
One of the responsibilities of those who work in science is to communicate findings. Communication means that we must generate written or spoken materials that will be understood and, often, must do so by reporting measurements. Measurements must be performed and reported in a standardized procedure or the communications will be misunderstood.
Chemistry and physics measure kinds of quantities such as length, velocity, volume, mass, and energy. All measurements are expressed using a number and a unit. The number is used to tell us how many of the units are contained in the quantity being measured. The unit tells us the specific nature of the dimension—measuring in feet is different than measuring in liters. If you are not comfortable with exponents and scientific notation (Examples: 1 × 104, 3 × 10–9, or 106) and the rules for dealing with significant figures, please refer to Appendices A and B for help.
Dimensional calculations are simplified if the unit for each kind of measure is expressed in terms of special reference units. The reference dimensions for mechanics are length, mass, and time. Other measurements performed are expressed in terms of these reference dimensions; units associated with speed contain references to length and time—mi/hr or m/s. Some units are simple multiples of the reference unit—area is expressed in terms of length squared (m2) and volume is length cubed (in3). Other reference dimensions, such as those used to express electrical and thermal phenomena, will be introduced later.
There are differing systems of measurement in use throughout the world, making the ability to convert values between systems important (convert inches to centimeters, or pounds to kilograms).
A system known as SI from the French name, Système International d’Unités, has been adopted by many international bodies, including the International Union of Pure and Applied Chemistry, to institute a standard for measurements. In SI, the reference units for length, mass, and time are meter, kilogram, and second, with the symbols m, kg, and s, respectively.
A multiplier can be used to represent values larger or smaller than the basic unit (gram, liter, meter, etc.). The multipliers are ten raised to a specific power, as listed in Table 1-1. This system avoids the necessity of having different basic units, such as the inch, foot, yard, or ounce, pint, quart, gallon, etc. The multiplier abbreviation precedes the symbol of the base unit with neither a space nor punctuation; an example is m in mL, the milliliter (10–3 L). Since, for historical reasons, the SI reference unit for mass, kilogram, already has a prefix, multiples for mass should be derived by applying the multiplier to the unit gram rather than kilogram—then, 10–9 kg is expressed in micrograms (10–6 g), abbreviated μg.

Simple units can be combined to produce compound units that can be manipulated algebraically.
EXAMPLE 1 The unit for volume in SI is the cubic meter (m3), since

EXAMPLE 2 The unit for speed is a unit for length (distance) divided by a unit for time:

EXAMPLE 3 The unit for density is the unit for mass divided by the unit for volume:

Symbols for compound units may be expressed in the following formats:
1. Multiple of units. Example: kilogram second.
(a) 
(b) 
2. Division of units. Example: meter per second.
(a) 
(b) 
The use of per in a word definition is equivalent to divide by in the mathematical form (refer to 2(a) directly above). Also, symbols are not handled as abbreviations; they are not followed by a period unless at the end of a sentence.
There are non-SI units that are widely used. Table 1-2 provides a list of commonly used symbols, both SI and non-SI. The listed symbols are used in this book; however, there are others that will be introduced at appropriate places to aid in solving problems and communicating.
Table 1-2 Some SI and Non-SI Units
Temperature can be defined as that property of a body which determines the direction of the flow of heat. This means that two bodies at the same temperature placed in contact with each other will not display a transfer of heat. On the other hand, if there are two bodies of differing temperatures in contact, the heat will flow from the hotter to the cooler. The SI unit for temperature is the kelvin; 1 kelvin (K) is defined as 1/273.16 times the triple point temperature. The triple point is the temperature at which liquid water is in equilibrium with ice (solid water) at the pressure exerted by water vapor only. Most people are more familiar with the normal freezing point of water (273.15 K), which is just below the triple point of water (0.01 K). The normal freezing point of water is the temperature at which water and ice coexist in equilibrium with air at standard atmospheric pressure (1 atm).
The SI unit of temperature is so defined that 0 K is the absolute zero of temperature. The SI or Kelvin scale is often called the absolute temperature scale. Although absolute zero does not appear to be attainable, it has been approached to within 10–4 K.
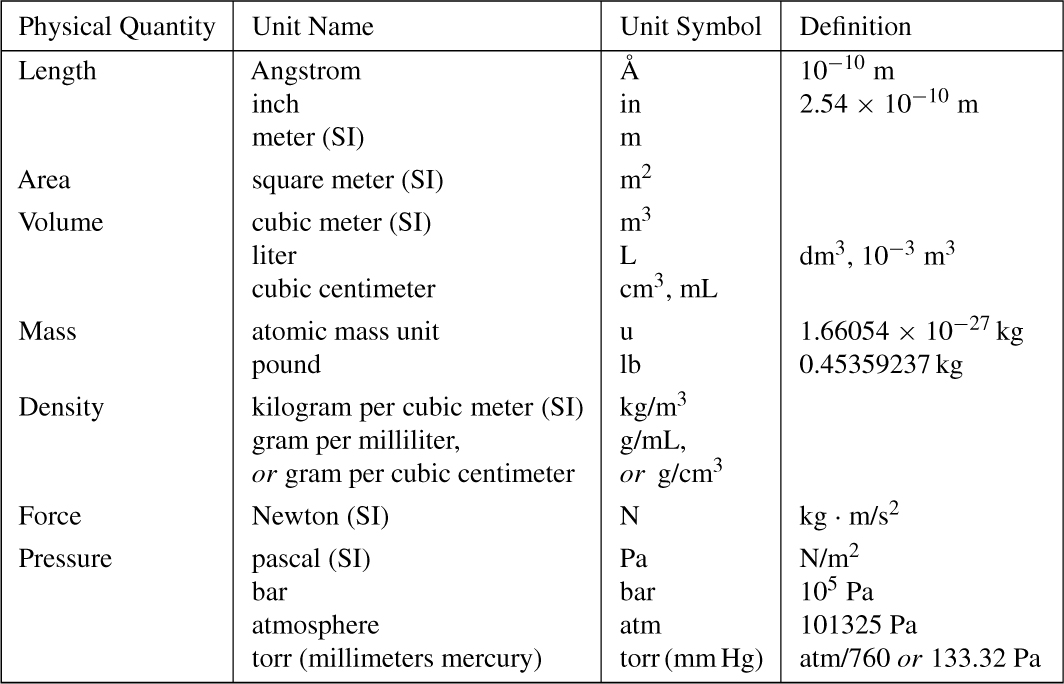
On the commonly used Celsius scale (old name: the centigrade scale), a temperature difference of one degree is the same as one degree on the Kelvin scale. The normal boiling point of water is 100°C; the normal freezing point of water is 0°C; and absolute zero is –273.15°C.
A difference of one degree on the Fahrenheit scale is exactly 5/9 K. The normal boiling point of water is 212°F; the normal freezing point of water is 32°F; and absolute zero is –459.67°F.
Figure 1-1 illustrates the relationships between the three scales. Converting one scale into another is by the equations below. The equation on the right is a rearrangement of the equation on the left. We suggest you know one equation, substitute values and solve for the unknown, rather than taking the time to memorize two equations for essentially the same calculation.

Fig. 1-1
It is human nature to leave out the units associated with measurements (e.g., cm, kg, g/mL, ft/s); however, leaving out the units is a good way to get into trouble when working problems. Keeping the units in the problem and paying attention to them as the problem progresses will help determine if the answer is correctly presented. When physical quantities are subjected to mathematical operations, the units are carried along with the numbers and undergo the same operations as the numbers. Keep in mind that quantities cannot be added or subtracted directly unless they have not only the same dimensions, but also the same units. Further, units can be canceled during multiplication and/or division operations. The units of the answer must match the nature of the dimension (e.g., length cannot be expressed in grams).
EXAMPLE 4 We cannot add 5 hours (time) to 20 miles/hour (speed) since time and speed have different physical significance. If we are to add 2 lb (mass) and 4 kg (mass), we must first convert lb to kg or kg to lb. Quantities of various types, however, can be combined in multiplication or division, in which the units as well as the numbers obey the algebraic laws of multiplication, squaring, division, and cancellation. Keeping these concepts in mind:
1. 6 L + 2L = 8L
2. (5 cm)(2 cm2) = 10 cm3
3. (3 ft3)(200 lb/ft3) = 600 lb
4. (2 s)(3 m/s2) = 6 m/s
5. 
One way of looking at problems is to follow what happens to the units. This technique is referred to in textbooks as the factor-label method, the unit-factor method, or dimensional analysis. In essence, the solution of the problem goes from unit(s) given by the problem to the desired final unit(s) by multiplying by a fraction called a unit-factor or just factor. The numerator and denominator of the factor must represent the same quantity (mL/mL, ft/ft, not mL/L, ft/in).
EXAMPLE 5 Convert 5.00 inches to centimeters.
The appropriate unit-factor is 2.54 cm/1 in. The setup for this problem is achieved by presenting the factor to the problem value of 5.00 inches so that the like dimensions cancel.

Notice that the units of inches (in) will cancel and leave only the units of centimeters (cm).
EXAMPLE 6 What is the weight in grams of seven nails from a batch of nails that weighs 0.765 kg per gross?

As with Example 5, following the cancellation of the units will help you see how the problem is solved.
The solution contains a unit-factor of mixed dimensions (0.765 kg/1 gross nails). The unit-factor is not composed of universally equivalent measures because different kinds of nails will weigh differently for each gross of nails. Many similar examples will be encountered during your studies and throughout this book.
When we work problems, we assume that the calculator is working properly; the numbers were all put into the calculator; and that we keyed them in correctly. Suppose that one or more of these suppositions is incorrect; will the incorrect answer be accepted? A very important skill is to determine, by visual inspection, an approximate answer. Especially important is the correct order of magnitude, represented by the location of the decimal point (or the power of 10). Sometimes the answer may contain the correct digits, but the decimal point is in the wrong location. A little practice to learn how to estimate answers and a few seconds used to do so when working problems can boost accuracy (and your grades) significantly.
EXAMPLE 7 Consider the multiplication: 122 g × 0.0518 = 6.32 g. Visual inspection shows that 0.0518 is a little more than 1/20th (0.05); the value of 1/20th of 122 is a little more than 6. This relationship tells us that the answer should be a little more than 6 g, which it is. Suppose that the answer were given as 63.2 g; this answer is not logical because it is much larger than the estimated answer of somewhere around 6 g.
Estimates of the answer only need to supply us with a rough value, often called a guesstimate. Actually, these guesstimates may need to be only accurate enough to supply the appropriate place for the decimal point.
EXAMPLE 8 Calculate the power required to raise 639 kg mass 20.74 m in 2.120 minutes. The correct solution is:

Even though you may not be familiar with the concepts and units, you can judge whether or not the answer is logical. A guesstimate can be generated quickly by writing each term in exponential notation, using one significant figure. Then, mentally combine the powers of ten and the multipliers separately to estimate the result like this:

1.1. The following examples illustrate conversions among various units of length, volume, or mass:
1 inch = 2.54 cm = 0.0254 m = 25.4 mm = 2.54 × 107 nm
1 foot = 12 in = 12 in × 2.54 cm/in = 30.48 cm = 0.3048 m = 304.8 mm
1 liter = 1 dm3 = 10–3m3
1 mile = 5280 ft = 1.609 × 105cm = 1.609 × 103m = 1.609 km = 1.609 × 106mm
1 pound = 0.4536 kg = 453.6 g = 4.536 × 105mg
1 metric ton = 1000 kg = 106 g(or 1 × 106 g)
1.2. Convert 3.50 yards to (a) millimeters, (b) meters. According to Table 1-2, the conversion factor used to move between the English and metric system (SI) units is 1 in/2.54 cm (2.54 × 10–2 m).
(a) 
Note that the use of three successive conversion factors was necessary. The units yd, in, and cm cancel out leaving the required unit, mm.
(b) 
1.3. Convert (a) 14.0 cm and (b) 7.00 m to inches.
(a) 
The conversion factor used in the first part, (a), is expressed on one line (1 in/254 cm) in part (b). The one-line version is much more convenient to type and write for many people.
(b) 
Note: The solution directly above contains sets of parentheses that are not truly necessary. The authors take the liberty throughout this book of using parentheses for emphasis, as well as for the proper isolation of data.
1.4. How many square inches are in one square meter?
A square meter has two dimensions—length and width (A = L × W). If we calculate the length of one meter in inches, all we need to do is square that measurement.

Note that the conversion factor is a ratio; it may be squared without changing the ratio, which leads us to another setup for the solution. Pay particular attention to the way in which the units cancel.

1.5. (a) How many cubic centimeters are in one cubic meter? (b) How many liters are in one cubic meter? (c) How many cubic centimeters are in one liter?
(a) 
(b) 
(c) 
The answers can also be written as 1 × 106 cm3, 1 × 103 L, and 1 × 103 cm3 respectively.
1.6. Find the capacity in liters of a tank 0.6 m long (L), 10 cm wide (W), and 50 mm deep (D).
Since we are given the dimensions of the tank and V = L × W × D (depth = height, the more traditional name for the dimension), all that we really need to do is convert the various expressions to dm (1 dm3 = 1L).

1.7. Determine the mass of 66 lb of sulfur in (a) kilograms and (b) grams. (c) Find the mass of 3.4 kg of copper in pounds.
(a) 66 lb = (66 lb)(0.4536 kg/lb) = 30 kg or 66 lb = (66 lb)(1 kg/2.2 lb) = 30 kg
(b) 66 lb = (66 lb)(453.6 g/lb) = 30,000 g or 3.0 × 104 g
(c) 3.4 kg = (3.4 kg)(2.2 lb/kg) = 7.5lb
1.8. Fatty acids spread spontaneously on water to form a monomolecular film. A benzene solution containing 0.10 mm3 of stearic acid is dropped into a tray full of water. The acid is insoluble in water, but spreads on the surface to form a continuous film covering an area of 400 cm2 after all of the benzene has evaporated. What is the average film thickness in (a) nanometers and (b) angstroms?
Since 1 mm3 = (10–3 m)3 = 10–9 m3 and 1 cm2 = (10–2 m)2 = 10–4 m2
(a) 
(b) Film thickness = 2.5 × 10–9 m × 1010 Å/m = 25Å
1.9. A pressure of one atmosphere is equal to 101.3 kPa. Express this pressure in pounds force (lbf) per square inch. (The pound force—lbf—is equal to 4.448 newtons, N.)

Notice that the conversion factor between meters (m) and inches (in) is squared to give the conversion factor between m2 and in2.
1.10. An Olympic-class sprinter can run 100 meters in about 10.0 seconds. Express this speed in (a) kilometers per hour and (b) miles per hour.
(a) 
(b) 36.0 km/hr × 1 mi/1.609 km = 22.4 mi/hr
Notice that the (b) portion of this problem requires the information from the (a) part of the problem.
1.11. New York City’s 7.9 million people in 1978 had a daily per capita consumption of 656 liters of water. How many metric tons (103 kg) of sodium fluoride (45% fluorine by weight) would be required per year to give this water a tooth-strengthening dose of 1 part (by weight) fluorine per million parts water? The density of water is 1.000 g/cm3, or 1.000 kg/L.
A good start is to calculate the mass of water, in tons, required per year.

Note that all units cancel except metric tons water/yr; it is needed for the next step.
Now, set up and calculate the total mass of sodium fluoride, in tons, required each year.

1.12. In a measurement of air pollution, air was drawn through a filter at the rate of 26.2 liters per minute for 48.0 hours. The filter gained 0.0241 grams in mass because of entrapped solid particles. Express the concentration of solid contaminants in the air in units of micrograms per cubic meter.

1.13. Calculate the density, in g/cm3, of a body that weighs 420 g (i.e., has a mass of 420 g) and has a volume of 52 cm3.

1.14. Express the density of the above body in the standard SI unit, kg/m3.

1.15. What volume will 300 g of mercury occupy? The density of mercury is 13.6 g/cm3.

1.16. The density of cast iron is 7200 kg/m3. Calculate its density in pounds per cubic foot.

The two conversions were borrowed from Problem 1.1.
1.17. A casting of an alloy in the form of a disk weighed 50.0 g. The disk was 0.250 inches thick and had a diameter of 1.380 inches. What is the density of the alloy, in g/cm3?

1.18. The density of zinc is 455 lb/ft3. Find the mass in grams of 9.00 cm3 of zinc.
Let us start the solution by calculating the density in g/cm3.

Then, we can determine the total mass of the zinc.

1.19. Battery acid has a density of 1.285 g/cm3 and contains 38% by weight H2SO4. How many grams of pure H2SO4 are contained in a liter of battery acid?
1cm3 of acid has a mass of 1.285 g. Then, 1 L of acid (1000 cm3) has a mass of 1285 g. Since 38.0% by weight (by mass) of the acid is pure H2SO4, the amount of H2SO4 in 1 L of battery acid is

Formally, the above solution can be expressed as follows:

The information provided in the problem generated the conversion factor utilizing the ratio of pure H2SO4 to H2SO4 solution.

It is extremely important to note that this conversion factor is only good for the conditions of this problem. However, this conversion factor does mean that every 100 g of this particular acid solution contains 38 g H2SO4, information that is important in both the logical and the formal explanations above. Liberal use of special conversion factors will be made in subsequent chapters where conversion factors are generated and valid for only particular cases. Of course, universally valid conversions will also be used as indicated.
1.20. (a) Calculate the mass of pure of HNO3 per cm3 of the concentrated acid which assays 69.8% by weight HNO3 and has a density of 1.42 g/cm3. (b) Calculate the mass of pure HNO3 in 60.0 cm3 of concentrated acid. (c) What volume of concentrated acid contains 63.0 g of pure HNO3?
(a) 1 cm3 of acid has a mass of 1.42 g. Since 69.8% of the total mass of the acid is pure HNO3, the number of grams of HNO3 in1cm3 is

(b) The mass of the HNO3 in 60.0 cm3 of acid = (60.0 cm3)(0.991 g/cm3) = 59.5 g HNO3
(c) 63.0 g HNO3 is contained in

1.21. Ethyl alcohol (a) boils at 78.5°C and (b) freezes at –117°C, at one atmosphere of pressure. Convert these temperatures to the Fahrenheit scale.
Use this conversion:

(a) 
(b) 
1.22. Mercury (a) boils at 675°F and (b) solidifies at –38.0°F, at one atmosphere of pressure. Express these temperatures in degrees Celsius.

(a) 
(b) 
1.23. Change (a)40°C and (b) –5°C to the Kelvin scale.
Use this conversion:
°C + 273 = K
(a) 40°C + 273 = 313 K
(b) –5°C + 273 = 268 K
1.24. Convert (a) 220 K and (b) 498 K to the Celsius scale.
Use this conversion:
K – 273 =° C
(a) 220 K – 273 = –53°C
(b) 498 K – 273 = 225°C
1.25. During the course of an experiment, laboratory temperature rose 0.8°C. Express this rise in degrees Fahrenheit.
Temperature intervals are converted differently than are temperature readings. For intervals, it is seen from Fig. 1-1 that
100°C = 180°F or 5°C = 9°F
therefore

1.26. (a) Express 3.69 m in kilometers, in centimeters, and in millimeters. (b) Express 36.24 mm in centimeters and in meters.
Ans. (a) 0.00369 km, 369 cm, 3690 mm; (b) 3.624 cm, 0.03624 m
1.27. Determine the number of (a) millimeters in 10 in, (b) feet in 5 m, (c) centimeters in 4 ft 3 in.
Ans. (a) 254 mm; (b) 16.4 ft; (c) 130 cm
1.28. A long shot is in the 300 yard range, but is within the training parameters for a SWAT officer. How far is the target as measured in (a) feet, (b) meters, and (c) kilometers?
Ans. (a) 900 ft; (b) 274 m; (c) 0.27 km
1.29. A recovered bullet is found to be from a 38 special revolver. The bullet measures 0.378 inches in diameter; what must you record in terms of the metric system using cm?
Ans. 1.04 cm
1.30. Express in cm (a) 14.0 in, (b) 7.00 yd.
Ans. (a) 35.6 cm; (b) 640 cm
1.31. A roll of the yellow crime scene tape contains 250 yards of tape. An area of a grassy field to be marked off is a rectangle 42 m by 31 m; how many yards of tape will be left?
Ans. 90 yd
1.32. A ¼ mile long suspension bridge is being planned which will require 16 miles of 150 strand (150 wires twisted) cable to be placed. What is the minimum (ignoring length for twisting) length in km of wire the cable manufacturer needs to have to produce the cable?
Ans. 3862 km
1.33. The average man can run at a top speed of 22 mph. Express this speed in (a) kilometers per hour and (b) meters per second.
Ans. (a) 35.4 km/h; (b) 9.83 m/s
1.34. Convert the molar volume, 22.4 liters, to cubic centimeters, to cubic meters, and to cubic feet.
Ans. 22,400 cm3; 0.0224 m3; 0.791 ft3
1.35. Express the weight (mass) of 32 g of oxygen in milligrams, in kilograms, and in pounds.
Ans. 32,000 mg; 0.032 kg; 0.0705 lb
1.36. How many grams in 5.00 lb of copper sulfate? How many pounds in 4.00 kg of mercury? How many milligrams in 1 lb 2 oz of sugar?
Ans. 2270 g; 8.82 lb; 510,000 mg
1.37. Convert the weight (mass) of a 2176 lb compact car to (a) kilograms; (b) metric tons; (c) U.S. tons (1 ton = 2000 lb).
Ans. (a) 987 kg; (b) 0.987 metric ton; (c) 1.088 ton (U.S.)
1.38. The steel used in the fabrication of the cable (16 mi, diameter 12 cm; assume solid; Vcylinder = πr2h) for the bridge in Problem 1.32 has the density of 8.65 g/cm3. The cable can be drawn from a solid block of the metal. What would that block weigh in (a) kg? (b) in lbs? (c) in tons?
Ans. (a) 1.01 × 107 kg; (b) 2.2 × 107 lb; (c) 1110 tons (1.01 × 104 metric tons)
1.39. The color of light depends on its wavelength. The longest visible rays, at the red end of the visible spectrum, are 7.8 × 10–7 m in length. Express this length in micrometers, in nanometers, and in angstroms.
Ans. 0.78 μm; 780 mm; 7800 Å
1.40. An average person should have no more than 60 grams of fat in their daily diet. A package of chocolate chip cookies is labeled “1 portion is 3 cookies” and also “fat: 6 grams per portion.” How many cookies can you eat before exceeding 50% of the recommended maximum fat intake?
Ans. 15 cookies
1.41. In a crystal of platinum, the centers of the atoms are 2.8 Å apart along the direction of the closest packing. How many atoms would lie on a one-centimeter line in this direction?
Ans. 3.5 × 107 atoms
1.42. The blue iridescence of butterfly wings is due to striations that are 0.15 μm apart, as measured by the electron microscope. What is this distance in centimeters? How does this spacing compare with the wavelength of blue light, about 4500 Å?
Ans. 1.5 × 10–5 cm, 1/3 wavelength of blue light
1.43. An average man requires about 2.00 mg of riboflavin (vitamin B2) per day. How many pounds of cheese would a man have to eat per day if this were his only source of riboflavin and if the cheese were to contain 5.5 μg of riboflavin per gram?
Ans. 0.80 lb/day
1.44. When a sample of blood from a healthy person is diluted to 200 times its initial volume and microscopically examined in a layer 0.10 mm thick, an average of 30 red blood cells are found in each 100 × 100 micrometer square. (a) How many red cells are in a cubic millimeter of blood? (b) The red blood cells have an average life of 1 month, and the blood volume of a particular patient is about 5 L. How many red blood cells are generated every second in the bone marrow of the patient?
Ans. (a) 6× 106 cells/mm3; (b)1 × 107 cells/s
1.45. A porous catalyst for chemical reactions has an internal surface area of 800 m2 per cm3 of bulk material. Fifty percent of the bulk volume consists of the pores (holes), while the other 50% of the volume is made up of the solid substance. Assume that the pores are all cylindrical tubules of uniform diameter d and length l, and that the measured internal surface area is the total area of the curved surfaces of the tubules. What is the diameter of each pore? (Hint: Find the number of tubules per bulk cm3, n, in terms of l and d, by using the formula for the volume of a cylinder V = 0.25 πd2l. Then apply the surface-area formula, S = πdl, to the cylindrical surfaces of n tubules.)
Ans. 25 Å
1.46. Suppose that a rubber tire loses a layer one molecule thick from its surface during each revolution on the pavement. (By “molecule” you should infer one monomer unit.) Assume that the molecules average 7.50 Å in thickness, that the tire tread is 35.6 cm in radius, and 19.0 cm wide. On a 483 km drive from Pittsburgh to Philadelphia (a) how much is the radius reduced (in mm), and (b) what volume of rubber (in cm3) is lost from each tire?
Ans. (a) 0.162 mm; (b) 68.8 cm3
1.47. Refer to Problem 1.46. If the tire has a density of 963 kg/m3, calculate the mass in grams lost by each tire on the trip.
Ans. 66.3 g
1.48. The density of water is 1.000 g/cm3 at 4°C. Calculate the density of water in pounds per cubic foot at the same temperature.
Ans. 62.4 lb/ft3
1.49. There is an estimate that a cube 60 ft by 60 ft by 60 ft would contain all of the gold ever mined and refined. Considering that the density of pure gold is 19.3 g/cm3, calculate the mass in (a) kilograms, (b) pounds, and (c) tons represented by this estimate.
Ans. (a) 1.18 × 108 kg; (b)5.36 × 107 lb; (c) 26,800 tons (1.18 × 105 metric tons)
1.50. A difference of no more than 0.0013 grams/cm3 from the average density (7.700 g/mL) is normal for empty 9 mm shells (the part that held the propellant) from ABC, Inc.. Two fired shells from a 9 mm handgun were found and taken to the lab. The shells were identified as from ABC, were weighed, and the volumes were measured using displacement of water (#1: 3.077 g and 0.399 mL and #2: 3.092 g and 0.402 mL). Could these shells be from the same lot?
Ans. They could be from the same lot. The first shell, #1, had a density 0.012 from the average and the second shell, #2, was 0.008 g/mL from the average. This is only one test of many.
1.51. The silica gel which is used to protect sealed overseas shipments from moisture seepage has a surface area of 6.0 × 102 m2 per kilogram. What is the surface area in square feet per gram?
Ans. 6.5 × 103 ft2/g
1.52. There is reason to think that the length of the day, determined from the earth’s period of rotation, is increasing uniformly by about 0.0001 s every century. What is this variation in parts per billion (ppb)?
Ans. 3 × 10–4s per 109 s(or 3 × 10–4ppb)
1.53. The average content of bromine in the Atlantic Ocean is 65 parts per million (ppm) by weight. Assuming 100% recovery, how many cubic meters of ocean water must be processed to produce 0.61 kg of bromine? Assume that the density of seawater is 1.0 × 103 kg/m3.
Ans. 9.4 m3
1.54. An important physical quantity’s value is 8.314 joules or 0.08206 liter · atmosphere. What is the conversion factor from joules to liter · atmospheres?
Ans. 101.3 J/L · atm
1.55. Find the density of ethyl alcohol if 80.0 cm3 weighs 63.3 g.
Ans. 0.791 g/cm3
1.56. Find the volume in liters of 40 kg of carbon tetrachloride, CCl4. (Density = 1.60 g/cm3.)
Ans. 25 L
1.57. A type of plastic foam has a density of 17.7 kg/m3. Calculate the mass in pounds of an insulating slab 4.0 ft wide, 8.0 ft long, and 4.0 in thick.
Ans. 11.8 lb
1.58. Air weighs about 8 lb per 100 cubic feet. Find its density in (a) grams per cubic foot, (b) grams per liter, and (c) kilograms per cubic meter.
Ans. (a) 36 g/ft3; (b) 1.3 g/L; (c) 1.3 kg/m3
1.59. The estimates for the caloric content of food are: 9.0 Cal/g for fats, and 5.0 Cal/g for carbohydrates and proteins. A breakfast muffin contains 14% by weight of fat, 64% carbohydrate, and 7% protein (the rest is water, which has no calories). Does it meet the criterion of 30% or less calories from fat, which is recommended for the U.S. population?
Ans. Yes, 26% of the calories are from fat.
1.60. A wood block, 10 in × 6.0 in × 2.0 in, has a weight of 3 lb 10 oz. What is the density of the wood in SI units?
Ans. 840 kg/m3
1.61. An alloy was machined into a flat disk 31.5 mm in diameter and 4.5 mm thick. A hole 7.5 mm in diameter was drilled through the center. The disk weighed 20.2 g. What was the density of the alloy in SI units?
Ans. 6100 kg/m3
1.62. A glass vessel weighed 20.2376 g when empty and 20.3102 g when filled to an etched mark with water at 4°C. The same vessel was then dried and filled to the same mark with a solution at 4°C. The vessel was then found to weigh 20.3300 g. What is the density of the solution?
Ans. 1.273 g/cm3
1.63. A sample of lead shot weighing 321 g was added to a graduated cylinder partially filled with isopropyl alcohol (enough to cover the lead completely). As a result the alcohol level rose 28.3 mL. What is the density of the lead in SI units? (The density of isopropyl alcohol is 0.785 g/cm3.)
Ans. 1.13 × 104kg/m3
1.64. A sample of concentrated sulfuric acid is 95.7% H2SO4 by weight and its density is 1.84 g/cm3.(a) How many grams of pure H2SO4 are contained in one liter of the acid? (b) How many cubic centimeters of acid contain 100 g of pure H2SO4?
Ans. (a) 1760 g; (b) 56.8 cm3
1.65. A quick method of determining density utilizes Archimedes’ principle, which states that the buoyant force on an immersed object is equal to the weight of the liquid displaced. A bar of magnesium metal attached to a balance by a fine thread weighed 31.13 g in air and 19.35 g when completely immersed in hexane (Dhexane = 0.659 g/cm3). See Fig. 1-2. Calculate the density of this sample of magnesium in SI units.
Ans. 1741 kg/m3

Fig. 1-2
1.66. An electrolytic tin-plating process gives a coating 30 millionths of an inch thick. How many square meters can be coated with one kilogram of tin, density 7300 kg/m3?
Ans. 180 m2
1.67. A piece of gold leaf (density 19.3 g/cm3) weighing 1.93 mg can be beaten further into a transparent film covering an area of 14.5 cm2. (a) What is the volume of 1.93 mg of gold? (b) What is the thickness of the transparent film, in angstroms?
Ans. (a)1 × 10–4 cm–3; (b) 690 Å
1.68. Calculate the length (km and mi) of the gold leaf mentioned in Problem 1.67 that can be beaten out if the width is 6 inches. Note: The moon is 2.4 × 105 mi and the sun is 9.3 × 107 mi (both averages).
Ans. 1.7 × 1011 km, 1 × 106 mi
1.69. A piece of capillary tubing was calibrated in the following manner: A clean sample of the tubing weighed 3.247 g. A thread of mercury, drawn into the tubing, occupied a length of 23.75 mm, as observed under a microscope. The weight of the tubing with the mercury was 3.489 g. The density of mercury is 13.60 g/cm3. Assuming that the capillary bore is a uniform cylinder, find the diameter of the bore.
Ans. 0.98 mm
1.70. The General Sherman tree, located in Sequoia National Park, is believed to be the most massive of living things. If the overall density of the tree trunk is assumed to be 850 kg/m, calculate the mass of the tree trunk by assuming that it may be approximated by two right conical frusta having lower and upper diameters of 11.2 and 5.6 m, and 5.6 and 3.3 m, respectively, and respective heights of 2.4 and 80.6 m. A frustum is a portion of a cone bounded by two planes, both perpendicular to the axis of the cones. The volume of a frustum is given by
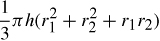
where h is the height and r1 and r2 are the radii of the circular ends of the frusta.
Ans. 1.20 × 106 kg = 1200 metric tons
1.71. (a) Convert 88°F to °C; 16°F to °C; 130°F to °C. (b) Convert 35°C to °F; 2°C to °F; –29°C to °F.
Ans. (a) 31°C, –9°C, 54°C; (b) 95°F, 36°F, –20°F
1.72. Convert the following temperatures: –149.7°C to °F; –396.0°F to °C; 1555°C to °F.
Ans. –237.5°F, –237.8°C, 2831°F
1.73. The temperature of dry ice (sublimation temperature at normal pressure) is –109°F. Is this higher or lower than the temperature of boiling ethane (a component of bottled gas), which is –88°C?
Ans. higher
1.74. An ill person has a temperature of 103 °F, about the same temperature as a healthy cat. What is the temperature in (a) C and (b) kelvins?
Ans. (a) 39.4°C; (b) 312.6 K
1.75. Gold has been mined and refined for many thousands of years, certainly before electric furnaces and other high-temperature devices were possible. The melting point of gold is 1064°C; express this temperature in terms of the Kelvin and Fahrenheit scales.
Ans. 1303 K and 1947°F
1.76. Metal contracts and expands with temperature changes. A metal bar is being used to build part of the deck of an oil rig for the North Sea and must be able to withstand –45°C. State the temperature in (a) °F and (b) in the Kelvin scale.
Ans. (a) –49°F; (b) 228 K
1.77. Gabriel Fahrenheit in 1714 suggested for the zero point on his scale the lowest temperature then obtainable from a mixture of salts and ice, and for his 100° point he suggested the highest known normal animal temperature. Express these “extremes” in Celsius.
Ans. –17.8°C, 37.8°C
1.78. Sodium metal has a very wide liquid range, melting at 98°C and boiling at 892°C. Express the liquid range in degrees Celsius, kelvins, and degrees Fahrenheit.
Ans. 794°C, 794 K, 1429°F
1.79. Convert 298 K, 892 K, and 163 K to degrees Celsius.
Ans. 25°C, 619°C, –110°C
1.80. Express 11 K and 298 K in degrees Fahrenheit.
Ans. –440°F, 77°F
1.81. Convert 23°F to degrees Celsius and kelvins.
Ans. –5°C, 268K
1.82. An accelerant is suspected when a vehicle fire is so hot that the glass in the windshield melted. The melting point of this car’s glass (essentially SiO2) is 1698°C. Convert that temperature to (a) the Kelvin scale and (b) the Fahrenheit scale.
Ans. (a 1971 K; (b) 3088° F
1.83. At what temperature have the Celsius and Fahrenheit readings the same numerical value?
Ans. –40°
1.84. A water-stabilized electric arc was reported to have reached a temperature of 25,600°F. On the absolute scale, what is the ratio of this temperature to that of an oxyacetylene flame (3500°C)?
Ans. 3.84
1.85. Construct a temperature scale in which the freezing and boiling points of water are 100° and 400°, respectively, and the degree interval is a constant multiple of the Celsius degree interval. What is the absolute zero on this scale, and what is the melting point of sulfur (MP = 444.6°C)?
Ans. –719°, 1433.8°
1.86. Normal body temperature is 98.6°F, but the internal temperature (liver temperature) of a deceased person found in an apartment is at 91.5°F. The expected temperature drop under the conditions in the apartment is 1°C for each hour and 15 minutes after death. (a) Express the body temperatures in °C. (b) How long ago did this person die? (Only an estimate can be derived from these data and the cooling rate.)
Ans. (a) 37°C and 33°C; (b) 6 hours, approximately