The general principles of chemical equilibrium (Chapter 16) apply to reactions of neutral molecules and to reactions of ions. Chemical equilibria are of special interest, not only because they are used in commercial processes, but also because many of the reactions involved in life are equilibrium reactions. As in Chapter 16, concentrations will be expressed in mol/L and will be referred to in the mathematical relationships by enclosing the substance in square brackets. Further, these chapters are dedicated to the discussion of aqueous solutions. In other words: if the solvent is not identified, it is to be taken as water.
According to the classical definition as formulated by Arrhenius, an acid is a substance that can yield H+ in aqueous solution. Strong acids are those that ionize completely in water, such as HClO4 and HNO3. These acids ionize by means of
Weak acids are those that do not ionize completely and the dissociation of these acids provides us with an equilibrium reaction. A couple of examples are HC2H3O2 and HNO2.
An equilibrium constant can be calculated. Since the substance on the left of the written reaction is an acid and is behaving as one by releasing H+, the equilibrium constant is given a special symbol, Ka. For acetic acid, the Ka is calculated by
Note that the Ka expression is set up in the same way as the K’s in Chapter 16: Ka is the product of the products divided by the product of the reactants, as in (17-1) above. As with any K, pure solids and liquids (including liquid water, the solvent, in these solutions) are not included in the K expression.
Bases are those substances that ionize in water to release OH– ions. NaOH is a strong base, ionizing completely in water to yield Na+ and OH– ions. However, even those hydroxide bases that do not dissolve well, such as Ca(OH)2, do ionize completely to the extent they dissolve. A weak base is one that does not ionize completely. As with the acids, a K expression can be calculated, and that expression is referred to as Kb (the K for a base, as in (17-4) below).
An interesting situation that may occur when ammonia, NH3, dissolves in water is that hydroxide ions, OH–, appear in the solution and the concentration is measurable. The implication is that NH4OH forms, then ionizes to yield ammonium and hydroxide ions. This is logical, but NH4OH has not been detected in aqueous solution. Since the OH– concentration is only a few percent of the ammonia concentration, NH3 is considered a weak base.
The Brönsted-Lowry definition of an acid takes into account the nature of the solvent. Although water does not ionize well, it does ionize to a small extent. The result is the appearance of H+ and OH– ions in an equilibrium equation, which is
A point of this reaction is the release of H+ ions—the Brönsted-Lowry approach considers this the appearance of a proton from the acid. A Brönsted-Lowry acid is a proton donor. Note that the hydrogen ion is a proton, hydrogen’s nucleus without the electron found in the atom. Then, a Brönsted-Lowry acid must contain a hydrogen. Of course, if the solvent were not to be water, this statement may not work because the cation released could be other than the hydrogen ion, but there might be other ions performing the same service (liquid ammonia autoionizes, Problem 17.3).
The base in the Brönsted-Lowry concept is any substance that can accept the proton; it can even be the solvent. A Brönsted-Lowry base has an electron pair (a lone pair) that will accept the proton. The point that needs to be stressed here is that the proton is involved in both the definition of an acid (donates a proton) and a base (accepts a proton).
The Brönsted-Lowry concept looks at the equilibrium reaction and ties the acid on the left to a base on the right, called a conjugate acid-base pair or, more simply, a conjugate pair. Suppose we were to consider an acid reacting with a compound in equilibrium with the acid’s anion and the products, as
The conjugate pair would contain the acid, HA, on the left and A– on the right (bold participants). A– is the result of acid’s loss of its proton (H+). This relationship can be read as “A– is the conjugate base of the acid, HA.” A– is a base, because in the reverse reaction (reading from right to left), it will accept a proton (H+) and become the starting compound, HA.
B is a base, because it will accept the proton, whereas BH+ is an acid. BH+ is an acid because, if the reaction is read from right to left, it will give up the proton (H+). So, the relationship can be read as “B is the conjugate base of the acid, BH+.”
Note that HA and B are not necessarily neutral. They could be ions that are capable of acting as an acid or a base. This is one of the features of the Brönsted-Lowry concept that broadens the definitions of acids and bases over the Arrhenius concept—there are many more substances that can behave as acids or bases. Further, we can write the reaction including the solvent, water in this case, and the associated Ka.
Notice that water is not included in the Ka; it is a pure liquid and is omitted, as discussed in Chapter 16.
In a way similar to (17-3), we can write the ionization of the weak base, ammonia, and its Kb.
Water can act as either an acid or a base, depending on the circumstances. This ability to act as either an acid or a base is referred to by stating that water is amphoteric. Water serves as a base in (17-3) and as an acid in (17-4). Note that the bare H+ (a proton) becomes the hydronium ion, H3O+, which is a hydrated proton (H3O+ is H+ + H2O) because the bare proton does not really exist in solution. When we write the equilibrium constant expression for an aqueous equilibrium, we can use either the hydrogen ion, H+, or the hydrated form, H3O+. Although the proton is hydrated in aqueous solution (as is the hydroxide), the use of H+ and H3O+ is up to the style of the person working the problem and the problem itself. More often than not, leaving out water on both sides of the equation is used to keep the solutions to the problems visually simple. So long as water is in its standard state (liquid), it is not included in the K expression and, therefore, not necessary in the chemical equation.
The strengths of acids can be compared in terms of their Ka’s; the stronger the acid, the larger its Ka. This statement also applies to bases and their Kb’s—the larger the Kb, the stronger the base. Also, the strengths of acids and bases are due to the magnitude of their respective K’s in solvents other than water. For instance, HNO3 is a strong acid in water and it is a weak acid in ethanol solvent—a Ka can be determined that is much smaller than that in water.
Acids and bases, according to the Lewis concept, present an even more general picture than the two previous concepts. The Lewis acid is a structure which has an affinity for electron pairs—it can accept a share in a pair of electrons. A Lewis base is the structure that provides the electron pair. Notice the use of the word structure; this means that the Lewis acid or base does not necessarily have to be a compound. As a matter of fact, parts of a compound can function within the Lewis concept. An example of part of a compound acting is the amino group, —NH2, which is included as the “amino” part of amino acids. There is an unshared pair of electrons on the nitrogen which can be shared, making the amino group a base. Additionally, by the definition, the hydrogen ion is the acid, not the acetic acid molecule.
Some other possible Lewis acids can be transition-metal ions, which can react with ligands (bases) to form complexes. Other substances that are short electrons are like BF3, which can react with a base like NH3 to form a compound, as below:
Since water is amphiprotic (meaning it can act as both an acid by releasing H+ and as a base by releasing OH–), every aqueous solution is characterized by autoionization, the process in which one H2O molecule transfers a proton to another water molecule. The autoionization of water always occurs, whether or not there are other acids or bases in solution. A special K is assigned to the reaction:
This is an example of a reaction in which we chose to write H+ instead of H3O+, which is an acceptable procedure. As mentioned above, since water is the solvent, we know that all ions are hydrated and can take that for granted while writing the simpler form of the ion (H+, instead of H3O+). Regardless, if water is included in the written reaction, it is not included in the Kw expression as it is a pure liquid. In this book, the problems involving concentrations of nonelectrolytes do not exceed 1M and the concentrations of electrolytes do not exceed 0.1 M. For solutions containing larger concentrations of ions, the same laws of equilibrium apply if proper correction is made for the electrical interactions between ions, which is not covered in this book. Instead, examples have been chosen for which the numerical solutions should be correct to within 10 percent, even without such corrections.
At 25°C, Kw = [H+][OH–] = 1.00 × 10–14; this value should be memorized (another factor related to water). In pure water (no solutes present), the concentrations of H+ and OH– must be equal. Therefore, at 25°C,
We can define a neutral solution as one in which 
. The value of Kw varies with temperature; for instance, at 0°C, Kw = 0.34 × 10–7; however, most problems are written at 25°C or assuming 25°C when the temperature is not specified.
An acid solution is one that has a [H+] greater than 10–7 M. A basic solution is one in which the [H+] is less than 10–7 M. Having a hydrogen ion concentration less than 10–7 means that the hydroxide ion concentration is greater than 10–7 M. It is important to note that as the hydrogen ion concentration decreases, the hydroxide ion increases, and, of course, the reverse is true.
The acidity or alkalinity (basic extent) of a solution is often expressed by its pH, defined as
We prefer to use the left-hand definition in this book, pH = —log[H+]. Similarly, we can define as
Taking the -log of both sides of (17-5), we find that the two measures are related by
Note: These notations become more understandable if you consider that p stands for “take the negative log” of whatever follows. The following variable can be [H+], [OH–], for even K, as we will see shortly.
Table 17-1 summarizes the pH and pOH scales at 25°C.
The value of pKa is a convenient expression for the expression of acid strength (pKb for a base). pKa is defined as —log Ka. An example is an acid with the ionization constant of 10–4; it will have a pKa of 4. Similarly, pKb = —log Kb for base values.
A salt containing at least one ion which is conjugate to a weak acid or base undergoes a reaction with water of an acid-base nature. Let us look at NaC2H3O2, a salt produced from a strong base, NaOH, and a weak acid, HC2H3O2. The acetate ion in sodium acetate is conjugate to the acetic acid, a weak acid. The acetate ion is a base and can accept a proton from an acid or from the solvent (water):
The above reaction is called hydrolysis (literally, splitting water). As a result of this process, a solution of sodium acetate in water is basic because an excess of OH– is produced; the OH– released from the above reaction is added to pure water (neutral). Note that the reaction (17-5) is the sum of the reactions (17-3) and (17-7). The equilibrium constants for these three reactions must then be related as follows (see Problem 16.14):
An equation of the type (17-8) applies to the hydrolysis of any species which is the conjugate base to an acid having an ionization constant Ka. Some examples are CN–, HS–, SCN–, 
. Since hydrolysis involves a reverse of acid dissociation, the tendency toward hydrolysis runs opposite to the tendency of the conjugate acid toward ionization. The weaker the acid, the greater the difficulty of removing a proton from the acid, and the easier for its anion (its conjugate base) to attach a proton from water (that is, to hydrolyze). This relationship appears mathematically as the inverse proportionality between Ka of the acid and Kb of the conjugate base. Acetic acid is a moderately weak acid, and the acetate ion hydrolyzes to a slight extent. HCN is a very weak acid and the cyanide ion, CN–, hydrolyzes to a great extent. Chloride ion, on the other hand, does not undergo the hydrolysis reaction at all. The reason is that its conjugate acid, HCl, is a strong acid and cannot exist to any appreciable extent in dilute aqueous solution because Cl– is an extremely weak base.
There is a clear example of a cation behaving as an acid. 
is quite capable of losing a proton (the fourth hydrogen, which is really a hydrogen nucleus, H+), and the conjugate base, NH3, appears. Because of this situation, a solution of ammonium chloride, NH4Cl, would be acidic.
Ka for can be obtained from Kb for NH3, its conjugate base, by rearranging equation (17-8).
Many heavy metal cations hydrolyze to some extent in aqueous solution in a reaction characterized by an equilibrium constant, Ka. As an example,
This reaction is sometimes written with the hydrated forms of ions to show that the hydrated ferric ion, like the neutral acids, demonstrates its acidity by loss of a proton.
The two equations, (17-9) and the one directly above, are equivalent.
There are conditions under which a solution is resistant to a change in pH. For instance, distilled (or deionized) water, if totally neutral when produced, has a pH of 7.00. However, if that water is stored in containers that let in the smallest amount of air, the pH of the “pure” water drops into the acid range. A pH of 6.0 is not uncommon in the supposedly pure water used in laboratories. If it were possible to treat the water so that the H+ that appears when CO2 dissolves and reacts could be neutralized, the pH of the water would remain at or near 7.00. CO2 and H2O react as follows; H+ end up in the solution:
A buffer solution (or a buffered solution) is a solution that is resistant to change when small amounts of acid or bases are added. Such a solution contains relatively large amounts of both a weak acid (or weak base) and its strong salt (one that ionizes very well). If a small amount of a strong acid (or base) is added to a buffer, most of the added H+ (or OH–) will combine with an equivalent amount of the weak base (or acid) of the buffer to form the conjugate acid (or base) of that weak base (or acid). The result is that the hydrogen ion and hydroxide concentrations in the solution display very little change.
Any pair of weak acid and base can be used to form a buffer solution, so long as each can form its conjugate base or acid in aqueous solution.
EXAMPLE 1 A particularly simple and common case of the buffer solution is one in which the weak acid and weak base are conjugates of each other. We could choose acetic acid as the weak acid and the acetate ion is, then, the weak base. Since relatively large amounts of each are needed, it would not be possible to use just a solution of the acid because the ionization equilibrium favors the acid to a large extent. However, we can still make an acid-acetate buffer by these methods:
1. Dissolve a relatively large amount of acetic acid and an acetate salt in water. The salt must be a strong salt, one that ionizes to a large extent, if not completely. NaCH2H3O2 and KCH2H3O2 are good choices for salts as they are strong salts, ionizing completely, and are inexpensive (an important point).
2. Dissolve a relative large amount of acetic acid in water. Partially neutralize the acid by adding some strong base, like NaOH. The amount of acetate formed will be equivalent to the amount of strong base added. The amount of acetic acid left in solution will be the starting amount minus the amount converted to acetate.
3. Dissolve a relatively large amount of an acetate salt in water, preferably a strong salt. Partially neutralize the acetate by adding some strong acid, like HCl. The amount of acetic acid formed will be equivalent to the amount of strong acid added. The amount of acetate ion left in solution will be the starting amount minus the amount converted to acetic acid.
The ratio of acetic acid to acetate in solution can be chosen to provide a desired [H+] or pH for the buffer solution. Usually, the ratio is kept within the limits of 10 and 0.1. Let us look at the equilibrium reaction for this system and the associated calculation for Ka:
The rearrangement above can be expressed in a generalized form:
Taking the logarithms of (17-10) and reversing the signs yields a convenient form:
An indicator is used to give a visual indication of the pH of a solution. Like a buffer, it is a conjugate acid-base pair; however, indicators are used in such small amounts (a couple of drops) that the pH of the solution is not affected. The pH of the solution determines the ratio of the acid form to the conjugate base form of the indicator. Each form of the indicator has a definite color, so it is easy to see the change from the acid to the conjugate base as the dominant form in solution—that is the indicator of the pH of that solution. If the acid dissociation of the indicator is written as follows:
If the ratio exceeds about 10:1, the color will appear to be purely that of HIn, the acid form. If the ratio is less than roughly 0.1, the color will be purely that of the base form, In–. There is a change from color to color generally through a mixing or blending of colors. As an example, if the extreme colors are yellow and blue, the intermediate will be a gradual change from yellow-green through green to blue-green. The gradual change occurs over a 100-fold range in [H+], about 2 pH units, with the pKa near the center of the range. A variety of indicators is known, each with its own pKa and range of color change. (Note that the greater the difference in color intensity between the acid and base forms, the further off-center will be pKa.)
If multiple ionizations are possible, as in H2S, H2CO3, and H3PO4, each stage of ionization has its own equilibrium constant, K1, K2, etc. The subscripts are numbers representing the ionization in stages starting with the ionization of the molecule (K1) and continuing in order (1, 2, 3, etc.). H2S ionizes in steps:
The secondary ionization constant of polyprotic acids is always smaller than the primary (K2 < K1); the tertiary, K3, is even smaller; and so on.
We should make it clear at this point that [H+] is the actual concentration of hydrogen ions in solution, regardless of the source. In an aqueous mixture containing more than one acid, the different acids all contribute to the hydrogen ion concentration, but there is only one value of [H+] in any given solution. That value must simultaneously satisfy the equilibrium conditions for all the different acids present. Although it may seem complex to solve a problem in which there are lots of equilibria, simplifications can be made when all sources but one make a small enough contribution that it can be insignificant (less than 10 percent in this book) to the total concentration of the ion.
In the case of polyprotic acids, K1 is often so much greater than K2 that only the K1 equilibrium need be considered to calculate [H+] in a solution of the acid. Examples where this assumption may and may not be made will be given in specific Solved Problems with the reasoning included.
Another problem of interest is the calculation of the concentration of the divalent ion (2–) in a solution of a weak polyprotic acid, when the total [H+] is essentially due to a stronger acid present in the solution or to a buffer. In such a case, the concentration of the divalent ion can best be calculated by multiplying the expressions for K1 and K2. Again, illustrating with H2S, we find the following:
When a base is added in small increments to a solution of acid, the pH of the solution rises on each addition of base. When the pH is plotted against the amount of base added, the steepest rise occurs at the equivalence point (when the acid is exactly neutralized). This region of steepest rise is called the end point, and the whole process of base addition and determination at the end point is called titration. The graph showing the change of pH during the titration is called a titration curve. Example 2 discusses the titration curve with reference to Fig. 17-1a and 17-1b.
Fig. 17-1
EXAMPLE 2 Figure 17-1a shows the titration of one strong acid and one weak acid, separately, with a strong base. Figure 17-1b shows the titration of one strong base and one weak base, separately, with a strong acid. All four titrations are performed at 25°C. All reagents are 0.100 M so that the end point always occurs on the addition of exactly 50.0 mL of titrant (known concentration solution added during titration). The strong acid is HCl and the weak acid is HC4H7O3; the strong base is NaOH and the weak base is NH3. Note: HC4H7O3 is β-hydroxybutyric acid.
All curves display a very sharp rise or fall in pH at the end point. When HCl is titrated (Fig. 17-1a), the pH rises slowly until very near the end point. The rise at the end point is much greater than for HC4H7O3, which starts at a higher pH, has an initial rapid rise, reverses its curvature, and eventually undergoes the very sharp rise typical of the end point. Beginning slightly beyond the end point, the two curves are identical. The titration curves for NaOH and NH3 (Fig. 17-1b) are almost mirror images of those for HCl and HC4H7O3 with decreasing pH. There is no practical reason for using a weak reagent as a titrant. If, for instance, NH3 were to be used in place of NaOH in Fig. 17-1a, the curve would level off beyond the end point at least 3 pH units lower, making the end point more difficult to spot.
The points along a titration curve can be calculated by methods previously discussed in this chapter. Basically, there are four regions making up a titration curve. Consider the titration of acid with strong base.
1. Starting point: 0% neutralization.
In the case of the strong acid, [H+] in the initial solution is simply the molar concentration of the acid. In the case of a weak acid, [H+] is calculated by the method used to determine the extent of ionization of any weak acid in terms of its ionization constant and molar concentration.
2. Approach to the end point: 5% to 95% neutralization.
For the case of the strong acid, the neutralization reaction is as follows.
H+ + OH– → H2O
This reaction may be assumed to go to completion to the extent of the amount of base added. The amount of unreacted H+ is then the difference between the initial amount of H+ and the amount neutralized. To determine [H+], allowance is made for the dilution effect of increasing the total volume of solution on the addition of base (also a solution).
For the case of a weak acid, the neutralization reaction may be written as
The amount of hydroxybutyrate ion, 
, is equal to the amount of base added. The amount of acid, HC4H7O3, that has not ionized is the difference between the initial amount and the amount neutralized. Then,
The above is Equation (17-10); solutions in this region of a weak acid titration are buffers.
3. The end point: 100% neutralization.
The pH at the end point is the same as for a solution of a salt containing the ions remaining at neutralization, NaCl or NaC4H7O3. NaCl solutions are neutral (pH = 7); however, NaC4H7O3 hydrolyzes and the pH can be evaluated by solving the hydrolysis equilibria. The HC4H7O3–NaOH titration has a pH greater than 7 at the end point because of the hydrolysis of the hydroxybutyrate ion.
4. Extension beyond the end point: Over 105% neutralization.
With NaOH as the titrant, the excess OH– beyond that needed for neutralization accumulates in the solution. The [OH–] is calculated in terms of this excess and the total volume of the solution [H+] can then be calculated from the Kw relationship, which is as follows:
It makes no difference whether the acid titrated was weak or strong.
Points within 5% of the starting point or 5% of the end point can be calculated by the same equilibria, but some of the simplifying assumptions made above would no longer be valid.
Polyprotic acids, like H3PO4, may have two or more distinct end points corresponding to neutralization of the first, second, and subsequent hydrogens. In such a case, each end point would occur at a different pH.
The calculations for the titration curves of bases with strong acid (Fig. 17-1b) are done by similar methods.
The end point of a titration, the region of the steepest rise in the titration curve, can be determined experimentally if an instrument is available for measuring the pH after each addition of base. A simpler means is to introduce into the solution a small amount of an indicator chosen so that its range lies within the steep vertical portion of the curve. This ensures a sharp color change at the end point.
17.1. Write the formulas for the conjugate bases of the following acids: (a) HCN; (b) 
; (c) 
; (d) C2H5OH; (e) HNO3.
In each case, the conjugate base is derived from the acid when it loses a proton (H+) from the highly electronegative oxygen, rather than from carbon. If there is no oxygen, as in (a) and (c), the proton will be lost from the most electronegative element to which it is bonded (the carbon and nitrogen, respectively, in these cases). (a) CN–; (b) 
; (c) N2H4; (d) C2H5O–; (e) 
17.2. Write the formulas for the conjugate acids of the following bases: (a) HC2H3O2; (b) ; (c) C5H5N; (d) ; (e) OH–.
In each case, the conjugate acid is formed from the base by the addition of a proton. The proton is added to oxygen in (a) or to nitrogen in (c) and (d), all of which have unshared pairs available to which the proton is attracted. In (a), the proton is added to the carbonyl oxygen (—C=O).
(a) 
. This species might form in liquid acetic acid on the addition of a strong acid.
(b) 
can serve as both an acid [Problem 17.1(b)] and a base.
(c) C5H5NH+.
(d) 
. Bases, like acids, can be multifunctional. The second proton is accepted by N2H4, but only with great difficulty.
(e) H2O.
17.3. Liquid NH3, like water, is an amphiprotic solvent. Write the equation for its autoionization.
Note that, as NH3 replaces H2O, the ammonium ion occupies the same position as H+ in the autoionization of water. And, of course, the amide ion takes the place of the hydroxide ion.
17.4. Aniline, C6H5NH2, is a weak organic base in aqueous solutions. Suggest a solvent in which aniline would become a strong base.
The solvent needed to do the job is one that has appreciably stronger acid properties than water. One such solvent, in which aniline is a strong base, is liquid acetic acid or any other acidic solvent with greater acid properties than water.
17.5. NH4ClO4 and HClO4 · H2O both crystallize in the same orthorhombic structure, having unit-cell volumes of 0.395 and 0.370 nm3, respectively. How do you account for the similarity in crystal structure and crystal dimensions?
Both are ionic substances with lattice sites occupied by cations and anions. In perchloric acid monohydrate, the cation is H3O+ and there are no water molecules of hydration. The cations in the two crystals, H3O+ and 
, should occupy nearly equal amounts of space because they are isoelectronic (having the same number of electrons).
Historical note: The data in this problem have been cited as one of the proofs for the existence of the hydroniumion, H3O+.
17.6. (a) Give an explanation for the decreasing acid strength in the series HClO4, HClO3, HClO2. (b) What would be the relative basic strengths of 
, (c) Keeping in mind the discussion of (a), how do you account for the fact that there is very little difference in acid strength in the series H3PO4, H3PO3, H3PO2?
(a) The Lewis structures are
Since oxygen is more electronegative than chlorine, each terminal oxygen tends to withdraw electrons from the chlorine and, in turn, from the O—H bond. This withdrawal leads to an increasing tendency for the proton (H+) to dissociate. In general, the greater the number of terminal oxygens in an oxygen-containing acid with the same central atom, the stronger the acid.
(b) Members of a conjugate acid-base pair stand in complementary relationship to each other—the stronger an acid, the weaker its conjugate base. This results in the order of decreasing basic strength, which is 
(reversed for increasing acid strength).
(c) The hydrogens in these acids are not all bonded to oxygens. The Lewis structures are
The number of terminal oxygen atoms, one, is exactly the same in all three acids, so that, according to (a), no great differences in acidity are expected. Since the electronegativities of P and H are almost the same, there is no tendency for the phosphorus-bonded H to ionize, nor to influence the ionization of the oxygen-bonded H’s.
17.7. How do you account for the formation of S2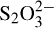
from 
and S in terms of Lewis acid theory?
The sulfur atom is electron-deficient and can be regarded as an acid. is the base, for which an octet structure can be written with an unshared pair proving its base character.
17.8. In combustion analysis of organic compounds, solid NaOH is used to absorb the CO2 from the combustion gases. Account for this reaction in terms of Lewis acid-base theory.
Because the oxygen in the OH– ion has three unshared pairs of unshared electrons, it is a Lewis base. Understanding how CO2 functions as an acid relies on noting that the carbon in CO2 is sp hybridized, but by reverting to sp2 hybridization, as in , an orbital is made available to accept the base pair.
17.9. At 25°C, a 0.0100M NH3 solution is 4.1% ionized. Assuming no volume changes, calculate (a) the concentration of OH– and 
ions; (b) the concentration of molecular ammonia; (c) the ionization constant of aqueous ammonia; (d) [OH–] after 0.0090 mol NH4Cl is added to 1 L of the above solution; (e) [OH–] of a solution prepared by dissolving 0.010 mol NH3 and 0.0050 mol HCl per liter.
The label on a solution refers to the stoichiometric or weight composition, not the concentration of any particular component in an ionic equilibrium. In other words, 0.0100 M NH3 means that the solution was produced from 0.0100 mol ammonia and the necessary water to make a liter of solution. It does not mean that the concentration of the un-ionized ammonia in the solution, [NH3], is 0.0100.
(b) 
(c) 
(d) Since the base is so slightly ionized, we may assume that (1) the 
is completely derived from NH4CI and that (2) the [NH3] at equilibrium is the same as the stoichiometric molar concentration of the base. Then,
The addition of NH4Cl holds back the ionization of NH3. This action reduces greatly the [OH–] of the solution. This action of shifting the reaction by means of two sources of the same ion is called the common-ion effect.
Alternate method: There were a lot of assumptions made in the above solutions, but there is a way to work without making assumptions. The technique involves writing the reaction and then making a table below that equation holding the information given in the problem so that the answers can be derived by direct, mathematical means. Water is a pure liquid in this reaction and is not included in K.
This yields a quadratic equation, which can be solved by the usual methods. Clearing fractions and ignoring for the moment the rules of significant digits,
The quadratic equation must be used for the solution for x as follows:
and, since one possible answer is negative, the other value, x = 1.94 × 10–5, is the only logical choice.
Clearly, making simplifying assumptions provides for a large reduction in labor for this problem and others. However, for many students, the table provides a good system of bookkeeping and helps when putting together the solution. Once x has been found, substituting into the last line above will provide the concentrations of all species present. Recall that water is the solvent and, since it is a pure liquid, its concentration is constant and not included in the K expression.
(e) Since HCl is a strong acid, the 0.0050 mol of HCl will react completely with the 0.0050 mol of NH3 to form 0.0050 mol . Of the original 0.0100 mol of NH3, only half will remain as ammonia that is not ionized.
Check of assumption: The amount of contributed by the dissociation of NH3 must be equal to the amount of OH–, or 1.75 × 10–5 mol/L. This is quite small compared with the 0.0050 mol/L formed by the neutralization of NH3 with HCl.
17.10. Calculate the molarity at which an acetic acid solution is 2.0% ionized. Ka at 25°C for HC2H3O2 is 1.75 × 10–5.
Let x be the molar concentration of acetic acid. Then,
The approximation is well within 10%, which allows us to ignore 0.020x.
Solving:
17.11. Calculate the percent ionization of a 1.00 M HCN (hydrocyanic acid); Ka of HCN is 4.93 × 10–10.
Since H+ and CN– are present in the solution only as a result of the ionization, their concentrations must be equal. Assume that [H+] from the ionization of water is not significant.
Let x = [H+] = [CN–]. Such being the case, [HCN] = 1.00 – x. Let us assume that x will be very small compared to 1.00, so that [HCN] = 1.00, which should be within the allowed error of 10%. Then,
Check of assumptions: (1) (x = 2.22 × 10–5) is very small compared with 1.00; (2) the [H+] in neutral water is only 1 × 10–7, which is less than 1% of x. Also, the ionization of water is suppressed even more by the presence of the acid because the added hydrogen ion from the acid shifts the ionization of water toward the water (H2O 
H+ + OH–).
17.12. The [H+] in a 0.020 M solution of benzoic acid is 1.1 × 10–3. Calculate Ka for the acid, HC7H5O2.
Since the hydrogen ion and benzoate ion come only from the ionization of the acid, their concentrations are equal. The contribution of H+ by the ionization of water is insignificant.
17.13. The ionization constant for formic acid, HCO2H, is 1.77 × 10–4. What is the percent ionization of a 0.00100 M solution of formic acid?
Let 
Then [HCO2H] = 0.00100 – x. Assume, as in Problem 17.11, that the percent ionization is less than 10% and that the formic acid concentration, 0.00100 – x, may be approximated as 0.00100. Then,
In checking the assumption, we see that x is not insignificant compared with 0.0010. Therefore, the assumption and the solution based on it must be rejected and the full quadratic form of the equation must be solved. (Refer to Problem 17.9 for the techniques involved.)
Solving: x = 3.4 × 10–4. Note that we rejected the negative root, –5.2 × 10–4 (negative concentration?).
This exact solution (34% ionization) shows that the solution based on the original assumption was almost 25% too high.
The pitfall introduced by this problem is making the assumption as to the significance of x in 0.00100 – x and, after calculations, finding that the assumption was incorrect. Then, we had to do the work all over again with x included. There is a way of getting around such false assumptions called the five percent rule. This rule states that x may be omitted as being insignificant if x is less than 5% of the number it is being subtracted from (or added to). In other words, the value of x is so small that it doesn’t make any difference if it is or is not subtracted from (or added to) the number. Notice that the chemical equation produces 2 ions in this problem. If, since these two ions are multiplied together (squared, if they are the same concentration), we were to take the square root of K, it would approximate the value of x. If that value, the square root of Ka, is less than 5% of the number it is being subtracted from, it is insignificant. The square root of Ka, (1.77 × 10–4)1/2, is 0.0133 and 5% of 0.00100 is 0.00005. Since the square root of Ka is larger than the 5% approximation, it cannot be ignored.
17.14. What concentration of acetic acid is needed to give a [H+] of 3.5 × 10–4? Ka is 1.75 × 10–5.
Let x be the number of moles acetic acid per liter.
17.15. A 0.100 M solution of an acid (density = 1.010 g/mL) is 4.5% ionized. Calculate the freezing point of the solution. The molar mass of the acid is 300.
Since we are dealing with a freezing-point change, we must know the molality of the solution, and we can use any volume of solution for the calculations—using 1 L is convenient.
If the acid were not ionized at all, the freezing-point lowering (Chapter 14) would be
However, because of the ionization, the total number of dissolved particles is greater than 0.102 mol per kg solvent. The freezing-point depression is determined by the total number of dissolved particles, regardless of whether they are charged (ions) or uncharged (molecules).
Let a = fraction ionized. For every mole of acid added to the solution, there will be (1 – a) moles of un-ionized acid at equilibrium, a moles of H+, and a moles of anion base conjugate to the acid. This gives us a total of (1 + a) moles of dissolved particles. Then, the molality with respect to all dissolved particles is (1 + a) times the molality calculated without regard to ionization.
The freezing point of the solution is –0.198°C.
17.16. A solution was made up to be 0.0100 M HC2H2O2Cl, chloroacetic acid, and also 0.0020 M NaC2H2O2Cl. Ka for chloroacetic acid is 1.40 × 10–3. Calculate [H+].
Instead of making the 10% assumption, as has been done in most of the problems above, let us apply the 5% rule. Solving this problem is made easier by recording the reaction involved and doing the bookkeeping under the reactions, as was introduced in Problem 17.9
The 0.0020 anion added in the first line recognizes that sodium salts ionize completely in aqueous solution. We now have to substitute into the Ka expression, but do we have to add x on the right and subtract x on the left? The square root of Ka is 0.037, which is larger than 5% of 0.0020 (0.0001) on the right and also larger than 5% of 0.0100 on the left. This means that we cannot ignore the value of x anywhere in this setup. Then,
After solving this equation in the ax2 + bx + c = 0 format and applying the quadratic formula, we find that the hydrogen ion concentration is 2.4 × 10–3 M.
Note that, had we made the assumption that x was not significant, we would have discovered that it could not be left out and would have been required to redo the problem, doubling the work.
17.17. Calculate [H+] and 
in a solution that is 0.100 M HC2H3O2 and 0.050 M HCl. Ka for acetic acid is 1.75 × 10–5.
HCl contributes so much more H+ than acetic acid that we can take [H+] as equal to the molar concentration of the HCl, 0.050; this is another example of the common-ion effect.
Then, if = x, we have [HC2H3O2] = 0.100 – x, which we can assume is 0.100.
Check of assumption: (1) The contribution of acetic acid to [H+], x, is quite small compared with 0.050; (2) x is definitely small compared with 0.100.
17.18. Calculate [H+], , and [CN–] in a solution that is 0.100 M in HC2H3O2 (Ka = 1.75 × 10–5) and 0.200 M in HCN (Ka = 4.93 × 10–10).
This problem is similar to the preceding one; one of the acids, acetic, completely dominates the other in terms of contribution to the total [H+] of the solution. We base this assumption on the fact that the Ka for acetic acid is so much greater than the one for hydrocyanic acid. We will check the assumption after solving the problem. Let us start by treating the acetic acid as if the hydrocyanic were not present.
Let [H+] = = x; then, [HC2H3O2] = 0.100 – x, and this is taken to be 0.100 because of the small expected value of x. Actually, the five percent rule tells us that the value of x is approximately 0.0042, which is less than 5% of 0.100, which is 0.005, telling us that x can be omitted.
Check of assumption: x is very small compared to 0.100.
Now we treat the HCN equilibrium established at a value of [H+] determined by the acetic acid, 1.32 × 10–3. Let [CN–]= y; then [HCN] = 0.200 – y ≈ 0.200, because the square root of Ka is so small compared to 0.200 that it is not significant. And
Check of assumption: (1) y is small compared with 0.200; (2) the amount of H+ contributed by HCN is equal to the amount of CN– formed (7.5 × 10–8 mol/L) and is small compared with the amount of H+ contributed by HC2H3O2 (1.32 × 10–3 mol/L).
17.19. Calculate [H+] in a solution that is 0.100 M HCOOH (Ka = 1.77 × 10–4) and 0.100M HOCN (Ka = 3.3 × 10–4).
This is a case in which two weak acids both contribute to [H+]; however, neither one is a much larger contributor than the other. Both need to be considered for their contributions. Let us do the bookkeeping for both equilibria and see where that leads us.
The final line is based on the assumption that x and y are both small compared to 0.100 at the 10% level.
Dividing the HOCN equation by the HCOOH equation,
Subtracting the HCOOH equation from the HOCN equation,
Substitute y = 1 .86x into the last equation and solving: x = 2.5 × 10–3. Then
Check of assumptions: The values of x and y are not much less than 10% of 0.100, which is pressing the 10% limit of error generally allowed in this chapter. Note that, if the five percent rule were to be applied, there would be a great deal more calculation involved due to the necessary use of the quadratic formula. The point is that you need to be aware of how much error is allowed and stick to that limit.
17.20. Calculate the [H+] and the [OH–] in 0.100 M HC2H3O2 which is 1.31% ionized.
From acetic acid,
Note that [H+] is calculated as if the HC2H3O2 were the only contributor, whereas [OH–] is based on the ionization of water. If water ionizes to supply OH–, it must supply an equal amount of H+ at the same time. Implied in this solution is the assumption that water’s contribution to [H+], 7.6 × 10–12 mol/L, is negligible compared with that of the HC2H3O2. Actually, this assumption is valid in all but the most dilute acid solutions. In calculating [OH–], water is the only source and it therefore cannot be overlooked.
17.21. Determine the [OH–] and the [H+] in a 0.0100 M ammonia solution which is 4.1% ionized.
In this problem, we have made the assumption that the contribution of water to [OH–] (equal to [H+], or 2.4 × 10– M) is negligible compared with that of NH3. Kw is used to calculate [H+], since water is the only supplier of H+. In general, [H+] for acidic solutions can be calculated without regard to the water equilibrium; then Kw is used to calculate [OH–]. Conversely, [OH–] for basic solutions can usually be calculated without regard to the water equilibrium; then, Kw is used to calculate [H+].
17.22. Express the following H+ concentrations in terms of pH: (a) 1 × 10–3 M, (b) 5.4 × 10–9 M.
(a) pH = –log[H+] = 3, (b) pH = –log[H+] = 8.27.
Enter the molar concentration into your calculator, then press the log button. Remember to reverse the sign of the answer because taking the –log [H+] is the same as –1 × log[H+].
17.23. Calculate the pH values (100% ionization) of (a) 4.9 × 10–4 Nacid, (b) 0.0016 N base.
(a) 3.31; (b) 14 = pH + pOH is the relationship needed for this calculation. Recall that p means “take the negative log” of whatever follows. Then, pH = 14 – pOH, and the hydroxide ion concentration comes directly from the problem. So, pH = 14 – 2.8 = 11.2.
17.24. Change the following pH values to [H+] values: (a) 4, (b) 3.6.
(a) Since pH = –log[H+] then,
Taking the antilog of both sides will prove the answer. Then,
(b) Using the same technique as in (a), [H+] = 2.5 × 10–4.
17.25. What is the pH of (a) 5.0 × 10–8 M HCl, (b) 5.0 × 10–10 M HCl?
(a) If we were to consider only the contribution of the HCl to the acidity of the solution, [H+] would be 5.0 × 10–8 and the pH would be greater than 7, which is a pH indicating a base. We have to take into account the contribution of water to the total acidity, something we have not done in previous problems because the acids and bases way overshadowed water’s effect. The bookkeeping is
Kw = [H+][OH–] = (5.0 × 10–8 + x)(x) = 1.00 × 10–14
From the quadratic equation: x = 7.8 × 10–8. Then, [H+] = (5.0 × 10–8 + x) = 1.28 × 10–7, and
(b) Although the method of (a) could be used here, the problem can be simplified by noting that HCl is so dilute as to make only a small contribution to [H+] as compared with the ionization of water. We may therefore write directly: [H+] = 1.00 × 10–7 and pH 7.00.
17.26. Calculate the extent of hydrolysis in a 0.0100 M solution of NH4Cl. Kb for NH3 is 1.75 × 10–5.
By the reaction equation, equal amounts of NH3 and H+ are formed. Let x = [NH3] = [H+].
and
Check of approximation: x is very small compared with 0.0100.
17.27. Calculate [OH–] in a 1.00 M solution of NaOCN; Ka for HOCN is 3.5 × 10–4.
Since the source of the OH– and HOCN is the hydrolysis reaction, they must exist in equal concentrations. Let x = [OH–] = [HOCN]. Then
and
Check of approximation: x is very small compared with 1.00.
17.28. The acid ionization (hydrolysis) constant of Zn2+ is 3.3 × 10–10. (a) Calculate the pH of 0.0010 M ZnCl2. (b) What is the basic dissociation constant of Zn(OH)+?
(a) 
Let x = [Zn(OH)+] = [H+]. Then, [Zn2+] = 0.0010 – x ≈ 0.0100, and
Check of approximation: x is very small compared with 0.0010.
(b) 
17.29. Calculate the extent of hydrolysis and the pH of 0.0100 M NH4C2H3O2. Ka for HC2H3O2 is 1.75 × 10–5 and Kb for NH3 is also 1.75 × 10–5.
The problem illustrates a situation where both the cation and anion hydrolyze.
By coincidence, the hydrolysis constants for these two ions are identical. The production of H+ by hydrolysis must, therefore, exactly equal the production of OH– by 
hydrolysis. The H+ and OH– formed by hydrolysis neutralize each other to maintain the original water equilibrium. The solution is neutral, [H+] = [OH–] = 1.00 × 10–7; the pH is 7.00.
For hydrolysis,
Let x = [NH3]. Then 0.0100 – x = 
and
The percent hydrolysis of acetate must also be 0.57% because the equilibrium constant for the hydrolysis is the same as for 
.
In comparing the results of this problem with Problem 17.26, note that the percent hydrolysis of is greater in the presence of a hydrolyzing anion (like acetate). The reason is that the removal of some of the products of the two hydrolyses, H+ and OH–, by the water equilibrium reaction 
allows both hydrolyses to proceed to an increasing extent.
17.30. Calculate the pH in 0.100 M NH4OCN. Kb for NH3 is 1.75 × 10–5 and Ka for HOCN is 3.5 × 10–4.
As in Problem 17.29, both cation and anion hydrolyze. Since NH3 is a weaker base than HOCN is an acid, hydrolyzes more than OCN–, and the pH of the solution is less than 7. In order to preserve electrical neutrality, there cannot be an appreciable difference between and [OCN–]. (If there is a slight difference, it can be accounted for by the [H+] or [OH–].) Therefore, [NH3] must be practically equal to [HOCN], and we will assume that they are for this problem.
Let x = [NH3] = [HOCN]; then, 0.100 – x = = [OCN–].
and
and
Dividing (1) by (2),
Also, [H+] and [OH–] must satisfy the Kw relationship:
Multiplying (3) by (4), we obtain:
Check of assumption: Our assumption that [NH3] = [HOCN] is valid only if [H+] and [OH–] are much smaller than [NH3] and [HOCN]. We will solve for x, the [NH3] or [HOCN]. From (1),
Both [H+] and [OH–] are small compared with x.
It appears from the solution to this problem that the pH is independent of the concentration of NH4OCN, and this is true at sufficiently high concentrations. However, x decreases with the initial concentration, as is shown in (5), so that, at much lower concentrations, the simplifying assumptions are no longer valid. Note: The problem can still be solved by insisting on conservation of electrical charge, but the solution becomes very complicated.
17.31. Calculate [H+] of 0.10 M H2S. K1 and K2 for H2S are 1.0 × 10–7 and 1.2 × 10–13.
By far, most of the H+ results from the primary ionization: H2S H+ + S– because K1 is so much larger than K2.
Let x = [H+] = [HS–]. Then, [H2S] = 0.10 – x ≈ 0.10.
Check of assumptions: (1) x is definitely small compared with 0.10. (2) For the above value of [H+] and [HS–], the extent of the second dissociation is given by
The extent of the second dissociation is so small that it does not either lower [HS–] or raise [H+] as calculated from the first dissociation significantly. Notice that in a solution of a polyprotic acid the concentration of the conjugate base resulting from the second dissociation is equal to K2. This result is general whenever the extent of the second dissociation is less than 5% (an application of the five percent rule).
17.32. Calculate the concentration of 
(a) in 0.010 M H2C8H4O4, (b) in a solution which is 0.10 M H2C8H4O4 and 0.020 M HCl. The ionization constants for H2C8H4O4, phthalic acid, are
(a) If there were no second dissociation, the [H+] could be calculated on the basis of K1.
Note that it was necessary to solve the quadratic to obtain x. If we assume that the second dissociation does not appreciably affect [H+] or [HC8H4O4–], then
Check of assumption: The extent of the second dissociation relative to the first is sufficiently small to validate the assumption as follows:
(b) The [H+] in solution may be assumed to be essentially all from the HCl. Also, this large common-ion concentration reduces the ionization of phthalic acid, so that we assume that 
. The most convenient equation to use is the K1K2 equation, since all the concentrations for this equation are known, except for one.
Check on assumption: Solving for the first dissociation,
The amount of H+ contributed by this dissociation, 6.5 × 10–4 mol/L, is less that 10% of the amount contributed by HCl (0.020 mol/L). The amount of the H+ contributed by the second dissociation is still less.
17.33. Calculate the extent of hydrolysis of 0.005 M K2CrO4. The ionization constants of H2CrO4 are K1 = 0.18, K2 = 3.2 × 10–7.
Just as in the ionization of polyprotic acids, so in the hydrolysis of their salts, the reaction proceeds in successive stages. The extent of the second stage is generally very small compared with the first. This is particularly true in this case, where H2CrO4 is quite a strong acid with respect to its first ionization and much weaker in the second ionization. The equation of interest is
which indicates that the conjugate acid of the hydrolyzing 
is 
. As the ionization constant for is K2, the basic hydrolysis constant for the reaction is Kw/K2.
Let x = [OH–] = []. Then, [] = 0.005 – x ≈ 0.005 and
Check assumption: x is quite small compared with 0.005.
17.34. What is the pH of 0.0050 M Na2S? For H2S, K1 = 1.0 × 10–7 and K2 = 1.2 × 10–13.
As in Problem 17.33, the first stage of hydrolysis, leading to HS–, by far overshadows the second stage.
Because of the large value for Kb, it cannot be assumed that the equilibrium concentration of S2– is approximately 0.0050 mol/L. In fact, the hydrolysis is so extensive that most of the S2– is converted to HS–.
Let x = [S2–], then [HS–] = [OH–] = 0.0050 – x, and
Check of assumption: Consider the second stage of hydrolysis:
Solve for [H2S] by assuming the values of [OH–] and [HS–] already calculated above.
The extent of the second hydrolysis compared with the first, (1.6 × 10–7) to (4.7 × 10–3), is very small.
17.35. Calculate [H+], 
and 
in 0.0100 M H3PO4. K1, K2, and K3 are 7.52 × 10–3, 6.23 × 10–8, and 4.5 × 10–13, respectively.
We begin by assuming that H+ comes mostly from the first stage of dissociation and that the concentration of any anion formed by one stage of an ionization is not appreciably lowered by the second state of ionization.
Let 
Then [H3PO4] = 0.0100 – x, and
We next take the above values for [H+] and 
to solve for 
Check of assumption: The extent of the second dissociation compared with the first is very small, 6.23 × 10–8 compared to 5.7 × 10–3.
The next step would be to perform the same calculations using K3 and the associated reaction, but we note that K3 is very small as compared with K2, the point being that the values that would be calculated are expected to be of little significance in comparison to the results of the previous K values.
17.36. What is the pH of 0.0100 M NaHCO3? K1 and K2 for H2CO3 are 4.3 × 10–7 and 5.61 × 10–11.
(Note: H2CO3 in aqueous solution is in equilibrium with dissolved CO2, the majority species. The value of K1 given here is based on the total concentration of both of these neutral species. Since there is no effect on the stoichiometry or charge balance, the problem can be worked as if all the neutral species were in the form H2CO3.)
This problem is somewhat similar to Problem 17.30 because there is one reaction tending to make the solution acid (the K2 acid dissociation of 
to yield H+) and another reaction tending to make the solution basic (the hydrolysis of ).
We notice that the hydrolysis constant for reaction (2) is related to K1, because both hydrolysis and the K1 equilibrium involve H2CO3 and . We see that the equilibrium constant for (2) is greater than that for (1); then, the pH is definitely going to exceed 7.
We assume that, after the self-neutralization of both, [H+] and [OH–] were so small as to have no appreciable effect on the ionic charge balance. Therefore, electrical neutrality can be preserved only by maintaining a fixed total anionic charge among the various carbonate species. This is true since the cationic charge remains at 0.0100 M, which is the concentration of Na+, regardless of the acid-base equilibria. In other words, for every negative charge removed by the conversion of to H2CO3, another negative charge is created by converting to
This leads to the following conditions:
Multiplying (3) and (4), while recalling that [H+][OH–] = 1.00 × 10–14, we have
Provisional check: 2x is small compared with 0.0100.
We return now to (3).
Final check: Both [H+] and [OH–] are small compared with x and will have no appreciable effect on the electrical charge balance.
Alternatively, [H+] could have been calculated from K1 only; the result would have been the same.
17.37. A buffer solution of pH 8.50 is desired. (a) Starting with 0.0100 mol KCN and the usual inorganic reagents of the laboratory, how would you prepare 1 L of the buffer solution? Ka for HCN is 4.93 × 10–10.
(b) By how much would the pH change after the addition of 5 × 10–5 mol HClO4 to 100 mL of the buffer?
(c) By how much would the pH change after the addition of 5 × 10–5 mol NaOH to 100 mL of the buffer?
(d) By how much would the pH change after the addition of 5 × 10–5 mol NaOH to 100 mL pure water?
(a) To find the desired [H+]:
Taking the antilog of both sides:
The buffer solution could be prepared by mixing CN– (weak base, using a strong salt, such as KCN as it ionizes completely) with HCN (weak acid) in the proper proportions to satisfy the Ka for HCN.
and, by rearrangement and solving,
The ratio of CN– to HCN (0.154:1) can be attained if some of the CN– is neutralized with a strong acid, like HCl, to form an equivalent amount of HCN. The total cyanide available for both forms is 0.0100 mol. Let x = [HCN]; then [CN–] = 0.0100 – x. Substituting in (1) directly above,
The buffer solution can be prepared by dissolving 0.0100 mol KCN and 0.0087 mol HCl in sufficient water to make up 1 L of solution.
(b) 100 mL of the buffer contains
and
The addition of 5 × 10–5 mol of strong acid converts more CN– to HCN. The amount of HCN will be
and the amount of CN– will be
Only the ratio of the two concentrations is needed.
The drop in pH caused by the addition of the acid is 8.50 – 8.24, or 0.26 pH units.
(c) The addition of 5 × 10–5 mol of a strong base will convert an equivalent amount of HCN to CN–.
The rise in pH caused by the addition of the base is 8.66 – 8.50, or 0.16 pH units.
(d)
and
Pure water has a pH of 7.00. The rise caused by the addition of the base is 10.70 – 7.00, or 3.70 pH units. Note that this rise is quite large when compared to the rise due to addition to the buffer solution. Recall that the buffer is capable of absorbing hydrogen and/or hydroxide ions with little change; pure water cannot do that.
17.38. If 0.00010 mol H3PO4 were to be added to a solution well buffered at pH 7.00, what are the relative proportions for the four forms: H3PO4, 
, 
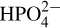, and 
K1 = 7.52 × 10–3, K2 = 6.23 × 10–8, and K3 = 4.5 × 10–13.
In the previous problem, we expected some pH change, but in this problem we can assume that the pH is not changed by the addition of the very small amount of phosphoric acid mentioned because it is “well buffered,” meaning that it is extremely resistant to pH change. Then, if [H+] is fixed, the ratio of two of the desired concentrations can be calculated from each of the ionization constant equations.
Since the ratio 
is very small and the ratio 
is very large, practically all of the material will exist as and 
The sum of the amounts of these two ions will be practically equal to 0.00010 mol. If the total volume is 1 L, the sum of these two ion concentrations will be 0.00010 M.
Let x = 
then 
= 0.00010 – x. Then
A total volume of 1 L was selected for convenience in illustrating the relative concentrations. However, the same ratios of concentrations would be valid for any reasonable choice of total volume.
17.39. Ka for HC2H3O2 is 1.75 × 10–5. A 40.0-mL sample of 0.0100M acetic acid is titrated with 0.0200M NaOH. Calculate the pH after the addition of (a) 3.0 mL; (b) 10.0 mL; (c) 20.0 mL; (d) 30.0 mL of NaOH solution.
We can keep track of the changing amounts of various species and the increasing volume by a bookkeeping system, such as Table 17-2.
Note that the amount of acetic acid neutralized (amount of 
) follows the amount of OH– added, up to complete neutralization. Additional OH–, having no more acid to neutralize, accumulates in the solution. Up to the end point, the amount of HC2H3O2 remaining is obtained by simply subtracting the amount of from the initial amount of HC2H3O2. At the end point and beyond, however, [HC2H3O2] cannot be set equal to zero, but must be deduced from the hydrolysis equilibrium.
(a) and (b). The numerical values for the concentrations are not needed for these parts of the problem; however, the ratio of the conjugate acid to base is required.
The solution at the end point is the same as 6.7 × 10–3 M Na2C2H3O2; consider its hydrolysis:
Let [HC2H3O2] = [OH–] = x, and [C2H3O2] = 6.7 × 10–3 – x ≈ 6.7 × 10–3. Then
Check of assumption: x is quite small compared with 6.7 × 10–3.
(d) From the extra OH– beyond that needed to neutralize all the acetic acid, we know that
17.40. Calculate a point on the titration curve for the addition of 2.0 mL of 0.0100 M NaOH to 50.0 mL of 0.0100M chloroacetic acid, HC2H2O2Cl. Ka = 1.40 × 10–3.
The simplifying assumption made in Problem 17.39 just won’t work in this problem. If the amount of chloroacetate ion formed were to be equivalent to the amount of NaOH added, we would have
Amount OH– added = (0.0020 L)(0.010 mol/L) = 2.0 × 10–5 mol
Total volume = 0.0520 L
This answer simply won’t work because the [H+] cannot possibly be more than the beginning molar concentration of the acid. Apparently the amount of chloroacetate ion is greater than the equivalent amount of base added. This fact is related to the relatively strong acidity of the acid and to the appreciable ionization of the acid, even before the titration begins. Mathematically, this is taken into account by an equation of electroneutrality, according to which there must be equal numbers of cations and anions in solution.
It is safe to drop the [OH–] in (4) in this case because it is so much smaller than any of the others. [Na+] is obtained from the amount of NaOH added (complete ionization) and the total volume of solution.
Chloroacetate ion can be calculated from (4) and (5) while omitting [OH–] from consideration.
The undissociated acid concentration is the total molar concentration of acid minus [C2H2O2Cl–].
Note that (6) and (7) differ from (1) and (2) only in the inclusion of the [H+] terms.
Now, we may return to the ionization equilibrium for the acid.
The solution to the quadratic equation is [H+] = 2.8 × 10–3, and pH = –log [H+] = 2.55.
The complication treated in this problem occurs whenever, during a partial neutralization, [H+] or [OH–] cannot be neglected in comparison with the concentrations of other ions in solution. This is likely to be the case near the beginning of the titration of an acid which is only moderately weak.
17.41. An acid-base indicator has a Ka of 3.0 × 10–5. The acid form is red and the basic form is blue. (a) By how much must the pH change in order to change from 75% red to 75% blue? (b) For which of the titrations shown in Fig. 17-1a and 17.1b would this indicator be a good choice?
(a)
The change in pH is 5.00 – 4.05 = 0.95 pH units.
(b) The indicator changes color between pH 4 and pH 5 (Fig. 17-1b). With the use of HCl, the pH is falling rapidly in this range; the indicator would be suitable for both of them. In the titration of HCl with NaOH in Fig. 17-1a, the pH is rising rapidly in this range; the indicator can be used. The indicator, however, would not be suitable for the HC4H7O3 titration, which would change from red to blue long before the end point is reached.
Notes:
1. The numerical values tabulated for equilibrium constants differ in various books. The values selected for this book are internally consistent, and the calculated answers are based on values given here. The temperature is assumed to be 25°C, unless there is a specific statement to the contrary.
2. Some of the problems at the end of the sections on Acids and Bases, Hydrolysis, Polyprotic Acids, and Buffers involve multiple equilibria. They may be omitted in a simplest treatment of ionic equilibria.
17.42. A certain reaction is catalyzed by acids. The catalytic activity for 0.1 M solutions of acids in water was found to decrease in the order: HCl, HCOOH, HC2H3O2. The same reaction takes place in anhydrous ammonia, but the three acids all have the same catalytic effect in 0.1 M solutions. Explain.
Ans. The order of catalytic activity in water is the same as the order of acidity. In anhydrous ammonia, a stronger base than water (i.e., a more efficient proton acceptor), all three acids are strong.
17.43. The amino acid glycine exists predominantly in the form +NH3CH2COO–. Write the formulas for (a) the conjugate base and (b) the conjugate acid of glycine.
Ans. (a)NH2CH2COO–; (b) +NH3CH2COOH
17.44. In the reaction of BeF2 with 2F– to form 
, which reactant is the Lewis acid and which is the Lewis base?
Ans. BeF2 is the acid and F– is the base.
17.45. The conjugate acid of nitric acid loses a water molecule in certain solvents. Explain how the resulting entity can still act as an acid in the Lewis sense.
Ans. 
would be the conjugate acid of nitric acid (the result of HNO3 +H+). Then, → H2O + 
(refer below for nitrite)
Nitrogen can go from sp to sp3 hybridization providing an empty orbital for a base pair. (Note similar behavior of CO2 in Problem 17.8.)
17.46. Is acetic acid a weaker or stronger acid in the following solvents as compared to water? (a) hydrazine, N2H4; (b) sulfur dioxide, SO2; (c) methanol, CH3OH; (d) liquid hydrogen cyanide, HCN; (e) liquid sulfuric acid, H2SO4.
Ans. (a) stronger; (b) weaker; (c) weaker; (d) weaker; (e) weaker
17.47. The self-ionization constant for pure formic acid, 
has been estimated as 10–6 at room temperature. What percentage of formic acid molecules in pure formic acid, HCOOH, are converted to formate ion? The density of formic acid is 1.22 g/mL.
Ans. 0.004%
17.48. Calculate the ionization constant of formic acid, HCOOH, which ionizes 4.2% in 0.10 M solution.
Ans. 1.8 × 10–4
17.49. A solution of acetic acid is 1.0% ionized. What must be the molar concentration of acetic acid and the [H+] of the solution? Ka of HC2H3O2 is 1.75 × 10–5.
Ans. 0.17M HC2H3O2, 1.7 × 10–3 M H+
17.50. The ionization constant of ammonia in water is 1.75 × 10–5. Determine (a) the degree of ionization and (b) the [OH–] of a 0.08 M solution of NH3.
Ans. (a) 1.5%; (b) 1.2 × 10–3 M OH–
17.51. Chloroacetic acid, a monoprotic acid, has a Ka of 1.40 × 10–3. Calculate the freezing point of a 0.10 M solution of this acid. Assume that the numerical value of the molar and molal concentrations are the same.
Ans. –0.21°C
17.52. Determine the [OH–] of a 0.0500 M solution of ammonia to which has been added sufficient NH4Cl to make the total equal to 0.100.Kb for ammonia is 1.75 × 10–5.
Ans. 8.8 × 10–6
17.53. Find the value of the [H+] in a liter of solution in which are dissolved 0.080 mol HC2H3O2 and 0.100 mol NaC2H3 O2. Ka for acetic acid is 1.75 × 10–5.
Ans. 1.4 × 10–5
17.54. A 0.025 M solution of monobasic acid had a freezing point of –0.060°C. What are Ka and pKa for the acid? Assume that at this low concentration, molality is equal to molarity.
Ans. 3.0 × 10–3, 2.52
17.55. What is in a solution of 0.0200 M NH3 and 0.0100 M KOH? Kb for NH3 is 1.75 × 10–5.
Ans. 3.5 × 10–5
17.56. What molarity of NH3 provides 1.5 × 10–3 M OH–? Kb for NH3 is 1.75 × 10–5.
Ans. 0.13 M
17.57. What is [HCOO–] in a solution that is both 0.015 M HCOOH and 0.020 M HCl? Ka for HCOOH is 1.8 × 10–4.
Ans. 1.4 × 10–4
17.58. What are 
, and 
in a solution that is 0.030 M HC3H5O3 and 0.100 M HOC6H5? Ka-values for HC3H5O3 and HOC6H5 are 3.1 × 10–5 and 1.05 × 10–10, respectively.
Ans. [H+]= 9.6 × 10–4, 
= 9.6 × 10–4, = 1.1 × 10–8
17.59. Find the value of [OH–] in a solution made by dissolving 0.0050 mol each of ammonia and pyridine in enough water to make 200 mL of solution. Kb for ammonia and pyridine are 1.75 × 10–5 and 1.78 × 10–9, respectively. What are the concentrations of ammonium and pyridinium ions?
Ans. [OH–] = = 6.6 × 10–4, [pyridinium ion] = 6.7 × 10–8
17.60. Consider a solution of a monoprotic weak acid with acidity constant Ka. Calculate the minimum concentration, C, for which the percent ionization is less than 10%.
Ans. C = 90 Ka
17.61. What is the percent ionization of 0.0065 M chloroacetic acid? Ka = 1.40 × 10–3.
Ans. 37%
17.62. What concentration of dichloroacetic acid gives a [H+] of 8.5 × 10–3? Ka = 3.32 × 10–2.
Ans. 1.07 × 10–2M
17.63. Calculate [H+] in a 0.200 M dichloroacetic acid solution that is also 0.100 M sodium dichloroacetate. Ka for dichloroacetic acid is 3.32 × 10–2.
Ans. 0.066 M
17.64. How much solid sodium dichloroacetate should be added to a liter of 0.100M dichloroacetic acid to reduce the hydrogen ion concentration to 0.030 M? Ka for dichloroacetic acid is 3.32 × 10–2. Assume no change in concentration on the addition of the solid.
Ans. 0.047 mol
17.65. Calculate [H+] and [C2HO2Cl–] in solution that is 0.0100 M HCl and 0.0100 M HC2HO2Cl2. Ka for HC2HO2Cl2(dichloroacetic acid) is 3.32 × 10–2.
Ans. 0.0167, 0.0067
17.66. Calculate [H+], , and 
in a solution that is 0.0200 M HC2H3O2 and 0.0100 M HC7H5O2. Ka for HC2H3O2 is 1.75 × 10–5; Ka for HC7H5O2 is 6.46 × 10–5.
Ans. 1.00 × 10–3, 3.5 × 10–4, 6.5 × 10–4
17.67. Liquid ammonia (am) ionizes to a slight extent. The ion product, 
, at –50°C has a Kam of 10–30. How many amide ions, 
, are present per mm3 of pure liquid ammonia?
Ans. 6.0 × 102
17.68. Calculate the molar concentration of ammonium ions in a liter of liquid ammonia at –50°C (see previous problem), in which 10.0 grams each of NH4Cl and sodium amide (NaNH2) were dissolved.
Ans. 1.4 × 10–29 M
17.69. Assuming complete ionization, what are the pH and pOH of the following solutions? (a) 0.00345 N acid; (b) 0.000775 N acid; (c) 0.00868 N base.
Ans. (a) pH = 2.46, pOH = 11.54; (b) 3.11, 10.89; (c) 11.95, 2.05
17.70. Convert the following pH values to [H+] values: (a)4; (b)7; (c) 2.50; (d) 8.26.
Ans. (a)10–4; (b)10–7; (c)3.2 × 10–3; (d)5.5 × 10–9
17.71. The[H+]of an HNO3 solution is 1 × 10–3, and the [H+] of an NaOH solution is 1 × 10–12. What are the molar concentration and pH of each solution?
Ans. 0.001 M HNO3, pH = 3; 0.01 M NaOH, pH = 12
17.72. (a) Calculate [H+] and [OH–] in an 0.0010 M solution of a monobasic acid which is 4.2% ionized. (b) What is the pH of the solution? (c) What are Ka and pKa for the acid?
Ans. (a)[H+] = 4.2 × 10–5, [OH–] = 2.4 × 10–10; (b) pH = 4.38; (c) Ka = 1.8 × 10–6, pKa = 5.74
17.73. (a) Calculate [OH–] and [H+] in a 0.10 N solution of a weak base which is 1.3% ionized. (b) What is the pH of the solution?
Ans. (a)[OH–] = 1.3 × 10–3,[H+] = 7.7 × 10–12;(b) pH = 11.11
17.74. (a) What is the pH of a solution containing 0.010 mol HCl per liter? (b) Calculate the change in pH if 0.020 mol NaC2H3O2 is added to a liter of this solution. Ka of HC2H3O2 is 1.75 × 10–5.
Ans. (a) Initial pH = 2.0; (b) Final pH = 4.76
17.75. The value of Kw at the physiological temperature (normal human body temperature, 37°C) is 2.4 × 10–14. What is the pH of the neutral point of water at this temperature, where there are equal numbers of H+ and OH–?
Ans. 6.81
17.76. Calculate the pH of 1.0 × 10–7 M NaOH. What percentage of the added base was neutralized by the H+ present in the water and what percentage remained to make the solution basic?
Ans. 7.21; 38% was neutralized; 62% remained
17.77. (a) What is the pH of 7.0 × 10–8 M HC2H3O2? (b) What is the concentration of un-ionized acetic acid? Ka is 1.75 × 10–5 (Hint: Assume complete ionization of the acetic acid in solving for [H+].)
Ans. (a) 6.85; (b) 5.6 × 10–10
17.78. Calculate [OH–] in a 0.0100 M C6H5NH2 (aniline). Kb for the basic dissociation is 4.3 × 10–10. What is the [OH–] in a 0.0100 M solution of aniline hydrochloride, which contains the ion 
Ans. 2.1 × 10–6, 2.1 × 10–11
17.79. Calculate the percent hydrolysis in a 0.0100 M solution of KCN. Ka for HCN is 4.93 × 10–10.
Ans. 4.5%
17.80. The basic ionization constant for hydrazine, N2H4, is 9.6 × 10–7. What would be the percent hydrolysis of 0.100 M N2H5Cl, a salt containing the acid ion conjugate to hydrazine base?
Ans. 0.032%
17.81. Calculate the pH of a moderately concentrated solution of pyridinium acetate, (C5H5NH)(C2H3O2). Ka for acetic acid is 1.75 × 10–5 and for pyridinium ion is 5.6 × 10–6.
Ans. 5.00
17.82. A 0.25 M solution of pyridinium chloride, C5H6N+Cl–, was found to have a pH of 2.93. What is Kb for the basic dissociation of pyridine, C5H5N?
Ans. 1.8 × 10–9
17.83. Ka for the acid ionization of Fe3+ to Fe(OH)2+ and H+ is 6.5 × 10–3. What is the maximum pH value which could be used so that at least 95% of the total iron(III) in a dilute solution is in the Fe3+ form?
Ans. 0.91
17.84. A 0.010M solution of PuO2(NO3)2 was found to have a pH of 3.80. What is the hydrolysis constant, Ka, for 
, and what is Kb for PuO2OH+?
Ans. Ka = 2.5 × 10–6, Kb = 4.0 × 10–9
17.85. Calculate the pH of 1.00 × 10–3 M sodium phenolate, NaOC6H5. Ka for HOC6H5 is 1.28 × 10–10.
Ans. 10.39
17.86. Calculate [H+] and [CN–] in 0.0100 M NH4CN. Ka for HCN is 4.93 × 10–10 and Kb for NH3 is 1.75 × 10–5.
Ans. 5.3 × 10–10, 4.8 × 10–3
17.87. Calculate the [H+] of a 0.050 M H2S solution. K1 of H2S is 1.0 × 10–7.
Ans. 7.1 × 10–5
17.88. What is [S2–] in a 0.0500 M H2S solution. K2 of H2S is 1.2 × 10–13.
Ans. 1.2 × 10–13
17.89. What is [S2–] in a solution that is 0.050 M H2S and 0.0100 M HCl? Refer to previous two problems.
Ans. 6.0 × 10–18
17.90. (a) Calculate the [HS–] in the solution in the preceding problem. (b) If sufficient ammonia were added to buffer the solution at pH = 4.37, what would be the concentrations of S2– and HS–?
Ans. (a) 5.0 × 10–7; (b)[S2–] = 3.3 × 10–13, [HS–] = 1.2 × 10–4
17.91. K1 and K2 for oxalic acid, H2C2O4, are 5.9 × 10–2 and 6.4 × 10–5, respectively. What is [OH–] in 0.0050 M Na2C2O4?
Ans. 8.8 × 10–7
17.92. Malonic acid is a dibasic acid having K1 = 1.49 × 10–3 and K2 = 2.03 × 10–6. Calculate the concentration of the divalent malonate ion in (a) 0.0010 M malonic acid, (b) a solution that is 0.00010 M malonic acid and 0.00040 M HCl.
Ans. (a) 2.0 × 10–6; (b) 3.2 × 10–7
17.93. What is the pH of a 0.010 M solution of H3PO4. K1 = 7.52 × 10–3, K2 = 6.23 × 10–8.
Ans. 2.24
17.94. (a) Calculate [H+] in a 0.0060 M H2SO4 solution. The first ionization of H2SO4 is complete and the second ionization has a Ka of 1.20 × 10–2. (b) What is the sulfate concentration in this solution?
Ans. (a)[H+] = 9.4 × 10–3; (b) 
= 3.4 × 10–3
17.95. Ethylenediamine, NH2C2H4NH2, is a base that can add one or two protons. The successive pKb values for the reaction of the neutral base and that of the monovalent (+1) cation with water are 3.288 and 6.436, respectively. In a 0.0100 M solution of ethylenediamine, what are the concentrations of the singly charged cation and of the doubly charged cation?
Ans. 2.03 × 10–3 mol/L, 3.66 × 10–7 mol/L
17.96. Suppose 0.0100 mol NaOH were added to a liter of the solution in the preceding problem. What would the concentrations of singly charged and doubly charged cations be after the addition?
Ans. 5.1 × 10–4M, 1.88 × 10–8M
17.97. Suppose that, instead of 0.0100 mol NaOH, 0.0100 mol HCl had been added to the solution in the previous problem. Calculate the molar concentrations of the singly charged cation, doubly charged cation, and neutral ethylenediamine.
Ans. 0.010; 2.7 × 10–4; 2.7 × 10–4
17.98. The pK1 and pK2 for pyrophosphoric acid are 0.85 and 1.49. Neglecting the third and fourth dissociations of this tetraprotic acid, what would be the concentration of the doubly charged anion in a 0.050 M solution of the acid?
Ans. 1.5 × 10–2M
17.99. What is 
in a 0.00100 M Na2CO3 solution after the hydrolysis reactions have come to equilibrium? K1 and K2 for H2CO3 are 4.30 × 10–7 and 5.61 × 10–11.
Ans. 6.6 × 10–4
17.100. Calculate the pH of 0.050 M NaH2PO4 and of 0.00200 M Na3PO4. K1, K2, and K3 of H3PO4 are 7.52 × 10–3, 6.23 × 10–8, and 4.5 × 10–12.
Ans. 4.7, 11
17.101. Citric acid is a polyprotic acid with pK1, pK2, and pK3 equal to 3.15, 4.77, and 6.39, respectively. Calculate the concentrations of H+, the singly charged anion, the doubly charged anion, and the triply charged anion in 0.0100 M citric acid.
Ans. 2.3 × 10–3M; 2.3 × 10–3 M; 1.7 × 10–5M; 2.9 × 10–9M
17.102. The amino acid glycine, NH2CH2COOH, is basic because of its –NH2 group and acidic because of its –COOH group. By a process equivalent to base dissociation, glycine can gain an additional proton to form+NH3CH2COOH. The resulting cation may be considered to be a diprotic acid, since one proton from the —COOH group and one proton from the positively charged –NH3 group may be lost. The pKa values for these processes are 2.35 and 9.78. In a 0.0100 M solution of neutral glycine, what is the pH and what percent of the glycine is in the cationic form at equilibrium?
Ans. 6.14, 0.016%
17.103. A buffer solution was prepared by dissolving 0.0200 mol propionic acid and 0.0150 mol sodium propionate in enough water to make 1 L of solution. (a) What is the pH of the buffer? (b) What would be the pH change if 1.0 × 10–5 mol HCl were added to 10 mL of the buffer? (c) What would be the pH change if 1.0 × 10–5 mol NaOH were added to 10 mL of the buffer? Ka for propionic acid is 1.34 × 10–5.
Ans. (a) 4.75; (b) –0.05; (c) +0.05
17.104. The base imidazole had a Kb of 1.11 × 10–7.(a) In what amounts should 0.0200 M HCl and 0.0200 M imidazole be mixed to make 100 mL of a buffer at pH 7.00? (b) If the resulting buffer is diluted to 1 L, what is the pH of the dilute buffer?
Ans. (a) 34 mL acid, 66 mL base; (b) 7.00
17.105. In the titration of HCl with NaOH represented in Fig. 17-1 a, calculate the pH after the addition of a total of 20.0, 30.0, and 60.0 mL of NaOH.
Ans. 1.37; 1.60; 11.96
17.106. In the titration of β-hydroxybutytric acid, HC4H7O3, with NaOH (Fig. 17-1a), calculate the pH after the addition of a total of 20.0, 30.0, and 70.0 mL of NaOH. pKa for HC4H7O3 is 4.70.
Ans. 4.52; 4.88; 12.22
17.107. In the titration of NH3 with HCl (Fig. 17-1b), calculate the total volume of the HCl solution needed to bring the pH to 10.00 and to 8.00. Kb for NH3 is 1.75 × 10–5.
Ans. 7.4 mL, 47.3 mL
17.108. Bromcresol green, a dye, has a pKa value of 4.95. For which of the four titrations shown in Fig. 17-1 would bromcresol green be a suitable end-point indicator?
Ans. HCl vs. NaOH, NaOH, vs. HCl, NH3 vs. HCl
17.109. Bromphenol blue is an indicator with a Ka value of 5.84 × 10–5. What percentage of this indicator is in its basic form at a pH of 4.84?
Ans. 80%
17.110. Calculate the pH and [NH3] at the end point in the titration of NH3 with HCl, at the concentrations indicated in Fig. 17-1b. Kb for NH3 is 1.75 × 10–5.
Ans. 5.28, 5.3 × 10–6
17.111. If 0.00200 mol of citric acid is dissolved in 1 L of a solution buffered at pH 5.00 (without changing the volume), what will be the equilibrium concentrations of citric acid, its singly charged anion, the doubly charged anion, and the triply charged anion? Use the pK values from Problem 17.101.
Ans. 5.0 × 10–6M; 3.6 × 10–4M; 6.1 × 10–4M; 2.5 × 10–5 M
17.112. If 0.000500 mol NaHCO3 is added to a large volume of a solution buffered at pH 8.00, how much material will exist in each of the three forms, H2CO3, , and 
? For H2CO3, K1 is 4.30 × 10–7 and K2 is 5.61 × 10–11.
Ans. 1.14 × 10–5mol; 4.86 × 10–4mol; 2.73 × 10–6mol
17.113. A buffer solution of pH 6.71 can be prepared by using solutions of NaH2PO4 and Na2HPO4. If 0.0050 mol NaH2PO4 is weighed out, how much Na2HPO4 must be used to make 1 L of the solution? Take K values from Problem 17.100.
Ans. 0.0016 mol
17.114. How much NaOH must be added to 1 L of 0.010 M H3BO3 to make a buffer solution of pH 10.10? H3BO3 is a monoprotic acid with Ka = 5.8 × 10–10.
Ans. 0.0088 mol.
17.115. A buffer solution was prepared by dissolving 0.050 mol formic acid and 0.060 mol sodium formate in enough water to make 1 L of solution. Ka for formic acid is 1.77 × 10–4.(a) Calculate the pH of the solution. (b) If this solution were to be diluted to ten times its volume, what would be the pH? (c) If the solution in (b) were to be diluted to ten times its volume, what would be the pH?
Ans. (a) 3.83; (b) 3.85; (c) 4.00
17.116. Consider the titration curve of a 0.100 M solution of a weak acid, HA, for which Ka = 2.00 × 10–4, using 0.100 M strong base. Calculate the pH at (a) the beginning (before any base); (b) the half-way point; (c) the end point of the titration.
Ans. (a) 2.35; (b) 3.70; (c) 8.20
17.117. The three points determined in the preceding problem were easy to calculate. They enable one to make a good sketch of the titration curve. Other intermediate values, e.g., 10%, 75%, etc., are also easy to calculate, but it may be more challenging to calculate points very near the beginning and end. Determine the pH in this titration (a) after 1% of the base is added, and (b) after 99% addition.
Ans. (a) 2.41; (b) 5.7
