In this chapter, we deal with two aspects of the connection between chemistry and electricity. The first is electrolysis, the splitting (lysis) of compounds when electricity passes through the solutions involved. The second topic is galvanic cell action, which is the generation of electricity (a flow of electrons) during chemical reaction.
The coulomb (C) is the SI unit of electrical charge. From the point of view of fundamental particles, the elementary unit (Chapter 8) is the charge of one proton (or an electron, which is equal in size, opposite in charge). No chemical particle is known whose charge is not a multiple of this elementary charge, which is 1.602 × 10–19 C.
Electrical current is the rate of flow of a charge. The SI unit is the ampere (A), which is the flow rate of one coulomb per second (1 A = 1 C/s).
The electrical potential difference between two points in a circuit causes the transfer of charge from one point to the other. The volt (V) is the SI unit of electrical potential. When a charge of 1 C moves through a potential of 1 V, it gains 1 J of energy. Summarized:
The watt (W) is the SI unit of power (electrical and others). One watt is developed when 1J of work is performed in 1 s. From (19-1),
Fig. 19-1
In electrochemistry, we are normally concerned with direct current (DC) for reasons mentioned later. However, the above discussion of units applies equally well to alternating current (AC), the type of power normally used in the home and the laboratory.
1. The mass of any substance liberated or deposited at an electrode is proportional to the electrical charge (i.e., the number of coulombs) that has passed through the electrolyte.
2. The masses of different substances liberated or deposited by the same amount of electricity (i.e., the same number of coulombs) are proportional to the equivalent masses (Chapter 12) of the substances.
These laws (determined by Michael Faraday over a half century before the discovery of the electron) can now be shown to be simple consequences of the electrical nature of matter. In any electrolysis, an oxidation must occur at the anode to supply the electrons that leave this electrode. Also, a reduction must occur at the cathode removing electrons coming into the system from an outside source (battery or other DC source). By the principle of continuity of current, electrons must be discharged at the cathode at exactly the same rate at which they are supplied to the anode. By definition of the equivalent mass for oxidation-reduction reactions, the number of equivalents of electrode reaction must be proportional to the amount of charge transported into or out of the electrolytic cell. Further, the number of equivalents is equal to the number of moles of electrons transported in the circuit. The Faraday constant (F) is equal to the charge of one mole of electrons, as shown in this equation:
The symbol Na is Avogadro’s number of electrons and e is the elementary charge, 1.602 × 10–19 C/e–. As has been utilized in previous chapters, n(e–) may be used for moles of electronic charge, the number of equivalents.
The equivalent mass needed for electrolytic calculations can be found by inspecting the balanced half-reaction for the electrode process. For instance, the reduction of Cu2+ is
The equivalent mass of copper is the amount of copper involved with one mole of electrons; there are two moles of electrons required for each mole of copper. Therefore, the equivalent mass of copper is 
the molar mass. Suppose the reaction for the reduction of copper were to be
then the equivalent mass of copper would be one mole. Note that one mole of copper is reduced by one mole of electrons in this case.
Suppose we had these reactions:
In the case of (a), an equivalent mass would be one mole iron (1e–), but an equivalent mass for (b) would be 
mole Fe (3e–).
Many oxidation-reduction reactions may be carried out in such a way as to generate electricity. These cells are known as voltaic (older term: galvanic) cells. In principle, any spontaneous, oxidation-reduction reaction (aqueous) can be set up to generate electricity by the following requirements:
1. The oxidizing and reducing agents are not in physical contact with each other, but are continued in separate compartments (half-cells). Each half-cell contains a solution and a conductor (electrode), which is usually a metal.
2. The reducing or oxidizing agent in a half-cell may be either the electrode itself, a solid substance deposited on the electrode, a gas which bubbles around the electrode, or a solute in solution which bathes the electrode. Just as in electrolysis, the electrode at which reduction occurs is the cathode and that at which oxidation occurs is the anode. (Hint: Oxidation-anode and reduction-cathode are alphabetical.)
3. The solutions of the two half-cells are connected in some way that allows ions to move between them. Among the possible arrangements are (a) careful layering of the less dense solution over the more dense solution; (b) separation of the two solutions by a porous substance, such as unglazed porcelain or a fibrous substance soaked in an electrolyte; or (c) insertion of a connecting electrolyte solution (a salt bridge) between the two solutions.
The potential developed across the two electrodes causes an electrical current to flow and the half-cell reactions to proceed so long as there is a complete circuit and reactants. The flow of electricity must travel essentially in a circle; the e– flow starts somewhere, flows out, and returns to the flow’s origin.
Figure 19-1(a) shows a galvanic cell in which each half-cell consists of a metal in contact with a solution of the ions of the same metal. The direction of the reaction, direction of the current, and the voltage have been arrived at by the methods described in the following sections. There are different structures for half-cells depending on the states of matter of reactants and products. Figure 19-1(b) shows a setup for a hydrogen (gas) half-cell in which the reduced form (H2 gas) is adsorbed onto the surface of platinum. The platinum electrode is inert and serves as a conductor of the electrons involved. Figure 19-1(c) is a half-cell in which the electrode is platinum (inert, but a conductor of electrons), but both the oxidized and reduced forms are in solution.
This chapter deals primarily with reactions in aqueous media, but the principles can be extended to fuel cells and other batteries like the high-temperature batteries with exotic nonaqueous electrolytes.
The reaction occurring in each half-cell may be represented by an ion-electron partial equation of the type described in Chapter 11. The whole-cell operation involves a flow of electrons in an external circuit. The electrons generated in the oxidation half-reaction (oxidation) enter the anode, travel through the external circuit to the cathode, and are taken up by the half-reaction (reduction) that occurs at the cathode. Since the overall charge of a complete set of reactions must be neutral, the number of electrons given off at the anode (oxidation reaction) and those taken up at the cathode (reduction reaction) must be exactly the same number. This is also required of the combining (adding together) of the two half-reactions involved to produce the summation reaction as in Chapter 11. As with the balanced reactions in previous chapters, there will be no electrons written into the summation reaction.
In the half-cell containing the cathode, the oxidation product accumulates while the half-cell is operating. The reducing agent is also located in this half-cell (it is the substance being oxidized). The reducing agent and its oxidation product are known as a couple and are in the same half-cell. Similarly, the other half-cell contains a couple consisting of the oxidizing agent and its reduction product. A particular couple, consisting of both product and reactant of an oxidation-reduction half-reaction, may be the reducing part of the galvanic cell and sometimes the oxidizing part—the role depends on what the other couple is. The (Fe3+/Fe2+) couple, for example, takes on an oxidizing role when paired against the strongly reducing (Zn2+/Zn) couple. On the other hand, (Fe3+|Fe2+) takes a reducing role when paired against the strongly oxidizing (Ce4+|Ce3+) couple. The notation used toward the end of this paragraph, (Fe3+|Fe2+) as an example, has the oxidized form (Fe3+) on the left, a vertical line separating the components of the half-cell, and the reduced form, (Fe2+), on the right.
Each couple has the ability to consume electrons. This ability can be assigned by numerical value, called the electrode potential. The electrode potential is the potential of a half-cell compared to the hydrogen cell (hydrogen standard cell), which is taken to produce 0.000 volts. When two couples are combined into a whole cell, the couple with the higher electrode potential provides the oxidizing agent, absorbs electrons from the external circuit at its electrode, and is positive. The other couple provides the reducing agent, delivers electrons from its electrode to the external circuit, and is negative. The driving force for the flow of current is the algebraic difference between the two potentials. This difference is equal to the voltage output of the cell under standard conditions.
The numerical value of an electrode potential depends on the nature of the particular chemicals, the temperature, and on the concentrations of the various members of the couple. For the purposes of reference, half-cell potentials are taken at the standard states of all chemicals. Standard state is defined as 1 atm pressure of each gas (the difference between 1 bar and 1 atm is insignificant for the purposes of this chapter), the pure substance of each liquid or solid, and 1 molar concentrations for every nongaseous solute appearing in the balanced half-cell reaction. Reference potentials determined with these parameters are called standard electrode potentials and, since they are represented as reduction reactions (Table 19-1), they are more often than not referred to as standard reduction potentials (E°). E° is also used to represent the standard potential, calculated from the standard reduction potentials, for the whole cell. Some values in Table 19-1 may not be in complete agreement with some sources, but are used for the calculations in this book.
Table 19-1 Standard Reduction Potentials at 25°C
A couple with a large positive E°, like (F2|F–), is strongly oxidizing, captures electrons from the electrode, and is experimentally positive with respect to the hydrogen electrode. Conversely, a couple with a large negative E°, like (Li+|Li), is strongly reducing and therefore undergoes oxidation, transferring electrons to the electrode. Such a standard half-cell is negative when compared to a standard hydrogen electrode since the external circuit receives electrons from the half-cell’s electrode.
There is a way of combining two half-cell reactions, in which the electrons do not cancel. This cannot correspond to a whole cell, since its electrons always cancel. The situation to which we refer is a hypothetical one used to calculate an unknown half-cell potential on the basis of two known half-cell potentials. In such a case, the electron number cannot be left out and is algebraically added. As discussed in the next section, if n is the number of electrons in a half-reaction, nE° is proportional to the free energy associated with it. As in Chapter 16, when we add two reactions, we may also add their free energies to get the free energy of the overall (net) reaction. The rule for this case is as follows:
If two reduction half-reactions are added or subtracted to give a third reduction half-reaction, the two nE° products are added or subtracted correspondingly to give the nE° value for the resulting half-reaction.
EXAMPLE 1 Calculate E° for the (Fe3+|Fe) couple using values from Table 19-1.
Since nE° for the resulting half-reaction is –0.11 V, and n is 3, E° must be –0.11/3 = –0.0367 V.
This rule makes it possible to reduce the length of compiled tables, since many half-reactions can be computed, even if they are not tabulated.
The discussion following (16-4) indicated that the decrease in free energy of a system can be equated to the maximum amount of work the system can perform at constant temperature and pressure in forms other than expansive or contractive work. At this point, we can make use of that principle by noting from (19-1) that the electrical work performed by a galvanic cell is equal to the voltage times the electrical charge transferred at either electrode. For the passage of n moles of electrons, the charge transferred is nF. This tells us that the electrical work in joules equals nFE. The maximum amount of work performed by a galvanic cell is the value of nFE under conditions where the electrode processes are reversible. Reversibility may be approximated for many electrodes if the cell potential is measured at very low current; such measurements are the basis of the values using the construction of tables, like Table 19-1. Since the electrical work is the only form of work other than expansive or contractive work performed in the typical galvanic cell, the free-energy principle may be stated as
The dependence of a cell potential on the concentrations of the reactants and products may be derived from the known dependence of G upon concentration, (16-6).
As in Chapter 16, (19-4) uses R = 8.3145 J/K and ΔG is in joules. When all reactants and products are in the standard states, Q = 1 (Chapter 16) and E = E°. Substitution into (19-4) provides the Nernst equation:
When the constants are combined and the natural logarithm converted to a common logarithm, the expression for the potential (in volts) at 25°C becomes
In (19-6), n has been made dimensionless. For a half-reaction, n is the number of electrons in the half-equation; for the whole-cell reaction, n is the number of electrons in one of the multiplied half-equations before canceling the electrons. The Nernst equation is closely related to the laws of chemical equilibrium. Le Chatelier’s principle applies to the potential of a cell in the same sense as it applies to the yield of an equilibrium process. Since Q is a fraction that has product concentrations in the numerator (top) and reactant concentrations in the denominator (bottom), an increased concentration of the product reduces the potential and an increased concentration of reactant raises the potential.
The same type of equation may be used to describe the concentration dependence of the potential of a single half-cell (i.e., the electrode potential). In this case, Q contains terms in the numerator containing the products of the balanced half-cell reaction written as a reduction. The terms in the denominator contain the reactants. Neither the numerator nor the denominator contain electron(s). For example:
Spontaneous oxidation-reduction reactions
If the potential of a whole cell is positive, the free-energy change is negative, according to (19-3). Then, the corresponding oxidation-reduction reaction is spontaneous as written. The galvanic cell would operate spontaneously with electrons provided to the external circuit at the half-cell where oxidation takes place. If the potential is negative, the free-energy is positive, and the corresponding reaction does not take place spontaneously. These statements about the direction of spontaneous reaction are valid whether the reaction is set up as a galvanic cell or as an ordinary process where the reactants and products are all mixed in the same vessel. This is true because the free-energy change for a reaction depends on the concentrations, but not on the way in which the reaction is carried out. In particular, if both reduced and oxidized members of the two couples are mixed (all at standard states), any reducing agent can reduce an oxidizing agent occurring higher in the table of standard electrode potentials. The same rule of relative position may be applied for general values of concentrations, with E for each half-cell, as computed from the Nernst equation, replacing E°. Usually, the qualitative prediction based on E° values is not changed, even for moderate deviations from standard states, if the two E° values are separated by at least several tenths of a volt.
It should be noted that predictions under this rule indicate what reactions might occur, but says nothing about the rate at which they do occur.
Electrode reactions in electrolysis
An oxidation-reduction reaction that is not spontaneous, for which the calculated cell potential is negative, may be induced by electrolysis. This reaction can be due to an external electrical potential to force electrons into the couple undergoing reduction and to extract electrons from the couple undergoing oxidation. The minimum external potential required for electrolysis is the value of the calculated cell potential for the reaction.
Under nearly reversible conditions, the following rule applies:
Of all possible reductions that might occur during electrolysis at a cathode, the one for which the electrode potential is algebraically greatest is the most likely.
Of course, the reverse is also true: the most probable oxidation at the anode is that for which the electrode potential is algebraically the least. In applying the rule, we must keep in mind that (a) a solute molecule or ion may undergo oxidation or reduction; (b) the anode electrode may itself undergo oxidation; (c) the solvent may undergo oxidation or reduction.
EXAMPLE 2 Let us illustrate possibility (c) for water at 25°C.
Reduction of molecular hydrogen is found in Table 19-1:
Assume that H2 gas is allowed to accumulate to a partial pressure of 1 atm. In neutral solutions, where [H+] = 10–7 and the H2 pressure retains its unit value. the calculation is
Water is much more difficult to reduce, but hydrogen is easier to oxidize in neutral solutions than in acids.
For the oxidation of water to molecular oxygen, the most appropriate entry in Table 19-1 is
The standard states to which this E° value refers are 1 atm for oxygen gas and 1 mol/L for H+. We can calculate E for the above half-cell for neutral solutions, in which [H+] = 10–7, by using the Nernst equation. Assuming the oxygen remains at its standard state, P(O2) = 1 atm,
Then, it is harder for oxygen to be reduced, but easier for water to be oxidized, in neutral than in acid solutions.
19.1. A lamp draws a current of 2.0 A. Find the charge in coulombs used by the lamp in 30 s.
19.2. What is the time required to pass 36,000 C through an electroplating bath using a current of 5 A?
19.3. A generator delivers 15 A at 120 V. (a) Calculate the power in kW supplied by the generator. (b) How much electrical energy, in kilowatt-hours, is supplied by the generator in 2 hours? (c) What is the cost of this energy at 6¢ per kilowatt-hour?
(a) 
(b) 
(c) 
19.4. A resistance heater was wound around a 50-g metallic cylinder. A current of 0.65 A was passed through the heater for 24 s while the measured voltage drop across the heater was 5.4 V. The temperature of the cylinder was 22.5°C before the heating period and 29.8°C afterward. On this basis, what is the specific heat of the cylinder metal in J/g · K?
The last equation above is solved and the specific heat = 0.23 J/g · K.
19.5. How many electrons per second pass through a cross section of copper wire carrying 10–16 A?
19.6. Exactly 0.2 mol of electrons are passed through three electrolytic cells in series. One contains silver ion, the next zinc ion, and the last iron(III) ion. Assume that the only cathode reaction in each cell is the reduction of the ion to metal. How many grams of each metal will be deposited?
One mole of electrons deposits 1 eq of an element. Equivalent masses of Ag+, Zn2+, and Fe3+ are
Then, applying the information from the problem and that found directly above:
19.7. A current of 5.00 A flowing for 30 min deposits 3.048 g Zn at the cathode. Calculate the equivalent mass of zinc from this information.
19.8. A certain current liberates 0.504 g of hydrogen in 2 hours. How many grams of oxygen and copper (from Cu2+ solution) can be liberated by the same current during the same time?
Masses of different substances liberated by the same number of coulombs are proportional to their equivalent masses. The equivalent mass of hydrogen is 1.008 g; of oxygen, 8.00 g; of copper, 31.8 g.
Then, 0.500 eq of any element can be liberated under the same conditions.
The equivalent mass of any substance in an electrolysis is determined from the balanced half-reaction. For the liberation of oxygen from water, the anode reaction is
The molar mass of O2 is 32.00. The equivalent mass is the molar mass divided by the number of electrons which must flow to produce one molecule, or 32.00/4 = 8.00.
19.9. The same quantity of electricity that liberated 2.158 g Ag was passed through a solution of a gold salt and 1.314 g Au were deposited. The equivalent mass of silver is 107.9 g. Calculate the equivalent mass of gold and provide the oxidation state of the gold in this salt.
Since 1.314 g Au must represent 0.02000 eq, then
The oxidation state is the number of electrons needed to form one gold atom by reduction.
And, since this is a reduction, the oxidation number of the gold involved is positive, Au3+.
19.10. How long would it take to deposit 100 g Al from an electrolytic cell containing Al2O3 at a current of 125 A?
The equivalent mass of Al from Al3+ and further calculations are
19.11. A current of 15.0 A is used to plate nickel on a surface from a NiSO4 bath. Both Ni and H2 are formed at the cathode. The current efficiency with respect to the formation of Ni is 60%. (a) How many grams of Ni are plated on the cathode per hour? (b) What is the thickness of the plating if the cathode consists of a sheet of metal 4.0 cm square, which is coated on both facts? (Density of Ni is 8.9 g/cm3) (c) What volume of H2 (S.T.P.) is formed per hour?
(b) The calculations are based on the determination of the area of both sides of the metal sheet and the determination of the total volume of the plated Ni.
(c) This part of the problem is similar to previously worked problems. For a bit of variety, we show the use of the faraday, F, a somewhat-out-of date unit which is one mole of electrons.
19.12. How many coulombs must be supplied to a cell for the electrolytic production of 245 g NaClO4 from NaClO3? Because of side reactions, the anode efficiency is only 60% for the reaction.
First, it is necessary to know the equivalent mass of NaClO4 for this reaction. The balanced anode reaction is as follows:
19.13. What is the standard potential of a cell that uses the (Zn2+|Zn) and (Ag+|Ag) couples? Which couple is negative? Write the equation for the cell reaction occurring at standard states.
The standard potentials for (Zn2+|Zn) and (Ag+|Ag) are –0.763 V and 0.799 V from Table 19-1. The standard potential of the cell is the difference between these two numbers, 0.779 V – (–0.763) = 1.542 V. The silver potential is higher, and this means that the silver ion is the oxidizing agent. The zinc couple provides the reducing agent and is the negative electrode. The equation for the cell is
19.14. Can Fe3+ oxidize Br– to Br2 under the circumstances in which Table 19-1 is constructed?
From Table 19-1, which provides the values at 25°C, 1 atm, and standard states, the (Fe3+|Fe2+) couple has a lower standard reduction potential, 0.771 V, than the (Br2|Br–) couple, 1.065 V. Therefore Fe2+ can reduce Br2, but Br– cannot reduce Fe3+. This also means that Fe3+ cannot oxidize Br–.
19.15. What is the standard electrode potential for 
in acid solution? ([H+] = 1.00 M)
The reduction half-reaction for the couple is
The reaction can be written as the difference of two half-reactions whose reduction potentials are listed in Table 19-1. The nE° values can be calculated as standard reduction potentials so long as one is reversed to an oxidation. The reversal of the reaction results in the opposite sign for the potential.
19.16. Predict the stabilities at 25°C of aqueous solutions of the uncomplexed intermediate oxidation states of (a) thallium and (b) copper.
(a) The question is whether the intermediate state, Tl+, spontaneously decomposes into the lower and higher states, Tl and Tl3+. We can take the reaction to be
This reaction could be written in the ion-electron method as
In (1), the (Tl+|Tl) couple functions as the oxidizing agent; in (2), the (Tl3+|Tl+) couples functions as the reducing agent. The reaction would occur at standard concentrations if E° for the reducing couple were to be less than E° for the oxidizing couple. Since the reduction potential of 1.25 V is greater than –0.336 V, the reaction cannot occur as written. We can now conclude that Tl+ does not spontaneously decompose to Tl and Tl3+. Actually, the reverse reaction is the spontaneous reaction: 2Tl + Tl3+ → 3Tl+.
(b) As in (a), we can take the following reaction to incorporate both possibilities:
The ion-electron partial reactions are as follows:
This process could occur if E° for the supposed reducing couple, (Cu2+|Cu+), were to be less than E° for the oxidizing couple, (Cu+|Cu). If we use the method of Problem 19.15, we calculate 0.16 V, which is less than 0.52 V. Therefore, Cu+ is unstable in solution. Compounds of Cu+ can exist only as extremely insoluble substances or as such stable complexes that only a very small concentration of free Cu+ can exist in solution.
19.17. (a) What is the potential of the cell containing the (Zn2+|Zn) and (Cu2+|Cu) couples, if the Zn2+ and Cu2+ concentrations are 0.1 M and 10–9 M, respectively at 25°C? (b) What is ΔG for the reduction of 1 mol of Cu2+ by Zn at the indicated concentrations of the ions, and what is ΔG° for the reaction, both at 25°C?
(a) The cell reaction is Zn + Cu2+ → Zn2+ + Cu, with an n-value of 2.
E°, the standard cell potential, is equal to the difference between the standard electrode potentials.
Q, the concentration function, does not include terms for solid metals, because the metals are in their standard states.
(b) From (19-3)
19.18. By how much is the oxidizing power of the 
couple decreased if the H+ concentration is decreased from 1M to 10–4M at 25°C?
The half-cell reaction for this reduction is
with an n-value of 5 because Mn goes from Mn7+ in Mn
to Mn2+. Assume that only the H+ concentration deviates from 1 mol/L.
The couple has moved down the table 0.38 V from its standard value. This is a position of less oxidizing power.
19.19. In the continued electrolysis of each of the following solutions at pH 7.0 and 25°C, predict the main product at each electrode if there are no (irreversible) electrode polarization effects: (a) 1 M NiSO4 with palladium electrodes; (b) 1 M NiBr2 with inert electrodes; (c)1 M Na2SO4 with Cu electrodes.
(a) Cathode reaction. The following two possible reduction processes may be considered:
By the rule that the most probable cathode process is that for which the corresponding electrode potential is algebraically greatest, the hydrogen couple is favored as a standard cell. Allowing for the effect of the pH 7.0 buffer, however, E for (2) is lowered to –0.41 V, as calculated in Example 2. The reduction of nickel is the favored process at this pH.
Anode reaction. Three possible oxidation processes may be considered, the reverses of the following reduction half-reactions:
The standard potentials are reasonable values to take into consideration with (4) and (5). Although the initial concentration of Pd2+ and S2
are zero, they would increase during prolonged electrolysis if these species were the principal products. In the case of (3), however, the buffering of the solution prevents the buildup of [H+], and it would be more appropriate to take the E-value calculated for pH 7.0 in Example 2, 0.82 V. It is apparent that of the three, (3) has the smallest E-value and the reverse of (3) would occur most readily among the possible anode reactions.
In conclusion, the electrode processes to be expected are:
(b) Cathode reaction. As in (a), Ni reduction would occur.
Anode reaction. The expression “inert electrode” is often used to indicate that we may neglect reaction of the electrode itself. This can be due to the high value of its electrode potential or because of polarization effects related to the preparation of the electrode surface. The remaining possible anode reactions are the reverses of the following:
When the E-value for (3) is calculated as 0.82 V for pH 7.0, as in (a), oxygen evolution takes precedence.
(c) Cathode reaction. The new couple to be considered is the sodium couple, which is
This E-value is much lower algebraically than that of (2), the evolution of H2 at pH 7.0. –0.41 V. Therefore, hydrogen evolution will occur at the cathode.
Anode reaction. In addition to (3) and (5), the reaction of the Cu anode must be considered, the reverse of which is
Process (8) has the lowest E-value, and copper going into solution, the reverse of (8), would take precedence over oxygen evolution.
In this example, the sodium sulfate solution was not at all involved in the reaction, but served as an electrical conductor. Eventually, as Cu2+ builds up and copper migrates to the cathode, reaction (8) will replace reaction (2) as the cathode reaction.
19.20. Knowing that Ksp for AgCl is 1.8 × 10–10, calculate E for a silver-silver chloride electrode immersed in 1M KCl at 25°C.
The electrode process is a special case of the (Ag+|Ag) couple, except that silver in the +1 oxidation state collects as solid AgCl on the electrode itself. Even solid AgCl, however, has some Ag+ in equilibrium with it in solution. This [Ag+] can be calculated from the Ksp equation as follows:
This value for [Ag+] can be inserted into the Nernst equation for the (Ag+|Ag) half-reaction.
19.21. From data in Table 19-1, calculate the overall stability constant, Ks, of [Ag(S2O3)2]3– at 25°C.
There are two entries in the table for couples connecting the zero and +1 states of silver.
Process (1) refers to the couple in which Ag+ is at standard concentrations; the Ag+ concentration to which E° refers is that value which satisfies the complex ion equilibrium when the other species are at standard concentration. The formation reaction for this complex is:
In other words, the standard conditions for couple (2) may be thought of as a nonstandard condition, [Ag+] = 1/Ks, for couple (1). The Nernst equation for (1) gives us
from which
19.22. (a) At equal concentrations of Fe2+ and Fe3+, what must [Ag+] be so that the voltage of the galvanic cell made from the (Ag+|Ag) and (Fe3+|Fe2+) electrodes equals zero? (b) Determine the equilibrium constant at 25°C for the reaction under standard conditions. The reaction for this cell is:
(a) For the reaction as written,
Then, from the Nernst equation (only 1 e– is involved),
Taking the antilog of both sides of the equation, we find that the [Ag+] would be 0.34 M.
(b) To find the equilibrium constant, we must combine the relationship between K and ΔG°, (16-8), with the relationship between ΔG° and E° obtained from (19-3), ΔG° = –nFE°.
Note that the same combination of constants (of value 0.0592 at 25°C) occurs here as in the Nernst equation.
Part (a) above could have been solved alternatively by using the equilibrium constant, noting that [Fe2+] = [Fe3+] and solving for [Ag+]:
The two methods must be equivalent because the voltage of a galvanic cell becomes zero when the two couples are at equilibrium with each other.
19.23. An excess of liquid mercury was added to an acidified 1.00 × 10–3 M Fe3+ solution. It was found that only 5.4% of the iron remained as Fe3+ at equilibrium at 25°C. Calculate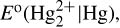 
assuming
The first step is to calculate the equilibrium constant for the reaction. At equilibrium,
Liquid mercury is in excess and is in its standard state (included in the K expression).
The standard potential of the cell may be calculated from the relationship found in Problem 19.22(b).
For the reaction as written,
or
19.24. How many coulombs per hour pass through an electroplating bath using a current of 5 A?
Ans. 1.8 × 104 C/h
19.25. Calculate the cost at $0.05 per kilowatt-hour of operating an electric motor using 15 A at 110 V for 8hours.
Ans. $0.66
19.26. A tank containing 0.2m3 of water was used as a constant-temperature bath. How long would it take to heat the bath from 20°C to 25°C with a 250-W immersion heater? Assume no heat loss.
Ans. 4.6h
19.27. The specific heat of a liquid was measured by placing 100 g of the liquid in a calorimeter. The liquid was heated by an electrical immersion coil. The heat capacity of the calorimeter and coil was previously determined as 31.4 J/K. With the 100-g sample in place, a current of 0.500 A was passed through the coil for 3 min. The voltage across the terminals of the coil was measured to be 1.50 V. The temperature of the sample rose 0.800°C. Find the specific heat of the liquid.
Ans. 1.37 kJ/kg · K
19.28. The heat of solution of NH4NO3 in water was determined by measuring the amount of electrical work needed to compensate for the cooling which would otherwise occur when the salt dissolves. After the NH4NO3 was added to water, electrical energy was provided by passage of a current through a resistance coil until the temperature of the solution reached the value it had before the addition of the salt. In a typical experiment, 4.4g NH4NO3 were added to 200 g H2O. A current of 0.75 A was provided through the heater coil and the voltage was 6.0 V. The current was applied for 5.2 minutes. Calculate ΔH for the solution of 1 mol NH4NO3 in enough water to give the same concentration as was attained in the above experiment.
Ans. 25.5 kJ
Note: Unless indicated otherwise, the efficiency is 100% for all electrodes.
19.29. What current is required to pass 1 mol of electrons per hour through an electroplating cell? How many grams of aluminum will be liberated by 1 mol of electrons? How many moles of Cd/mol e–?
Ans. 26.8 A; 8.99 g Al; 56.2 g Cd
19.30. What mass of aluminum is deposited by 40 A in 30 minutes?
Ans. 6.7 g Al
19.31. How many amperes are required to deposit 5.00 g Au/h from a solution of a Au3+ salt?
Ans. 2.04 A
19.32. How many hours will it take to produce 100 lb of electrolytic chorine from NaCl in a cell that carries 1000 A? The anode efficiency for the chlorine half-reaction is 85%.
Ans. 40.4 h
19.33. A quantity of electricity passes through two separate electrolytic cells; one contains a solution of AgNO3 and the other contains a solution of SnCl2. If 2.00 g Ag are deposited in one cell, how many grams Sn are deposited in the other cell?
Ans. 1.10 g Sn
19.34. An electrolytic cell contains a solution of CuSO4 and an anode of impure copper. How many kilograms of copper will be refined (deposited on the cathode) by 150 A over 12.0 h? The copper deposited on the cathode comes from the solution; however, that copper deposited is replaced from the anode. This is a technique of separating the copper from the impurities in the anode (refining).
Ans. 2.13 kg Cu
19.35. A fuel cell designed for a spaceship is powered by the overall reaction:
2H2 + O2 → 2H2O
The cell delivers a steady current of 10.0 A and is fed H2 gas from a 3.5 ft3 tank at 2000 psi and 31 °C. How long will the cell run? (psi = lb/in2 from Problem 1.9)
Ans. 1.04 × 107 seconds (121 days)
19.36. Hydrogen peroxide, H2O2, can be prepared by the successive reactions below:
The first reaction is an electrolytic reaction; the second is a steam distillation. What current would have to be used in the first reaction to produce enough (NH4)2S2O8 to yield 100 g of pure H2O2 per hour from the second reaction? Assume 50% anode current efficiency.
Ans. 315 A
19.37. A lead-acid battery, as used in cars, uses the following reaction at the anode:
Suppose that this is a 75 ampere-hours battery, meaning that the battery will put out 1 amp for 75 hours (or 75 amps for 1 hour). What is the mass of lead that would be used up during a complete discharge of the battery?
Ans. 290 g Pb
19.38. The reaction presented in this problem is that of the anode and the cathode added together. Suppose we are still interested in a 75 ampere-hour battery, what mass of lead and lead(IV) oxide must be used in the construction of the battery?
Ans. 290 g Pb and 335 g PbO2
19.39. An important measure of the efficiency of a battery is the energy density, the amount of energy delivered divided by the mass of reactants consumed. For comparison purposes, calculate the energy density of (a) the 2.00 V (approximate) lead storage battery that discharges by the following reaction:
Pb + PbO2 + 2H2SO4 → 2PbSO4 + 2H2O
(b) and calculate the energy density of a 1.30 V (approximate) NiCad battery, which discharges by
Cd + 2NiOOH + 2H2O → Cd(OH)2 + 2Ni(OH)2
Note that these calculations do not take into account such practical factors as the cost of the chemicals required, fraction of reactants not utilized, or nonreactive structural materials. These factors and others add to the cost of the batteries.
Ans. (a) 601 kJ/kg; (b) 756 kJ/kg
19.40. Engineers interested in developing low-weight batteries have turned to the Group IA elements Li and Na, both of which, in addition to their low equivalent mass, have a very negative reduction potential. (Because the electrolytes are not aqueous, the battery voltages cannot be calculated accurately from tabulations such as Table 19-1. The voltages given below are very rough estimates.) Calculate the energy densities of (a) the approximately 3.00 V lithium-titanium(IV) sulfide battery, and (b) the approximately 2.60 V sodium-sulfur battery. The discharge reactions are
Ans. (a) 2.43 × 103 kJ/kg; (b) 4.56 × 103 kJ/kg
19.41. Predict the principal product at each electrode in the continued electrolysis at 25°C of each of the following: (a) 1 M Fe2(SO4)3 with inert electrodes in 0.10 M H2SO4; (b) 1 M LiCl with silver electrodes; (c) 1 M FeSO4 with inert electrodes at pH 7.0; (d) molten NaF with inert electrodes.
Ans. (a) Fe2+ and O2; (b) H2 and AgCl; (c) H2 and Fe3+; (d) Na and F2
19.42. A voltaic cell was operated under almost ideally reversible conditions at a current of 10–16 A. (a) At this current, how long would it take to deliver 1 mol e–? (b) How many electrons would be delivered by the cell to a pulsed measuring circuit in 10 ms?
Ans. (a) 3 × 1013 years; (b) 6e–
19.43. The quantity of antimony in a solution can be determined by converting it to the +3 oxidation state and titrating with standard iodine in bicarbonate solution:
In a variation of this method, particularly useful when dealing with very small samples, excess iodide ion is added to the solution and the requisite iodine is generated by electrolysis:
Determine the mass of antimony in a solution which required a steady current of 23.2 milliamperes for 182 s to reach the end point in the above “coulometric” titration.
Ans. 2.66 mg Sb
All problems refer to 25° C.
19.44. (a) What is the standard potential of a cell made up of (Cd2+|Cd) and (Cu2+|Cu) couples? (b) Which couple is positive?
Ans. (a) 0.74 V; (b) (Cu2+1 Cu)
19.45. What is the standard potential of a cell containing the (Sn2+|Sn) and (Br2|Br–) couples?
Ans. 1.20V
19.46. Why are Co3+ salts unstable in water?
Ans. Co3+ can oxidize H2O, the principal products being Co2+ and O2.
19.47. If H2O2 is mixed with Fe2+, which reaction is more likely: the oxidation of Fe2+ to Fe3+ or the reduction of Fe2+ to Fe? In answering, write the reaction for each possibility and calculate the standard potential of the equivalent electrochemical cell.
Ans. More likely: H2O2 + 2H+ + 2Fe2+ → 2H2O + 2Fe3+; E° = 0.99 V
Less likely: H2O2 + Fe2+ → Fe + O2 + 2H+. The reverse of this reaction occurs with a standard potential of 1.14 V.
19.48. What substance can be used to oxidize fluorides to fluorine?
Ans. Fluorides may be oxidized during electrolysis, but not chemically by any substance listed in Table 19-1.
19.49. Are Fe2+ solutions stable in air? Why can such solutions be preserved by the presence of iron nails?
Ans. They are not stable because the O2 oxidizes Fe2+ to Fe3+, but the Fe in the nails reduces Fe3+ to Fe2+.
19.50. What is the standard potential of the (Tl3+|Tl) electrode?
Ans. 0.72V
19.51. Which of the following intermediate oxidation states is stable with respect to the possible oxidation reactions of the elements in oxygen-free noncomplexing media: germanium(II), tin(II)?
Ans. tin(II)
19.52. Would H2O2 behave as oxidant or reductant with respect to each of the following couples at standard concentrations: (a)(I2|I–); (b) 
(c) (Fe3+|Fe2+)?
Ans. (a) oxidant; (b) reductant; (c) both; in fact, very small amounts of iron salts in either +2 or +3 oxidation states catalyze the self-oxidation-reduction of H2O2.
19.53. What is the potential of a cell containing two hydrogen electrodes, the negative one in contact with 10–8 MH+ and the positive one in contact with 0.025 M H+?
Ans. 0.379 V
19.54. The cell in the preceding problem is, in a sense, a pH meter. Suppose one half-cell contained 1.00 M H+, the standard state. Describe the relationship (at 25°C) between the pH of the other half-cell and the observed voltage (connecting the positive terminal of the meter to the standard half-cell).
Ans. V = 0.0592pH units
19.55. A voltmeter can replace the traditional indicator in titrations by making the titration vessel a half-cell (with an appropriate electrode) and connecting it to a reference half-cell via a salt bridge. To follow the titration in Problem 18-57, a silver/silver chloride electrode is inserted into the halide solution, and the reference half-cell is a silver/silver chloride electrode immersed in 1.00 M KCl. The reference electrode goes to the positive terminal of the voltmeter. Calculate the voltage reading at each of the five points in the titration specified in Problem 18.56.
Ans. (a) 0.179 V; (b) –0.101 V; (c) –0.195V; (d) –0.288V; (e) –0.399V
19.56. The burning of methanol could be the basis of a convenient fuel cell. The anode reaction is
The cathode reaction is the same as in the successful hydrogen-oxygen fuel cell:
Calculate the voltage of this fuel cell (for the standard states). (Hint: Use data from Table 16-1.)
Ans. E° = 1.213 V
19.57. (a) Calculate the potential of the (Ag+|Ag) couple with respect to (Cu2+|Cu) if the concentration of Ag+ and Cu2+ are 4.2 × 10–6 and 3.2 × 10–3 M, respectively. (b) What is the value of ΔG for the reduction of 1 mol Cu2+ by Ag at the indicated ion concentration?
Ans. (a) 0.23 V; (b) –44kJ
19.58. Copper can reduce zinc ions if the resultant copper ions can be kept at a sufficiently low concentration by the formation of an insoluble salt. What is the maximum concentration of Cu2+ in solution if this reaction is to occur (assume 1 M Zn2+)?
Ans. 7 × 10–38M Cu2+
19.59. Evaluate the equilibrium constant for the following reaction at 298 K:
Ans. 0.5
19.60. When a rod of metallic lead was added to a 0.0100 M solution of [Co(en)3]3+, it was found that 68% of the cobalt complex was reduced to [Co(en)3]2+ by the lead. Find the value of K at 298 K for
Ans. 0.0154
19.61. A (Tl+|Tl) couple was prepared by saturating 0.1 M KBr with TlBr and allowing the Tl+ from the relative insoluble bromide to come to equilibrium. This couple was observed to have a potential of –0.443 V with respect to a (Pb2+|Pb) couple in which the Pb2+ was 0.1 molar. What is the solubility product of TlBr?
Ans. 3.7 × 10–6
19.62. Kd for the complete dissociation of [Ag(NH3)2]+ into Ag+ and NH3 is 6.0 × 10–8. Calculate E° for the following half-reaction (refer to Table 19-1):
Ans. 0.372 V
19.63. Calculate Kd for the formation of [PdI4]2– from Pd2+ and I–.
Ans. 1 × 1025
19.64. Reference tables give the following entry:
Combining this information with relevant entries in Table 19-1, find K1 for the acid dissociation of H2O2.
Ans. 1 × 10–12