
Fig. 1-0: Earth from space. (Courtesy of NASA; image created by Reto Stöckli, Nazmi El Saleous, and Marit Jentoft-Nilsen, NASA GSFC)
At the moments when we are able to separate ourselves from our daily concerns and ponder deeply, most of us have encountered fundamental questions of our existence as human beings. Where do we come from? What happened before humans appeared on Earth? Where do the stars come from? Do we have a place in planetary evolution? Are there others like us out there somewhere?
These questions are common to all of us, irrespective of national origin or political persuasion. They are the stuff of myths, creation stories, philosophy, and religion throughout human history. Today major aspects of these questions are susceptible to rigorous scientific inquiry. In this book we explore these questions, the scientific story of creation, the history of the universe that has permitted planetary takeover by an intelligent civilization.
The story begins with the inception of our universe by the Big Bang, through the formation of the elements in stars, to the formation of our solar system, the evolution of our world that became home to life and ultimately to human beings who can question and begin to understand the universal processes from which we are derived. Viewed on the largest scale, this story is the central story of our existence. It relates us to the beginning, to all of natural history, and to everything we can observe. While this book has a primary aim to present some of the current scientific knowledge on these topics, a secondary aim is to encourage a mode of thinking that is often latent for us—how we are derived from and related to a larger world.
The approach to this understanding of the world we inhabit and to which we are inextricably linked requires a range of scales that is difficult for us to encompass, from the atomic to the universal. The story also cannot be told by reduction to its smallest parts. Relationships among the parts and evolution through time also are necessary, a “systems” approach to scientific understanding. From a systems perspective, stars, planets, and life have a set of properties in common that appear to be characteristics of many of the “natural systems” of which the universe is made.
The origin and evolution of our inhabited world is both a single subject and a topic of enormous diversity. It is “natural science” in the sense the term was used hundreds of years ago—the understanding of nature—but with a vastly greater panorama of scientific fields and data. The fields include the fundamental sciences of physics, chemistry, and biology, and also the integrative and historical sciences of astronomy and earth science. Most subjects broached in this book could each occupy an entire term of study, so the task is daunting for all of us.
Our aim is to explore Earth’s history in detail as an example of a habitable planet, and from that history try to deduce the likelihood of similar histories occurring elsewhere. Within this story there are large numbers of exciting scientific developments and outstanding questions. And the story is the grandest that can be told, the scientific creation story of the universe whose evolution has led to us, human beings who are able to question and investigate the origin of our existence and the universal laws that led to us and surround us.
One of the challenges we face is that the range of scales we will need to encompass is almost unfathomable, from the minute atoms of which we and our planet are made, to the grander scales of solar system and universe of which we are a minuscule part. The smallest scales pertain to how atoms are formed and how molecules combine. The smallest scale of concern to us is the size of the hydrogen nucleus—a starting point for all atoms—which is 0.000000000000001 meters (m) in size. Dealing with very small (or very large) numbers is obviously cumbersome, so we will use exponential notation and abbreviations (Table 1-1). The hydrogen nucleus has a diameter of 10–15 m. At vastly larger scales, stellar distances are measured in light years—the distance light travels in a year. Since the speed of light is 3 × 108 m/sec multiplied by the ~3 × 107 seconds in a year, a light year is 9 × 1015 meters. The nearest star is 3 light years away, our galaxy the Milky Way is 100,000 light years across, and the universe is estimated to be billions of light years in diameter, or ~1026 m. Hence, our task encompasses 1026m /10–15m, or 41 orders of magnitude in terms of distance!
Table 1-1
Exponential units and names

Similar large magnitudes exist for time. As we will discover in Chapter 2, the age of the universe is roughly 14 billion years (14 Ga), or 4.2 × 1017 seconds. The time of the atomic reactions that are involved in the creation of matter can be nanoseconds (10–9 seconds). Our range of time encompasses 26 orders of magnitude.
The challenge of working with these huge ranges of time and space is that our experience as human beings is so limited. The same size of figure on a page (Fig. 1-1) can be used to portray vastly different scales. We might tell the story of the evolution of the universe taking place over billions of years with the flavor of a story about our summer vacation—without recognizing the difference in scale between the story of everything and that of our small life. The journey through the story of the universe will make much more sense if we remain mindful at each moment of the scale of the phenomena we are investigating.
Fig. 1-1: Two subjects considered in this book, galaxies and atoms. In this figure they take up about the same space on the page but differ in actual size by more than 25 orders of magnitude. (a) Spiral galaxy NGC 1309 (http://hubblesite.org; NASA, ESA, the Hubble Heritage Team [STScI/AURA], and A. Riess [STScI]); (b) Schematic portrayal of the carbon atom. Carbon has the symbol C, atomic number 6, and mass 12. The size of the nucleus is greatly expanded in order to make it visible.
Our approach in this book is to try to relate the smallest of parts to the largest of systems. This may appear to contrast with the traditional scientific approach of so-called reductionism. Much scientific understanding has come about by discovering governing mathematical equations, or laws, that account for diverse phenomena. In this approach, understanding comes from our ability to “reduce” the whole to the fundamental laws of physics from which all phenomena arise. Then phenomena calculated at the most fundamental level can, at least in theory, explain and predict the whole.
The great scientific revolution of the seventeenth century exemplifies the power of the reductionist approach. Newton’s mathematical expression of gravity was able to account for Kepler’s laws describing the motion of the planets around the sun and the careful measurements of falling objects carried out by Galileo. The big idea stemming from Newton’s successes was that fundamental physical laws, described by mathematical equations, can explain everything we see. Today we are probably only partially able to conceive of the wonder of these results when they first appeared—everything we observe, from the tiny scale of a rolling marble to the movements of celestial objects, governed by mathematical law discernible by the mind of man. As Alexander Pope wrote of Newton’s discoveries:
Nature and Nature’s laws lay hid in night: God said, Let Newton be! and all was light.
Emerging from these startling successes came the idea of the “clockwork universe,” where everything is explained by physical law rather than divine intervention. Once the laws are understood, everything can be accurately described and predicted through calculation. This is often understood as the fundamental scientific approach.
An aspect of this approach is the belief that understanding complex phenomena comes from breaking them down to their simplest parts. If we wish to accurately describe a crystal or a gas, the behavior of individual atoms provides the ultimate answer, and if we wish to understand the behavior of individual atoms, we must understand subatomic particles and quantum theory, and ultimately the strings of string theory. Understanding then comes from isolation of variables, improvement of the resolution and precision of observation, and discoveries of fundamental laws from which calculations are theoretically possible from first principles.
In this way, phenomena that appear to be miraculous become explained. Any human being prior to the scientific revolution, if they were to hear an amplified sound system or view images on a television screen, might believe they were in the presence of a miracle (or more likely the presence of the devil). But once the machine is taken apart and all the components are understood, the actions of physical laws appear. Understanding the operation of some of the electronic components would require reduction and observation to microscopic levels, ultimately down to the fundamental particles that make up the atoms involved. The same approach applies to the processes of life. The “miracle” of medications derives from understanding the processes of the body and the action of the drug on the molecular scale. The apparent miracle of evolution can be reduced to individual mutations of DNA molecules. Many of the topics of this book reflect the efficacy of this approach. Understanding how laws that operate at small scales manifest on much larger scales is one of the great triumphs of the scientific method.
Despite its obvious successes, however, reductionism falls short when we try to calculate or understand many natural phenomena. From the practical point of view, very few natural phenomena can actually be calculated from first principles. Let’s take a simple example of calculating the atmospheric pressure at some point on the surface of Earth, say at the top of your head as you read this book. This is a straightforward, one-dimensional problem that involves simply summing the weight of the atmospheric column directly above you. We can measure pressure very precisely indeed—what would it take to calculate it as well as we can measure it?
To calculate it, we would need to know the density of the atmosphere at each point along the column. Thermodynamics helps with the general pressure-temperature-volume relations, but quantitative thermodynamic calculations apply best to closed systems, and the air over your head is in movement. The density of air also depends on the concentration of water vapor, which can vary both laterally and vertically. Winds are a response to pressure gradients, so pressure changes continually owing to movements and forces exterior to your personal atmospheric column. We could take an average temperature profile for this time of year, and assume a clear sky with constant relative humidity and no wind, but that gives an approximate pressure, nowhere near as precise as what we can measure. We could send a probe up through the atmosphere and measure the temperature and water vapor, but that is a bit like simply measuring the pressure, and by the time we got the data and processed it, the atmosphere could have undergone small changes from time of day and weather, leading to small errors.
This simple example illustrates the fundamental point that natural systems at any moment can never be specified completely. They are open systems without clear boundaries. Energy and material continually flow in and out; physical and chemical properties are not constant and homogeneous. For the gases of the atmosphere, the water of the ocean, the rocks of Earth’s mantle, the liquid metal of Earth’s outer core, or the plasma of the sun’s interior, pressure and temperature change in space and time, mass and energy are constantly flowing in and out of the system, and we cannot make enough measurements to define accurately the state of the system on any but approximate scales, or as a long-term or broadly spaced average.
This state of affairs influences our ability to calculate and predict. Every calculation requires specification of initial conditions. Calculation of the weather tomorrow starts from our knowledge of the weather today. Initial conditions for real systems can never be measured simultaneously everywhere. Predictions become difficult for the immediate future, and progressively more uncertain for more distant times. This is particularly true for systems that contain “feedback,” where movement in one direction causes a countervailing movement. This common characteristic of the real world often even leads to chaos.
Nowhere is the uncertainty of prediction more evident than chaotic systems. Chaos occurs in common equations where the outcome is so sensitive to the tiniest of changes in initial conditions or constants in the equations that long-term prediction is impossible. A simple illustration of this point comes from a time series generated by a “feedback” equation where the initial value of x is permitted to vary between 0 and 1. Subsequent values of x are then calculated with the following equation:

A is a constant. To construct the time series, the equation is used repeatedly with the output from one step used as the input for the next step, i.e., xn+1 = F(xn). Whenever x is large, the Ax term gets larger, but the (1 – x) term gets smaller, and vice versa. This is a negative feedback, where an increase in one term causes a decrease in the other. Negative feedbacks are very important in many natural processes. If A = 3 and we start with a value of x = 0.5, then F(x) = 0.75. For the next step, x = 0.75 and F(x) = 0.5625 and so on. This can easily be set up on a spreadsheet or a simple computer program to calculate what happens after large numbers of steps—a recommended exercise for the reader.
Equation (1-1) is an inverted parabola (see Fig. 1-2), and we can track the evolution of the time series as a path from one point on the parabola to the next. Figure 1-3a illustrates what happens to a time series for moderate values of A. When A = 2, the system proceeds rapidly to a steady-state value of 0.5, while for A = 2.8 the steady-state value is near 0.64. The steady state values for a particular value of A are independent of the initial value of x. The time series begins to exhibit more interesting behavior once A exceeds values of 3.0. For values of 3.2, for example (Fig. 1-3b) the time series proceeds to an oscillation between two states, also independent of the initial value of x. For A = 3.9, no such regularity appears in the result—no matter how many the number of steps.
Fig. 1-2: Illustration of the behavior of time series controlled by the simple function generated by Ax(1 – x) for different values of A. Both illustrated time series begin with the same starting value for x, xo = 0.2. For A = 2, the time series (squares) marches along the curve to a constant value. For A = 3.9, the time series (dots) is chaotic and never reaches a fixed value.
To have a more comprehensive view of the behavior of this simple function, Figure 1-4 plots on the vertical axis the range of values of x obtained after a large number of steps, for different values of A plotted along the horizontal axis. For values of A less than 3, the time series arrives at a steady state value, independent of the starting value of x. Up to values of A less than (~3.45) the time series oscillates between two values. At values of A slightly above this number there are four stable oscillating states, and the number of stable states increases up to values of A of about 3.57, above which chaos begins. Then values vary over large ranges in almost random fashion between an upward and lower bound. Steady-state values reappear for A = 3.83, and then chaos reappears up to values of 4. For the chaotic states, the most minuscule change in the value of A leads to a completely different series of results, such that the state of the system at future time cannot be predicted.
Fig. 1-3: Progression of values for a time series using Equation 1-1 for different values of A and two different starting values for x, x0= 0.2 and x0= 0.9; (a) for A=2.8, independent of starting value, the time series reaches a common value of F(x) = 0.64; (b) for A = 3.2, the time series reaches a steady state where it oscillates between two values; (c) for A=3.9 no steady state is reached, and the value after a fixed number of steps is very sensitive to even very small changes in the initial input value.
Fig. 1-4: Illustration of how the time series generated by Ax(1 – x) varies with different values of A. For A less than three, a constant steady state is obtained independent of initial conditions. Then there are two states, then four. At values of A greater than about 3.6, there is chaotic behavior. Within the chaos, there are limited regions where steady-state values again are obtained (blown up for clarity in the lower panel). The figures show the range of states reached after time series of >100 steps.
Table 1-2
Demonstration of chaos
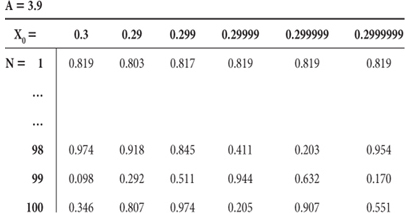
Output values of x for A = 3.9 after iterations (H) of Equation 1-1 for values of X0 near 0.3. After the first iteration, the values are all very similar to three decimal places (they differ at more significant figures). But after 98–100 steps the results are chaotic, and do not converge on the calculation for X0 = .3 as X0 gets closer and closer to 0.3 starting from 0.29. Similar chaos would result from infinitesimal changes in the value of A.
In the chaotic regime, the result after a fixed number of steps also varies with minuscule changes in initial conditions—i.e., the initial value of x—and these changes are nonintuitive. Table 1-2 illustrates the result after 100 steps of the time series for A = 3.9. No matter how precisely the initial value is specified, while the first step is the same, the final value after a sufficient number of steps can vary across the entire range. “Extreme sensitivity to initial conditions” is the hallmark of chaotic systems and has been described by the so-called butterfly effect, where the beating of a butterfly’s wings in China could lead eventually to a hurricane in the Atlantic.
The weather is a familiar example of a chaotic system. There are upper and lower bounds of temperature that characterize the seasons, and prediction is quite good for periods of hours. But last night’s weather forecast in Boston predicted rain with one inch of snow accumulation overnight. Today the skies are gray, but no precipitation has fallen. What will the weather be two weeks from now? It will still be the same season, but accurate weather prediction is not possible. To the extent that natural systems are chaotic, their behavior cannot be calculated precisely, even if the governing equations are known exactly.
Another characteristic of natural systems is self-similarity, or their tendency to exhibit fractal behavior. A geometric object that is fractal looks exactly the same when it is examined over a very large range of scales. For fractal systems you cannot tell the size of an object without a scale bar. Great canyons can extend over thousands of kilometers, but the topography of a single streambed or a rivulet on a mud flat can have very similar ratios of width to depth and the same sinuosity (Fig. 1-5). Benoit Mandelbrot illustrated this concept beautifully in a paper entitled “How Long Is the Coast of Britain?” The coastline looks similarly irregular at small scales and large scales. And the length of the coastline depends entirely on the size of ruler used to measure it—the smaller the ruler, the longer the coastline. For example, if you can measure the distance around every pebble the coastline becomes very long indeed! There is no single answer to the question of length unless the ruler size is specified. Donald Turcotte has demonstrated the huge number of natural processes that exhibit fractal behavior.
Of course, these various challenges do not mean that scientific understanding is not possible. Great discoveries lie in the determination of fundamental laws and equations. Nor are the calculations useless. Even with Equation (1-1), increased precision of initial conditions means that more extended prediction is possible—the first few steps in the time series are increasingly well established. And even for long-time series there are upper and lower bounds that are not exceeded.
There is nonetheless a practical and philosophical dilemma for reductionism. In principle, everything can be reduced to the smallest phenomena from which everything else derives. In practice, even a straightforward phenomenon such as water flowing out of a garden hose cannot be predicted quantitatively from first principles. There is a gap between our practical experience of nature and the pure laws governing phenomena. The laws remain true and nature cannot defy them; but the gap can never, even theoretically, be filled.
Fig. 1-5: Examples of dendritic drainage patterns. Zooming in on one small part of it gives similar pattern rules to the whole image. Simply from looking at the image, it is not possible to tell the scale because the pattern exists over a large range of scale. Can you find which image is a blowup from the other? (Copyright © 1995–2008 Calvin J. Hamilton and courtesy of NASA; http://www.solarviews.com/huge/earth/yemen.jpg)
On a more human level of what we perceive as understanding, reductionism also falls short. A cell is much more than a collection of reactions among chemicals. It has functions that cannot be inferred or understood from the atomic scale. It has a history, is descended from ancestors going back in time to the origin of life, and relates to its surroundings in ways that must be observed to be understood. It has a relationship both to the underlying molecular scale and the next larger scale (e.g., the organism) of which it is a part. Properties apparent from a larger scale often cannot be inferred from the individual parts of the smaller scale. An understanding of any natural phenomenon requires knowledge of its constituent parts and their relationship to each other, and to the larger world of which the phenomenon is a part.
Including relationship in the understanding of phenomena has come to be called systems thinking. This approach recognizes the necessity of accurately describing both the reduced components and the relationships among them. To put it simply, reductionism assumes that the whole can be reduced to the sum of the parts. Systems thinking asserts that the whole is greater than the sum of the parts, and that there are “emergent properties” that arise from the whole that could never be understood or predicted from a reductionist approach. The most obvious example is any living organism. For an individual cell, its DNA might be very precisely defined, but its living manifestation requires complex feedbacks and relationships on a variety of scales in an inevitably open system. Systems biology, for example, stems from the recognition that individual biological components such as DNA or RNA can only be fully understood through their relationship to the larger scales—organelles, cells, organs, and so on. This concept expands to larger scales. An animal can never be fully understood from even highly precise understanding of the properties of the individual cells. The relationships among the cells that make it up and its relationship to the larger ecosystem in which it lives must be included. An ecosystem can never be understood from isolated consideration of the individual plants and animals, and also exists in the context of various planetary conditions such as soils, elevation, and climate. The universe would not be able to be fully understood from a detailed understanding of individual galaxies.
Another important aspect of all these examples is that they are in movement. “Relationship” includes transport of matter and energy. Understanding of a cell, an organism, an ecosystem, or a planet is not fully revealed by a snapshot. Observation in action is necessary.
To illustrate these principles we can consider a simple object like a mechanical watch. If we spread the parts out on the table in front of us, there is much we can learn from investigating the gears, the nature of the spring, and so on. We can investigate the detailed chemical make-up of the pieces and even their atomic structure. However, seeing all these pieces separately, even understanding them down to the level of individual atoms, would not allow us to predict what functions they all served. Once the watch was put together a new understanding would emerge—we could see how all the parts relate to one another, the driving mechanism of the spring, the meshing of the gears, the place of the watch face. Only once the watch is put in motion, however, does the mechanism become clear—with a new appreciation for the details and complexity of the parts, and the appreciation of precise timekeeping. Still, however, the watch remains an isolated mechanical object, with no relationship to a larger world. When it is on someone’s wrist, and used to monitor and guide the movements of the person’s day, its function becomes still more evident, and we are forced to deal with the big idea of time. We might then also consider the history of watchmaking and time, and how the measure of time, represented by the watch, has related to the detailed development of human civilization.
This simple example illustrates some of the basic principles that apply to systems:
• The full significance of the watch could never be predicted (without advance knowledge) from the description of the parts, and particularly not from their description on an atomic scale.
• Understanding the relationships among the parts creates an entirely different phenomenon than the parts themselves.
• A fuller understanding is not possible without observing the watch in movement, and realizing that without movement it has no function.
• The function of the watch is still not evident until it is understood in its relationship to the larger system represented by the human being.
• There is evolution over time in this larger relationship that relates to development of a still larger system.
Looking from the largest scale down, the precise mechanisms of the watch can be understood and placed in an appropriate context. That is, vision downward in scale can show how the smallest scales relate to the largest. From the smallest scale, vision upward is very limited. The spring in the watch, for example, knows what it is connected to and that it moves back and forth—the full dimensions of the watch described above are not perceptible.
You will notice that there is no figure illustrating a system. Why not? Because systems involve relationship, cycles, feedbacks, and movement. They cannot be adequately represented by a static figure on a page.
While systems thinking has very broad applicability, our concern relates to the natural systems of the world around us. Observation of these systems suggests a suite of shared characteristics.
The drive toward equilibrium, a minimum energy state where there is no further tendency to change, is one of the fundamental principles of chemistry and physics. Falling objects come to rest at the lowest energy state; chemical reactions proceed to completion where no further reaction occurs. While this driving force is manifest everywhere, natural systems, even when they are at steady state, are usually far from equilibrium. At equilibrium, properties such as temperature and pressure are constant throughout the system, and the system is isolated from external influences. That is not the natural world! One of the benefits of laboratory experiences is that when we actually try to measure properties at equilibrium, it becomes evident that controlling the conditions for such perfection to appear is very difficult indeed. Natural systems are not isolated. Matter flows in and out; properties such as temperature and pressure change continuously. Natural phenomena do not exist in static equilibrium states, but are in movement at all scales.
Instead, a characteristic of most natural systems is disequilibrium. Often this condition reflects a balance of forces and fluxes that leads to a steady-state disequilibrium where the natural system remains within narrow bounds, perched at a disequilibrium state. All living organisms reflect this state, for example. Our body temperatures are maintained within a narrow range irrespective of the temperature of our surroundings, sustained by the food and air we take in and various feedbacks that maintain the temperature. Most of the molecules that make up life are out of equilibrium with oxygen and decay rapidly once they are no longer metabolically sustained. Earth’s atmosphere is in a disequilibrium state, its temperature sustained by the continuous influx of solar energy and the warming effects of greenhouse gases coming from Earth’s interior and modulated by life. The sun is not at equilibrium, but reflects a balance between gravitational forces leading to contraction, and expansion forces coming from heating of its interior by nuclear fusion. Energy flows continuously outward. The forces toward equilibrium are acting everywhere, but the state is one of disequilibrium.
Another characteristic of systems is that they can become increasingly complex and organized with time. This characteristic also appears contradictory from the point of view of equilibrium. Part of the force toward equilibrium is the inevitability of increased entropy, or randomness, or the decay of order. Two separate gases mix to homogeneity, temperature differences become homogenous, or potential energy is released to minimum energy states. How then can a relatively stable state far from equilibrium be maintained, with order preserved or increasing? Why doesn’t the system simply move to its minimum energy, equilibrium state and rest there?
Equilibrium applies to isolated systems that move toward and then maintain a minimum energy state. To be maintained far from equilibrium, an external source of energy is necessary. The sun is maintained by the energy provided by nuclear fusion. Earth receives energy from the sun and also from decay of radioactive elements. Life on Earth is sustained by the sun. Absent the external energy, all of these would decay to a static equilibrium state. It is the external energy source that also permits evolution to increasing order within the system. In the largest context, disorder increases.
Despite being out of equilibrium, natural states often occupy a narrow range of states that can persist despite significant changes in external conditions. How can such states be maintained?
There are various mechanisms that permit stability despite variations in energy input. For example, when we boil the water, the water is maintained at a steady-state temperature different from its surroundings by an external heat source. What makes the temperature difference with the room possible? The external energy source. And then what keeps the temperature of the water constant? Why doesn’t its temperature rise to be the same as the flame that heats it?
When water boils, the liquid is converted into gas. This requires a great deal of energy—the energy of vaporization. While to heat one gram of water by one degree takes one calorie, to convert that gram of water to gas takes 539 calories. Once water begins to boil, any additional energy that is added does not raise the temperature but just converts the liquid water to gaseous steam. If we plot temperature vs. time as we add energy to the water, we get the plot shown in Figure 1-6. Note that there is a long stretch of time where the temperature is constant. If we reduce the heat input, the water boils more slowly; if we increase the heat, the water boils more quickly, absorbing all the additional energy being added. Hence the boiling water responds to changes in heat input in a way that maintains the constant temperature in the pot—a steady state despite changes in the energy source or external environment. Many more complex chemical phenomena also have such properties.
Fig. 1-6: The temperature of water subjected to external heat over a period of time. The water initially heats up rapidly, but once it reaches the boiling point, the temperature remains constant until all the water has turned to steam.
Feedback occurs when the system is maintained at steady state because the response “feeds back” to control the input. Another example from the kitchen is the oven’s thermostat. Once it is set to a particular temperature, the heat source goes on when the temperature is below the set point, and turns off once the temperature is above it. The external energy source permits the oven to be far from equilibrium with the kitchen; the mechanism of the thermostat provides the feedback that maintains the temperature within a narrow range.
The thermostat is an example of negative feedback. The negative feedback maintains the system at steady state. Increased input triggers a response that counteracts or turns off the input. This principle of negative feedback is an essential component of natural systems.
There also can be positive feedbacks, where the response becomes amplified rather than damped. The oven has a positive feedback when a small spark of electrical current trips a switch that releases a large gas supply. An important natural example of positive feedback occurs in the climate system. Carbon dioxide is a greenhouse gas, but it is at low concentrations that absent emissions from humans would be about 300 parts per million (ppm) in the atmosphere. Increases in CO2 increase the temperature of the atmosphere a little bit, causing more water vapor to be created. Water vapor is also a greenhouse gas, and there is lots of water vapor in the atmosphere. Because there is so much water, there is a much greater warming effect than would be caused by the CO2 alone. Therefore, the water amplifies the temperature increase. The same process works in the opposite direction—lowering CO2 lowers temperature slightly, which reduces water vapor, which lowers temperature much more. Positive feedback amplifies small changes.
Fig. 1-7: Illustration of feedback influencing Earth’s climate stability. Increases in CO2 (e.g., from volcanic eruptions) lead to a small temperature increase, which causes increased water in the atmosphere. Water is also a greenhouse gas and causes temperature to increase further. This is a positive feedback—higher temperatures cause still higher temperatures. The increased temperature then enhances weathering, which adds Ca to the ocean causing removal of CO2 through precipitation of CaCO3 (limestone). This is a negative feedback—higher temperatures lower CO2, which lowers temperatures. The negative feedback in this system occurs on long timescales.
Both positive and negative feedbacks are important in natural systems (Fig. 1-7). Positive feedbacks cause rapid response and sensitivity to small changes; negative feedbacks provide balance and stability. Both are important factors in maintaining steady-state disequilibrium, and natural systems often have complex interplays between positive and negative feedbacks, which can make them very difficult to model accurately. Increased water vapor, for example, while increasing the greenhouse effect also leads to more cloud cover, which is a negative feedback because clouds reflect sunlight back into space. Therefore, climate models will be very sensitive to the assumptions made about the relative importance of the positive and negative feedback associated with water vapor.
Chemical cycles are also a requirement for long-term stability far from equilibrium. Cycling in itself implies lack of equilibrium, because at equilibrium there is no movement and a static state, while in systems there is circulation in continual movement. For systems to have longevity, they must be able to persist over long periods of time. To persist over time and maintain a steady-state disequilibrium, materials cannot be exhausted, and hence natural systems must recycle.
Many parts of the Earth system illustrate this recycling. Rocks are formed, eroded, deposited as sediments, heated, melted, and erupted to form again (Fig. 1-8). On geological timescales, rocks are continually in movement. Water goes through the rock cycle, and it also has a cycle on a much shorter timescale (Fig. 1-9). If the ocean only evaporated, then it would rapidly diminish in size and increase in salinity, and the “waste product” of water vapor would have to be stored somewhere. There would be no steady state and no longevity. Instead, the water vapor turns into rain that flows back into the ocean, eroding the continents in the process. The ocean is maintained in volume and salinity, and the eroding power of the water contributes to the recycling of continental crust and the maintenance of continental volume and elevation in steady state. The various parts of the Earth system—rock, water, atmosphere—are all involved in interrelated cycles where matter is continually in motion and is used and reused in the various planetary processes. Without interlocked cycles and recycling, Earth could not function as a system.
This discussion leads to a list of shared characteristics of natural systems:
• Natural systems are invariably in movement.
• They are sustained by an external energy source and energy flow through the system.
• Matter cycles through the system, providing sustainability through recycling.
• The system is maintained over a narrow range of states, but these states are normally “steady-state disequilibrium.”
• Feedbacks operate to sustain steady-state conditions
• The system is nested within a larger scale and relates to or contains within it systems at a smaller scale.
• There is change with time—creation, long-term evolution, and eventual death.
Fig. 1-8: Illustration of the rock cycle during the operation of plate tectonics. New igneous rocks are generated by melting of the mantle at ocean ridges and by volcanism at convergent margins. Erosion and sediment transport lead to the depositions of sediments. The sediments and igneous rocks are both metamorphosed as they are subjected to the higher temperatures and pressures of Earth’s interior. If the metamorphism gets hot enough, melting begins and new igneous rocks are generated. Metamorphism can also lead to release of fluids that can trigger melting. The circular diagram in the lower right illustrates the rock cycle in more schematic and general terms. The rock cycle operates on timescales of millions of years.
Fig. 1-9: Illustration of the water cycle. Evapotranspiration and rain operate on very short time scales (weather). The groundwater portion of the cycle has longer timescales, >1000 yrs.
This set of characteristics applies to a range of scales—cells, animals, ecosystems, planets, stars, and so on. Let us consider how Earth fits these characteristics:
• In the last fifty or so years we have come to recognize the movements in all Earth’s layers, including the plates at the surface, the mantle, and the core as well as the atmosphere and ocean.
• Earth has two important external energy sources: the sun and the “battery power” of radioactivity stored in Earth since its formation. This energy flows continuously between the various components of the Earth system.
• All of Earth’s reservoirs have chemical cycles where matter is added to, circulates through, and is removed from the various reservoirs. Earth recycles—elements are cycled through the parts of the system and reused.
• Earth has maintained a narrow range of states throughout most of its history. The temperature range of the atmosphere/ocean system has been above the freezing point and well below the boiling point of water for billions of years, maintaining conditions suitable for life. The tectonic plates have moved over the surface for a similar period of time, and for all of Earth’s history that we have access to there have been continents as well as oceans, suggesting only modest changes in sea level.
• Each Earth reservoir is sustained by feedbacks.
• Earth is dependent on the larger-scale solar system, and contains within it smaller-scale natural systems (e.g., the ocean, ecosystems).
• Earth had a beginning at the dawn of the solar system, and evidence for evolution and change abounds. As our energy sources have changed, there has been evolution in the behavior of the solid earth, and striking evolution in the complexity of life and its relationship to ocean, atmosphere, and crust. Ultimately, as the energy sources from the sun and radioactivity decay, Earth will die.
James Lovelock has postulated that the steady-state disequilibrium that is characteristic of Earth’s surface makes it a “living organism,” for which he has suggested the name Gaia. This suggestion has raised some controversy, because there are obviously discrepancies between biological life and Gaia—Darwinian evolution and reproduction being the most obvious. What Earth and life do have in common is the shared characteristics of natural systems. These shared characteristics are not limited to the organic envelope of the Earth that Lovelock called Gaia. The Earth system includes the movements of the plates of the solid earth as well as the interior all the way down to the inner core. Therefore, if one asks of natural systems the general question, “On what principles does the system work?” then Earth and life work in similar ways. They both have the shared characteristics of natural systems. One might ask the question whether the universe taken as a whole operates with the same characteristics, out of equilibrium, powered by the Big Bang, with cycles of chemicals and energy in a long-term evolutionary process. From this perspective, then, there is a commonality extending from microcosmic to macrocosmic scales. Systems appear to be the way the universe works.
A diversity of scales and approaches is necessary to approach an understanding of the development of a habitable planet. The largest scale is that of the universe, billions of light years in size and more than 10 billion years of time. The smallest scale we will deal with is the construction of atoms from neutrons and protons, 41 orders of magnitude smaller where reactions happen in nanoseconds.
A reductionist approach to science implies that understanding and causality can be determined by reduction to the smallest scales. We need this approach to understand many of the materials and processes of stars, Earth, and life. Despite its explanatory power, reductionism is incomplete. For such calculations, initial conditions need to be specified and boundaries defined. For natural systems such as planets, initial conditions can never be specified completely and boundaries are open. Furthermore, many equations that describe natural processes exhibit chaotic behavior that prevents accurate calculation over long time periods.
Natural systems such as stars, Earth, and life have properties that are not revealed by an exclusively reductionist approach. They have states that are out of equilibrium and that are maintained at steady state by a balance of forces and continuous movement of matter and energy through the system. Systems thinking states that the properties of the whole cannot be inferred from the properties of the parts. Relationships among the parts and their evolution in time are essential. Most natural systems are also nested, containing within them systems of a smaller scale and being a part of systems at a larger scale. From a systems approach, Earth and life share many common characteristics, the characteristics of natural systems. Understanding of such systems requires knowledge of the constituent parts, the energy that drives the system, the cycles and feedbacks that relate the parts, the nested systems at larger and smaller scales, and the inevitable evolution over time that tells the story of our inhabited world. These are our tasks in the remaining chapters.
Fritjof Capra. 1997. The Web of Life. New York: Anchor Books.
James Gleick. 1998. Chaos. New York: Penguin Books.
James Lovelock. 1995. The Ages of Gaia. New York: W. W. Norton & Co.
Benoit Mandelbrot. 1982. The Fractal Geometry of Nature. New York: W. H. Freeman & Co.