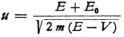20. Schrödinger to Lorentz
Zürich
6 June 1926
My dear Professor Lorentz,
You have rendered me the extraordinary honor of subjecting the train of thought in my latest papers to a profound analysis and criticism on eleven closely written pages. I cannot find words with which to thank you sufficiently for this precious gift that you have thereby made to me; I am deeply distressed that I have made such excessive demands on your time in this way. My thanks consist of—continuing these demands; but at least only for reading, and you have even given me permission to inform you about my attitude to the exceptionally interesting and important new viewpoints which your letter opens up. Please allow me to do this without directly answering the individual suggestions and doubts point by point; it is hardly likely that you still remember or have a copy of these in order. Also, much that I should like to say refers to several places in your letter.
1. You mention the difficulty of projecting the waves in q-space, when there are more than three coordinates, into ordinary three dimensional space and of interpreting them physically there. I have been very sensitive to this difficulty for a long time but believe that I have now overcome it. I believe, (and I have worked it out at the end of the third article), that the physical meaning belongs not to the quantity itself but rather to a quadratic function of it. There I chose the real part of 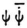 , where ψ is taken to be complex in the obvious way (for criticism, see below) and the bar denotes the complex conjugate. Now I want to choose more simply
, where ψ is taken to be complex in the obvious way (for criticism, see below) and the bar denotes the complex conjugate. Now I want to choose more simply 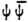 , that is, the square of the absolute value of the quantity ψ. If we now have to deal with N particles, then
, that is, the square of the absolute value of the quantity ψ. If we now have to deal with N particles, then 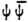 (just as ψ itself) is a function of 3N variables or, as I want to say, of N three dimensional spaces, R1,R2, …, RN. Now first let R1 be identified with the real space and integrate
(just as ψ itself) is a function of 3N variables or, as I want to say, of N three dimensional spaces, R1,R2, …, RN. Now first let R1 be identified with the real space and integrate 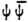 over R2, …,RN; second, identify R2 with the real space and integrate over R1,R3, …,RN; and so on. The N individual results are to be added after they have been multiplied by certain constants which characterize the particles, (their charges, according to the former theory). I consider the result to be the electric charge density in real space. In this manner one obtains for an atom with many electrons exactly what Born-Heisenberg-Jordan designate as the transition probability, with the new and plausible meaning “component of the electric moment”, (strictly speaking that partial moment which oscillates with the emission frequency in question).
over R2, …,RN; second, identify R2 with the real space and integrate over R1,R3, …,RN; and so on. The N individual results are to be added after they have been multiplied by certain constants which characterize the particles, (their charges, according to the former theory). I consider the result to be the electric charge density in real space. In this manner one obtains for an atom with many electrons exactly what Born-Heisenberg-Jordan designate as the transition probability, with the new and plausible meaning “component of the electric moment”, (strictly speaking that partial moment which oscillates with the emission frequency in question).
What is unpleasant here, and indeed directly to be objected to, is the use of complex numbers. ψ is surely fundamentally a real function and therefore in Eq. (35) of my third paper
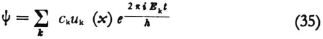
I should be good and write a cosine instead of the exponential, and ask myself: is it possible in addition to define the imaginary part unambiguously without reference to the whole behavior of the quantity in time, but rather referring only to the real quantity itself and its time and space derivatives at the point in question. This actually can be done, at least for ψ. I write the “wave equation” for the sake of brevity in the form

where L[] means a certain differential operator. Furthermore let ψr be the real wave function, the only one known originally, therefore the real part of ψ whose imaginary part is to be defined in addition. That can be done this way:
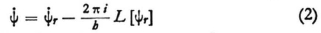
By this method, therefore, the magnitude of 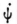 is in any case represented by the space and time derivatives of the real quantity ψr, independent of the complex representation; so that one does not get into difficulty even if there is a ψr that does not correspond to a stationary super-position of proper oscillations. Now to be sure one has only
is in any case represented by the space and time derivatives of the real quantity ψr, independent of the complex representation; so that one does not get into difficulty even if there is a ψr that does not correspond to a stationary super-position of proper oscillations. Now to be sure one has only 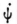 and integration with respect to time would involve an undetermined additive purely imaginary function of the coordinates. I do not know yet whether this can be fixed in a rational way. Probably there is nothing that prevents us in practice from replacing ψ by
and integration with respect to time would involve an undetermined additive purely imaginary function of the coordinates. I do not know yet whether this can be fixed in a rational way. Probably there is nothing that prevents us in practice from replacing ψ by 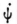 throughout the argument cited first, since all eigenvalues are really almost equally large because of the large additive constant that they contain, and of which you also speak. If this constant is fixed to be mc2` (or an integer multiple of it), which is practically inevitable, then the differences in the eigenvalues become very small compared to the eigenvalues themselves, of the order of the relativistic correction.
throughout the argument cited first, since all eigenvalues are really almost equally large because of the large additive constant that they contain, and of which you also speak. If this constant is fixed to be mc2` (or an integer multiple of it), which is practically inevitable, then the differences in the eigenvalues become very small compared to the eigenvalues themselves, of the order of the relativistic correction.
2. You often touch on the point that the “wave equation” (1) is still not the fundamental equation of the problem, because it no longer contains any time derivatives but has instead the integration constant E. Also the equation does not hold in general but only for such solutions u that depend on time through the factor { }21. But the latter is equivalent to
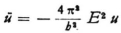
One can eliminate E between (1) and (2)22 and one obtains
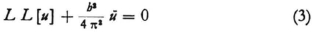
This might well be the general wave equation which no longer contains the integration constant E but contains time derivatives instead. It is of completely the same type as the equation for a vibrating plate (which contains the repeated Laplacian operator), and no longer of the simple type of the vibrating membrane. It took me a terribly long time to discover this simple fact. Of course one can now go backwards again from equation (3) by trying the form
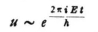
and trying to split (3) according to the pattern
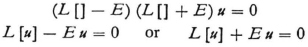
as in the case of the vibrating plate. That one obtains all solutions this way has to be proved afterwards by investigation of the completeness of the system of functions that is found. (Naturally it makes no difference that two equations with different signs for E result, because E is an undetermined constant, still to be determined; one does not therefore obtain any new solutions in addition.)
3. Allow me to send you, in an enclosure, a copy of a short note in which something is carried through for the simple case of the oscillator which is also an urgent requirement for all more complicated cases, where however it encounters great computational difficulties. (It would be nicest if it could be carried through in general, but for the present that is hopeless.) It is a question of really establishing the wave groups (or wave packets) which mediate the transition to macroscopic mechanics when one goes to large quantum numbers. You see from the text of the note, which was written before I received your letter, how much I too was concerned about the “staying together” of these wave packets. I am very fortunate that now I can at least point to a simple example where, contrary to all reasonable conjectures, it still proves right.
I hope that this is so, in any event for all those cases where ordinary mechanics speaks of quasi-periodic motions. Let us accept this as secured or conceded for once; there still always remains the difficulty of the completely free electron in a complete field-free space. Would you consider it a very weighty objection against the theory if it were to turn out that the electron is incapable of existing in a completely field-free space? Or perhaps even that “free” electrons do not permanently keep their identities at all in the usual sense? That speaking of individual electrons in a bundle of cathode rays perhaps means only that the bundle has a certain “granular” structure, in just the same way that many phenomena have made this seem plausible for a bundle of light rays, where in both cases neither a pure wave description nor a pure particle description exactly reaches the truth, but rather something in between that we have not yet adequately achieved.
4. I should like to add a few more remarks to the considerations in the enclosed note, the most important of which seems to me to be this: one should not set the individual proper oscillations of the wave theory in parallel with the individual stationary orbits of the Bohr theory. For if one does that the transition from micromechanics to macromechanics by means of the correspondence principle is absolutely impossible. One can even see how for large quantum number (A >> 1) the individual Bohr orbits are built up by a superposition of very many proper oscillations which are relatively closely adjacent to one another. It would be possible for imposed couplings between the amplitudes and phases of adjacent proper oscillations to persist, perhaps in such a way that one obtains all possible states of the oscillator, while one allows the quantity A to assume all possible positive values, (the whole aggregate then must still be thought of as multiplied by 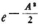 so that the integral
so that the integral 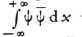 will be independent of A.) In the limiting case of very small A one obtains at first only the fundamental oscillation; with increasing A the higher oscillations are gradually excited and the center of gravity gradually shifts to higher and higher quantum numbers.
will be independent of A.) In the limiting case of very small A one obtains at first only the fundamental oscillation; with increasing A the higher oscillations are gradually excited and the center of gravity gradually shifts to higher and higher quantum numbers.
But for the present these are just chimeras; it could be completely different. In no case do I consider it correct to speak of the energy of the individual proper oscillation, measured perhaps by the square of its amplitude. In my view the latter has nothing to do with energy but rather with charge. The only property of the individual proper oscillation that has anything to do with energy is its frequency, I believe.
The question naturally arises: but why must I supply a quite definite amount of energy to the atom in order just to excite a definite proper oscillation? Now “supply a definite amount of energy” really means here either “bombard with electrons of definite velocity” or “irradiate with light of definite frequency”. As far as the latter is concerned you will know better than I that a physicist of the old days would have opened wide his eyes and his mouth if someone had said to him: to irradiate with light of definite frequency “means” to supply a definite amount of energy. He would have looked for a very much more obvious explanation in resonance. The basis for the statement just made, which would be so hard to understand for the physicist of the old days, can be seen in the fact that light of a definite frequency is always capable of producing the same physical effects as electrons of a definite velocity. From the fact of this equivalence the opposite conclusion can, however, be drawn with the same inevitability, or lack of inevitability: the electron moving with a definite velocity must be a wave phenomenon whose frequency is that of the fight which is experimentally equivalent to it with regard to the excitation of resonance. I consider one conclusion to be as one-sided as the other, the truth lying somewhere in the middle.
5. You discuss the question of the explanation of radiation by means of beats or by means of difference tones in a very penetrating way that is also very instructive for me. I must frankly admit that up to now I have not made enough of a conceptual distinction between these two things. I was so extremely happy, first of all, to have arrived at a picture in which at least something or other really takes place with that frequency which we observe in the emitted light that, with the rushing breath of a hunted fugitive, I fell upon this something in the form in which it immediately offered itself, namely as the amplitudes periodically rising and falling with the beat frequency. By this I only meant: there is a conceivable mechanism by means of which these rising and falling amplitudes can excite light of equal frequency. The frequency discrepancy in the Bohr model, on the other hand, seems to me, (and has indeed seemed to me since 1914), to be something so monstrous, that I should like to characterize the excitation of light in this way as really almost inconceivable. Between the alternatives of beats or difference tones, however, I obviously declare myself for the latter. That of course only means that it is not at all necessary for everything to happen strictly linearly; otherwise the most beautiful beat frequency remains eternally ineffectual.
6. I am surprised that at one point in your letter you take strong offense at what you describe in the words “the radiation is considered to be something of secondary importance, as something that depends on terms in the fundamental equations that one even neglects in first approximation (in deriving the wave equation)”. In case I understand you correctly I must declare that I would consider the opposite to be a serious stumbling block if it were to be proposed.
And that would be because I believe that the significance of the radiation terms for atomic dynamics is grasped correctly, so far as orders of magnitude are concerned, by the older theories, and indeed it was not the Bohr theory that did this first, but rather the electron theory. The radiation terms play a thoroughly secondary role in both theories. The main force exerted by the self field on the electron in the theory of electrons is the inertial force. The radiation force appears first as the second term in a series expansion and is really always very small compared to the inertial force in the typical electronic motions that occur. In the Bohr model too the radiation reaction force is completely disregarded first of all, and the whole model is built up without it. It does not come in until afterwards and then through two things: first through the assumption of a lack of sharpness of the levels (determined just by the classical radiation force), and second, through the “electron jumps”. The latter, to be sure, can no longer be compared directly to anything else with respect to order of magnitude because of their bizarre discontinuity. But since the frequency with which the jumps occur is still calculated from the radiation force by using the correspondence principle, it can be seen that it is to be put on the same level as the latter so far as order of magnitude is concerned. I am therefore quite satisfied that the wave mechanics seems to be in agreement with the older theories on this point insofar as the reaction of the radiation on the radiating system is insignificant enough so that it can be neglected to the first approximation in setting up its “equation of motion.”
Through your discussion I have become absolutely certain that the addition of these terms must necessarily put an end to the linear character of the equations of motion, and I consider this an exceptionally important piece of knowledge.
7. From the wave equation itself and from the assumption about the group velocity you again derive in reverse the expression in Eq. (6) of my second paper for the wave velocity, from which I started:
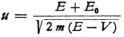
The constant E0 is formally absent from my equations, yet I emphasized (p. 10 of that paper) that E and V individually are obviously determined only up to an additive constant. I took particular pleasure in calling special attention (at that very place) to the circumstance that the wave length is independent of this constant, just because the wave length determines the order of magnitude of the orbital dimensions at which quantum phenomena begin to appear.
Then, at a place later on, you emphasize that, just because of this unalterably fixed wave length, the dimensions of the electron are certainly of at least the same order of magnitude as the Bohr elliptic orbits of low quantum number, and that it is in no way possible to construct wave packets which revolve in these orbits and are small compared to the dimensions of the orbit. I do not know whether I am correct in reading an “unfortunately” between the lines. But I believe that the enclosed note shows you that, in any event, I never cherished this wish for the orbits of low quantum number. In my view these states are something that differs toto genere from electron orbits; not until the high quantum numbers does classical mechanics gradually assume its rights again, just as the diffraction image of a slit is gradually transformed into its shadow image if you slowly pull the sides of the slit apart.
8. In conclusion may I emphasize several serious difficulties of a fundamental nature in the matrix mechanics, (without any connection with your letter), which have gradually become clear to me and in which I see an advantage in the wave mechanics, quite apart from its intuitive clarity.
Most important of these is the symmetrization of the Hamiltonian function. I have spoken about this in considerable detail on page 14 of my third article. But what I had not clearly recognized yet at that time was and is that the rules set up for this purpose by Born, Jordan and Heisenberg are actually false if one applies them to generalized coordinates; they are correct only in Cartesian coordinates. That has turned out simply empirically in the calculations of Dirac and Pauli; that symmetrization is then chosen which leads to something reasonable. Heisenberg, in a summarizing article in the Mathematische Annalen23, has therefore decided to lay down the rule that the Hamiltonian must be taken over from the classical theory in Cartesian coordinates. In doing so he does not, however, explicitly retract the abovementioned strictly false generalization to arbitrary coordinates (given earlier in a paper with Born and Jordan in the Zeitschrift für Physik.) Furthermore there are still situations left that are completely undetermined, such as the symmetric or the asymmetric top, since here returning to Cartesian coordinates is not only cumbersome but even impossible so long as it has not been decided how “rigid connections” are to be interpreted in the new mechanics.
Wave mechanics, on the other hand, is directly applicable to arbitrary coordinates and allows the energy levels to be calculated without even having to know the connection between the general coordinates and Cartesian coordinates.
A second point is that wave mechanics always yields completely determined eigenvalues, apart perhaps from one additive constant (which is of no consequence in the energy differences). In matrix mechanics this seems to be very difficult at least, and I am not sure if at times there are not still some things that are indefinite in principle. Dirac (Proc. Roy. Soc.)24 and Wentzel (Zeitschrift fur Physik)25 calculate for pages and pages on the hydrogen atom, (Wentzel relativistically, too), and finally the only thing missing in the end result is just what one is really interested in, namely, whether the quantization is in “half integers” or “integers”!* Thus, Wentzel does indeed find “exactly the Sommerfeld fine structure formula” but for the reasons mentioned the result is completely worthless for comparison with experiment. The relativistic treatment by means of wave mechanics, which is just as simple, results unambiguously in half integral azimuthal and radial quanta, just like the classical treatment. (I did not publish the calculation at the time because this result just showed me that something was still missing; that something is certainly Goudsmit and Uhlenbeck’s idea.) As a side remark, Wentzel’s procedure is so constituted that if he were to push through to the result, his result would probably be false,* * because he takes the problem as two dimensional rather than three dimensional. That is not permited, as I stressed in my second article, p. 32, and, because of the complete mathematical equivalence of wave mechanics and the Göttingen mechanics, it is also certainly not permitted in the latter. Wave mechanics also allows one to perceive clearly the reason for this, because a wave motion in two dimensions is obviously something completely different from a wave motion in three dimensions. In the Göttingen mechanics on the other hand one cannot really understand, so far as I can see, why the reduction of the problem by the use of an integral should be forbidden. At least the reason is not very evident or else it would not be generally used.
I am afraid, Professor Lorentz, that I have taken up a great deal of your time again with this long letter. But your criticism of my attempt—kind, penetrating, and yet, despite all your misgivings, well-meaning—allows me to hope that one or another of the ideas that you induced will be of interest to you. I am quite convinced that I have not been able to dispel all your misgivings; to tell the truth, I have more than enough of them myself, and in all these considerations I perceive no more than the first pale glimmerings of what I hope is the dawn of a more profound understanding.
I must also thank you very much for something else, and that is the charming picture with which you rewarded all those who demonstrated their respect for you (on the occasion of your festival day26) by what was, at least in my case, unfortunately a purely symbolic action. The delightful picture will always be a beautiful reminder of the days of unalloyed pleasure that I was allowed to spend under your guidance in Brussels two years ago.27
I beg you always to be assured of the sincere admiration and respect of
Yours faithfully,
E. Schrödinger
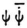 , where ψ is taken to be complex in the obvious way (for criticism, see below) and the bar denotes the complex conjugate. Now I want to choose more simply
, where ψ is taken to be complex in the obvious way (for criticism, see below) and the bar denotes the complex conjugate. Now I want to choose more simply 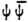 , that is, the square of the absolute value of the quantity ψ. If we now have to deal with N particles, then
, that is, the square of the absolute value of the quantity ψ. If we now have to deal with N particles, then 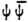 (just as ψ itself) is a function of 3N variables or, as I want to say, of N three dimensional spaces, R1,R2, …, RN. Now first let R1 be identified with the real space and integrate
(just as ψ itself) is a function of 3N variables or, as I want to say, of N three dimensional spaces, R1,R2, …, RN. Now first let R1 be identified with the real space and integrate 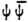 over R2, …,RN; second, identify R2 with the real space and integrate over R1,R3, …,RN; and so on. The N individual results are to be added after they have been multiplied by certain constants which characterize the particles, (their charges, according to the former theory). I consider the result to be the electric charge density in real space. In this manner one obtains for an atom with many electrons exactly what Born-Heisenberg-Jordan designate as the transition probability, with the new and plausible meaning “component of the electric moment”, (strictly speaking that partial moment which oscillates with the emission frequency in question).
over R2, …,RN; second, identify R2 with the real space and integrate over R1,R3, …,RN; and so on. The N individual results are to be added after they have been multiplied by certain constants which characterize the particles, (their charges, according to the former theory). I consider the result to be the electric charge density in real space. In this manner one obtains for an atom with many electrons exactly what Born-Heisenberg-Jordan designate as the transition probability, with the new and plausible meaning “component of the electric moment”, (strictly speaking that partial moment which oscillates with the emission frequency in question).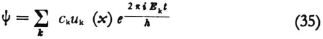

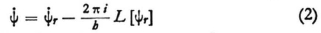
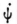 is in any case represented by the space and time derivatives of the real quantity ψr, independent of the complex representation; so that one does not get into difficulty even if there is a ψr that does not correspond to a stationary super-position of proper oscillations. Now to be sure one has only
is in any case represented by the space and time derivatives of the real quantity ψr, independent of the complex representation; so that one does not get into difficulty even if there is a ψr that does not correspond to a stationary super-position of proper oscillations. Now to be sure one has only 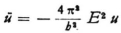
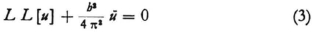
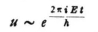
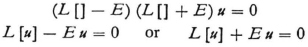
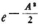 so that the integral
so that the integral 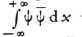 will be independent of A.) In the limiting case of very small A one obtains at first only the fundamental oscillation; with increasing A the higher oscillations are gradually excited and the center of gravity gradually shifts to higher and higher quantum numbers.
will be independent of A.) In the limiting case of very small A one obtains at first only the fundamental oscillation; with increasing A the higher oscillations are gradually excited and the center of gravity gradually shifts to higher and higher quantum numbers.