16 April 1926
Dear Colleague,
Professor Planck pointed your theory out to me with well justified enthusiasm, and then I studied it too, with the greatest interest. In the process one doubt has arisen which I hope you can dispel for me. If I have two systems that are not coupled to each other at all, and if E1 is an allowed energy value of the first system and E2 an allowed energy value of the second, then E1 + E2 = E must be an allowed energy value of the total system consisting of both of them. I do not, however, understand how your equation
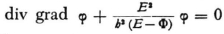
is to express this property.
So that you can see what I mean, I put down another equation that would satisfy this condition:
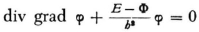
For, the two equations
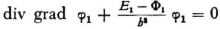
(valid for the phase space of the first system)
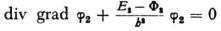
(valid for the phase space of the second system) have as a consequence
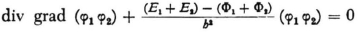
(valid in the combined q- space).
As proof one need only multiply the equations by φ2 and φ1 respectively and add. φ1 φ2 would, therefore, be a solution of the equation for the combined system, belonging to the energy value E, + E2.
I have tried in vain to establish a relationship of this sort for your equation.
It also seems to me that the equation ought to have such a structure that the integration constant of the energy does not appear in it; this also holds for the equation I have constructed, but despite that I have not been able to assign a physical significance to it, a matter on which I have not reflected sufficiently.
With warmest greetings from
A. Einstein
The idea of your article shows real genius.8