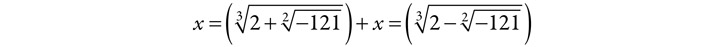
Abstract: Robert Tragesser comments on Stefania Centrone’s Logic and Philosophy of Mathematics in the Early Husserl.
Keywords: Stefania Centrone, Edmund Husserl, phenomenology of mathematics
First I should say I don’t think a “commentary” is the same thing as a “review.” What I have done—given the limited time—is to select some views or ideas of Husserl’s that Stefania Centrone has unearthed or reconstructed in her study,2 and to comment on them. They are mainly views about formal logic and about the philosophy or foundations of mathematics. I am going to comment on them from the perspective of my ongoing rethinking of Husserlian phenomenology.
My principal interest has been the phenomenological philosophy of mathematical thought. Over all these years, Husserl’s own writings have not been as helpful as I had hoped they would be. In no small part this has to do with the sketchiness of his thinking in print about formal logic and his not knowing how to draw upon or (until very late) even show much interest in the inner history of mathematics, which I now think is necessary for an adequate phenomenological investigation of the nature or natures of mathematical thought. And if it is true, as Peter Simons says in the Foreward to Early Husserl book, that “Husserl never changed his view as to the nature of natural numbers as properties of collections or multitudes, so on the substantial issue of the correct ontology of arithmetic, he was unmoved,”3 this suggests strongly to me that Husserl was not substantially rethinking the natural numbers as his phenomenological ontology developed, and it is very odd that as he was beginning to realize that genetic phenomenology must draw on history (albeit it in a certain subtle sense at which he seems not to have arrived) we have an essay on the origin of geometry but not on the origin of arithmetic (on these last matters, the publication of Burt Hopkins’s The Origin of the Logic of Symbolic Mathematics4 will help us tremendously).
When long ago I began reading the Logical Investigations I was excited when Husserl suggested that one application of his investigations would be to make sense of the “imaginary” or “impossible” or “nonsensical” apparent pseudo-numbers that were finding a deep role in mathematics, but disappointed when it seemed he never did this (at least in the texts available). I think it has been a problem for many of us, Husserl’s obscure references to Bolzano compounded with Husserl’s not presenting a formal-symbolic logic; it was too hard or seemingly unrewarding a problem to study Bolzano and to work out just what Husserl was taking, and not taking, from Bolzano. When I received Early Husserl in mid-February 2011, it was pleasing to find that its chapter 2 makes a breakthrough contribution to our understanding of Husserl in relation to Bolzano, and chapter 3, “The Imaginary in Mathematics,” digs out of Husserl’s sketchy writings work he had actually done on the problem of mathematical imaginaries or impossibles, albeit that his thinking was apparently in the main what we would call metamathematical, with very little attention to the problem of which would become one of the main problems of his phenomenological thinking in the Logical Investigations and, say, the Formal and Transcendental Logic, namely the problem of missing or suppressed validative thinking in logic and mathematics.
I had, and have, difficulty in quite knowing how to relate to Early Husserl. Its essay on Husserl and Frege is brilliant criticism, a most significant and enlivening of what had seemed to me to be a very tired and unenlightening literature. But there are significant lacunae and shortfalls, especially in chapter 3 on the imaginary in mathematics. I’m sure this has to do with the source material in Husserl—he just did not execute nor point very far how his program to deal with the “imaginaries” or “impossibles” was to be carried through, so we only get fragments—albeit very nobly reconstructed by Centrone. At the same time, one of the central notions, called by Husserl “universal arithmetic,” immediately creates a problem. Husserl considers “all numerical systems”5 and “each numerical system will be axiomatized by a different arithmetic.”6 For Husserl, “universal arithmetic is the part that all these theories have in common.” I cannot think of what that part might be. Centrone seems vague on this score, when she says “numerical systems have the peculiarity that the objects of their fields can be ordered by a total order relation (obviously, with the exception of that of the complex numbers).” Is the common part that makes up universal arithmetic really more “common but with of course these exceptions”? And if there is “the system of rules of calculation that is valid in all these systems,” what do they look like (the general forms and the specific forms), and what are they? What would a general form of multiplication look like, if that’s the sort of thing that’s at issue? It seems that, beginning with the axiomatized arithmetic of the finite cardinal numbers, and its specific operations, we somehow move onto another arithmetic (say, M) by noticing that some specification of a general operation (say minus—but I’d like to know how qua general operation this is understood) in the cardinal arithmetic has a condition attached to it, for example, (a –b) is not admitted, has no sense, if b > a, is specified in the other arithmetic by removing that prohibition. But just where and how does this get us? It seems we are already given axiomatizations of all the arithmetics. It seems moreover that the fundamental and foundationally clarifying question should be: how do the arithmetics and their axiomatizations come about, and are they to be somehow validated? There are many puzzles here. But perhaps Husserl didn’t take them up, and that’s why Centrone didn’t, never mind providing enough detail for Centrone to solve them.
I want now to comment on the question of “the existence” of mathematicals. This was inspired by appendix 6 of chapter 3 of The Imaginary in Mathematics. The appendix is titled “Husserl’s Existential Axiomatics.” Centrone observed that for Husserl, “an axiom-system defines a field only if it includes existential axioms of this type,” for example, “There is a determinate number—let us denote it by ‘1’—such that for each a it holds: a × 1 = a and 1 × a = a.” When setting up an axiom system “We establish existential axioms that determine which objects belong in the field.” (Curiously, Centrone gives an axiomatization of second order Peano arithmetic7 without existential axioms.)
Do “existential axioms” introduce assumptions of existence that have to be validly discharged in order for the system to be sound or valid or acceptable or true? For example, is ZF set theory, which has an axiom asserting the existence of infinite sets, no good unless we, external to the theory, establish that infinite sets do indeed exist? Or, if someone could demonstrate external to the theory that infinite sets do not exist, would that show that ZF is false or vacuous or no good? Employing Husserl’s metamathematics, Centrone investigates some functions of existential axioms, distinguishing different sorts of existential axioms and their effect on the theory. But I don’t think that Centrone addresses the question about whether or not existential axioms are needed. It seems that the idea of them was introduced by Hilbert and Bernays because of some need to assure the existence of the mathematicals of the domain or field considered, and that same felt need motivated Dedekind to try to prove the existence of an infinite system as part of his foundations for arithmetic. I believe that on their conception existential assumptions as assumptions were discharged, made acceptable or even validated by means of a finitary consistency proof. If that could be done, what, then was the weight of the existential axioms? It would seem that that sort of “existence” would not have satisfied Dedekind’s felt need for a proof of existence. The close of the appendix on existential axiomatics proposes that Husserl’s attitude toward the being of mathematical domains is that they are constituted via a notion of what Kit Fine calls “procedural postulationism.”8 Centrone finds this notion in the background of Husserl’s thinking about extending theories, one being introducing new existential axioms. She overhears in this Kit Fine’s introduction postulate: “Introduce new objects into the domain!”
What is missing here is something that would be of central importance to the later Husserl, namely, motivation and the validating sense of doing that with a particular theory and a particular existential axiom. It’s not the formal freedom to, say, extend a theory that’s the central thing, but the point of doing that, the sense of it and the contribution that’s made to mathematics.
Indeed, one can’t just introduce an object into a domain. The “object” must in some sense be, and, in mathematics, the being of beings in a mathematical domain is contingent upon the being of the domain. It would make no sense just to inject, say, i into a domain. The being-sense of mathematical domains and their beings is given, I would argue, by Husserl’s Thesis of Reason (suitably otherwise expressed) in Ideas I §142. It’s a characterization of the being sense “being in and through truth.” This would have to be discussed in another and longer time- but, as we will briefly see below, the imaginary numbers a+bi were accepted with equal rights in their being with the natural numbers when we learned how to think and learn and reason about them, and did so with ever increasing success and power.
Let me pause to discuss a theme from Bolzano: “Methodenreinheit: in order to arrive at a certain proposition we should not use concepts that are extraneous to it.”9 It frequently happens that in the proof of a difficult theorem, concepts or theorems from other branches of mathematics are employed in the proof (e.g., complex analysis in the proof of a number theoretic theorem). Then there might be a sometimes long quest for one of those pure proofs typically called “elementary proofs.” Although it’s called “elementary,” it’s because it’s “elemental,” more or less only containing concepts in the proposition of the theorem, but typically it is a long and quite tricky or difficult proof. Although they can see that it is a correct proof, even experts might have a difficult time achieving an insightful understanding of the proof. It has become a commonplace in mathematics that other branches of mathematics can facilitate our proving theorems in a given perhaps difficult branch. Contemplating such non-elementary proofs may yield a fresh, insightful understanding—an insightful understanding that can contribute to finding solutions to other problems or proofs of more general theorems or a better understanding of the theorem it proved, or even a better understanding of the other branch of mathematics brought in to help prove the theorem. It was an important moment when in Husserl’s Formal and Transcendental Logic, he observed in §30, prepared for by the discussion of sense in the Prolegomena: in a formal axiomatic system, one does not have axioms, proof, theorems, but, rather, axiom-forms, proof-forms, theorem-forms (my paraphrasing). The difference between axioms and axiom-forms, proofs and proof forms, theorem and theorem forms is that sense is suppressed or abstracted from the axioms to obtain the axiom forms, theorem to obtain theorem forms, proof to obtain proof forms. It’s the sense that is needed for the sake of insightful understanding. At the same time, formalization (with suppression of sense) is what is needed in order, as in the Hilbert school, to make mathematical theories and proofs objects for mathematical investigation. But sense and sense-giving is needed for insightful understanding. As I suggested above, as presented in chapter 3 of Early Husserl, we see Husserl suppressing sense and losing a sense of the importance of understanding in mathematics and the sciences. By the time of the Logical Investigations, and increasingly so through the Ideas and the Formal and Transcendental Logic, we see Husserl struggling to find his way to cogent thinking about sense, especially in relation to the constitution of beings and truth.
When we are learning, mastering, and practicing some mathematics, we tend to become technique-oriented: “integration by parts is what is needed here”; or “completing the square” is what is needed there; or “this is just the thing for some Fourier analysis”; and we’ve lost our sense of how or why the technique is working, or we aren’t in a position to think about a way of solving our problem in a more economical or fruitful way. Or to notice something interesting you do not understand, and perhaps to work out some problems whose solution would help you understand that.
The rather intense discourse on the need for sense-investigation and radical sense investigation is in the Introduction to Husserl’s Formal and Transcendental Logic. Our understanding, our sense, of things we deal with, whether in mathematics, the sciences, or life, tends to get lost in our routines and techniques, and generally fail either to keep the sense of things before us or keep the sense of things coherent, not widersinnig. “Thus men live in a world [whether that world be a small province of mathematics or the full life-world] that has become unintelligible, in which they ask in vain for the wheretofore, the sense, which was once so doubtless and accepted by the understanding.” Radical sense explication or reawakening is what is needed to bring the sense of things back into mind, and perhaps find our sense is so corrupted as to need a serious, bottom-up reworking. The historian of mathematics Gert Shubring on the highly problematic imbroglio of mathematical sense making its way down to the nineteenth century:
Deidier’s textbook [on arithmetic and algebra] is not only a revealing example for the possibility of different epistemological concepts coexisting in a “superposition” of various historical “layers.” It serves at the same time as a first proof the developments of concepts and style need not occur in a “one dimensional” and cumulative way, but the ruptures and reversions to forms prevailing at an earlier time may very well occur.10
A major source of what emerged as incoherencies, lapses, and conflicts of sense was the predominant notion that mathematics is the science of magnitude and quantity (e.g., line lengths, angles, distances, weight, motions, collections), entities that could be reasoned about through assigned measures or relations of proportion, via arithmetic or algebra. It was important that relations of >, <, = held between them, although these relations had different senses for different magnitudes and quantities. The arithmetic and algebraic operations had to make sense in terms of the magnitudes or metaphysics of the magnitudes that were the subject of a mathematical problem. If, in the solutions to problems, a–2 or 0 showed up as solutions, or operations on them seemed to be required in order to advance to the solution of a problem, there was the problem of making sense of them and operations on them, such as (−5) × (−7), or √−1 or 0. Mathematics was here and there deceptively shored up, or openly ridiculed, and thereby made near unintelligible by a patchwork of metaphysics.
At the close of his 1891 Foreword to Philosophy of Arithmetic, Husserl indicated what he expected to be the content of a promised second volume, remarking: “Perhaps no unfavorable bias against my aspirations will be evoked beforehand if I say that I owe the basic conceptualization to the study of Gauss’s [1831] report—much read, and still only partially exploited—on the biquadratic [residues](II).”11,12 In that report, Gauss calls 1, 2, 3, 4, 5, … “the real numbers.” Therein he defends “the impossible or imaginary numbers,” including, especially the complex numbers a + bi as having equal rights with “the real numbers” (meaning here the natural numbers). The complex numbers can no more be called ‘fictional’ than can the natural numbers—“the real numbers”—be called ‘fictional.’ The complex numbers are equally as “real” as the natural numbers. Indeed, Riemann believed that the complex numbers a + bi with integral a and b were more fundamental than the integers.
Here is a quote from the 1831 Gauss report relevant to some discussion in Early Husserl: “The mathematician abstracts totally from the nature of the objects and the content of their relations; he is concerned solely with the counting and comparison of the relations among themselves.”13 Recall Centrone: “At the time of this lecture Husserl conceives of a formal theory, in the narrow sense of the word, as a collection of axioms that are purely formal, mutually consistent and independent and, in a broader sense, as also including all propositions derivable from the axioms “in a purely logical way …,” that is the theorems of the theory. The related field or object-domain is in turn considered as “a field of objects in general,” determined only by the fact that it “falls under” certain axioms of this or that form. “We call an object field thus defined a formally defined manifold hence determines only the relations that occur among the elements of the manifold, leaving the nature of the elements undetermined.”14 This is just Gauss’s thought far better expressed.
After sketching some patterns of integers of interest in the theory of quadratic residues that are in need of proof, Gauss writes15 (I paraphrase) that one can make progress here only by methods that are entirely new; for them it is necessary, indeed for the true grounding of the theory of quadratic residues, one must extend the field of higher arithmetic into the imaginary integers a + bi, and must concede to the latter the same legitimacy as the real integers. As soon as one has seen this, that theory appears in an entirely new light, and its results acquire a startling simplicity.
The first has to do with the beginning of a two-fold revolution in mathematics that developed in the nineteenth and early twentieth centuries. It has to do with making abstract structure the principal concern of mathematics and the evolution of pure mathematics. That stripping away of concern with the nature of objects and the contents of relations closed the door to all of that incoherence sunken into mathematicals, that was holding back mathematics, making it more something that tried and puzzled the understanding than fostered it.
Mathematicians of the eighteenth century—even Euler—can be seen to be doing mathematics by means of a style of calculating with “forms (or formulas) without content.”16 Initiated with Gauss, Cauchy, Dirichlet, continued by Riemann (taking some inspiration from the philosopher Herbart), Dedekind, Weierstrass, Hilbert and growing numbers took up and developed what was spoken of as a new conceptual approach, “to put thoughts in the place of calculations,” cultivating, practicing, “the art of solving problems with a minimum of blind calculations and a maximum of insightful thoughts. One of the stories we hear about Hilbert was how he solved a difficult open problem with a logical proof that took only a page, beating out Gordan, the creator of the problem, who had spent countless months trying to calculate its solution with those “formulas without content.” It’s worth mentioning that the formulas were “without content” because the content that had been put into them was that confused quasi-metaphysics spoken of above in the quote from Schubring.
Centrone mentions several times that Husserl required that a mathematical field or domain be developed under a concept and embody that concept.17 This is a part of the new conceptual approach that in part made the nineteenth-century mathematics so revolutionary. By way of illustration, we have Centrone’s surprising account of Husserl’s characterization of operations of calculation, yielding the equivalent of Turing machines or partial recursive functions 35 years before Turing gave his analysis. Another illustration: I recently read that Cantor had quite insisted that a principal conception under which he developed transfinite set theory—a theory which is of course now axiomatized and very well developed, its “sets” being as it were now logically constituted rather than quasi-metaphysically, quasi-psychologically constituted (e.g., there is absolutely no problematic issue about a set’s unity or how many can be one)—the conception (although not the whole of it) was that sets will have cardinal numbers. Indeed, there is a theorem proved in ZFC that all sets have cardinal numbers—Cantor succeeded.
The revolution of which Centrone spoke, quoting Howard Stein—mathematics becoming in major part the theory of abstract structures—emerged in a natural way as the new conceptual approach worked its way through the century.18
In 1545, Cardan made public a formal or formulaic process for solving cubic equations. When this was applied to, for example, x3= 15x + 4, the formula yielded an ostensibly “impossible number,” whereas it ought to have been a real root:
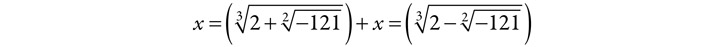
But it follows from some invented and correct formal calculations by Bombelli that x = 4. Whenever the quadratic formula yielded an imaginary number, mathematicians just crossed it out as an absurd or impossible root. Bombelli applied Cardano’s formula for roots of cubics to a cubic and got three roots of this form. At least one of them should have been real. Bombelli worked out some algebra for complex numbers and was able to show that it was equal to 4. Leibniz got very excited when he learned of this.19 Why? It showed that there was much more than nonsense to the complex numbers. It upped their status as genuine no-nonsense mathematical beings, and the computations by Bombelli opened up the way to an algebra for them. Listen to Craig Smorynski:
My second aim was to include the proofs of some results of importance one way or another for the history of mathematics that are neglected in the modern curriculum. The most obvious of these is the oft-cited necessity of introducing complex numbers in applying the algebraic solution of cubic equations. This solution … was a major occurrence in our history. It was the first substantial piece of mathematics in Europe that was not a mere extension of what the Greeks had done and thus signified the coming of age of European mathematics. The fact that the solution, in the case of three distinct real roots to a cubic, necessarily involved complex numbers … made inevitable the acceptance and study of these numbers.20
Notice how both Gauss and Smorynski see “the complex numbers a + bi” as necessary to our understanding of other mathematical structures. Their being is not in some individual (or primary or secondary) substances they denote, but in their function that gives them the power to illuminate other mathematicals. If space permitted, I’d go through Ideas I §86 to explore this function. In order to do this, we must work in as it were the informal or concrete mathematics of the complex numbers rather than in their formal-axiomatic counterpart. The latter is what is needed for metamathematical investigations, but the informal is what is needed for phenomenological sense-investigations.
In any case, it was for the best that Husserl was distanced from the Hilbert school and its suppressions of sense, sense being the engine of thought.
The New Yearbook for Phenomenology and Phenomenological Philosophy XII (2012): 327–35
© Acumen Publishing Ltd. 2013 ISSN: 1533-7472 (print); 2157-0752 (online)
1. Robert Tragesser is author of Phenomenology and Logic and Husserl and Realism in Logic and Mathematics.
2. Stefania Centrone, Logic and Philosophy of Mathematics in the Early Husserl (Dordrecht: Springer, 2010); henceforth cited as Early Husserl.
3. Peter Simons, “Foreword,” in Early Husserl, iv.
4. Burt C. Hopkins, The Origin of the Logic of Symbolic Mathematics: Edmund Husserl and Jacob Klein (Bloomington, IN: Indiana University Press, 2011).
5. Early Husserl, 160.
6. Early Husserl, 160.
7. Early Husserl, 199
8. Early Husserl, 209–10.
9. Early Husserl, 118–27.
10. Gert Schubring, Confl icts between Generalization, Rigor, and Intuition: Number Concepts Underlying the Development of Analysis in 17–19th Century (Berlin: Springer, 2005), 87.
11. Gauss’s report, philosophically related matters, and a brief exposition are available (in English) in the monumental From Kant to Hilbert: A Source Book in the Foundations of Mathematics, 2 vols, ed. William B. Ewald (Oxford: Oxford University Press, 1996), vol. I, 293–313.
12. Edmund Husserl, Philosophy of Arithmetic, trans. Dallas Willard (Dordrecht: Kluwer, 2003), 8.
13. Gauss; ibid., 132.
14. Early Husserl, 155–6.
15. Ibid., Ewald, 308–9.
16. This is discussed at great length in a forthcoming book, Adventures in Formalism, by the mathematical logician (and now historian of mathematics) Craig Smorynski.
17. E.g., Early Husserl, §2.4.
18. Early Husserl, 154.
19. Gottfried Wilhelm Leibniz, Philosophical Papers and Letters, 2nd edition, ed. Leroy E. Loemker (Dordrecht: Kluwer, 1989); 544 [GM., 94]
20. Craig Smorynski, History of Mathematics: A Supplement (Berlin: Springer, 2008), 8.