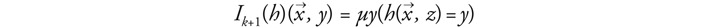
Abstract: Mark van Atten reviews Stefania Centrone’s Logic and Philosophy of Mathematics in the Early Husserl, which addresses Husserl’s technical ideas on mathematics and logic. By ‘the early Husserl’ Centrone means primarily Husserl in the period from the Philosophy of Arithmetic (1891) to the Logical Investigations (1900/1901). The review focuses on what in the reviewer’s opinion are the two most important systematic claims in the book: the claim that in the Philosophy of Arithmetic, Husserl defines the class now known as that of the partially recursive functions, and the claim that the notion of (relative) definiteness of an axiom system is to be understood as its syntactical completeness.
Keywords: Stefania Centrone, Edmund Husserl, phenomenology of mathematics
In Stefania Centrone’s Logic and Philosophy of Mathematics in the Early Husserl,2 what the author means by ‘the early Husserl’ is primarily Husserl in the period from the Philosophy of Arithmetic (1891) to the Logical Investigations (1900/1901).3 The book’s three chapters can be read practically independently of one another: chapter 1, “Philosophy of Arithmetic”; chapter 2, “The Idea of Pure Logic”; and chapter 3 “The Imaginary in Mathematics.” The first chapter is devoted to Husserl’s work of the same name and some related texts; the second, to Husserl’s indebtedness to Bolzano; the third, to the notion of definiteness of an axiom system and of a manifold. As far as exposition is concerned, the second chapter is perhaps the most original contribution.4
The book makes a detailed and convincing case that these ideas of the early Husserl were rich and avant-garde; the very fact that Husserl’s texts can give rise to the wealth of formal reconstructions and related historical considerations that Centrone presents testifies to that. On the other hand, I agree with Mirja Hartimo’s remark in her own (useful and different) review of this book that, contrary to the book’s title, not much philosophy of mathematics can be found in it.5 What the book does not provide either, but was indeed not designed to provide, is any new contribution to or insight in descriptive psychology or phenomenology; such parts on descriptive psychology as the book contains are expository, and there is no attempt to employ it in a critical evaluation of some of Husserl’s philosophical claims.
Th at does not at all mean, however, that this book is of no interest to phenomenologists. Indeed, one transcendental phenomenologist who was much interested in this particular part of Husserl’s early work, and who was confident about the possibility to integrate it into a transcendental–phenomenological philosophy of mathematics, was Husserl himself, as is clear from his remarks in Formal and Transcendental Logic; this is dealt with in chapter 3.
Not being well versed in Bolzano’s philosophy, I will not attempt a critical discussion of chapter 2 here. The remainder of this review will be limited to what, to my mind, are the two most important systematic claims defended in the other two chapters: the claim in chapter 1 (suggested by Ettore Casari) that the class H of functions that Husserl defines in the Philosophy of Arithmetic is extensionally equivalent to the class of the partial recursive functions Pμ, and the claim in chapter 3 that the notion of (relative) definiteness of an axiom system is to be understood as its syntactical completeness. Th ese claims are of major importance, and merit detailed discussion: the conceptual analysis of computability was one of the most important problems in twentieth-century foundations of mathematics, and the notion(s) of definiteness guided Husserl’s thought on formal theories through his whole career. Any strong, systematic claims that the book proposes on these topics, as well as the arguments proposed to defend them, should therefore be considered at leisure.
The crucial part of a demonstration of the first claim would be to show that H is, like Pμ, closed under minimization; that is, for every total function h in H of k + 1 arguments, H should also contain a function that yields μy(h(x→ , y) = 0) (‘the smallest y such that (h(x→ , y) = 0)’), if such a y exists, and diverges otherwise.6 The argument that Centrone presents for her thesis that this is indeed the case is not altogether satisfying. She first proposes to define Husserl’s inversion operator in terms of precisely the minimization operator:
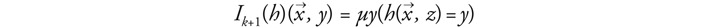
Not surprisingly, this makes the subsequent proof of closure of H under minimization easy. The reconstruction would, however, be none the weaker for it, if it could be shown that Husserl himself knew (of) the minimization operator. However, Centrone mentions (57) that he never considers it, and she says that her definition may therefore seem rather ad hoc (60). She then goes on to propose an alternative definition of inversion that uses only ingredients that are explicit in Husserl’s text. It uses the definite description operator ℩x… (‘the unique x, if it exists, such that …’), which for Husserl clearly is a basic operator:
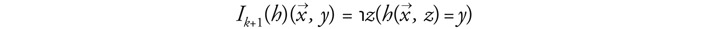
Incidentally, the other inversion functions Ii (59) can be obtained from this one by using the appropriate projection functions and primitive recursion. Centrone (61) points out that, while the price to pay is that inversion thus defined is not as generally applicable as on the first definition,7 all the examples of inversion that Husserl actually gives still work fine. However, Centrone then remarks that she does not know whether under this second definition of inversion closure of H under minimization is still provable (61). Later on in the book (98 and 212) she seems to have forgotten her own reservations, stating that her proof “represents a substantially new result.”
Neither of Centrone’s explorations of definitions of the inversion operator as presented in her book, then, ends in a convincing argument for the extensional equivalence of H and Pμ. On the other hand, the objection to the first definition may be mitigated by observing (as Centrone does not) that it is hard to see how a general inversion function could be implemented as a computable operator if not in terms of a search from 0 on. Moreover, also on the basis of the second definition of inversion H is indeed closed under minimization, as can be demonstrated as follows. Define8
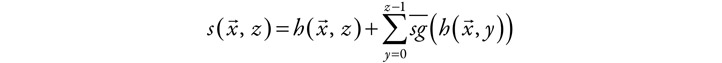
where ̄sg is the inverted sign function given by ̄sg (0) = 1 and ̄sg (x + 1) = 0.
As h is in H by hypothesis, and s is primitive recursive in h, s is in H as well. We have s(x, z) = 0 exactly if z is the smallest y such that h(x , y) = 0. For there are two jointly necessary and sufficient conditions for a given z to have that property: h(x→ , z) = 0 should be 0, and this should not be the case for any y smaller than z. The two addends in the definition of s give penalties, so to speak, for the failure of the conditions they correspond to.
Using the inversion function defined in terms of ℩, the minimization operator can now be defined thus:9
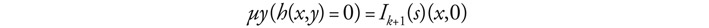
Once one has the equivalence of the classes H and Pμ in hand, a further ingredient is necessary to argue that H indeed exhausts the class of all computable functions, namely, (something to the effect of) the Church–Turing thesis, according to which the formally defined notion of partial recursiveness is the correct analysis of the intuitive notion of computability. Centrone is of course aware of this (60), but does not elaborate the point. It is worth emphasizing, however, that Husserl does not offer such a further ingredient. Centrone writes:
The problem of finding an adequate mathematical characterization (or definition) of the intuitive notion of computability has received various answers much later (since 1933–1934), and, to the best of our knowledge, nobody has ever thought of Husserl as someone who has anything to contribute to this issue. (98)
She takes her analysis to show that this attitude toward Husserl is not correct. I disagree. Certainly, Husserl’s formulation of the need for a general theory of operations was groundbreaking. But as he did not then attempt to provide such a theory, he contributed nothing to solving the greater difficulty, which lies not in defining ever larger classes of computable functions, but in arguing that a given class contains exactly all of them. Interestingly, when Turing in 1936 did (decisively) contribute to the discussion by proposing an argument why computability should be analysed as partial recursiveness,10 he did so, as Husserl might have attempted but did not, by engaging in an exercise of a descriptive-psychological or phenomenological nature. Turing reflected on the acts an idealized computing human may engage in, and on how these acts depend on, and are constrained by, properties of his mind and of his capacities for observation. Turing then observed that the simplest of these operations, to which the more complicated ones can be reduced, can be mimicked by a machine, and showed that the class of functions computable by such a machine and that of the partial recursive functions coincide. It was this analysis, of a type that had not yet figured in the discussion,11 that fully convinced Gödel (and others) that partial recursiveness indeed exactly captures the intuitive notion of computability; the suggestion had been made before, but then Gödel had not been prepared to believe it.12
The second systematic claim in Centrone’s book that I should like to discuss has to do with Husserl’s notion of a definite axiom system. Over the years, up to Formal and Transcendental Logic, this notion changed a bit, in ways discussed by Centrone; here, I will be concerned with the notion as it appears in the Doppelvortrag in Göttingen, 1901. Centrone warns (in the light of later developments in logic, rightly so) that Husserl (like others) at the time was not at all clear about the distinction between syntax and semantics,13 and that he “seems to regard syntactical talk and semantical talk as coming more or less to the same thing” (168–9). Th ere would seem to be no reason, then, to expect that his writings on topics where this distinction is important admit of a coherent or preferred reading at all. On the other hand, Husserl’s remarks are, all the same, strongly suggestive of various notions of modern logic. Be that as it may, Centrone goes on to propose interpretations of relative and absolute definiteness that wholly depend on being precise about the distinction between syntax and semantics: relative definiteness is construed as syntactical completeness, and absolute definiteness as categoricity. My remark concerns relative definiteness.
Centrone’s short argument (169) for identifying Husserl’s relative definiteness with syntactical completeness starts from a passage from the second Doppelvortrag which she quotes as follows:
An irreducible axiom system … is definite … when no independent axiom can be added which is constructed only from the concepts already defined (of course, also, none can be withdrawn, since otherwise the axiom-system would not be irreducible).
She then points out that, if one nevertheless does add such a further axiom, this results in inconsistency.14 Th is, in turn, is (classically) equivalent to syntactic completeness: for any closed formula φ of the system, either φ or ¬φ is derivable in the system. She then claims that “Husserl seems to be fully aware of this equivalence,” quoting him as follows:
But I can also say: I define an axiom system, which formally defines a field of objects in such a way that every meaningful question for this field of objects finds its answer by means of the axiom-system; or that every proposition that is meaningful in virtue of the axioms … either follows from the axioms or contradicts them.
However, the part she replaced by an ellipsis reads: “if we limit it exclusively to the objects grounded as existing through the axioms.”15 Th ere would be no reason at all for Husserl to add this qualification if what he has in mind indeed corresponds to the notion of syntactical completeness, for which no consideration on the interpretation of the axiom system is relevant. Given that Centrone’s concern here is “to provide further textual evidence for our interpretation of definiteness as syntactic completeness” (169), she should not have omitted Husserl’s qualification, but have given an explanation why, as she must think, it wouldn’t affect her proposal. Precisely this qualification plays a central role in Da Silva’s earlier, alternative interpretation of relative definiteness as syntactical completeness restricted to formulas that, through the device of relativized quantification, are only about objects in a privileged domain;16 and whether one finally agrees with his interpretation or not, any critical discussion of it should take his motivation into account. However, in Centrone’s brief remarks on Da Silva’s analysis (176–7), it is passed over in silence. Centrone makes the sensible objection that this privileged domain need not be definable in the language of the system. But as she does not take Husserl’s qualification into consideration, the question whether this is an objection only to Da Silva’s reading of Husserl or (also) to Husserl is not addressed; doing so might, whatever the answer turns out to be, have suggested further reflections on her own proposal. Similarly, Centrone’s discussion would have been instructively richer if, instead of merely recording (178n.123) the incompatibility of her interpretation with that of another participant in the discussion, Hartimo, she had paused to consider what in Husserl’s texts under discussion may have actually motivated Hartimo to hold (rightly or wrongly) that relative definiteness means categoricity.17
Th is book provides an efficient and clear presentation, in today’s terms, of the early Husserl’s technical ideas on mathematics and logic, in particular in relation to those of his predecessors and contemporaries. Th is is both its principal and its strongest point. Its attempts at defending larger systematic claims on the basis of these reconstructions, however, are not quite as successful.
The New Yearbook for Phenomenology and Phenomenological Philosophy XII (2012): 370–76
© Acumen Publishing Ltd. 2013 ISSN: 1533-7472 (print); 2157-0752 (online)
1. Mark van Atten is researcher for the Centre National de la Recherche Scientifique (CNRS) in Paris. His main areas of research are philosophy of mathematics and idealistic philosophy; he works in particular on Brouwer and Gödel from a Husserlian point of view. He is the author of On Brouwer (2004), Brouwer Meets Husserl. On the Phenomenology of Choice Sequences (2007), and editor (with P. Boldini, M. Bourdeau, and G. Heinzmann) of One Hundred Years of Intuitionism (1907–2007). The Cerisy Conference (2008).
2. Stefania Centrone, Logic and Philosophy of Mathematics in the Early Husserl (Dordrecht: Springer, 2010).
3. It would have been only natural to include more than a passing reference to the logic lectures of 1902–3. E. Husserl, Logik. Vorlesung 1902/03, ed. E. Schuhmann (Dordrecht: Kluwer, 2001).
4. While Centrone (perhaps justifiably) complains about a lack of attention to the role of Bolzano in early Husserl’s thought (146), two obvious references from the not-so-distant past are not on her list: C. Beyer, Von Bolzano zu Husserl (Dordrecht: Kluwer, 1996) and R. Rollinger, Husserl’s Position in the School of Brentano (Dordrecht: Kluwer, 1999). Conversely, there are works listed in the bibliography that are not actually referred to, for example the entries Føllesdal 1995 and Van Atten 2002, both of which are moreover somewhat removed from the topics in the book.
5. M. Hartimo, “Review of Stefania Centrone, Logic and Philosophy of Mathematics in the Early Husserl,” Philosophia Mathematica 18(3) (2010), 344–9, here 349.
6 x→ is a (possibly empty) sequence of k parameters.
7. Consider a function h with h(0) = 1 and h(1) = 1. Th en μz(h(z)) = 1 yields 0 but ℩z(h(z) = 1 is undefined.
8. The definition of such a function s is known from, e.g., T. Skolem, Selected Works in Logic, ed. J. Fenstad (Oslo: Universitetsforlaget, 1954), 567.
9. Centrone (61) states the condition that this second inversion operator only be applied to functions that are injective in their last argument. The function s does not in general, i.e. for arbitrary h, satisfy this condition, but note that its definition guarantees that it does in the special case s(x→ , z) = s(x→, z) = 0: if s(x→ , y) = 0 then z = y. As only this special case is used in the definition of μ given here, inversion defined in terms of the ℩-operator can be safely applied to it.
10. A. Turing, “On Computable Numbers, with an Application to the Entscheidungsproblem,” Proceedings of the London Mathematical Society, II, Series 42 (1936), 230–65.
11. Also in 1936, and independently of Turing, Post had devised a somewhat similar analysis: E. Post, “Finite Combinatory Processes—Formulation 1,” Journal of Symbolic Logic 1 (1936), 103–5.
12. See K. Gödel, Collected Works vol. I: Publications 1929–1936, ed. S. Feferman et al. (Oxford: Oxford University Press, 1986), 348n.3 and 369–71. A very good account of this episode is W. Sieg, “Step by Recursive Step: Church’s Analysis of Effective Calculability,” Bulletin of Symbolic Logic 3 (1997), 154–80. Note that at issue here is the notion of computability by a finite mechanical procedure; unlike Turing, Gödel became convinced that there are also finite procedures that are not mechanical. Th ere might then be functions that are computable by the human mind but not by a machine. See K. Gödel, Collected Works vol. II: Publications 1938–1974, ed. S. Feferman et al. (Oxford: Oxford University Press, 1990), 306.
13. Brouwer was clear about this in his dissertation (in Dutch) of 1907, and he communicated it to Hilbert in conversations in 1909. See L. E. J. Brouwer, Collected Works vol. 1: Philosophy and Foundations of Mathematics, ed. A. Heyting (Amsterdam: Elsevier, 1975), 94, 410.
14. Centrone does not quote any passage here in which Husserl explicitly says (as in the passage above he does not) that the result of adding a further axiom is inconsistency, but that is probably taken for granted. One can be found in E. Husserl, Philosophy of Arithmetic, trans. D. Willard (Dordrecht: Kluwer, 2003), 438 (K I 26/36).
15. Also in the previously quoted passage, the part that Centrone decided to leave out referred to the domain of objects. In Willard’s translation, it reads in full: “An irreducible axiom system is definite which delimits (or grounds as existing) a formal domain of objects in such a way that for this domain—that is, if one preserves the identity of the axiom system, and if one presupposes that no further objects are defined and thereby assumed as existing—no independent axiom can be added which is constructed purely from the concepts already defined (of course, also, none can be withdrawn, since otherwise the axiom system would not be irreducible).” Husserl, Philosophy of Arithmetic, 434.
16. J. da Silva, “Husserl’s Two Notions of Completeness. Husserl and Hilbert on Completeness and Imaginary Elements in Mathematics,” Synthese 125 (2000), 417–38.
17. M. Hartimo, “Towards Completeness: Husserl on Theories of Manifolds 1890–1901,” Synthese 156 (2007), 281–310.