
A special technique is used to express, and to make calculations involving, gigantic and minuscule numbers. The scheme is like using a mathematical telescope or microscope. How many grains of sand are there on all the beaches in the world? What is the ratio of the diameter of a golf ball to the diameter of the moon? How many times brighter is the sun than a birthday candle?
Subscripts are used to modify the meanings of units, constants, and variables. A subscript is placed to the right of the main character (without spacing) and is set below the base line. Superscripts almost always represent exponents (the raising of a base quantity to a power). A superscript is placed to the right of the main character (without spacing) and is set above the base line.
Numeric subscripts are never italicized. Alphabetic subscripts sometimes are. Here are three examples of subscripted quantities:

Ordinary numbers are not normally modified with subscripts, so you are not likely to see expressions like this:
35
−9.7755π
−16x
Constants and variables can come in many “flavors.” Some physical constants are assigned subscripts by convention. An example is me, representing the mass of an electron at rest. Sometimes, points in three-dimensional space are represented using ordered triples like (x1,x2,x3) rather than (x, y, z). This subscripting scheme becomes especially convenient if you’re talking about points in a higher-dimensional space, for example, (x1,x2,x3,. . .,x26).
Numeric superscripts are never italicized, but alphabetic superscripts usually are. Examples of superscripted quantities are:
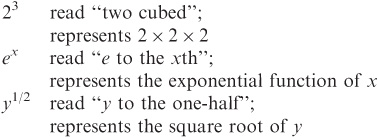
There is a significant difference between 23 and 2! There’s also a big difference between the expression e that symbolizes the natural-logarithm base (approximately 2.71828) and ex, which can represent e raised to a variable power, or which is sometimes used in place of the words “exponential function.” Those little superscripts have a huge effect.
Scientists and engineers express extreme numerical values using power-of-10 notation, also called scientific notation.
A numeral in standard power-of-10 notation is written as follows:
m.n1 n2n3. . .np × 10z
where the dot (·) is a period, written on the base line (not a raised dot indicating multiplication), and is called the radix point or decimal point. The numeral m (to the left of the radix point) is a digit from the set {1, 2, 3, 4, 5, 6, 7, 8, 9}. The numerals n1, n2, n3, and so on up to np (to the right of the radix point) are digits from the set {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}. The value z, which is the power of 10, can be any integer: positive, negative, or zero. Here are some examples of numbers written in standard scientific notation:
2.56 × 106
8.0773 × 10−18
1.000 100
In certain countries, and in some old books and papers, a slight variation on the above theme is used. The alternative power-of-10 notation requires that m always be equal to 0. When the above quantities are expressed this way, they appear as decimal fractions larger than 0 but less than 1, and the value of the exponent is increased by 1 compared with the standard form:
0.256 × 107
0.80773 × 10−17
0.1000 × 101
These expressions represent the same numbers as the previous three, even though they’re written differently.
The multiplication sign in a power-of-10 expression can be denoted in various ways. Most scientists in America use the cross symbol (×), as in the examples shown above. But a small dot raised above the base line (·) is sometimes used to represent multiplication in power-of-10 notation. When written that way, the above numbers look like this in the standard form:
2.56 · 106
8.0773 · 10−18
1.000 · 100
This small dot should not be confused with a radix point. The dot symbol is preferred when multiplication is required to express the dimensions of a physical unit. An example is the kilogram-meter per second squared, which is symbolized kg · m/s2 or kg · m · s−2·
Another alternative multiplication symbol in power-of-10 notation is the asterisk (*). You will occasionally see numbers written like this:
2.56 * 106
8.0773 * 10−18
1.000 * 100
Once in a while, you will have to express numbers in power-of-10 notation using plain, unformatted text. This is the case, for example, when transmitting information within the body of an e-mail message (rather than as an attachment). Some calculators and computers use this system. The letter E indicates that the quantity immediately following is a power of 10. In this format, the above quantities are written:
2.56E6
8.0773E−18
1.000E0
In an alternative format, the exponent is always written with two numerals, and always includes a plus sign or a minus sign, so the above expressions
2.56E+06
8.0773E–18
1.000E+00
Another alternative is to use an asterisk to indicate multiplication, and the symbol ˆ to indicate a superscript, so the expressions look like this:
2.56 * 10 ˆ6
8.0773 * 10 ˆ–18
1.000 * 10 ˆ0
In all of these examples, the numerical values represented are identical. Respectively, if written out in full, they are:
2,560,000
0.0000000000000000080773
1.000
As you can see, power-of-10 notation makes it possible to easily write down numbers that denote unimaginably gigantic or tiny quantities. Consider the following:
2.55 × 1045,589
−9.8988 × 10−7,654,321
Imagine the task of writing either of these numbers out in ordinary decimal form! In the first case, you’d have to write the numerals 255, and then follow them with a string of 45,587 zeros. In the second case, you’d have to write a minus sign, then a numeral zero, then a radix point, then a string of 7,654,320 zeros, then the numerals 9, 8, 9, 8, and 8. Now consider these two numbers:
2.55 × 1045,592
−9.8988 × 10−7,654,318
These look a lot like the first two, don’t they? Look more closely. Both of these new numbers are 1000 times larger than the original two. You can tell by looking at the exponents. Both exponents are larger by 3. The number 45,592 is 3 more than 45,591, and the number −7,754,318 is 3 larger than −7,754,321. (Numbers grow larger in the mathematical sense as they become more positive or less negative.) The second pair of numbers is 3 orders of magnitude larger than the first pair of numbers. They look almost the same here, and they would look essentially identical if they were written out in full decimal form. But they are as different as a meter is from a kilometer.
The order-of-magnitude concept makes it possible to construct number lines, charts, and graphs with scales that cover huge spans of values. Three examples are shown in Fig. 3-1. Drawing A shows a number line spanning 3 orders of magnitude, from 1 to 1000. Illustration B shows a number line spanning 10 orders of magnitude, from 10−3 to 107. Illustration C shows a graph whose horizontal scale spans 10 orders of magnitude, from 10−3 to 107, and whose vertical scale extends from 0 to 10.
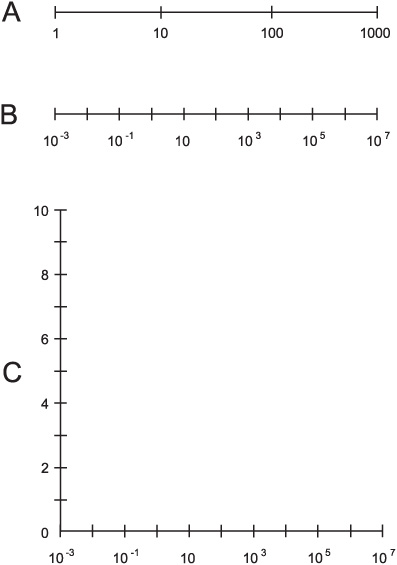
Fig. 3−1. At A, a number line spanning three orders of magnitude. At B, a number line spanning 10 orders of magnitude. At C, a coordinate system whose horizontal scale spans 10 orders of magnitude, and whose vertical scale extends linearly from 0 to 10.
If you’re astute, you’ll notice that while the 0-to-10 scale is the easiest to directly envision, we can’t really say how many orders of magnitude it covers. This is because, no matter how many times you cut a nonzero number to 1/10 its original size, you can never reach zero. In a certain sense, a linear scale (a scale where all the graduations are the same distance apart) ranging from 0 to any positive or negative value covers infinitely many orders of magnitude.
In printed literature, power-of-10 notation is generally used only when the power of 10 is large or small. If the exponent is between −2 and 2 inclusive, numbers are written out in plain decimal form as a rule. If the exponent is −3 or 3, numbers are sometimes written out, and are sometimes written in power-of-10 notation. If the exponent is −4 or smaller, or if it is 4 or larger, values are expressed in power-of-10 notation as a rule.
Some calculators, when set for power-of-10 notation, display all numbers that way, even those that normally shouldn’t be. This can be confusing, especially when the power of 10 is zero and the calculator is set to display a lot of digits. Most people understand the expression 8.407 more easily than 8.407000000E+00, for example, even though they represent the same number.
Special verbal prefixes, known as prefix multipliers, are commonly used by physicists and engineers to express orders of magnitude. Table 3-1 shows the prefix multipliers used for factors ranging from 10−24 to 1024.
By how many orders of magnitude does a terahertz differ from a megahertz? (The hertz is a unit of frequency, equivalent to a cycle per second.)
Refer to Table 3-1. A terahertz represents 1012 hertz, and a megahertz represents 106 hertz. The exponents differ by 6. Therefore, a terahertz differs from a megahertz by 6 orders of magnitude.
What, if anything, is wrong with the number 344.22 × 107 as an expression in power-of-10 notation?
Table 3-1 Prefix multipliers and their abbreviations.
This is a legitimate number, but it is not written in the correct format for scientific notation. The number to the left of the multiplication symbol should be at least 1, but smaller than 10. To convert the number to the proper format, first divide the portion to the left of the “times sign” by 100, so it becomes 3.4422. Then multiply the portion to the right of the “times sign” by 100, increasing the exponent by 2 so it becomes 109. This produces the same number in correct power-of-10 format: 3.4422 × 109.
Let’s see how power-of-10 notation works when we want to do simple arithmetic using extreme numbers.
Addition is best done by converting the numbers to ordinary decimal form before performing the operation. Scientific notation doesn’t work very well with addition unless both numbers happen to be expressed in the same power of 10. Here are a couple of examples:
(3.045 × 105) + (6.853 × 106)
= 304,500 + 6,853,000
= 7,157,500
= 7.1575 × 106
(3.045 × 10_4) + (6.853 × 10−7)
= 0.0003045 + 0.0000006853
= 0.0003051853
= 3.051853 × 10−4
(3.045 × 105) + (6.853 × 10−)
= 304,500 + 0.0000006853
= 304,500.0000006853
= 3.045000000006853 × 105
Subtraction follows the same basic rules as addition:
(3.045 × 105)−(6.853 × 106)
= 304,500 – 6,853,000
= –6,548,500
= –6.548500 × 106
(3.045 × 10−4)−(6.853 × 10−7)
= 0.0003045 − 0.0000006853
= 0.0003038147
= 3.038147 × 10–4
(3.045 × 105)–(6.853 × 10–7)
= 304,500 – 0.0000006853
= 304,499.9999993147
= 3.044999999993147 × 105
When numbers are multiplied in power-of-10 notation, the coefficients (the numbers to the left of the multiplication symbol) are multiplied by each other. Then the exponents are added. Finally, the product is reduced to standard form. Here are three examples, using the same three number pairs as before:
(3.045 × 105) × (6.853 × 106)
= (3.045 × 6.853)×(105 × 106)
= 20.867385 × 10(5+6)
= 20.867385 × 1011
= 2.0867385 × 1012
= (3.045 × 10−4) × (6.853 × 10−7)
= (3.045 × 6.853)×(10−4 × 10−7)
= 20.867385 × 10[−4+(−7)]
= 20.867385 × 10−11
= 2.0867385 × 10−10
= (3.045 × 105)×(6.853 × 10−7)
= (3.045 × 6.853) × (105 × 10−7)
= 20.867385 × 10(5−7)
= 20.867385 × 10−2
= 2.0867385 × 10−1
= 0.20867385
This last number is written out in plain decimal form because the exponent is between −2 and 2 inclusive.
When numbers are divided in power-of-10 notation, the coefficients are divided by each other. Then the exponents are subtracted. Finally, the quotient is reduced to standard form. Here’s how division works, with the same three number pairs we’ve been using:
(3.045 × 105)/(6.853 × 106)
= (3.045/6.853) × (105/106)
≈ 0.444331 × 10(5−6)
= 0.444331 × 10−1
= 0.0444331
(3.045 × 10−4)/(6.853 × 10−7)
= (3.045/6.853) × (10−4/10−7)
≈ 0.444331 × 10[−4−(−7)]
= 0.444331 × 103
= 4.44331 × 102
= 444.331
= (3.045/6.853)×(105/10−7)
≈ 0.444331 × 10[5−(−7)]
= 0.444331 × 1012
= 4.44331 × 1011
Note the squiggly equal signs (≈) in the above equations. This symbol means “is approximately equal to.” The numbers here don’t divide out neatly, so the decimal portions are approximated.
When a number is raised to a power in scientific notation, both the coefficient and the power of 10 itself must be raised to that power, and the result multiplied. Consider this example:
(4.33 × 105)3
= (4.33)3 × (105)3
= 81.182737 × 10(5×3)
= 81.182737 × 1015
= 8.1182727 × 1016
If you are a mathematical purist, you will notice gratuitous parentheses in the second and third lines here. These are included to minimize the chance for confusion. It is more important that the result of a calculation be correct than that the expression be mathematically lean.
Let’s consider another example, in which the exponent is negative:
(5.27 × 10−4)2
=(5.27)2 × (10−4)2
=27.7729 × 10(−4×2)
=27.7729 × 10−8
=2.77729 × 10−7
To find the root of a number in power-of-10 notation, think of the root as a fractional exponent. The square root is equivalent to the 1/2 power. The cube root is the same thing as the 1/3 power. In general, the nth root of a number (where n is a positive integer) is the same thing as the 1/n power. When roots are regarded this way, it is easy to multiply things out in exactly the same way as is done with whole-number exponents. Here is an example:
(5.27×10−4)1/2
= (5.27)1/2× (10−4)1/2
≈2.2956 × 10[−4×(1/2)]
= 2.2956 × 10−2
= 0.02956
Note the squiggly equal sign in the third line. The square root of 5.27 is an irrational number, and the best we can do is to approximate its decimal expansion because it cannot be written out in full. Also, the exponent in the final result is within the limits for which we can write the number out in plain decimal form, so power-of-10 notation is not needed to express the end product here.
State the rule for multiplication in scientific notation, using the variables u and v to represent the coefficients and the variables m and n to represent the exponents.
Let u and v be real numbers greater than or equal to 1 but less than 10, and let m and n be integers. Then the following equation holds true:
(u×10m)(v×10n= uv × 10(m+n)
PROBLEM 3-4
State the rule for division in scientific notation, using the variables u and v to represent the coefficients and the variables m and n to represent the exponents.
Let u and v be real numbers greater than or equal to 1 but less than 10, and let m and n be integers. Then the following equation holds true:
(u×10m)/(v×10n=u/v × 10(m-n)
State the rule for exponentiation in scientific notation, using the variable u to represent the coefficient, and the variables m and n to represent the exponents.
Let u be a real number greater than or equal to 1 but less than 10, and let m and n be integers. Then the following equation holds true:
(u × 10m)n = un× 10(mn)
Exponents m and n can be real numbers in general. They need not be restricted to integer values. But that subject is too advanced for this chapter. We’ll be dealing with them in Chapter 14, when we get to logarithms and exponential functions.
Numbers in the real world are not always exact. This is especially true in observational science and in engineering. Often, we must approximate. There are two ways of doing this: truncation (simpler but less accurate) and rounding (a little more difficult, but more accurate).
The process of truncation involves the deletion of all the numerals to the right of a certain point in the decimal part of an expression. Some electronic calculators use truncation to fit numbers within their displays. For example, the number 3.830175692803 can be shortened in steps as follows:

Rounding is the preferred method of rendering numbers in shortened form. In this process, when a given digit (call it r) is deleted at the right-hand extreme of an expression, the digit q to its left (which becomes the new r after the old r is deleted) is not changed if 0 ≤ r ≤ 4. If 5 ≤ r ≤ 9, then q is increased by 1 (“rounded up”). Most electronic calculators use rounding rather than truncation. If rounding is used, the number 3.830175692803 can be shortened in steps as follows:

PRECEDENCE
In scientific notation, as in regular arithmetic, operations should be performed in a certain order when they appear together in an expression. When more than one type of operation appears, and if you need to simplify the expression, the operations should be done in the following order:
• Simplify all expressions within parentheses, brackets, and braces from the inside out.
• Perform all exponential operations, proceeding from left to right.
• Perform all products and quotients, proceeding from left to right.
• Perform all sums and differences, proceeding from left to right.
Here are two examples of expressions simplified according to the above rules of precedence. Note that the order of the numerals and operations is the same in each case, but the groupings differ.
3.4 × 105 + 5.0 × 10−4
= (3.4 × 105) + (5.0 × 10−4)
= (340,000 + 0.0005)
= 3.400005 × 105
3.4 ×(105 + 5.0)× 104
= 3.4 × 100,005 × 10,000
= 3,400,170,000
= 3.40017 × 109
Suppose you’re given a complicated expression and there are no parentheses, brackets, or braces in it. This is not ambiguous if the above-mentioned rules are followed. Consider this example:
z = −3x3 + 4x2y - 12xy2 - 5y3
If this were written with parentheses, brackets, and braces to emphasize the rules of precedence, it would look like this:
z = [-3(x3)] + {4[(x2)y]} - {12[x(y2)]} - [5(y3)]
Because we have agreed on the rules of precedence, we can do without the parentheses, brackets, and braces. Nevertheless, if there is any doubt about a crucial equation, you’re better off to use a couple of unnecessary parentheses than to make a costly mistake.
What is the value of 2 + 3 × 4 + 5?
First, perform the multiplication operation, obtaining the expression 2 + 12 + 5. Then add the numbers, obtaining the final value 19. Therefore:
2 + 3 × 4 + 5 - 19
The number of significant figures, also called significant digits, in a power-of-10 number is important in real-world mathematics, because it indicates the degree of accuracy to which we know a particular value.
When multiplication, division, or exponentiation is done using power-of-10 notation, the number of significant figures in the result cannot legitimately be greater than the number of significant figures in the least-exact expression. You might wonder why, in some of the above examples, we come up with answers that have more digits than any of the numbers in the original problem. In pure mathematics, where all numbers are assumed exact, this is not an issue. But in real life, and especially in experimental science and engineering, things are not so clean-cut.
Consider the two numbers x = 2.453 × 104 and y = 7.2 × 107. The following is a perfectly valid statement in pure mathematics:
xy = 2.453 × 104 × 7.2 × 107
= 2.453 × 7.2 × 1011
= 17.6616 × 1011
= 1.76616 × 1012
But if x and y represent measured quantities, as in experimental physics for example, the above statement needs qualification. We must pay close attention to how much accuracy we claim.
When you see a product or quotient containing a bunch of numbers in scientific notation, count the number of single digits in the coefficients of each number. Then take the smallest number of digits. That’s the number of significant figures you can claim in the final answer or solution.
In the above example, there are four single digits in the coefficient of x, and two single digits in the coefficient of y. So you must round off the answer, which appears to contain six significant figures, to two. It is important to use rounding, and not truncation. You should conclude that:
xy = 2.453 × 104 × 7.2 × 107
=1.8 × 1012
In situations of this sort, if you insist on being rigorous, you should use squiggly equal signs throughout, because you are always dealing with approximate values. But most folks are content to use ordinary equals signs. It is universally understood that physical measurements are inherently inexact, and writing squiggly lines can get tiresome.
Suppose you want to find the quotient x/y instead of the product xy? Proceed as follows:
x/y = (2.453 × 104)/(7.2 × 107)
= (2.453/7.2)× 10−3
= 0.3406944444. . .× 10−3
= 3.406944444. . . × 10−4
= 3.4 × 10−4
Sometimes, when you make a calculation, you’ll get an answer that lands on a neat, seemingly whole-number value. Consider x =1.41421 and y = 1.41422. Both of these have six significant figures. The product, taking significant figures into account, is:
xy = 1.41421 × 1.41422
= 2.0000040662
= 2.00000
This looks like it’s exactly equal to 2. In pure mathematics, 2.00000 = 2. But in practical math, those five zeros indicate how near the exact number 2 we believe the resultant to be. We know the answer is very close to a mathematician’s idea of the number 2, but there is an uncertainty of up to plus-or-minus 0.000005 (written ±0.000005). When we claim a certain number of significant figures, zero is as important as any of the other nine digits in the decimal number system.
When measured quantities are added or subtracted, determining the number of significant figures can involve subjective judgment. The best procedure is to expand all the values out to their plain decimal form (if possible), make the calculation as if you were a pure mathematician, and then, at the end of the process, decide how many significant figures you can reasonably claim.
In some cases, the outcome of determining significant figures in a sum or difference is similar to what happens with multiplication or division. Take, for example, the sum x + y, where x = 3.778800 × 10–6 and y - 9.22 × 10–7. This calculation proceeds as follows:
x = 0.000003778800
y = 0.000000922
x + y = 0.0000047008
= 4.7008 × 10–6
= 4.70 × 10–6
In other instances, one of the values in a sum or difference is insignificant with respect to the other. Let’s say that x =3.778800 × 104, while y = 9.22 × 10–7. The process of finding the sum goes like this:
x = 37,788.00
y = 0.000000922
x + y = 37,788.000000922
= 3.7788000000922 × 104
In this case, y is so much smaller than x that it doesn’t significantly affect the value of the sum. Here, it is best to regard y, in relation to x or to the sum x + y, as the equivalent of a gnat compared with a watermelon. If a gnat lands on a watermelon, the total weight does not appreciably change, nor does the presence or absence of the gnat have any effect on the accuracy of the scales. We can conclude that the “sum” here is the same as the larger number. The value y is akin to a nuisance or a negligible error:
x + y = 3.778800 × 104
What is the product of 1.001 × 105 and 9.9 × 10–6, taking significant figures into account?
Multiply the coefficients and the powers of 10 separately:
(1.001 × 105)(9.9 × 10−6)
= (1.001 × 9.9)× (105 × 10–6)
= 9.9099 × 10−1
= 0.99099
We must round this to two significant figures, because that is the most we can legitimately claim. The expression does not have to be written out in power-of-10 form. Therefore:
(1.001 × 105)(9.9 × 10-6)= 0.99
Refer to the text in this chapter if necessary. A good score is eight correct. Answers are in the back of the book.
1. Two numbers differ in size by exactly 4 orders of magnitude. This is a factor of:
(a) 4
(b) 16
(c) 256
(d) 10,000
2. Suppose the population of a certain city is found to be 226,496 people. What is this expressed to three significant figures in power-of-10 notation?
(a) 2.26 × 105
(b) 2.27 × 105
(c) 227,000
(d) 2.26E+06
3. Suppose we invent a new unit called the widget (symbol: Wi). What should we call a quantity of 10–12 Wi?
(a) One milliwidget (1 mWi).
(b) One nanowidget (1 nWi).
(c) One picowidget (1 pWi).
(d) One kilowidget (1 kWi).
4. What is the value of 5 × 32 - 5?
(a) 20
(b) 40
(c) 220
(d) There is no way to tell; this is an ambiguous expression.
5. What is 8.899 × 105 - 2.02 × 10−12, taking significant figures into account?
(a) 2.02 × 10−12
(b) 9 × 105
(c) 6.88 × 105
(d) 8.899 × 105
6. What is the product of 8.72 × 105 and 6.554 × 10−5, taking significant figures into account?
(a) 57.2
(b) 57.15
(c) 57.151
(d) 57.1509
7. Suppose a mathematical expression contains addition, multiplication, and exponentiation, all without any parentheses, brackets, or braces. Which operation should be performed last?
(a) The exponentiation.
(b) The multiplication.
(c) The addition.
(d) It doesn’t matter.
8. Suppose we measure a quantity and get 5.53 × 104 units, accurate to three significant figures. Within what range of whole-number units can we say the actual value is?
(a) 55,299 units to 56,301 units.
(b) 55,290 units to 56,310 units.
(c) 55,250 units to 55,349 units.
(d) 55,200 units to 55,299 units.
9. What is the proper power-of-10 way of writing 416,803?
(a) 416.803 × 103
(b) 41.6803E+04
(c) 0.0416803 × 107
(d) None of the above.
10. What is the order in which the operations should be performed in the following expression?
S = x(y + z)- w2
(a) Addition, then subtraction, then exponentiation, and finally multiplication.
(b) Addition, then exponentiation, then multiplication, and finally subtraction.
(c) Multiplication, then exponentiation, then subtraction, and finally addition.
(d) Subtraction, multiplication, exponentiation, and finally addition.