
Rates of change can sometimes be expressed in terms of mathematical constants. In this chapter, we’ll examine a few of the ways this can happen.
The simplest changeable quantities can be written as lists of numbers whose values repeatedly increase or decrease by a fixed amount. Here are some examples:
A = 1, 2, 3, 4, 5, 6
B = 0, −1, −2, −3, −4, −5
C = 2, 4, 6, 8
D = −5, −10, −15, −20
E = 4, 8, 12, 16, 20, 24, 28,. . .
F = 2, 0, −2, −4, −6, −8, −10,. . .
The first four of these sequences are finite. The last two are infinite, as indicated by the three dots following the last term in each case.
In each of the six sequences shown above, the values either increase (A, C, and E) or else they decrease (B, D, and F). In all six sequences, the “spacing” between numbers is constant throughout. Note:
• The values in A always increase by 1.
• The values in B always decrease by 1.
• The values in C always increase by 2.
• The values in D always decrease by 5.
• The values in E always increase by 4.
• The values in F always decrease by 2.
Each sequence has a starting point or first number. After that, succeeding numbers can be predicted by repeatedly adding a constant. If the added constant is positive, the sequence increases. If the added constant is negative, the sequence decreases.
Let s0 be the first number in a sequence S, and let c be a constant. Imagine that S can be written in this form:
S = s0, (s0 + c), (s0 + 2c), (s0 + 3c),. . .
for as far as the sequence happens to go. Such a sequence is called an arithmetic sequence or an arithmetic progression. In this context, the word “arithmetic” is pronounced “air-ith-MET-ick.”
The numbers s0 and c can be whole numbers, but that is not a requirement. They can be fractions such as 2/3 or −7/5. They can be irrational numbers such as the square root of 2. As long as the separation between any two adjacent terms in a sequence is the same, the sequence is an arithmetic progression. In fact, even if s0 and c are both equal to 0, the resulting sequence is an arithmetic progression.
A series is, by definition, the sum of all the terms in a sequence. For any arithmetic sequence, the corresponding arithmetic series can be defined only if the sequence is finite. That means it must have a finite number of terms. For the above sequences A through F, let the corresponding series be called A+
A+ = 1 + 2 + 3 + 4 + 5 + 6 = 21
B+ = 0 + (−1) + (−2) + (−3) + (−4) + (−5) = −15
C+ = 2 + 4 + 6 + 8 = 20
D+ = (−5) + (−10) + (−15) + (−20) = −50
E+ is not defined
F+ is not defined
When you see a long sequence of numbers, you should be able to tell without much trouble whether or not it’s an arithmetic sequence. If it isn’t immediately obvious, you can conduct a test: subtract each number from the one after it. If all the differences are the same, then the sequence is an arithmetic sequence.
Imagine that you see a long sequence of numbers, and some of the intermediate values are missing. An example of such a situation is shown in Table 14–1. It’s not too hard to figure out what the missing values are, once you realize that this is an arithmetic sequence in which each term has a value that is 3 larger than the term preceding it. The 4th term has a value of 14, and the 9th term has a value of 29. The process of filling in missing intermediate values in a sequence is a form of interpolation. We might call the process of filling in Table 14–1 arithmetic interpolation.
It is possible to “predict” what the next numbers are, or would be if a series were lengthened. Table 14–2 illustrates an example of this type of situation.
Table 14–1 A sequence with some intermediate values missing. They can be filled in by interpolation.

Table 14–2 Extension of an arithmetic sequence can be done by extrapolation.

The values keep getting smaller by 2. The 7th number is 20. Therefore, the 8th number must be 18, the 9th number must be 16, the 10th number must be 14, and the 11th number must be 12. This extension process constitutes a form of extrapolation, so we can call the process of filling in Table 14–2 arithmetic extrapolation.
An arithmetic sequence looks like a set of points when plotted in Cartesian (rectangular) coordinates. The term number or position in the sequence is depicted on the horizontal axis, and it plays the role of the independent variable. The term value is plotted against the vertical axis, and it plays the role of the dependent variable.
Figure 14–1 shows examples of two arithmetic sequences as they appear when graphed. (The dashed lines connect the dots, but they aren’t actually parts of the sequences.) Note that the dashed lines are straight. One sequence is increasing, and the dashed line connecting this set of points ramps upward as you go toward the right. Because this sequence is finite, the dashed line ends at the final point (6,6). The other sequence is decreasing, and the dashed line for it ramps downward as you go toward the right. This sequence is infinite, as shown by the three dots at the end of the string of numbers, and also by the arrow at the right-hand end of the dashed line.
When any arithmetic sequence is graphed in this way, its points lie along a straight line. The slope m of the line depends on whether the sequence increases (positive slope) or decreases (negative slope). In fact, m is exactly equal to the constant c.
When interpolating or extrapolating any sequence, you must be sure to check out enough values to know that you’re looking at a true sequence, and not just a string of numbers. If the string has only two or three values that increase by the same amount, you don’t have enough information to be
Fig. 14–1. When the values of the terms in an arithmetic sequence are plotted in rectangular coordinates, the points always fall along straight lines.
sure you’re observing an arithmetic sequence. You need at least four or five values.
There’s another way to go wrong when attempting to interpolate a sequence. If the missing values are alternate numbers, you can be deceived. The examples in Tables 14–3A, B, and C provide a vivid illustration of how far astray you can go if you jump to conclusions about filling in a sequence with alternate terms missing! The plot in Fig. 14–2 illustrates this graphically.
Consider again the general formula for an arithmetic sequence S:
S = s0, (s0 + c), (s0 + 2c), (s0 + 3c),. . .
Suppose s0 = 5 and c = 3. List the first 10 terms of an infinite sequence that follows this form and has these values.
The first number is 5, and the numbers increase by 3 every time thereafter. So:
S = 5, 8, 11, 14, 17, 20, 23, 26, 29, 32, . . .
Is the following sequence an arithmetic sequence? If so, what are the values s0 (the starting value) and c (the constant of change)?
S = 2, 4, 8, 16, 32, 64, . . .
This is not an arithmetic sequence. The numbers do not increase at a steady rate. There is a pattern, however: each number in the sequence is twice as large as the number before it. We’ll look at this type of series shortly.
Is the following sequence an arithmetic sequence? If so, what are the values s0 (the starting value) and c (the constant of change)?
S = 100, 135, 170, 205, 240, 275, 310, . . .
Fig. 14–2. Graphical portrayal of mistaken interpolation.
This is an arithmetic sequence, at least for the numbers shown (the first seven terms). In this case, s0 = 100 and c = 35.
Another type of progression has values that are repeatedly multiplied by some constant. Here are a few examples:
G = 1, 2, 4, 8, 16, 32
H = 1, −1, 1, −1, 1, −1, . . .
I = 1, 10, 100, 1000
J = −5, −15, −45, −135, −405
K = 3, 9, 27, 81, 243, 729, 2187,. . .
L = ½, ¼, 1/8, 1/16, 1/32,. . .
Sequences G, I, and J are finite. Sequences H, K, and L are infinite, as indicated by the three dots following the last term in each sequence.
Examine the six sequences above. Upon casual observation, they appear to be much different from one another. But in all six sequences, each term is a specific and constant multiple of the term before it. Note:
• The values in G progress by a constant factor of 2.
• The values in H progress by a constant factor of −1.
• The values in I progress by a constant factor of 10.
• The values in J progress by a constant factor of 3.
• The values in K progress by a constant factor of 3.
• The values in L progress by a constant factor of ½.
Each sequence has a starting point or first number. After that, succeeding numbers are generated by repeated multiplication by a constant. If the constant is positive, the values in the sequence stay “on the same side of 0” (they either remain positive or remain negative). If the constant is negative, the values in the sequence “alternate to either side of 0” (if a given term is positive, the next is negative, and if a given term is negative, the next is positive).
Let t0 be the first number in a sequence T, and let k be a constant. Imagine that T can be written in this form:
T = t0, t0k, t0k2, t0k3, t0k4, . . .
for as long as the sequence goes. Such a sequence is called a geometric sequence or a geometric progression.
If k happens to be equal to 1, the sequence consists of the same number, listed over and over. If k = −1, the sequence alternates between t0 and its negative. If t0 is less than −1 or greater than 1, the values get farther and farther from 0. If t0 is between (but not including) −1 and 1, the values get closer and closer to 0. If t0 = 1 or t0 = −1, the values stay the same distance from 0.
The numbers t0 and k can be whole numbers, but this is not a requirement. As long as the multiplication factor between any two adjacent terms in a sequence is the same, the sequence is a geometric progression. In the last sequence, k = ½. This is an especially interesting sequence, as we’ll see in a moment.
For a geometric sequence, the corresponding geometric series, which is the sum of all the terms, can always be defined if the sequence is finite. Sometimes the sum of all the terms can be defined even if the sequence is infinite.
For the above sequences G through L, let the corresponding series be called G+ through L+. Then:
G+ = 1 + 2 + 4 + 8 + 16 + 32 = 63
H+ = 1 −1 + 1 −1 + 1 −1 + . . . = ?
I+ = 1 + 10 + 100 + 1000 = 1111
J+ = −5 −15 −45 −135 −405 = −605
K+ = “blows up” and is not defined
L+ = ½ + ¼ + 1/8 + 1/16 + 1/32 + . . . = ?
The finite series G+, I+, and J+ are straightforward enough. The infinite series H+ seems unable to settle on 0 or 1, repeatedly hitting both. It’s tempting to say that H+ is a number with two values at once, and a fascinating theory can be built around the notion of multi-valued numbers. But in conventional math, we have to say that H+ is not definable as a number. The infinite series K+ runs off “out of control” and is an example of a divergent series, because its values keep on getting farther and farther away from 0 without limit.
That leaves us with L+. What’s going on with this series?
When we have an infinite sequence and we start to add up its numbers, we get another sequence of numbers representing the sums. These sums are called partial sums. For the above sequences H, K, and L, the partial sums, which we will denote using asterisk superscripts instead of plus-sign subscripts, go like this:
H = 1, −1, 1, −1, 1, −1, . . .
H* = 1, 0, 1, 0, 1, 0, . . .
K = 3, 9, 27, 81, 243, 729, 2187, . . .
K* = 3, 12, 39, 120, 363, 1092, 3279, . . .
L = ½, ¼, 1/8, 1/16, 1/32
L* = ½, ¾, 7/8, 15/16, 31/32 . . .
The partial sums denoted by H* and K* don’t settle down on anything. But the partial sums denoted by L* seem to approach 1. They aren’t skyrocketing off into uncharted territory, and they aren’t alternating between or among any multiple numbers. They are under control. The partial sums in L* seem to have a clear destination that they could reach, if only they had an infinite amount of time to get there.
It turns out that L+, representing the sum of the infinite string of numbers L, adds up to exactly 1! We can demonstrate this by observing that the partial sums “close in” on a value of 1. As the position in the sequence of partial sums, L*, gets farther and farther along, the denominators keep doubling, and the numerator is always 1 less than the denominator. In fact, if we want to find the nth number Ln in the sequence of partial sums L*, we can calculate it by using the following formula:
Ln = (2n −1)/2n
As n becomes large, 2n becomes large much faster, and the proportional difference between 2n −1 and 2n becomes smaller and smaller. When n is extremely large, the quotient (2n −1)/2n is almost exactly equal to 1. We can make the quotient as close to 1 as we want by going out far enough in the series of partial sums, but we can never make it bigger than 1. The series L+ is said to converge on the number 1, and as such it is an example of a convergent series.
When you see a long sequence of numbers, you can usually figure out, without much effort, whether or not it’s a geometric sequence. If it isn’t immediately obvious, you can conduct a test: divide each number by the one before it. If all the quotients are the same, then the sequence is a geometric sequence.
Now imagine, as you did with the arithmetic sequences earlier in this chapter, that you’re given a long string of numbers, but some of them are missing. An example of such a situation is shown in Table 14–4. It’s easy to determine the missing values, once you notice that this is a geometric sequence in which each term is twice as big as the term preceding it. The 4th term has a value of 8, and the 9th term has a value of 256. We can call the process of filling in Table 14–4 an example of geometric interpolation.
Table 14–4 Another example of a sequence with some intermediate values missing. The missing values can be filled in by interpolation.

Table 14–5 Extension of a geometric sequence can be done by extrapolation.

Just as a geometric sequence can be interpolated, it’s also possible to “predict” what the next numbers are, or would be if the series were lengthened. Table 14–5 illustrates an example of this type of situation. The values in this sequence are repeatedly cut in half. The 7th number is ½. Therefore, the 8th number must be ¼, the 9th number must be 1/8, the 10th number must be 1/16, and the 11th number must be 1/32. We can call the process of filling in Table 14–5 geometric extrapolation.
A geometric sequence, like an arithmetic sequence, looks like a set of points when plotted on a Cartesian plane. Figure 14–3 shows examples of two geometric sequences as they appear when graphed. (The dashed curves aren’t actually parts of the sequences.) Note that the dashed curves are not straight, but they are smooth.
One of the sequences in Fig. 14–3 is increasing, and the dashed curve connecting this set of points goes upward as you move to the right. Because this sequence is finite, the dashed curve ends. The other sequence is decreasing, and the dashed curve goes downward and approaches 0 as you move to the right. This sequence is infinite, as shown by the three dots at the end of the string of numbers, and also by the arrow at the right-hand end of the dashed curve.
If a geometric sequence has a negative factor, that is, if k < 0, the plot of the points alternates back and forth on either side of 0. In this case, the points fall along two different curves, one above the horizontal axis and
Fig. 14–3. Plots of values of the terms in two different geometric sequences.
the other below. If you want to see what happens in a case like this, try plotting an example. Try setting t0 = 64 and k = −½, and plot the resulting points.
Suppose you get a certificate of deposit (CD) at your local bank for $1000.00, and it earns interest at the annualized rate of exactly 5% per year. How much will this CD be worth at the end of 6 years, assuming a constant interest rate? Round all figures off to the nearest cent at the end of every year.
The CD will be worth $1340.10 after 6 years. To calculate this, multiply $1000 by 1.05, then multiply this result by 1.05, and repeat this process a total of six times. The resulting numbers are a geometric progression.
• After 1 year: $1000.00 × 1.05 = $1050.00
• After 2 years: $1050.00 × 1.05 = $1102.50
• After 3 years: $1102.50 × 1.05 = $1157.63
• After 4 years: $1157.63 × 1.05 = $1215.51
• After 5 years: $1215.51 × 1.05 = $1276.29
• After 6 years: $1276.29 × 1.05 = $1340.10
Is the following sequence a geometric sequence? If so, what are the values t0 (the starting value) and k (the factor of change)?
T = 3, −6, 12, −24, 48, −96, . . .
This is a geometric sequence. The numbers change by a factor of −2. Each number in the sequence is the product of −2 and the number before it. In this case, t0 = 3 and k = −2.
Is the following sequence a geometric sequence, an arithmetic sequence, or neither? Is there any pattern to it? If so, what is the pattern?
T = 10, 13, 17, 22, 28, 35, 43, . . .
This is not a geometric sequence. It isn’t an arithmetic sequence either. But there is a pattern. The difference between the first and second numbers is 3, the difference between the second and third numbers is 4, the difference between the third and fourth numbers is 5, and so on; the difference keeps increasing by 1 for each succeeding pair of numbers. (Some sequences have patterns that are subtle indeed. Computers can be helpful in analyzing such sequences.)
Suppose a particular species of cell undergoes mitosis (splits in two) without fail every half hour, precisely on the half hour. We take our first look at a petri dish at 12:59 p.m., and find 3 cells. At 1:00 p.m., mitosis occurs for all the cells at the same time, and then there are 6 cells in the petri dish. At 1:30 p.m., mitosis occurs again, and then there are 12 cells. How many cells are there in the petri dish at 4:01 p.m.?
There are 3 hours and 2 minutes between 12:59 p.m. and 4:01 p.m. This means that mitosis takes place 7 times: at 1:00, 1:30, 2:00, 2:30, 3:00, 3:30, and 4:00. Table 14–6 illustrates the scenario. There are 384 cells at 4:01 p.m., just after the 7th mitosis event that occurs at 4:00.
Table 14–6 Table for Problem 14–7.

The idea of the geometric progression, in which a value is repeatedly multiplied by some constant, can be extended into the general realm of continuous-curve functions. In an exponential function, a constant is raised to some variable power.
Until now, the notion of “raising something to a power” has been kept simple because we’ve dealt only with whole-number exponents. For example, when a variable x is raised to the power of 5, we write it as x5. When some constant k is raised to the power of 10, we write it as k10. But what about exponents that are not whole numbers? What, for example, is meant by the expression x1.5 or 72/3 or z−8/5? What if an exponent is an irrational number such as π, the ratio of a circle’s circumference to its diameter?
All scientific calculators, and even some ordinary ones, have a key marked something like “xy” or “xˆy.” This is literally read as, “x to the yth power.” To find the value of, say, 31.5, you first enter the number 3, then you hit the “xy” or “xˆy” key, and finally you enter 1.5. This should give you a result of 5.19615. . . . To find the value of 32.88, you first enter the number 3, then you hit the “xy” or “xˆy” key, and finally you enter 2.88. This will give you 23.6651. . . . You can even find the value of 3 raised to some power between 0 and 1, or less than 0 (that is, negative).
The general term exponential refers to the raising of a constant to some power, where that power can be any sort of number. An exponential function is the raising of a constant to a variable power. Suppose the following relationship exists among three real numbers a, x, and y:
y = ax
In this case, x is the independent variable and y is the dependent variable. The constant a is called the base.
The two most common exponential-function bases are 10 and the natural exponential base. The natural exponential base is symbolized by the lowercase, italicized letter e, and is an irrational number. It is approximately equal to 2.71828.
Base–10 exponentials are also known as common exponentials. For example:
10−3000 = 0.001
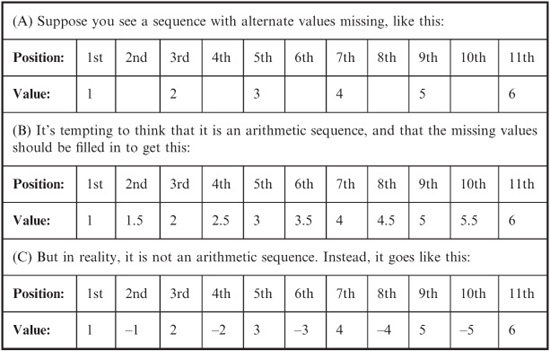
Figure 14–4 is an approximate graph of the function y = 10x. The domain of this function encompasses the entire set of real numbers. The range is limited to positive real numbers only.
Base-e exponentials are also known as natural exponentials. For example:
e−3.000 ≈ 2.71828−3.000 ≈ 0.04979
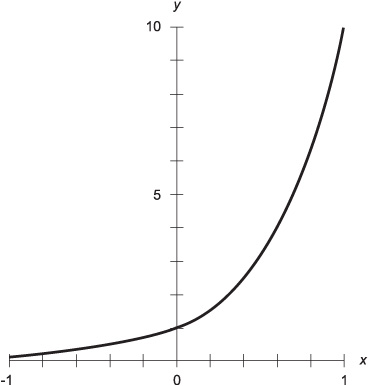
Fig. 14–4. Approximate graph of the common exponential function.
Fig. 14–5. Approximate graph of the natural exponential function.
Figure 14–5 is an approximate graph of the function y = ex. The domain encompasses the entire set of real numbers. The range is limited to positive real numbers only.
Common and natural exponentials are easy to find. All you have to do is get, and use, a scientific calculator. The calculator can show us only the first few digits of the result, so the answer is usually not exact, but it’s a good enough approximation for most purposes.
Exponential functions allow us to manipulate numbers in ways that can be useful in the sorts of work you’re likely to encounter these days. Here are some of the most common “laws” concerning exponentials. These laws, like the basic rules of arithmetic, are worth memorizing. That idea is repulsive to some folks, but it’s the truth. It is good to know the following rules by heart.
Suppose that x is a real number. The reciprocal of the common (base–10) exponential of x is equal to the common exponential of the negative of x:
1/(10x) = 10−x
The reciprocal of the natural (base-e) exponential of x is equal to the natural exponential of the negative of x:
1/(ex)= e−x
Let x and y be real numbers. The product of the common exponentials of x and y is equal to the common exponential of the sum of x and y. You might recognize this rule from all the way back in Chapter 3, when we worked with power-of–10 notation. When two numbers in scientific notation are multiplied, the powers of 10 add:
(10x)(10y) = 10(x+y)
The product of the natural exponentials of x and y is equal to the natural exponential of the sum of x and y:
(ex)(ey) = e(x+y)
Let x and y be real numbers. The ratio (quotient) of the common exponentials of x and y is equal to the common exponential of the difference between x and y. This rule, too, appeared in Chapter 3. When two extreme numbers are divided in scientific notation, their powers of 10 subtract:
10x/10y = 10(x−y)
The ratio of the natural exponentials of x and y is equal to the natural exponential of the difference between x and y:
ex/ey = e(x−y)
Let x and y be real numbers. The yth power of the quantity 10x is equal to the common exponential of the product xy:
(10x)y = 10(xy)
The yth power of the quantity ex is equal to the natural exponential of the product xy:
(ex)y = e(xy)
Suppose a scientist, Professor P, has developed a theory to the effect that the world population increases exponentially with time. Imagine that the present population of the world has been accurately determined, and we assign this number (whatever it happens to be) the value 100%, or “exactly 1 population unit.” Professor P then tells us that every 100 years, the population increases by precisely a factor of 10, known as an order of magnitude. Suppose the theory of Professor P is correct, and that the theory remains valid for millennia to come. What will be the world’s “people count,” in population units, 100 years from now? What will it be in 200 years? In 300 years?
In 100 years (1 century from now), the world’s “people count” will be 101, or 10, population units. In 200 years (2 centuries), it will be 102, or 100, population units. In 300 years, it will be 103, or 1000, population units. This means that in a century, the world will contain 10 times as many people as it does now; in 2 centuries the world will have 100 times as many people as it does now; in 3 centuries there will be 1000 times as many people on the planet as there are today. Let’s hope that Professor P’s theory doesn’t hold true that long!
Write down an exponential equation showing the world population p, in population units, as a function of time t, in centuries, according to the theory of Professor P. Assume that t = 0 right now.
The equation looks like this:
p = 10t
You can check this out by plugging in values for t. If t = 0, then p = 100 = 1. If t = 1, then p = 101 = 10. If t = 2, then p = 102 = 100. If t = 3, then p = 103 = 1000. These results agree with those obtained in Solution 14–8.
According to the theory of Professor P, how many people, in population units, will inhabit the world 150 years from now?
To solve this problem, we use the equation from Solution 14–9, and plug in the value t = 1.5. This gives us a population p as follows:
p = 101.5
How do we calculate the value of an expression like 101.5? It’s easy if you have a scientific calculator that includes exponential functions. Use the “xy” or “xˆy” key. Your calculator might also have a “10x” key. In any event, you should obtain the value p = 31.62, which we can round off to 32. This means that in 150 years, according to the theory of Professor P, the world population will be 32 times as great as it is right now.
A logarithm (sometimes called a log) is an exponent to which a constant is raised to obtain a given number. Suppose the following relationship exists among three real numbers a, x, and y:
ay = x
Then y is the base-a logarithm of x. This expression is written
y =logax
The two most common logarithm bases are 10 and e, the same as the exponential bases.
Base–10 logarithms are also known as common logarithms or common logs. In equations, common logarithms are denoted by writing “log” without a subscript, or occasionally “log” with a subscript 10. For example:
log 100 = log10100 = 2.00
Fig. 14–6. Approximate graph of the common logarithm function.
Figure 14–6 is an approximate graph of the function y = log x. The domain is limited to the positive real numbers. The range encompasses the entire set of real numbers.
Base-e logarithms are also called natural logs or Napierian logs. In equations, the natural-log function is usually denoted “ln” or “loge.” For example:
In 2.71828 = loge2.71828 ≈ 1.00000
Figure 14–7 is an approximate graph of the function y = In x. The domain is limited to the positive real numbers, just as in the case of the common log function. The range of the natural log function, also like the common log function, encompasses the entire set of real numbers.
Common and natural logarithms can be easily and quickly found using a scientific calculator. That’s all you have to know for practical purposes.
Fig. 14–7. Approximate graph of the natural logarithm function.
Once you have learned which keys to use (the instructions can help you with this if it isn’t obvious), finding logarithms is painless.
Logarithmic functions, like their exponential-function counterparts, make it possible to work with numbers in unique ways. And, as with exponentials, logarithms have a way of coming up in work nowadays. Here are some rules you should know about logarithmic functions.
If x and y are both positive real numbers, the common logarithm of the product is equal to the sum of the common logarithms of the individual numbers:
log xy = log x + log y
The natural logarithm of the product is equal to the sum of the natural logarithms of the individual numbers:
In xy = In x + In y
Let x and y be positive real numbers. The common logarithm of their ratio, or quotient, is equal to the difference between the common logarithms of the individual numbers:
log(x/y) = log x − log y
The natural logarithm of their ratio, or quotient, is equal to the difference between the natural logarithms of the individual numbers:
ln(x/y) = ln x − ln y
Let y be a real number, and let x be a positive real number. The common logarithm of x raised to the power y can be expressed as a product:
log xy = y log x
The natural logarithm of x raised to the power y can be expressed as a product:
In xy = y In x
Let x be a positive real number. The common logarithm of the reciprocal of x is equal to the negative of the common logarithm of x, as follows:
log(1/x) = −logx
The natural logarithm of the reciprocal of x is equal to the negative of the natural logarithm of x, as follows:
In(1/x) = −In x
Let x be a positive real number. Let y be any real number except 0. The common logarithm of the yth root of x (also denoted as x to the 1/y power) is given by:
log x(1/y) = (log x)/y
The natural logarithm of the yth root of x (also denoted as x to the 1/yth power) is given by:
ln x(1/y) = (ln x)/y
If you have ever done serious work with high-fidelity (hi-fi) equipment, you’ve heard about units called decibels, symbolized dB. The decibel is a logarithmic unit. It is used to express the relative intensity of sound waves, radio signals, and even visible light.
The concept of the decibel evolved because our senses perceive variable effects according to the logarithm of the intensity, not in direct proportion to the intensity. This is a defense mechanism against the harshness of the world. If we perceived phenomena such as sound and light in direct proportion to their true levels, the variability would be overwhelming. We might not be able to hear someone whispering a meter away, yet a trumpet blast from across a room would knock us out. We might not be able to see the full moon on a clear night, but we would be blinded by the light of a cloudy day.
Imagine two sounds having the same frequency and wave shape, such as middle C played on a trombone. Call them “sound number 1” and “sound number 2.” Imagine that a trombone plays note 1, pauses for a moment, and then plays note 2. Notes 1 and 2 differ in intensity by 1 dB if the change is just barely enough so that a listener can tell the difference when the change is expected. This turns out to be a difference in audio power of approximately 26%, or a ratio of 1.26:1. If the change is not expected, the smallest detectable audio power difference is about 100%, or a ratio of 2:1 (believe it or not).
If P1 is the power (in watts) contained in sound 1 and P2 is the power (also in watts) contained in sound 2, their relationship in decibels, R, is given by this formula:
R = 10log(P2/P1)
This formula also works for radio-signal power and light-brilliance power. If we know the relationship R in decibels between phenomenon number 1 and phenomenon number 2, then the actual power ratio P2/P1 is a common exponential function of R, as follows:
P2/P1 = 10(R/10)
Suppose two sounds differ in volume by a power ratio of 2:1, which allegedly is the smallest difference a listener can detect if the change is not anticipated. What is the ratio in decibels?
Use the formula above. Let P2 = 2 and P1 = 1. Then:
R = 10log(P2/P1)
= 10log(2/1)
= 10 log 2
= 10 × 0.30103
= 3.0103 dB
We can round this off to 3 dB.
Suppose you are listening to a musical recording and the needles on your hi-fi amplifier are peaking at a reading of 0 dB. You boost the volume until the needles kick up to +10 dB. By what factor have you increased the audio power level?
In the formula, set R = 10 because the change in sound volume is +10 dB. From this, calculate the audio power ratio:
P2/P1 = 10(R/10)
= 10(10/10)
= 101
= 10
This means you have increased the audio power by a factor of 10:1.
Logarithms make it possible to graph certain functions that don’t lend themselves to clear portrayal on the rectangular (Cartesian) coordinate plane. This is done by making the increments on one or both axes proportional to the logarithm of the variable value, rather than directly proportional to the variable value. A scale or axis in which the sizes of the increments are in direct proportion to the variable value is called a linear scale or a linear axis. A scale or axis in which the sizes of the increments are in proportion to the logarithm of the variable value is called a logarithmic scale or a logarithmic axis.
Figure 14–8 shows semilogarithmic (semilog) coordinates for defining points in a portion of the xy-plane. The independent-variable (x) axis is linear, and the dependent-variable (y) axis is logarithmic. In this example, functions can be plotted with domains and ranges as follows:
−1 ≤ x ≤ 1
0.1 ≤ y ≤ 10
The y axis in Fig. 14–8 spans two orders of magnitude (powers of 10). The span could be larger or smaller than this, but in any case the y values cannot extend all the way down to 0. This is because the logarithm of 0 is undefined.
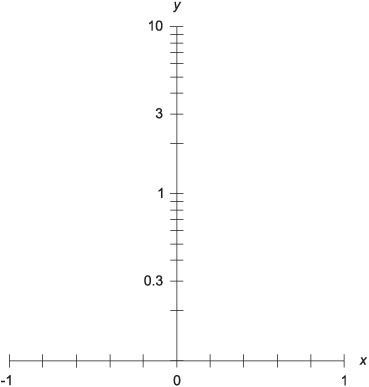
Fig. 14–8. Semilog xy-plane with linear x axis and logarithmic y axis.
Fig. 14–9. Semilog xy-plane with logarithmic x axis and linear y axis.
Figure 14–9 shows a different sort of semilog coordinate system for defining points in a portion of the xy-plane. Here, the independent-variable (x) axis is logarithmic, and the dependent-variable (y) axis is linear. In this example, functions can be plotted with domains and ranges as follows:
0.1 ≤ x ≤ 10
−1 ≤ y ≤ 1
The x axis in Fig. 14–9 spans two orders of magnitude. The span could be larger or smaller, but in any case the x values cannot extend all the way down to 0.
Figure 14–10 shows log-log coordinates for defining points in a portion of the xy-plane. Both axes are logarithmic. In this example, functions can be plotted with domains and ranges as follows:
0.1 ≤ x ≤ 10
0.1 ≤ y ≤ 10
Fig. 14–10. Log-log xy-plane. Both axes are logarithmic.
Fig. 14–11. Illustration for Problem 14–13.
The axes in Fig. 14–10 span two orders of magnitude. The span of either axis could be larger or smaller, but in any case the values cannot extend all the way down to 0.
In semilog coordinates, graph the world population p, in population units, as a function of time t, in centuries, according to the theory of Professor P. Show the function over the domain from t = 0 (right now) to t = 2 (2 centuries, or 200 years, from now). Use a linear scale for the horizontal axis and a logarithmic scale for the vertical axis.
Refer to Fig. 14–11. Note that the graph is a straight line. One of the major assets of semilogarithmic coordinates is the fact that they can show exponential and logarithmic functions as straight lines, rather than as curves.
Refer to the text in this chapter if necessary. A good score is eight correct. Answers are in the back of the book.
1. Imagine a frog that jumps halfway to a wall. After 10 seconds, it jumps halfway to the wall again. After another 10 seconds, it jumps halfway to the wall once again. It keeps repeating this process. In theory, how long will it take to reach the wall after its first jump?
(a) More information is needed to answer this question.
(b) 102, or 100, seconds.
(c) 210, or 1024, seconds.
(d) It will never reach the wall.
2. Imagine a frog that jumps halfway to a wall. After 4 seconds, it jumps halfway to the wall again. After 2 seconds, it jumps halfway to the wall again. After 1 second, it jumps halfway to the wall again. The frog keeps repeating this process, but the intervals between jumps keep getting half as long: ½ second, then ¼ second, and so on. In theory, how long will it take to reach the wall, if we start timing it the moment it finishes its first jump?
(a) More information is needed to answer this question.
(b) 8 seconds.
(d) 28, or 256, seconds.
3. Consider this sum of numbers:
S = 4 −4 + 4 −4 + 4 −4 + 4 −4 + . . .
Which of the following statements is true?
(a) S is a convergent series.
(b) S is an arithmetic series.
(c) S is an infinite series.
(d) S is not a series.
4. What is the base–10 logarithm of 0.00001?
(a) e/10
(b) −e/10
(c) 5
(d) −5
5. Which of the following points cannot, in theory, be shown on a log-log (x,y) coordinate system?
(a) The point corresponding to x = 1 and y = 1.
(b) The point corresponding to x = 0 and y = 1.
(c) The point corresponding to x = 10 and y = 10.
(d) The point corresponding to x = 0.1 and y = 0.1.
6. What is the natural logarithm of e?
(a) 0
(b) 1
(c) e
(d) 1/e
7. Suppose a sequence of numbers is such that each value is exactly 4 less than the value before it. This is an example of
(a) a geometric progression
(b) an arithmetic progression
(c) a logarithmic progression
(d) a fractional progression
8. Suppose you’re listening to a compact disc on your new high-powered stereo sound system. The VU (volume unit) meter needles are kicking up to the points marked 0 dB, exactly where the black lines end and the red lines begin. If you increase the gain so the needles are kicking up to + 6 dB in the red zone, the sound power coming from the speakers has approximately
(a) doubled
(b) quadrupled
(c) increased by a factor of 6
(d) increased by a factor of 26, or 64
9. Suppose you take a 4-week temporary job with a 5-day work week. The boss promises that you’ll be paid daily in US dollars ($): $1.00 at the end of the first day, $2.00 at the end of the second day, and doubling each day after that for the entire period. What should this indicate to you?
(a) The boss is a liar or an unwise wealthy person.
(b) The payment is meager, and you should look for another job.
(c) Your accumulated pay, day by day, will represent a convergent series.
(d) Nothing, without more information.
10. Suppose a sequence of numbers is such that each value is exactly 25% of the value before it. This is an example of
(a) a geometric progression
(b) an arithmetic progression
(c) a logarithmic progression
(d) a fractional progression