Do not refer to the text when taking this test. You may draw diagrams or use a calculator if necessary. A good score is at least 30 correct. Answers are in the back of the book. It’s best to have a friend check your score the first time, so you won’t memorize the answers if you want to take the test again.
1. The binary number 10010 is equivalent to the decimal number
(a) 8
(b) 12
(c) 16
(d) 18
(e) 34
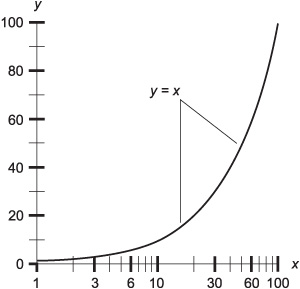
2. In the graph of Fig. Test 1-1, how many orders of magnitude are shown on the horizontal axis?
(a) 1
(b) 2
(c) 10
(d) 100
(e) Infinitely many.
Fig. Test 1-1. Illustration for Part One Test Questions 2 and 3.
3. In Fig. Test 1-1, why does the graph of y = x look like a curve, not a straight line?
(a) Because one scale is linear (graduated evenly) and the other is not.
(b) Because neither scale is linear.
(c) Because both scales are linear.
(d) Because y is not a function of x in this example.
(e) Because the two scales encompass the same range of values.
4. Suppose you graph the barometric pressure at 30-minute intervals during the passage of a hurricane, with time on the horizontal scale and pressure (in millibars) on the vertical scale. After you have plotted the points, you connect them with a curve that represents your “best educated guess” as to the moment-to-moment pressure. In this graph, the pressure is
(a) the independent variable
(b) the dependent variable
(c) a function
(d) a relation
(e) a coefficient
5. In the graph described in the previous question, suppose you connect the points with straight lines to get an approximate graph of the barometric pressure plotted with respect to time. This lets you infer the pressure at any given point in time according to
(a) extrapolation
(b) inversion
(d) exponentiation
(e) curve fitting
6. In the graph described in Question 4, suppose you connect the points with a “best educated guess” curve in an attempt to create a precise, moment-to-moment graph of the barometric pressure plotted with respect to time. This lets you infer the pressure at any given point in time according to
(a) extrapolation
(b) inversion
(c) linear interpolation
(d) exponentiation
(e) curve fitting
7. Consider a number that is equal to 5.00 × 220. In power-of-10 notation, rounded to three significant figures, this is
(a) 5.24 × 106
(b) 2.00 × 103
(c) 5.12 × 103
(d) 1.00 × 1020
(e) impossible to determine without more information
8. Fig. Test 1-2 shows the speed of an accelerating car (in meters per second) as a function of time (in seconds). The fact that the graph is a straight line indicates that the rate of acceleration (expressed in meters per second per second, or m/s2) is constant. What is this constant acceleration?
(a) 1 m/s2
(b) 2 m/s2
(c) 10 m/s2
(d) 20 m/s2
(e) It cannot be determined without more information.
9. In the scenario shown by Fig. Test 1-2, suppose a mass of one kilogram (1 kg) is substituted for the car. According to the laws of physics, constant acceleration of an object having constant mass is produced by a constant force or thrust. Force is expressed in units of kilogram-meters per second per second (kg · m/s2), also known as newtons (N), as you learned in Chapter 4. What force, in newtons, is necessary to cause a 1-kg mass to accelerate at the rate shown by the graph?
(a) 1 N
(b) 2 N
Fig. Test 1-2. Illustration for Part One Test Questions 8 and 9.
(c) 10 N
(d) 20 N
(e) It cannot be determined without more information.
10. In a graph intended to show the correlation between two variables, the total absence of any correlation is indicated by points that
(a) all lie near a horizontal line
(b) all lie near a vertical line
(c) are scattered all over the graph
(d) all lie tightly clustered near the center of the graph
(e) are arranged in some manner other than the four described above
11. How does a numeral differ from a number?
(a) A number represents a diagram, but a numeral represents a set.
(b) A numeral is a symbol that represents a number.
(c) A number is a symbol that represents a numeral.
(d) Numerals are letters of the alphabet, but numbers are symbols such as the plus sign, the minus sign, and the forward slash.
(e) There is no difference.
12. What is the value of 3 – 5 × 6/3 + 10?
(a) 6
(b) –9/10
(c) –40
(d) 3
(e) It is undefined, because it is ambiguous as written.
13. In a vertical bar graph, function values are portrayed as
(a) the heights of bars having equal width
(b) the widths of bars having equal height
(c) points connected by straight lines
(d) points connected by a curve
(e) points plotted all by themselves, not connected by anything
14. The milligram is a unit of
(a) temperature
(b) electrical quantity
(c) brightness of light
(d) frequency
(e) mass
15. The mole is an example of a
(a) linear unit
(b) nonlinear unit
(c) dimensional unit
(d) dimensionless unit
(e) temporal unit
16. The sum of two integers
(a) is always an integer
(b) is always a positive integer
(c) cannot be a rational number
(d) is never zero
(e) is always a dependent variable
17. A radian is equivalent to approximately
(a) 57.3 meters of displacement
(b) 57.3 degrees of angular measure
(c) 57.3 degrees Kelvin
(d) 57.3 degrees Fahrenheit
(e) 57.3 degrees Celsius
18. In order to get the Fahrenheit (°F) temperature when the Kelvin temperature (°K) is known, this formula is commonly used:
°F = 1.800 × °K – 459.67
Suppose we are told that the temperature outdoors is 300 °K. What is the temperature in °F to the maximum justifiable number of significant figures?
(a) 80.3 °F
(b) 80.33 °F
(c) –287 °F
(e) None of the above.
19. If the independent and dependent variables of a function are reversed, the result
(a) is always a function
(b) is sometimes a function
(c) is never a function
(d) is not defined
(e) has negative correlation
20. Suppose there are two quantities, and one of them is exactly 0.001 the size of the other. These quantities differ by
(a) 0.001 orders of magnitude
(b) 1 order of magnitude
(c) 3 orders of magnitude
(d) 10 orders of magnitude
(e) 1000 orders of magnitude
21. In the octal system, the number 67 is followed by the number
(a) 68
(b) 69
(c) 70
(d) 77
(e) 100
22. The numbers –6.78870000 × 10–6 and –6.7887 × 10–6 differ in the sense that
(a) the first is expressed with a greater degree of accuracy than the second
(b) the first is four orders of magnitude larger than the second
(c) the first is only a small fraction of the second
(d) the first is rounded, but the second is truncated
(e) the first is the reciprocal of the second
23. Every rational number is
(a) a natural number
(b) an integer
(c) a real number
(d) positive
(e) nonzero
24. Consider that a meter (m) is equivalent to 39.37 inches (in), a foot (ft) is equivalent to 12.000 in, and a statute mile (mi) is equivalent to 5280 ft. Based on this information, how many feet are there in a kilometer?
(a) 3281 ft
(b) 1609 ft
(c) 440.0 ft
(d) 1.732 × 104 ft
(e) More information is needed to calculate this.
25. Based on the information given in the previous question, how many millimeters (mm) are there in a statute mile?
(a) 6.336 × 104 mm
(b) 1.341 × 105 mm
(c) 1.609 × 106 mm
(d) 6.336 × 107 mm
(e) More information is needed to calculate this.
26. In the hexadecimal system, the number 11 is followed by the number
(a) 12
(b) A
(c) B
(d) 1A
(e) 1B
27. How many radians are there in a degree Kelvin?
(a) Approximately 57.3, the same number of degrees as there are in a radian.
(b) Approximately 273.15, the difference between °K and °C.
(c) Approximately 360, the number of degrees in a complete circle.
(d) It depends on the radius of the circle under consideration.
(e) This question is meaningless because the units are incompatible.
28. Suppose a and b are rational numbers, both larger than 1 but less than 10, and both expressed in decimal form to the same number of significant figures. Suppose m and n are integers. What is the product of a × 10m and b × 10n?
(a) There is no way to express this in the general case.
(b) (a + b) × 10mn
(c) ab × 10mn
(d) ab × (10m)n
(e) ab × 10(m + n)
29. The steradian is a unit of
(a) solid angular measure
Fig. Test 1-3. Illustration for Part One Test Questions 30 and 31.
(b) temperature
(c) visible-light brightness
(d) frequency
(e) electrical current
30. In Fig. Test 1-3, the gray shaded area represents
(a) the set A – B
(b) the set A ∩ B
(c) the set A ∪ B
(d) the set A ⊆ B
(e) the set A
31. In Fig. Test 1-3, which of the points P, Q, or R lies within the set A ∩ B?
(a) Point P only.
(b) Point Q only.
(c) Points P and R.
(d) Points Q and R.
(e) None of the points.
32. In Fig. Test 1-4, the point shown represents
(a) a natural number
(b) an integer
(c) a rational number
(d) an irrational number
(e) none of the above
33. A one-dimensional graph, consisting of two scales lined directly up against each other, is called a
(a) linear comparison
(b) bar graph
(c) correlation graph
(d) nomograph
(e) functional graph
Fig. Test 1-4. Illustration for Part One Test Question 32.
34. One millionth of a kilometer is equal to
(a) 1 meter
(b) 10 meters
(c) 1 millimeter
(d) 10 millimeters
(e) 1 micrometer
35. In a graph intended to show the correlation between two variables, strong negative correlation is indicated by points that
(a) all lie near a horizontal line
(b) all lie near a vertical line
(c) are scattered all over the graph
(d) all lie tightly clustered near the center of the graph
(e) are arranged in some manner other than the four described above
36. Suppose you are performing calculations on a computer, and you end up with the expression 5.000000000E–45. This is
(a) a number between 0 and 1
(b) a number greater than 1
(c) a number between –1 and 0
(d) a number less than –1
(e) a number too large to be defined
37. The reciprocal of 5.000000000E–45 can be expressed as
(a) 2 × 10–44
(b) 2 × 1044
(c) 5 × 1045
(d) 5 × 1044
(e) none of the above
38. In Fig. Test 1-5, the solid curve represents an approximation of stock price versus time, based on points plotted
(a) continuously
(b) at regular time intervals
Fig. Test 1-5. Illustration for Part One Test Questions 38 and 39.
(c) at regular stock-price intervals
(d) at random
(e) by extrapolation
39. In Fig. Test 1-5, suppose stock price is considered as a function of time. We can call this
(a) a nondecreasing function
(b) a nonincreasing function
(c) both a nondecreasing and a nonincreasing function
(d) neither a nondecreasing nor a nondecreasing function
(e) a relation, but not a legitimate function
40. In the hexadecimal number system, the single-digit numerals are
(a) 1 and 2
(b) 1, 2, 3, 4, 5, 6, 7, 8, 9, and 10
(c) 1, 2, 3, 4, 5, 6, 7, and 8
(d) 1, 2, 3, and 4
(e) none of the above