p, whose value at every point of X is that supremum, belongs to A. The mapping of A into itself is called a functional quantifier; it is easy to verify that it satisfies the conditionsGENERAL THEORY
1. Introduction.—It is well known that when a logician speaks of the proposi-tional calculus and when a mathematician speaks of Boolean algebras there is a sense in which they are talking about the same thing. What, in that sense, is the mathematical version of the so-called first-order functional calculus? Several answers to this question have been proposed in recent years;1 the most satisfying of these answers is the concept of cylindric algebra introduced by Tarski and Thompson. The answer offered in this note (namely, polyadic Boolean algebra) differs from previous proposals mainly in being able to imitate the substitution processes that give the functional calculi their characteristic flavor. The imitation appears to be successful. It turns out, for example, just as it does in the propositional case, that the customary approach to the functional calculus can be viewed as nothing but a detailed description of the symbolism of a free polyadic algebra.
It should be emphasized that the theory of polyadic algebras is discussed here not as a possible tool for solving problems about the foundations of mathematics, but as an independently interesting part of modern algebra. The possibility of making a dictionary that translates logical terms (such as interpretation and semantic completeness) into algebraic terms (such as homomorphism and semisimplicity) is to be regarded as merely an amusing by-product of the discussion.
2. Monadic Algebras.—If a proposition is taken to mean an element of a Boolean algebra B, then it is natural to interpret a propositional function as a function from some set X in to B. The set A* of all such functions is a Boolean algebra with respect to the pointwise operations. A functional monadic algebra is a Boolean subalgebra A of A* such that, for each p in A, the range of p has a supremum in B, and such that the (constant) function p, whose value at every point of X is that supremum, belongs to A. The mapping of A into itself is called a functional quantifier; it is easy to verify that it satisfies the conditions
for all p and q in A. (Properly speaking, should be called a functional existential quantifier; universal quantifiers are defined by an obvious dualization.) A general concept that applies to any Boolean algebra is obtained by abstraction from the functional case: a quantifier is a mapping of a Boolean algebra into itself satisfying (Q1)–(Q3). (This concept occurs also in the announcement of the results of Tarski and Thompson.) A monadic algebra is a Boolean algebra with a quantifier.
The entire theory of Aristotelian (syllogistic) logic is easily subsumed under the elementary algebraic theory of monadic algebras.
3. Polyadic Algebras,—Propositional functions of several variables are treated by considering functions from a Cartesian power, say XI, into a Boolean algebra B. Even if the index set I is infinite, the interesting functions are those that depend on finitely many co-ordinates only. The set A* of all such functions is a Boolean algebra, as before.
Let T* be the semigroup of all transformations of I into itself (not necessarily one-to-one and not necessarily onto). Every element τ of T* induces a Boolean endomorphism p → τp on A*, defined by allowing τ to act on the indices of the coordinates of the argument of p. [Example: if I = {1, 2, 3} and if τ is the cyclic permutation (1, 2, 3), then τp(x1 x2, x3) = p(x2, x3, x1).]
If x 
XI and J ⊂ I, it is natural to consider the set of points in XI that can be obtained by varying arbitrarily those co-ordinates of x whose index is in J. [Example: if I = {1, 2, 3}, x = (x1 x2, x3), and J = {1, 3}, then the set so obtained consists of all points whose second co-ordinate is x2.] If p A* and if the image of that set under p has a supremum in B, that supremum is denoted by Jp(x) ; if J contains only one element, say i, it is convenient to write i for J.
A functional polyadic algebra (in more detail, a B-valued functional polyadic algebra with domain X) is a Boolean subalgebra A of A* such that, for each p in A, (1)jp(x) exists whenever J ⊂ I and x XI, (2) the function Jp belongs to A whenever J ⊂ I, and (3) τρ A whenever x T*. Because of the finiteness condition imposed on the elements of A*, it turns out that it is sufficient to assume (1) and (2) for finite subsets J and to assume (3) for finite transformations τ; the infinite ones can then be recaptured. (A transformation in T* is finite if it coincides with the identity transformation outside some finite subset of I. The set T of all finite transformations is a subsemigroup of T*.)
The operators J are quantifiers on A; the quantifiers J (J finite) and the endo-morphisms τ(τ finite) have the following properties.
(The transformation τ is said to be one-to-one on τ−1J if it never maps two distinct elements of I on the same element of J.)
The superficially complicated results (P5) and (P6) are merely a telegraphic summary of the usual intuitively obvious relations between quantification and substitution. A couple of examples will make them clear. Suppose that i and j are distinct elements of I, and let τ be the transformation that maps i on j and maps everything else (including j) on itself. Since τ agrees with the identity outside {i}, it follows from (P5) that τi = i. This relation corresponds to the familiar fact that once a variable has been quantified, the replacement of that variable by another one has no further effect. To get another example, note, for the same τ, that τ−1{i} is empty; it follows from (P6) and (P1) that iτ = τ. This relation corresponds to the familiar fact that once a variable has been replaced by another one, a quantification on the replaced variable has no further effect.
Once again a general concept is obtained by abstraction. A polyadic algebra is a Boolean algebra A, an index set I (whose elements are called variables), a correspondence from finite subsets of I to quantifiers on A, and a correspondence from finite transformations on I to Boolean endomorphisms on A, such that (P1)–(P7) are satisfied. It is useful to know that, just as in the functional case, the infinite quantifiers and endomorphisms can be defined in terms of the finite ones, and these extended operators satisfy the same conditions as their finite counterparts.
4. Polyadic Logics.—The usual machinery of universal algebra is immediately applicable to polyadic Boolean algebras ; terms such as subalgebra, homomorphism, kernel, ideal, maximal ideal, simple algebra, and free algebra are defined as always. The essential point is to insist, in every case, that the corresponding Boolean concepts be invariant under the operators (quantifiers and endomorphisms) that define the polyadic structure. (Caution: polyadic algebras with different sets of variables are distinct types of algebraic systems. A homomorphism, for instance, is defined only between algebras with the same sets of variables. The situation is analogous to the theory of groups with operators.) A minor difficulty occurs in the definition of a free algebra: because of the assumed finiteness condition (P7), a polyadic algebra can never be really free. The difficulty is easily conquered by an appropriate relativization of the concept of freedom.
With the algebraic nomenclature at hand, many logical terms are easily translatable into algebraic language. A polyadic logic, to begin with, is defined as a pair (A, I), where A is a polyadic algebra and I is a polyadic ideal in A. The motivation for this definition is the logical concept of refutability. In the customary treatment of logic, certain elements of an appropriate algebraic system (usually, though only implicitly, a polyadic algebra) are called refutable. From the algebraic point of view the definition of refutability in any particular case is inessential. What is important is the structure of the set I of all refutable elements; it turns out (and intuitive considerations demand that it should turn out so) that I is a polyadic ideal. (This discussion is, in fact, the dual of the usual one; reasons of algebraic convenience make refutability a more desirable concept than provability.)
A polyadic logic (A, I) is simply consistent if I is a proper ideal in A (not everything is refutable). Simple consistency is equivalent to the requirement that for no element p of A do both p and p' belong to I (where p' is the Boolean complement, or negation, of p). A polyadic logic (A, I) is simply complete if either I = A or else I is a maximal ideal in A. Simple completeness is equivalent to the requirement that, for every closed element p of A, either p or p' belongs to I. (An element p of A is closed if Ip = p) In these terms the celebrated Gödel incompleteness theorem asserts that certain important polyadic logics are either incomplete or inconsistent.
5. Semantic Completeness.—Since every simply consistent polyadic logic (A, I) is easily studied in terms of the associated polyadic quotient algebra A/I, there is no essential loss of generality in restricting attention to algebras instead of logics. It is, of course, necessary to keep in mind that the reduction to algebras reduces some non-trivial logical concepts to trivialities; thus, for instance, the only “refutable” element of A/I is the zero element.
“Semantic” concepts refer to the representation theory of polyadic algebras. (The intrinsic, or structural, concepts of the preceding section are usually called “syntactic”) Representation theory proceeds, as always, by selecting a class of particularly simple and “concrete” polyadic algebras and asking to what extent every algebra is representable in terms of algebras of that class. For intuitively obvious reasons the logically important “concrete” algebras are the two-valued functional algebras, i.e., the functional algebras whose elements are functions from a Cartesian power XI into the two-element Boolean algebra. Such algebras are called models.
An interpretation of an algebra A in a model B is a polyadic homomorphism from A onto B. An element p of an algebra A is universally invalid if it is “false” in every interpretation, i.e., in algebraic language, if φρ = 0 whenever φ is a homomorphism from A on a model. (Once again, the present discussion is the dual of the usual one.) The algebra A is semantically complete if the only universally invalid element is 0. In logical terms, A is semantically complete if every universally invalid element is refutable, or, dually, if every universally valid element is provable.
6. Constants.—An important concept in the representation theory of polyadic algebras is that of a constant. Intuitively, a constant is something that can be substituted for a variable ; in the functional case a typical example of a constant is an element of the domain. The algebraic essence of the concept is captured by examining (either in terms of intuitive logic or in a functional example) the effect of replacing some of the variables (say the ones corresponding to a finite subset J of I) by an intuitively conceived constant. Abstraction from these special cases suggests the following definition. A constant (of a polyadic algebra A with variables I) is a mapping J → c(J) from finite subsets of I to Boolean endomorphisms of A such that :
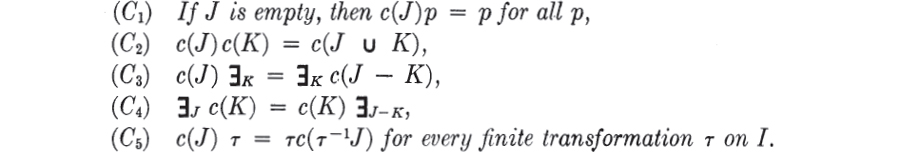
There are simple examples of polyadic algebras that do not possess any constants. A polyadic algebra A with variables I is rich if, whenever p A and i I, there exists a constant c such that ip = c(i)p. (In highly informal language: there is a witness to every existential proposition.) The most important fact about rich algebras is that there are enough of them.
THEOREM 1. Every polyadic algebra is isomorphic to a subalgebra of a rich algebra.
The idea of the proof of Theorem 1.1 is most easily illustrated by sketching the proof of a special case. Suppose that A is a polyadic algebra with variables I, and suppose that p0 A and i0 I. Let I+ bea set containing one more element than I, and consider a free polyadic algebra, with variables I+, generated by the elements of A. If that free algebra is reduced modulo all the relations that hold among the elements of A, the result is a polyadic algebra A+ with variables I+ (and hence, a fortiori, with variables I) that includes A. If, for every finite subset J of I, c(J) is defined to be the Boolean endomorphism of A+ induced by the transformation on I+ that replaces thp elements of J by the new element of I+ and is otherwise equal to the identity, then c is a constant of the algebra A+ regarded as having the variables of I only. One more reduction, modulo the relation i0p0 = c(i0)p0, yields a polyadic extension of A that is rich enough, at least, to supply a witness for i0p0.
7. Semisimplicity.—The simplest representation theorem for polyadic algebras follows easily from an algebraic adaptation of the method of Rasiowa and Sikorski;2 an analogue of this result for cylindric algebras was announced by Tarski.3
THEOREM 2. Every polyadic algebra with an infinite set of variables is isomorphic to a functional algebra.
Unfortunately Theorem 2.2 does not yield enough information about the structure of a general polyadic algebra. To state the desired sharper result, it is convenient to introduce the functional counterpart of the concept of richness. A functional algebra A with variables I and domain X is functionally rich if, whenever p A, i I, and x XI, there exists a point y of XI such that all the co-ordinates of y, with the possible exception of the i co-ordinate, are the same as the corresponding co-ordinates of x and such that ip (x) = p(y)·
THEOREM 3. Every polyadic algebra A with variables I is isomorphic to a subalgebra of a rich functional algebra the cardinal number of whose domain is less than or equal to the sum of the cardinal numbers of A and of I.
The proof of Theorem 3.3 is based on Theorem 1.1 ; the method is a modification of the one introduced by Henkin.4 To construct the promised functional algebra, it is necessary to construct a domain X and a value algebra B. The role of X is played by a sufficiently large set of constants for a rich polyadic extension of the given algebra A, and the role of B is played by A itself.
The algebraic analogues of the Skolem-Löwenheim theorem and the Gödel completeness theorem are relatively easy consequences of Theorem 3.3. To discuss the latter, for instance, consider a functionally rich B-valued functional algebra, and let φ0 be an arbitrary Boolean homomorphism from B to the two-element Boolean algebra. The assumption of richness implies that the application of φ0 to the values of the elements of the functional algebra induces a polyadic homomorphism φ into a two-valued functional algebra; more precisely, φ is defined by φp(x) = φ0 [p(x)]. This technique, combined with Theorem 3.3, yields the following basic result.
THEOREM 4. Every simple polyadic algebra is isomorphic to a model.
The method of Rasiowa and Sikorski also serves to prove a theorem of this type, and it is in some respects simpler than Henkin’s; its disadvantage is that it works under severe infinity and countability restrictions only.
The converse of Theorem 4.4 is true, easy, and, incidentally, independent of the preceding relatively high-powered representation theorems.
THEOREM 5. Every model is simple.
Since, on universal algebraic grounds, the kernel of a polyadic homomorphism is a maximal ideal if and only if its range is simple, semantic completeness is equivalent to the requirement that the intersection of all maximal ideals is {0}. Since, in analogy with other parts of algebra, it is natural to call a polyadic algebra satisfying this condition semisimple, it follows that a polyadic algebra is semantically complete if and only if it is semisimple. It is now easy to state the algebraic version of the Gödel completeness theorem.
THEOREM 6. Every polyadic algebra is semisimple.
The assertion of Theorem 6.6 for a polyadic algebra with the empty set of variables (i.e., for an ordinary Boolean algebra) is the most important part of Stone’s theorem on the representation of Boolean algebras. Theorem 6.6 is, in fact, a relatively easy consequence of Stone’s theorem ; it is much nearer to the surface than, for instance, Theorem 3.3. In other words, the hard thing in proving Gödel’s completeness theorem is not to prove semisimplicity but to prove the appropriate representation theorem (Theorem 4.4) that guarantees that semisimplicity is the right thing to prove.
1 A. Tarski, J. Symbolic Logic, 6, 73–89 (1941); C. J. Everett and S. Ulam, Amer. J. Math., 68, 77–88 (1946); F. I. Mautner, Amer. J. Math., 68, 345–384 (1946); A. Tarski and F. B. Thompson, Bull. Amer. Math. Soc, 58, 65 (1952).
2 H. Rasiowa and R. Sikorski, Fund. Math., 37,193–200 (1950).
3 A. Tarski, Bull. Amer. Math. Soc., 58, 65 (1952).
4 L. Henkin, J. Symbolic Logic, 14, 159–66 (1949)