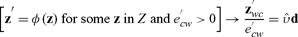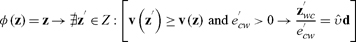| 5 |
Class in catallaxy |
| |
|
| |
A. J. Julius |
A degree of freedom
A capitalist economy is capable of an uncountable infinity of distributions of income between the capitalists who own its nonlabor inputs and the workers who turn those inputs into outputs. The resolution of this indeterminacy falls to the customary or contested institutions and practices that organize competition and bargaining among and between capitalists and workers.
I will argue here for a version of this indeterminacy thesis. The thesis is often raised in opposition to a Walrasian picture of economic life. My argument for it will begin at the starting point of most Walrasian economic explanations and predictions. Describing a population of persons in terms of their consumption preferences, their initial holdings of goods, and their access to technologies for producing new goods, I will suppose that these persons come together to exchange their goods or labor, each acting to improve her or his own consumption prospects, and I will ask where such exchanges take the economy as a whole. “Pretty much anywhere; depends on the institutions” is the answer that I’ll defend.
Two classes
Consider a population of M + N persons falling into two classes, capitalists indexed by c = 1,2,…,M and workers indexed by w = M + 1,M + 2,…,M + N.
Before production or exchange the cth capitalist owns a collection of previously produced quantities of n kinds of goods, indicated by a nonnegative n-vector ωc.1 She consumes quantities of the n goods at two dates, separated by a period of production. A continuous increasing concave function uc represents her preferences over consumption sequences described by pairs of nonnegative n-vectors (yc, 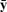 c). Every capitalist has access to the same Leontief production technology characterized by a productive, indecomposable n × n matrix of material input requirements A and a nonnegative n-vector of labor requirements l. For any nonnegative n-vector xc, a capitalist who employs lxc units of labor on Axc units of nonlabor inputs acquires [I — A]xc as a net output of the n goods.
c). Every capitalist has access to the same Leontief production technology characterized by a productive, indecomposable n × n matrix of material input requirements A and a nonnegative n-vector of labor requirements l. For any nonnegative n-vector xc, a capitalist who employs lxc units of labor on Axc units of nonlabor inputs acquires [I — A]xc as a net output of the n goods.
Each worker has a unit of labor power, a capacity to work throughout the production period. She owns no other resources. She consumes goods only at the start of the period. The wth worker’s preferences are represented by a continuous increasing concave uw(yw, hw) on her consumption yw and on the fraction of the period hw transforms after she works outside the home.
Let me emphasize that I am simply assuming that the capitalists own produced goods and no labor, that the workers own labor and no produced goods, that the capitalists have access to a technology that is closed off to the workers, and that the capitalists face a decision about how to allocate their consumption over time while the workers consume their wage goods right away. I adopt these assumptions because they underwrite an especially simple characterization of class income distributions in the exchange equilibria of a production economy where production takes time.2
The question of exchange
The capitalists would like to spread their consumption into the future. They can do this only if some worker will work up some capitalist’s input stocks into goods available at the end of the period. For their part the workers would also like to consume something. But they will eat only if previously produced goods now owned by the capitalists come into the workers’ possession.
Suppose that workers try to sell their labor power to capitalists for consumption goods to be delivered before production. Suppose that every capitalist, while trying to buy labor from the workers, also seeks to buy and sell previously and prospectively produced goods that yield a better profile of consumption. What is going to happen? Which exchanges will take place, bringing about which division of labor and which distribution of income?
Price-taking equilibrium
A Walrasian economist tries to answer these questions by imposing a special structure on the exchange of goods and labor. She describes a set of perfectly competitive markets where labor, previously produced goods, and prospectively produced goods are traded all at once and each at a uniform price. Every participant in these markets, believing that she can carry out any transaction she can afford at the given prices, opts for a transaction, production, and consumption plan that promises a final bundle of goods that she weakly prefers to all other affordable and productively attainable bundles. The Walrasian economist then looks for a system of uniform prices that directs these traders toward mutually consistent plans.
Continuing the earlier example, we can suppose that the capitalists contract for pre- and post-production deliveries of material goods and that workers commit fractions of their labor time to capitalists’ production projects while purchasing consumption goods to be delivered at the start of the period. Faced with a wage rate ν, an n-vector p of prices for goods delivered before production, and an n-vector 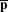 of prices for goods delivered after production, a capitalist chooses a production plan xc and a consumption plan yc,
of prices for goods delivered after production, a capitalist chooses a production plan xc and a consumption plan yc,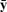 c that maximize uc(yc,
c that maximize uc(yc, 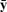 c) subject to the budget
c) subject to the budget
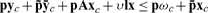 |
(1) |
A worker chooses a nonnegative yw and a hw in [0, 1] to maximize her own uw (yw, hw) subject to
 |
(2) |
So everyone makes a plan that she likes no less than any other plan she can afford at the prices she takes as given.
A price-taking equilibrium is a list of prices (p*, 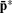 , ν*) and a complex of consumption and production plans (yc*,
, ν*) and a complex of consumption and production plans (yc*, 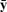 c*, xc*)c=1,2,…,M and consumption and labor plans (yw*, hw*)w=M+1,M+2,…,M+N that solve these constrained-maximization problems for those prices and that together satisfy
c*, xc*)c=1,2,…,M and consumption and labor plans (yw*, hw*)w=M+1,M+2,…,M+N that solve these constrained-maximization problems for those prices and that together satisfy
Under the guidance of these prices people apparently plan to consume or employ in aggregate no more of each commodity than they’re collectively holding or planning to produce.
Although it is billed as a model of exchange, this idealization prescinds from any direct representation of transactions between traders. The omission is said to be explained by the focus on equilibrium. So long as everyone trades at the same prices, and so long as those prices call up consistent plans, it makes no difference who trades what with whom. Everyone puts in what she plans to put in and takes out what she plans to take out. What everyone plans to do adds up to something that they can all do.
Interest, profit, and wage
Suppose that as part of her initial endowment a capitalist owns a unit of the ith good. Starting from a plan that meets her budget constraint with strict equality, she decides to postpone her consumption of that unit to the end of the production period. If she sells the unit for immediate delivery, she can afford to purchase  units of the good for her later consumption. In effect she makes a loan of this good to someone who consumes it or uses it in production, and the “own rate of interest” defined in
units of the good for her later consumption. In effect she makes a loan of this good to someone who consumes it or uses it in production, and the “own rate of interest” defined in
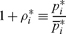 |
(6) |
measures her return on this commodity loan. At a constrained utility maximum
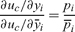 |
(7) |
and so in equilibrium
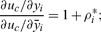
this interest rate also reports the capitalists’ marginal rate of substitution between earlier and later consumption of the good.
Unless the input prices p are proportional to the output prices 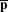 , these own-interest rates will vary from commodity to commodity. But by turning to production we can find a kind of equalization of return.
, these own-interest rates will vary from commodity to commodity. But by turning to production we can find a kind of equalization of return.
Equilibrium prices must satisfy
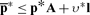 |
(8) |
If this inequality were not met for some good, then, by producing greater and greater quantities of that good, a household could afford larger and larger consumption bundles delivering ever greater utility, and no constrained maximum would exist. For any good i that’s to be produced it must be that
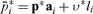 |
(9) |
so that all operated activities make the maximum profit of zero.
With a commodity bundle d serving as numéraire, an undiscounted profit rate on the production activity ai, l may be defined as in
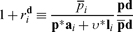 |
(10) |
This measures a capitalist household’s return on the material goods and wage payments tied up during the production period, using the undiscounted prices corresponding to the numéraire. Since every operated activity satisfies (9), the first ratio on the right-hand side equals 1, and in fact
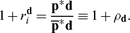 |
(11) |
Profit rates on operated activities, measured in the undiscounted prices associated with a numéraire of d, are equalized at the own-rate of interest of that composite commodity.3
Taking the cth capitalist’s budget constraint (1) to be satisfied with equality and substituting from the zero-profit condition, you may write the value of her consumption of the newly produced goods 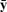 c as
c as
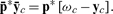 |
(12) |
These magnitudes can in turn be expressed in d-units by dividing through by 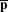 *d and substituting from (11) to arrive at
*d and substituting from (11) to arrive at
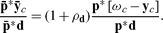 |
(13) |
The value in d-units of the capitalist’s consumption of the produced good equals the value in d-units of the inputs she’s contributed to production, marked up by the own-rate interest of the composite commodity d.
For a given numéraire d, then, the real wage νd* ≡ ν*/p*d and the composite own rate ρd* make a low-dimensional representation of the distribution of income between capital and labor inhering in the equilibrium prices.
Distribution by tastes, technology, and endowment
Suppose it were true that, for each possible technology, allocation of endowments, and specification of preferences, there’s a unique equilibrium configuration of prices and plans. As we’ve just seen, the equilibrium prices include a price for labor and a profile of ratios between the input and output prices of the produced goods — a wage rate and a structure of interest rates. The Walrasian economist explains this distribution of income between labor and capital as an incident of the unique socially consistent configuration of price-taking market interaction motivated and constrained by the given endowments, tastes, and technology.
To offer this explanation is to propose a strong division of explanatory labor between the market and other social institutions or practices. Public taxation and spending; the legal recognition and enforcement of property; the organization of family life; material culture; collective bargaining and shopfloor conflict; norms of deference, solidarity, or justice: any of these might help to explain the prevailing distribution, but their roles are necessarily limited. They can help to cause or to constitute the endowments, tastes, and technology that the market maps to a price-taking equilibrium. Or they can serve to redistribute commodities and income away from that equilibrium. They do not directly interact with or compose the market’s own exchange and production processes that decide which distribution results from the market’s data of endowments, tastes, and technology. These institutions are kept to the background, their influence felt only in the prehistory or the aftermath of market exchange.
Exogenous distribution
A classical economist asks which system of temporally invariant goods prices, profit rates, and wage rates supports a sustainable pattern of production by equalizing rates of profit across the activities operated in that pattern. Applied to the Leontief technology and numéraire defined earlier, these conditions are
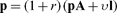 |
(14) |
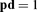 |
(15) |
The classical economist finds this equal-profit-rate condition met at each of a continuum of price systems. She notices that the profit rate and the real wage vary inversely across that continuum. And she argues that extramarket institutions resolve this indeterminacy by imposing a boundary condition on distribution that selects a (price, profit, wage) system from the continuum of possibilities. She has in mind that custom, policy, bargaining, or class struggle can dictate a particular value for the real wage, for example, and that commodity prices form to equalize profit rates at that wage. In this way the classical economist reaches her own version of the indeterminacy thesis that I set out in the first section.4
The price system (14, 15) is sometimes promoted as a rival to the Walrasian intertemporal equilibrium described in earlier sections. I’ve never been sure what that rivalry amounts to or how we should go about picking a winner. The Walrasian model, like the classical one, calls for an equalization of profit rates. The crucial differentia of (14, 15) are apparently twofold. First, those equations presuppose that inputs and outputs are sold atconstant relative prices. And, second, they accommodate this restriction on prices by abstracting away any requirement that demand not exceed an aggregate supply that is limited by the endowments of labor and produced goods. Why should we suppose that prices are constant? Why should we ignore an end owment-constrained balance of supply and demand? Then again, why not?5
Sidestepping these questions about the classical assumptions, I want now to point out that the Walrasian assumptions give rise to two grave internal problems. We can solve those problems, I will claim next, if we relax the Walrasian’s special restrictions on exchange in favor of a more general characterization of genuinely decentralized market interaction. This catallactic conception will turn out to sponsor a version of the indeterminacy thesis championed by the classical economist.
Why these prices?
The Walrasian economist says that equilibrium prices organize the exchange and production decisions of individual actors into a consistent macroscopic pattern. A closer look shows this to be false. To bring out the deepest difficulties I will go on supposing that only one equilibrium exists. The question to ask first is whether people will come to trade at the equilibrium prices that correspond to their tastes, technology, and endowments.
Suppose that everyone believes that prices will form such that everyone can carry out a constrained-best price-taking plan at those prices. And suppose that everyone knows the endowments, preferences, and technology that characterize the rest of the economy. And suppose that everyone can compute the corresponding unique equilibrium. Then everyone will infer that others will trade at that equilibrium’s prices, and she will set out to trade at them herself.
But this is silly. Not only does it require universal economic sophistication, universal computational prowess, and universal knowledge of the economy’s structure. It also attributes to every trader the belief that all traders will converge on price expectations that allow for mutually consistent price-taking behavior economywide. What would warrant that belief? Since the argument now underway is meant to show that trade will take place at the equilibrium prices, it should in any case not assume that this belief is warranted.
A second possibility is that people will arrive at the equilibrium as the asymptotically stable rest point of some exchange process through which people trade their goods and labor at initially non-equilibrium prices. It’s an awkward proposal. By the definition of equilibrium the price-taking transaction behavior given in the section Price-taking Equilibrium cannot be universalized outside equilibrium. We’ll need a different characterization of transactions. Any such characterization must feature some market actors whose actions help to determine the prices at which goods are traded. And it must limit a person’s transactions to those that particular trading partners are willing to carry out. The disequilibrium process is thus bound to show a qualitative discontinuity with the price-taking exchange behavior of the section Price-taking Equilibrium, whose outstanding features are that no person can affect prices and that a person’s transactions are limited only by her own budget constraint in those prices.6
Suppose that these perplexities are somehow overcome. Suppose that, starting from the initial endowments, people follow a disequilibrium trading process until it converges to an equilibrium price system and allocation. On their way to equilibrium people will have traded goods at non-equilibrium prices. The “endowments” that define their equilibrium destination are not the actual holdings of goods with which they began. The supposed convergence of this disequilibrium process to a price-taking equilibrium fails to imply that, starting from their actual endowments, people will reach the equilibrium prices that the Walrasian theory assigns to that starting point.7
Why these quantities?
A second problem strikes me as even more serious. Put aside the doubts just aired. Suppose that people come to believe that trade will take place at the equilibrium prices corresponding to their original endowments. What will they do then? The Walrasian answers that they will arrange to trade and produce goods in a socially consistent pattern. But this answer is also unsupported.
In equilibrium every operated activity earns zero profits. Every capitalist is indifferent between all intensities of operation of any mixture of those activities. She is happy to produce nothing. She is happy to produce on a vast scale whose input requirements dwarf the economy’s aggregate endowment. And she is equally content with all intermediate possibilities.
When the Walrasian economist observes that at the equilibrium prices capitalists are willing to produce in a pattern that clears the markets for goods and labor, she forgets to add that they’re also willing to produce in any of an uncountable infinity of non-market-clearing patterns. Prices do not live up to their reputation for organizing a socially consistent program of production by the many producers.8
Starting over
I conclude that we should not hold onto the Walrasian’s special structure for exchange. Throwing it off, we are free to return to a less restricted version of the question of exchange with which I started. When people set out to exchange goods and labor with one another, each so as to improve her or his own consumption prospects, where will her or his exchanges take the economy as a whole?
Catallactic exchange
I’ll now assume that persons meet to consider possible contracts arranging for deliveries of goods before or after the production period or for labor during it.9 Let the vectors zjk,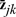 describe the deliveries called for under any contracts extant between the jth and the kth actors. A positive (negative) ith component in zjk indicates that the kth (jth) person is to deliver to the jth (kth) a quantity of the ith good equal in magnitude to that component. Let the number ecw describe the fraction of the wth worker’s labor time that she’s contracted to spend on the cth capitalist’s production. Let
describe the deliveries called for under any contracts extant between the jth and the kth actors. A positive (negative) ith component in zjk indicates that the kth (jth) person is to deliver to the jth (kth) a quantity of the ith good equal in magnitude to that component. Let the number ecw describe the fraction of the wth worker’s labor time that she’s contracted to spend on the cth capitalist’s production. Let
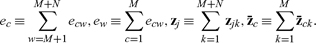 |
(16) |
And let a vector z concatenate all the zjk, 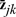 , ecw, ewc representing the capitalists’ and workers’ contractually obligated deliveries.
, ecw, ewc representing the capitalists’ and workers’ contractually obligated deliveries.
The cth capitalist chooses a production and consumption plan to maximize her utility, given that she will give or take the goods or labor that she’s contracted for:
Let the function vc (z) report the solution value of this problem.10 For her part the wth worker is represented by a
I’ll collect all persons’ value functions as v(z).
Let Z be the set of possible states z such that for all w 0 ≤ ew ≤ 1 and such that for all c the constraints (18, 19, 20) are met for some nonnegative production plan xc. For any z in Z, then, everyone can deliver the goods or labor she’s obligated to provide under the contracts in that z. Because labor power and the nonlabor inputs are in fixed supply, Z is bounded.
A negotiation process unfolding over rounds t = 1,2,3,… determines for each zt the new state zt+1 of contracts that results from agreements reached during the tth round. I’ll assume that any one such process can be represented by some continuous φ : Z → Z such that a solution of
 |
(24) |
for an initial z0 with all components equal to zero represents a path of contracts negotiated under the process.
I’ll assume throughout that
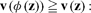 |
(25) |
no change to the contracts makes a person worse off. I will assume throughout that
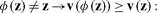 |
(26) |
any change in the contracts makes someone strictly better off. Finally, I will assume in the next five sections that
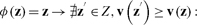 |
(27) |
contracts go unchanged only if no feasible change would make someone better off while making no one worse off.
Catallactic equilibrium
A state that satisfies the consequent of (27) I’ll call a catallactic equilibrium. I’ll now show that, for any continuous φ : Z → Z satisfying (25, 26, 27), every negotiation path zt solving (24) converges to such an equilibrium.
Because zt is confined to the bounded set Z, there is an infinite subsequence {tτ} for which the limit
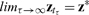 |
(28) |
exists. Let zt* be the negotiation path that solves (24) given the limit point z* as its initial position. Solutions of (24) are continuous with respect to their initial positions, so
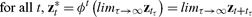 |
(29) |
where φt is the tth iterate of the function φ. Now consider the sum of the households’ values
 |
(30) |
This function is bounded and — by (25) — nondecreasing on any solution path, and there exists the limit
 |
(31) |
The sum of value functions is continuous, and so
 |
(32) |
So V is in fact constant on the path zt*. But V can be constant only if
 |
(33) |
since by (26) any change in some contract would yield a strictly greater value of V. So by (27) any such limit point is an equilibrium.11
The question of exchange reconsidered
My question was “What will happen when capitalists and workers set out to trade so as to improve their consumption prospects?” My new answer is that they’ll converge to a catallactic equilibrium where no one is worse off than before trade. The set of such equilibria forms a continuum, and a series of individually advantageous exchanges will convey the economy to some point on that continuum.12
This answer marks a twofold improvement over the Walrasian one. First, the equilibria it mentions are the asymptotically stable rest points of dynamical systems representing the decentralized market interactions that it describes. There is no mystery as to how people find their way to these equilibria.
Second, people reach equilibrium intending to produce goods in a socially consistent pattern. Everyone has contracted toreceiveor supply particular quantities of labor and produced inputs, and they have contracted to deliver particular outputs. Bound by their contracts, people are planning to produce as much of each good altogether as they’re altogether planning to consume. A web of informationally decentralized, contractually specified individual quantity constraints secures the coordination of production that centrally broadcast uniform prices fail to achieve.
Power-dependent distribution
Every negotiation path ends up somewhere in the equilibrium set. But it depends for its particular destination on the institutions of bargaining and on the balances of power that shape them.
For one very crude illustration of that dependence, suppose that at every round of negotiation a worker is grouped with one or several capitalists to consider changes to their contracts. Agreed changes maximize a weighted sum of the parties’ value functions, subject to their existing contracts with outsiders and to the further condition that no one be made worse off.
If in every such meeting the worker’s value function carries no weight in the sum to be maximized, contracts converge to an equilibrium in which for every worker
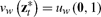 |
(34) |
and the capitalists claim all gains to trade realized along the way. If instead the capitalists’ value functions take zero weight, then in equilibrium
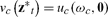 |
(35) |
and all benefit redounds to the workers.
Intermediate weightings presumably split the cooperative surplus in ways that are harder to analyze at this level of abstraction. But the comparison between these extremes is already enough to show that the distribution generated from a particular constellation of tastes, technology, and endowment can favor workers or capitalists according as the institutional configuration of bargaining tilts toward one or the other class.
Shadow prices in equilibrium
Let (pc, 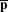 c ,νc) be the Lagrange multipliers or shadow prices corresponding to the jth capitalist’s optimal program at the equilibrium contracts. Every capitalist’s prices are, in equilibrium, proportional to some (p*,
c ,νc) be the Lagrange multipliers or shadow prices corresponding to the jth capitalist’s optimal program at the equilibrium contracts. Every capitalist’s prices are, in equilibrium, proportional to some (p*, 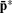 , ν*), and the shadow prices (pw, νw) supporting a worker’s program are also proportional to (p*, ν*).
, ν*), and the shadow prices (pw, νw) supporting a worker’s program are also proportional to (p*, ν*).
Suppose that were false. It would follow that some pattern Δz of feasible small deviations from the economy’s equilibrium contract state would satisfy
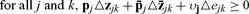 |
(36) |
and
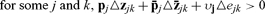 |
(37) |
Since by an envelope theorem the vector of an actor’s shadow prices coincides with the gradient of her value function, these small changes would help the jth actor and hurt no one, contradicting the definition of equilibrium.
Let’s go ahead and normalize the capitalists’ shadow prices in equilibrium to (p*, 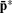 , ν*) and the workers’ multipliers to (p*, ν*). These have a familiar structure. The Kuhn–Tucker conditions for a solution of each capitalist’s maximization problem include that
, ν*) and the workers’ multipliers to (p*, ν*). These have a familiar structure. The Kuhn–Tucker conditions for a solution of each capitalist’s maximization problem include that
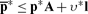 |
(38) |
with
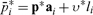 |
(39) |
for any good that’s produced. Equilibrium shadow prices equalize discounted shadow profits at zero.
Path-dependent distribution
A person’s final consumption is decided, not by these shadow prices, but by the history of the exchange and labor agreements she’s reached on the way to equilibrium. Most of those arranged for transfers of goods or labor at ratios different from the equilibrium prices. It follows that, while shadow prices in catallactic equilibrium mimic Walrasian market prices by annihilating discounted profits, my earlier Walrasian analysis of capitalists’ income in terms of those prices does not carry over to catallaxy. Let me explain.
The Kuhn–Tucker conditions for a constrained maximum of the cth capitalist’s utility include the equalities
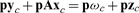 |
(40) |
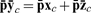 |
(41) |
and
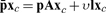 |
(42) |
A rearrangement gives
 |
(43) |
Because workers don’t participate in the market for prospectively produced goods, it turns out that
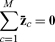 |
(44) |
and so that
 |
(45) |
The capitalists’ aggregate consumption of produced goods, as valued in the equilibrium shadow prices, equals the aggregate value of the material inputs they’ve invested plus a further term
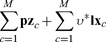 |
(46) |
that subtracts the shadow value of the wage goods they collectively deliver to the workers from the shadow value of the workers’ labor. This number might be negative or positive. It won’t be zero except by fluke.
In the corresponding price-taking equilibrium, on the other hand, capitalist consumption satisfies
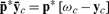
The value of capitalists’ consumption in catallaxy is greater or less than in this price-taking equilibrium according to how the negotiation of wage agreements outside equilibrium made for a positive or negative value of (46).
The section Interest and Profit also pointed out that in the price-taking equilibrium

a capitalist’s real consumption in d units equals her investment marked up by the own rate of interest of the numéraire commodity, which relates the marginal utilities of earlier and later consumption. In catallaxy, by contrast, the right-hand side of this expression bears the further term
 |
(47) |
Again this may be positive or negative. It will take different values for different capitalists. And its values will depend on the particular institutionally determined negotiation path by which the equilibrium was approached. There’s no hope of equating the value of capitalists’ consumption with the value of their investments marked up by a uniform rate of return, defined from the equilibrium prices and expressing the capitalists’ substitution between immediate and deferred consumption.
An exogenous real wage
Consider a negotiation process that, in place of (27), obeys, for some  and d,
and d,
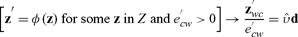 |
(48) |
and
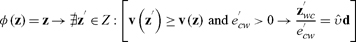 |
(49) |
and that also satisfies my original assumptions (25) and (26). This process requires that labor be paid in units of the numéraire bundle d at the given real wage  . And it allows a contract state to persist only if no change consistent with this real-wage condition improves some person’s situation while worsening no one’s.
. And it allows a contract state to persist only if no change consistent with this real-wage condition improves some person’s situation while worsening no one’s.
It’s easy to show that every path of a continuous process φ that obeys (25, 26, 48,49) converges to a state that satisfies the consequent of (49).13 For any  that’s not too large, this equilibrium supports production projects that pay a real wage of
that’s not too large, this equilibrium supports production projects that pay a real wage of  to every worker they employ.
to every worker they employ.
This result makes another interesting contrast with the Walrasian outlook on class. To impose an exogenous real wage on the Walrasian system is to force an excess supply (or demand) in its market for labor. By the accounting identity known as Walras’ Law this calls for an offsetting excess demand (or supply) in some other market. Price-taking equilibrium has no room for a politically concerted or culturally conventional real wage.
The catallactic conception is more permissive. It allows that where tradition or politics dictates a particular value for the real wage, a series of individually advantageous decentralized agreements will reconcile individual production and consumption plans to that distributive boundary condition. It gives another glimpse of social possibilities that were not dreamt of in the Walrasian philosophy.14
Notes
1 I’ll reserve boldfaced symbols for vectors or vector-valued functions. I’ll write the scalar product of vectors x and y as xy. That x ≥ y is that no component of x is less than the corresponding component of y. That x ≥ y is that x ≥ y and x ≠ y. I’ll use the subscript i for an arbitrary good and j or k for an arbitrary actor of either class.
2 Roemer (1982) stages a variety of capitalist class structures in Walrasian general equilibrium.
3 This conception of profit rates in the undiscounted price system of an intertemporal general equilibrium is due to Malinvaud (1972: ch. 10). See also Duménil and Lévy (1985).
4 Sraffa (1960) gives the authoritative modern statement of this classical idea. My way of contrasting the explanatory structures of Walrasian and classical price theory follows Marglin (1984). Mandler (1999a) and Mandler (1999b: ch. 2) also ascribe an indeterminacy thesis to Sraffa.
5 Hahn (1982a) presses these points.
6 This discontinuity between equilibrium and disequilibrium was pointed out by Arrow (1959).
7 Fisher (1983) emphasizes that, if equilibrium is reached by disequilibrium trade, the initial endowments fail to play their expected role in determining the final prices and allocation.
8 Linearity is not crucial for this conclusion. Any constant-returns technology, for example, would require a zero-profit equilibrium price system that leaves the scale of individual production undetermined.
9 This conception of genuinely decentralized exchange, which can be traced back at least to Edgeworth (1881), was most recently retrieved by Axtell (2005) and by Foley (2010).
10 I’m writing this value function as a function of the entire contract state z for convenience’s sake. A person’s solution depends only on her own contracts.
11 This convergence proof closely follows the argument of Uzawa (1962). For other discussions of the stability of catallactic processes see Smale (1976), Hahn (1982b), Axtell (2005), and Foley (2010).
12 To confirm that it’s a continuum, notice that for any convex combination of the individual value functions, a contract state z that maximizes that combination subject to the constraint that every person be able to fulfill her contracts given her endowments, is a catallactic equilibrium. Thanks to the continuity of the value functions, the solutions of these problems are continuous in the weights assigned to the value functions. By setting all but one weight to zero, you ensure that only the person receiving positive weight is strictly better off in the associated solution, so there must be several distinct solutions corresponding to different weightings. So the equilibrium set must include an uncountable infinity of distinct contract states.
13 Take another look at the argument of the section Catallactic Equilibrium. Before its final sentence, that argument appeals only to the properties (25) and (26). Since the exogenous-wage process has those properties as well, the argument shows that every solution of this process has some limit point z* such that z* = φ (z*). In light of (49) it must be that this z* satisfies the consequent of that conditional.
14 I learned the catallactic conception of exchange from Duncan Foley, and this chapter runs variations on themes from Foley (2010). To my fellow students in his microeconomic theory course at the New School this chapter will also read as a poor fascimile of his lecture notes for that magnificent class. I thank Foley along with Rajiv Sethi, Gil Skillman, Peter Skott, Roberto Veneziani, Luca Zamparelli, and two anonymous readers of an earlier draft.
References
Arrow, K. J. (1959) “Toward a theory of price adjustment,” in Abramovitz, M. (ed.) The Allocation of Economic Resources, Palo Alto, CA: Stanford University Press.
Axtell, R. (2005) “The complexity of exchange,” Economic Journal, 115: 193–210.
Duménil, G. and Lévy, D. (1985) “The classicals and the neoclassicals: a rejoinder to Hahn,” Cambridge Journal of Economics, 9(4): 327–;345.
Edgeworth, F. Y. (1881) Mathematical Psychics, London: Kegan Paul.
Fisher, F. (1983) Disequilibrium Foundations of Equilibrium Economics, Cambridge, UK: Cambridge University Press.
Foley, D. K. (2010) “What’s wrong with the fundamental existence and welfare theorems?” Journal of Economic Behavior and Organization, 75(2): 115–131.
Hahn, F. (1982a) “The neo-Ricardians,” Cambridge Journal of Economics, 6: 353–374.
Hahn, F. (1982b) “Stability,” in Arrow, K. and Intriligator, M. (eds) Handbook of Mathematical Economics vol. 2, Amsterdam: Elsevier.
Malinvaud, E. (1972) Lectures on Microeconomic Theory, Amsterdam: North-Holland.
Mandler, M. (1999a) “Sraffian indeterminacy in general equilibrium,” Review of Economic Studies, 66: 693–711.
Mandler, M. (1999b) Dilemmas in Economic Theory, Oxford: Oxford University Press.
Marglin, S. (1984) Growth, Distribution, and Prices, Cambridge, MA: Harvard University Press.
Roemer, J. (1982) A General Theory of Exploitation and Class, Cambridge, MA: Harvard University Press.
Smale, S. (1976) “Exchange processes with price adjustment,” Journal of Mathematical Economics, 3: 211–226.
Sraffa, P. (1960) Production of Commodities by Means of Commodities. Cambridge, UK: Cambridge University Press.
Uzawa, H. (1962) “On the stability of Edgeworth’s barter process,” International Economic Review, 3: 218–232.
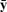 c). Every capitalist has access to the same Leontief production technology characterized by a productive, indecomposable n × n matrix of material input requirements A and a nonnegative n-vector of labor requirements l. For any nonnegative n-vector xc, a capitalist who employs lxc units of labor on Axc units of nonlabor inputs acquires [I — A]xc as a net output of the n goods.
c). Every capitalist has access to the same Leontief production technology characterized by a productive, indecomposable n × n matrix of material input requirements A and a nonnegative n-vector of labor requirements l. For any nonnegative n-vector xc, a capitalist who employs lxc units of labor on Axc units of nonlabor inputs acquires [I — A]xc as a net output of the n goods.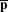 of prices for goods delivered after production, a capitalist chooses a production plan xc and a consumption plan yc,
of prices for goods delivered after production, a capitalist chooses a production plan xc and a consumption plan yc,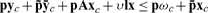

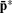 , ν*) and a complex of consumption and production plans (yc*,
, ν*) and a complex of consumption and production plans (yc*, 
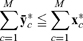

 units of the good for her later consumption. In effect she makes a loan of
units of the good for her later consumption. In effect she makes a loan of 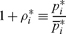
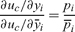
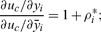
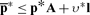
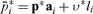
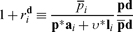
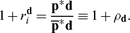
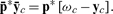
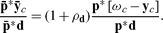
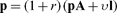
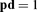
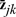 describe the deliveries called for under any contracts extant between the jth and the kth actors. A positive (negative) ith component in zjk indicates that the kth (jth) person is to deliver to the jth (kth) a quantity of the ith good equal in magnitude to that component. Let the number ecw describe the fraction of the wth worker’s labor time that she’s contracted to spend on the cth capitalist’s production. Let
describe the deliveries called for under any contracts extant between the jth and the kth actors. A positive (negative) ith component in zjk indicates that the kth (jth) person is to deliver to the jth (kth) a quantity of the ith good equal in magnitude to that component. Let the number ecw describe the fraction of the wth worker’s labor time that she’s contracted to spend on the cth capitalist’s production. Let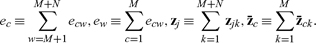
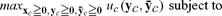

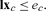
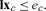

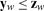
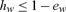

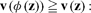
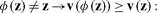
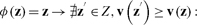
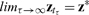
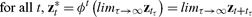




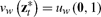
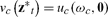
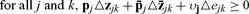
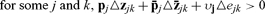
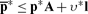
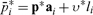
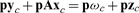
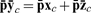
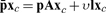

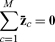

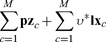
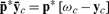


 and d,
and d,