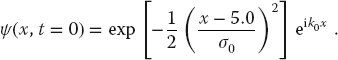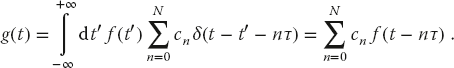12
Fourier Analysis: Signals and Filters
12.1 Fourier Analysis of Nonlinear Oscillations
Consider a particle oscillating either in the nonharmonic potential of (8.5):
or in the perturbed harmonic oscillator potential (8.2),
While free oscillations in these potentials are always periodic, they are not sinusoidal. Your problem is to take the solution of one of these nonlinear oscillators and expand it in a Fourier basis:
For example, if your oscillator is sufficiently nonlinear to behave like the sawtooth function (Figure 12.1a), then the Fourier spectrum you obtain should be similar to that shown in Figure 12.1b.
In general, when we undertake such a spectral analysis we want to analyze the steady-state behavior of a system. This means that we have waited for the initial transient behavior to die out. It is easy to identify just what the initial transient is for linear systems, but may be less so for nonlinear systems in which the “steady state” jumps among a number of configurations. In the latter case, we would have different Fourier spectra at different times.
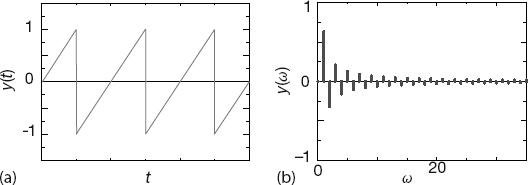
Figure 12.1 (a) A sawtooth function that repeats infinitely in time. (b) The Fourier spectrum of frequencies contained in this function (natural units). Also see Figure 1.9 in which we show the result of summing a finite number of terms of this series.
12.2 Fourier Series (Math)
Part of our interest in nonlinear oscillations arises from their lack of study in traditional physics courses where linear oscillations, despite the fact that they are just a first approximation, are most often studied. If the force on a particle is always toward its equilibrium position (a restoring force), then the resulting motion will be periodic, but not necessarily harmonic. A good example is the motion in a highly anharmonic potential with 
in (12.1) that produces an x(t) looking like a series of pyramids; this motion is periodic but not harmonic.
In a sense, our approach is the inverse of the traditional one in which the fundamental oscillation is determined analytically and the higher frequency overtones are determined by perturbation theory (Landau and Lifshitz, 1976). We start with the full (numerical) periodic solution and then decompose it into what may be called harmonics. When we speak of fundamentals, overtones, and harmonics, we speak of solutions to the linear boundary-value problem, for example, of waves on a plucked violin string. In the latter case, and when given the correct conditions (enough musical skill), it is possible to excite individual harmonics or sums of them in the series
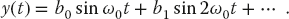
Anharmonic oscillators vibrate at a single frequency (which may vary with amplitude) but not with a sinusoidal waveform. Although it is mathematically proper to expand nonlinear oscillations in a Fourier series, this does not imply that the individual harmonics can be excited (played).
You may recall from classical mechanics that the general solution for a vibrating system can be expressed as the sum of the normal modes of that system. These expansions are possible only if we have linear operators and, subsequently, the principle of superposition: If 
are solutions of some linear equation, then 
is also a solution. The principle of linear superposition does not hold when we solve nonlinear problems. Nevertheless, it is always possible to expand a periodic solution of a nonlinear problem in terms of trigonometric functions with frequencies that are integer multiples of the true frequency of the nonlinear oscillator.1) This is a consequence of Fourier’s theorem being applicable to any single-valued periodic function with only a finite number of discontinuities. We assume we know the period T, that is,
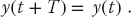
This tells us the true frequency ω:
A periodic function (usually designated as the signal) can be expanded as a series of harmonic functions with frequencies that are multiples of the true frequency:
This equation represents the signal y(t) as the simultaneous sum of pure tones of frequency nω. The coefficients an and bn measure the amount of cos nωt and sin nωt present in y(t), respectively. The intensity or power at each frequency is proportional to 
.
The Fourier series (12.7) is a “best fit” in the least-squares sense of Chapter 7, because it minimizes 
, where i denotes different measurements of the signal. This means that the series converges to the average behavior of the function, but misses the function at discontinuities (at which points it converges to the mean) or at sharp corners (where it overshoots). A general function y(t) may contain an infinite number of Fourier components, although low-accuracy reproduction is usually possible with a small number of harmonics.
The coefficients an and bn in (12.7) are determined by the standard techniques for orthogonal function expansion. To find the coefficients, multiply both sides of (12.7) by cos n
t or sin nt, integrate over one period, and project a single an or bn:
As seen in the bn coefficients (Figure 12.1b), these coefficients usually decrease in magnitude as the frequency increases, and can enter with a negative sign, the negative sign indicating the relative phase.
Awareness of the symmetry of the function y(t) may eliminate the need to evaluate all the expansion coefficients. For example,
- a0 is twice the average value of y:
(12.9)
- For an odd function, that is, one for which
, and only half of the integration range is needed to determine bn:
(12.10)However, if there is no input signal for
, we do not have a truly odd function, and so small values of an may occur. - For an even function, that is, one for which
, and only half the integration range is needed to determine an:
(12.11)
12.2.1 Examples: Sawtooth and Half-Wave Functions
The sawtooth function (Figure 12.1) is described mathematically as
It is clearly periodic, nonharmonic, and discontinuous. Yet it is also odd and so can be represented more simply by shifting the signal to the left:
Although the general shape of this function can be reproduced with only a few terms of the Fourier components, many components are needed to reproduce the sharp corners. Because the function is odd, the Fourier series is a sine series and (12.8) determines the bn values:
The half-wave function
is periodic, nonharmonic (the upper half of a sine wave), and continuous, but with discontinuous derivatives. Because it lacks the sharp corners of the sawtooth function, it is easier to reproduce with a finite Fourier series. Equation 12.8 determines
12.3 Exercise: Summation of Fourier Series
Hint: The program FourierMatplot.py written by Oscar Restrepo performs a Fourier analysis of a sawtooth function and produces the visualization shown in Figure 1.9b. You may want to use this program to help with this exercise.
- Sawtooth function: Sum the Fourier series for the sawtooth function up to order n = 2, 4, 10, 20, and plot the results over two periods.
- a) Check that in each case, the series gives the mean value of the function at the points of discontinuity.
- b) Check that in each case the series overshoots by about 9% the value of the function on either side of the discontinuity (the Gibbs phenomenon).
- Half-wave function: Sum the Fourier series for the half-wave function up to order n = 2, 4, 10, 50 and plot the results over two periods. (The series converges quite well, doesn’t it?)
12.4 Fourier Transforms (Theory)
Although a Fourier series is the right tool for approximating or analyzing periodic functions, the Fourier transform or integral is the right tool for nonperiodic functions. We convert from series to transform by imagining a system described by a continuum of “fundamental” frequencies. We thereby deal with wave packets containing continuous rather than discrete frequencies.2) While the difference between series and transform methods may appear clear mathematically, when we approximate the Fourier integral as a finite sum, the two become equivalent.
By analogy with (12.7), we now imagine our function or signal y(t) expressed in terms of a continuous series of harmonics (inverse Fourier transform):
where for compactness we use a complex exponential function.3) The expansion amplitude Y() is analogous to the Fourier coefficients (an, bn), and is called the Fourier transform of y(t). The integral (12.18) is the inverse transform because it converts the transform to the signal. The Fourier transform converts the signal y(t) to its transform Y(ω):
The 
factor in both these integrals is a common normalization in quantum mechanics, but maybe not in engineering where only a single 1/2π factor is used. Likewise, the signs in the exponents are also conventions that do not matter as long as you maintain consistency.
If y(t) is the measured response of a system (signal) as a function of time, then Y(ω) is the spectral function that measures the amount of frequency ω present in the signal. In many cases, it turns out that Y(ω) is a complex function with both positive and negative values, and with powers-of-ten variation in magnitude. Accordingly, it is customary to eliminate some of the complexity of Y(ω) by making a semilog plot of the squared modulus 
vs ω. This is called a power spectrum and provides an immediate view of the amount of power or strength in each component.
If the Fourier transform and its inverse are consistent with each other, we should be able to substitute (12.18) into (12.19) and obtain an identity:
For this to be an identity, the term in braces must be the Dirac delta function:
While the delta function is one of the most common and useful functions in theoretical physics, it is not well behaved in a mathematical sense and misbehaves terribly in a computational sense. While it is possible to create numerical approximations to 
, they may well be borderline pathological. It is certainly better for you to do the delta function part of an integration analytically and leave the nonsingular leftovers to the computer.
12.5 The Discrete Fourier Transform
If y(t) or Y(ω) is known analytically or numerically, integrals (12.18) and (12.19) can be evaluated using the integration techniques studied earlier. In practice, the signal y(t) is measured at just a finite number N of times t, and these are all we have as input to approximate the transform. The resultant discrete Fourier transform is an approximation both because the signal is not known for all times, and because we must integrate numerically (Briggs and Henson, 1995). Once we have a discrete set of (approximate) transform values, they can be used to reconstruct the signal for any value of the time. In this way, the DFT can be thought of as a technique for interpolating, compressing, and extrapolating the signal.
We assume that the signal y(t) is sampled at (N + 1) discrete times (N time intervals), with a constant spacing 
between times:
In other words, we measure the signal y(t) once every hth of a second for a total time of T. This correspondingly define the signal’s period T and the sampling rate s:
Regardless of the true periodicity of the signal, when we choose a period T over which to sample the signal, the mathematics will inevitably produce a y(t) that is periodic with period T,
We recognize this periodicity, and ensure that there are only N independent measurements used in the transform, by defining the first and last y’s to be equal:
If we are analyzing a truly periodic function, then the N points should span one complete period, but not more. This guarantees their independence. Unless we make further assumptions, the N independent data y(tk) can determine no more than N independent transform values 
.
The time interval T (which should be the period for periodic functions) is the largest time over which we measure the variation of y(t). Consequently, it determines the lowest frequency contained in our Fourier representation of y(t),
The full range of frequencies in the spectrum ωn are determined by the number of samples taken, and by the total sampling time T = Nh as
Here ω0 = 0 corresponds to the zero-frequency or DC component of the transform, that is, the part of the signal that does not oscillate.
The discrete Fourier transform (DFT) algorithm follows from two approximations. First we evaluate the integral in (12.19) from time 0 to time T, over which the signal is measured, and not from 
. Second, the trapezoid rule is used for the integration4):
To keep the final notation more symmetric, the step size h is factored from the transform Y and a discrete function Yn is defined as
With this same care in accounting, and with 
, we invert the Yn’s:
Once we know the N values of the transform, we can use (12.34) to evaluate y(t) for any time t. There is nothing illegal about evaluating Yn and yk for arbitrarily large values of n and k, yet there is also nothing to be gained either. Because the trigonometric functions are periodic, we just get the old answers:
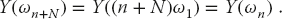
Another way of stating this is to observe that none of the equations change if we replace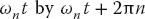 
. There are still just N independent output numbers for N independent inputs, and so the transform and the reconstituted signal are periodic.
We see from (12.29) that the larger we make the time T = Nh over which we sample the function, the smaller will be the frequency steps or resolution.5) Accordingly, if you want a smooth frequency spectrum, you need to have a small frequency step 2π/T, which means a longer observation time T. While the best approach would be to measure the input signal for all times, in practice a measured signal y(t) is often extended in time (“padded”) by adding zeros for times beyond the last measured signal, which thereby increases the value of T artificially. Although this does not add new information to the analysis, it does build in the experimentalist’s view that the signal has no existence, or no meaning, at times after the measurements are stopped.
While periodicity is expected for a Fourier series, it is somewhat surprising for Fourier a integral, which have been touted as the right tool for nonperiodic functions. Clearly, if we input values of the signal for longer lengths of time, then the inherent period becomes longer, and if the repeat period T is very long, it may be of little consequence for times short compared to the period. If y(t) is actually periodic with period Nh, then the DFT is an excellent way of obtaining Fourier series. If the input function is not periodic, then the DFT can be a bad approximation near the endpoints of the time interval (after which the function will repeat) or, correspondingly, for the lowest frequencies.
The DFT and its inverse can be written in a concise and insightful way, and be evaluated efficiently, by introducing a complex variable Z for the exponential and then raising Z to various powers:
With this formulation, the computer needs to compute only powers of Z. We give our DFT code in Listing 12.1. If your preference is to avoid complex numbers, we can rewrite (12.37) in terms of separate real and imaginary parts by applying Euler’s theorem with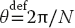 
:
Readers new to DFTs are often surprised when they apply these equations to practical situations and end up with transforms Y having imaginary parts, despite the fact that the signal y is real. Equation 12.40 should make it clear that a real signal 
will yield an imaginary transform unless 
. This occurs only if y(t) is an even function over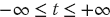 
and we integrate exactly. Because neither condition holds, the DFTs of real, even functions may have small imaginary parts. This is not as a result of an error in programming, and in fact is a good measure of the approximation error in the entire procedure.
The computation time for a DFT can be reduced even further by using fast Fourier transform algorithm, as discussed in Section 12.9. An examination of (12.37) shows that the DFT is evaluated as a matrix multiplication of a vector of length N containing the Z values by a vector of length N of y value. The time for this DFT scales like N2, while the time for the FFT algorithm scales as N log2 N. Although this may not seem like much of a difference, for N = 102–3, the difference of 103–5 is the difference between a minute and a week. For this reason, it is the FFT is often used for online spectrum analysis.
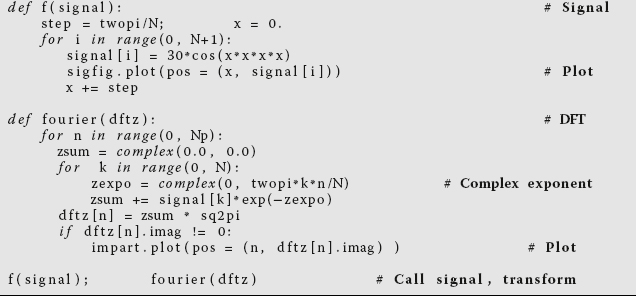
Listing 12.1 DFTcomplex.py uses the built-in complex numbers of Python to compute the DFT for the signal in method f(signal).
12.5.1 Aliasing (Assessment)
The sampling of a signal by DFT for only a finite number of times (large Δt) limits the accuracy of the deduced high-frequency components present in the signal. Clearly, good information about very high frequencies requires sampling the signal with small time steps so that all the wiggles can be included. While a poor deduction of the high-frequency components may be tolerable if all we care about are the low-frequency components, the inaccurate high-frequency components remain present in the signal and may contaminate the low-frequency components that we deduce. This effect is called aliasing and is the cause of the Moiré pattern distortion in digital images.
As an example, consider Figure 12.2 showing the two functions 
, with their points of overlap in bold. If we were unfortunate enough to sample a signal containing these functions at the times t = 0, 2, 4, 6, 8, then we would measure 
and assume that there was no signal at all. However, if we were unfortunate enough to measure the signal at the filled dots in Figure 12.2 where 
, specifically, t = 0, 12/10, 4/3, …, then our Fourier analysis would completely miss the high-frequency component. In DFT jargon, we would say that the high-frequency component has been aliased by the low-frequency component. In other cases, some high-frequency values may be included in our sampling of the signal, but our sampling rate may not be high enough to include enough of them to separate the high-frequency component properly. In this case some high-frequency signals would be included spuriously as part of the low-frequency spectrum, and this would lead to spurious low-frequency oscillations when the signal is synthesized from its Fourier components.
More precisely, aliasing occurs when a signal containing frequency f is sampled at a rate of s = N/T measurements per unit time, with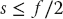 
. In this case, the frequencies f and f – 2s yield the same DFT, and we would not be able to determine that there are two frequencies present. That being the case, to avoid aliasing we want no frequencies f > s/2 to be present in our input signal. This is known as the Nyquist criterion. In practice, some applications avoid the effects of aliasing by filtering out the high frequencies from the signal and then analyzing only the remaining low-frequency part. (The low-frequency sinc filter discussed in Section 12.8.1 is often used for this purpose.) Although filtering eliminates some high-frequency information, it lessens the distortion of the low-frequency components, and so may lead to improved reproduction of the signal.
Figure 12.2 A plot of the functions sin(πt/2) and sin(2πt). If the sampling rate is not high enough, these signalsmay appear indistinguishable in a Fourier decomposition. If the sample rate is too low and if both signals are present in a sample, the deduced low-frequency component may be contaminated by the higher frequency component signal.
If accurate values for the high frequencies are required, then we will need to increase the sampling rate s by increasing the number N of samples taken within the fixed sampling time T = Nh. By keeping the sampling time constant and increasing the number of samples taken, we make the time step h smaller and we pick up the higher frequencies. By increasing the number N of frequencies and that you compute, you move the previous higher frequency components in closer to the middle of the spectrum, and thus away from the error-prone ends.
If we increase the total time sampling time T = Nh and keep h the same, then the sampling rate s = N/T = 1/h remains the same. Because 
, this makes ω1 smaller, which means we have more low frequencies recorded and a smoother frequency spectrum. And as we said, this is often carried out, after the fact, by padding the end of the data set with zeros.
Listing 12.2 DFTreal.py computes the discrete Fourier transform for the signal in method f(signal) using real numbers.
12.5.2 Fourier Series DFT (Example)
For simplicity, let us consider the Fourier cosine series:
Here 
is the actual period of the system (not necessarily the period of the simple harmonic motion occurring for a small amplitude). We assume that the function y(t) is sampled for a discrete set of times
Because we are analyzing a periodic function, we retain the conventions used in the DFT and require the function to repeat itself with period T = Nh; that is, we assume that the amplitude is the same at the first and last points:
This means that there are only N independent values of y being used as input. For these N independent yk values, we can determine uniquely only N expansion coefficients ak. If we use the trapezoid rule to approximate the integration in (12.42), we determine the N independent Fourier components as
Because we can determine only N Fourier components from N independent y(t) values, our Fourier series for the y(t) must be in terms of only these components:
In summary, we sample the function y(t) at N times, t1, …, tN. We see that all the values of y sampled contribute to each ak. Consequently, if we increase N in order to determine more coefficients, we must recompute all the an values. In the wavelet analysis in Chapter 13, the theory is reformulated so that additional samplings determine higher spectral components without affecting lower ones.
12.5.3 Assessments
Simple analytic input It is always good to do simple checks before examining more complex problems, even if you are using a package’s Fourier tool.
- Sample the even signal
(12.47)
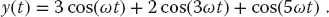
- a) Decompose this into its components.
- b) Check that the components are essentially real and in the ratio 3 : 2 : 1 (or 9 : 4 : 1 for the power spectrum).
- c) Verify that the frequencies have the expected values (not just ratios).
- d) Verify that the components resum to give the input signal.
- e) Experiment on the separate effects of picking different values of the step size h and of enlarging the measurement period T = Nh.
- Sample the odd signal
(12.48)Decompose this into its components; then check that they are essentially imaginary and in the ratio 1 : 2 : 3 (or 1 : 4 : 9 if a power spectrum is plotted) and that they resum to give the input signal.
- Sample the mixed-symmetry signal
(12.49)Decompose this into its components; then check that there are three of them in the ratio 5 : 2 : 1 (or 25 : 4 : 1 if a power spectrum is plotted) and that they resum to give the input signal.
- Sample the signal
Compare and explain the results obtained by sampling (a) without the 5, (b) as given but without the 2, and (c) without the 5 and without the 2.
- In our discussion of aliasing, we examined Figure 12.2 showing the functions
. Sample the function
(12.50)and explore how aliasing occurs. Explicitly, we know that the true transform contains peaks at
. Sample the signal at a rate that leads to aliasing, as well as at a higher sampling rate at which there is no aliasing. Compare the resulting DFTs in each case and check if your conclusions agree with the Nyquist criterion.
Highly nonlinear oscillator Recall the numerical solution for oscillations of a spring with power p = 12 (see (12.1)). Decompose the solution into a Fourier series and determine the number of higher harmonics that contribute at least 10%; for example, determine the n for which 
. Check that resuming the components reproduces the signal.
Nonlinearly perturbed oscillator Remember the harmonic oscillator with a nonlinear perturbation (8.2):
For very small amplitudes of oscillation 
, the solution x(t) essentially should be only the first term of a Fourier series.
- We want the signal to contain “approximately 10% nonlinearity.” This being the case, fix your value of α so that
is the maximum amplitude of oscillation. For the rest of the problem, keep the value of α fixed. - Decompose your numerical solution into a discrete Fourier spectrum.
- Plot a graph of the percentage of importance of the first two, non-DC Fourier components as a function of the initial displacement for
. You should find that higher harmonics are more important as the amplitude increases. Because both even and odd components are present, Yn should be complex. Because a 10% effect in amplitude becomes a 1% effect in power, make sure that you make a semilog plot of the power spectrum. - As always, check that resumations of your transforms reproduce the signal.
(Warning: The ω you use in your series must correspond to the true frequency of the system, not the ω0 of small oscillations.)
12.5.4 Nonperiodic Function DFT (Exploration)
Consider a simple model (a wave packet) of a “localized” electron moving through space and time. A good model for an electron initially localized around x = 5 is a Gaussian multiplying a plane wave:
This wave packet is not an eigenstate of the momentum operator 6) p = id/dx and in fact contains a spread of momenta. Your problem is to evaluate the Fourier transform
as a way of determining the momenta components in (12.52).
12.6 Filtering Noisy Signals
You measure a signal y(t) that obviously contains noise. Your problem is to determine the frequencies that would be present in the spectrum of the signal if the signal did not contain noise. Of course, once you have a Fourier transform from which the noise has been removed, you can transform it to obtain a signal s(t) with no noise.
In the process of solving this problem, we examine two simple approaches: the use of autocorrelation functions and the use of filters. Both approaches find wide applications in science, with our discussion not doing the subjects justice. We will see filters again in the discussion of wavelets in Chapter 13.
12.7 Noise Reduction via Autocorrelation (Theory)
We assume that the measured signal is the sum of the true signal s(t), which we wish to determine, plus some unwelcome noise n(t):
Our first approach at removing the noise relies on that fact that noise is a random process and thus should not be correlated with the signal. Yet what do we mean when we say that two functions are not correlated? Well, if the two tend to oscillate with their nodes and peaks in much the same places, then the two functions are clearly correlated. An analytic measure of the correlation of two arbitrary functions y(t) and x(t) is the correlation function
where τ, the lag time, is a variable. Even if the two signals have different magnitudes, if they have similar time dependences except for one lagging or leading the other, then for certain values of τ the integrand in (12.55) will be positive for all values of t. For those values of τ, the two signals interfere constructively and produce a large value for the correlation function. In contrast, if both functions oscillate independently regardless of the value of τ, then it is just as likely for the integrand to be positive as to be negative, in which case the two signals interfere destructively and produce a small value for the integral.
Before we apply the correlation function to our problem, let us study some of its properties. We use (12.18) to express c, y*, and x in terms of their Fourier transforms:
Because ω, ω′, and ω″ are dummy variables, other names may be used for these variables without changing any results. When we substitute these representations into definition (12.55) of the correlation function and assume that the resulting integrals converge well enough to be rearranged, we obtain
where the last line follows because ω″ and ω are equivalent dummy variables. Equation 12.57 says that the Fourier transform of the correlation function between two signals is proportional to the product of the transform of one signal and the complex conjugate of the transform of the other. (We shall see a related convolution theorem for filters.)
Figure 12.3 (a) A function that is a signal plus noise s(t) + n(t); (b) the autocorrelation function vs. time deduced by processing this signal; (c) the power spectrum obtained from autocorrelation function; (d) the signal plus noise after passage through a low-pass filter.
A special case of the correlation function c(τ) is the autocorrelation function A(τ). It measures the correlation of a time signal with itself:
This function is computed by taking a signal y(t) that has been measured over some time period and then averaging it over time using y(t + τ) as a weighting function. This process is also called folding a function onto itself (as might be done with dough) or a convolution. To see how this folding removes noise from a signal, we go back to the measured signal (12.54), which was the sum of pure signal plus noise s(t) + n(t). As an example, in Figure 12.3a we show a signal that was constructed by adding random noise to a smooth signal. When we compute the autocorrelation function for this signal, we obtain a function (Figure 12.3b) that looks like a broadened, smoothed version of the signal y(t).
We can understand how the noise is removed by taking the Fourier transform of s(t) + n(t) to obtain a simple sum of transforms:
Because the autocorrelation function (12.58) for 
involves the second power of y, is not a linear function, that is, 
, but instead
If we assume that the noise n(t) in the measured signal is truly random, then it should average to zero over long times and be uncorrelated at times t and t + τ. This being the case, both integrals involving the noise vanish, and so
Thus, the part of the noise that is random tends to be averaged out of the autocorrelation function, and we are left with an approximation of the autocorrelation function of the pure signal.
So how does this help us? Application of (12.57) with 
tells us that the Fourier transform A(ω) of the autocorrelation function is proportional to 
:
The function is the power spectrum of the pure signal. Thus, evaluation of the autocorrelation function of the noisy signal gives us the pure signal’s power spectrum, which is often all that we need to know. For example, in Figure 12.3a we see a noisy signal, the autocorrelation function (Figure 12.3b), which clearly is smoother than the signal, and finally, the deduced power spectrum (Figure 12.3c). Note that the broadband high-frequency components characteristic of noise are absent from the power spectrum.
You can easily modify the sample program DFTcomplex.py in Listing 12.1 to compute the autocorrelation function and then the power spectrum from A(τ). We present a program NoiseSincFilter.py on the instructor’s site that does this.
12.7.1 Autocorrelation Function Exercises
- Imagine that you have sampled the pure signal
(12.64)Although there is just a single sine function in the denominator, there is an infinite number of overtones as follows from the expansion
(12.65)
- a) Compute the DFT S(ω). Make sure to sample just one period but to cover the entire period. Make sure to sample at enough times (fine scale) to obtain good sensitivity to the high-frequency components.
- b) Make a semilog plot of the power spectrum .
- c) Take your input signal s(t) and compute its autocorrelation function A(τ) for a full range of τ values (an analytic solution is okay too).
- d) Compute the power spectrum indirectly by performing a DFT on the autocorrelation function. Compare your results to the spectrum obtained by computing directly.
- Add some random noise to the signal using a random number generator:
(12.66)where α is an adjustable parameter. Try several values of α, from small values that just add some fuzz to the signal to large values that nearly hide the signal.
- a) Plot your noisy data, their Fourier transform, and their power spectrum obtained directly from the transform with noise.
- b) Compute the autocorrelation function A(τ) and its Fourier transform A(ω).
- c) Compare the DFT of A(τ) to the true power spectrum and comment on the effectiveness of reducing noise by use of the autocorrelation function.
- d) For what value of α do you essentially lose all the information in the input?
12.8 Filtering with Transforms (Theory)
A filter (Figure 12.4) is a device that converts an input signal f(t) to an output signal g(t) with some specific property for g(t). More specifically, an analog filter is defined (Hartmann, 1998) as integration over the input function:
The operation indicated in (12.67) occurs often enough that it is given the name convolution and is denoted by an asterisk *. The function h(t) is called the response or transfer function of the filter because it is the response of the filter to a unit impulse:
Equation 12.67 states that the output g(t) of a filter equals the input f(t) convoluted with the transfer function h(t – τ). Because the argument of the response function is delayed by a time τ relative to that of the signal in integral (12.67), τ is called the lag time. While the integration is over all times, the response of a good detector usually peaks around zero time. In any case, the response must equal zero for τ > t because events in the future cannot affect the present (causality).
The convolution theorem states that the Fourier transform of the convolution g(t) is proportional to the product of the transforms of f(t) and h(t):
Figure 12.4 A schematic of an input signal f(t) passing through a filter h that outputs the function g(t).
The theorem results from expressing the functions in (12.67) by their transforms and using the resulting Dirac delta function to evaluate an integral (essentially what we did in our discussion of correlation functions).
Regardless of the domain used, filtering as we have defined it is a linear process involving just the first powers of f. This means that the output at one frequency is proportional to the input at that frequency. The constant of proportionality between the two may change with frequency and thus suppress specific frequencies relative to others, but that constant remains fixed in time. Because the law of linear superposition is valid for filters, if the input to a filter is represented as the sum of various functions, then the transform of the output will be the sum of the functions’ Fourier transforms.
Filters that remove or decrease high-frequency components more than they do low-frequency ones, are called low-pass filters. Those that filter out the low frequencies are called high-pass filters. A simple low-pass filter is the RC circuit shown in Figure 12.5a. It produces the transfer function
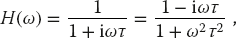
where τ = RC is the time constant. The ω2 in the denominator leads to a decrease in the response at high frequencies and therefore makes this a low-pass filter (the iω affects only the phase). A simple high-pass filter is the RC circuit shown in Figure 12.5b. It produces the transfer function
H = 1 at large ω, yet H vanishes as ω → 0, as expected for a high-pass filter.
Filters composed of resistors and capacitors are fine for analog signal processing. For digital processing we want a digital filter that has a specific response function for each frequency range. A physical model for a digital filter may be constructed from a delay line with taps at various spacing along the line (Figure 12.6)
Figure 12.5 (a) An RC circuit arranged as a low-pass filter. (b) An RC circuit arranged as a high-pass filter.
Figure 12.6 A delay-line filter in which the signal at different times is scaled by different amounts ci.
(Hartmann, 1998). The signal read from tap n is just the input signal delayed by time nτ, where the delay time τ is a characteristic of the particular filter. The output from each tap is described by the transfer function 
, possibly with scaling factor cn. As represented by the triangle in Figure 12.6b, the signals from all taps are ultimately summed together to form the total response function:
In the frequency domain, the Fourier transform of a delta function is an exponential, and so (12.72) results in the transfer function
where the exponential indicates the phase shift from each tap.
If a digital filter is given a continuous time signal f(t) as input, its output will be the discrete sum
And of course, if the signal’s input is a discrete sum, its output will remain a discrete sum. In either case, we see that knowledge of the filter coefficients ci provides us with all we need to know about a digital filter. If we look back at our work on the DFT in Section 12.5, we can view a digital filter (12.74) as a Fourier transform in which we use an N-point approximation to the Fourier integral. The cns then contain both the integration weights and the values of the response function at the integration points. The transform itself can be viewed as a filter of the signal into specific frequencies.
12.8.1 Digital Filters: Windowed Sinc Filters (Exploration) 
Problem Construct digital versions of high-pass and low-pass filters and determine which filter works better at removing noise from a signal.
Figure 12.7 The rectangle function rect(ω) that is constant for a finite frequency interval. The Fourier transform of this function is sinc(t).
A popular way to separate the bands of frequencies in a signal is with a windowed sinc filter (Smith, 1999). This filter is based on the observation that an ideal low-pass filter passes all frequencies below a cutoff frequency ωc, and blocks all frequencies above this frequency. And because there tends to be more noise at high frequencies than at low frequencies, removing the high frequencies tends to remove more noise than signal, although some signal is inevitably lost. One use for windowed sinc filters is in reducing aliasing in DFTs by removing the high-frequency component of a signal before determining its Fourier components. The graph in Figure 12.1b was obtained by passing our noisy signal through a sinc filter (using the program NoiseSincFilter.py).
If both positive and negative frequencies are included, an ideal low-frequency filter will look like the rectangular pulse in frequency space (Figure 12.7):
Here rect(ω) is the rectangular function. Although maybe not obvious, a rectangular pulse in the frequency domain has a Fourier transform that is proportional to the sinc function in the time domain (Smith, 1991)
where the πs are sometimes omitted. Consequently, we can filter out the high-frequency components of a signal by convoluting it with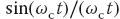 
, a technique also known as the Nyquist–Shannon interpolation formula. In terms of discrete transforms, the time-domain representation of the sinc filter is simply
Because all frequencies below the cutoff frequency ωc are passed with unit amplitude, while all higher frequencies are blocked, we can see the importance of a sinc filter.
In practice, there are a number of problems in using sinc function as the filter. First, as formulated, the filter is noncausal; that is, there are coefficients at negative times, which is nonphysical because we do not start measuring the signal until t = 0. Second, in order to produce a perfect rectangular response, we would have to sample the signal at an infinite number of times. In practice, we sample at (M + 1) points (M even) placed symmetrically around the main lobe of sin(πt)/πt, and then shift times to purely positive values via
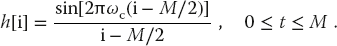
As might be expected, a penalty is incurred for making the filter discrete; instead of the ideal rectangular response, we obtain some Gibbs overshoot, with rounded corners and oscillations beyond the corner.
There are two ways to reduce the departures from the ideal filter. The first is to increase the length of times for which the filter is sampled, which inevitably leads to longer compute times. The other way is to smooth out the truncation of the sinc function by multiplying it with a smoothly tapered curve like the Hamming window function:
In this way, the filter’s kernel becomes
The cutoff frequency ωc should be a fraction of the sampling rate. The time length M determines the bandwidth over which the filter changes from 1 to 0.
Exercise Repeat the exercise that added random noise to a known signal, this time using the sinc filter to reduce the noise. See how small you can make the signal and still be able to separate it from the noise.
12.9 The Fast Fourier Transform Algorithm
We have seen in (12.37) that a discrete Fourier transform can be written in the compact form as
Even if the signal elements yk to be transformed are real, Z is complex, and therefore we must process both real and imaginary parts when computing transforms. Because both n and k range over N integer values, the 
multiplications in (12.81) require some N2 multiplications and additions of complex numbers. As N gets large, as happens in realistic applications, this geometric increase in the number of steps leads to long computation times.
In 1965, Cooley and Tukey discovered an algorithm7) that reduces the number of operations necessary to perform a DFT from N2 to roughly N log2 N (Cooley, 1965; Donnelly and Rust, 2005). Although this may not seem like such a big difference, it represents a 100-fold speedup for 1000 data points, which changes a full day of processing into 15 min of work. Because of its widespread use (including cell phones), the fast Fourier transform algorithm is considered one of the 10 most important algorithms of all time.
The idea behind the FFT is to utilize the periodicity inherent in the definition of the DFT (12.81) to reduce the total number of computational steps. Essentially, the algorithm divides the input data into two equal groups and transforms only one group, which requires ~ (N/2)2 multiplications. It then divides the remaining (nontransformed) group of data in half and transforms them, continuing the process until all the data have been transformed. The total number of multiplications required with this approach is approximately N log2 N.
Specifically, the FFT’s time economy arises from the computationally expensive complex factor 
having values that are repeated as the integers n and k vary sequentially. For instance, for N = 8,
where we include 
for clarity. When we actually evaluate these powers of Z, we find only four independent values:
When substituted into the definitions of the transforms, we obtain
We see that these transforms now require 8 × 8 = 64 multiplications of complex numbers, in addition to some less time-consuming additions. We place these equations in an appropriate form for computing by regrouping the terms into sums and differences of the y’s:
Note the repeating factors inside the parentheses, with combinations of the form 
. These symmetries are systematized by introducing the butterfly operation (Figure 12.8). This operation takes the yp and yq data elements from the left wing and converts them to the yp + Zyq elements in the right wings. In Figure 12.9 we show what happens when we apply the butterfly operations to an entire FFT process, specifically to the pairs (y0, y4), (y1 y5), (y2, y6), and (y3, y7). Note how the number of multiplications of complex numbers has been reduced: For the first butterfly operation there are 8 multiplications by Z0; for the second butterfly operation there are 8 multiplications, and so forth, until a total of 24 multiplications are made in four butterflies. In contrast, 64 multiplications are required in the original DFT (12.91).
Figure 12.8 The basic butterfly operation in which elements yp and yq on the left are transformed into yp + Zyq and yp – Zyq on the right.
12.9.1 Bit Reversal
The reader may have observed in Figure 12.9 that we started with eight data elements in the order 0–7 and that after three butterfly operators we obtained transforms in the order 0, 4, 2, 6, 1, 5, 3, 7. The astute reader may further have observed that these numbers correspond to the bit-reversed order of 0–7. Let us look into this further. We need 3 bits to give the order of each of the 8 input data elements (the numbers 0–7). Explicitly, on the left in Table 10.1 we give the binary representation for decimal numbers 0–7, their bit reversals, and the corresponding decimal numbers. On the right we give the ordering for 16 input data elements, where we need 4 bits to enumerate their order. Notice that the order of the first 8 elements differs in the two cases because the number of bits being reversed differs. Also note that after the reordering, the first half of the numbers are all even and the second half are all odd.
Figure 12.9 The butterfly operations performing a FFT on the eight data on the left leading to eight transforms on the right. The transforms are different linear combinations of the input data.
The fact that the Fourier transforms are produced in an order corresponding to the bit-reversed order of the numbers 0–7 suggests that if we process the data in the bit-reversed order 0, 4, 2, 6, 1, 5, 3, 7, then the output Fourier transforms will be ordered (see Table 10.1). We demonstrate this conjecture in Figure 12.10, where we see that to obtain the Fourier transform for the eight input data, the butterfly operation had to be applied three times. The number 3 occurs here because it is the power of 2 that gives the number of data; that is, 23 = 8. In general, in order for a FFT algorithm to produce transforms in the proper order, it must reshuffle the input data into bit-reversed order. As a case in point, our sample program starts by reordering the 16 (24) data elements given in Table 12.1. Now the four butterfly operations produce sequentially ordered output.
Table 12.1 Reordering for 16 data complex points.
| Order | Input data | New order |
| 0 | 0.0 + 0.0i | 0.0 + 0.0i |
| 1 | 1.0 + 1.0i | 8.0 + 8.0i |
| 2 | 2.0 + 2.0i | 4.0 + 4.0i |
| 3 | 3.0 + 3.0i | 12.0 + 12.0i |
| 4 | 4.0 + 4.0i | 2.0 + 2.0i |
| 5 | 5.0 + 5.0i | 10.0 + 10.i |
| 6 | 6.0 + 6.0i | 6.0 + 6.0i |
| 7 | 7.0 + 7.0i | 14.0 + 14.0i |
| 8 | 8.0 + 8.0i | 1.0 + 1.0i |
| 9 | 9.0 + 9.0i | 9.0 + 9.0i |
| 10 | 10.0 + 10.i | 5.0 + 5.0i |
| 11 | 11.0 + 11.0i | 13.0 + 13.0i |
| 12 | 12.0 + 12.0i | 3.0 + 3.0i |
| 13 | 13.0 + 13.0i | 11.0 + 11.0i |
| 14 | 14.0 + 14.i | 7.0 + 7.0i |
| 15 | 15.0 + 15.0i | 15.0 + 15.0i |
| Binary-Reversed 0–7 | Binary-Reversed 0–16 | ||||
| Dec | Bin | Rev | Dec Rev | Rev | Dec Rev |
| 0 | 000 | 000 | 0 | 0000 | 0 |
| 1 | 001 | 100 | 4 | 1000 | 8 |
| 2 | 010 | 010 | 2 | 0100 | 4 |
| 3 | 011 | 110 | 6 | 1100 | 12 |
| 4 | 100 | 001 | 1 | 0010 | 2 |
| 5 | 101 | 101 | 5 | 1010 | 10 |
| 6 | 110 | 011 | 3 | 0110 | 6 |
| 7 | 111 | 111 | 7 | 1110 | 14 |
| 8 | 1000 | — | — | 0001 | 1 |
| 9 | 1001 | — | — | 1001 | 9 |
| 10 | 1010 | — | — | 0101 | 5 |
| 11 | 1011 | — | — | 1101 | 13 |
| 12 | 1100 | — | — | 0011 | 3 |
| 13 | 1101 | — | — | 1011 | 11 |
| 14 | 1101 | — | — | 0111 | 7 |
| 15 | 1111 | — | — | 1111 | 15 |
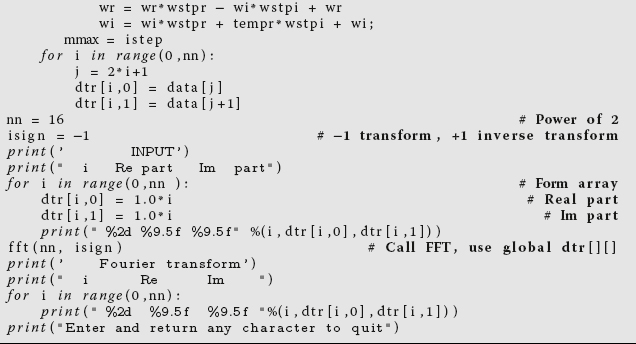
12.10 FFT Implementation
The first FFT program we are aware of was written in Fortran IV by Norman Brenner at MIT’s Lincoln Laboratory (Higgins, 1976) and was hard for us to follow. Our (easier-to-follow) Python version is in Listing 12.3. Its input is N = 2n data to be transformed (FFTs always require that the number of input data are a power of 2). If the number of your input data is not a power of 2, then you can make it so by concatenating some of the initial data to the end of your input until a power of 2 is obtained; because a DFT is always periodic, this just starts the period a little earlier. Our program assigns complex numbers at the 16 data points
Figure 12.10 A modified FFT in which the eight input data on the left are transformed into eight transforms on the right. The results are the same as in the previous figure, but now the output transforms are in numerical order whereas in the previous figure the input signals were in numerical order.
reorders the data via bit reversal, and then makes four butterfly operations. The data are stored in the array dtr[max,2], with the second subscript denoting real and imaginary parts. We increase the speed further by using the 1D array data to make memory access more direct:
which also provides storage for the output. The FFT transforms data using the butterfly operation and stores the results back in dtr[,], where the input data were originally.
12.11 FFT Assessment
- Compile and execute
FFT.py. Make sure you understand the output. - Take the output from
FFT.py, inverse-transform it back to signal space, and compare it to your input. (Checking that the double transform is proportional to itself is adequate, although the normalization factors in (12.37) should make the two equal.) - Compare the transforms obtained with a FFT to those obtained with a DFT (you may choose any of the functions studied before). Make sure to compare both precision and execution times.
Listing 12.3 FFT.py computes the FFT or inverse transform depending upon the sign of isign.
