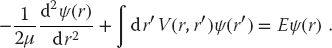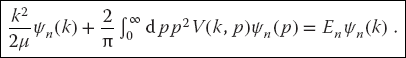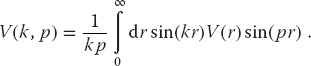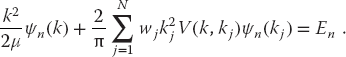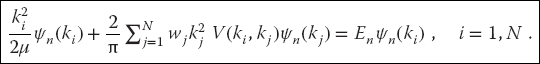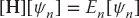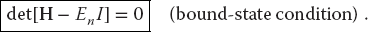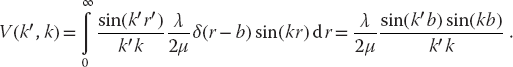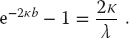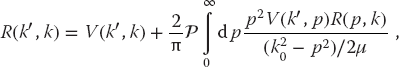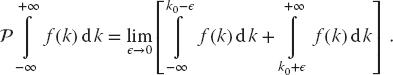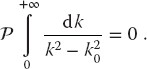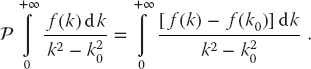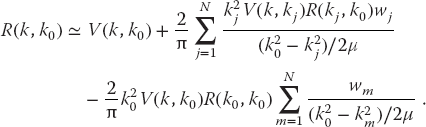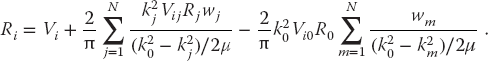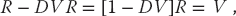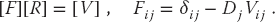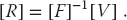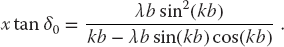26
Integral Equations of Quantum Mechanics
26.1 Bound States of Nonlocal Potentials
Problem A particle undergoes a many-body interaction with a medium (Figure 26.1). Although, we can write down the many-body Schrödinger equation that describes this interaction as the sum of many potentials, the number of coordinates involved is too large for a practical solution. Instead theorists have derived an effective single-particle potential that accounts for the many particles present by having the potential that is nonlocal, that is, the effective potential at r that depends on the wave function at the r′ values of the other particles (Landau, 1996):
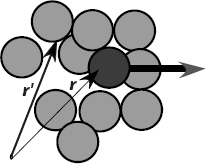
Figure 26.1 A dark particle moving in a dense medium in which it interacts with all particles present. The nonlocality of the potential felt by the dark particle at r arises from the interactions at all r′.
This type of interaction leads to a Schrödinger equation which is a combined integral and differential (“integrodifferential”) equation:
Your problem is to figure out how to find the bound-state energies En and wave functions ψn for the equation in (26.2).1)
26.2 Momentum–Space Schrödinger Equation (Theory)
One way of dealing with (26.2) is by going to momentum space where it becomes the integral equation (Landau, 1996)
We restrict our solution to angular momentum l = 0 partial waves, but for simplicity of notation we do not include an index to indicate that. In (26.3), V(k, p) is the momentum–space representation (double Fourier transform) of the coordinate-space potential,
ψn(k) is the momentum–space wave function (the probability amplitude for finding the particle with momentum k), and is the Fourier transform of ψn(r):
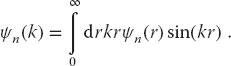
Equation 26.3 is an integral equation for ψn(k). It differs from an integral representation of ψn(k), because the integral in it cannot be evaluated until ψn(p) is known. Although this may seem like an insurmountable barrier, we will transform this equation into a matrix equation that can be solved with the matrix techniques discussed in Chapter 6.
26.2.1 Integral to Matrix Equations
We approximate the integral over the potential as a weighted sum over N integration points (usually Gauss quadrature points2)) for p = kj, j = 1, N:
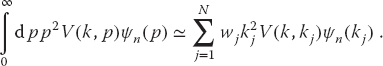
This converts the integral equation (26.3) to the algebraic equation
Equation 26.7 contains the N unknown function values ψn(kj), the unknown En, as well as the unknown functional dependence of ψn(k). We eliminate the functional dependence of ψn(k) by restricting the solution to the same values of k = ki as used in the approximation of the integral, which means that we are solving for wave function for k values on the grid of Figures 26.2. This leads to a set of N coupled linear equations in (N + 1) unknowns:
As a concrete example, for N = 2 we have two simultaneous linear equations
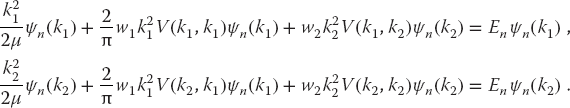
Figure 26.2 The grid of momentum values on which the integral equation is solved.
Of course, realistic examples require more than two integration points for precision.
We write our coupled equations (26.8) in the matrix form as
or as explicit matrices
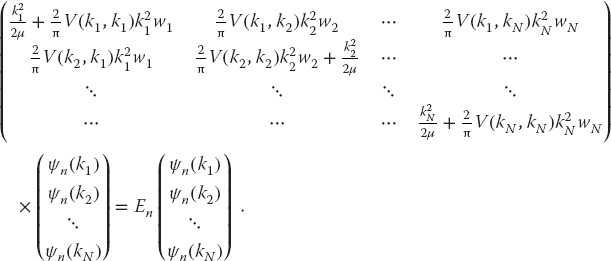
Equation 26.9 is the matrix representation of the Schrödinger equation (26.3). The wave function ψn(k) on the grid is the N × 1 vector
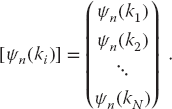
The astute reader may be questioning the possibility of solving N equations for (N + 1) unknowns, ψn(ki), and En. Only sometimes, and only for certain values of En (eigenvalues), will the computer be able to find solutions. To see how this arises, we try to apply the matrix inversion technique (which we will use successfully for scattering in Section 26.3). We rewrite (26.9) as
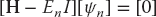
and multiply both sides by the inverse of [H – EnI] to obtain the formal solution
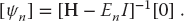
This equation tells us that (1) if the inverse exists, then we have the trivial solution ψn ≡ 0, which is not revealing, and (2) for a nontrivial solution to exist, our assumption that the inverse exists must be incorrect. Yet we know from the theory of linear equations that the inverse fails to exist when the determinant vanishes:
Equation 26.14 is the N + 1th equation needed to find unique solutions to the eigenvalue problem. Although, there is no guarantee that solutions of (26.14) can always be found, if they are found they are the desired eigenvalues of (26.9).
26.2.2 Delta-Shell Potential (Model)
To keep things simple and to have an analytic answer to compare with, we consider the local delta-shell potential:
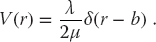
This might be a good model for an interaction that occurs when two particles are predominantly a fixed distance b apart. We use (26.4) to determine its momentum–space representation:
Beware: We have chosen this potential because it is easy to evaluate the momentum–space matrix element of the potential. However, its singular nature in r space leads to (26.16) having a very slow falloff in k space, and this causes the integrals to converge so slowly that numerics are not as precise as we would like.
If the energy is parameterized in terms of a wave vector κ by En = −κ2/2μ, then for this potential there is, at most, one bound state and it satisfies the transcendental equation (Gottfried, 1966)
Note that bound states occur only for attractive potentials. For the present case, this requires λ < 0.
Exercise Pick some values of b and λ and verify that (26.17) can be solved for κ.
26.2.3 Binding Energies Solution
An actual computation may follow two paths. The first calls subroutines to evaluate the determinant of the [H − EnI] matrix in (26.14), and then to search for those values of energy for which the computed determinant vanishes. This provides En, but not wave functions. The other approach calls an eigenproblem solver that may give some or all eigenvalues and eigenfunctions. In both the cases, the solution is obtained iteratively, and you may be required to guess starting values for both the eigenvalues and eigenvectors. In Listing 26.1, we present our solution of the integral equation for bound states of the delta-shell potential using the NumPy matrix library and the gauss method for Gaussian quadrature points and weights.
Listing 26.1 Bound.py solves the Lippmann–Schwinger integral equation for bound states within a delta-shell potential. The integral equations are converted to matrix equations using Gaussian grid points, and they are solved with linalg.
- Write a program, or modify ours, to solve the integral equation (26.9) for the delta-shell potential (26.16). Either find the En’s for which the determinant vanishes or, find the eigenvalues and eigenvectors for this H.
- Set the scale by setting 2μ = 1 and b = 10.
- Set up the potential and Hamiltonian matrices V(i, j) and H(i, j) for Gaussian quadrature integration with at least N = 16 grid points.
- Adjust the value and sign of λ for bound states. A good approach is to start with a large negative value for λ and then make it less negative. You should find that the eigenvalue moves up in energy.
- Note: Your eigenenergy solver may return several eigenenergies. The true bound state will be at negative energy and change little as the number of grid points changes. The others are numerical artifacts.
- Try increasing the number of grid points in steps of 8, for example, 16, 24, 32, 64, …, and see how the energy changes.
- Extract the best value for the bound-state energy and estimate its precision by seeing how it changes with the number of grid points.
- If you are solving the eigenvalue problem, check your solution by comparing the RHS and LHS in the matrix multiplication [H][ψn] = En[ψn].
- Verify that, regardless of the potential’s strength, there is only a single bound state and that it gets deeper as the magnitude of λ increases. Compare with (26.17).
26.2.4 Wave Function (Exploration)
- Determine the momentum–space wave function ψn(k) using an eigen problem solver. Does ψn(k) fall off at k → ∞? Does it oscillate? Is it well behaved at the origin?
- Using the same points and weights as used to evaluate the integral in the integral equation, determine the coordinate-space wave function via the Bessel transform
(26.18)
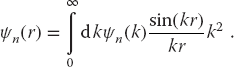
Does ψn(r) fall off as you would expect for a bound state? Does it oscillate? Is it well behaved at the origin? - Compare the r dependence of this ψn(r) to the analytic wave function:
(26.19)
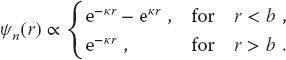
26.3 Scattering States of Nonlocal Potentials 
Problem Again we have a particle interacting with the nonlocal potential discussed for bound states (Figure 26.3a), only now the particle has sufficiently high energy that it scatters from rather than binds with the medium. Your problem is to determine the scattering cross section for scattering from a nonlocal potential.
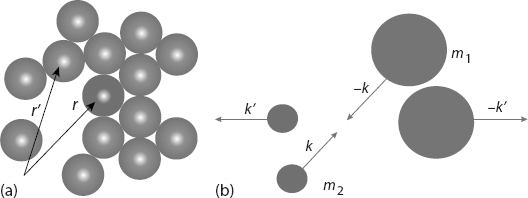
Figure 26.3 (a) A projectile (dark particle at r) scattering from a dense medium. (b) The same process viewed in the CM system where the projectile and target always have equal and opposite momenta.
26.4 Lippmann–Schwinger Equation (Theory)
Because experiments measure scattering amplitudes and not wave functions, it is more direct to have a theory dealing with amplitudes rather than wave functions.3) An integral form of the Schrödinger equation dealing with the scattering amplitude R is the Lippmann–Schwinger equation:
where the symbol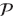 
in (26.20) indicates the Cauchy principal-value prescription for avoiding the singularity arising from the zero of the denominator (we discuss how to do that next). As for the bound-state problem, this equation is for partial wave l = 0 and 
= 1. In (26.20), the momentum k0 is related to the energy E and the reduced mass μ by
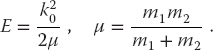
The initial and final COM momenta k and k′ are the momentum–space variables. The experimental observable that results from a solution of (26.20) is the diagonal matrix element R(k0, k0), which is related to the scattering phase shift δ0 and thus the cross section:
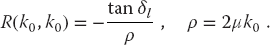
Note that (26.20) is not just the evaluation of an integral, it is an integral equation in which R(p, k) is integrated over all p. Yet because R(p, k) is unknown, the integral cannot be evaluated until after the equation is solved!
26.4.1 Singular Integrals (Math)
A singular integral
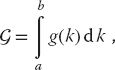
is one in which the integrand g(k) is singular at a point k0 within the integration interval [a, b], yet with the integral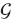 
remaining finite. (If the integral itself were infinite, we could not compute it.) Unfortunately, computers are notoriously bad at dealing with infinite numbers, and if an integration point gets too near the singularity, overwhelming subtractive cancellation or overflow may occur. Consequently, we apply some results from complex analysis before evaluating singular integrals numerically.4)
In Figure 26.4, we show three ways to avoid the singularity of an integrand. The paths in Figure 26.4a and b move the singularity slightly off the real k-axis by giving the singularity a small imaginary part ±iє. The Cauchy principal-value prescription 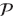in Figure 26.4c is seen to follow a path that “pinches” both sides of the singularity at k0, but does not to pass through it:
The preceding three prescriptions are related by the identity
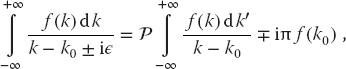
which follows from Cauchy’s residue theorem.
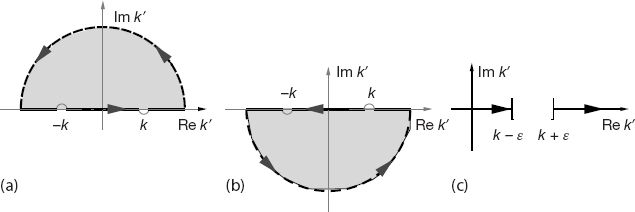
Figure 26.4 Three different paths in the complex k′ plane used to evaluate line integrals when there are singularities. Here the singularities are at k and −k, and the integration variable is k′.
26.4.2 Numerical Principal Values
A direct numerical evaluation of the principal value limit (26.24) is troublesome because of the large cancellations that occur near the singularity. A better algorithm follows from the mathematical theorem
This equation says that the curve of 1/(k − k0) as a function of k has equal and opposite areas on both sides of the singular point k0. If we break the integral up into one over positive k and one over negative k, a change of variable k → −k permits us to rewrite (26.26) as
We observe that the principal-value exclusion of the singular point’s contribution to the integral is equivalent to a simple subtraction of the zero integral (26.27):
Note that there is no 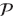on the RHS of (26.28) because the integrand is no longer singular at k = k0 (it is proportional to the d f / dk) and can therefore be evaluated numerically using the usual rules. The integral (26.28) is called the Hilbert transform of f and also arises in subjects like inverse problems.
26.4.3 Reducing Integral Equations to Matrix Equations (Method)
Now that we can handle singular integrals, we go back to reducing the integral equation (26.20) to a set of linear equations that can be solved with matrix methods. We start by rewriting the principal-value prescription as a definite integral (Haftel and Tabakin, 1970):
We convert this integral equation to linear equations by approximating the integral as a sum over N integration points (usually Gaussian) kj with weights wj:
We note that the last term in (26.30) implements the principal-value prescription and cancels the singular behavior of the previous term. Equation 26.30 contains the (N + 1) unknowns R(kj, k0) for j = 0, N. We turn it into (N + 1) simultaneous equations by evaluating it for (N + 1) k values on a grid (Figure 26.2) consisting of the observable momentum k0 and the integration points:
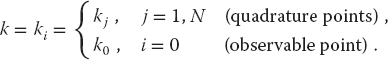
There are now (N + 1) linear equations for (N + 1) unknowns Ri ≡ R(ki, k0):
We express these equations in the matrix form by combining the denominators and weights into a single denominator vector D:
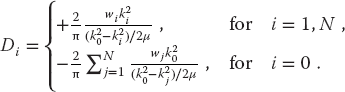
The linear equations (26.32) now assume the matrix form
where R and V are column vectors of length N + 1:
We call the matrix [1 − DV] in (26.34) the wave matrix F and write the integral equation as the matrix equation
With R the unknown vector, (26.36) is in the standard form AX = B, which can be solved by the mathematical subroutine libraries discussed in Chapter 6.
26.4.4 Solution via Inversion, Elimination
An elegant (but alas not most efficient) solution to (26.36) is by matrix inversion:
Because the inversion of even complex matrices is a standard routine in mathematical libraries, (26.37) is a direct solution for the R amplitude. Unless you need the inverse for other purposes (like calculating wave functions), a more efficient approach is to use Gaussian elimination to find an [R] that solves [F][R] = [V] without computing the inverse.
Listing 26.2 Scatt.py solves the Lippmann–Schwinger integral equation for scattering froma delta-shell potential. The singular integral equations are regularized by a subtraction, converted to matrix equations using Gaussian grid points, and then solved with matrix library routines.
26.4.5 Scattering Implementation
For the scattering problem, we use the same delta-shell potential (26.16) discussed in Section 26.2.2 for bound states:
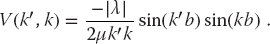
This is one of the few potentials for which the Lippmann–Schwinger equation (26.20) has an analytic solution (Gottfried, 1966) with which to check:
Our results were obtained with 2μ = 1, λb = 15, and b = 10, the same as in (Gottfried, 1966). In Figure 26.5, we give a plot of sin2 δ0 vs. kb, which is proportional to the scattering cross section arising from the angular momentum l = 0 phase shift. It is seen to reach its maximum values at energies corresponding to resonances. In Listing 26.2, we present our program for solving the scattering integral equation using the NumPy Linear Algebra matrix library and the gauss method for quadrature points. For your implementation:
- Set up the matrices
V[], D[], and F[,]. Use at least N = 16 Gaussian quadrature points for your grid. - Calculate the matrix F−1 using a library subroutine.
- Calculate the vector R by matrix multiplication R = F−1V.
- Deduce the phase shift δ from the i = 0 element of R:
(26.40)
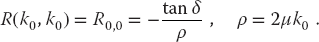
- Estimate the precision of your solution by increasing the number of grid point in steps of two (we found the best answer for N = 26). If your phase shift changes in the second or third decimal place, you probably have that much precision.
- Plot sin2 δ vs. energy
starting at zero energy and ending at energies where the phase shift is again small. Your results should be similar to those in Figure 26.5. Note that a resonance occurs when δl increases rapidly through π/2, that is, when sin2 δ0 = 1. - Check your answer against the analytic results (26.39).
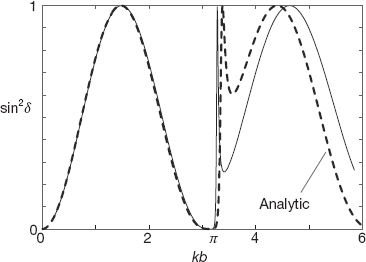
Figure 26.5 The energy dependence of the cross section for l = 0 scattering from an attractive delta-shell potential with λb = 15. The dashed curve is the analytic solution (26.39), and the solid curve results from numerically solving the integral Schrödinger equation, either via direct matrix inversion or via LU decomposition.
26.4.6 Scattering Wave Function (Exploration)
The F−1 matrix that occurred in our solution to the integral equation
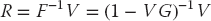
is actually quite useful. In scattering theory, it is known as the wave matrix because it is used in expansion of the wave function:
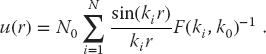
Here N0 is a normalization constant and the R amplitude is appropriate for standing-wave boundary conditions. So once we know F1, we also know the wave function.
- Plot u(r) and compare it to a free wave.