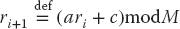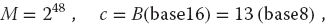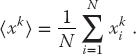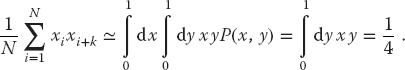4
Monte Carlo: Randomness, Walks, and Decays

---

This chapter starts with a discussion of how computers generate numbers that appear random, but really are not, and how we can test that. After discussing how computers generate pseudorandom numbers, we explore how these numbers are used to incorporate the element of chance into simulations. We do this first by simulating a random walk and then by simulating the spontaneous decay of an atom or nucleus. In Chapter 5, we show how to use these random numbers to evaluate integrals,and in Chapter 17, we investigate the use of random numbers to simulate thermal processes and the fluctuations of quantum systems.

---

4.1 Deterministic Randomness

Some people are attracted to computing because of its deterministic nature; it is nice to have a place in one’s life where nothing is left to chance. Barring machine errors or undefined variables, you get the same output every time you feed your program the same input. Nevertheless, many computer cycles are used for Monte Carlo calculations that at their very core include elements of chance. These are calculations in which random-like numbers generated by the computer are used to simulate naturally random processes, such as thermal motion or radioactive decay, or to solve equations on the average. Indeed, much of computational physics’ recognition has come about from the ability of computers to solve previously intractable problems using Monte Carlo techniques.

4.2 Random Sequences (Theory)

We define a sequence r₁, r₂, … as random if there are no correlations among the numbers. Yet being random does not mean that all the numbers in the sequence are equally likely to occur. If all the numbers in a sequence are equally likely to occur, then the sequence is called uniform, which does not say anything about being random. To illustrate, 1, 2, 3, 4, … is uniform but probably not random. Furthermore, it is possible to have a sequence of numbers that, in some sense, are random but have very short-range correlations among themselves, for example,

(4.1)

have short-range but not long-range correlations.

Mathematically, the likelihood of a number occurring is described by a distribution function P(r), where P(r) dr is the probability of finding r in the interval [r, r + dr]. A uniform distribution means that P(r) = a constant. The standard random-number generator on computers generates uniform distributions between 0 and 1. In other words, the standard random-number generator outputs numbers in this interval, each with an equal probability yet each independent of the previous number. As we shall see, numbers can also be more likely to occur in certain regions than other, yet still be random.

By their very nature, computers are deterministic devices and so cannot create a random sequence. Computed random number sequences must contain correlations and in this way cannot be truly random. Although it may be a bit of work, if we know a computed random number r_m and its preceding elements, then it is always possible to figure out r_m+1. For this reason, computers are said to generate pseudorandom numbers (yet with our incurable laziness we will not bother saying “pseudo” all the time). While more sophisticated generators do a better job at hiding the correlations, experience shows that if you look hard enough or use pseudorandom numbers long enough, you will notice correlations. A primitive alternative to generating random numbers is to read in a table of truly random numbers determined by naturally random processes such as radioactive decay, or to connect the computer to an experimental device that measures random events. These alternatives are not good for production work, but have actually been used as a check in times of doubt.

4.2.1 Random-Number Generation (Algorithm)

The linear congruent or power residue method is the common way of generating a pseudorandom sequence of numbers over the interval [0, M – 1]. To obtain the next random number r_i+1, you multiply the present random number r_i by the constant a, add another constant c, take the modulus by M, and then keep just the fractional part (remainder)¹⁾:

(4.2)

(4.3)

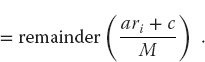
The value for r₁ (the seed) is frequently supplied by the user, and mod is a built-in function on your computer for remaindering. In Python, the percent sign % is the modulus operator. This is essentially a bit-shift operation that ends up with the least significant part of the input number and thus counts on the randomness of round-off errors to generate a random sequence.

For example, if c = 1, a = 4, M = 9, and you supply r₁ = 3, then you obtain the sequence

(4.4)

(4.5)

(4.6)

(4.7)

(4.8)

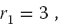
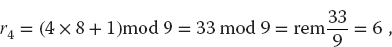
We get a sequence of length M = 9, after which the entire sequence repeats. If we want numbers in the range [0, 1], we divide the r’s by M = 9 to obtain

(4.9)

This is still a sequence of length 9, but is no longer a sequence of integers. If random numbers in the range [A, B] are needed, you only need to scale:

(4.10)

As a rule of thumb: Before using a random-number generator in your programs, you should check its range and that it produces numbers that “look” random.

Although not a mathematical proof, you should always make a graphical display of your random numbers. Your visual cortex is quite refined at recognizing patterns and will tell you immediately if there is one in your random numbers. For instance, Figure 4.1 shows generated sequences from “good” and “bad” generators, and it is clear which is not random. (Although if you look hard enough at the random points, your mind may well pick out patterns there too.)

The linear congruent method (4.2) produces integers in the range [0, M − 1] and therefore becomes completely correlated if a particular integer comes up a second time (the whole cycle then repeats). In order to obtain a longer sequence, a and M should be large numbers but not so large that ar_i−1 overflows. On a computer using 48-bit integer arithmetic, the built-in random-number generator may use M values as large as 2⁴⁸ 3 × 10¹⁴. A 32-bit generator may use M = 2³¹ 2 × 10⁹. If your program uses approximately this many random numbers, you may need to reseed (start the sequence over again with a different initial value) during intermediate steps to avoid the cycle repeating.

Figure 4.1 (a) A plot of successive random numbers (x, y) = (r_i, r_i+1) generated with a deliberately “bad” generator, (b) A plot generated with the built in random number generator. While the plot (b) is not the proof that the distribution is random, the plot (a) is a proof enough that the distribution is not random.

Your computer probably has random-number generators that are better than the one you will compute with the power residue method. In Python, we use random.random(), the Mersenne Twister generator. We recommend that you use the best one you can find rather than write your own. To initialize a random sequence, you need to plant a seed in it. In Python, the statement random.seed(None) seeds the generator with the system time (see Walk.py in Listing 4.1). Our old standard, drand48, uses:

(4.11)

(4.12)

4.2.2 Implementation: Random Sequences

For scientific work, we recommend using an industrial-strength random-number generator. To see why, here we assess how bad a careless application of the power residue method can be.

1. Write a simple program to generate random numbers using the linear congruent method (4.2).
2. For pedagogical purposes, try the unwise choice: (a, c, M, r₁) = (57, 1, 256, 10). Determine the period, that is, how many numbers are generated before the sequence repeats.
3. Take the pedagogical sequence of random numbers and look for correlations by observing clustering on a plot of successive pairs (x_i, y_i) = (r_2i−1, r₂i), i = 1, 2, … (Do not connect the points with lines.) You may “see” correlations (Figure 4.1), which means that you should not use this sequence for serious work.
4. Make your own version of Figure 4.2; that is, plot r_i vs. i.
5. Test the built-in random-number generator on your computer for correlations by plotting the same pairs as above. (This should be good for serious work.)
6. Test the linear congruent method again with reasonable constants like those in (4.11) and (4.12). Compare the scatterplot you obtain with that of the built-in random-number generator. (This, too, should be good for serious work.)

4.2.3 Assessing Randomness and Uniformity

Because the computer’s random numbers are generated according to a definite rule, the numbers in the sequence must be correlated with each other. This can affect a simulation that assumes random events. Therefore, it is wise for you to test a random-number generator to obtain a numerical measure of its uniformity and randomness before you stake your scientific reputation on it. In fact, some tests are simple enough for you to make it a habit to run them simultaneously with your simulation. In the examples to follow, we test for randomness and uniformity.

1. Probably the most obvious, but often neglected, test for randomness and uniformity is just to look at the numbers generated. For example, Table 4.1 presents some output from Python’s random method. If you just look at these numbers you will know immediately that they all lie between 0 and 1, that they appear to differ from each other, and that there is no obvious pattern (like 0.3333).
2. As we have seen, a quick visual test (Figure 4.2) involves taking this same list and plotting it with r_i as ordinate and i as abscissa. Observe how there appears to be a uniform distribution between 0 and 1 and no particular correlation between points (although your eye and brain will try to recognize some kind of pattern if you look long enough).

   

   Figure 4.2 A plot of a uniform pseudorandom sequence r_i, vs. i. The points are connected to make it easier to follow the order. While this does not prove that a distribution is random, it at least shows the range of values and that there is fluctuation.

   Table 4.1 A table of a uniform, pseudo-random sequence r_i generated by Python’s random method.

   0.046 895 024 385 081 75	0.204 587 796 750 397 95	0.557 190 747 079 725 5	0.056 343 366 735 930 88
   0.936 066 864 589 746 7	0.739 939 913 919 486 7	0.650 415 302 989 955 3	0.809 633 370 418 305 7
   0.325 121 746 254 331 9	0.494 470 371 018 847 17	0.143 077 126 131 411 28	0.328 581 276 441 882 06
   0.535 100 168 558 861 6	0.988 035 439 569 102 3	0.951 809 795 307 395 3	0.368 100 779 256 594 23
   0.657 244 381 503 891 1	0.709 076 851 545 567 1	0.563 678 747 459 288 4	0.358 627 737 800 664 9
   0.383 369 106 540 338 07	0.740 022 375 602 264 9	0.416 208 338 118 453 5	0.365 803 155 303 808 7
   0.748 479 890 046 811 1	0.522 694 331 447 043	0.148 656 282 926 639 13	0.174 188 153 952 713 6
   0.418 726 310 120 201 23	0.941 002 689 012 048 8	0.116 704 492 627 128 9	0.875 900 901 278 647 2
   0.596 253 540 903 370 3	0.438 238 541 497 494 1	0.166 837 081 276 193	0.275 729 402 460 343 05
   0.832 243 048 236 776	0.457 572 427 917 908 75	0.752 028 149 254 081 5	0.886 188 103 177 451 3
   0.040 408 674 172 845 55	0.146 901 492 948 813 34	0.286 962 760 984 402 3	0.279 150 544 915 889 53
   0.785 441 984 838 243 6	0.502 978 394 047 627	0.688 866 810 791 863	0.085 104 148 559 493 22
   0.484 376 438 252 853 26	0.194 793 600 337 003 66	0.379 123 023 471 464 2	0.986 737 138 946 582 1

3. A simple test of uniformity evaluates the kth moment of a distribution:
   (4.13)

   If the numbers are distributed uniformly, then (4.13) is approximately the moment of the distribution function P(x):

   (4.14)

   If (4.14) holds for your generator, then you know that the distribution is uniform. If the deviation from (4.14) varies as then you also know that the distribution is random because the result derives from assuming randomness.

4. Another simple test determines the near-neighbor correlation in your random sequence by taking sums of products for small k:
   (4.15)

   If your random numbers x_i and x_i+k are distributed with the joint probability distribution P(x_i, x_i+k) = 1 and are independent and uniform, then (4.15) can be approximated as an integral:

   (4.16)

   If (4.16) holds for your random numbers, then you know that they are uniform and independent. If the deviation from (4.16) varies as , then you also know that the distribution is random.

5. As we have seen, an effective test for randomness is performed by making a scatterplot of (x_t = r_2i, y_i = r_2i+1) for many i values. If your points have noticeable regularity, the sequence is not random. If the points are random, they should uniformly fill a square with no discernible pattern (a cloud) (as in Figure 4.1b).
6. Test your random-number generator with (4.14) for k = 1, 3, 7 and N = 100, 10 000, 100 000. In each case print out
   (4.17)

   to check that it is of the order 1.

4.3 Random Walks (Problem)

Consider a perfume molecule released in the front of a classroom. It collides randomly with other molecules in the air and eventually reaches your nose despite the fact that you are hidden in the last row. Your problem is to determine how many collisions, on the average, a perfume molecule makes in traveling a distance R. You are given the fact that a molecule travels an average (root-mean-square) distance r_rms between collisions.

Listing 4.1 Walk.py calls the random-number generator from the random package. Note that a different seed is needed to obtain a different sequence.

4.3.1 Random-Walk Simulation

There are a number of ways to simulate a random walk with (surprise, surprise) different assumptions yielding different physics. We will present the simplest approach for a 2D walk, with a minimum of theory, and end up with a model for normal diffusion. The research literature is full of discussions of various versions of this problem. For example, Brownian motion corresponds to the limit in which the individual step lengths approach zero, and with no time delay between steps. Additional refinements include collisions within a moving medium (abnormal diffusion), including the velocities of the particles, or even pausing between steps. Models such as these are discussed in Chapter 16, and demonstrated by some of the corresponding applets given online.

In our random-walk simulation (Figure 4.3) an artificial walker takes sequential steps with the direction of each step independent of the direction of the previous step. For our model, we start at the origin and take N steps in the xy plane of lengths (not coordinates)

(4.18)

Although each step may be in a different direction, the distances along each Cartesian axis just add algebraically. Accordingly, the radial distance R from the starting point after N steps is

(4.19)

If the walk is random, the particle is equally likely to travel in any direction at each step. If we take the average of a large number of such random steps, all the cross terms in (4.19) will vanish and we will be left with

(4.20)

where is the root-mean-square step size.

To summarize, if the walk is random, then we expect that after a large number of steps the average vector distance from the origin will vanish:

(4.21)

Yet does not vanish. Equation 4.20 indicates that the average scalar distance from the origin is 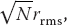where each step is of average length r_rms. In other words, the vector endpoint will be distributed uniformly in all quadrants, and so the displacement vector averages to zero, but the average length of that vector does not. For large N values, (the value if all steps were in one direction on a straight line), but does not vanish. In our experience, practical simulations agree with this theory, but rarely perfectly, with the level of agreement depending upon the details of how the averages are taken and how the randomness is built into each step.

Figure 4.3 (a) A schematic of the N steps in a random walk simulation that end up a distance R from the origin. Note how the Δx’s for each step add vectorially. (b) A simulated walk in 3D from Walk3D.py.

4.3.2 Implementation: Random Walk

The program Walk.py in Listing 4.1 is a sample random-walk simulation. It is key element is random values for the x and y components of each step,

Here we omit the scaling factor that normalizes each step to length 1. When using your computer to simulate a random walk, you should expect to obtain (4.20) only as the average displacement averaged over many trials, not necessarily as the answer for each trial. You may get different answers depending on just how you take your random steps (Figure 4.4b).

Start at the origin and take a 2D random walk with your computer.

1. To increase the amount of randomness, independently choose random values for Δx' and Δy' in the range [−1, 1]. Then normalize them so that each step is of unit length
   (4.22)
2. Use a plotting program to draw maps of several independent 2D random walks, each of 1000 steps. Using evidence from your simulations, comment on whether these look like what you would expect of a random walk.

   

   Figure 4.4 (a) The steps taken in seven 2D random walk simulations. (b) The distance covered in two walks of N steps using different schemes for including randomness. The theoretical prediction (4.20) is the straight line.

3. If you have your walker taking N steps in a single trial, then conduct a total number of trials. Each trial should have N steps and start with a different seed.
4. Calculate the mean square distance R² for each trial and then take the average of R² for all your K trials:
   (4.23)
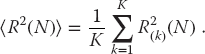
5. Check the validity of the assumptions made in deriving the theoretical result (4.20) by checking how well
   (4.24)

   Do your checking for both a single (long) run and for the average over trials.

6. Plot the root-mean-square distance as a function of -Values of N should start with a small number, where is not expected to be accurate, and end at a quite large value, where two or three places of accuracy should be expected on the average.
7. Repeat the preceding and following analysis for a 3D walk as well.

4.4 Extension: Protein Folding and Self-Avoiding Random Walks

A protein is a large biological molecule made up of molecular chains (the residues of amino acids). These chains are formed from monomers, that is, molecules that bind chemically with other molecules. More specifically, these chains consist of nonpolar hydrophobic (H) monomers that are repelled by water, and polar (P) monomers that are attracted by water. The actual structure of a protein results from a folding process in which random coils of chains rearrange themselves into a configuration of minimum energy. We want to model that process on the computer.

Although molecular dynamics (Chapter 18) may be used to simulate protein folding, it is much slower than Monte Carlo techniques, and even then, it is hard to find the lowest energy states. Here we create a simple Monte Carlo simulation in which you to take a random walk in a 2D square lattice (Yue et al., 2004). At the end of each step, you randomly choose an H or a P monomer and drop it on the lattice, with your choice weighted such that H monomers are more likely than P ones. The walk is restricted such that the only positions available after each step are the three neighboring sites, with the already-occupied sites excluded (this is why this technique is known as a self-avoiding random walk).

The goal of the simulation is to find the lowest energy state of an HP sequence of various lengths. These then may be compared to those in nature. Just how best to find such a state is an active research topic (Yue et al., 2004). The energy of a chain is defined as

(4.25)

where is a positive constant and f is the number of H–H neighbor not connected directly (P–P and H–P bonds do not count at lowering the energy). So if the neighbor next to an H is another H, it lowers the energy, but if it is a P it does not lower the energy. We show a typical simulation result in Figure 4.5, where a light dot is placed half way between two H (dark-dot) neighbors. Accordingly, for a given length of chain, we expect the natural state(s) of an H–P sequence to be those with the largest possible number f of H–H contacts. That is what we are looking for.

1. Modify the random walk program we have already developed so that it simulates a self-avoiding random walk. The key here is that the walk stops at a corner, or when there are no empty neighboring sites available.
2. Make a random choice as to whether the monomer is an H or a P, with a weighting such that there are more H’s than P’s.
3. Produce a visualization that shows the positions occupied by the monomers, with the H and P monomers indicated by different color dots. (Our visualization, shown in Figure 4.5, is produced by the program ProteinFold.py, available on the Instructor’s site.)
4. After the walk ends, record the energy and length of the chain.

   

   Figure 4.5 Two self-avoiding random walks that simulate protein chains with hydrophobic (H) monomers in light gray, and polar (P) monomers in black. The dark dots indicate regions where two H monomers are not directly connected.

5. Run many folding simulations and save the outputs, categorized by length and energy.
6. Examine the state(s) of the lowest energy for various chain lengths and compare the results to those from molecular dynamic simulations and actual protein structures (available on the Web).
7. Do you think that this simple model has some merit?
8. Extend the folding to 3D.

4.5 Spontaneous Decay (Problem)

Your problem is to simulate how a small number N of radioactive particles decay.²⁾ In particular, you are to determine when radioactive decay looks like exponential decay and when it looks stochastic (containing elements of chance). Because the exponential decay law is a large-number approximation to a natural process that always leads to only a small number of nuclei remaining, our simulation should be closer to nature than is the exponential decay law (Figure 4.6). In fact, if you “listen” to the output of the decay simulation code, what you will hear sounds very much like a Geiger counter, an intuitively convincing demonstration of the realism of the simulation.

Spontaneous decay is a natural process in which a particle, with no external stimulation, decays into other particles. Although the probability of decay of any one particle in any time interval is constant, just when it decays is a random event. Because the exact moment when any one particle decays is always random, and because one nucleus does not influence another nucleus, the probability of decay is not influenced by how long the particle has been around or whether some other particles have decayed. In other words, the probability P of any one particle decaying per unit time interval is a constant, yet when that particle decays it is gone forever. Of course, as the total number N of particles decreases with time, so will the number that decay per unit time, but the probability of any one particle decaying in some time interval remains the same as long as that particle exists.

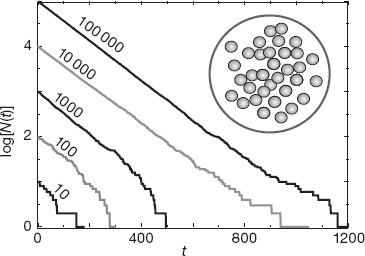
Figure 4.6 Circle: A sample containing N nuclei, each of which has the same probability of decaying per unit time, Graphs: Semilog plots of the number of nuclei vs. time for five simulations with differing initial numbers of nuclei. Exponential decay would be a straight line with bumps, similar to the initial behavior for N = 100 000.

4.5.1 Discrete Decay (Model)

Imagine having a sample containing N(t) radioactive nuclei at time t (Figure 4.6 circle). Let ΔN be the number of particles that decay in some small time interval Δt. We convert the statement “the probability P of any one particle decaying per unit time is a constant” into the equation

(4.26)

(4.27)

where the constant λ is called the decay rate and the minus sign indicates a decreasing number. Because N(t) decreases in time, the activity ΔN(t)/Δt (sometimes called the decay rate) also decreases with time. In addition, because the total activity is proportional to the total number of particles present, it is too stochastic with an exponential-like decay in time. (Actually, because the number of decays ΔN(t) is proportional to the difference in random numbers, its tends to show even larger statistical fluctuations than does N(t).)

Equation 4.27 is a finite-difference equation relating the experimentally quantities N(t), ΔN(t), and Δt. Although a difference equation cannot be integrated the way a differential equation can, it can be simulated numerically. Because the process is random, we cannot predict a single value for ΔN(t), although we can predict the average number of decays when observations are made of many identical systems of N decaying particles.

4.5.2 Continuous Decay (Model)

When the number of particles N → ∞ and the observation time interval Δt → 0, our difference equation becomes a differential equation, and we obtain the familiar exponential decay law (4.27):

(4.28)

This can be integrated to obtain the time dependence of the total number of particles and of the total activity:

(4.29)

(4.30)

In this limit, we can identify the decay rate λ with the inverse lifetime:

(4.31)

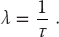
We see from its derivation that the exponential decay is a good description of nature for a large number of particles where ΔN/N 0. However, in nature N(t) can be a small number, and in that case we have a statistical and not a continuous process. The basic law of nature (4.26) is always valid, but as we will see in the simulation, the exponential decay (4.30) becomes less and less accurate as the number of particles gets smaller and smaller.

4.5.3 Decay Simulation with Geiger Counter Sound

A program for simulating radioactive decay is surprisingly simple but not without its subtleties. We increase time in discrete steps of Δt, and for each time interval we count the number of nuclei that have decayed during that Δt. The simulation quits when there are no nuclei left to decay. Such being the case, we have an outer loop over the time steps Δt and an inner loop over the remaining nuclei for each time step. The pseudocode is simple (as is the code):

When we pick a value for the decay rate λ = 1/τ to use in our simulation, we are setting the scale for times. If the actual decay rate is λ = 0.3 × 10⁶ s⁻¹ and if we decide to measure times in units of 10⁻⁶ s, then we will choose random numbers 0 ≤ r_i 1, which leads to λ values lying someplace near the middle of the range (e.g., λ 0.3). Alternatively, we can use a value of λ = 0.3 × 10⁶ s⁻¹ in our simulation and then scale the random numbers to the range 0 ≤ r_i ≤ 10⁶. However, unless you plan to compare your simulation to experimental data, you do not have to worry about the scale for time but instead should focus on the physics behind the slopes and relative magnitudes of the graphs.

Listing 4.2 DecaySound.py simulates spontaneous decay in which a decay occurs if a random number is smaller than the decay parameter. The winsound package lets us play a beep each time there is a decay, and this leads to the sound of a Geiger counter.

Decay.py is our sample simulation of the spontaneous decay. An extension of this program, DecaySound.py, in Listing 4.2, adds a beep each time an atom decays (unfortunately this works only with Windows). When we listen to the simulation, it sounds like a Geiger counter, with its randomness and its slowing down with time. This provides some rather convincing evidence of the realism of the simulation.

4.6 Decay Implementation and Visualization

Write a program to simulate the radioactive decay using the simple program in Listing 4.2 as a guide. You should obtain results like those in Figure 4.6.

1. Plot the logarithm of the number left In N(t) and the logarithm of the decay rate ΔN(t)/Δt(= 1) vs. time. Note that the simulation measures time in steps of Δt (generation number).
2. Check that you obtain what looks like the exponential decay when you start with large values for N(0), but that the decay displays its stochastic nature for small N(0). (Large N(0) values are also stochastic; they just do not look like it.)
3. Create two plots, one showing that the slopes of N(t) vs. t are independent N(0) and another showing that the slopes are proportional to the value chosen for λ.
4. Create a plot showing that within the expected statistical variations, In N(t) and In ΔN(t) are proportional.
5. Explain in your own words how a process that is spontaneous and random at its very heart can lead to the exponential decay.
6. How does your simulation show that the decay is exponential-like and not a power law such as N = βt^−α?

1) You may obtain the same result for the modulus operation by subtracting M until any further subtractions would leave a negative number; what remains is the remainder.

2) Spontaneous decay is also discussed in Chapter 7, where we fit an exponential function to a decay spectrum.