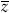The Princeton Guide to Evolution

III.5

Phenotypic Selection on Quantitative Traits

Edmund D. Brodie III

OUTLINE

1. How selection works

2. Selection is a statistical process

3. The genetic response to selection

4. Modes of selection

5. The multidimensional phenotype

6. Indirect selection and misleading covariances

7. Genetic correlations and correlated response to selection

Natural selection is the primary driver of adaptive evolution. Despite its power as a force of change over time, it is a remarkably simple process with only a few basic criteria. Whenever variation in a trait is associated with differences in reproductive success, selection occurs. This fundamental relationship between phenotype and fitness is measured as a covariance, and allows for a quantitative assessment of the strength of selection. Selection can occur in different modes that have distinct effects on the distributions of traits. While directional selection that changes the average character is most commonly considered, stabilizing and disruptive selection can directly impact the variance of a trait. Hundreds of studies of selection suggest that each of these modes is common in natural populations, and that directional selection tends to be strongest in magnitude. Correlational selection simultaneously affects two or more traits and can result in integration of characters within an organism. Relatively few studies have attempted to examine correlational selection in the wild. Genetic architecture determines whether and how any of these forms of selection are transmitted across generations. Selection can cause lasting changes only when traits are heritable and offspring resemble their parents. When traits are inherited together, selection on one trait can drag other traits along in a correlated response. Such indirect effects of correlations limit the independent evolution of single traits and can constrain evolution of the phenotype as a whole.

GLOSSARY

Correlated Response to Selection. The change in a trait across generations due to genetic correlations with another trait experiencing selection.

Covariance. A statistical measure of the degree to which two characters vary together; when standardized it is known as the correlation.

Fitness. How much an individual contributes to future generations, usually measured empirically as total lifetime reproductive success of an individual.

Frequency Distribution. Describes the probability of observing a particular value of a trait in a population. Usually assumed to be bell shaped or “normal,” with the mean near the peak of the bell and the width of the curve measured by the variance.

Heritability. The resemblance of parents and offspring measured as the proportion of phenotypic variance in a trait due to the additive effects of genes.

Indirect Selection. Selection experienced by a trait not because it is causally related to fitness but because it is correlated with another trait that is.

Multivariate. Comprising more than one character or dimension; for example, a multivariate phenotype exhibits many traits at once.

Phenotype. Any observable characteristic of an organism; collectively, all its traits and their patterns of integration.

Population. A collection of sexually reproducing individuals with the potential to interbreed. For asexual organisms, a group of individuals of a single species in a local area.

Variance. The statistical spread of a distribution measured as the average squared deviation from the mean of the distribution; distributions with high variance are wider than those with low variance.

When Darwin and Wallace independently conceived of natural selection as the primary driver of evolutionary change, they imagined a process operating on all forms of life to gradually modify them to be better suited to the environmental challenges facing them. The forms better suited to survival and reproduction leave more copies of themselves and replace the alternatives in a population, leading over time to changes in forms from the ancestral condition, an idea that became known as descent with modification. This simple idea transformed human thinking about life on earth and remains one of the most important intellectual contributions in history.

Although Darwin and Wallace wrote specifically about “natural selection,” we now understand the same general process of selection to apply across the spectrum of biological systems. Sexual selection is a subcategory of natural selection that operates through differences in the ability of organisms to acquire mates. Humans practice artificial selection to improve crops and livestock and to change the qualities of cultivated forms of plants and pet animals. Accidental selection resulting from the application of antibiotics and other biocides often leads to the evolution of resistance in pathogens and pests, posing serious problems in pest control. All these forms of selection operate in the same way and have similar impacts on populations, natural or managed.

1. HOW SELECTION WORKS

The power of selection, as both a process and a concept, lies in its simplicity. Only three conditions are necessary, and sufficient, for selection to cause change over time. When these three requisites are met, populations will change because of selection, and adaptive evolution will proceed, as follows:

1. Variation. Differences among individuals are the essential substrate on which selection works. Without such differences, some forms that are more successful than others could not exist. The source of the variation is not important for this criterion. The phenotypic differences might arise through influences of environment, different abilities to acquire resources, or fundamental genetic differences. Traits may vary quantitatively, as in differences in body mass, the length of a wing, or the number of flowers on an inflorescence, or variation might be qualitative, as in song forms of a bird, the presence of horns, or the color of flowers. So long as the traits of one individual are not identical to those of others, selection can occur.

2. Heritability. In order for the effects of selection to have lasting consequences across generations, offspring must resemble their parents. Heritable variation is essential as the mechanism of transmission of selection in one generation to the distribution of traits in the next. Darwin did not have a clear understanding of how inheritance worked when he described selection, but he nonetheless emphasized that resemblance among relatives was essential to the process. With the rediscovery of Mendel’s work on particulate inheritance in the early 1900s, biologists began to understand the mechanism by which offspring reliably expressed traits similar to their parents. We now usually think of heritability as having a genetic basis, but some consistent environmental influences such as cultural transmission can satisfy the same criterion.

3. Differential Reproduction. The crux of the selection argument is that some individuals are more successful than others. Success is measured in terms of the number of copies of oneself left in the subsequent generation. This success in representation in the next generation is known to evolutionary biologists as fitness and is most easily measured as the number of offspring produced in a lifetime. It is fitness relative to others within a population that matters to selection, not the absolute amount of reproductive success. Selection essentially compares variants within a population, so a variant needs only to perform better than alternatives to be successful.

Whenever these three criteria are met, it is unavoidable that selection will cause changes to the mean and/or variance of traits in a population. Those variants that are associated with higher relative fitness will leave more offspring in subsequent generations, and heritability ensures that those offspring resemble their parents. Whether the differences in reproduction come about through the struggle for existence in the wild, or through humans selecting the breeding stock for a domestic improvement plan, the process is the same.

The two-part nature of evolution by natural selection becomes clear from this dissection. Phenotypic selection works within a generation whenever some trait values are associated with differential reproductive success. Inheritance then mediates the effects of phenotypic selection to determine evolutionary change. This separation of the force and response to the force allows us to understand in detail the contributions of each component of the process.

2. SELECTION IS A STATISTICAL PROCESS

The language typically used to discuss selection—active terms like the “force” of selection, identifying “agents” and “targets” of selection, and labeling some traits as “favored” by selection—obscures how straightforward the process is. In fact, selection requires no consciousness, no end goal, and no long-term direction. Even the idea that selection is a “process” is a bit misleading.

In fact, phenotypic selection is nothing more than a simple statistical by-product. To understand why, it helps to think of the traits of organisms in terms of distributions. For any variable trait in a population of organisms, say, body size or running speed, we can measure the population in terms of its frequency distribution. Usually that distribution is shaped something like a normal or “bell” curve, with the mean or average value of the trait near the peak of the bell, and the spread of the curve measured by the variance. Fitness or reproductive success has a similar kind of distribution with its own mean and variance.

Selection as a statistical process becomes apparent when we consider these distributions together in a bivariate form. On an x-y plot we can represent each individual in the population in terms of its trait value (x) and its reproductive success (y). This bivariate distribution determines whether a trait experiences selection or not. If some values of the trait are associated with higher values of reproductive success, then selection occurs.

This association is measured as the covariance. The covariance is the key to understanding selection on quantitative traits because it determines the strength of the relationship between fitness and a trait. If the covariance is positive, large values of a trait are disproportionately reproduced, whereas smaller values of a trait are overproduced if the covariance is negative. If the covariance is zero, then all values are equally reproduced on average and no selection occurs.

What we are trying to understand with selection is whether and how the average trait changes over time—will body mass, for example, get larger or smaller because of differences in reproductive success? In the early 1970s, George Price demonstrated that this change was neatly and fully predicted by the covariance between fitness and phenotype. Without going into Price’s full mathematical proof, the simplest form of the Price equation shows that the change in the average trait, Δ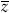, can be expressed in terms of the covariance of fitness, w, and that trait, z:

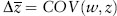
The Price equation underscores the statistical nature of selection. Any trait that covaries with fitness, whether the association is causal or not, will experience selection. Whether the covariance obtains because some lizards are fast enough to outrun predators and others are not, or because humans choose to plant seeds from only the sweetest watermelons, the inequality in reproductive success is what drives the selection. The covariance is easy to measure and provides a metric for the strength of total selection on a trait known as the phenotypic selection differential, s. The variance in fitness itself is known as the opportunity for selection because it places a limit on the strength of selection on any character. Without variance in fitness, there could be no covariance between fitness and phenotype.

3. THE GENETIC RESPONSE TO SELECTION

The type of selection described above is a purely phenotypic process. It happens in one generation, and it changes distributions of traits within that generation. In order for the phenotypic selection to have evolutionary consequences, changes that take place in one generation must be transmitted to the next; this is where inheritance comes into play.

It is easiest to understand how this works by considering the simple form of truncation selection, in which every individual above a threshold value survives and breeds; those below die and leave no offspring. Truncation selection is often practiced in agricultural contexts to improve the quality of crops, but it can occur in nature too. In the interaction between Japanese weevils and Camellia fruits, a female weevil uses her long beak to chew through a protective fruit coat into the seed to lay her eggs. Camellia fruits with coats thicker than the beak length of weevils survive, but those with thinner coats are parasitized and eaten by weevil larvae. This form of truncation selection results in an increase in the mean fruit coat thickness of surviving fruits compared to the population as a whole.

To determine whether fruit coat thickness evolves, we have to know whether the trait is heritable. In the most general sense, a trait is heritable if offspring resemble their parents more than they do other adults. More specifically, we are interested in the portion of resemblance that is likely to be passed along generation after generation, which is determined by the proportion of total phenotypic variation attributable to additive genetic effects. Additive genetic effects have the same influences on trait variation regardless of the genetic background, so these are most generally expected to transmit change across many generations.

Graphically, a heritability plot shows a positive relationship between the average traits of parents and their offspring (figure 1A). The stronger the relationship, the greater the proportion of variance explained by additive genetic effects. The slope of this regression is equal to the heritability of a trait. Regardless of heritability, the mean of the trait in the offspring generation is expected to be the same as the mean in the parent generation in the absence of selection. The effects of selection on distribution of the trait in the offspring generation can be seen by noting the parents that survive and reproduce after truncation selection (figure 1). In the case of Camellia fruits, only trees that make a fruit coat thicker than the length of the beak of local weevils will successfully reproduce. The difference between the mean of all possible parents and the mean of those that do reproduce is the phenotypic selection differential, s, the same value as predicted by Price’s equation, Δ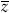, and described above. The difference between the mean offspring trait and the mean that would have been produced if all possible parents had reproduced equally is the response to selection, R. It is predicted by the product of the heritability, h², and the phenotypic selection differential, s.

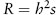
This relationship is famously known as the breeder’s equation. The stronger the heritability (which, as a ratio of variances, is bound between 0 and 1), the more faithfully the effects of selection in one generation are translated into phenotypic change across generations. Fruit coat thickness in Camellia is known to have a heritability around 0.7. While the strength of selection on Camellia varies greatly among populations, it averages around s = 0.1, indicating that fruit coat thickness changes around one-tenth of a standard deviation each generation. The fruit coat of Camellia differs fivefold across islands in the Pacific, matching the beak length of weevils on each island, suggesting that evolutionary response has occurred.

Figure 1. Heritability plot and response to selection. (A) The relationship between the average of a trait in two parents (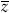) and the average trait of the offspring they produce. The slope of the relationship is the heritability of the trait. On the margins are the frequency distributions of each generation (solid curves). The means of each generation will be the same in the absence of selection. If truncation selection occurs and only parents with traits above a threshold value reproduce (solid symbols), the distributions change (dashed curves), with new means. At the top of the plot, the mean of the parent generation is increased, and this difference is s, the selection differential. (B and C) Response to selection without the distributions or the parent-offspring pairs. The means of the parent generation and the offspring that would be produced are shown as . After truncation selection, the mean of the parent distribution becomes * and the difference between the parent means is the strength of selection, s. Heritability determines the average traits of the offspring that would be produced after selection, 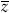*. The difference between mean of the offspring produced and those that might have been produced is the response to selection, 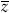. The same strength of selection, s, can generate a strong response (B) or a weak response (C) depending on the heritability of a trait.

The breeder’s equation is based on statistical principles, and the estimates of heritability and phenotypic selection that go into it are notoriously approximate. Nonetheless, this simple product of selection in one generation and genetic basis of response across generations is remarkably accurate at predicting quantitative evolutionary changes. One particularly impressive example comes from a field study of the alpine skypilot flower in Colorado. Candace Galen bred plants to obtain a heritability estimate for flower size (h^2≈ 1.0) and observed pollinator behavior to determine the strength of the selection differential on the same trait (s = 0.07 – 0.17). Combining the estimates using the breeder’s equation, she predicted that flower size should increase 4–17 percent per generation because of the preferences of bumble bees for larger flowers. By following the population across generations, she was able to detect an observed evolutionary increase of 9 percent, firmly within the range of her predictions.

4. MODES OF SELECTION

Selection can take several different statistical forms having very distinct consequences for the evolution of quantitative traits (see chapter III.3). When one thinks of selection that changes form, driving adaptation of the kind associated with classic evolutionary radiations like leg lengths of Anolis lizards on Caribbean islands and the beak depth of finches on the Galápagos, this is generally called directional selection. Directional selection changes the mean of a trait and is visualizable as a monotonically increasing (or decreasing) function of fitness with phenotype (figure 2A). Truncation selection is an extreme form of directional selection. Sexual selection, such as that documented by Carl Gerhardt and colleagues in which female gray tree frogs prefer males with longer calls, typically generates directional selection.

Figure 2. Modes of selection. Selection functions relating fitness (w) to trait variation are shown at the top of each plot, with the frequency distributions of the trait below. The general change in the frequency distribution due to selection within a generation is shown with a black dashed line. If heritability results in a response to selection, the long-term effect of selection is shown in the dashed gray distribution. (A) Directional selection; (B) stabilizing selection; (C) disruptive selection; (D) correlational selection (shown as a saddle-shaped contour plot, wherein lines on the surface indicate equal fitness and peaks are denoted with a +; bivariate frequency distributions are shown as ellipses).

It is often assumed that most traits of organisms are relatively well adapted to their current environments. This means that neither larger nor smaller values of traits should be associated with higher fitness; instead, it is the intermediate values of traits that have highest relative fitness, so the resulting selection function is nonlinear with an intermediate peak. Stabilizing (or optimizing) selection acts to reduce the variance in a distribution without changing the average value of a trait (figure 2B). For this reason it is usually regarded as a mechanism of stasis and stability rather than one that generates new adaptations; however, the shape of a phenotypic distribution may be considered adaptive at the population level.

Whereas stabilizing selection occurs because the individuals with the most deviant trait values have lowest fitness, in disruptive selection these individuals fare best and the intermediate values fare worst. Disruptive selection is the mathematical opposite of stabilizing selection; the resultant function is convex, whereas that of stabilizing selection is concave (figure 2C). The effect of disruptive selection is to inflate the variance of a distribution, and in this way it acts to promote polymorphism within populations. Most cases of disruptive selection in nature involve relatively distinct forms with alternative strategies, such as those of black-bellied seedcrackers, in which birds with different bill shapes specialize on alternative food types. Field studies conducted by Tom Smith in Cameroon demonstrated that birds with intermediate bill shapes are less efficient at foraging on either food type, thereby suffering lower fitness.

Disruptive selection is expected to be uncommon because it is unstable over time. As the phenotypic distribution of a trait shifts toward one side or the other of the convex function, the prevailing effect of selection in the population becomes more directional. For disruptive selection to persist, temporal fluctuations in selection must occur. The most important of these may be negative frequency-dependent selection, in which the fitness associated with a trait value depends on its relative frequency. If rare values always have higher fitness, this has the effect of rocking the convex function back and forth across generations, thus maintaining the average form of disruptive selection through time. Negative frequency-dependent selection has been observed in a variety of species with polymorphic trophic strategies and color patterns. Flower color polymorphisms such as the yellow or purple inflorescences of the orchid Dactylorhiza sambucina may be maintained in this fashion. Pollinators of D. sambucina receive no reward for visitation, and they learn to avoid the most commonly encountered flower color, thus lending an advantage to rare types.

Phenotypic selection of each mode has been widely documented in nature (see chapter III.7). Joel Kingsolver and his colleagues have reviewed the majority of these studies and revealed that directional selection is the mode most commonly observed. The strength of directional selection, particularly when it results from sexual selection, is stronger than many researchers expect, averaging around s = 0.15, or a change of 15 percent of one standard deviation each generation. Despite the presumption that most selection should be stabilizing, it is not as commonly observed as directional selection. In fact, disruptive selection is detected at nearly the same frequency and the same strength as stabilizing selection. These patterns may be influenced by the tendency of researchers to study selection in traits they suspect to be experiencing directional selection, and by the statistical difficulty in detecting nonlinear functions.

5. THE MULTIDIMENSIONAL PHENOTYPE

Each of the above modes of selection assumes that relationships exist between fitness and single traits in isolation. In fact, organisms comprise an uncountable number of traits that both function and are inherited as part of an integrated whole. This fact renders selection and response multivariate problems that must consider whether and to what extent traits are correlated to make accurate predictions about evolutionary change.

A character sometimes does not experience selection alone, but does so in combination with another. Neither individual trait covaries with fitness, nor is there a discernible function relating variance in fitness to the individual trait; when the two traits are considered simultaneously, however, a pattern may emerge, a mode known as correlational selection, which describes selection on combinations of traits rather than on individual characters in isolation. The effect of correlational selection is to change the bivariate distribution of traits without necessarily changing the mean of either character (figure 2D). Field studies of the northwestern garter snake showed this mode of selection with respect to escape behavior and color patterns. No covariance between fitness and either the number of reversals during escape or the degree of stripedness was observed, indicating that snakes had an equal probability of survival regardless of these traits, when viewed individually. However, when both traits were examined together, correlational selection was detected. Survival was highest for snakes that had striped patterns and made few reversals, or for those with spotted patterns that performed many reversals. Snakes with the other two possible combinations had lower survival. This form of selection acts to increase the correlation between behavior and color pattern, thus shaping the integration of the multivariate phenotype.

Correlational selection can take several shapes with slightly different effects. The selection on garter snakes described above can be envisioned as a saddle-shaped function in bivariate space (plate 2). Much like disruptive selection, the highest fitness is associated with extreme combinations of traits while the opposite combinations of extremes have the lowest fitness. This form of selection is sometimes called epistatic because it is the interaction between traits, rather than the traits themselves, that predicts fitness. Any trait value of one character could have the same fitness, depending on the value of a second character with which it is paired. A second form of correlational selection can be envisioned as a ridge of higher fitness along a line of matching trait values. In this case, there is no particular advantage to having extreme phenotypes, but rather to being equally matched. This ridge form of selection also leads to increased correlations among traits and builds integration across the phenotype. Several studies of birds and insects, including Dolph Schluter’s 1994 analysis of survival in song sparrows, have revealed matching correlational selection for body mass and wing size, suggesting that a range of body sizes are equally fit as long as they are paired with appropriate-sized wings. Correlational selection is understudied in nature, owing in part to the logistical challenges of studying multivariate functions.

6. INDIRECT SELECTION AND MISLEADING COVARIANCES

Selection is typically thought of as a causal process, but this interpretation contradicts the covariance approach. To be sure, covariances can arise because of causation, but they do not require functional relationships to occur. Statistical analyses of selection alone can rarely demonstrate causal links; experimental approaches are normally required to disentangle such paths.

Correlated characters make the problem particularly confounding. If two characters are positively correlated, one trait might covary with fitness because it is correlated with another trait that is functionally more important. Flat-tailed horned lizards of the North American Southwest have a crown of bony projections around the skull presumably used in defense against predators. Kevin Young and colleagues used the covariance approach to show that the length of the parietal horns on the back of the head covaried strongly with survival in the face of attack by shrikes; however, the length of parietal horns strongly correlates with the length of squamosal horns on the side of the head. Squamosal horns, too, covary with survival. Both types of horns are positively correlated with overall body size, which also covaries with fitness. Each of these traits experiences phenotypic selection, but that does not imply that each is causally important.

This problem is known as indirect (or correlated, distinct from “correlational”) selection. In the example above, it is assumed from behavioral studies that the parietal horns are important in defense because they are used to stab predators in the face during attacks. If the length of parietal horns drives the variation in survival, then squamosal horns might experience indirect selection because they are correlated with the causally important trait. A functional relationship between one trait and fitness causes all correlated traits to experience selection as well. In a landmark paper in the early 1980s, Russell Lande and Steve Arnold described an analytical approach that helped disentangle the multivariate problem. Using multiple regression, it is possible to determine how much of the covariance between a trait and fitness is independent of other correlated traits. This approach has changed the way that selection is studied in the wild, and it ameliorates the problem of confounding trait correlations.

7. GENETIC CORRELATIONS AND CORRELATED RESPONSE TO SELECTION

A different set of correlations changes the way selection is transmitted across generations. Genetic correlations describe how traits are inherited together and can arise from a variety of mechanisms. Pleiotropy occurs whenever a gene or group of genes influences variation in multiple traits at once. Pleiotropic effects can be generated whenever a single gene product like an enzyme is used in common developmental pathways or influences the expression of more than one character. The endocrine system is a common example, wherein a single product like testosterone determines the expression of behavioral traits including aggression and parental care, morphological traits like body size, and physiological traits like immune function.

Genetic correlations also occur whenever independent genes become associated statistically or physically. When two genes are found close together on a chromosome, they are physically linked, and recombination between them is unlikely. Alleles at these genes form nonrandom combinations known as linkage disequilibrium that is measured as a genetic correlation. Even without physical linkage, patterns of assortative mating and selection (such as the correlational selection described above) can lead to combinations of alleles occurring together more often than expected by chance, and likewise generating genetic correlations.

When selection occurs on one trait, all the genetically correlated traits will respond to that selection, even if they experience no selection themselves. This correlated response to selection occurs because selection on one trait in the parent generation also changes the distribution of the genetic variance in correlated traits. Just as heritability causes evolution across generations in a single trait, genetic correlations cause correlated evolution in linked traits. This effect is clear when we consider traits expressed in both sexes. Silene latifolia is a dioecious plant, with male and female reproductive structures on separate plants. Because flower size in both sexes is controlled by many of the same genes, the flower size of males and females is strongly genetically correlated. Lynda Delph and colleagues have demonstrated that natural selection favors large female flowers, in part because they can make more seeds. At the same time, selection favors many small flowers in males, because that is how they increase their mating success. In an artificial selection experiment, Delph allowed only the smallest female flowers to reproduce, causing an evolutionary reduction in female flower size as predicted. Male flower size, too, responded to this selection with a reduction in size. Even though males experienced no selection directly, the genetic correlation between the sexes was enough to drag along the evolution of a second trait.

This experiment highlights the usual interpretation that genetic correlations can constrain evolutionary response (see chapter III.8). In Silene, male and female flowers are selected in opposite directions, creating a conflict in selection. Genetic correlations cause selection on one sex to drag the other along in the same direction in evolutionary time; thus the positive genetic correlation acts as a constraint against selection favoring different flower sizes in the two sexes. More generally, genetic correlations and the correlated responses to selection they cause are expected to constrain phenotypic evolution, because selection on a single trait will cause changes throughout the integrated phenotype.