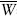The Princeton Guide to Evolution

Genetic Load

Aneil F. Agrawal

OUTLINE

1. Genetic load

2. Mutation load

3. Other types of load

4. Consequences of load

At a cursory level, evolution by natural selection is simple. Some genotypes are better than others. Those genotypes increase in frequency, wiping out the alternatives. The population then consists of only the best genotype(s). Once this has occurred, the population has achieved its maximum fitness. However, a number of phenomena—especially those processes that generate the variation necessary for adaptation—prevent populations from achieving this selective nirvana in which only the best genotype exists. In other words, nonoptimal genotypes persist at equilibrium. The presence of these nonoptimal genotypes means that the average fitness of individuals within the population is lower than the fitness of the best genotype; this reduction in fitness is genetic load.

GLOSSARY

Epistasis. The deviation in fitness of a genotype carrying multiple mutations from its expected fitness based on independent effects of individual mutations.

Genetic Load. The reduction in mean fitness due to the presence of nonoptimal genotypes.

Mean Fitness. In the context of load, mean fitness refers to the average fitness relative to the optimal genotype.

Mutation Load. The reduction in mean fitness due to the presence of deleterious alleles maintained by mutation-selection balance; it is one form of genetic load.

1. GENETIC LOAD

For a number of reasons, a population can harbor genotypes that are less fit than the optimal genotype. Such a population carries a genetic load because the average fitness is less than it could be. Here we will consider several types of genetic load, though mutation load will be discussed in greatest detail. Usually, x load can be interpreted as meaning how much more fit would the average individual be if one could stop x from happening. For example, a mutation load of 60 percent (L_mut = 0.6) means that as a result of new deleterious mutations, the average individual is 60 percent less fit than the best genotype. If mutation could be stopped, selection would eventually eliminate all deleterious alleles, so that all remaining individuals would possess the best genotype, thereby increasing this relative measure of mean fitness by 60 percent.

As discussed in greater detail below, theory tells us that some types of genetic load can be shockingly large, meaning that mean fitness is much lower than it could be; however, even when the load is high, it is unclear whether this “matters.” Some have argued that the burden of high genetic loads might severely threaten population persistence. Others have argued that genetic load is no more than a mathematical construct with no meaningful consequences. The truth lies somewhere in between, with the answer depending on the circumstances and also the metric used to assess what it means to “matter.” These issues will be discussed in the final section.

2. MUTATION LOAD

The Classic Theory

The vast majority of mutations that affect fitness are deleterious (see chapter IV.2). Because selection should eliminate such alleles, one might naively assume that deleterious mutations are an uninteresting and unimportant part of evolutionary biology; however, more careful consideration of the problem changes that perspective. Although selection pushes deleterious alleles out of populations, new mutations are constantly being introduced. Thus, no population can ever be free of deleterious alleles. For example, recent estimates from the 1000 Genomes project and other sources suggest that the average person carries several hundred (or more) deleterious alleles.

In a classic theory paper, J.B.S. Haldane (1937) considered the equilibrium between the opposing forces of selection and mutation. Consider a single autosomal locus in a diploid organism where the wild-type allele A mutates to the deleterious allele a at rate μ. Given the fitness relationships W_AA = 1, W_Aa = 1 – hs, and W_aa = 1 – s, the mean fitness in the population is 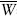= 1 – 2q(1 – q)hs – q²s, where q is the frequency of the deleterious allele.

At equilibrium, the deleterious allele is expected to exist at a low, but nonzero, frequency, q≈μ/hs (assuming that μ ≪ hs). Because the deleterious allele is rare at equilibrium (q ≪ 1), mean fitness is well approximated by 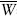≈ 1−2qhs≈1−2μ. We can define the mutation load as the reduction in mean fitness when mutation occurs relative to what it would be in the absence of mutation,

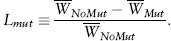
In the case of our single locus model, this becomes

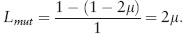
This remarkable result says that the mean fitness is reduced by an amount 2μ relative to what it would be in the absence of mutation (when all individuals would be of type AA). Counter to common intuition, the reduction in mean fitness is independent of the strength of selection (hs) against the mutation. This is because if a mutation were to be more strongly selected, it would be rarer at equilibrium (q ≈ μ/hs), but each copy present would cause a bigger effect on mean fitness; these two opposing effects of hs cancel out in calculating the mean.

With a realistic per locus mutation rate of μ = 10^-6, the mutation load from our single locus model is so small, it seems hardly worth our time to consider it at all; however, we must remember that deleterious mutations are occurring at all n loci in the genome. As a first approximation to calculating the genome-wide mutation load, Haldane made two simplifying assumptions: (1) genes affect fitness independently (no epistasis), and (2) deleterious alleles are randomly distributed across loci (no linkage disequilibrium). Under these assumptions, the mean fitness with respect to the entire genome is simply the product of the mean fitnesses with respect to each individual locus,

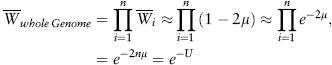
where U = 2nμ is the average number of new mutations per diploid genome per generation. This calculation leads to some disturbing conclusions once we start considering real values of U. While a fair bit of uncertainty remains in estimates of U, there is good evidence that many multicellular eukaryotes have deleterious mutation rates in the range of U = 1 (see chapter IV.2). By the equation above, we obtain 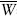= e^-1 = 0.37, implying a mutation load of more than 60 percent. This major reduction in mean fitness is not due to any one particular deleterious allele being common but rather to the presence of many different rare mutations, perhaps all of very small effect, dispersed across the genome.

Before proceeding, it is worth making a few semantic clarifications. The use of the term mutation load here follows the formal mathematical definition above, but readers should use caution when interpreting its usage elsewhere. Sometimes, “mutation load” is used more loosely to describe any scenario where deleterious alleles are present, often in reference to the relative commonness of such alleles, or the ways they affect the genetic variance in fitness, the consequences of inbreeding, or the risk of extinction. The formal definition above pertains precisely to the reduction in “mean fitness,” but interpreting this can be tricky. Mutation load is best thought of as the degree to which the average individual would be less fit relative to a mutation-free individual placed in the population. Mean fitness as used in the current context is not defined in terms of absolute fitness in a way relating directly to population size or growth, an issue to be discussed later. In addition, beneficial mutations are not considered here, even though they are incredibly important for adaptive evolution and fitness. The purpose of excluding beneficial mutations is to focus on the effects of deleterious mutations. Arguably, a more accurate term for the ideas discussed here would be deleterious mutation load rather than just “mutation load,” as we are interested in quantifying the impact of deleterious mutations, not all mutations; nonetheless, the traditional terminology is used here.

Extending the Theory

Building from earlier work, Kondrashov and Crow (1988) provided a more general analysis of mutation load that does not depend on any assumptions about gene interaction or linkage disequilibrium. Their analysis shows that load is , where 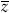and 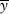are the mean numbers of mutations carried by the winners and losers of selection, respectively. This result can be understood as follows. Each generation, U mutations per individual enter the population. At equilibrium, the same number of mutations must be removed by selection. The mutation load can be thought of as the individuals who die, or otherwise fail to contribute to the next generation, in order to remove these mutations. The difference is the number of mutations eliminated per selective death, when an individual dies or fails to reproduce because of its genotype. (The concept applies more generally than survival versus death; for example, a mutant individual who produces 10 percent fewer offspring can be thought of as representing 10 percent of a selective death.) If many mutations can be eliminated at once by killing off a few individuals, the load will be smaller than if it takes many selective deaths to remove the same number of mutations. In practice, it is difficult to determine for particular scenarios, limiting the application of the elegant general result above. Nonetheless, the general result helps us interpret more specific results.

Perhaps the best-known extension of the mutation load theory pertains to the role of epistasis or gene interaction. For example, consider the fitnesses of the following haploid genotypes: W_AB = 1, W_Ab = 0.9, and W_aB = 0.9. If the double mutant has a fitness of W_ab = 0.6, then its fitness is worse than expected based on each of the single mutation effects, and we would describe this as synergistic or negative epistasis. If the double mutant had a fitness of W_ab = 0.85 (i.e., better than expected), we would say there is positive epistasis. Compared with Haldane’s prediction, mutation load is larger when there is positive epistasis but lower when there is negative epistasis. With strong negative epistasis (especially truncation selection), load can be greatly reduced because many mutations can be eliminated per selective death (i.e., > 1); however, empirical studies have shown that some gene combinations show positive epistasis but others show negative epistasis, with no strong general trend toward one type of epistasis.

Inbreeding can also reduce mutation load, especially if deleterious alleles are strongly recessive. The clustering of alleles through inbreeding (i.e., excess of homozygosity) allows more deleterious alleles to be eliminated with each selective death (see chapter IV.6). Like typical inbreeding, population structure can also create an excess of homozygotes and therefore also reduce mutation load; however, with population structure, the ecology of selection is important, especially if individuals compete primarily against their relatives for resources. If mutants compete against their mutant relatives, rather than against wild types, their deleterious effects may be sheltered from selection, thereby increasing the load.

Under fairly general circumstances, the load of asexual populations is given by Haldane’s result of L = 1 – e^-U. Though epistasis and dominance affect mutation load in sexual populations, they do not affect the load of asexual populations. This discrepancy serves as an important reminder that it is not the form of selection alone that determines the efficiency with which deleterious alleles are removed by selection; the distribution of deleterious alleles with respect to one another—which is affected by sexual processes such as segregation, recombination, and inbreeding—is also important. Because asexual and sexual populations can have different mutation loads under the same circumstances, population geneticists have wondered whether this may contribute to maintenance of sex.

Empirical Evidence

At least with respect to some groups of multicellular eukaryotes, deleterious mutation rates should be large enough (on the order of 1) to substantially reduce mean fitness according to Haldane’s prediction; moreover, there is much evidence that deleterious mutations exist in natural populations. In some cases, specific alleles causing particular genetic diseases have been identified. Inbreeding depression is a common observation in many taxa and is largely attributable to the presence of (partially) recessive deleterious mutations. Molecular population geneticists often find an excess of rare variants at nonsynonymous sites, the expected signature of segregating deleterious mutations.

Although there is little doubt that many deleterious alleles segregate in natural populations, and that new ones are entering populations at a high rate, we do not know if their effect on mean fitness is anything close to the magnitude of Haldane’s prediction. Despite the potentially massive effects of mutation load, they have never been quantified. The primary reason is that it is impossible to identify a mutation-free genotype to serve as a reference. One possible solution is to identify a high-fitness genotype to serve as reference. Because it can never be known if this is the best possible genotype, any measure of load using this genotype as a reference must be considered a lower bound on the mutation load. For example, with U = 1 and hs = 0.01, the mean number of mutations per individual is 100 under Haldane’s assumptions. The best genotype one would be likely to find (even with considerable effort) would be expected to have at least 80 mutations. Thus, the true load would be L = 1 – e^-U = 0.63, whereas the measured load using the “best available” genotype as a reference would be 0.18.

It should be possible to gain insight into the problem by manipulating the mutation rate and comparing the average fitness of individuals from populations of high and low mutation rates. Although this would not be true load because no mutation-free genotype would be present, one could obtain a measure of the load of the high mutation rate population relative to that of the low mutation rate population. Under Haldane’s assumptions, the relative load is given by the difference in mutation rates, L_relative = 1 – exp(U_Low – U_High). Provided the difference in mutation rates between treatments is on the order of 1, we would expect a sizeable relative load, if Haldane was even approximately correct. Bruce Wallace (1991) conducted this type of experiment by maintaining some populations of Drosophila melanogaster under normal conditions while other populations were exposed to X-ray radiation each generation. He found differences in fitness of 5–30 percent; however, these results are difficult to interpret for three reasons. It is unknown the degree to which X-ray radiation increased mutation rate. Though reasonable, the fitness assays he performed would not be considered particularly accurate reflections of fitness, compared with more modern assays. Finally, it is possible that the X-ray procedure may have resulted in inadvertent selection for somewhat different phenotypes than the control (e.g., X-ray resistance); nonetheless, these studies by Wallace represent one of the only attempts to examine the ways in which mutation-selection balance affects mean fitness. There is clearly a need for more studies of this nature.

3. OTHER TYPES OF LOAD

Drift Load

Drift load is sometimes viewed casually as a type of mutation load, though others like to keep the concepts separate. Drift load usually refers to the reduction in fitness due to the deviation of deleterious alleles away from their deterministic expected value under mutation-selection balance (e.g., q = μ/hs). When selection is weak relative to the inverse of the population size, s ≪ 1/4N_e, then the fate of a deleterious allele is more strongly determined by neutral processes than by selection. Deleterious alleles may drift to high frequencies or even reach fixation, thereby reducing fitness. In populations of reasonable size, only very minor deleterious alleles can drift all the way to fixation. Unlike rare segregating deleterious mutations, fixed mutations provide a likely target for compensatory adaptation, especially if a single beneficial mutation can compensate for multiple fixed deleterious effects.

Migration Load

Divergent ecological selection can favor alternative alleles in subpopulations connected by migration. Conceptually, migration load is very similar to mutation load. Just as deleterious alleles are constantly entering a population through mutation, locally maladapted alleles can be maintained within subpopulations through migration. At equilibrium, the frequency of a maladapted allele is q ≈ m/hs (assuming m ≪ hs), where m is the migration rate. The presence of these alleles reduce mean fitness, creating a single-locus load of L = 2m. Although only a small fraction of loci are likely to experience divergent ecological selection, the load per affected locus is likely much larger than that from mutation-selection balance, because migration can be much stronger than mutation, that is, m ≫ μ. A number of empirical studies provide suggestive evidence that maladapted alleles appear to be maintained by migration-selection balance, but there are no direct estimates of the migration load itself.

Segregation and Recombination Load

Although sexual reproduction does not change allele frequencies, it can change the way alleles are distributed with respect to one another. Because selection is expected to result in an excess of good combinations, rearranging these combinations through segregation and recombination can result in lower fitness. This is the essence of segregation and recombination load.

The simplest scenario to consider is a single locus model with heterozygote advantage: W_AA = 1 – s, W_Aa = 1, W_aa = 1 – t. In the absence of segregation, the population would evolve to consist entirely of heterozygotes and mean fitness would be 1; however, because of sex (specifically, segregation), homozygotes are present at equilibrium. The equilibrium allele frequency is q = s/(s + t), resulting in a mean fitness of 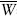= 1 – st/(s+t), which confers a segregation load of L = st/(s + t). Although only a small fraction of loci may be subject to heterozygote advantage, each one can make a substantial contribution to genetic load (relative to a single gene at mutation-selection balance). If we imagine that 50 loci (of the 10,000+ genes in a typical eukaryote) are subject to heterozygote advantage with s = t = 0.05, then we expect a segregation load of about 70 percent, assuming independent fitness effects.

Segregation load need not require heterozygote advantage. Consider the case of a recessive lethal: W_AA = W_Aa = 1 and W_aa = 0. In a facultatively sexual organism where asexual reproduction is common, the allele can accumulate to a reasonably high frequency in the heterozygous state. Whenever sex occurs, segregation will reduce fitness by converting healthy heterozygotes into lethal homozygotes, thereby reducing mean fitness.

Just as segregation disrupts favorable intralocus associations, recombination can break up favorable interlocus associations (e.g., coadapted gene complexes). By converting fit genotypes to less fit ones, recombination can reduce mean fitness, and this is the recombination load.

As reviewed by Becks and Agrawal (2011), a number of experimental studies in facultatively sexual organisms (e.g., Chlamydomonas, Daphnia, rotifers) have found that sexually derived offspring have substantially lower mean fitness than asexually derived offspring. This “sex load” could be due to segregation load and/or recombination load, as both genetic processes are involved in sex. A study in Drosophila melanogaster found that recombinant chromosomes were less fit than nonrecombinant chromosomes, reflecting a recombination load.

Gender Load

Because males and females share largely the same genome (excepting Y and W chromosomes), one or both sexes can be constrained from achieving its optimal phenotype when sex-specific optima differ. Analogous to migration between habitats, biparental inheritance continually moves alleles back and forth between the sexes. Populations may fix alleles that are a selective compromise between the sexes, though suboptimal for both genders. This represents a “fixed” gender load, which is quite hard to detect. Alternatively, balancing selection between the sexes can maintain diversity within populations, resulting in a “segregating” gender load. Such segregating polymorphisms should create genotypes that develop into above-average females but below-average males, or vice versa. This type of negative intrasexual genetic correlation in fitness has been observed in several insect and plant systems. In principle, a more direct measure of the gender load could be obtained by preventing gene flow between the sexes. Prasad et al. (2007) used cytogenetic tricks in Drosophila so that much of the genome was transmitted patrilineally (e.g., Y-like) and thereby became subject to selection only in males. After 25 generations of being free from selection in females, the resulting genomes produced males that were 15 percent more fit than controls. This represents a lower bound to the segregating gender load.

The gender load described above results from opposing selection on the sexes with respect to the same gene(s), that is, intralocus sexual conflict. A second type of gender load results from interlocus sexual conflict. This occurs when the sexes are in conflict over a “shared” trait, such as remating rate, for example, males typically want to mate more frequently than is optimal for females. A different set of genes (and phenotypes) may underlie a male’s ability to influence remating rate from those possessed by a female (e.g., male courtship traits vs. female preference functions). Evolutionary advances by each sex prevent one or both sexes from reaching its optimal value. Because this scenario does not involve opposing selection between the sexes at the gene level, it is more likely to contribute to fixed than segregating gender load.

Substitution Load

Evolution by natural selection is not a magical transformation of poor genotypes into good ones. Rather it is replacement process; good alleles spread to fixation by outcompeting the alternative. The removal of these less fit types was described by Haldane as the “cost of natural selection.” The associated term substitution load can be confusing, because adaptive substitution hardly seems to involve a load as it obviously increases fitness, rather than decreases it. The substitution load refers to the selective deaths required to make a substitution via replacement relative to an imaginary scenario whereby substitution was by instantaneous (and magical) transformation. Formally, the load resulting from increasing an allele at frequency p to fixation is L_sub = 2 ln(1/p). This represents the number of selective deaths per capita but is somewhat different from other loads as it is distributed across many generations. When selection is strong, this load is concentrated into fewer generations. Some have argued that the substitution load may set an upper limit on the number of simultaneous substitutions in a limited time, especially in organisms that do not have large amounts of reproductive excess to “absorb” selective losses. Another interpretation of this result is that assuming the population is initially viable, it is not possible for selection to be very strong at multiple newly substituting loci unless the most fit and least fit genotypes are capable of producing vastly different numbers of offspring. Because the lower limit on reproduction is zero, the maximum difference in fitness is limited by the upper bound on absolute fitness, which is lower for organisms such as elephants than for flies.

4. CONSEQUENCES OF LOAD

Under reasonable conditions, the predicted loads from mutation, migration, segregation, and antagonistic selection between the sexes can be very large. But does it matter? From one perspective, the answer is a definitive yes; individuals are of lower genetic quality than they otherwise would be, and this is inherently interesting. From another perspective, the answer is a more ambiguous maybe. Consider that a recent estimate for genome-wide deleterious mutation rate in humans is U = 4.2. Following Haldane, this predicts 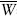= 0.015, or a load of 98.5 percent. That is a massive mutation load! But what does this mean?

In principle, this means that the average individual from the real population would have a fitness of less than 2 percent if he or she were placed in a population with no deleterious alleles at all. Other potentially misleading interpretations of load are also used; for example, a load of L is sometimes taken to mean that if the average real individual is capable of producing n offspring, then an unloaded individual should be capable of producing n_unloaded = n/(1 – L) offspring. Using human values of L = 98 percent and n = 10, then n_unloaded = 500.

This value seems ridiculous, so we should consider it carefully. First, we should acknowledge our limited ability to assess the plausibility of this number. It is unlikely that any human, or any other large mammal, has fewer than 100 deleterious mutations, so we have no real basis to evaluate what might be possible in the absence of any deleterious mutations. Second, the calculation uses n = 10 based on potential reproductive capacity, but in reality, the average individual produces fewer offspring; in a stable population the average female produces n = 2 offspring, reducing maximum reproductive capacity to a lower, but still large, value of n_unloaded = 100. Of course, the reason most individuals do not realize their reproductive capacity is because of competition for limited resources. This leads to the third, and probably most important, issue. Load refers to fitness relative to the optimal type, not to absolute fitness. Much of the load may be manifest as reduced competitive ability; if so, it is misleading to attempt to calculate maximum reproductive capacity. An unloaded individual may have no greater reproductive capacity, but rather be much more likely to obtain the resources necessary to reach that potential when in competition with loaded individuals. Conversely, the average individual carrying about 700 deleterious alleles may not seem too unfit if competing against others carrying a similar mutational burden, rather than against a hypothetical mutant-free genotype. From this perspective, one might argue that load does not really “matter” too much with respect to realized absolute fitness.

We can continue this line of thinking with respect to population-level consequences of load. Usually, demography is not a simple linear function of the average “genetic quality” relative to the optimal genotype. Consequently, it is hard to predict whether load will have any meaningful population-level consequences. Consider the scenario above involving a resource-limited population in which much of the load is expressed as reduced competitive ability. Those with more loaded genotypes allow those with less loaded genotypes to succeed. If there were no loaded genotypes, then ecological (nonselective) deaths due to resource limitation would replace genetic (selective) ones. In this case, population size can be largely unaffected by the amount of load. This can explain how populations persist in the face of seemingly “unbearable” loads.

The scenario above, with complete ecological compensation for selective deaths, represents one extreme. Whenever load directly affects birth or death rates or the ability to convert resources into survival or reproduction, load is likely to have demographic consequences, even if resource limitation imposes additional density regulation. Moreover, most discussion of load ignores the importance of interspecific competition. When two closely related species compete, their loads relative to one another will either affect their abundances quantitatively or, more importantly, determine whether there is coexistence or competitive exclusion. This latter notion is implicit in load-based hypotheses for the sexual populations competing against their obligately asexual sister taxa. Although the ecological consequences of load have received little attention in more general contexts, this neglect is unjustified. It remains a major empirical challenge to find useful ways to measure load in terms of the decline in fitness relative to the optimal genotype and also its demographic and ecological consequences.