Mathematical Models of the Real World
This introductory chapter discusses mathematical models, sketches the mathematical tools for their analysis, defines systems in general and systems of decisions in particular. Games are introduced from a general point of view and it is indicated how they may arise in combinatorial, economic, social, physical and other contexts.
1.Mathematical modelling
Mathematics is the powerful human instrument to analyze and to structure observations and to possibly discover natural “laws”. These laws are logical principles that allow us not only to understand observed phenomena (i.e., the so-called real world) but also to compute possible evolutions of current situations, and thus to attempt a “look into the future”.
Why is that so? An answer to this question is difficult if not impossible. There is a wide-spread belief that mathematics is the language of the universe.1 So everything can supposedly be captured by mathematics and all mathematical deductions reveal facts about the real world. I do not know whether this is true. Even if it were, one would have to be careful with real-world interpretations of mathematics, nonetheless. A simple example may illustrate the difficulty:
While apples on a tree are counted in terms of natural numbers, it would certainly be erroneous to conclude: for every natural number n, there exists a tree with n apples. In other words, when we use the set of nonnegative integers to describe the number of apples on a tree, our mathematical model will comprise mathematical objects that have no real counterparts.
Theoretically, one could try to get out of the apple dilemma by restricting the mathematical model to those numbers n that are realized by apple trees. But such a restricted model would be of no practical use as neither the set of such apple numbers n nor its specific algebraic structure is explicitly known. Indeed, while the sum m + n of two natural numbers m and n is a natural number, it is not clear whether the existence of two apple trees with m resp. n apples guarantees the existence of an apple tree with m + n apples.
In general, a mathematical model of a real-world situation is, alas, not necessarily guaranteed to be absolutely comprehensive. Mathematical conclusions are possibly only theoretical and may suggest objects and situations which do not exist in reality. One always has to double-check real-world interpretations of mathematical deductions and ask whether an interpretation is “reasonable” in the sense that it is commensurate with one’s own personal experience.
In the analysis of a game-theoretic situation, for example, one may want to take the psychology of individual players into account. A mathematical model of psychological behavior, however, is typically based on assumptions whose accuracy is unclear. Consequently, mathematically established results within such models must be interpreted with care, of course.
Moreover, similar to physical systems with a large number of particles (like molecules), game-theoretic systems with many agents (e.g., traffic systems and economies) are too complex to analyze by following each of the many agents individually. Hence a practical approach will have to concentrate on “group behavior” and consider statistical parameters that average over individual numerical attributes.
Having cautioned the reader about the real-world interpretation of mathematical deductions, we will concentrate on mathematical models (and their mathematics) and leave the interpretation to the reader. Our emphasis is on game-theoretic models. So we should explain what we understand by this.
A game involves players that perform actions which make a given system go through a sequence of states. When the game ends, the system is in a state according to which the players receive rewards (or are charged with costs or whatever). Many game theorists think of a “player” as a humanoid, i.e., a creature with human feelings, wishes and desires, and thus give it a human name.2
Elements of a mathematical model, however, do not have humanoid feelings per se. If they are to represent objects with wishes and desires, these wishes and desires must be explicitly formulated as mathematical optimization challenges with specified objective functions and restrictions. Therefore, we will try to be neutral and refer to “players” often just as agents with no specified sexual attributes. In particular, an agent will typically be an “it” rather than a “he” or a “she”.
This terminological neutrality makes it clear that mathematical game theory comprises many more models than just those with human players. As we will see, many models of games, decisions, economics and social sciences have the same underlying mathematics as models of physics and informatics.
Note on continuous and differentiable functions. Real world phenomena are often modelled with continuous or even differentiable functions. However,
•There exists no practically feasible test for the continuity or the differentiability of a function!
Continuity and differentiability, therefore, are assumptions of the model builder. These assumptions appear often reasonable and produce good results in applications. Moreover, they facilitate the mathematical analysis. Yet, their appropriateness cannot be proven by tests and experiments. The reader should be aware of the difference between a mathematical model and its physical origin.
Note on algorithms and computational complexity. Game-theoretic questions naturally call for mathematical computations within appropriate models. This will become clear in the present text, which also tries to exhibit important links to mathematical optimization theory. However, here is not the place to discuss specific mathematical optimization procedures per se. There is an abundance of classical mathematical literature on the latter, which can be consulted by the interested reader.
The question of the complexity of computations within particular game-theoretic models has attracted the interest of theoretical computer science and created the field of algorithmic game theory,3 whose details would exceed the frame and aim of this text and are, therefore, not addressed either.
2.Mathematical preliminaries
The reader is assumed to have basic mathematical knowledge (at least at the level of an introductory course on linear algebra). Nevertheless, it is useful to review some of the mathematical terminology. Further basic facts are outlined in the Appendix.
2.1.Functions and data representation
A function f : S → W assigns elements f(s) of a set W as values to the elements s of a set S. One way of looking at a function is to imagine a measuring device “f” which produces the result f(s) upon the input s:
We denote the collection of all W-valued functions with domain S as
and think of an element f ∈ WS also as a parameter vector whose coordinates fs are indexed by the elements s ∈ S and have values fs = f(s) ∈ W.
There is a dual way of looking at this situation where the roles of the function f and the variable s are reversed. The dual viewpoint sees s as a probe which produces the value f(s) when exposed to f:
If S is small, the function f can be presented by a table which displays the total effect of f on S:
The dual viewpoint would fix an element s ∈ S and evaluate the effect of the measuring devices f1, . . . , fk, for example, and thus represent an individual element s ∈ S by a k-dimensional data table:
The dual viewpoint is typically present when one tries to describe the state σ of an economic, social or physical system 
via the data values f1(σ), f2(σ), . . . , fk(σ) of statistical measurements f1, . . . , fk with respect to k system characteristics:
The two viewpoints are logically equivalent. Indeed, the dual perspective sees the element s ∈ S just like a function 
with values
Also the first point of view is relevant for data representation. Consider, for example, a n-element set
In this context, a function f : N → {0, 1} may represent a subset Sf of N, via the identification
REMARK 1.1. The vector f in (1) is the incidence vector of the subset Sf. Denoting by 
the collection of all subsets of N and writing 2 = {0, 1}, the context (1) establishes the correspondence
NOTA BENE. (0, 1)-valued functions can also have other interpretations, of course. Information theory, for example, thinks of them as bit vectors and thus as carriers of information.
An abstract function is a purely mathematical object with no physical meaning by itself. It obtains a concrete meaning only within the modelling context to which it refers.
EX. 1.1. The so-called HEISENBERG and the SCHRÖDINGER pictures of quantum theory are dual to each other in the sense of the present section.4
Notation. When we think of a function f : S → W as a data representative, we think of f as a coordinate vector f ∈ WS with coordinate components fs = f(s) and also use the notation
In the case S = {s1, s2, s3 . . . }, we may write
Matrices. The direct product of two sets X and Y is the set of all ordered pairs (x, y) of elements x ∈ X and y ∈ Y, i.e.,
A function A : X × Y → W can be imagined as a matrix with rows labeled by the elements x ∈ X and columns labeled by the elements y ∈ Y:
The function values Axy are the coefficients of A. We express this point of view in the shorthand notation
The matrix form suggests to relate similar structures to A. The transpose of the matrix A ∈ WX×Y, for example, is the matrix
In the case X = {1, 2, . . . , m} and Y = {1, 2, . . . , n}, one often simply writes
REMARK 1.2 (Row and column vectors). When one thinks of a coordinate vector f ∈ WX as a matrix having just f as the only column, one calls f a column vector. If f corresponds to a matrix with f as the only row, f is a row vector. So:
Graphs. A (combinatorial) graph G = G(X) consists of a set X of nodes (or vertices) whose ordered pairs (x, y) of elements are viewed as arrows or (directed) edges between nodes:
Denoting, as usual, the set of all real numbers by ℝ, an ℝ-weighting of G is an assignment of real number values axx to the nodes x ∈ X and axy to the other edges (x, y) and hence corresponds to a matrix
with X as its row and its column index set and coefficients Axy = axy.
REMARK 1.3. Although logically equivalent to a matrix, a graph representation of data is often more intuitive in dynamic contexts.
A directed edge e = (x, y) may, for example, represent a road along which one can travel from x to y in a traffic context. In another context, e could also indicate a possible transformation of x into y, etc.
The edge weight ae = axy could be the distance from x to y or the strength of an action exerted by x onto y, etc.
2.2.Algebra of functions and matrices
While the coefficients of data vectors or matrices can be quite varied (colors, sounds, configurations in games, etc.), we will typically deal with numerical data so that coordinate vectors have real numbers as their component values. Hence we deal with coordinate spaces of the type
Addition and scalar multiplication. The sum f + g of two coordinate vectors f, g ∈ ℝS is the vector of component sums (f + g)s = fs + gs, i.e.,
For any scalar λ ∈ ℝ, the scalar product λf multiplies each component of f ∈ ℝS by λ:
WARNING. There are many — quite different — notions for “multiplication” operations with vectors.
Products. The (function) product f • g of two vectors f, g ∈ ℝS is the vector with the componentwise products, i.e.,
In the special case of matrices A, B ∈ ℝX×Y the function product of A and B is called the HADAMARD5 product
WARNING. The HADAMARD product is quite different than the standard matrix multiplication rule (3) below.
Norm and inner products. Data vectors have typically only finitely many components. This means: One deals with parameter vectors f ∈ ℝS where S is a finite set. Assuming S to be finite, the following notions are mathematically well-defined since they involve sums with only finitely many summands:
The (euclidian) norm of a vector f ∈ ℝS is the parameter
The inner product of the vectors f, g ∈ ℝS is the real number (!):
which allows us to express the norm as
For finite matrices A, B ∈ ℝX×Y, we have the completely analogous notions:
Orthogonality. The idea of a norm is motivated by geometric considerations which suggest to interpret the norm ∥f∥ as the length of the vector f. One says that f, g ∈ ℝS are orthogonal if they satisfy the so-called Theorem of PYTHAGORAS, i.e.,the relation
REMARK 1.4. Notice that the “Theorem of PYTHAGORAS”(2) is actually not a theorem but a definition (for the notion of orthogonality) in the context of the algebraic structure ℝS.
LEMMA 1.1 (Orthogonality). Assuming S finite, one has for the coordinate vectors f, g ∈ ℝS:
Proof. Straightforward exercise.
The standard matrix product. If we have matrices A ∈ ℝX×Y and B ∈ ℝY×Z, every row vector Ax of A is an element of ℝY and every column vector Bz of B is an element of ℝY. So the corresponding inner products
are well-defined. The matrix AB ∈ ℝX×Z of all those inner products is called the (standard) product of A and B.
The standard product of matrices A ∈ ℝX×Y and B ∈ ℝU×Z is ONLY declared in the case U = Y and, then, defined as the matrix
If we think of f, g ∈ ℝS as column vectors, then fT defines a matrix with just one row fT and g a matrix with just one column. With this understanding, we find
EX. 1.2. If f, g ∈ ℝn are column vectors, then fTg is formally a (1 × 1)-matrix with the single coefficient 〈f|g〉. This is to be clearly distinguished from the (n × n)-matrix
EX. 1.3 (Trace). The trace tr C of a matrix C is the sum of its diagonal elements. Show for the matrices A, B ∈ ℝX×Y:
Linear maps. Recall that one may think of a matrix A ∈ ℝm×n as the parametrization of a linear map f : ℝn → ℝm that assigns to the n unit vectors ui ∈ ℝn the n column vectors of A:
A general member of ℝn is a linear combination of the n unit vectors ui with scalar coefficients λi. Linearity of f means:
and hence
REMARK 1.5. Where I ∈ ℝn×n is the (n × n) identity matrix (with column vectors ui), one has
In contrast, assuming A ∈ ℝn×n, the HADAMARD product yields a diagonal matrix:
Hilbert spaces. If S is an infinite set, both the sum f + g and the HADAMARD product f • g are well-defined for any f, g ∈ ℝS. However, the notions of norms and inner products become vague because of the infinite sums in their definitions.
As a way around this difficulty, let us call a parameter vector f ∈ ℝS a HILBERT6 vector if
| (H1) | Only a countable number of coefficients fs of f are non-zero. |
| (H2) |  |
Let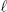 
2(S) denote the so-called HILBERT space of all HILBERT vectors in ℝS. 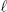2(S) is a vector space over the scalar field ℝ in the sense
As one knows form the algebra of series with at most countably many summands, norms and inner products are well-defined scalar numbers for all vectors in the HILBERT space 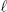2(S).
While much of mathematical game theory can be developed in the more general setting of HILBERT spaces, we will be mostly concerned with finite-dimensional coordinate spaces in this introductory text.
EX. 1.4. Show that all finite-dimensional real coordinate spaces are HILBERT spaces. In fact, one has:
2.3.Numbers and algebra
The set ℝ of real numbers has an algebraic structure under the usual addition and multiplication rules for real numbers. ℝ contains the set of natural numbers
The computational rules of ℝ may also be applied to ℕ because sums and products of two natural numbers yield natural numbers.7 Similar algebraic rules can be defined on other sets. We give two examples below.
REMARK 1.6. There is the philosophical issue whether “0” is a natural number, which corresponds to the question whether an entity can be a “set” when it is empty, i.e., contains no element.8 For clarification, we therefore employ the notation
for the set of natural numbers including 0.
Complex numbers. There is no real number r ∈ ℝ with the property r2 = −1. To remedy this deficiency, one may introduce a new “number” i and do computations with it like it were a real number with the property
In doing so, one arrives at more general numbers of the form z = a + ib, with a and b being real numbers. The set
is the set of complex numbers. The special number
is the so-called imaginary unit. Using the algebraic rules of ℝ and always keeping i2 = −1 in mind, one can perform the usual computations with additions, subtractions, multiplications and divisions in ℂ.
EX. 1.5. Assume that numbers a, b, c, d ∈ ℝ are given such that
Express the real numbers c and d in terms of the real numbers a and b.
A sober, neutral look at the matter reveals that we have imposed an algebraic structure on the set ℝ × ℝ of pairs (a, b) of real numbers with the computational rules
If we identify the pair (1, 0) with the real number 1 and the pair (0, 1) with the imaginary unit i, we observe
It is straightforward to check that the rules (4) correspond precisely to the computational rules for complex numbers.
Another interesting view on complex numbers is offered by their representation as (2 × 2)-matrices:
EX. 1.6. Show: The sum and the product of two complex numbers is compatible with the matrix sum and (standard) matrix product of their representation of type (5).
We will see in Chapter 9 how the matrix representation (5) captures the basic idea of interaction among two agents and provides the fundamental link to the mathematical model underlying quantum theory.
For computational purposes, we retain:
Algebra in ℂ follows the same rules as algebra in ℝ with the additional rule
Binary algebra. Define an addition ⊕ and a multiplication ⊗ on the 2-element set 
= {0, 1} according to the following tables:
Also in this binary algebra, division is possible in the sense that the equation
has a unique solution y “for every” x ≠ 0.9
Vector algebra. Complex numbers allow us to define sums and products of vectors with complex coefficients in analogy with real sums and products.
The same is true for vectors with (0, 1)-coefficients under the binary algebraic rules.10
REMARK. Are there clearly defined “correct” or “optimal” addition and multiplication rules on data structures that would reveal their real-world structure mathematically?
The answer is “no” in general. The imposed algebra is always a choice of the mathematical analyst — and not of “mother nature”. It often requires care and ingenuity. Moreover, different algebraic setups may reveal different structural aspects and thus lead to additional insight.
2.4.Probabilities, information and entropy
Consider n mutually exclusive events E1 , . . . , En, and expect that any one of these, say Ei, indeed occurs “with probability” pi = Pr(Ei). Then the parameters pi form a probability distribution p ∈ ℝℇ on the set ℇ = {E1, . . . , En}, i.e., the pi are nonnegative real numbers that sum up to 1:
If we have furthermore a measuring or observation device f that produces the number fi if Ei occurs, then these numbers have the expected value
In a game-theoretic context, a probability is often a subjective evaluation of the likelihood for an event to occur. The gambler, investor, or general player may not know in advance what the future will bring, but has more or less educated guesses on the likelihood of certain events. There is a close connection with the notion of information.
Intensity. We think of the intensity of an event E as a numerical parameter that is inversely proportional to its probability p = Pr(E) with which we expect its occurrence to be: the smaller p, the more intensely felt is an actual occurrence of E. For simplicity, let us take 1/p as our objective intensity measure.
REMARK 1.7 (FECHNER’S law). According to FECHNER,11 the intensity of a physical stimulation is physiologically felt on a logarithmic scale. Well-known examples are the Richter scale for earthquakes or the decibel scale for the sound.
Following FECHNER,we feel the intensity of an event E that we expect with probability p on a logarithmic scale and hence according to a function of type
where loga p is the logarithm of p relative to the basis a > 0 (see Ex. 1.7). In particular, the occurrence of an “impossible” event, which we expect with zero probability, has infinite intensity
NOTA BENE. The mathematical intensity of an event depends only on the probability p with which it occurs — and not (!) on its interpretation within a modelling context or its “true nature” in a physical environment.
EX. 1.7 (Logarithm). Recall from real analysis: For any given positive numbers a, x > 0, there is a unique number y = loga x such that
where e = 2.718281828... is EULER’s12 number, the notation ln x = loge x is commonly used. ln x is the so-called natural logarithm with the function derivative
Two logarithm functions loga x and logb x differ just by a multiplicative constant. Indeed, one has
and hence
Information. In SHANNON’s13 [42] fundamental theory of information, the parameter
is the quantity of information provided by an event E that occurs with probability p. Note that the probability value p can be regained from the information quantity I2(p):
This relationship shows that “probabilities” can be understood as numerical parameters that capture the amount of information (or lack of information) we have on the occurrence of events.
Entropy. The expected quantity of information provided by the family
of events with the probability distribution π = (p1, . . . , pn) is known as its entropy
where, by convention, one sets 0 · log2 0 = 0. Again, it should be noticed:
H2(ℇ) just depends on the parameter vector π — and not on a real-world interpretation of ℇ.
REMARK 1.8. Entropy is also a fundamental notion in thermodynamics, where it serves, for example, to define the temperature of a system.14 Physicists prefer to work with base e rather than base 2 and thus with ln x instead of log2 x, i.e., with the accordingly scaled entropy
3.Systems
A system is a physical, economic, or other entity that is in a certain state at any given moment. Denoting by the collection of all possible states σ, we identify the system with . This is, of course, a very abstract definition. In practice, one will have to describe the system states in a way that is suitable for a concrete mathematical analysis. To get a first idea of what is meant, let us look at some examples.
Chess. A system arises from a game of chess as follows: A state of chess is a particular configuration C of the chess pieces on the chess board, together with the information which of the two players (“B” or “W”) is to draw next. If 
is the collection of all possible chess configurations, a state could thus be described as a pair
In a similar way, a card game takes place in the context of a system whose states are the possible distributions of cards among the players together with the information which players are to move next.
Economies. The model of an exchange economy involves a set N of agents and a set 
of certain specified goods. A bundle for agent i ∈ N is a data vector
where the component bG indicates that the bundle b comprises bG units of the good G ∈ . Denoting by 
the set of all possible bundles, we can describe a state of the exchange economy by a data vector
that specifies each agent i’s particular bundle βi ∈ .
Closely related is the description of the state of a general economy. One considers a set 
of economic statistics E. Assuming that these statistics take numerical values ϵE at a given moment, the corresponding economic state is given by the data vector
having the statistical values ϵE as its components.
Decisions. In a general decision system 
, we are given a finite set
of agents and assume that each agent i ∈ N has to make a decision of a given type, i.e., we assume that each i has to designate an element di in its individual “decision set” Di. The joint decision of the members of N is then a n-dimensional data vector
and thus describes a decision state of the set N. In the context of game theory, decisions of agents often correspond to choices of strategies from certain strategy sets.
Decision systems are ubiquitous. In the context of a traffic situation, for example, N can be a set of persons who want to travel from individual starting points to individual destinations. Suppose that each person i ∈ N selects a path Pi from a set 
i of possible paths in order to do so. Then a state of the associated traffic system is a definite selection π of paths by the members of the group N and thus a data vector with path-valued components:
3.1.Evolutions
An evolution φ of a system over a time frame T is a function
with the interpretation: The system is in the state φ(t) at time t. While the notion of “time” is a philosophically unclear issue, let us keep things simple and understand by a time frame just a set T of real numbers.
The time frames that are relevant in game-theoretic models are typically discrete in the sense that game-theoretic evolutions are observed at well-defined and well-separated time points t. So our time frames are of the type
Rather than speaking of the state σn = φ(tn) of a system at time t = tn under the evolution φ, it is often convenient to simply refer to the index n as the counter for the time elapsed. Hence an evolution φ corresponds to a sequence of states:
A game Γ involves a set N of agents (or players) and a system relative to which the game is played. A concrete game instance γ starts with some initial state σ0 ∈ and consists of a sequence of moves, i.e., of state transitions
that are feasible according to the rules of Γ. After t steps, the system has evolved from state σ0 into a state σt in a sequence of (feasible) moves
We refer to the associated sequence γt = σ0σ1 · · · σt–1σt as the stage of Γ at time t and denote the set of all possible stages after t steps by
If the game instance γ ends in stage γt = σ0σ1 · · · σt, then σt is the final state of γ.
REMARK 1.9. It is important to note that there may be many finite state sequences γ in that are not feasible according to the rules of Γ and, therefore, are not stages of Γ.
Abstract games. The preceding informal discussion indicates how a game can be defined from an abstract point of view:
•A game Γ on a system is, by definition, a collection of finite state sequences γ = σ0σ1 . . . σt with the property
The members γ ∈ Γ are called the stages of Γ.
Chess would thus be abstractly defined as the set of all possible finite sequences of legal chess moves. This set, however, is infinitely large and impossibly difficult to handle computationally.
In concrete practical situations, a game Γ is characterized by a set of rules that allow us to check whether a state sequence γ is feasible for Γ, i.e., belongs to that potentially huge set Γ. The rules typically involve also a set N of players (or agents) that “somehow” influence the evolution of a game by exerting certain actions and making certain choices at subsequent points in time t = 0, 1, 2, . . ..
Let us remain a bit vague on the precise mathematical meaning of “influence” at this point. It will become clear in special game contexts later.
In an instance of chess, for example, one knows which of the players is to move at a given time t. This player can then move the system deterministically from the current state σt into a next state σt+1 according to the rules of chess. Many games, however, involve stochastic procedures (like rolling dice or shuffling cards) whose outcome is not known in advance and make it impossible for a player to select a desired subsequent state with certainty.
REMARK 1.10. When a game starts in a state σ0 at time t = 0, it is often not clear in what stage γ it will end (or whether it ends at all).
Objectives and utilities. The players in a game may have certain objectives according to which they try to influence the evolution of a game. A rigorous mathematical model requires these objectives to be clearly formulated in mathematical terms, of course. A typical example of such objectives is a family U of utility functions
which associate with each player i ∈ N real numbers ui(γ) ∈ ℝ as its utility value once the stage γ ∈ Γ is realized.
Its expected utility is, of course, of importance for the strategic decision of a player in a game. We illustrate this with an example in a betting context.
EX. 1.8. Consider a single player with a capital of 100 euros in a situation where a bet can be placed on the outcome of a (0, 1)-valued stochastic variable X with probabilities
Assume:
•If the player invests f euros into the game and the event {X = 1} occurs, the player will receive 2f euros. In the event {X = 0} the investment f will be lost.
Question: What is the optimal investment amount f* for the player?
To answer it, observe that the player’s total portfolio after the bet is
For the sake of the example, suppose that the player has a utility function u(x) and wants to maximize the expected utility of x, that is the function
Let us consider two scenarios:
(i) u(x) = x and hence the expected utility
with derivative
If p < 1/2, the derivative is negative and, therefore, g(f) monotonically decreasing in f. Consequently f* = 0 would be the best decision.
In the case p > 1/2, g(f) is monotonically increasing and, therefore, the optimal utility is to be expected from the full investment f* = 100.
(ii) u(x) = ln x and hence
In this case, g(f) increases monotonically until f = 100(p − q) and decreases monotonically afterwards. So the best investment choice is
If p < q, we have 100(p – q) < 0. Hence f* = 0 would be the best investment choice.
NOTA BENE. The player in Ex. 1.8 with utility function u(x) = x risks a complete loss of the capital in the case p > 1/2 with probability q.
A player with utility function u(x) = ln x will never experience a complete loss of the capital.
EX. 1.9. Analyze the betting problem in Ex. 1.8 for an investor with utility function u(x) = x2.
REMARK 1.11 (Concavity). Utility functions which represent a gain are typically “concave”, which intuitively means that the marginal utility gain is higher when the reference quantity is small than when it is big.
As an illustration, assume that u : (0, ∞) → ℝ is a differentiable utility function. Then the derivative u′(x) represents the marginal utility value at x. u is concave if the derivative function
decreases monotonically with x.
The logarithm function f(x) = ln x has the strictly decreasing derivative f′(x) = 1/x and is thus an (important) example of a concave utility.
Profit and cost. In a profit game the players i are assumed to aim at maximizing their utility ui. In a cost game one tries to minimize one’s utility to the best possible.
REMARK 1.12. The notions of profit and cost games are closely related: A profit game with the utilities ui is formally equivalent to a cost game with utilities ci = – ui.
Terminology. A game with a set n of players is a so-called n-person game.15 The particular case of 2-person games is fundamental, as will be seen later.
Decisions and strategies. In order to pursue its objective in an n-person game, an agent i may choose a strategy si from a set Si of possible strategies. The joint strategic choice
typically influences the evolution of the game. We illustrate the situation with a well-known game-theoretic puzzle:
EX. 1.10 (Prisoner’s dilemma). There are two agents A, B and the data matrix
A and B play a game with these rules:
(1)A chooses a row i and B a column j of U.
(2)The choice (i, j) entails that A is “penalized” with the value 
and B with the value 
.
This 2-person game has an initial state σ0 and four other possible states (1, 1), (1, 2), (2, 1), (2, 2), which correspond to the four coordinate positions of U.
The agents have to decide on strategies i, j ∈ {1, 2}. Their joint decision (i, j) will move the game from σ0 into the final state σ1 = (i, j). So the game ends at time t = 1. The utility of player A is then the value . B has the utility value .
This game is usually understood as a cost game, i.e., A and B aim at minimizing their utilities. What should A and B do optimally?
REMARK 1.13 (Prisoner’s dilemma). The utility matrix U in (10) yields a version of the so-called Prisoner’s dilemma, which is told as the story of two prisoners A and B who can either individually “confess” or “not confess” to the crime they are jointly accused of. Depending on their joint decision, they supposedly face prison terms as specified in U. Their “dilemma” is:
•No matter what decisions are taken, at least one of the prisoners will feel that he has taken the wrong decision in the end.
_____________________________
1 GALILEO GALILEI (1564–1642).
2 Alice and Bob are quite popular choices.
3 See, e.g., NISAN et al. [35].
4 cf. Chapter 9.4.1.
5 J. HADAMARD (1865–1963).
6 D. HILBERT (1862–1943).
7 Though the same is not guaranteed for subtractions and divisions, of course.
8 In Europe, for example, the idea and mathematical use of a number “zero” became customary not before the 13th century.
9 There is actually only one such case: y = x = 1.
10 An application of binary algebra is the analysis of winning strategies for nim games in Section 2.6.
11 G.TH. FECHNER (1801–1887).
12 L. EULER (1707–1783).
13 C.E. SHANNON (1916–2001).
14 Chapter 7 relates the notion of temperature also to game-theoretic activities.
15 Even if the players are not real “persons”.