Multilinear Products

A.1 Introduction

The material in this appendix is much more abstract than that which has previously appeared. Accordingly, many of the proofs will be omitted. Also, we motivate the material with the following observation.

Let S be a basis of a vector space V. Theorem 5.2 may be restated as follows.

THEOREM 5.2:   Let g : S → V be the inclusion map of the basis S into V. Then, for any vector space U and any mapping f : S → U; there exists a unique linear mapping f^* :V → U such that f = f^* · g.

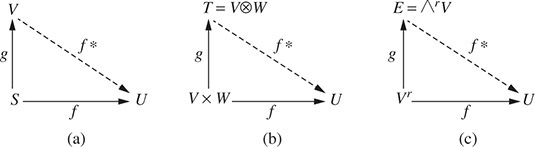
Another way to state the fact that f = f^* · g is that the diagram in Fig. A-1(a) commutes.

Figure A-1

A.2 Bilinear Mapping and Tensor Products

Let U, V, W be vector spaces over a field K. Consider a map

f : V × W → U

Then f is said to be bilinear if, for each ν ∈ V; the map f_v : W → U defined by f_v (w) = f(ν, w) is linear; and, for each w ∈ W; the map f_w : V → U defined by f_w (v) = f (ν, w) is linear.

That is, f is linear in each of its two variables. Note that f is similar to a bilinear form except that the values of the map f are in a vector space U rather than the field K.

DEFINITION A.1:   Let V and W be vector spaces over the same field K. The tensor product of V and W is a vector space T over K together with a bilinear map g : V W → T; denoted by g (v, w) = ν ⊗ w; with the following property: (*) For any vector space U over K and any bilinear map f : V × W → U there exists a unique linear map f^– : T → U such that f^– g = f.

The tensor product (T, g) [or simply T when g is understood] of V and W is denoted by V ⊗ W; and the element ν ⊗ w is called the tensor of ν and w.

Another way to state condition (*) is that the diagram in Fig. A-1(b) commutes. The fact that such a unique linear map f* exists is called the “Universal Mapping Principle” (UMP). As illustrated in Fig. A-1(b), condition (*) also says that any bilinear map f : V × W → U “factors through” the tensor product T = V ⊗ W: The uniqueness in (*) implies that the image of g spans T; that is, span (ν ⊗ w) = T.

THEOREM A.1:   (Uniqueness of Tensor Products) Let (T, g) and (T^′; g^′) be tensor products of V and W. Then there exists a unique isomorphism h:T → T^′ such that hg = g^′.

Proof. Because T is a tensor product, and g^′ :V W → T^′ is bilinear, there exists a unique linear map h :T → T^′ such that hg = g^′: Similarly, because T^′ is a tensor product, and g′ : V ⊗ W → T^′ is bilinear, there exists a unique linear map h^′ :T^′ → T such that h^′g⁰ = g: Using hg = g^′, we get h^′hg = g: Also, because T is a tensor product, and g : V ⊗ W → T is bilinear, there exists a unique linear map h^– : T → T such that h^–g = g: But 1_T} = g: Thus, h^′h = h^– = 1_T. Similarly, hh⁰ = 1_T^′: Therefore, h is an isomorphism from T to T^′:

THEOREM A.2:   (Existence of Tensor Product) The tensor product T = V ⊗ W of vector spaces V and W over K exists. Let {ν₁, … ; ν_m} be a basis of V and let {w₁, … ; w_n} be a basis of W. Then the mn vectors

form a basis of T. Thus, dim T = mn = (dim V) dim (W):

Outline of Proof. Suppose {ν_1; … ; ν_m} is a basis of V, and suppose { w₁, … ; w_n } is a basis of W. Consider the mn symbols {t_iji = i; … ; m; j = 1; … ; n}. Let T be the vector space generated by the t_ij. That is, T consists of all linear combinations of the t_ij with coefficients in K. [See Problem 4.137.]

Let ν ∈ V and w ∈ W. Say

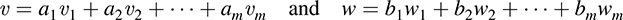
Let g: V × W → T be defined by

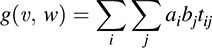
Then g is bilinear. [Proof left to reader.]

Now let f : V × W → U be bilinear. Because the t_ij form a basis of T, Theorem 5.2 (stated above) tells us that there exists a unique linear map f^* :T → U such that f^– t_ij. Then, for 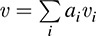and 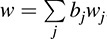we have

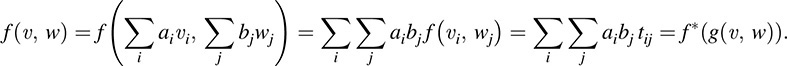
Therefore, f = f^*g where f* is the required map in Definition A.1. Thus, T is a tensor product.

Let be any basis of V and be any basis of W.

Let ν ∈ V and w ∈ W and say

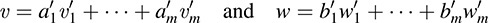
Then

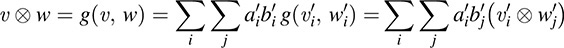
Thus, the elements 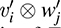span T. There are mn such elements. They cannot be linearly dependent because {t_ij} is a basis of T, and hence, dim T = mn. Thus, the 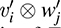form a basis of T.

Next we give two concrete examples of tensor products.

EXAMPLE A.1 Let V be the vector space of polynomials P_{r–1 (x) and let W be the vector space of polynomials Ps–1(y). Thus, the following from bases of V and W, respectively,}

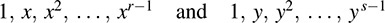
In particular, dim V = r and dim W = s: Let T be the vector space of polynomials in variables x and y with basis

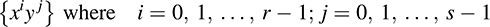
Then T is the tensor product V W under the mapping

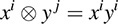
For example, suppose ν = 2 ∈ 5x + 3x³ and w = 7y + 4y². Then

EXAMPLE A.2

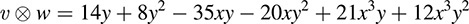
Let V be the vector space of m × n matrices over a field K and let W be the vector space of p × q matrices over K. Suppose A = [a₁₁] belongs to V, and B belongs to W. Let T be the vector space of mp × nq matrices over K. Then T is the tensor product of V and W where A ⊗ B is the block matrix

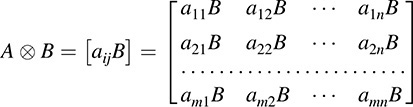
For example, suppose 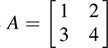and 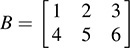. Then

Isomorphisms of Tensor Products

First we note that tensoring is associative in a cannonical way. Namely,

THEOREM A.3:   Let U, V, W be vector spaces over a field K. Then there exists a unique isomorphism

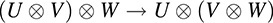
such that, for every u ∈ U; v ∈ V; w ∈ W,

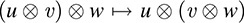
Accordingly, we may omit parenthesis when tensoring any number of factors. Specifically, given vectors spaces V₁, V₂, … ; V_m over a field K, we may unambiguously form their tensor product

V₁ ⊗ V₂ ⊗ … ⊗ V_m

and, for vectors ν_j in V_j, we may unambiguously form the tensor product

v₁ ⊗ v₂ ⊗ … ⊗ v_m

Moreover, given a vector space V over K, we may unambiguously define the following tensor product:

^rV = V V … V (r factors)

Also, there is a canonical isomorphism

(⊗^rV) ⊗ (⊗ ^sV) → ^r+sV

Furthermore, viewing K as a vector space over itself, we have the canonical isomorphism

K ⊗ V → V

where we define a ⊗ v = av:

A.3 Alternating Multilinear Maps

Let f : V^r → U where V and U are vector spaces over K. [Recall V^r = V × V × … × V, r factors.]

(1) The mapping f is said to be multilinear or r-linear if f (v₁, … ; v_r) is linear as a function of each v_j when the other v_i’s are held fixed. That is,

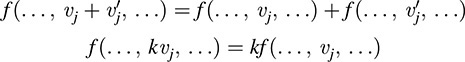
where only the jth position changes.

(2) The mapping f is said to be alternating if

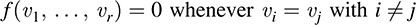
One can easily show (Prove!) that if f is an alternating multilinear mapping on V^r, then

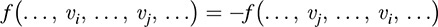
That is, if two of the vectors are interchanged, then the associated value changes sign.

EXAMPLE A.3 (Determinants)

The determinant function D: M → K on the space M of n n matrices may be viewed as an n-variable function

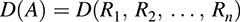
defined on the rows R₁, R₂, … ; R_n of A. Recall (Chapter 8) that, in this context, D is both n-linear and alternating.

We now need some additional notation. Let K = k₁, k₂, … ; k_r denote an r-list (r-tuple) of elements from (I_n = 1; 2; … ; n). We will then use the following notation where the v_k’s denote vectors and the a_ik’s denote scalars:

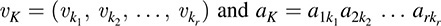
Note ν_K is a list of r vectors, and a_K is a product of r scalars.

Now suppose the elements in K = k₁, k₂, … ; k_r ½ are distinct. Then K is a permutation s_K of an r-list J = [i₁, i₂, … ; i_r] in standard form, that is, where i₁ < i₂ < … < i_r. The number of such standard-form r-lists J from I_n is the binomial coefficient:

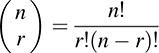
[Recall sign (σ_K) = (–1)^mK where m_K is the number of interchanges that transforms K into J.]

Now suppose A = a_ij is an r × n matrix. For a given ordered r-list J, we define

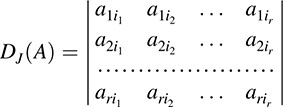
That is, D_J (A) is the determinant of the r × r submatrix of A whose column subscripts belong to J.

Our main theorem below uses the following “shuffling” lemma.

LEMMA A.4   Let V and U be vector spaces over K, and let f : V^r → U be an alternating r-linear mapping. Let ν₁, ν₂, … ; ν_n be vectors in V and let A = a_ij be an r × n matrix over K where r ≥ n. For i = 1; 2; … ; r, let

Then

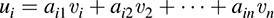
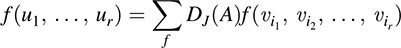
where the sum is over all standard-form r-lists J = {i₁, i₂, … ; i_r}.

The proof is technical but straightforward. The linearity of f gives us the sum

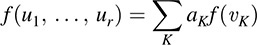
where the sum is over all r-lists K from {1; … ; n}. The alternating property of f tells us that f (v_K) = 0 when K does not contain distinct integers. The proof now mainly uses the fact that as we interchange the v_j’s to transform

so that i₁ < … < i_r, the associated sign of a_K, will change in the same way as the sign of the corresponding permutation σ_K changes when it is transformed to the identity permutation using transpositions.

We illustrate the lemma below for r = ∈ and n = 3.

EXAMPLE A.4 Suppose f : V² → U is an alternating multilinear function. Let ν₁, ν₂, ν₃ ∈ V and let u; w 2 V. Suppose

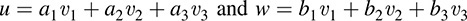
Consider

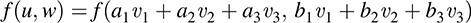
Using multilinearity, we get nine terms:

(Note that J = [1; 2], J^′ = [1; 3] and J^″ = 2; 3 ½ are the three standard-form 2-lists of I = 1; 2; 3 ½.) The alternating property of f tells us that each f (v_i, v_i) = 0; hence, three of the above nine terms are equal to 0. The alternating property also tells us that f(v_i, v_f) = f (v_f ; v_r). Thus, three of the terms can be transformed so their subscripts form a standard-form 2-list by a single interchange. Finally we obtain

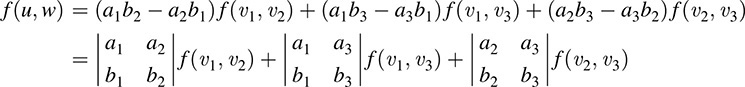
which is the content of Lemma A.4.

A.4 Exterior Products

The following definition applies.

DEFINITION A.2:   Let V be an n-dimensionmal vector space over a field K, and let r be an integer such that 1 ≥ r ≥ n. The r-fold exterior product (or simply exterior product when r is understood) is a vector space E over K together with an alternating r-linear mapping g: V^r → E, denoted by g(v₁, … ; v_r) = v₁ Λ … Λ v_r, with the following property: (*) For any vector space U over K and any alternating r-linear map f : V^r → U there exists a unique linear map f^* : E → U such that f^* · g = f.

The r-fold tensor product (E, g) (or simply E when g is understood) of V is denoted by Λ^rV, and the element ν₁ Λ … Λ ν_r is called the exterior product or wedge product of the ν_i’s.

Another way to state condition (*) is that the diagram in Fig. A-1(c) commutes. Again, the fact that such a unique linear map f* exists is called the “Universal Mapping Principle (UMP)”. As illustrated in Fig. A-1 (c), condition (*) also says that any alternating r-linear map f : V^r → U “factors through” the exterior product E = Λ^r V. Again, the uniqueness in (*) implies that the image of g spans E; that is, span ν₁ Λ … Λ v_r ( ) = E.

THEOREM A.5:   (Uniqueness of Exterior Products) Let (E, g) and E^′; (g⁰) be r-fold exterior products of V. Then there exists a unique isomorphism h : E → E^′ such that hg = g^′.

The proof is the same as the proof of Theorem A.1, which uses the UMP.

THEOREM A.6:   (Existence of Exterior Products) Let V be an n-dimensional vector space over K. Then the exterior product E = Λ^r V exists. If r > n, then E = {0}. If r ≥ n, then 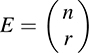. Moreover, if [ν₁, … ; ν_n is a basis of V, then the vectors

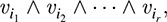
where 1 ≥ i₁ < i₂ < …. < i_r n, form a basis of E.

We give a concrete example of an exterior product.

EXAMPLE A.5 (Cross Product)

Consider V = R³ with the usual basis (i, j, k). Let E = Λ²V. Note dim V = 3: Thus, dim E = 3 with basis i Λ j; i Λ k; j Λ k: We identify E with R³ under the correspondence

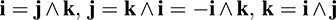
Let u and w be arbitrary vectors in V = R³, say

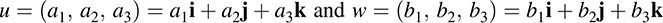
Then, as in Example A.3,

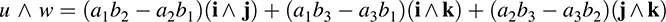
Using the above identification, we get

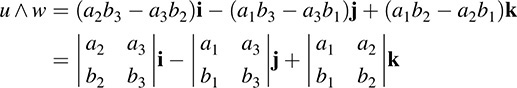
The reader may recognize that the above exterior product is precisely the well-known cross product in R³.

Our last theorem tells us that we are actually able to “multiply” exterior products, which allows us to form an “exterior algebra” that is illustrated below.

THEOREM A.7:   Let V be a vector space over K. Let r and s be positive integers. Then there is a unique bilinear mapping

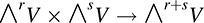
such that, for any vectors u_i, w_j in V,

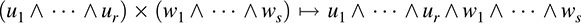
EXAMPLE A.6 We form an exterior algebra A over a field K using noncommuting variables x, y, z. Because it is an exterior algebra, our variables satisfy:

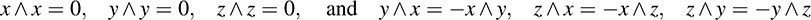
Every element of A is a linear combination of the eight elements 1;

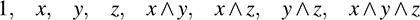
We multiply two “polynomials” in A using the usual distributive law, but now we also use the above conditions. For example,

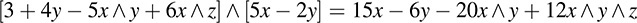
Observe we use the fact that