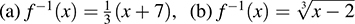Linear Mappings

5.1 Introduction

The main subject matter of linear algebra is the study of linear mappings and their representation by means of matrices. This chapter introduces us to these linear maps and Chapter 6 shows how they can be represented by matrices. First, however, we begin with a study of mappings in general.

5.2 Mappings, Functions

Let A and B be arbitrary nonempty sets. Suppose to each element in a ∈ A there is assigned a unique element of B; called the image of a. The collection f of such assignments is called a mapping (or map) from A into B, and it is denoted by

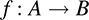
The set A is called the domain of the mapping, and B is called the target set. We write f(a), read “f of a,” for the unique element of B that f assigns to a ∈ A.

One may also view a mapping f : A → B as a computer that, for each input value a ∈ A, produces a unique output f(a) ∈ B.

Remark:   The term function is used synonymously with the word mapping, although some texts reserve the word “function” for a real-valued or complex-valued mapping.

Consider a mapping f : A → B. If A^′ is any subset of A, then f(A^′) denotes the set of images of elements of A^′; and if B^′ is any subset of B, then f⁻¹(B^′) denotes the set of elements of A; each of whose image lies in B. That is,

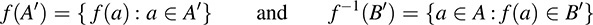
We call f(A^′) the image of A^′ and f⁻¹(B^′) the inverse image or preimage of B^′. In particular, the set of all images (i.e., f(A)) is called the image or range of f.

To each mapping f : A → B there corresponds the subset of A × B given by {(a, f(a)) : a ∈ A}. We call this set the graph of f. Two mappings f : A → B and g : A → B are defined to be equal, written f = g, if f (a) = g(a) for every a ∈ A —that is, if they have the same graph. Thus, we do not distinguish between a function and its graph. The negation of f = g is written f ≠ g and is the statement:

Sometimes the “barred” arrow ↦ is used to denote the image of an arbitrary element x ∈ A under a mapping f : A → B by writing

x ↦ f(x)

This is illustrated in the following example.

EXAMPLE 5.1

(a) Let f : R → R be the function that assigns to each real number x its square x². We can denote this function by writing

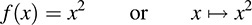
Here the image of −3 is 9, so we may write f(−3) = 9. However, f⁻¹ (9) = {3, −3}. Also, f(R) = [0, ∞) = {x : x ≥ 0} is the image of f.

(b) Let A = {a, b, c, d} and B = {x, y, z, t}. Then the following defines a mapping f : A → B :

The first defines the mapping explicitly, and the second defines the mapping by its graph. Here,

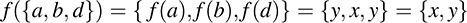
Furthermore, f(A) = {x, y, z} is the image of f.

EXAMPLE 5.2 Let V be the vector space of polynomials over R, and let p(t) = 3t² − 5t + 2.

(a) The derivative defines a mapping D : V → V where, for any polynomials f(t), we have D(f) = df/dt. Thus,

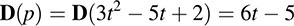
(b) The integral, say from 0 to 1, defines a mapping J : V → R. That is, for any polynomial f(t),

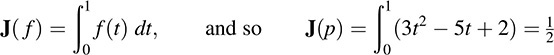
Observe that the mapping in (b) is from the vector space V into the scalar field R, whereas the mapping in (a) is from the vector space V into itself.

Matrix Mappings

Let A be any m × n matrix over K. Then A determines a mapping F_A : Kⁿ → K^m by

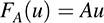
where the vectors in Kⁿ and K^m are written as columns. For example, suppose

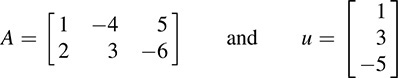
then

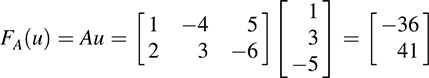
Remark:   For notational convenience, we will frequently denote the mapping F_A by the letter A, the same symbol as used for the matrix.

Composition of Mappings

Consider two mappings f : A → B and g : B → C, illustrated below:

The composition of f and g, denoted by g ° f, is the mapping g ° f : A → C defined by

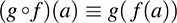
That is, first we apply f to a ∈ A, and then we apply g to f (a) ∈ B to get g(f (a)) ∈ C. Viewing f and g as “computers,” the composition means we first input a ∈ A to get the output f (a) ∈ B using f, and then we input f (a) to get the output g(f (a)) ∈ C using g.

Our first theorem tells us that the composition of mappings satisfies the associative law.

THEOREM 5.1:   Let f : A → B, g : B → C, h : C → D. Then

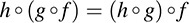
We prove this theorem here. Let a ∈ A. Then

Thus, (h ° (g ° f))(a) = ((h ° g) ° f)(a) for every a ∈ A, and so h ° (g ° f) = (h ° g) ° f.

One-to-One and Onto Mappings

We formally introduce some special types of mappings.

DEFINITION:   A mapping f : A → B is said to be one-to-one (or 1-1 or injective ) if different elements of A have distinct images; that is,

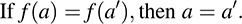
DEFINITION:   A mapping f : A → B is said to be onto (or f maps A onto B or surjective ) if every b ∈ B is the image of at least one a ∈ A.

DEFINITION:   A mapping f : A → B is said to be a one-to-one correspondence between A and B (or bijective) if f is both one-to-one and onto.

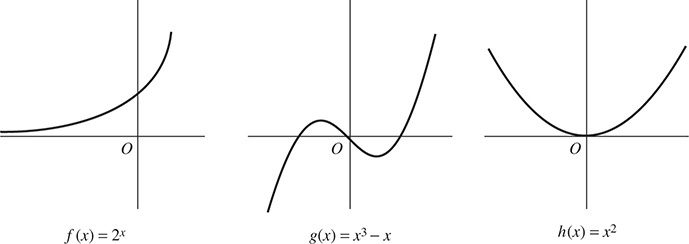
EXAMPLE 5.3 Let f : R → R, g : R → R, h : R → R be defined by

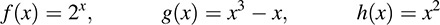
The graphs of these functions are shown in Fig. 5-1. The function f is one-to-one. Geometrically, this means that each horizontal line does not contain more than one point of f. The function g is onto. Geometrically, this means that each horizontal line contains at least one point of g. The function h is neither one-to-one nor onto. For example, both 2 and −2 have the same image 4, and −16 has no preimage.

Figure 5-1

Identity and Inverse Mappings

Let A be any nonempty set. The mapping f : A → A defined by f(a) = a—that is, the function that assigns to each element in A itself—is called identity mapping. It is usually denoted by 1_A or 1 or I. Thus, for any a ∈ A, we have 1_A(a) = a.

Now let f : A → B. We call g : B → A the inverse of f, written f⁻¹, if

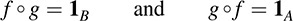
We emphasize that f has an inverse if and only if f is a one-to-one correspondence between A and B; that is, f is one-to-one and onto (Problem 5.7). Also, if b ∈ B, then f⁻¹ (b) = a, where a is the unique element of A for which f(a) = b

5.3 Linear Mappings (Linear Transformations)

We begin with a definition.

DEFINITION:   Let V and U be vector spaces over the same field K. A mapping F : V → U is called a linear mapping or linear transformation if it satisfies the following two conditions:

(1) For any vectors υ, w ∈ V, F(υ + w) = F(υ)+ F(w).

(2) For any scalar k and vector υ ∈ V, F(kυ) = kF(υ).

Namely, F : V → U is linear if it “preserves” the two basic operations of a vector space, that of vector addition and that of scalar multiplication.

Substituting k = 0 into condition (2), we obtain F(0) = 0. Thus, every linear mapping takes the zero vector into the zero vector.

Now for any scalars a, b ∈ K and any vector υ, w ∈ V, we obtain

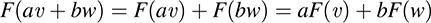
More generally, for any scalars a_i ∈ K and any vectors υ_i ∈ V, we obtain the following basic property of linear mappings:

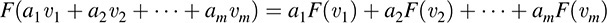
Remark 1:   A linear mapping F : V → U is completely characterized by the condition

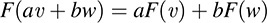
and so this condition is sometimes used as its defintion.

Remark 2:   The term linear transformation rather than linear mapping is frequently used for linear mappings of the form F : Rⁿ → R^m.

EXAMPLE 5.4

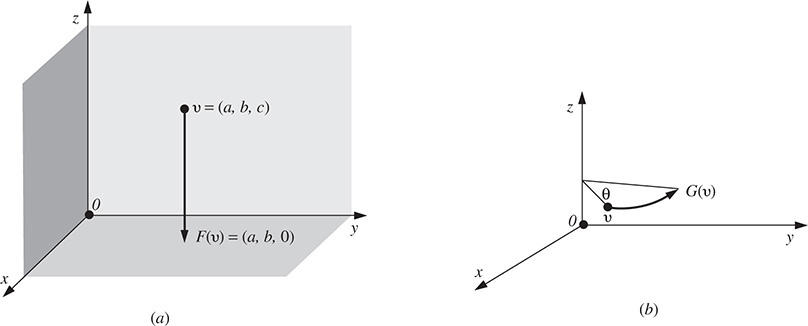
(a) Let F : R³ → R³ be the “projection” mapping into the xy-plane; that is, F is the mapping defined by F(x, y, z) = (x, y, 0). We show that F is linear. Let υ = (a, b, c) and w = (a^′, b^′, c^′). Then

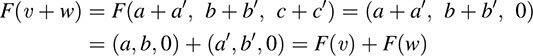
and, for any scalar k,

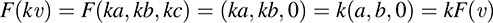
Thus, F is linear.

(b) Let G : R² → R² be the “translation” mapping defined by G(x, y) = (x + 1, y + 2). [That is, G adds the vector (1, 2) to any vector υ = (x, y) in R².] Note that

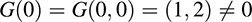
Thus, the zero vector is not mapped into the zero vector. Hence, G is not linear.

EXAMPLE 5.5 (Derivative and Integral Mappings) Consider the vector space V = P (t) of polynomials over the real field R. Let u(t) and υ(t) be any polynomials in V and let k be any scalar.

(a) Let D : V → V be the derivative mapping. One proves in calculus that

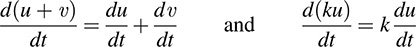
That is, D(u + υ) = D(u)+ D(υ) and D(ku) = kD(u). Thus, the derivative mapping is linear.

(b) Let J : V → R be an integral mapping, say

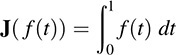
One also proves in calculus that,

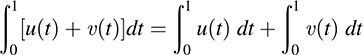
and

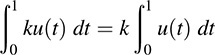
That is, J(u + υ) = J(u) + J(υ) and J(ku) = kJ(u). Thus, the integral mapping is linear.

EXAMPLE 5.6 (Zero and Identity Mappings)

(a) Let F : V → U be the mapping that assigns the zero vector 0 ∈ U to every vector υ ∈ V. Then, for any vectors υ, w ∈ V and any scalar k ∈ K, we have

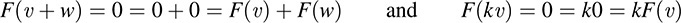
Thus, F is linear. We call F the zero mapping, and we usually denote it by 0.

(b) Consider the identity mapping I : V → V, which maps each υ ∈ V into itself. Then, for any vectors υ, w ∈ V and any scalars a, b ∈ K, we have

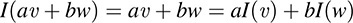
Thus, I is linear.

Our next theorem (proved in Problem 5.13) gives us an abundance of examples of linear mappings. In particular, it tells us that a linear mapping is completely determined by its values on the elements of a basis.

THEOREM 5.2:   Let V and U be vector spaces over a field K. Let {υ₁, υ₂, …, υ_n} be a basis of V and let u₁, u₂, …, u_n be any vectors in U. Then there exists a unique linear mapping F : V → U such that F(υ₁) = u₁, F(υ₂) = u₂, …, F(υ_n) = u_n.

We emphasize that the vectors u₁, u₂, …, u_n in Theorem 5.2 are completely arbitrary; they may be linearly dependent or they may even be equal to each other.

Matrices as Linear Mappings

Let A be any real m × n matrix. Recall that A determines a mapping F_A : Kⁿ → K^m by F_A(u) = Au (where the vectors in Kⁿ and K^m are written as columns). We show F_A is linear. By matrix multiplication,

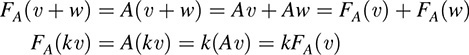
In other words, using A to represent the mapping, we have

Thus, the matrix mapping A is linear.

Vector Space Isomorphism

The notion of two vector spaces being isomorphic was defined in Chapter 4 when we investigated the coordinates of a vector relative to a basis. We now redefine this concept.

DEFINITION:   Two vector spaces V and U over K are isomorphic, written V ≅ U, if there exists a bijective (one-to-one and onto) linear mapping F : V → U. The mapping F is then called an isomorphism between V and U.

Consider any vector space V of dimension n and let S be any basis of V. Then the mapping

x ↦ (v)_s

which maps each vector υ ∈ V into its coordinate vector [υ]_S, is an isomorphism between V and Kⁿ.

5.4 Kernel and Image of a Linear Mapping

We begin by defining two concepts.

DEFINITION:   Let F : V → U be a linear mapping. The kernel of F, written Ker F, is the set of elements in V that map into the zero vector 0 in U; that is,

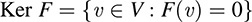
The image (or range) of F, written Im F, is the set of image points in U; that is,

Im F = fu ∈ U : there exists υ ∈ V for which F(υ) = u}

The following theorem is easily proved (Problem 5.22).

THEOREM 5.3:   Let F : V → U be a linear mapping. Then the kernel of F is a subspace of V and the image of F is a subspace of U.

Now suppose that υ₁, υ₂, …, υ_m span a vector space V and that F : V → U is linear. We show that F(υ₁), F(υ₂), …, F(υ_m) span Im F. Let u ∈ Im F. Then there exists υ ∈ V such that F(υ) = u. Because the υ_i’s span V and υ ∈ V, there exist scalars a₁, a₂, …, a_m for which

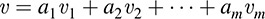
Therefore,

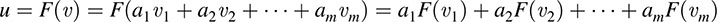
Thus, the vectors F(υ₁), F(υ₂), …, F(υ_m) span Im F.

We formally state the above result.

PROPOSITION 5.4:   Suppose υ₁, υ₂, …, υ_m span a vector space V, and suppose F : V → U is linear. Then F(υ₁), F(υ₂), …, F(υ_m) span Im F.

EXAMPLE 5.7

(a) Let F : R³ → R³ be the projection of a vector υ into the xy-plane [as pictured in Fig. 5-2(a)]; that is,

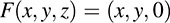
Clearly the image of F is the entire xy -plane—that is, points of the form (x, y, 0). Moreover, the kernel of F is the z-axis—that is, points of the form (0, 0, c ). That is,

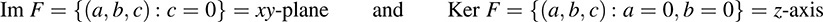
(b) Let G : R³ → R³ be the linear mapping that rotates a vector υ about the z-axis through an angle θ [as pictured in Fig. 5-2(b)]; that is,

Figure 5-2

Observe that the distance of a vector υ from the origin O does not change under the rotation, and so only the zero vector 0 is mapped into the zero vector 0. Thus, Ker G = {0}. On the other hand, every vector u in R³ is the image of a vector υ in R³ that can be obtained by rotating u back by an angle of θ. Thus, Im G = R³, the entire space.

EXAMPLE 5.8 Consider the vector space V = P(t) of polynomials over the real field R, and let H : V → V be the third-derivative operator; that is, H[f(t) = d³f/dt³. [Sometimes the notation D³ is used for H, where D is the derivative operator.] We claim that

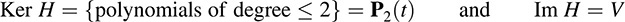
The first comes from the fact that H(at² + bt + c) = 0 but H(tⁿ) ≠ 0 for n ≥ 3. The second comes from that fact that every polynomial g(t) in V is the third derivative of some polynomial f(t) (which can be obtained by taking the antiderivative of g(t) three times).

Kernel and Image of Matrix Mappings

Consider, say, a 3 × 4 matrix A and the usual basis {e₁, e₂, e₃, e₄} of K⁴ (written as columns):

Recall that A may be viewed as a linear mapping A : K⁴ → K³, where the vectors in K⁴ and K³ are viewed as column vectors. Now the usual basis vectors span K⁴, so their images Ae₁, Ae₂, Ae₃, Ae₄ span the image of A. But the vectors Ae₁, Ae₂, Ae₃, Ae₄ are precisely the columns of A :

Thus, the image of A is precisely the column space of A.

On the other hand, the kernel of A consists of all vectors υ for which Aυ = 0. This means that the kernel of A is the solution space of the homogeneous system AX = 0, called the null space of A.

We state the above results formally.

PROPOSITION 5.5:   Let A be any m × n matrix over a field K viewed as a linear map A : Kⁿ → K^m. Then

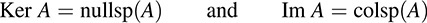
Here colsp(A) denotes the column space of A, and nullsp(A) denotes the null space of A.

Rank and Nullity of a Linear Mapping

Let F : V → U be a linear mapping. The rank of F is defined to be the dimension of its image, and the nullity of F is defined to be the dimension of its kernel; namely,

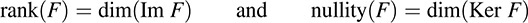
The following important theorem (proved in Problem 5.23) holds.

THEOREM 5.6   Let V be of finite dimension, and let F : V → U be linear. Then

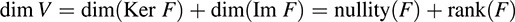
Recall that the rank of a matrix A was also defined to be the dimension of its column space and row space. If we now view A as a linear mapping, then both definitions correspond, because the image of A is precisely its column space.

EXAMPLE 5.9 Let F : R⁴ → R³ be the linear mapping defined by

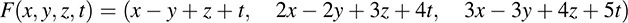
(a) Find a basis and the dimension of the image of F.

First find the image of the usual basis vectors of R⁴,

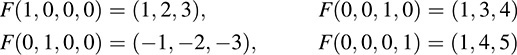
By Proposition 5.4, the image vectors span Im F. Hence, form the matrix M whose rows are these image vectors and row reduce to echelon form:

Thus, (1, 2, 3) and (0, 1, 1) form a basis of Im F. Hence, dim(Im F) = 2 and rank(F) = 2.

(b) Find a basis and the dimension of the kernel of the map F.

Set F(υ) = 0, where υ = (x, y, z, t),

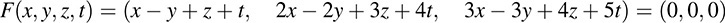
Set corresponding components equal to each other to form the following homogeneous system whose solution space is Ker F :

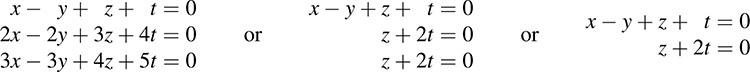
The free variables are y and t. Hence, dim(Ker F) = 2 or nullity(F) = 2.

(i) Set y = 1, t = 0 to obtain the solution (1, 1, 0, 0),

(ii) Set y = 0, t = 1 to obtain the solution (1, 0, −2, 1).

Thus, (−1, 1, 0, 0) and (1, 0, −2, 1) form a basis for Ker F.

As expected from Theorem 5.6, dim(Im F) + dim(Ker F) = 4 = dim R⁴.

Application to Systems of Linear Equations

Let AX = B denote the matrix form of a system of m linear equations in n unknowns. Now the matrix A may be viewed as a linear mapping

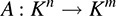
Thus, the solution of the equation AX = B may be viewed as the preimage of the vector B ∈ K^m under the linear mapping A. Furthermore, the solution of the associated homogeneous system

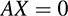
may be viewed as the kernel of the linear mapping A. Applying Theorem 5.6 to this homogeneous system yields

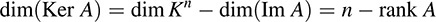
But n is exactly the number of unknowns in the homogeneous system AX = 0. Thus, we have proved the following theorem of Chapter 4.

THEOREM 4.19: The dimension of the solution space W of a homogenous system AX = 0 of linear equations is s = n − r, where n is the number of unknowns and r is the rank of the coefficient matrix A.

Observe that r is also the number of pivot variables in an echelon form of AX = 0, so s = n − r is also the number of free variables. Furthermore, the s solution vectors of AX = 0 described in Theorem 3.14 are linearly independent (Problem 4.52). Accordingly, because dim W = s, they form a basis for the solution space W. Thus, we have also proved Theorem 3.14.

5.5 Singular and Nonsingular Linear Mappings, Isomorphisms

Let F : V → U be a linear mapping. Recall that F(0) = 0. F is said to be singular if the image of some nonzero vector υ is 0—that is, if there exists υ ≠ 0 such that F(υ) = 0. Thus, F : V → U is nonsingular if the zero vector 0 is the only vector whose image under F is 0 or, in other words, if Ker F = {0}.

EXAMPLE 5.10 Consider the projection map F : R³ → R³ and the rotation map G : R³ → R³ appearing in Fig. 5-2. (See Example 5.7.) Because the kernel of F is the z-axis, F is singular. On the other hand, the kernel of G consists only of the zero vector 0. Thus, G is nonsingular.

Nonsingular linear mappings may also be characterized as those mappings that carry independent sets into independent sets. Specifically, we prove (Problem 5.28) the following theorem.

THEOREM 5.7:   Let F : V → U be a nonsingular linear mapping. Then the image of any linearly independent set is linearly independent.

Isomorphisms

Suppose a linear mapping F : V → U is one-to-one. Then only 0 ∈ V can map into 0 ∈ U, and so F is nonsingular. The converse is also true. For suppose F is nonsingular and F(υ) = F(w), then F(υ − w) = F(υ) − F(w) = 0, and hence, υ w = 0 or υ = w. Thus, F(υ) = F(w) implies υ = w—that is, F is one-to-one. We have proved the following proposition.

PROPOSITION 5.8:   A linear mapping F : V → U is one-to-one if and only if F is nonsingular.

Recall that a mapping F : V → U is called an isomorphism if F is linear and if F is bijective (i.e., if F is one-to-one and onto). Also, recall that a vector space V is said to be isomorphic to a vector space U, written V ≅ U, if there is an isomorphism F : V → U.

The following theorem (proved in Problem 5.29) applies.

THEOREM 5.9:   Suppose V has finite dimension and dim V = dim U. Suppose F : V → U is linear. Then F is an isomorphism if and only if F is nonsingular.

5.6 Operations with Linear Mappings

We are able to combine linear mappings in various ways to obtain new linear mappings. These operations are very important and will be used throughout the text.

Let F : V → U and G : V → U be linear mappings over a field K. The sum F + G and the scalar product kF, where k ∈ K, are defined to be the following mappings from V into U :

We now show that if F and G are linear, then F + G and kF are also linear. Specifically, for any vectors υ, w ∈ V and any scalars a, b ∈ K,

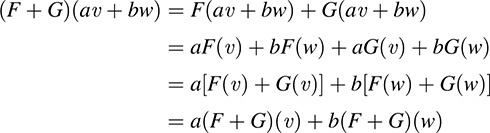
and

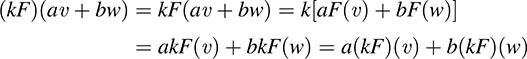
Thus, F + G and kF are linear.

The following theorem holds.

THEOREM 5.10: Let V and U be vector spaces over a field K. Then the collection of all linear mappings from V into U with the above operations of addition and scalar multiplication forms a vector space over K.

The vector space of linear mappings in Theorem 5.10 is usually denoted by

Hom(V, U)

Here Hom comes from the word “homomorphism.” We emphasize that the proof of Theorem 5.10 reduces to showing that Hom(V, U) does satisfy the eight axioms of a vector space. The zero element of Hom(V, U) is the zero mapping from V into U, denoted by 0 and defined by

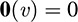
for every vector υ ∈ V.

Suppose V and U are of finite dimension. Then we have the following theorem.

THEOREM 5.11: Suppose dim V = m and dim U = n. Then dim[Hom(V, U) = mn.

Composition of Linear Mappings

Now suppose V, U, and W are vector spaces over the same field K, and suppose F : V → U and G : U → W are linear mappings. We picture these mappings as follows:

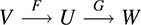
Recall that the composition function G ° F is the mapping from V into W defined by (G ° F)(υ) = G(F(υ)). We show that G ° F is linear whenever F and G are linear. Specifically, for any vectors v, w ∈ V and any scalars a, b ∈ K, we have

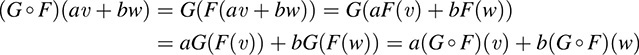
Thus, G ° F is linear.

The composition of linear mappings and the operations of addition and scalar multiplication are related as follows.

THEOREM 5.12:   Let V, U, W be vector spaces over K. Suppose the following mappings are linear:

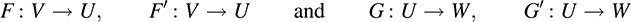
Then, for any scalar k ∈ K:

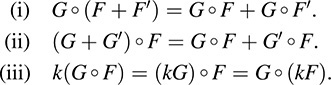
5.7 Algebra A(V) of Linear Operators

Let V be a vector space over a field K. This section considers the special case of linear mappings from the vector space V into itself—that is, linear mappings of the form F: V → V. They are also called linear operators or linear transformations on V. We will write A(V), instead of Hom(V, V), for the space of all such mappings.

Now A(V) is a vector space over K (Theorem 5.8), and, if dim V = n, then dim A(V) = n². Moreover, for any mappings F, G ∈ A(V), the composition G ° F exists and also belongs to A(V). Thus, we have a “multiplication” defined in A(V). [We sometimes write FG instead of G ° F in the space A(V).]

Remark: An algebra A over a field K is a vector space over K in which an operation of multiplication is defined satisfying, for every F, G, H ∈ A and every k ∈ K:

(i) F(G + H) = FG + FH,

(ii) (G + H)F = GF + HF,

(iii) k(GF) = (kG)F = G(kF).

The algebra is said to be associative if, in addition, (FG)H = F(GH).

The above definition of an algebra and previous theorems give us the following result.

THEOREM 5.13:   Let V be a vector space over K. Then A(V) is an associative algebra over K with respect to composition of mappings. If dim V = n, then dim A(V) = n².

This is why A(V) is called the algebra of linear operators on V.

Polynomials and Linear Operators

Observe that the identity mapping I: V → V belongs to A(V). Also, for any linear operator F in A(V), we have FI = IF = F. We can also form “powers” of F. Namely, we define

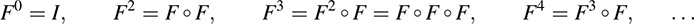
Furthermore, for any polynomial p(t) over K, say,

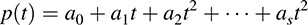
we can form the linear operator p(F) defined by

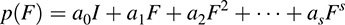
(For any scalar k, the operator kI is sometimes denoted simply by k.) In particular, we say F is a zero of the polynomial p(t) if p(F) = 0.

EXAMPLE 5.11 Let F : K³ → K³ be defined by F(x, y, z) = (0, x, y). For any (a, b, c) ∈ K³,

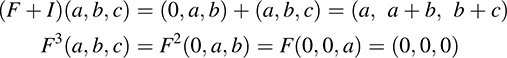
Thus, F³ = 0, the zero mapping in A(V). This means F is a zero of the polynomial p(t) = t³.

Square Matrices as Linear Operators

Let M = M_n,n be the vector space of all square n × n matrices over K. Then any matrix A in M defines a linear mapping F_A : Kⁿ → Kⁿ by F_A(u) = Au (where the vectors in Kⁿ are written as columns). Because the mapping is from Kⁿ into itself, the square matrix A is a linear operator, not simply a linear mapping.

Suppose A and B are matrices in M. Then the matrix product AB is defined. Furthermore, for any (column) vector u in Kⁿ,

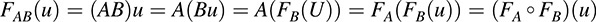
In other words, the matrix product AB corresponds to the composition of A and B as linear mappings. Similarly, the matrix sum A + B corresponds to the sum of A and B as linear mappings, and the scalar product kA corresponds to the scalar product of A as a linear mapping.

Invertible Operators in A(V)

Let F: V → V be a linear operator. F is said to be invertible if it has an inverse—that is, if there exists F^-1 in A(V) such that FF^-1 = F^-1F = I. On the other hand, F is invertible as a mapping if F is both one-to-one and onto. In such a case, F^-1 is also linear and F^-1 is the inverse of F as a linear operator (proved in Problem 5.15).

Suppose F is invertible. Then only 0 ∈ V can map into itself, and so F is nonsingular. The converse is not true, as seen by the following example.

EXAMPLE 5.12 Let V = P (t), the vector space of polynomials over K. Let F be the mapping on V that increases by 1 the exponent of t in each term of a polynomial; that is,

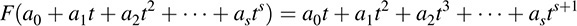
Then F is a linear mapping and F is nonsingular. However, F is not onto, and so F is not invertible.

The vector space V = P (t) in the above example has infinite dimension. The situation changes significantly when V has finite dimension. Namely, the following theorem applies.

THEOREM 5.14:   Let F be a linear operator on a finite-dimensional vector space V. Then the following four conditions are equivalent.

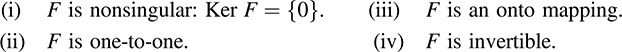
The proof of the above theorem mainly follows from Theorem 5.6, which tells us that

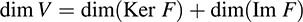
By Proposition 5.8, (i) and (ii) are equivalent. Note that (iv) is equivalent to (ii) and (iii). Thus, to prove the theorem, we need only show that (i) and (iii) are equivalent. This we do below.

(a) Suppose (i) holds. Then dim(Ker F) = 0, and so the above equation tells us that dim V = dim(Im F). This means V = Im F or, in other words, F is an onto mapping. Thus, (i) implies (iii).

(b) Suppose (iii) holds. Then V = Im F, and so dim V = dim(Im F). Therefore, the above equation tells us that dim(Ker F) = 0, and so F is nonsingular. Therefore, (iii) implies (i).

Accordingly, all four conditions are equivalent.

Remark: Suppose A is a square n × n matrix over K. Then A may be viewed as a linear operator on Kⁿ. Because Kⁿ has finite dimension, Theorem 5.14 holds for the square matrix A. This is why the terms “nonsingular” and “invertible” are used interchangeably when applied to square matrices.

EXAMPLE 5.13 Let F be the linear operator on R² defined by F(x, y) = (2x + y, 3x + 2y).

(a) To show that F is invertible, we need only show that F is nonsingular. Set F(x, y) = (0, 0) to obtain the homogeneous system 2x + y = 0 and 3x + 2y = 0

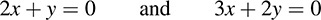
Solve for x and y to get x = 0, y = 0. Hence, F is nonsingular and so invertible.

(b) To find a formula for F^-1, we set F(x, y) = (s, t) and so F^-1 (s, t) = (x, y). We have

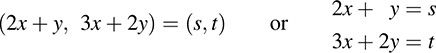
Solve for x and y in terms of s and t to obtain x = 2s – t, y = – 3s + 2t. Thus,

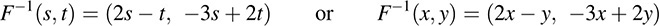
where we rewrite the formula for F^-1 using x and y instead of s and t.

SOLVED PROBLEMS

Mappings

5.1.   State whether each diagram in Fig. 5-3 defines a mapping from A = {a, b, c} into B = {x, y, z}.

(a) No. There is nothing assigned to the element b ∈ A.

(b) No. Two elements, x and z, are assigned to c ∈ A.

(c) Yes.

Figure 5-3

5.2.   Let f : A → B and g : B → C be defined by Fig. 5-4.

(a) Find the composition mapping (g ° f) : A → C.

(b) Find the images of the mappings f , g, g ° f.

Figure 5-4

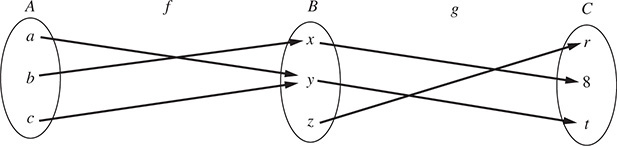
(a) Use the definition of the composition mapping to compute

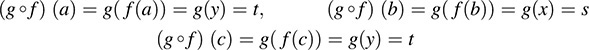
Observe that we arrive at the same answer if we “follow the arrows” in Fig. 5-4:

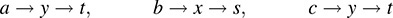
(b) By Fig. 5-4, the image values under the mapping f are x and y, and the image values under g are r, s, t.

Hence,

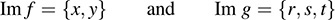
Also, by part (a), the image values under the composition mapping g ° f are t and s; accordingly, Im g ° f = {s, t}. Note that the images of g and g ° f are different.

5.3.   Consider the mapping F : R³ → R² defined by F(x, y, z) = (yz, x²). Find

(a) F(2, 3, 4); (b) F(5, 2, 7); (c) F^-1 (0, 0), that is, all υ ∈ R³ such that F(υ) = 0.

(a) Substitute in the formula for F to get F(2, 3, 4) = (3 ˙ 4, 2²) = (12, 4).

(b) F(5, -2, 7) = (-2 ˙ 7, 5²) = (14, 25).

(c) Set F(υ) = 0, where υ = (x, y, z), and then solve for x, y, z:

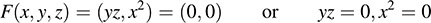
Thus, x = 0 and either y = 0 or z = 0. In other words, x = 0, y = 0 or x = 0, z = 0—that is, the z-axis and the y-axis.

5.4.   Consider the mapping F : R² → R² defined by F(x, y) = (3y, 2x). Let S be the unit circle in R², that is, the solution set of x² + y² = 1. (a) Describe F(S). (b) Find F^-1 (S).

(a) Let (a, b) be an element of F(S). Then there exists (x, y) ∈ S such that F(x, y) = (a, b). Hence,

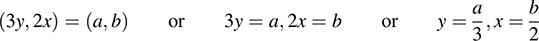
Because (x, y) ∈ S—that is, x² + y² = 1—we have

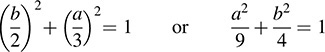
Thus, F(S) is an ellipse.

(b) Let F(x, y) = (a, b), where (a, b) ∈ S. Then (3y, 2x) = (a, b) or 3y = a, 2x = b. Because (a, b) ∈ S, we have a² + b² = 1. Thus, (3y)² +(2x)² = 1. Accordingly, F^-1 (S) is the ellipse 4x² + 9y² = 1.

5.5.   Let the mappings f : A → B, g : B → C, h : C → D be defined by Fig. 5-5. Determine whether or not each function is (a) one-to-one; (b) onto; (c) invertible (i.e., has an inverse).

(a) The mapping f : A → B is one-to-one, as each element of A has a different image. The mapping g : B → C is not one-to one, because x and z both have the same image 4. The mapping h : C → D is one-to-one.

(b) The mapping f : A → B is not onto, because z ∈ B is not the image of any element of A. The mapping g : B → C is onto, as each element of C is the image of some element of B. The mapping h : C → D is also onto.

(c) A mapping has an inverse if and only if it is one-to-one and onto. Hence, only h has an inverse.

Figure 5-5

5.6.   Suppose f : A → B and g : B → C. Hence, (g ° f) : A → C exists. Prove

(a) If f and g are one-to-one, then g ° f is one-to-one.

(b) If f and g are onto mappings, then g ° f is an onto mapping.

(c) If g ° f is one-to-one, then f is one-to-one.

(d) If g ° f is an onto mapping, then g is an onto mapping.

(a) Suppose (g ° f)(x) = (g ° f)(y). Then g(f (x)) = g(f (y)). Because g is one-to-one, f (x) = f (y). Because f is one-to-one, x = y. We have proven that (g ° f)(x) = (g ° f)(y) implies x = y; hence g ° f is one-to-one.

(b) Suppose c ∈ C. Because g is onto, there exists b ∈ B for which g(b) = c. Because f is onto, there exists a ∈ A for which f (a) = b. Thus, (g ° f)(a) = g(f (a)) = g(b) = c. Hence, g ° f is onto.

(c) Suppose f is not one-to-one. Then there exist distinct elements x, y ∈ A for which f (x) = f (y). Thus, (g ° f)(x) = g(f (x)) = g(f (y)) = (g ° f)(y). Hence, g ° f is not one-to-one. Therefore, if g ° f is one-toone, then f must be one-to-one.

(d) If a ∈ A, then (g ° f)(a) = g(f (a)) ∈ g(B). Hence, (g ° f)(A) ⊆ g(B). Suppose g is not onto. Then g(B) is properly contained in C and so (g ° f)(A) is properly contained in C; thus, g ° f is not onto. Accordingly, if g ° f is onto, then g must be onto.

5.7.   Prove that f : A → B has an inverse if and only if f is one-to-one and onto.

Suppose f has an inverse—that is, there exists a function f^-1 : B → A for which f^-1 °f = 1_A and f ° f^-1 = 1_B. Because1_A is one-to-one, f is one-to-one by Problem 5.6(c), and because 1_B is onto, f is onto by Problem 5.6(d); that is, f is both one-to-one and onto.

Now suppose f is both one-to-one and onto. Then each b ∈ B is the image of a unique element in A, say b*. Thus, if f (a) = b, then a = b*; hence, f (b*) = b. Now let g denote the mapping from B to A defined by b ↦ b*. We have

(i) (g ° f)(a) = g(f (a)) = g(b) = b* = a for every a ∈ A; hence, g ° f = 1_A.

(ii) (f ° g)(b) = f (g(b)) = f (b*) = b for every b ∈ B; hence, f ° g = 1_B.

Accordingly, f has an inverse. Its inverse is the mapping g.

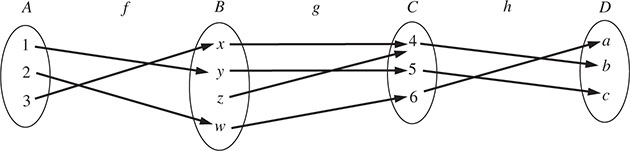
5.8.   Let f : R → R be defined by f (x) = 2x 𓴻 3. Now f is one-to-one and onto; hence, f has an inverse mapping f^-1. Find a formula for f^-1.

Let y be the image of x under the mapping f; that is, y = f (x)= 2x – 3. Hence, x will be the image of y under the inverse mapping f^-1. Thus, solve for x in terms of y in the above equation to obtain 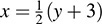. Then the formula defining the inverse function is 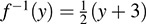, or, using x instead of .

Linear Mappings

5.9.   Suppose the mapping F : R² → R² is defined by F(x, y) = (x + y, x). Show that F is linear.

We need to show that F(υ + w) = F(υ)+ F(w) and F(kυ) = kF(υ), where u and υ are any elements of R² and k is any scalar. Let υ = (a, b) and w = (a', b'). Then

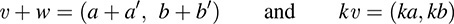
We have F(υ) = (a + b, a) and F(w) = (a' + b', a'). Thus,

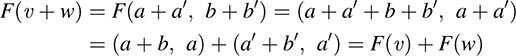
and

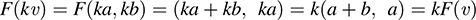
Because υ, w, k were arbitrary, F is linear.

5.10.   Suppose F : R³ → R² is defined by F(x, y, z) = (x + y + z, 2x – 3y + 4z). Show that F is linear.

We argue via matrices. Writing vectors as columns, the mapping F may be written in the form F(υ) = Aυ, where υ = [x, y, z]^T and

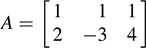
Then, using properties of matrices, we have

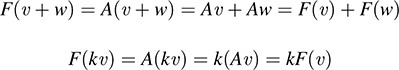
and

Thus, F is linear.

5.11.   Show that the following mappings are not linear:

(a) F : R² → R² defined by F(x, y) = (xy, x)

(b) F : R² → R³ defined by F(x, y) = (x + 3, 2y, x + y)

(c) F : R³ → R² defined by F(x, y, z) = (|x|, y + z)

(a) Let υ = (1, 2) and w = (3, 4); then υ + w = (4, 6). Also,

Hence,

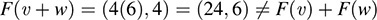
(b) Because F(0, 0) = (3, 0, 0) ≠ (0, 0, 0), F cannot be linear.

(c) Let υ = (1, 2, 3) and k = -3. Then kυ = (-3, -6, -9). We have

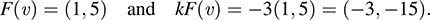
Thus,

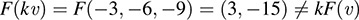
Accordingly, F is not linear.

5.12.   Let V be the vector space of n-square real matrices. Let M be an arbitrary but fixed matrix in V. Let F : V → V be defined by F(A) = AM + MA, where A is any matrix in V. Show that F is linear.

For any matrices A and B in V and any scalar k, we have

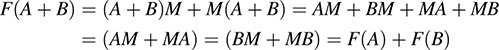
and

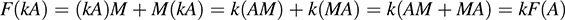
Thus, F is linear.

5.13.   Prove Theorem 5.2: Let V and U be vector spaces over a field K. Let {υ₁, υ₂,…, υ_n} be a basis of V and let u₁, u₂,…, u_n be any vectors in U. Then there exists a unique linear mapping F : V → U such that F(υ₁) = u₁, F(υ₂) = u₂,…, F(υ_n) = u_n.

There are three steps to the proof of the theorem: (1) Define the mapping F : V → U such that F(υ_i) = u_i, i = 1,…, n. (2) Show that F is linear. (3) Show that F is unique.

Step 1. Let υ ∈ V. Because {υ₁,…, υ_n} is a basis of V, there exist unique scalars a₁,…, a_n ∈ K for which υ = a₁υ₁ + a₂υ₂ + + a_nυ_n. We define F : V ∈ U by

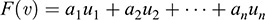
(Because the a_i are unique, the mapping F is well defined.) Now, for i = 1,…, n,

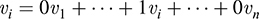
Hence,

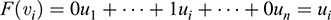
Thus, the first step of the proof is complete.

Step 2. Suppose υ = a₁υ₁ + a₂υ₂ +…+ a_nυ_n and w = b₁υ₁ + b₂υ₂+…+ b_nυ_n. Then

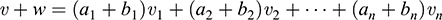
and, for any k ∈ K, kυ = ka₁υ₁ + ka₂υ₂ + … + ka_nυ_n. By definition of the mapping F,

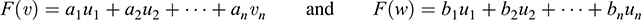
Hence

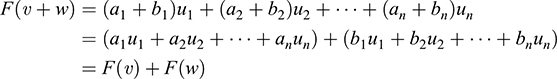
and

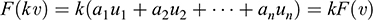
Thus, F is linear.

Step 3. Suppose G : V → U is linear and G(υ_i) = u_i, i = 1,…, n. Let

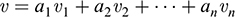
Then

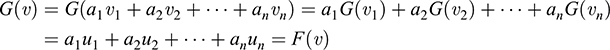
Because G(υ) = F(υ) for every υ ∈ V, G = F. Thus, F is unique and the theorem is proved.

5.14.   Let F : R² → R² be the linear mapping for which F(1, 2) = (2, 3) and F(0, 1) = (1, 4). [Note that {(1, 2), (0, 1)} is a basis of R², so such a linear map F exists and is unique by Theorem 5.2.] Find a formula for F; that is, find F(a, b).

Write (a, b) as a linear combination of (1, 2) and (0, 1) using unknowns x and y,

Solve for x and y in terms of a and b to get x = a, y = -2a + b. Then

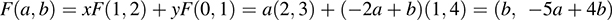
5.15.   Suppose a linear mapping F : V → U is one-to-one and onto. Show that the inverse mapping F^-1 : U → V is also linear.

Suppose u, u' ∈ U. Because F is one-to-one and onto, there exist unique vectors υ, υ' ∈ V for which F(υ) = u and F(υ') = u'. Because F is linear, we also have

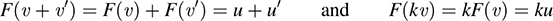
By definition of the inverse mapping,

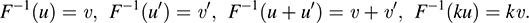
Then

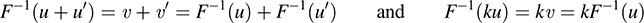
Thus, F^-1 is linear.

Kernel and Image of Linear Mappings

5.16.   Let F : R⁴ → R³ be the linear mapping defined by

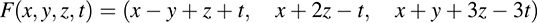
Find a basis and the dimension of (a) the image of F, (b) the kernel of F.

(a) Find the images of the usual basis of R⁴:

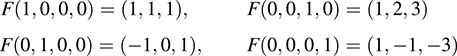
By Proposition 5.4, the image vectors span Im F. Hence, form the matrix whose rows are these image vectors, and row reduce to echelon form:

Thus, (1, 1, 1) and (0, 1, 2) form a basis for Im F; hence, dim(Im F) = 2.

(b) Set F(υ) = 0, where υ = (x, y, z, t); that is, set

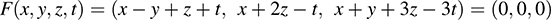
Set corresponding entries equal to each other to form the following homogeneous system whose solution space is Ker F:

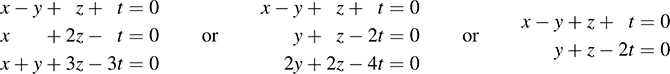
The free variables are z and t. Hence, dim(Ker F) = 2.

Thus, (2, 1, 1, 0) and (1, 2, 0, 1) form a basis of Ker F.

[As expected, dim(Im F) + dim(Ker F) = 2 + 2 = 4 = dim R⁴, the domain of F.]

5.17.   Let G : R³ → R³ be the linear mapping defined by

Find a basis and the dimension of (a) the image of G, (b) the kernel of G.

(a) Find the images of the usual basis of R³:

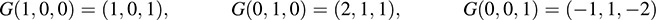
By Proposition 5.4, the image vectors span Im G. Hence, form the matrix M whose rows are these image vectors, and row reduce to echelon form:

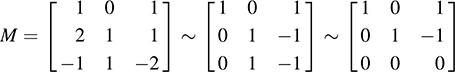
Thus, (1, 0, 1) and (0, 1, 1) form a basis for Im G; hence, dim(Im G) = 2.

(b) Set G(υ) = 0, where υ = (x, y, z); that is,

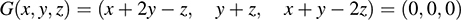
Set corresponding entries equal to each other to form the following homogeneous system whose solution space is Ker G:

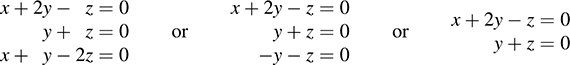
The only free variable is z; hence, dim(Ker G) = -1. Set z = -1; then y = -1 and x = 3. Thus, (3, -1, 1) forms a basis of Ker G. [As expected, dim(Im G)+ dim(Ker G) = 2 + 1 = 3 = dim R³, the domain of G.]

5.18.   Consider the matrix mapping A : R⁴ → R³, where . Find a basis and the dimension of (a) the image of A, (b) the kernel of A.

(a) The column space of A is equal to Im A. Now reduce A^T to echelon form:

Thus, {(1, 1, 3), (0, 1, 2)} is a basis of Im A, and dim(Im A) = 2.

(b) Here Ker A is the solution space of the homogeneous system AX = 0, where X = {x, y, z, t)^T. Thus, reduce the matrix A of coefficients to echelon form:

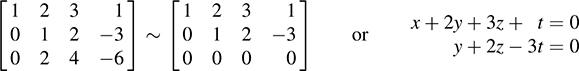
The free variables are z and t. Thus, dim(Ker A) = 2.

(i) Set z = 1, t = 0 to get the solution (1, -2, 1, 0).

(ii) Set z = 0, t = 1 to get the solution (-7, 3, 0, 1).

Thus, (1, -2, 1, 0) and (-7, 3, 0, 1) form a basis for Ker A.

5.19.   Find a linear map F : R³ → R⁴ whose image is spanned by (1, 2, 0, -4) and (2, 0, -1, -3).

Form a 4× 3 matrix whose columns consist only of the given vectors, say

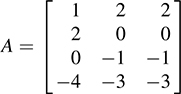
Recall that A determines a linear map A : R³ → R⁴ whose image is spanned by the columns of A. Thus, A satisfies the required condition.

5.20.   Suppose f : V → U is linear with kernel W, and that f (υ) = u. Show that the “coset” υ + W = {υ + w : w ∈ W} is the preimage of u; that is, f^-1 (u) = υ + W.

We must prove that (i) f^-1 (u) υ + W and (ii) υ + W ⊆ f^-1 (u).

We first prove (i). Suppose υ' ∈ f^-1. Then f (υ') = u, and so

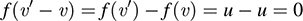
that is, υ' - υ ∈ W. Thus, υ = υ +(υ' - υ) ∈ υ + W, and hence f^-1 (u) ⊆ υ + W.

Now we prove (ii). Suppose υ' ∈ υ + W. Then υ' = υ + w, where w ∈ W. Because W is the kernel of f, we have f (w) = 0. Accordingly,

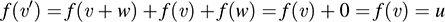
Thus, υ' ∈ f^-1

Both inclusions imply f^-1 (u) = υ + W.

5.21.   Suppose F : V → U and G : U → W are linear. Prove

(a) rank(G ° F) ≤ rank(G),

(b) rank(G ° F) ≤ rank(F).

(a) Because F(V) ⊆ U, we also have G(F(V)) ⊆ G(U), and so dim [G(F(V)) ≤ dim [G(U). Then rank(G ° F) = dim[(G ° F)(V) = dim [G(F(V)) ⊆ dim [G(U) = rank(G).

(b) We have dim [G(F(V)) ⊆ dim [F(V). Hence, rank(G ° F) = dim[(G ° F)(V) = dim [G(F(V)) ⊆ dim [F(V) = rank(F)

5.22.   Prove Theorem 5.3: Let F : V → U be linear. Then,

(a) Im F is a subspace of U, (b) Ker F is a subspace of V.

(a) Because F(0) = 0, we have 0 ∈ Im F. Now suppose u, u' ∈ Im F and a, b ∈ K. Because u and u' belong to the image of F, there exist vectors υ, υ' ∈ V such that F(υ) = u and F(υ') = u'. Then

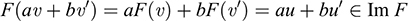
Thus, the image of F is a subspace of U.

(b) Because F(0) = 0, we have 0 ∈ Ker F. Now suppose υ, w ∈ Ker F and a, b ∈ K. Because υ and w belong to the kernel of F, F(υ) = 0 and F(w) = 0. Thus,

Thus, the kernel of F is a subspace of V.

5.23.   Prove Theorem 5.6: Suppose V has finite dimension and F : V → U is linear. Then

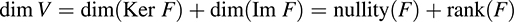
Suppose dim(Ker F) = r and {w₁,…, w_r} is a basis of Ker F, and suppose dim(Im F) = s and {u₁,…, u_s} is a basis of Im F. (By Proposition 5.4, Im F has finite dimension.) Because every u_j ∈ Im F, there exist vectors υ₁,…, υ_s in V such that F(υ₁) = u₁,…, F(υ_s) = u_s. We claim that the set

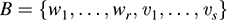
is a basis of V; that is, (i) B spans V, and (ii) B is linearly independent. Once we prove (i) and (ii), then dim V = r + s = dim(Ker F)+ dim(Im F).

(i) B spans V. Let υ ∈ V. Then F(υ) ∈ Im F. Because the u_j span Im F, there exist scalars a₁,…, a_s such that F(υ) = a₁u₁ +…+ a_su_s. Set 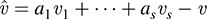. Then

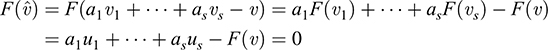
Thus, 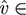Ker F. Because the w_i span Ker F, there exist scalars b₁,…, b_r, such that

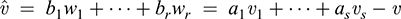
Accordingly,

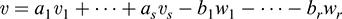
Thus, B spans V.

(ii) B is linearly independent. Suppose

where x_i, y_j ∈ K. Then

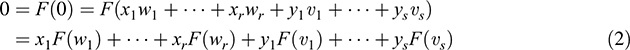
But F(w_i) = 0, since w_i ∈ Ker F, and F(υ_j) = u_j. Substituting into (2), we will obtain y₁u₁ + + y_su_s = 0. Since the u_j are linearly independent, each y_j = 0. Substitution into (1) gives x₁w₁ +…+ x_rw_r = 0. Since the w_i are linearly independent, each x_i = 0. Thus B is linearly independent.

Singular and Nonsingular Linear Maps, Isomorphisms

5.24.   Determine whether or not each of the following linear maps is nonsingular. If not, find a nonzero vector v whose image is 0.

(a) F : R² ∈ R² defined by F(x, y) = (x – y, x – y).

(b) G : R² ∈ R² defined by G(x, y) = (2x – 4y, 3x – 6y).

(a) Find Ker F by setting F(υ) = 0, where υ = (x, y),

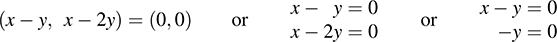
The only solution is x = 0, y = 0. Hence, F is nonsingular.

(b) Set G(x, y) = (0, 0) to find Ker G:

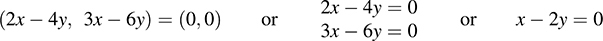
The system has nonzero solutions, because y is a free variable. Hence, G is singular. Let y = 1 to obtain the solution υ = (2, 1), which is a nonzero vector, such that G(υ) = 0.

5.25.   The linear map F : R² → R² defined by F(x, y) = (x – y, x – 2y) is nonsingular by the previous Problem 5.24. Find a formula for F^-1

Set F(x, y) = (a, b), so that F^-1 (a, b) = (x, y). We have

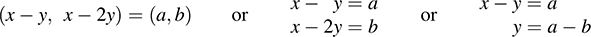
Solve for x and y in terms of a and b to get x = 2a –b, y = a – b. Thus,

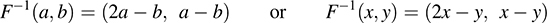
(The second equation is obtained by replacing a and b by x and y, respectively.)

5.26.   Let G : R² → R³ be defined by G(x, y) = (x + y, x – 2y, 3x + y).

(a) Show that G is nonsingular. (b) Find a formula for G^-1.

(a) Set G(x, y) = (0, 0, 0) to find Ker G. We have

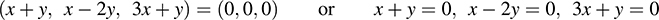
The only solution is x = 0, y = 0; hence, G is nonsingular.

(b) Although G is nonsingular, it is not invertible, because R² and R³ have different dimensions. (Thus, Theorem 5.9 does not apply.) Accordingly, G^-1 does not exist.

5.27.   Suppose that F : V ∈ U is linear and that V is of finite dimension. Show that V and the image of F have the same dimension if and only if F is nonsingular. Determine all nonsingular linear mappings T : R⁴ ∈ R³.

By Theorem 5.6, dim V = dim(Im F)+ dim(Ker F). Hence, V and Im F have the same dimension if and only if dim(Ker F) = 0 or Ker F = {0} (i.e., if and only if F is nonsingular).

Because dim R³ is less than dim R⁴, we have that dim(Im T) is less than the dimension of the domain R⁴ of T. Accordingly no linear mapping T : R⁴ ∈ R³ can be nonsingular.

5.28.   Prove Theorem 5.7: Let F : V ∈ U be a nonsingular linear mapping. Then the image of any linearly independent set is linearly independent.

Suppose υ₁, υ₂,…, υ_n are linearly independent vectors in V. We claim that F(υ₁), F(υ₂),…, F(υ_n) are also linearly independent. Suppose a₁F(υ₁) + a₂F(υ₂) +…+ a_nF(υ_n) = 0, where a_i ∈ K. Because F is linear, F(a₁υ₁ + a₂υ₂ +…+ a_nυ_n) = 0. Hence,

But F is nonsingular—that is, Ker F = {0}. Hence, a₁υ₁ + a₂υ₂ +…+ a_nυ_n = 0. Because the υ_i are linearly independent, all the a_i are 0. Accordingly, the F(v_i) are linearly independent. Thus, the theorem is proved.

5.29.   Prove Theorem 5.9: Suppose V has finite dimension and dim V = dim U. Suppose F : V → U is linear. Then F is an isomorphism if and only if F is nonsingular.

If F is an isomorphism, then only 0 maps to 0; hence, F is nonsingular. Conversely, suppose F is nonsingular. Then dim(Ker F) = 0. By Theorem 5.6, dim V = dim(Ker F)+ dim(Im F). Thus,

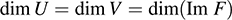
Because U has finite dimension, Im F = U. This means F maps V onto U. Thus, F is one-to-one and onto; that is, F is an isomorphism.

Operations with Linear Maps

5.30.   Define F : R³ → R² and G : R³ → R² by F(x, y, z) = (2x, y + z) and G(x, y, z) = (x – z, y). Find formulas defining the maps: (a) F + G, (b) 3F, (c) 2F – 5G.

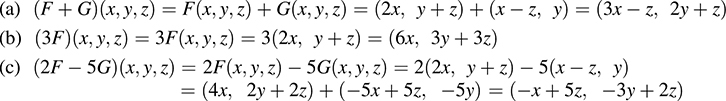
5.31.   Let F : R³ → R² and G : R² → R² be defined by F(x, y, z) = (2x, y + z) and G(x, y) = (y, x). Derive formulas defining the mappings: (a) G F, (b) F ° G.

(a) (G ° F)(x, y, z) = G(F(x, y, z)) = G(2x, y + z) = (y + z, 2x)

(b) The mapping F ° G is not defined, because the image of G is not contained in the domain of F.

5.32.   Prove: (a) The zero mapping 0, defined by 0(υ) = 0 ∈ U for every υ ∈ V, is the zero element of Hom(V, U). (b) The negative of F ∈ Hom(V, U) is the mapping (1)F, that is, F = ( 1)F.

Let F ∈ Hom(V, U). Then, for every υ ∈ V:

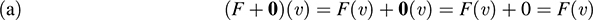
Because (F + 0)(υ) = F(υ) for every υ ∈ V, we have F + 0 = F. Similarly, 0 + F = F:

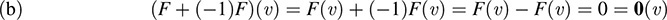
Thus, F +(-1)F = 0: Similarly (1)F + F = 0: Hence, -F = (-1)F:

5.33.   Suppose F₁, F₂,…, F_n are linear maps from V into U. Show that, for any scalars a₁, a₂,…, a_n, and for any υ ∈ V,

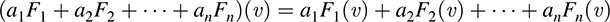
The mapping a₁F₁ is defined by (a₁F₁)(υ) = a₁F(υ). Hence, the theorem holds for n = 1. Accordingly, by induction,

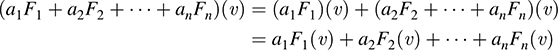
5.34.   Consider linear mappings F : R³ → R², G : R³ → R², H : R³ → R² defined by

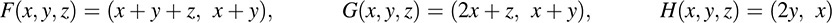
Show that F, G, H are linearly independent [as elements of Hom(R³; R²)].

Suppose, for scalars a; b; c ∈ K,

(Here 0 is the zero mapping.) For e₁ = (1; 0; 0) ∈ R³, we have 0(e₁) = (0; 0) and

Thus by (1), (a + 2b; a + b + c) = (0; 0) and so

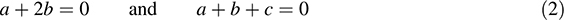
Similarly for e₂ = (0; 1; 0) ∈ R³, we have 0(e₂) = (0; 0) and

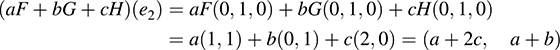
Thus,

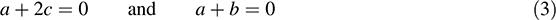
Using (2) and (3), we obtain

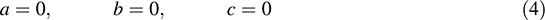
Because (1) implies (4), the mappings F, G, H are linearly independent.

5.35.   Let k be a nonzero scalar. Show that a linear map T is singular if and only if kT is singular. Hence, T is singular if and only if T is singular.

Suppose T is singular. Then T(υ) = 0 for some vector υ ≠ 0. Hence,

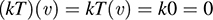
and so kT is singular.

Now suppose kT is singular. Then (kT)(w) = 0 for some vector w ≠ 0. Hence,

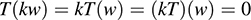
But k ≠ 0 and w ≠ 0 implies kw ≠ 0. Thus, T is also singular.

5.36.   Find the dimension d of:

(a) Hom(R³; R⁴), (b) Hom(R⁵; R³), (c) Hom(P₃(t); R²), (d) Hom(M_2;3; R⁴).

Use dim [Hom(V; U) = mn, where dim V = m and dim U = n.

(a) d = 3(4) = 12.

(b) d = 5(3) = 15.

(c) Because dim P₃(t) = 4, d = 4(2) = 8.

(d) Because dim M_2;3 = 6, d = 6(4) = 24.

5.38.   Prove Theorem 5.11. Suppose dim V = m and dim U = n. Then dim [Hom(V; U) = mn.

Suppose fv₁; …, v_mg is a basis of V and {u₁; …, u_n} is a basis of U. By Theorem 5.2, a linear mapping in Hom(V; U) is uniquely determined by arbitrarily assigning elements of U to the basis elements υ_i of V.We define

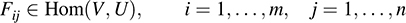
to be the linear mapping for which F_ij(υ_i) = u_j, and F_ij(υ_k) = 0 for k ≠ i. That is, F_ij maps υ_i into u_j and the other υ’s into 0. Observe that {F_ij} contains exactly mn elements; hence, the theorem is proved if we show that it is a basis of Hom(V; U).

Proof that {F_ij} generates Hom(V; U). Consider an arbitrary function F 2 Hom(V; U). Suppose F(υ₁) = w₁; F(υ₂) = w₂; …, F(υ_m) = w_m. Because w_k 2 U, it is a linear combination of the u’s; say,

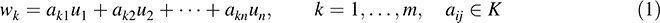
Consider the linear mapping 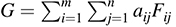. Because G is a linear combination of the F_ij, the proof that {F_ij} generates Hom(V; U) is complete if we show that F = G.

We now compute G(υ_k); k = 1; …, m. Because F_ij(υ_k) = 0 for k ≠ i and F_ki(υ_k) = u_i,

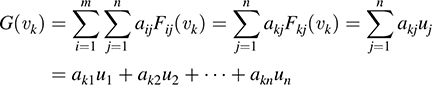
Thus, by (1), G(υ_k) = w_k for each k. But F(υ_k) = w_k for each k. Accordingly, by Theorem 5.2, F = G; hence, {F_ij} generates Hom(V; U).

Proof that {F_ij} is linearly independent. Suppose, for scalars c_ij ∈ K,

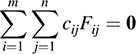
For υ_k; k = 1; …, m,

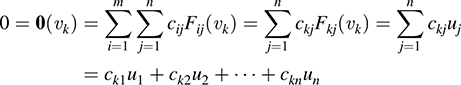
But the u_i are linearly independent; hence, for k = 1; …, m, we have c_k1 = 0; c_k2 = 0; …, c_kn = 0. In other words, all the c_ij = 0, and so {F_ij} is linearly independent.

5.38.   Prove Theorem 5.12: (i) G ° (F + F') = G ° F + G ° F'. (ii) (G + G') ° F = G ° F + G' ° F. (iii) k(G ° F) = (kG) ° F = G ° (kF).

(i) For every υ ∈ V,

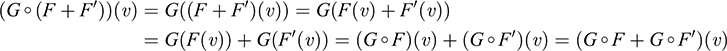
Thus, G (F + F') = G ° F + G ° F'.

(ii) For every υ ∈ V,

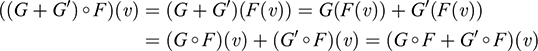
Thus, (G + G') ° F = G ° F + G' ° F.

(iii) For every υ ∈ V,

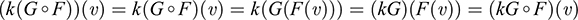
and

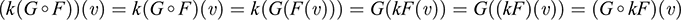
Accordingly, k(G ° F) = (kG) ° F = G ° (kF). (We emphasize that two mappings are shown to be equal by showing that each of them assigns the same image to each point in the domain.)

Algebra of Linear Maps

5.39.   Let F and G be the linear operators on R² defined by F(x; y) = (y; x) and G(x; y) = (0; x). Find formulas defining the following operators:

(a) F + G, (b) 2F – 3G, (c) FG, (d) GF, (e) F², (f) G².

(a) (F + G)(x; y) = F(x; y)+ G(x; y) = (y; x)+(0; x) = (y; 2x).

(b) (2F – 3G)(x; y) = 2F(x; y) 3G(x; y) = 2(y; x) 3(0; x) = (2y; x).

(c) (FG)(x; y) = F(G(x; y)) = F(0; x) = (x; 0).

(d) (GF)(x; y) = G(F(x; y)) = G(y; x) = (0; y).

(e) F²(x; y) = F(F(x; y)) = F(y; x) = (x; y). (Note that F² = I, the identity mapping.)

(f) G²(x; y) = G(G(x; y)) = G(0; x) = (0; 0). (Note that G² = 0, the zero mapping.)

5.40.   Consider the linear operator T on R³ defined by T(x; y; z) = (2x; 4x – y; 2x + 3y – z).

(a) Show that T is invertible. Find formulas for (b) T^-1, (c) T², (d) T^-2.

(a) Let W = Ker T. We need only show that T is nonsingular (i.e., that W = {0}). Set T(x; y; z)= (0; 0; 0), which yields

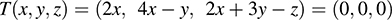
Thus, W is the solution space of the homogeneous system

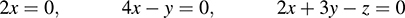
which has only the trivial solution (0, 0, 0). Thus, W = {0}. Hence, T is nonsingular, and so T is invertible.

(b) Set T(x; y; z) = (r; s; t) [and so T^-1(r; s; t) = (x; y; z)]. We have

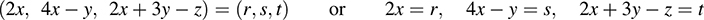
Solve for x, y, z in terms of r, s, t to get 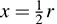, y = 2r – s, z = 7r – 3s – t. Thus,

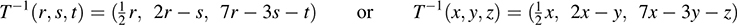
(c) Apply T twice to get

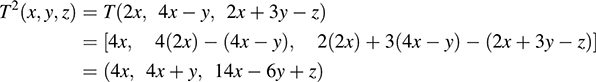
(d) Apply T

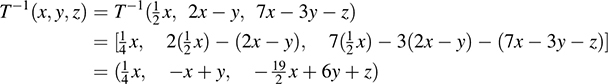
5.41.   Let V be of finite dimension and let T be a linear operator on V for which TR = I, for some operator R on V. (We call R a right inverse of T.)

(a) Show that T is invertible. (b) Show that R = T^-1.

(c) Give an example showing that the above need not hold if V is of infinite dimension.

(a) Let dim V = n. By Theorem 5.14, T is invertible if and only if T is onto; hence, T is invertible if and only if rank(T) = n. We have n = rank(I) = rank(TR) ≤ rank(T) ≤ n. Hence, rank(T) = n and T is invertible.

(b) TT^-1 = T^-1 T = I. Then R = IR = (T^-1T)R = T^-1 (TR) = T^-1 I = T^-1.

(c) Let V be the space of polynomials in t over K; say, p(t) = a₀ + a₁t + a₂t² +…+ a_st^s. Let T and R be the operators on V defined by

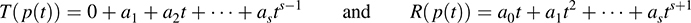
We have

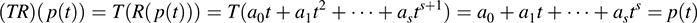
and so TR = I, the identity mapping. On the other hand, if k ∈ K and k ≠ 0, then

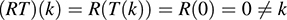
Accordingly, RT ≠ I.

5.42.   Let F and G be linear operators on R² defined by F(x; y) = (0; x) and G(x; y) = (x; 0). Show that

(a) GF = 0, the zero mapping, but FG ≠ 0.

(b) G² = G. (a) (GF)(x; y) = G(F(x; y)) = G(0; x) = (0; 0). Because GF assigns 0 = (0; 0) to every vector (x; y)in R²,it is the zero mapping; that is, GF = 0.

On the other hand, (FG)(x; y) = F(G(x; y)) = F(x; 0) = (0; x). For example, (FG)(2; 3) = (0; 2). Thus, FG ≠ 0, as it does not assign 0 = (0; 0) to every vector in R².

(b) For any vector (x; y) in R², we have G²(x; y)= G(G(x; y)) = G(x; 0)= (x; 0)= G(x; y). Hence, G² = G.

5.43.   Find the dimension of (a) A(R⁴), (b) A(P₂(t)), (c) A(M_2;3).

Use dim [A(V) = n² where dim V = n. Hence, (a) dim [A(R⁴) = 4² = 16, (b) dim [A(P₂(t)) = 3² = 9, (c) dim [A(M_2;3) = 6² = 36.

5.44.   Let E be a linear operator on V for which E² = E. (Such an operator is called a projection.) Let U be the image of E, and let W be the kernel. Prove

(a) If u ∈ U, then E(u) = u (i.e., E is the identity mapping on U).

(b) If E ≠ I, then E is singular—that is, E(υ) = 0 for some υ ≠ 0.

(c) V = U ⊕ W.

(a) If u ∈ U, the image of E, then E(υ) = u for some υ ∈ V. Hence, using E² = E, we have

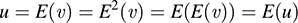
(b) If E ≠ I, then for some υ ∈ V, E(υ) = u, where υ ≠ u. By (i), E(u) = u. Thus,

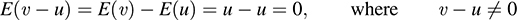
(c) We first show that V = U + W. Let υ ∈ V. Set u = E(υ) and w = υ – E(υ). Then

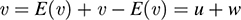
By deflnition, u = E(υ) ∈ U, the image of E. We now show that w ∈ W, the kernel of E,

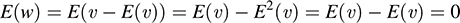
and thus w ∈ W. Hence, V = U + W.

We next show that U ∩ W = {0}. Let υ ∈ U ∩ W. Because υ ∈ U, E(υ) = υ by part (a). Because υ ∈ W, E(υ) = 0. Thus, υ = E(υ) = 0 and so U ∩ W = {0}.

The above two properties imply that V = U ⊕ W.

SUPPLEMENTARY PROBLEMS

Mappings

5.45.   Determine the number of different mappings from (a) {1; 2} into {1; 2; 3}; (b) {1; 2; …, r} into {1; 2; …, s}:

5.46.   Let f : R → R and g : R → R be defined by f (x) = x² + 3x + 1 and g(x) = 2x – 3. Find formulas defining the composition mappings: (a) f ° g; (b) g ° f ; (c) g ° g; (d) f ° f.

5.47.   For each mappings f : R → R find a formula for its inverse: (a) f (x) = 3x 7, (b) f (x) = x³ + 2.

5.48.   For any mapping f : A → B, show that 1_B ° f = f = f 1_A.

Linear Mappings

5.49.   Show that the following mappings are linear:

(a) F : R³ → R² defined by F(x; y; z) = (x + 2y – 3z; 4x – 5y + 6z).

(b) F : R² → R² defined by F(x; y) = (ax + by; cx + dy), where a, b, c, d belong to R.

5.50.   Show that the following mappings are not linear:

(a) F : R² → R² defined by F(x; y) = (x²; y²).

(b) F : R³ → R² defined by F(x; y; z) = (x + 1; y + z).

(c) F : R² → R² defined by F(x; y) = (xy; y).

(d) F : R³ → R² defined by F(x; y; z) = (|x|; y + z).

5.51.   Find F(a; b), where the linear map F : R² → R² is defined by F(1; 2) = (3; -1) and F(0; 1) = (2; 1).

5.52.   Find a 2 × 2 matrix A that maps

(a) (1; 3)^T and (1; 4)^T into (-2; 5)^T and (3; –1)^T, respectively.

(b) (2; -4)^T and (-1; 2)^T into (1; 1)^T and (1; 3)^T, respectively.

5.53.   Find a 2 × 2 singular matrix B that maps (1; 1)^T into (1; 3)^T.

5.54.   Let V be the vector space of real n-square matrices, and let M be a fixed nonzero matrix in V. Show that the first two of the following mappings T : V → V are linear, but the third is not:

(a) T(A) = MA, (b) T(A) = AM + MA, (c) T(A) = M + A.

5.55.   Give an example of a nonlinear map F : R² → R² such that F^-1 (0) = {0} but F is not one-to-one.

5.56.   Let F : R² → R² be defined by F(x; y) = (3x + 5y; 2x + 3y), and let S be the unit circle in R².(S consists of all points satisfying x² + y² = 1.) Find (a) the image F(S), (b) the preimage F^-1 (S).

5.57.   Consider the linear map G : R³ → R³ defined by G(x; y; z) = (x + y + z; y – 2z; y – 3z) and the unit sphere S₂ in R³, which consists of the points satisfying x² + y² + z² = 1. Find (a) G(S₂), (b) G^-1 (S₂).

5.58.   Let H be the plane x + 2y 3z = 4 in R³ and let G be the linear map in Problem 5.57. Find (a) G(H), (b) G^-1(H).

5.59.   Let W be a subspace of V. The inclusion map, denoted by i : W ,! V, is defined by i(w) = w for every w ∈ W. Show that the inclusion map is linear.

5.60.   Suppose F : V → U is linear. Show that F(-υ) = -F(υ).

Kernel and Image of Linear Mappings

5.61.   For each linear map F find a basis and the dimension of the kernel and the image of F:

(a) F : R³ → R³ defined by F(x; y; z) = (x + 2y – 3z; 2x + 5y – 4z; x + 4y + z),

(b) F : R⁴ → R³ defined by F(x; y; z; t) = (x + 2y + 3z + 2t; 2x + 4y + 7z + 5t; x + 2y + 6z + 5t).

5.62.   For each linear map G, find a basis and the dimension of the kernel and the image of G:

(a) G : R³ → R² defined by G(x; y; z) = (x + y + z; 2x + 2y + 2z),

(b) G : R³ → R² defined by G(x; y; z) = (x + y; y + z),

(c) G : R⁵ → R³ defined by

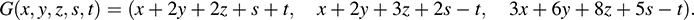
5.63.   Each of the following matrices determines a linear map from R⁴ into R³:

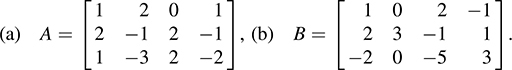
Find a basis as well as the dimension of the kernel and the image of each linear map.

5.64.   Find a linear mapping F : R³ → R³ whose image is spanned by (1, 2, 3) and (4, 5, 6).

5.65.   Find a linear mapping G : R⁴ → R³ whose kernel is spanned by (1, 2, 3, 4) and (0, 1, 1, 1).

5.66.   Let V = P₁₀(t), the vector space of polynomials of degree ≤ 10. Consider the linear map D⁴ denotes the fourth derivative d⁴(f)=dt⁴. Find a basis and the dimension of (a) the image of D⁴; (b) the kernel of D⁴.

5.67.   Suppose F : V → U is linear. Show that (a) the image of any subspace of V is a subspace of U; (b) the preimage of any subspace of U is a subspace of V.

5.68.   Show that if F : V → U is onto, then dim U ≤ dim V. Determine all linear maps F : R³ → R⁴ that are onto.

5.69.   Consider the zero mapping 0 : V → U defined by 0(υ) = 0; ∀ υ ∈ V. Find the kernel and the image of 0.

Operations with linear Mappings

5.70.   Let F : R³ → R² and G : R³ → R² be defined by F(x; y; z) = (y; x + z) and G(x; y; z) = (2z; x – y). Find formulas defining the mappings F + G and 3F – 2G.

5.71.   Let H : R² → R² be defined by H(x; y) = (y; 2x). Using the maps F and G in Problem 5.70, find formulas defining the mappings: (a) H ° F and H ° G, (b) F ° H and G ° H, (c) H ° (F + G) and H ° F + H ° G.

5.72.   Show that the following mappings F, G, H are linearly independent:

(a) F; G; H 2 Hom(R²; R²) defined by F(x; y) = (x; 2y), G(x; y) = (y; x + y), H(x; y) = (0; x),

(b) F; G; H 2 Hom(R³; R) defined by F(x; y; z) = x + y + z, G(x; y; z) = y + z, H(x; y; z) = x – z.

5.73.   For F; G ∈ Hom(V; U), show that rank(F + G) ≤ rank(F)+ rank(G). (Here V has finite dimension.)

5.74.   Let F : V → U and G : U → V be linear. Show that if F and G are nonsingular, then G ° F is nonsingular. Give an example where G ° F is nonsingular but G is not. [Hint: Let dim V < dim U.]

5.75.   Find the dimension d of (a) Hom(R²; R⁸), (b) Hom(P₄(t); R³), (c) Hom(M_2;4; P₂(t)).

5.76.   Determine whether or not each of the following linear maps is nonsingular. If not, find a nonzero vector v whose image is 0; otherwise find a formula for the inverse map:

(a) F : R³ → R³ defined by F(x; y; z) = (x + y + z; 2x + 3y + 5z; x + 3y + 7z),

(b) G : R³ → P₂(t) defined by G(x; y; z) = (x + y)t² +(x + 2y + 2z)t + y + z,

(c) H : R² → P₂(t) defined by H(x; y) = (x + 2y)t² +(x y)t + x + y.

5.77.   When can dim [Hom(V; U) = dim V?

Algebra of Linear Operators

5.78.   Let F and G be the linear operators on R² defined by F(x; y) = (x + y; 0) and G(x; y) = (y; x). Find formulas defining the linear operators: (a) F + G, (b) 5F – 3G, (c) FG, (d) GF, (e) F², (f) G².

5.79.   Show that each linear operator T on R² is nonsingular and find a formula for T^-1, where

(a) T(x; y) = (x + 2y; 2x + 3y), (b) T(x; y) = (2x 3y; 3x 4y).

5.80.   Show that each of the following linear operators T on R³ is nonsingular and find a formula for T^-1, where

(a) T(x; y; z) = (x 3y 2z; y – 4z; z); (b) T(x; y; z) = (x + z; x – y; y).

5.81.   Find the dimension of A(V), where (a) V = R⁷, (b) V = P₅(t), (c) V = M_3;4.

5.82.   Which of the following integers can be the dimension of an algebra A(V) of linear maps: 5, 9, 12, 25, 28, 36, 45, 64, 88, 100?

5.83.   Let T be the linear operator on R² defined by T(x; y) = (x + 2y; 3x + 4y). Find a formula for f (T), where

(a) f (t) = t² + 2t 3, (b) f (t) = t² – 5t – 2.

Miscellaneous Problems

5.84.   Suppose F : V → U is linear and k is a nonzero scalar. Prove that the maps F and kF have the same kernel and the same image.

5.85.   Suppose F and G are linear operators on V and that F is nonsingular. Assume that V has finite dimension. Show that rank(FG) = rank(GF) = rank(G).

5.86.   Suppose V has finite dimension. Suppose T is a linear operator on V such that rank(T²) = rank(T). Show that Ker T ∩ Im T = {0}.

5.87.   Suppose V = U ⊕ W. Let E₁ and E₂ be the linear operators on V defined by E₁(υ) = u, E₂(υ) = w, where υ = u + w, u ∈ U, w ∈ W. Show that (a) E²₁ = E₁ and E²₂ = E₂ (i.e., that E₁ and E₂ are projections); (b) E₁ + E₂ = I, the identity mapping; (c) E₁E₂ = 0 and E₂E₁ = 0.

5.88.   Let E₁ and E₂ be linear operators on V satisfying parts (a), (b), (c) of Problem 5.88. Prove

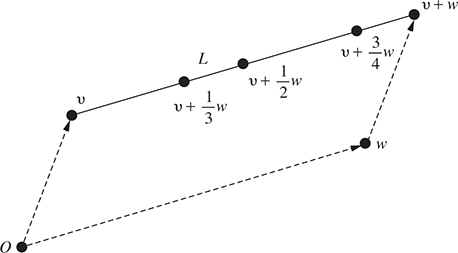
5.89.   Let v and w be elements of a real vector space V. The line segment L from v to v + w is defined to be the set of vectors v + tw for 0 ≤ t ≤ 1. (See Fig. 5.6.)

(a) Show that the line segment L between vectors v and u consists of the points:

(b) Let F : V → U be linear. Show that the image F(L) of a line segment L in V is a line segment in U.

Figure 5-6

5.90.   Let F : V → U be linear and let W be a subspace of V. The restriction of F to W is the map F|W : W → U defined by F|W(υ) = F(υ) for every υ in W. Prove the following:

(a) F|W is linear; (b) Ker(F|W) = (Ker F) ∩ W; (c) Im(F|W) = F(W).

5.91.   A subset X of a vector space V is said to be convex if the line segment L between any two points (vectors) P; Q ∈ X is contained in X. (a) Show that the intersection of convex sets is convex; (b) suppose F : V → U is linear and X is convex. Show that F(X) is convex.

ANSWERS TO SUPPLEMENTARY PROBLEMS

5.45.   (a) 3² = 9; (b) s^r

5.46.   (a) (f ° g)(x) = 4x² + 1, (b) (g ° f)(x) = 2x² + 6x – 1, (c) (g ° g)(x) = 4x – 9,

(d) (f ° f)(x) = x⁴ + 6x³ + 14x² + 15x + 5

5.47.   

5.49.   F(x; y; z) = A(x; y; z)^T, where (a)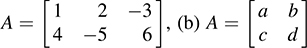

5.50.   (a) u = (2; 2), k = 3; then F(ku) = (36; 36) but kF(u) = (12; 12); (b) F(0) ≠ 0;

(c) u = (1; 2), υ = (3; 4); then F(u + υ) = (24; 6) but F(u)+ F(υ) = (14; 6);

(d) u = (1; 2; 3), k = 2; then F(ku) = (2; 10) but kF(u) = (2; 10).

5.51.   F(-a; b) = (a + 2b; -3a + b)

5.52. 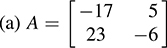  ; (b) None. (2; 4) and (1; 2) are linearly dependent but not (1, 1) and (1, 3).

5.53. 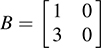   [Hint: Send (0; 1)^T into (0; 0)^T.]

5.55.   F(x; y) = (x²; y²)

5.56.   (a) 13x² – 42xy + 34y² = 1, (b) 13x² + 42xy + 34y² = 1

5.57.   (a) x² – 8xy + 26y² + 6xz – 38yz + 14z² = 1, (b) x² + 2xy + 3y² + 2xz – 8yz + 14z² = 1

5.58.   (a) x – y + 2z = 4, (b) x + 6z = 4

5.61.   (a) dim(Ker F) = 1, {(7; 2; 1)}; dim(Im F) = 2, {(1; 2; 1); (0; 1; 2)};

(b) dim(Ker F) = 2, {(2; 1; 0; 0); (1; 0; 1; 1)}; dim(Im F) = 2, {(1; 2; 1); (0; 1; 3)}

5.62.   (a) dim(Ker G) = 2, {(1; 0; 1); (1; 1; 0)}; dim(Im G) = 1, {(1; 2)};

(b) dim(Ker G) = 1, {(1; 1; 1)}; Im G = R², {(1; 0); (0; 1)};

(c) dim(Ker G) = 3, {(2; 1; 0; 0; 0); (1; 0; 1; 1; 0); (5; 0; 2; 0; 1)}; dim(Im G) = 2, {(1; 1; 3); (0; 1; 2)}

5.63.   (a) dim(Ker A) = 2, {(4; 2; 5; 0); (1; 3; 0; 5)}; dim(Im A) = 2, {(1; 2; 1); (0; 1; 1)};

(b) dim(Ker B) = 1, {(1; ²₃, 1; 1)}; Im B = R³

5.64.   F(x; y; z) = (x + 4y; 2x + 5y; 3x + 6y)

5.65.   F(x; y; z; t) = (x + y – z; 2x + y – t; 0)

5.66.   (a) {1; t; t²; …, t⁶}, (b) {1; t; t²; t³}

5.68.   None, because dim R⁴ > dim R³:

5.69.   Ker 0 = V, Im 0 = {0}

5.70.   (F + G)(x; y; z) = (y + 2z; 2x y + z), (3F – 2G)(x; y; z) = (3y – 4z; x + 2y + 3z)

5.71.   (a) (H ° F)(x; y; z) = (x + z; 2y), (H ° G)(x; y; z) = (x y; 4z);

(b) not defined; (c) (H ° (F + G))(x; y; z) = (H ° F + H ° G)(x; y; z) = (2x – y + z; 2y + 4z)

5.74.   F(x; y) = (x; y; y); G(x; y; z) = (x; y)

5.75.   (a) 16, (b) 15, (c) 24

5.76.   (a) υ = (2; 3; 1); (b) G^-1 (at² + bt + c) = (b – 2c; a – b + 2c; a + b – c);

(c) H is nonsingular, but not invertible, because dim P₂(t) > dim R².

5.77.   dim U = 1; that is, U = K.

5.78.   (a) (F + G)(x; y) = (x; x); (b) (5F 3G)(x; y) = (5x + 8y; 3x); (c) (FG)(x; y) = (x y; 0);

(d) (GF)(x; y) = (0; x + y); (e) F²(x; y) = (x + y; 0) (note that F² = F); (f) G²(x; y) = (x; – y).

[Note that G² + I = 0; hence, G is a zero of f (t) = t² + 1.]

5.79.   (a) T^-1 (x; y) = (3x + 2y; 2x y), (b) T^-1 (x; y) = (4x + 3y; 3x + 2y)

5.80.   (a) T^-1 (x; y; z) = (x + 3y + 14z; y – 4z; z), (b) T^-1 (x; y; z) = (y + z; y; x y – z)

5.81.   (a) 49, (b) 36, (c) 144

5.82.   Squares: 9, 25, 36, 64, 100

5.83.   (a) T(x; y) = (6x + 14y; 21x + 27y); (b) T(x; y) = (0; 0)—that is, f (T) = 0