Bilinear, Quadratic, and Hermitian Forms
12.1 Introduction
This chapter generalizes the notions of linear mappings and linear functionals. Specifically, we introduce the notion of a bilinear form. These bilinear maps also give rise to quadratic and Hermitian forms. Although quadratic forms were discussed previously, this chapter is treated independently of the previous results.
Although the field K is arbitrary, we will later specialize to the cases K = R and K = C. Furthermore, we may sometimes need to divide by 2. In such cases, we must assume that 1 + 1 ≠ 0, which is true when K = R or K = C.
12.2 Bilinear Forms
Let V be a vector space of finite dimension over a field K. A bilinear form on V is a mapping f:V × V → K such that, for all a, b ∈ K and all ui, νi ∈ V:
(i) f(au1 + bu2, v) = af(u1, v) + bf(u2, v),
(ii) f (u; av1 + bv2) = af (u; v1)+ bf (u; v2)
We express condition (i) by saying f is linear in the first variable, and condition (ii) by saying f is linear in the second variable.
(a) Let f be the dot product on Rn; that is, for u = (ai) and v = (bi),
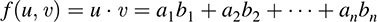
Then f is a bilinear form on Rn. (In fact, any inner product on a real vector space V is a bilinear form on V.)
(b) Let ϕ and σ be arbitrarily linear functionals on V. Let f:V × V → K be defined by f(u; v) = ϕ(u)σ(v). Then f is a bilinear form, because f and σ are each linear.
(c) Let A = [aij] be any n × n matrix over a field K. Then A may be identified with the following bilinear form F on Kn, where X = [x]i and Y = [y]i are column vectors of variables:
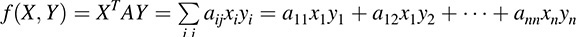
The above formal expression in the variables xi, yi is termed the bilinear polynomial corresponding to the matrix A. Equation (12.1) shows that, in a certain sense, every bilinear form is of this type.
Space of Bilinear Forms
Let B(V) denote the set of all bilinear forms on V. A vector space structure is placed on B(V), where for any f, g ∈ B(V) and any k ∈ K, we define f + g and kf as follows:
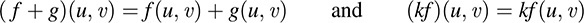
The following theorem (proved in Problem 12.4) applies.
THEOREM 12.1: Let V be a vector space of dimension n over K. Let {ϕ1, … ; ϕn} be any basis of the dual space V*. Then { fij : i; j = 1; … ; n} is a basis of B(V), where fij is defined by fij(u; v) = ϕi(u)ϕj(v). Thus, in particular, dim B(V) = n2.
12.3 Bilinear Forms and Matrices
Let f be a bilinear form on V and let S = {u1, … ; un} be a basis of V. Suppose u; v ∈ V and
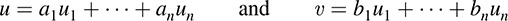
Then
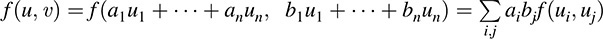
Thus, f is completely determined by the n2 values f(ui, uj).
The matrix A = [aij] where aij = f(ui, uj) is called the matrix representation of f relative to the basis S or, simply, the “matrix of f in S.” It “represents” f in the sense that, for all u, v ∈ V,
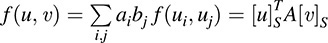
[As usual, [u]s denotes the coordinate (column) vector of u in the basis S.]
Change of Basis, Congruent Matrices
We now ask, how does a matrix representing a bilinear form transform when a new basis is selected? The answer is given in the following theorem (proved in Problem 12.5).
THEOREM 12.2: Let P be a change-of-basis matrix from one basis S to another basis S0. If A is the matrix representing a bilinear form f in the original basis S, then B = PTAP is the matrix representing f in the new basis S0.
The above theorem motivates the following definition.
DEFINITION: A matrix B is congruent to a matrix A, written B ≃ A, if there exists a nonsingular matrix P such that B = PTAP.
Thus, by Theorem 12.2, matrices representing the same bilinear form are congruent. We remark that congruent matrices have the same rank, because P and PT are nonsingular; hence, the following definition is well defined.
DEFINITION: The rank of a bilinear form f on V, written rank(f), is the rank of any matrix representation of f. We say f is degenerate or nondegenerate according to whether rank(f) < dim V or rank(f) = dim V.
12.4 Alternating Bilinear Forms
Let f be a bilinear form on V. Then f is called
(i) alternating if f(v, v) = 0 for every v ∈ V;
(ii) skew-symmetric if f(u, v) = –f(v, u) for every u, v ∈ V.
Now suppose (i) is true. Then (ii) is true, because, for any u; v; ∈ V,
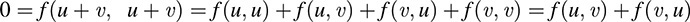
On the other hand, suppose (ii) is true and also 1 + 1 ≠ 0. Then (i) is true, because, for every v ∈ V, we have f(v, v) = f–(v, v). In other words, alternating and skew-symmetric are equivalent when 1 + 1 ≠ 0.
The main structure theorem of alternating bilinear forms (proved in Problem 12.23) is as follows.
THEOREM 12.3: Let f be an alternating bilinear form on V. Then there exists a basis of V in which f is represented by a block diagonal matrix M of the form
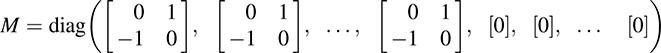
Moreover, the number of nonzero blocks is uniquely determined by f [because it is equal to 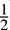 rank(f).
rank(f).
In particular, the above theorem shows that any alternating bilinear form must have even rank.
12.5 Symmetric Bilinear Forms, Quadratic Forms
This section investigates the important notions of symmetric bilinear forms and quadratic forms and their representation by means of symmetric matrices. The only restriction on the field K is that 1 + 1 ≠ 0. In Section 12.6, we will restrict K to be the real field R, which yields important special results.
Symmetric Bilinear Forms
Let f be a bilinear form on V. Then f is said to be symmetric if, for every u, v ∈ V,
f(u, v) = f(v, u)
One can easily show that f is symmetric if and only if any matrix representation A of f is a symmetric matrix.
The main result for symmetric bilinear forms (proved in Problem 12.10) is as follows. (We emphasize that we are assuming that 1 + 1 ≠ 0.)
THEOREM 12.4: Let f be a symmetric bilinear form on V. Then V has a basis {v1, … ; vn} in which f is represented by a diagonal matrix—that is, where f(vi, vj) = 0 for i ≠ j.
THEOREM 12.4: (Alternative Form) Let A be a symmetric matrix over K. Then A is congruent to a diagonal matrix; that is, there exists a nonsingular matrix P such that PTAP is diagonal.
Diagonalization Algorithm
Recall that a nonsingular matrix P is a product of elementary matrices. Accordingly, one way of obtaining the diagonal form D = PTAP is by a sequence of elementary row operations and the same sequence of elementary column operations. This same sequence of elementary row operations on the identity matrix I will yield PT. This algorithm is formalized below.
ALGORITHM 12.1: (Congruence Diagonalization of a Symmetric Matrix) The input is a symmetric matrix A = [aij] of order n.
Step 1. Form the n × 2n (block) matrix M = [A1, I], where A1 = A is the left half of M and the identity matrix I is the right half of M.
Step 2. Examine the entry a11. There are three cases.
Case I: a11 ≠ 0. (Use a11 as a pivot to put 0’s below a11 in M and to the right of a11 in A1:) For i = 2; … ; n:
(a) Apply the row operation “Replace Ri by –ai1R1 + a11Ri.”
(b) Apply the corresponding column operation “Replace Ci by ai1C1 + a11Ci.”
These operations reduce the matrix M to the form

Case II: a11 = 0 but akk ≠ 0, for some k > 1.
(a) Apply the row operation “Interchange R1 and Rk.”
(b) Apply the corresponding column operation “Interchange C1 and Ck.”
(These operations bring akk into the first diagonal position, which reduces the matrix to Case I.)
Case III: All diagonal entries aii = 0 but some aij ≠ 0.
(a) Apply the row operation “Replace Ri by Rj + Ri.”
(b) Apply the corresponding column operation “Replace Ci by Cj + Ci.”
(These operations bring 2aij into the ith diagonal position, which reduces the matrix to Case II.)
Thus, M is finally reduced to the form (*), where A2 is a symmetric matrix of order less than A.
Step 3. Repeat Step ∈ with each new matrix Ak (by neglecting the first row and column of the preceding matrix) until A is diagonalized. Then M is transformed into the form M0 = [D, Q], where D is diagonal.
Step 4. Set P = QT. Then D = PTAP.
Remark 1: We emphasize that in Step 2, the row operations will change both sides of M, but the column operations will only change the left half of M.
Remark 2: The condition 1 + 1 ≠ 0 is used in Case III, where we assume that 2aij ≠ 0 when aij ≠ 0.
The justification for the above algorithm appears in Problem 12.9.
EXAMPLE 12.2 Let 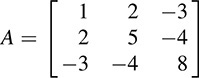 . Apply Algorithm 9.1 to find a nonsingular matrix P such that D = PTAP is diagonal.
. Apply Algorithm 9.1 to find a nonsingular matrix P such that D = PTAP is diagonal.
First form the block matrix M = [A, I] that is, let
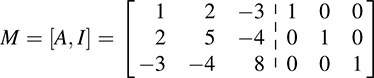
Apply the row operations “Replace R2 by –2R1 + R2” and “Replace R3 by 3R1 + R3” to M, and then apply the corresponding column operations “Replace C2 by –2C1 + C2” and “Replace C3 by 3C1 + C3” to obtain

Next apply the row operation “Replace R3 by 2R2 + R3” and then the corresponding column operation “Replace C3 by 2C2 + C3” to obtain
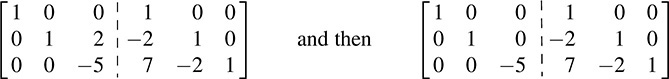
Now A has been diagonalized. Set
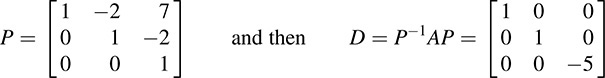
We emphasize that P is the transpose of the right half of the final matrix.
Quadratic Forms
We begin with a definition.
DEFINITION A: A mapping q:V → K is a quadratic form if q(v) = f(v, v) for some symmetric bilinear form f on V.
If 1 + 1 ≠ 0 in K, then the bilinear form f can be obtained from the quadratic form q by the following polar form of f:
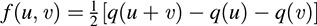
Now suppose f is represented by a symmetric matrix A = [aij], and 1 + 1 ≠ 0. Letting X = [x]i denote a column vector of variables, q can be represented in the form
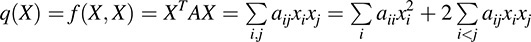
The above formal expression in the variables xi is also called a quadratic form. Namely, we have the following second definition.
DEFINITION B: A quadratic form q in variables x1, x2, … ; xn is a polynomial such that every term has degree two; that is,
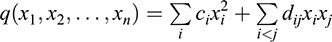
Using 1 + 1 ≠ 0, the quadratic form q in Definition B determines a symmetric matrix A = [aij] where 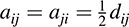 . Thus, Definitions A and B are essentially the same. If the matrix representation A of q is diagonal, then q has the diagonal representation
. Thus, Definitions A and B are essentially the same. If the matrix representation A of q is diagonal, then q has the diagonal representation
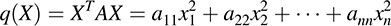
That is, the quadratic polynomial representing q will contain no “cross product” terms. Moreover, by Theorem 12.4, every quadratic form has such a representation (when 1 + 1 ≠ 0).
12.6 Real Symmetric Bilinear Forms, Law of Inertia
This section treats symmetric bilinear forms and quadratic forms on vector spaces V over the real field R. The special nature of R permits an independent theory. The main result (proved in Problem 12.14) is as follows.
THEOREM 12.5: Let f be a symmetric form on V over R. Then there exists a basis of V in which f is represented by a diagonal matrix. Every other diagonal matrix representation of f has the same number p of positive entries and the same number n of negative entries.
The above result is sometimes called the Law of Inertia or Sylvester’s Theorem. The rank and signature of the symmetric bilinear form f are denoted and defined by
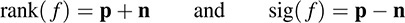
These are uniquely defined by Theorem 12.5.
A real symmetric bilinear form f is said to be
(i) positive definite if q(v) = f(v, v) > 0 for every v ≠ 0,
(ii) nonnegative semidefinite if q(v) = f(v; v) ≥ 0 for every v.
EXAMPLE 12.3 Let f be the dot product on Rn. Recall that f is a symmetric bilinear form on Rn. We note that f is also positive definite. That is, for any u = (ai) ≠ 0 Rn
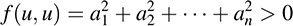
Section 12.5 and Chapter 13 tell us how to diagonalize a real quadratic form q or, equivalently, a real symmetric matrix A by means of an orthogonal transition matrix P. If P is merely nonsingular, then q can be represented in diagonal form with only 1’s and 1’s as nonzero coefficients. Namely, we have the following corollary.
COROLLARY 12.6: Any real quadratic form q has a unique representation in the form
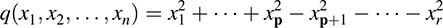
where r = p + n is the rank of the form.
COROLLARY 12.6: (Alternative Form) Any real symmetric matrix A is congruent to the unique diagonal matrix
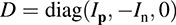
where r = p + n is the rank of A.
12.7 Hermitian Forms
Let V be a vector space of finite dimension over the complex field C. A Hermitian form on V is a mapping f:V × V → C such that, for all a; b ∈ C and all ui, v ∈ V,
(i) f(au1 + bu2, v) = af(u1, v)+ bf (u2, v),
(ii) 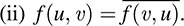
(As usual, k denotes the complex conjugate of k ∈ C.)
Using (i) and (ii), we get
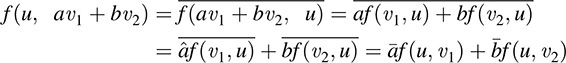
That is,
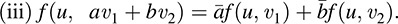
As before, we express condition (i) by saying f is linear in the first variable. On the other hand, we express condition (iii) by saying f is “conjugate linear” in the second variable. Moreover, condition (ii) tells us that 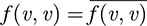 , and hence, f(v,v) is real for every v ∈ V.
, and hence, f(v,v) is real for every v ∈ V.
The results of Sections 12.5 and 12.6 for symmetric forms have their analogues for Hermitian forms. Thus, the mapping q : V ℯ C, defined by q(v) = f(v, v), is called the Hermitian quadratic form or complex quadratic form associated with the Hermitian form f. We can obtain f from q by the polar form
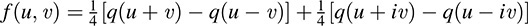
Now suppose S = {u1, … , un} is a basis of V. The matrix H = [h]ij where hij = f(ui, uj) is called the matrix representation of f in the basis S. By (ii), 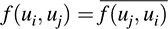 ; hence, H is Hermitian and, in particular, the diagonal entries of H are real. Thus, any diagonal representation of f contains only real entries.
; hence, H is Hermitian and, in particular, the diagonal entries of H are real. Thus, any diagonal representation of f contains only real entries.
The next theorem (to be proved in Problem 12.47) is the complex analog of Theorem 12.5 on real symmetric bilinear forms.
THEOREM 12.7: Let f be a Hermitian form on V over C. Then there exists a basis of V in which f is represented by a diagonal matrix. Every other diagonal matrix representation of f has the same number p of positive entries and the same number n of negative entries.
Again the rank and signature of the Hermitian form f are denoted and defined by
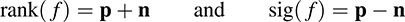
These are uniquely defined by Theorem 12.7.
Analogously, a Hermitian form f is said to be
(i) positive definite if q(v) = f(v, v) > 0 for every v ≠ 0,
(ii) nonnegative semidefinite if q(v) = f(v, v) ≥ 0 for every v.
EXAMPLE 12.4 Let f be the dot product on Cn; that is, for any u = (zi) and v = (wi) in Cn,
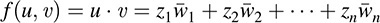
Then f is a Hermitian form on Cn. Moreover, f is also positive definite, because, for any u = (zi) ≠ 0 in Cn,
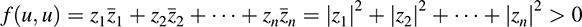
SOLVED PROBLEMS
Bilinear Forms
12.1. Let u = (x1, x2, x3) and v = (y1, y2, y3). Express f in matrix notation, where
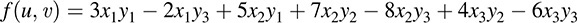
Let A = [aij], where aij is the coefficient of xiyj. Then
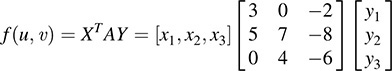
12.2. Let A be an n × n matrix over K. Show that the mapping f defined by f(X; Y) = XTAY is a bilinear form on Kn.
For any a, b ∈ K and any Xi Yi ∈ Kn,
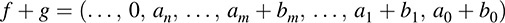
Hence, f is linear in the first variable. Also,
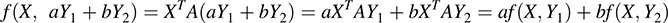
Hence, f is linear in the second variable, and so f is a bilinear form on Kn.
12.3. Let f be the bilinear form on R2 defined by

(a) Find the matrix A of f in the basis {u1 = (1, 0); u2 = (1, 1)}.
(b) Find the matrix B of f in the basis {v1 = (2, 1); v2 = (1, 1)}.
(c) Find the change-of-basis matrix P from the basis {ui} to the basis {vi}, and verify that B = PTAP.
(a) Set A = [aij], where aij = f(ui, uj). This yields

Thus, 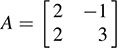 is the matrix of f in the basis fu1, u2}.
is the matrix of f in the basis fu1, u2}.
(b) Set B = [bij] , where bij = f(vi, vj). This yields

Thus, 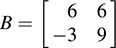 is the matrix of f in the basis {v1, v2}.
is the matrix of f in the basis {v1, v2}.
(c) Writing v1 and v2 in terms of the ui yields v1 = u1 + u2 and v2 = 2u1 u2. Then

and 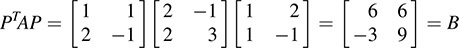
12.4. Prove Theorem 12.1: Let V be an n-dimensional vector space over K. Let {ϕ1, … ; ϕn} be any basis of the dual space V*. Then { fij : i, j = 1; … ; n} is a basis of B(V), where fij is defined by fij(u, v) = fi(u)fj(v). Thus, dim B(V) = n2.
Let {u1, … ; un} be the basis of V dual to {ϕi}. We first show that {fij} spans B(V). Let f ∈ B(V) and suppose f(ui, uj) = aij: We claim that f = Σi;j aij fij. It suffices to show that
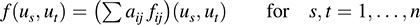
We have
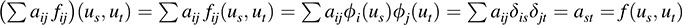
as required. Hence, {fij} spans B(V). Next, suppose P aijfij = 0. Then for s; t = 1; … ; n, 0 =
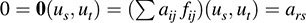
The last step follows as above. Thus, {fij} is independent, and hence is a basis of B(V).
12.5. Prove Theorem 12.2. Let P be the change-of-basis matrix from a basis S to a basis S′. Let A be the matrix representing a bilinear form in the basis S. Then B = PTAP is the matrix representing f in the basis S0.
Let u; v ∈ V. Because P is the change-of-basis matrix from S to S0, we have P[u]S0 = [u]S and also P[v]S0 = [v]S, hence, 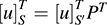 . Thus,
. Thus,
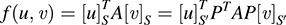
Because u and v are arbitrary elements of V, PTAP is the matrix of f in the basis S0.
Symmetric Bilinear Forms, Quadratic Forms
12.6. Find the symmetric matrix that corresponds to each of the following quadratic forms:
(a) q(x; y; z) = 3x2 + 4xy – y2 + 8xz – 6yz + z2,
(b) q0(x; y; z) = 3x2 + xz × 2yz, (c) q00(x; y; z) = 2x2 – 5y2 – 7z2
The symmetric matrix A = [aij] that represents q(x1, … ; xn) has the diagonal entry aii equal to the coefficient of the square term x2i and the nondiagonal entries aij and aji each equal to half of the coefficient of the cross-product term xixj. Thus,
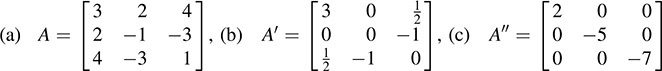
The third matrix A″ is diagonal, because the quadratic form q″ is diagonal; that is, q″ has no cross-product terms.
12.7. Find the quadratic form q(X) that corresponds to each of the following symmetric matrices:
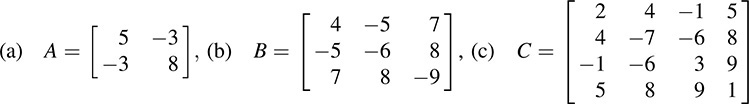
The quadratic form q(X) that corresponds to a symmetric matrix M is defined by q(X) = XTMX, where X = [x]i is the column vector of unknowns.
(a) Compute as follows:
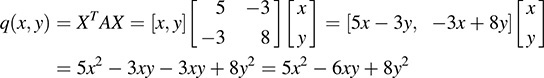
As expected, the coefficient 5 of the square term x2 and the coefficient 8 of the square term y2 are the diagonal elements of A, and the coefficient 6 of the cross-product term xy is the sum of the nondiagonal elements 3 and 3 of A (or twice the nondiagonal element 3, because A is symmetric).
(b) Because B is a three-square matrix, there are three unknowns, say x; y; z or x1, x2, x3. Then
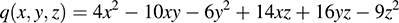
or
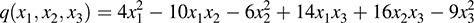
Here we use the fact that the coefficients of the square terms 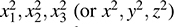 are the respective diagonal elements 4; –6; –9 of B, and the coefficient of the cross-product term xixj is the sum of the nondiagonal elements bij and bji (or twice bij, because bij = bji).
are the respective diagonal elements 4; –6; –9 of B, and the coefficient of the cross-product term xixj is the sum of the nondiagonal elements bij and bji (or twice bij, because bij = bji).
(c) Because C is a four-square matrix, there are four unknowns. Hence,
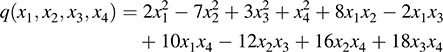
12.8. Let 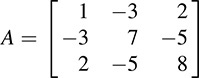 Apply Algorithm 12.1 to find a nonsingular matrix P such that D = PTAP is diagonal, and find sig(A), the signature of A.
Apply Algorithm 12.1 to find a nonsingular matrix P such that D = PTAP is diagonal, and find sig(A), the signature of A.
First form the block matrix M = [A, I] :
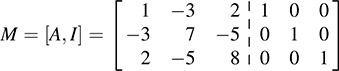
Using a11 = 1 as a pivot, apply the row operations “Replace R2 by 3R1 + R2” and “Replace R3 by 2R1 + R3” to M and then apply the corresponding column operations “Replace C2 by 3C1 + C2” and “Replace C3 by 2C1 + C3” to A to obtain

Next apply the row operation “Replace R3 by R2 + 2R3” and then the corresponding column operation “Replace C3 by C2 + 2C3” to obtain

Now A has been diagonalized and the transpose of P is in the right half of M. Thus, set

Note D has p = ∈ positive and n = 1 negative diagonal elements. Thus, the signature of A is sig(A) = p – n = 2 ∈ 1 = 1.
12.9. Justify Algorithm 12.1, which diagonalizes (under congruence) a symmetric matrix A.
Consider the block matrix M = [A, I]. The algorithm applies a sequence of elementary row operations and the corresponding column operations to the left side of M, which is the matrix A. This is equivalent to premultiplying A by a sequence of elementary matrices, say, E1, E2, … ; Er, and postmultiplying A by the transposes of the Ei. Thus, when the algorithm ends, the diagonal matrix D on the left side of M is equal to
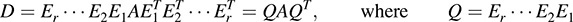
On the other hand, the algorithm only applies the elementary row operations to the identity matrix I on the right side of M. Thus, when the algorithm ends, the matrix on the right side of M is equal to
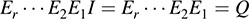
Setting P = QT, we get D = PTAP, which is a diagonalization of A under congruence.
12.10. Prove Theorem 12.4: Let f be a symmetric bilinear form on V over K (where 1 + 1 ≠ 0). Then V has a basis in which f is represented by a diagonal matrix.
Algorithm 12.1 shows that every symmetric matrix over K is congruent to a diagonal matrix. This is equivalent to the statement that f has a diagonal representation.
12.11. Let q be the quadratic form associated with the symmetric bilinear form f. Verify the polar identity 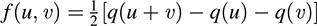 . (Assume that 1 + 1 ≠ 0.)
. (Assume that 1 + 1 ≠ 0.)
We have
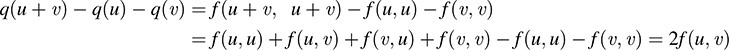
If 1 + 1 ≠ 0, we can divide by 2 to obtain the required identity.
12.12. Consider the quadratic form q(x, y) = 3x2 + 2xy y2 and the linear substitution

(a) Rewrite q(x, y) in matrix notation, and find the matrix A representing q(x, y).
(b) Rewrite the linear substitution using matrix notation, and find the matrix P corresponding to the substitution.
(c) Find q(s, t) using direct substitution.
(d) Find q(s; t) using matrix notation.
(a) Here 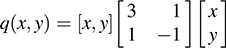 . Thus,
. Thus, 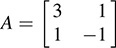 and q(x) = XTAX, where X = [x,y]T.
and q(x) = XTAX, where X = [x,y]T.
(b) Here xy 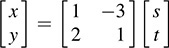 . Thus,
. Thus, 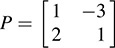 and
and 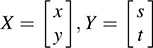
(c) Substitute for x and y in q to obtain
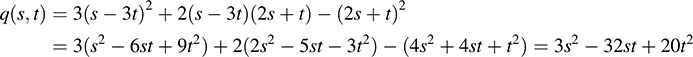
(d) Here q(X) = XTAX and X = PY. Thus, XT = YTPT. Therefore,
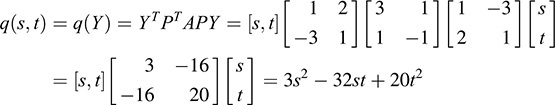
[As expected, the results in parts (c) and (d) are equal.]
12.13. Consider any diagonal matrix A = diag(a1, … ; an) over K. Show that for any nonzero scalars k1, … ; kn ∈ K, A is congruent to a diagonal matrix D with diagonal entries a1k21; … ; ank2n. Furthermore, show that
(a) If K = C, then we can choose D so that its diagonal entries are only 1’s and 0’s.
(b) If K = R, then we can choose D so that its diagonal entries are only 1’s, 1’s, and 0’s.
Let P = diag(k1, … ; kn). Then, as required,
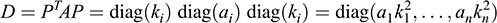
(a) Let P = diag(bi), where 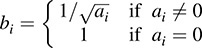
Then PTAP has the required form.
(b) Let P = diag(bi), where 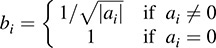
Then PTAP has the required form.
Remark: We emphasize that (b) is no longer true if “congruence” is replaced by “Hermitian congruence.”
12.14. Prove Theorem 12.5: Let f be a symmetric bilinear form on V over R. Then there exists a basis of V in which f is represented by a diagonal matrix. Every other diagonal matrix representation of f has the same number p of positive entries and the same number n of negative entries.
By Theorem 12.4, there is a basis {u1, … , un} of V in which f is represented by a diagonal matrix with, say, p positive and n negative entries. Now suppose {w1, … , wn} is another basis of V, in which f is represented by a diagonal matrix with p′ positive and n′ negative entries. We can assume without loss of generality that the positive entries in each matrix appear first. Because rank(f) = p + n = p′ + n0, it suffices to prove that p = p′.
Let U be the linear span of u1, … , up and let W be the linear span of wp0+1, … , wn. Then f(v, v) > 0 for every nonzero ν ∈ U, and f(v, v) 0 for every nonzero v ∈ W. Hence, U ∩ W = {0}. Note that dim U = p and dim W = n – p0. Thus,
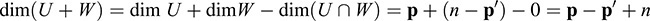
But dim(U + W) ≥ dim V = n; hence, p – p0 + n – n or p ≥ p0. Similarly, p0 p and therefore p = p0, as required.
Remark: The above theorem and proof depend only on the concept of positivity. Thus, the theorem is true for any subfield K of the real field R such as the rational field Q.
Positive Definite Real Quadratic Forms
12.15. Prove that the following definitions of a positive definite quadratic form q are equivalent:
(a) The diagonal entries are all positive in any diagonal representation of q.
(b) q(Y) > 0, for any nonzero vector Y in Rn.
Suppose 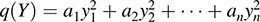 . If all the coefficients are positive, then clearly q(Y) > 0 whenever Y ≠ 0. Thus, (a) implies (b). Conversely, suppose (a) is not true; that is, suppose some diagonal entry ak ≥ 0. Let ek = (0; … ; 1; … 0) be the vector whose entries are all 0 except 1 in the kth position. Then q(ek) = ak is not positive, and so (b) is not true. That is, (b) implies (a). Accordingly, (a) and (b) are equivalent.
. If all the coefficients are positive, then clearly q(Y) > 0 whenever Y ≠ 0. Thus, (a) implies (b). Conversely, suppose (a) is not true; that is, suppose some diagonal entry ak ≥ 0. Let ek = (0; … ; 1; … 0) be the vector whose entries are all 0 except 1 in the kth position. Then q(ek) = ak is not positive, and so (b) is not true. That is, (b) implies (a). Accordingly, (a) and (b) are equivalent.
12.16. Determine whether each of the following quadratic forms q is positive definite:
(a) q(x; y; z) = x2 + 2y2 4xz 4yz + 7z2
(b) q(x; y; z) = x2 + y2 + 2xz + 4yz + 3z2
Diagonalize (under congruence) the symmetric matrix A corresponding to q.
(a) Apply the operations “Replace R3 by 2R1 + R3” and “Replace C3 by 2C1 + C3,” and then “Replace R3 by R2 + R3” and “Replace C3 by C2 + C3.” These yield
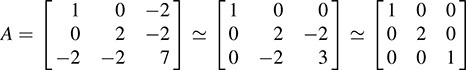
The diagonal representation of q only contains positive entries, 1, 2, 1, on the diagonal. Thus, q is positive definite.
(b) We have

There is a negative entry –2 on the diagonal representation of q. Thus, q is not positive definite.
12.17. Show that q(x, y) = ax2 + bxy + cy2 is positive definite if and only if a > 0 and the discriminant D = b2 – 4ac < 0.
Suppose v = (x,y) 0. Then either x ≠ 0 or y ≠ 0; say, y ≠ 0. Let t ≠ x/y. Then
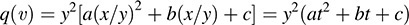
However, the following are equivalent:
(i) s = at2 + bt + c is positive for every value of t.
(ii) s = at2 + bt + c lies above the t-axis.
(iii) a > 0 and D = b2 – 4ac < 0.
Thus, q is positive definite if and only if a > 0 and D < 0. [Remark: D < 0 is the same as det(A) > 0, where A is the symmetric matrix corresponding to q.]
12.18. Determine whether or not each of the following quadratic forms q is positive definite:
(a) q(x, y) = x2 4xy + 7y2, (b) q(x, y) = x2 + 8xy + 5y2, (c) q(x; y) = 3x2 + 2xy + y2 Compute the discriminant D = b2 4ac, and then use Problem 12.17.
(a) D = 16 – 28 = 12. Because a = 1 > 0 and D < 0; q is positive definite.
(b) D = 64 – 20 = 44. Because D > 0; – q is not positive definite.
(c) D = 4 – 12 = – 8. Because a = 3 > 0 and D < 0; q is positive definite.
Hermitian Forms
12.19. Determine whether the following matrices are Hermitian:
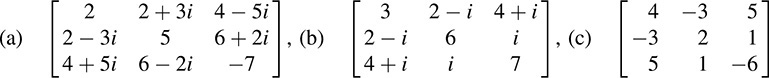
A complex matrix A = [aij] is Hermitian if A* = A—that is, if 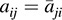
(a) Yes, because it is equal to its conjugate transpose.
(b) No, even though it is symmetric.
(c) Yes. In fact, a real matrix is Hermitian if and only if it is symmetric.
12.20. Let A be a Hermitian matrix. Show that f is a Hermitian form on Cn where f is defined by 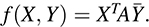
For all a, b ∈ C and all X1, X2, Y ∈ Cn,

Hence, f is linear in the first variable. Also,
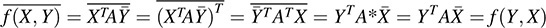
Hence, f is a Hermitian form on Cn.
Remark: We use the fact that  is a scalar and so it is equal to its transpose.
is a scalar and so it is equal to its transpose.
12.21. Let f be a Hermitian form on V. Let H be the matrix of f in a basis S = {ui} of V. Prove the following:
(a) 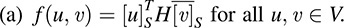
(b) If P is the change-of-basis matrix from S to a new basis S0 of V, then 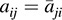 (or B = Q *HQ, where Q = P) is the matrix of f in the new basis S0.
(or B = Q *HQ, where Q = P) is the matrix of f in the new basis S0.
Note that (b) is the complex analog of Theorem 12.2.
(a) Let u, v ∈ V and suppose u = a1u1 + … + anun and v = b1u1 + + bnun. Then, as required,
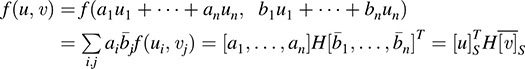
(b) Because P is the change-of-basis matrix from S to S0, we have P[u]S′ = [u] S and P[v] S0 = [v] S, hence, 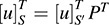 and
and 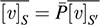 : Thus, by (a),
: Thus, by (a),
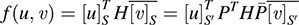
But u and v are arbitrary elements of V; hence, 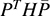 . is the matrix of f in the basis S0:
. is the matrix of f in the basis S0:
12.22. Let 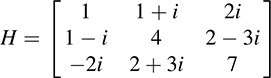 , a Hermitian matrix.
, a Hermitian matrix.
Find a nonsingular matrix P such that 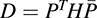 is diagonal. Also, find the signature of H.
is diagonal. Also, find the signature of H.
Use the modified Algorithm 12.1 that applies the same row operations but the corresponding conjugate column operations. Thus, first form the block matrix M = [H, I]:
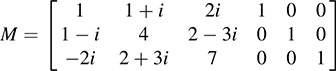
Apply the row operations “Replace R2 by (–1 + i)R1 + R2” and “Replace R3 by 2iR1 + R3” and then the corresponding conjugate column operations “Replace C2 by (–1 –i)C1 + C2” and “Replace C3 by 2iC1 + C3” to obtain

Next apply the row operation “Replace R3 by 5iR2 + 2R3” and the corresponding conjugate column operation “Replace C3 by 5iC2 + 2C3” to obtain

Now H has been diagonalized, and the transpose of the right half of M is P. Thus, set

Note D has p = 2 positive elements and n = 1 negative elements. Thus, the signature of H is sig(H) = 2 – 1 = 1.
Miscellaneous Problems
12.23. Prove Theorem 12.3: Let f be an alternating form on V. Then there exists a basis of V in which f is represented by a block diagonal matrix M with blocks of the form 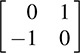 or 0. The number of nonzero blocks is uniquely determined by f [because it is equal to
or 0. The number of nonzero blocks is uniquely determined by f [because it is equal to 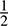 rank(f).
rank(f).
If f = 0, then the theorem is obviously true. Also, if dim V = 1, then f(k1u; k2u) = k1k2f (u, u) = 0 and so f = 0. Accordingly, we can assume that dim V > 1 and f ≠ 0.
Because f ≠ 0, there exist (nonzero) u1, u2 ∈ V such that f(u1, u2) ≠ 0. In fact, multiplying u1 by an appropriate factor, we can assume that f (u1; u2) = 1 and so f(u2, u1) = 1. Now u1 and u2 are linearly independent; because if, say, u2 = ku1, then f(u1, u2) = f(u1, ku1) = kf(u1, u1) = 0. Let U = span(u1, u2); then,
(i) The matrix representation of the restriction of f to U in the basis 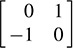 ,
,
(ii) If u ∈ U, say u = au1 + bu2, then
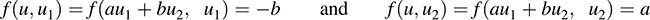
Let W consists of those vectors w ∈ V such that f(w, u1) = 0 and f(w; u2) = 0: Equivalently,
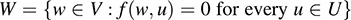
We claim that V = U ⊕ W. It is clear that U ∩ W = {0}, and so it remains to show that V = U + W. Let v ∈ V. Set
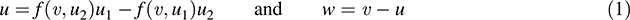
Because u is a linear combination of u1 and u2, u ∈ U.
We show next that w ∈ W. By (1) and (ii), f(u, u1) = f (v; u1); hence,
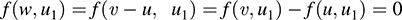
Similarly, f(u; u2) = f(u, u2)
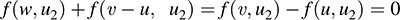
Then w ∈ W and so, by (1), v = u + w, where u ∈ W. This shows that V = U + W; therefore, V = U ⊕ W.
Now the restriction of f to W is an alternating bilinear form on W. By induction, there exists a basis u3, … , un of W in which the matrix representing f restricted to W has the desired form. Accordingly, u1, u2, u3, … ; un is a basis of V in which the matrix representing f has the desired form.
SUPPLEMENTARY PROBLEMS
Bilinear Forms
12.24. Let u = (x1, x2) and v = (y1, y2). Determine which of the following are bilinear forms on R2:
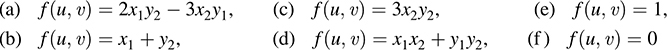
12.25. Let f be the bilinear form on R2 defined by
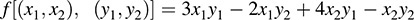
(a) Find the matrix A of f in the basis {u1 = (1; 1); u2 = (1; 2)}.
(b) Find the matrix B of f in the basis {v1 = (1; 1); v2 = (3; 1)}.
(c) Find the change-of-basis matrix P from {ui} to {vi}, and verify that B = PTAP.
12.26. Let V be the vector space of two-square matrices over R. Let 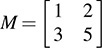 , and let f(A, B) = tr(ATMB), where A, B ∈ V and “tr” denotes trace. (a) Show that f is a bilinear form on V. (b) Find the matrix of f in the basis
, and let f(A, B) = tr(ATMB), where A, B ∈ V and “tr” denotes trace. (a) Show that f is a bilinear form on V. (b) Find the matrix of f in the basis
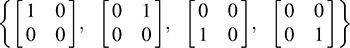
12.27. Let B(V) be the set of bilinear forms on V over K. Prove the following:
(a) If f, g ∈ B(V), then f + g, kg ∈ B(V) for any k ∈ K.
(b) If ϕ and σ are linear functions on V, then f(u, v) = f(u)s(v) belongs to B(V).
12.28. Let [f] denote the matrix representation of a bilinear form f on V relative to a basis {ui}. Show that the mapping f ℯ [f] is an isomorphism of B(V) onto the vector space V of n-square matrices.
12.29. Let f be a bilinear form on V For any subset S of V, let
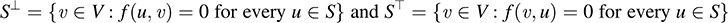
Show that: (a) ST and ST are subspaces of V; (b) Sj C S2 implies 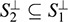 (c)
(c) 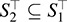 ;
;
12.30.. Suppose f is a bilinear form on V Prove that: rank( f) = dim V — dim V? = dim V — dim VT, and hence, dim V? = dim VT.
12.31. Let f be a bilinear form on V For each u 2 V, let U:V → K and w:V → K be defined by U(x) = f (x, u) and ũ(x) =f (u, x). Prove the following:
(a) ũ and u are each linear; i.e., w, u 2 V*,
(b) u → w and un u are each linear mappings from V into V *,
(c) rank( f) = rank(u ! u) = rank(u ! u).
12.32. Show that congruence of matrices (denoted by ') is an equivalence relation; that is,
(i) A ' A; (ii) If A ' B, then B ' A; (iii) If A ' B and B ' C, then A ' C.
Symmetric Bilinear Forms, Quadratic Forms
12.33. Find the symmetric matrix A belonging to each of the following quadratic forms:
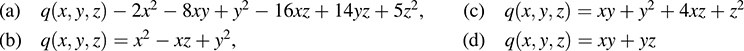
12.34. For each of the following symmetric matrices A, find a nonsingular matrix P such that D = PTAP is diagonal:
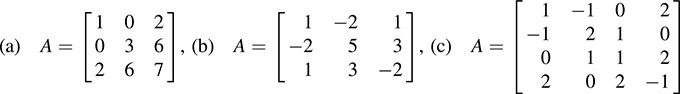
12.35. Letq(x, y) 2X2- 6xy — 3y2 and x = s + 2t, y =, 3s - t.
(a) Rewrite q(x, y) in matrix notation, and find the matrix A representing the quadratic form.
(b) Rewrite the linear substitution using matrix notation, and find the matrix P corresponding to the substitution.
(c) Find q(s, t) using (i) direct substitution, (ii) matrix notation.
12.36. For each of the following quadratic forms q(x, y, z), find a nonsingular linear substitution expressing the variables x, y, z in terms of variables r, s, t such that q(r, s, t) is diagonal:
(a) q(x, y, z) = x2 + 6xy + 8y2 — 4xz + 2yz — 9z2,
(b) q(x, y, z) = 2x2 — 3y2 + 8xz + 12yz + 25z2,
(c) q(x, y, z) = x2 + 2xy + 3y2 + 4xz + 8yz + 6z2.
In each case, find the rank and signature.
12.37. Give an example of a quadratic form q(x,y) such that q(u) = 0 and q(v) = 0 but q(u + v) = °.
12.38. Let S(V) denote all symmetric bilinear forms on V Show that
(a) S(V) is a subspace of B(V); (b) If dim V = n, then dim  .
.
12.39. Consider a real quadratic polynomial  where aij = aji.
where aij = aji.
(a) If a11 ≠ 0, show that the substitution
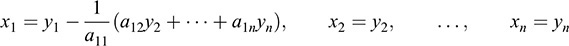
yields the equation 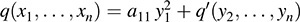 , where q0 is also a quadratic polynomial.
, where q0 is also a quadratic polynomial.
(b) If a11 = 0 but, say, a12 ≠ 0, show that the substitution x1 = y1 + y2;

yields the equation q(x1, … ; xn) = P bij yi yj, where b11 ≠ 0, which reduces this case to case (a).
Remark: This method of diagonalizing q is known as completing the square.
Positive Definite Quadratic Forms
12.40. Determine whether or not each of the following quadratic forms is positive definite:
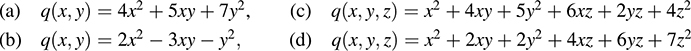
12.41. Find those values of k such that the given quadratic form is positive definite:
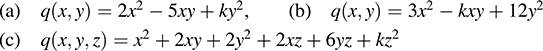
12.42. Suppose A is a real symmetric positive definite matrix. Show that A = PTP for some nonsingular matrix P.
Hermitian Forms
12.43. Modify Algorithm 12.1 so that, for a given Hermitian matrix H, it finds a nonsingular matrix P for which 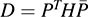 is diagonal.
is diagonal.
12.44. For each Hermitian matrix H, find a nonsingular matrix P such that D = PTH P is diagonal:
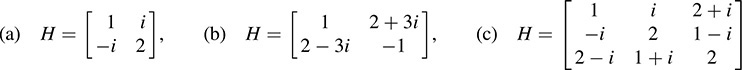
Find the rank and signature in each case.
12.45. Let A be a complex nonsingular matrix. Show that H = A*A is Hermitian and positive definite.
12.46. We say that B is Hermitian congruent to A if there exists a nonsingular matrix P such that 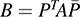 or, equivalently, if there exists a nonsingular matrix Q such that B = Q*AQ. Show that Hermitian congruence is an equivalence relation. (Note: If
or, equivalently, if there exists a nonsingular matrix Q such that B = Q*AQ. Show that Hermitian congruence is an equivalence relation. (Note: If  then
then 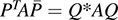 .)
.)
12.47. Prove Theorem 12.7: Let f be a Hermitian form on V. Then there is a basis S of V in which f is represented by a diagonal matrix, and every such diagonal representation has the same number p of positive entries and the same number n of negative entries.
Miscellaneous Problems
12.48. Let e denote an elementary row operation, and let f* denote the corresponding conjugate column operation (where each scalar k in e is replaced by 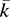 in f*). Show that the elementary matrix corresponding to f* is the conjugate transpose of the elementary matrix corresponding to e.
in f*). Show that the elementary matrix corresponding to f* is the conjugate transpose of the elementary matrix corresponding to e.
12.49. Let V and W be vector spaces over K. A mapping f : V W → K is called a bilinear form on V and W if
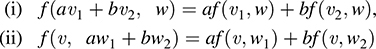
for every a, b ∈ K, vi ∈ V; wj ∈ W. Prove the following:
(a) The set B(V; W) of bilinear forms on V and W is a subspace of the vector space of functions from V × W into K.
(b) If {ϕ1, … ; ϕm} is a basis of V* and {σ1, … ; σn} is a basis of W*, then {fij : i = 1; … ; m; j = 1; … ; ng is a basis of B(V; W), where fij is defined by fij(v; w)= fi(v)sj(w). Thus, dim B(V; W) = dim V dim W. [Note that if V = W, then we obtain the space B(V) investigated in this chapter.]
12.50. Let V be a vector space over K. A mapping 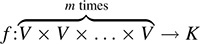 is called a multilinear (or m-linear) form on V if f is linear in each variable; that is, for i = 1; … ; m,
is called a multilinear (or m-linear) form on V if f is linear in each variable; that is, for i = 1; … ; m,
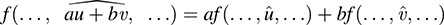
where  denotes the ith element, and other elements are held fixed. An m-linear form f is said to be alternating if f (v1, … vm) = 0 whenever vi = vj for i ≠ j. Prove the following:
denotes the ith element, and other elements are held fixed. An m-linear form f is said to be alternating if f (v1, … vm) = 0 whenever vi = vj for i ≠ j. Prove the following:
(a) The set Bm(V) of m-linear forms on V is a subspace of the vector space of functions from V × V × …. × V into K.
(b) The set Am(V) of alternating m-linear forms on V is a subspace of Bm(V).
Remark 1: If m = 2, then we obtain the space B(V) investigated in this chapter.
Remark 2: If V = Km, then the determinant function is an alternating m-linear form on V.
ANSWERS TO SUPPLEMENTARY PROBLEMS
Notation: M = [R1, R2,... denotes a matrix M with rows R1, R2, ….
12.24. (a) yes, (b) no,(c) yes, (d) no, (e) no, (f ) yes
12.25. (a) A = ½4; 1; 7; 3 , (b) B = ½0; 4; 20; 32 , (c) P = ½3; 5; 2; ∈
12.26. (b) ½1; 0; 2; 0; 0; 1; 0; 2; 3; 0; 5; 0; 0; 3; 0; 5
(a) [2, -4, 8; -4, 1,7; -8, 7, 5],
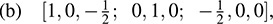
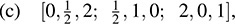
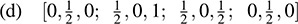
12.34. (a) P = ½1; 0; 2; 0; 1; 2; 0; 0; 1 ; D = diag(1; 3; 9);
(b) P = ½1; 2; 11; 0; 1; 5; 0; 0; 1 ; D = diag(1; 1; 28);
(c) P = ½1; 1; 1; 4; 0; 1; 1; 2; 0; 0; 1; 0; 0; 0; 0; 1 ; D = diag(1; 1; 0; 9)
12.35. A = ½2; 3; 3; 3 , P = [1; 2; 3; 1], q(s; t) = 43s2 4st + 17t2
12.36. (a) x = r – 3s – 19t, y = s + 7t, z = t; q(r, s, t) = r2 s2 + 36t2;
(b) x = r 2t, y = s + 2t, z = t, q(r, s, t) = 2r2 3s2 + 29t2;
(c) x = r – s t; y = s t; z = t; q(r, s, t) = r2 2s2
12.37. q(x, y) = x2 y2, u = (1; 1), v = (1; 1)
12.40. (a) yes,(b) no,(c) no,(d) yes
12.41. 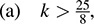 , (b) 12 < k < 12, (c) k > 5
, (b) 12 < k < 12, (c) k > 5
12.44. (a) P = [1, i, 0, 1], D = I; s = 2; (b) P = [1 ∈ + 3i 0, 1 , D = diag(1, 14), s = 0, (c) P = ½1; i, 3 + i, 0, 1, i, 0, 0, 1 , D = diag(1, 1, 4), s = 1
