1. Introduction to competition and stable coexistence
4. Competition and temperature
5. From models to reality: Future challenges
Numerous species commonly compose natural plant assemblages from the poles to the equator, and a wealth of classic ecological experiments have demonstrated that these often compete strongly with one another for resources such as nutrients or light. Theoretical ecologists have demonstrated that competing species are only expected to stably coexist (i.e., coexist in the long run) when each is protected from local extinction by density- or frequency-dependent processes that benefit it when rare, or equivalently, when the net negative effects of intraspecific (within-species) competition exceed those of interspecific (between-species) competition. Competition for nutrients, such as nitrogen and phosphorus, is “size symmetric” because smaller and larger individuals are potentially equal competitors on a per-biomass basis. In contrast, shoot competition for light is “size asymmetric” because taller individuals are advantaged irrespective of biomass. We describe the different modeling approaches that this difference requires. However, in either case, stable coexistence requires trade-offs such that species that are better competitors for one limiting nutrient or in one light environment are necessarily worse competitors for a second limiting nutrient or in a second light environment. As one important example of how these models might account for the stable coexistence of numerous species across landscapes, we consider the effects of habitat heterogeneity in mean growing season temperature coupled with trade-offs in performance among species at different mean temperatures. Finally, given our theoretical understanding, we close with a discussion of the current challenges to and opportunities for advancing our empirical understanding of competition and coexistence in the real world.
coexistence. The indefinite persistence of two or more species. The empirically relevant sort of coexistence is termed “stable coexistence” in which species will continue to persist in the face of perturbations in their abundances. It is important to note that species that co-occur may or may not be stably coexisting; it is possible that one or more species are on their way to local extinction at a time scale that might appear slow to a casual observer.
competition. Most broadly, an interaction between individuals in which neither benefits. Here, we are considering exploitation competition for limiting resources in which the resource consumed or intercepted by one individual is no longer available to the second individual, thereby decreasing its fitness.
exclusion. A condition in which a species is driven to local extinction as a consequence of a competitive interaction.
founder control. A condition in which the dominant species in a competitive interaction is the species that is initially most abundant.
interspecific competition. Competition among individuals of different species.
intraspecific competition. Competition among individuals of the same species.
invader/invasion. In the context of theoretical ecology, an invader is a species introduced at arbitrarily small abundance to a habitat of a resident species at equilibrium. The question is asked: will the invader increase in abundance? Note that this use of the term is different from the sense in which an “invader” may be a foreign species with negative ecological consequences.
local extinction. A condition in which a species is no longer present within a defined habitat area. Local extinction is very different from the common use of the term “extinction,” in which a species is no longer present anywhere.
resource. Broadly, something that may be consumed by one individual such that it is no longer available to another organism. Relevant resources for plants are nutrients, such as nitrogen, phosphorus, potassium, and micronutrients, along with light, water, and carbon dioxide.
Plant species, be they trees in tropical or temperate forests, forbs in prairies or tundra, or algae in lakes or oceans, frequently compete with other plant species for various limiting resources, such as nitrate, phosphate, and light (Harper, 1977). Plants are also impacted by interactions such as mutualism, predation, herbivory, and disease. Each of these interactions has the potential to influence both the types of habitats in which species occur and their abundances in those habitats. Here we focus on mechanisms of competition for nutrients and light and their influence on coexistence and competitive exclusion among competing plant species.
As developed in the pioneering work of Lotka and Volterra, competition between two species, or interspecific competition, is defined as an interaction in which an increase in the abundance of one species causes a decrease in the growth and abundance of the other species and vice versa. By removing neighboring plants from around a target plant and documenting an increase in the target plant’s growth rate, numerous experimental studies have shown that interspecific competition can be a strong force in plant communities. Competition between two individuals of the same species, intraspecific competition, is similarly defined and is almost certainly as strong as or stronger than interspecific competition.
Competition occurs because all vascular plants require light, water, and 20 or so mineral nutrients, including N, P, K, Ca, Mg, and various trace metals to survive and grow (e.g., Harper, 1977). As plants grow and consume these resources in a particular habitat, one or more resources become limiting because their rates of supply are insufficient to meet the demand from consumption. The outcome of the resultant resource competition may be exclusion or coexistence and depends on the dynamics of resource supply, on the resource requirements of the various species, and on the dependence of these factors on the physical attributes of the habitat, including its temperature, humidity, soil pH, slope, and aspect. The outcome of competition may also depend on initial species abundances. If each species maintains dominance whenever it is initially dominant, competition is said to be “founder controlled.”
Species will coexist if each species can increase when it is rare and other species are at equilibrial abundances. This generally requires that intraspecific competition be stronger than interspecific competition. The mere co-occurrence of two or more competing species does not necessarily mean that they are coexisting; some of these species may be on their way to local extinction, albeit too slowly to be detected by casual observation. Ecological theory provides a way to formally distinguish stable coexistence from competitive exclusion at any time scale. First, if a competition model has a multispecies equilibrium point at which competing species have abundances greater than zero, the stability of this point can be assessed mathematically. If species abundances return to the equilibrium point after abundances are perturbed away from that point, this indicates that coexistence is stable. However, it is also possible for two or more competing species to persist indefinitely even when they do not have a stable multispecies equilibrium point. In these cases, one way to test for stable coexistence is to determine if there is “mutual invasibility” of species within the model (note that “invasion” in this chapter has no connotation of processes related to problematic nonnative species). In the simple case of two species, A and B, one asks if the geometric mean growth rate of a relatively small number of As in a monoculture of Bs is positive. If so, species A is said to be able to invade species B. If B can also invade A, then each species increases when rare and is protected from local extinction. The two species stably persist (coexist), even though their abundances are not constant. If A can invade B but B cannot invade A, then species A will exclude species B. If neither species can invade an equilibrial population of the other, then there is founder control; the initial dominant will maintain dominance.
Although it is possible for many nutrients to limit growth, it is easiest to begin by considering a single consumer species and a single limiting nutrient (hereafter referred to more generically as a “resource”). A resource is considered limiting if increases/decreases in its supply lead to increases/decreases in the growth rate of the species (Tilman, 1982). To understand dynamics, we must consider the factors that control both the rates of growth and loss of a species and the rates of supply and consumption of the resource. Because many plants have indeterminate growth and must increase in mass by two to six or more orders of magnitude when growing from a seed to an adult plant, it is customary to consider the dynamics of plant biomass rather than the dynamics of the number of individuals (as often done for animal populations). Thus, the specific rate of growth or loss of plant biomass is represented by dB/dt 1/B, where B is biomass per unit area (for terrestrial plants) or per unit volume (for marine and freshwater planktonic algae).
The specific growth rate of a species is often a monotonically increasing but asymptotically saturating function, f[R], of the concentration or level of the limiting resource, R (figure 1A). Plant species experience a variety of sources of loss, including mortality and tissue loss from senescence, damage, herbivory, and disease. These losses, m, can be expressed in terms of density-independent changes in plant biomass, giving equation 1:
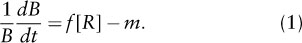
As a plant population grows, it will consume the limiting resource. To see this, consider the dynamics of the resource:
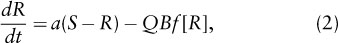
where S is the supply rate of all forms of resource R, a is the rate of conversion of currently plant-unavailable forms of this resource (such as, for example, soil organic compounds containing nitrogen) into a plant-available form (such as nitrate), and Q is the quota of this resource needed to make a unit of new biomass (e.g., the ratio of nitrogen in plant tissues to biomass). Equation 2 thus states that the rate of change in available resource, R, depends on its rates of supply, a (S – R), and consumption, QBf[R].
In combination, equations 1 and 2 state that, at equilibrium, a species growing by itself will reach a biomass at which growth and loss balance each other, at which resource supply and consumption balance each other, and thus, at which dB/dt = dR/dt = 0. This occurs when the balance between supply and consumption has reduced the level of the resource down to R* (figure 1A; Tilman, 1982). R* is the resource requirement of this species in the sense that it is the amount of resource at which resource-dependent growth balances all sources of loss (figure 1A). If the level of the resource were greater than R*, the abundance of the species would increase (dB/dt > 0) because growth would be greater than loss. Greater plant abundance would ultimately reduce the level of the resource to R*. If the level of the resource were less than R*, the abundance of the species would decrease (dB/dt < 0) because loss would be greater than growth. Less plant abundance would decrease resource consumption and ultimately increase the level of the resource to R*.
Figure 1. Details of resource consumption and competition for a single nutrient. (A) A single plant species growing on a single resource will reach equilibrium at resource concentration R*, where per capita growth, f (R), exactly balances per capita losses, m. (B) Depending on their physiology, morphology, and ecology, different species (e.g., Species A and Species B) are expected to have different resource-dependent growth rates and loss rates. As a consequence, different species are expected to have different R*values for a given resource. (C) When species compete for a single resource, the species with the lowest R* value is expected to win. The species with the lowest R* value reduces equilibrial resource concentrations to a level where the loss rates of its competitors exceed their growth rates, and they are driven locally extinct.
When two or more species compete for a single limiting soil resource, the long-term outcome of their competition, should an equilibrium be reached, is that the species with the lowest R* value (as determined by its physiology, morphology, and environmental conditions and their combined effects on f[R] and m; figure 1B) would win and exclude all other competitors (figure 1C). This occurs because the species with the lowest R* value would continue to increase in abundance until it had reduced the resource down to its R*. At this resource level, the growth rates of all other species would be less than their loss rates, causing them to decline in abundance until locally extinct. Thus, if there is only one limiting resource, coexistence is not possible at equilibrium; only a single species will persist.
There are two important points to be made about this result. First, note that the model is predictive in the sense that a species trait measured in monoculture (R* or physiological or morphological traits, such as root mass and fine root diameter, correlated with R* in a given environment) allows one to predict the outcome of competition. This is much different from phenomenological models, such as the Lotka-Volterra competition equations, in which the competition coefficients that might allow one to predict the outcome of competition are measurable only after a competition experiment has been performed (thereby making a prediction of the outcome unnecessary!).
Second, note that the model’s prediction that one species should displace all is at odds with the coexistence of numerous competing species in almost all natural ecosystems. This discrepancy suggests that one or more of the simplifying assumptions used in the model are violated in nature. This would not be surprising because the model implicitly assumes that there is only one limiting resource; that sites within a habitat do not differ in physical factors that may also limit growth, such as temperature, soil pH, and humidity; that plant abundances are not limited by dispersal; that interspecific interactions go to equilibrium; and that organisms on other trophic levels that might exert density- or frequency-dependent loss rates, such as herbivores, seed predators, pathogens, and mutualists, are unimportant. More complex and realistic theories have shown that addition of any one or more of these complexities of nature can allow many species to coexist, but only if species have appropriate trade-offs, as discussed below.
Few ecosystems have but a single limiting nutrient. Nutrient addition experiments in freshwater and marine ecosystems have shown that two or more nutrients often limit phytoplankton, especially nitrate, phosphate, silicate, and/or iron. The most commonly limiting nutrients in most terrestrial ecosystems are soil nitrogen and phosphorus. Other nutrients, especially potassium, calcium, or trace metals, can be limiting depending on the age and origin of the soil. Although not a nutrient per se, water is also limiting in many terrestrial ecosystems. In all but very nutrient poor or dry terrestrial ecosystems and in many freshwater and marine ecosystems, light also limits at least some plant species. We address the special case of light limitation in a separate section below.
Although a single number, R*, can summarize the competitive ability of a plant for a single limiting resource, resource-dependent growth isoclines are needed to do so for two or more limiting resources. A resource-dependent growth isocline defines the concentrations of all limiting resources for which a species has a given growth rate. The isocline defining the growth rate that is equal to the loss rate of a given species (i.e., dB/dt = 0), which is called the nullcline, is directly analogous to R* in its ability to predict the outcome of competition for two or more limiting resources. Most commonly, nullclines are plotted on graphs in which the axes represent the possible concentrations of limiting resources (figure 2A). When resource concentrations fall between the origin and a species’ nullcline, the species will experience greater loss than growth. When resource concentrations fall beyond the nullcline relative to the origin, the species will experience greater growth than loss (figure 2A).
The shape of the nullcline reflects the type of resources that are limiting. Most plant resources are nutritionally essential; individual plants must have N, P, K, etc., and they cannot eliminate their need for one of these elements by substituting increased amounts of a different element. Nutrients tend to be perfectly essential for morphologically simple plants, such as single-celled phytoplankton species. This means that the null-clines of algae tend to have right-angle corners (figure 2A), with each branch of the isocline representing the R* of the species for that resource. However, because higher plants can vary their morphology and the physiology of different tissue types, they have some ability to substitute one resource for the other when both are approximately equally limiting. Thus, they have interactive-essential resources: their nullclines tend to have rounded corners (figure 2B). The difference between perfectly essential and interactive-essential resources has no major qualitative effects on the outcomes of interspecific resource competition described below.
Figure 2. Details of resource consumption for two nutrients. (A) A nullcline defines the concentration of two resources for which a plant species will be in equilibrium, i.e., where dA/dt = 0 and per capita growth is exactly balanced by per capita loss. The nullcline shown depicts the response of a species to perfectly essential resources, such as nitrogen and phosphorus, where no amount of one resource can compensate for a deficit of the other resource. (B) A bent nullcline depicts the response of a species to interactive essential resources, where plants can somewhat shift investment toward physiological, morphological, or ecological structures that capture the most limiting resource. For example, a plant may invest less photosynthate in mycorrhizal associations and more photosynthate in the construction of fine roots when nitrogen is more Limiting than phosphorus. Characterizing resources as interactive essential instead of perfectly essential does not change the qualitative outcome of competition. (C) The intersection of the nullclines of two species is necessary, but not sufficient, for their coexistence. Their intersection implies that one species has a Lower R* value for one resource and that the other species has a Lower R* vaLue for the other resource. If coexistence does occur (see figure 3), equiLibriaL resource concentrations will be fixed at the intersection point. When the nullclines do not intersect (not shown), the species with Lower R* vaLues for both resources wiLL aLways win in competition, as in the case for a singLe resource.
Two species can stably coexist at equilibrium in a homogeneous habitat only if their nullclines cross, which occurs only if the species have an interspecific trade-off. For instance, consider species A and B of figure 2C. Species A has a lower requirement (i.e., a lower R* value) for R1 than species B, but species B has a lower requirement for R2 than species A. The two-species equilibrium point at which the nullclines cross shows the levels to which these two species would reduce R1 and R2 if they were to stably coexist at equilibrium. Although nullclines must cross for two species to coexist at equilibrium, that alone is not sufficient to ensure coexistence. The outcome of competition is also determined by their rates of consumption of the resources.
Assuming that each species forages optimally for these two resources, such that no resources are consumed that do not increase growth (i.e., no “luxury consumption,” a reasonable assumption given that resource consumption requires energy), each species will consume resources in the ratio defined by the slope of the line drawn from the corner of its nullcline to the origin. Hence, consumption may be represented by vectors, cA and cB, that take those slopes (figure 3A). Consider the habitat represented by the supply point (S1, S2) in figure 3A. Such habitats have intermediate rates of supply of the two limiting resources. At equilibrium, the consumption by the two competitors would reduce resources down to the two-species equilibrium point. Indeed, coexistence would occur for any habitats with supply points within the area bounded by the shaded triangle that extend the slopes of the consumption vectors of the two species away from the two-species equilibrium point (figure 3). This is because it is possible to create a linear combination of cA and cB that is exactly equal in magnitude and opposite in sign to the rate of resource replenishment, represented by the vector U, such that resource supply is exactly balanced by consumption (compare figures 3A and 3B) and dR/dt = 0.
Figure 3. The outcome of competition for two nutrients. For all three panels: Species A’s nullcline is solid and Species B’s nullcline is dashed. The vector cA represents Species A’s rate-of-consumption vector. By assumption of optimal foraging, its slope is fixed by the ratio of resource concentrations that limit Species A, i.e., the slope between the origin and the bend in Species A’s nullcline. Its magnitude is proportional to Species A’s equilibrial biomass. The vector cB is analogous for Species B. The vector U represents the rate of resource replenishment. The point (S1, S2) represents the supply concentration of the two resources in a given habitat. At equilibrium, U will point toward (S1, S2) and will be equal and opposite to the vector sum of the consumption vectors cA and cB. Because their slopes are fixed, coexistence will occur at equilibrium only when it is possible to add cA and cB from the nullcline intersection point such that their sum is equal and opposite to U. This will occur for all (S1, S2) inside the medium gray triangle (panels A and B). For all (S1, S2) inside the lightest gray area (panel C), Species A will win (cB = 0). For all (S1, S2) inside the darkest gray area (not shown), Species B will win (cA = 0). For all (S1, S2) inside the white area (not shown), both species will become locally extinct.
In habitats that have low rates of supply of R1 relative to R2, such as for the habitat depicted in figure 3C, both species are most limited by R1, and species A, which is the better competitor for R1 because it has a lower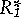 
, would competitively displace species B at equilibrium. Notice that because their slopes are fixed by assumption of optimal foraging, there is no linear combination of cA and cB in figure 3C that could exactly balance U, as in figures 3A and 3B. Similarly, species B would win for habitats that have low relative rates of supply of R2.
If species have trade-offs in their abilities to compete for two or more limiting resources, these trade-offs would mean that each species would have habitats, defined by supply rate of these resources, in which it would persist in competition with any other species. This is illustrated for four species (C, D, E, and F) competing for two limiting resources in figure 4A. Note that, with two limiting resources, only two species can stably coexist, at equilibrium, in any given habitat (i.e., any specific S1, S2) but that all four species can persist together in a landscape that has spatial heterogeneity in the supply rates of these resources as shown. Even more species could coexist with a fixed amount of heterogeneity if new species invaded with intermediate requirements for R1 and R2, an example of which is shown using a dashed nullcline in figure 4A. Alternatively, more species could coexist if the habitat encompassed even greater heterogeneity (not shown). The concept of trade-offs can easily be expanded to three or more resources.
The model of competition described above applies to competition for nutrients but not to competition for light (Tilman, 1988). To see why, first realize that the concentration to which a plant reduces a nutrient through consumption (R) is the same concentration at which it must subsequently extract the nutrient (R). In other words, the nutrient concentration it “gets” is the same as the nutrient concentration it “creates.” This is fundamentally different from competition for light: a tall tree intercepts full sunlight and reduces the intensity of light below its crown, such that trees below it receive less than full sunlight. Thus, the light level that the tall tree “gets” is distinct from the light level it “creates.”
Figure 4. The effect of heterogeneity in resource supply points and temperature on coexistence. (A) With two limiting resources, at most two species can stably coexist at a single resource supply point (S1, S2). However, if supply points shift across a landscape (as depicted by the circle and the range of S1 and S2), many species can coexist, provided a trade-off causes a lowered R* value for one resource to necessarily lead to an increased R* value for the other resource. Light gray regions depict those for which supply points will cause a single species to dominate. Dark gray regions depict those for which supply points will cause two species to stably coexist. Gray letters represent species nullclines. BLack Letters represent the suppLy point zones in which a species wiLL persist. The dashed nuLLcLine shows an exampLe of a new species that wouLd be abLe to invade and coexist in this Landscape. (B and C) HypotheticaL dependence of R* and Z* vaLues on mean growing season temperature. EcophysioLogicaL constraints suggest that those characteristics that wiLL Lead to Low R* vaLues or reLativeLy high Z* vaLues at one temperature shouLd prevent a species from having a Low R* vaLue or reLativeLy high Z* vaLue at a different temperature. Thus, heterogeneity in growing season temperature across a Landscape shouLd Lead to the coexistence of multiple species.
Weiner (1990) described differences in competitive interactions in terms of symmetry and asymmetry. “Size symmetric” competition occurs when larger individuals have no advantage over smaller individuals on a per-biomass basis, i.e., when the resource consumption of an individual is proportional to the biomass of its resource-capturing structures, such as roots for soil nutrients. “Size asymmetric” competition occurs when larger individuals take a disproportionate share of the resource, as is expected when taller plants preempt the light of shorter plants below them. Indeed, empirical studies have generally supported the idea that competition for soil resources is size symmetric, whereas competition for light is size asymmetric. Given size asymmetry, it is challenging to create a realistic mathematical model of light competition that is as simple and readily interpretable as the nutrient model described above.
Recently, S. W. Pacala and co-workers discovered an approach that allowed them to create a simple yet mechanistic and predictive analytical model of plant competition for light. Although their model is formulated explicitly for single-canopy forests, it is extendable to other plant communities. The model treats trees as morphologically plastic, as being able to “lean” toward gaps by concentrating their growth in areas of higher light, where the photosynthetic return on structural investment is greater. To a first approximation, termed the “perfect plasticity approximation” (PPA), the result of each tree’s individual plasticity and phototropism is canopy closure via tessellation, where each crown fills as much space as it can without growing into adjacent crowns. Moreover, under the PPA, the height above the ground at which each canopy crown touches an adjacent canopy crown tends toward a constant value across a forest canopy with a given set of species at a given stage of development.
Thus, forest trees may be classed as either in the canopy or in the understory and consequently subject to either full sunlight or the mean light remaining after transmission through the canopy. This has the dual advantage of simplifying the mathematics of a light competition model and yet making it more realistic (Adams et al., 2007). Consider a forest monoculture of species A at equilibrium. The forest consists of reproductive canopy trees and nonreproductive understory trees. The canopy trees reduce light to a level, LA, in the understory. Because the forest is assumed to be in equilibrium, each canopy tree exactly replaces itself over a lifetime of reproductive effort, on average. Understory trees grow at rate GD, A[L] and die at rate μD, A[L]. Canopy trees grow at rate GL, A, die at rate μL, A, and reproduce at rate FA per unit area of crown. Crown area, Π (αAD)2 and height, HA(D)ªβA, scale allometrically with trunk diameter, D. The equilibrial canopy height is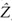 
A*.
Invasion of species A’s monoculture by a small number of species B individuals will be successful only if, on average, each invader produces more than one successful (i.e., reproductive) offspring. By assumption of the Adams et al. (2007) model, individuals reproduce only once they have reached the canopy. Thus, if some of the invaders die before reaching the canopy, successful invasion will depend on whether those individuals that do reach the canopy can produce enough successful offspring to make up for their loss. Resident species A can influence this process only by affecting the fraction, ζ, of invaders that survive to reach the canopy:
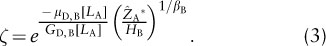
Adams et al. (2007) point out that invasion will be less likely if LA is smaller (by decreasing the invader’s understory growth rate, GD, B[LA], and increasing its mortality rate, μD, B[LA]) or if 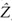A* is greater (by increasing the time required to reach the canopy and thus the likelihood of mortality before reaching the canopy).
If the crown transmissivities of the two species are equivalent, i.e., LA = LB, then Adams et al. (2007) demonstrate that light competition among trees is analogous to competition for a single soil resource, in the sense that one species is always expected to win, and the winner may be determined by examining the traits of the species in equilibrial monoculture. Specifically, the winner will be the tallest species, with the canopy height of species i, 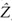A*, approximated by:
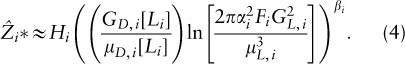
Foresters have long recognized that forest succession, which may be viewed as prolonged competitive exclusion, generally proceeds from shade-intolerant species to shade-tolerant species. Purves et al. (2008) showed that shade-intolerant species tend to have low 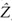A*, that shade-tolerant species tend to have high 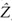A*, and that succession in the forests near the Great Lakes predictably proceeded from species with low 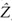A* to species with high 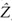A*. This suggests that, relative to the importance of other factors that affect light competition during succession, the crown transmissivities of different tree species may be effectively equivalent.
Clearly, numerous tree species stably coexist in most forests, an observation that is at odds with the prediction that the single species with the highest 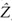A* should exclude all competitors. Again, this suggests that some of the model’s assumptions, which largely overlap with the assumptions of the simple model of competition for a single soil resource described in the previous section, are false. However, before introducing exogenous factors into the model to explain diversity, Adams et al. (2007) note that at least some coexistence may be explained if we relax the assumption that the transmissivities of different tree species are equal, i.e., let LA ≠ LB.
Adams et al. (2007) showed that it is possible for two species to coexist when competing for light if each species performs less well in the understory light environment that its canopy creates. Specifically, two species will coexist via competition for light when the species that casts more shade performs relatively better under less shade and the species that casts less shade performs relatively better under more shade. Each species creates the conditions that disfavor it. As discussed earlier, species are expected to stably coexist in resource-limited conditions when intraspecific competition is stronger than interspecific competition. Further theoretical and experimental work is needed to determine how likely this mechanism of coexistence might be relative to mechanisms that involve having both light and one or more additional factors limit plant growth.
The rates of photosynthesis, respiration, and other physiological processes of all plants are dependent on temperature during the growing season. Temperatures below freezing are a separate but equally important limiting factor for plants because a host of chemical and mechanical adaptations are needed for cells to avoid the damage that freezing can cause. Moreover, the magnitude of such adaptations increases for temperatures further below freezing. Here we consider just the effects of the mean temperature of the growing season on plant growth rates.
The net effect of the dependence of plant physiology on temperature is that each plant species should have a mean growing season temperature at which it performs best. For habitats in which a single nutrient is limiting, the R* of each species would be a function of mean growing season temperature, with each species having its lowest R* value at its optimal temperature (figure 4B). For habitats in which light is limiting, equilibrial canopy height, 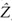*, will vary with temperature because of the dependence of growth, mortality, and fecundity rates on temperature.
Habitats have spatial variation in mean growing season temperature, such as along elevational gradients or among slopes with different aspects (north- versus south-facing slopes), and temporal variation, such as year-to-year or decade-to-decade differences. Such variation can allow numerous species to coexist. For example, the temperature-dependent R*values of figure 4B define the temperature ranges at which each species would be the superior competitor (figure 4B). Species A would dominate the coolest sites/times, species B would dominate warmer sites/times, and species C would dominate the warmest sites/times. Strictly interpreted, only a single species would persist in a given site, but all three species would stably coexist on the larger landscape that encompassed the temperature variation illustrated in figure 4B. Similarly, the 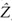* values of different species are expected to be maximal at a temperature for which they are well adapted, relative to other species at that temperature. Thus, across a landscape with variation in mean growing season temperature, the relative position of 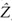* values would shift such that species A might win at lower temperatures, whereas species B might win at higher temperatures (figure 4C).
This coexistence occurs because plants, like all organisms, are constrained by trade-offs. No species has the lowest R* value or highest 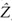* value for all temperatures. Rather, each species has a range of temperatures at which it is the superior competitor and a range for which it is inferior. Just such a trade-off is expected based on the temperature dependence of both the activation energy and the denaturation of enzymes. If such a trade-off were an unavoidable aspect of plant life, there could be many other species, each with its own optimal temperature, that could persist between species A and B (figure 4B, C). Indeed, there would be no simple limit to the number of competing species that could coexist on a single limiting resource, be it nutrients or light, in a landscape with spatial variation in growing season mean temperature.
The models described above provide several mechanisms, each of which, by itself, can maintain a potentially infinite number of stably coexisting species. The ecological literature is replete with other coexistence mechanisms that incorporate effects of space; disturbance and other nonequilibrium dynamics; or natural enemies on coexistence (see Further Reading). Given the appropriate trade-offs between species, most of these mechanisms can also maintain a potentially infinite number of stably coexisting species. The current and future challenge for ecology is determining which of these possible mechanisms actually maintain plant species diversity in nature. This is difficult for at least two reasons. First, feedbacks between plants and their abiotic and biotic environment and between soil biota and their abiotic and biotic environment make it difficult to isolate or manipulate only those aspects of the community or environment that theory suggests should impact some observable characteristic. For instance, it is difficult to remove specialized insect herbivores to test for their importance in diversity maintenance without also removing other insects, some of which may be mutualists.
The second difficulty lies in the long time scales over which many mechanisms are expected to operate, either because the dynamics are slow or because the mechanism relies on periodic but rare events. These defy detection in short-term field studies. As has happened in geology, substantial progress might be made if theoretical ecologists apply themselves to articulating short-term signatures of long-term mechanisms that field ecologists could then look for or test for. However, this appears more challenging in ecology than in geology because many of the most obvious signatures (e.g., particular rank abundance relationships) may be generated by multiple mechanisms. Alternatively, ecologists might turn to long-term data. For example, Purves et al. (2008) used long-term Forest Inventory and Analysis data (available from the U.S. Department of Agriculture) to parameterize and then test a variant of the light competition model described above and showed that the model largely predicted changes in total basal area, species composition, and the size structure of forest stands over 100 years of secondary succession. Unfortunately, such relevant long-term data are rare in ecology.
Despite these difficulties, many studies have demonstrated that particular mechanisms of coexistence may operate in particular habitats (Fargione and Tilman, 2002), typically by altering some aspect of the habitat and observing the predicted response. Such studies provide important insights into the ways particular mechanisms of coexistence operate and, to the extent that publications are not biased against negative results, provide data for broader conclusions via meta-analysis of multiple studies across a range of habitats and conditions. Although it might be intellectually gratifying to learn that just one mechanism maintains diversity throughout all of the varied biomes of the world, it seems much more likely that multiple mechanisms operate in any given habitat and that the relative importance of different mechanisms shifts across biomes and environmental gradients. In all cases, though, theory suggests that interspecific trade-offs will be both a root cause of coexistence of competing plant species and a useful signature of the mechanisms responsible for coexistence.
Adams, T. P., D. W. Purves, and S. W. Pacala. 2007. Understanding height-structured competition in forests: Is there an R* for light? Proceedings of the Royal Society B: Biological Sciences 274: 3039–3047.
Chesson, P. 2000. Mechanisms of maintenance of species diversity. Annual Review of Ecology and Systematics 31: 343–366. This review differentiates between the “equalizing” and “stabilizing” components of coexistence mechanisms. Chesson’s distinction has received considerable attention in the recent literature, especially in the debate between niche and neutral processes. See, for instance: Adler et al. 2007. A niche for neutrality. Ecology Letters 10: 95–104.
Fargione, J., and D. Tilman. 2002. Competition and coexistence in terrestrial plants. In U. Sommer and B. Worm, eds. Competition and Coexistence. Berlin: Springer-Verlag, 165–206. This review has a good discussion of the limited number of studies that have successfully identified mechanisms of coexistence operating in natural systems.
Harper, J. L. 1977. Population Biology of Plants. London: Academic Press. This volume is a classic synthesis of early work on plant competition.
Huisman, J., and F. J. Weissing. 1999. Biodiversity of plankton by species oscillations and chaos. Nature 402: 407–410. This article is an elegant account of how the number of coexisting species may greatly exceed the number of limiting resources. The authors use a variant of the soil resource model presented above and find that the dynamics of competition lead to chaos and, as a result, species coexistence.
Miller, T. E., J. H. Burns, P. Munguia, E. L. Walters, M. M. Kneitel, P. M. Richards, N. Mouquet, and H. L. Buckley. 2005. A critical review of twenty years’ use of the resource-ratio theory. The American Naturalist 165: 439–448. See also a reply by Wilson et al. and rejoinder by Miller et al. in 169: 700–708.
Purves, Drew W., Jeremy Lichstein, Nikolay Strigul, and Stephen W. Pacala. 2008. Predicting and understanding forest dynamics using a simple tractable model. Proceedings of the National Academy of Sciences 105: 17018–17022. This parameterized version of the light competition model presented above predicts the 100-year outcome of secondary succession in the forests of the Great Lakes states.
Tilman, D. 1982. Resource Competition and Community Structure. Princeton, NJ: Princeton University Press. This volume presents a detailed treatment of the soil resource competition model and its implications.
Tilman, D. 1988. Plant Strategies and the Dynamics and Structure of Plant Communities. Princeton, NJ: Princeton University Press. This volume presents a detailed treatment of a simulation model of plant allocation to leaves, roots, etc. and its effect on competition and coexistence.
Tilman, D., and S. Pacala. 1993. The maintenance of species richness in plant communities. In R. E. Ricklefs and D. Schluter, eds. Species Diversity in Ecological Communities. Chicago: The University of Chicago Press, 13–25. This is a review of coexistence mechanisms.
Weiner, J. 1990. Asymmetric competition in plant populations. Trends in Ecology and Evolution 5: 360–364. This article presents a clear presentation of the difference between symmetric” competition for soil resources and “asymmetric” competition for light.
