Civil engineers deal with three main tasks during their career: analysis, design and construction. When analysing, engineers are commonly required to verify and suggest means to comply with regulations or ways to improve the performance of a system, and, in doing so, they seek to achieve performance goals. In designing, engineers face the need to create built environment, and this typically results in conflicting objectives of professionalism, developer’s interests and resources. Finally, during construction, an engineer faces the need to allocate labour, equipment and materials to reach given milestones on time. However, timely achievement of such deadlines requires more intensive use of the resources mentioned which triggers project cost. Hence, the engineer is faced with two common conflicting goals: minimization of resource utilization and achievement of a certain level of quality and/or performance.
This morning, when you woke up, did the possibility to continue sleeping cross your mind? If so, then you had to make your first decision of the day. Why do you like to sleep? Your body gets some rest, you recover your energy and even your capability to learn reaches its highest point. So why then did you stand up and initiate your day instead of sleeping? You possibly either had breakfast, took a shower, exercised or finished your video game. Some time ago, economies defined a concept called utility, for you and me (who stay in bed for another 30 minutes). Sleeping gives us satisfaction, is valuable, is useful or, in other words, gives us utility. But the utility of sleeping was not as important for those who woke up and started their daily activities, perhaps because they have already slept for over 10 hours.
The amount of utility one gets out of sleeping decreases with time: sleeping after a long day of work/study has a very large utility, sleeping more after the first hour of dreaming has a large value (utility), sleeping after having dreamt for 6 hours still has some value (utility) and sleeping after 10 hours possibly has no value. This behaviour of decreasing value is formally called decreasing returns to scale: the more you get of something, the less you value it. Think of it as the amount of your favourite beverage: the first glass is amazing, the second glass is refreshing, the third glass is fine and the fourth glass is not so good.
Many other activities are valuable to an individual and provide him/her with utility. Eating, socializing and sleeping are just a few examples. An individual consumes food items to eat and in doing so has his or her own preferences: he may not like (and/or never) eat pork but love chocolate. In socializing, an individual perceives value out of activities and items: silver/gold jewellery, brand watches, fancy cars, visiting clubs, organizing parties at his place, attending conferences and seminars or publishing research in prestigious journals. All these activities require the consumption of goods. Goods cost money and money is in short supply (ask your parents if you do not believe me).
On a daily basis, individuals attempt to achieve the highest possible value of utility, and for that, they dedicate time and efforts to achieve what they want and are required to expend money. The problem of any individual is to maximize his utility given a certain amount of resources (time, money, ability).
A similar problem faces the junior engineer at my consulting company when I ask her to take care of the entire design process for a new building, including obtaining construction permits. She starts by meeting with the customer to learn his office space/functionality needs, then she has to conceptually design a building layout and validate the design with the customer. Assuming the client is happy, she will order the structural, mechanical and electrical engineers to design the corresponding components of the building. After a month or so, the blueprints will be ready and she will have to visit the municipality and other government institutions to obtain the required construction permits.
Why does she do all this? It sounds after all complicated and stressful. She perceives utility from the salary and the working experience. The company perceives utility out of the revenue (fees charged to the customer) minus the expenses we incur in (including her salary). Resources are involved in these activities and act as constraints: the company uses time from drawing technicians, structural, mechanical and electrical engineers; paper for the blueprints; computers that deteriorate for the designs and calculations; electricity; and pay rent for the building, among many others. The problem of any firm is to decide how much resources to use in order to spend as little as possible but yet to be able to satisfy its customers and obtain large amounts of profits.
The problems we have presented so far are given at a moment in time. The individual wants to achieve a large amount of utility today, and the company seek profits this month. Time complicates things and makes the problem more interesting (I bet you differ). The individual not only faces a maximization of utility today but for the rest of his life. Tomorrow and the day after and next year and in 5 years and in 20 years, he will wake up and will face a similar problem and will count with similar restrictions.
If I go to the cinemas twice a month, travel to sun destinations once every 2 months and attend one conference per year, I would like that to remain the same across time or to improve. Would you not? You eat your favourite meal once a week, purchase a new pair of shoes every month and go out with your friends every Friday. Would you not like being able to do any of those next year? Individuals get comfort out of the levels of consumption across time; they seek to have constant levels of consumption. In economic theory, this is called smooth consumption. In the same manner a company wishes to obtain every year similar amounts of profits; actually if you ask a financial planner, he will tell you the company seeks increasing (non-declining) levels of profits.
1.2 Objectives and Constraints
Seeking the largest amount of utility or profits is called maximization, and seeking the usage of the smallest amount of resources is called minimization. The amount to be minimized or maximized is called an objective. Restricting yourself to a given amount of some resource gives you a constraint. The amount of resources you will use is called decision variable or control variable. How effective you use your time, your machines, etc., gives you parameters which are typically related to productivity. Let us look at some examples.
Constraints impose limits to the ability of the decision maker, and they restrict the ‘universe’ of choices by considering what is feasible; for instance, producing a very large amount of ice cream may not be feasible because of storage limitations. Constraints can also limit our ability to combine resources, sometimes to produce goods or build, others to achieve intermediate elements.
The space of choices as delimited by the constraints is called feasible space. In general, one requires a ‘well-behaved’ feasible space as a requisite to solve an optimization problem and find a solution. What I mean by that will be the matter of another chapter. For now, let’s allow a loose usage of objective, constraints and decision variables.
1.3 Identifying Objectives and Constraints
One of the main issues when we deal with a problem is to narrow it down to its bare bones and capture its very nature. A model is after all a representation of reality that have abstracted many facts, concentrating only on the ones that matter for the decision maker. As a civil engineer, you will have to identify the objective as the most important element of your problem. Consider, for instance, a frequent flyer who takes flights every week but pays from his pocket.
Such traveller may wish to have a short flight, such that he arrives at his destination on time; he may want to be served free-of-charge meals or to be able to use an in-flight entertainment system with a good selection of free movies, TV shows, magazines, news, music and games. But if he pays from his pocket, the most important element for him will be the cost, how much he will have to pay overall for every trip, and hence, the objective will be the minimization of the cost.
The other elements will become constraints: the traveller may wish to have a minimum number of free films (say, one film for every 2 hours of flight time) and a minimum number of foods (say, one complete meal every 5 hours of flight). And possibly he may want to limit his options to no more than one stopover for every 6 hours of flight. All these elements turn out to be constraints. A rather different problem faces the top executive whose company pays for the flight. He does not care that much for the price of the flight; he cares for his comfort. Hence, he will try to maximize the number of amenities he counts with (number of features or conveniences). The constraint is perhaps not to expend more than the budget that the company provides him with for every trip.
The lesson learned is that an objective is nothing but a constraint without limitation, so objectives and constraints can be interchangeably used, but duplication should be avoided. Typically, we define only one objective and many constraints. In more advanced problems, one can have many objectives and even define a problem only in terms of multiple (conflicting) objectives.
One last word about constraints, sometimes we forget about evident constraints, such as the impossibility to use negative values (non-negativity), or the limitation of one choice every period. These types of constraints must also be defined. Many times we use some ‘black-box’ software to solve a problem for us, and as such having a correct problem definition results essential.
Building a model requires three major steps: (1) an identification of the very nature of the problem, (2) writing a mathematical formulation and (3) solving it. There is, however, not a given formula to do this. Understanding a problem requires us to identify the features that we have control over and that by manipulating could help us achieve a goal. Problems typically involve multiple dimensions and considerations of other systems commonly need to be removed or simplified in many cases.
1.4.1 Identifying the Nature of the Problem
If possible, start by constructing a sketch, scheme, diagram, table or any other visual representation of the problem and its mechanisms. This informal tool will definitely help you understand the problem’s nature. For any problem, look at its elements; write them down in a blank piece of paper, one by one, and use arrows to connect them and brackets to group them. Write them all down and somehow connect them.
Continue by exhaustively enlisting possible combinations of resources and how they may be limited; this will lead you to the constraints. More than that, it will allow you to identify decision variables. When writing constraints, bare in mind that constraints can be easily turn into objectives: so whenever you don’t see a limit, but there is a way to combine elements, you are possibly on the presence of an objective.
Enlist exhaustively all constraints and choose if possible one as your objective; if not, attempt to assign a relative importance to each on any scale (say 1–10). Once you have done so, assign letters to the elements that you have combined; use letters that make sense or simply use x with a subscript xi to differentiate among them. If more dimensions are involved (time, weather, alternative, origin, destination, etc.), expand the subscript to include this; the use of superscript is preferably reserved to cases where the quick visual distinction of the dimension being indexed really matters during the analysis.
1.4.2 Constructing a Mathematical Formulation
It is time now to formally express the problem. Start always with the objective. You have two choices: MAX for maximization or MIN for minimization. That depends on what your goal is. Underneath the objective, write the letter(s) that corresponds to the decision variable(s). Then continue by writing the following words: subject to or simply s.t., after which you will enlist the constraints including non-negativity and other logical constraints.
Let us look at a couple of simple examples. Imagine you are a town planner who just learnt that the federal and provincial government will fund 2/3 of a new pipeline project plus a water tank in order to secure water supply to your town. Records of water consumption for the entire town every month are available and based on previous observed history as shown on Table 1.1.
Population is stagnant (no growth) for the past 20 years. The federal government already established as a condition for funding that you should at least use a pipe such that you directly get in town a flow equivalent to the month with least requirement. What elements would you be interested on? Perhaps the capacity of the pipe and the tank? Now, how would you create the problem? Let us see: take a piece of paper and write the information that is given to you, and attempt to connect it.
TABLE 1.1
Water Consumption Demand
Month |
Consumption (×1000 m3) |
January |
72 |
February |
73 |
March |
75 |
April |
74 |
May |
77 |
June |
112 |
July |
120 |
August |
145 |
September |
110 |
October |
80 |
November |
75 |
December |
73 |
TABLE 1.2
Water Consumption: A First Attempt at Solving
Month |
Consumption (×1000 m3) |
Tank Capacity |
January |
72 |
0 |
February |
73 |
1 |
March |
75 |
3 |
April |
74 |
2 |
May |
77 |
5 |
June |
112 |
40 |
July |
120 |
48 |
August |
145 |
73 |
September |
110 |
38 |
October |
80 |
8 |
November |
75 |
3 |
December |
73 |
1 |
Perhaps some of your initial thoughts are whether to use the minimum of 72 as your pipe supply. You could even attempt to solve manually for the tank capacity. Table 1.2 is only intended to illustrate such approach.
According to this first approximation of our thoughts, we will need a water tank of 73 (×1000 m3). Although incorrect, this first approximation to the problem has taught us that we may well use a number such that the water tank never runs dry. Can we use the mid distance between lowest and highest demands, that is, average demand? Should this reduce to the minimum the tank capacity requirement? If you do so, you will find yourself in the position of Table 1.3. Most importantly, we have already identified that the objective is to minimize the monthly difference between demand and supply.
TABLE 1.3
Pipe Capacity as the Least-Square Difference
Month |
Demand (×1000 m3) |
Pipe Supply |
Monthly Deficit |
January |
72 |
90.5 |
18.5 |
February |
73 |
90.5 |
17.5 |
March |
75 |
90.5 |
15.5 |
April |
74 |
90.5 |
16.5 |
May |
77 |
90.5 |
13.5 |
June |
112 |
90.5 |
−21.5 |
July |
120 |
90.5 |
−29.5 |
August |
145 |
90.5 |
−54.5 |
September |
110 |
90.5 |
−19.5 |
October |
80 |
90.5 |
10.5 |
November |
75 |
90.5 |
15.5 |
December |
73 |
90.5 |
17.5 |
Even more our decision variable is such supply; let us call the pipe supply x and each month demand Di. So we want to minimize x − Di; as a matter of fact, this minimization is for every month, so we will write a summation and use i to represent the month, i will go from 1 to n = 12.
Additionally, note that this difference could give us positive or negative values, and at some point, they may cancel each other; so it is rather better to use the square of the difference to avoid this situation. This lead us to the following formulation.
The decision variable is x, and as we learnt from calculus, it suffices to take the first derivative of this expression with respect to x to obtain an answer which would be x = 90.5. If we add the values of column 4 of Table 1.3, we find that they add to zero; hence, we have truly minimized the difference.
Having found that 90.5 is the pipe capacity solves half of the problem. What is the tank’s required capacity? Is it 54.5 (i.e. the maximum deficit for the month of August)? From January to May there is an excess of water we could accumulate and start using it on June when the pipe does not provide us with enough water to cover the town’s needs (demand). If we do so, we would need to look at the monthly cumulative as shown in Table 1.4.
TABLE 1.4
Tank Capacity as the Maximum Deficit
Month |
Demand (×1000 m3) |
Pipe Supply |
Cumulative Deficit |
January |
72 |
90.5 |
18.5 |
February |
73 |
90.5 |
36 |
March |
75 |
90.5 |
51.5 |
April |
74 |
90.5 |
68 |
May |
77 |
90.5 |
81.5 |
June |
112 |
90.5 |
60 |
July |
120 |
90.5 |
30.5 |
August |
145 |
90.5 |
−24 |
September |
110 |
90.5 |
−43.5 |
October |
80 |
90.5 |
−33 |
November |
75 |
90.5 |
−17.5 |
December |
73 |
90.5 |
0 |
So you would have a tank of 43.5 (×1000 m3). If you select such capacity, you may be failing to consider how those elements from the real world that we neglected at the beginning of the problem may affect the required capacity of the tank.
We are making a huge investment on the premise that demand would not grow and that there are no losses of water on the system. What about pressure/pumping stations? Or simply the fact that we are only looking at monthly averages? And the daily demand could turn our results invalid. At least, we have been able to get a working model that we can now expand to incorporate the other factors.
Finally, before ending with this problem, let us look at the feasible space. What values of the decision variable can we take? As defined here the pipe supply can go from zero to any number; hence, there is no upper limit; hence is open (not closed), look the decision variable although continuous goes from (0, …) and the problem is unbounded, hence is not compact.
Thanks to the fact that the objective function moves in the direction of minimization, we can obtain an answer. If under any circumstance you were looking for the MAX, there would be no answer. We could, however, expand the problem and bring a monetary budget limitation, or a pumping capacity cap, and hence make it feasible by establishing an upper bound.
We will define here a problem that will inspire many sub-problems used through the text. We will start by attempting to define the decision-making world of civil engineers during their professional life. Acivil engineer is faced with either the design, construction or retrofit of infrastructure and buildings. If we look at buildings, the engineer will look at the use of the building and categorize it as residential, commercial, industrial, etc. For the design, the engineer faces the need to minimize the size of the foundation and the structure while restricted to standards specified by norms and codes. In addition, the engineer will look at the purpose of the building and attempt to minimize the amount of space while still complying with the number of parking spaces, offices, bathrooms and other elements as required by urban planning regulations and building by-laws.
When the engineer is tasked with the design of infrastructure, he will have to look at either surface or underground infrastructure and decide on the dimensions and features required as preconditioned by the demand (usage) from the public at large. For these, the engineer may need to play the role of planner and forecast demand for the infrastructure. Later on, the engineer will need to worry about how to maintain such infrastructure during its lifespan (Chapter 8).
Let us now set ourselves on the feet of a planner attempting to analyse the world of surface transportation demand and its links to urban planning and economic environment. This will be further explored in Chapter 6.
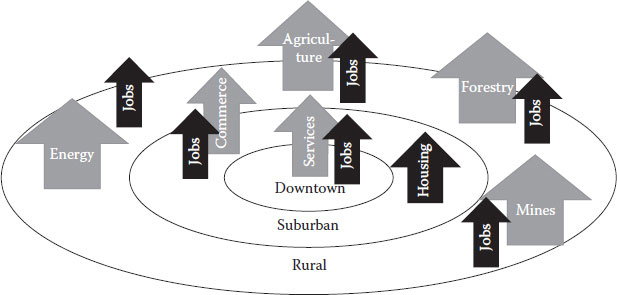
For simplicity, we will define a downtown area with suburbs and a rural region on the outskirts of our land use fabric. Land uses play an important role in defining the space of the problem; now is the time to bring the users. The decision makers will follow a positive self-selection process in which they will choose their location based on convenience; for per instance, housing will develop on the suburbs similar to retail stores. Government offices, service industries and company headquarters will locate in the downtown area. The labour market (i.e. employment or jobs) will hence concentrate there, but the other industries will attract some employment as well. In the rural area, we find basic industries (Chapter 6): agriculture, energy, forestry and raw materials. The reason behind this is the availability of such resources in such areas (Figure 1.1).
A flow of people (called commuters) will travel every day in the morning from their residences to the labour market and return back home in the afternoon. This defines the peak hours of the day. And for the civil engineer, this means the demand on mass transportation modes (trains, metro, buses, tramway, walk, bike and cars). Figure 1.2 illustrates the flow of commuting trips from housing to jobs.
A flow of commodities (goods) will be to move from the basic industries (energy, raw materials, wood, agriculture) to intermediate industries that will transform them into final goods. Energy will move as well but through wires (same as telephones and cable services such as the Internet). Figure 1.3 illustrates such flow.
A final movement of merchandises will flow from intermediate industries to final consumption markets (Figure 1.4). In this case, this is within the region or to other regions. A warning seems necessary, as suggested before the model has oversimplified reality and prevented the movement of raw materials to other regions.
FIGURE 1.1
A basic land use location set-up.
FIGURE 1.2
Commuting trips.
The condition that all raw materials will be transformed by local companies is one of such abstractions the decision maker or the planner will impose to simplify things, but that should be invoked back at the end when the analysis needs to be reconsidered in light of such limitations and simplifications.
It is always useful to explicitly state the assumptions of the model in a list format. For this example, we have several assumptions summarized in Table 1.5.
FIGURE 1.3
Freight trips to intermediate producers.
Now that the model and its environment have been defined, it is time to define the decision variable. If say a planner is looking to programme bus trips between two given points of a downtown area, she will be required to get the demand for trips between such given points. Call x your decision variable and use i to denote the origin and j to denote your destination; your decision variable turns out to be xij. To specify that the trips belong to passenger cars (c) and opposed to freight (f), we could use a superscript such that . If you care about time and want to include it as a dimension, then perhaps you can simply expand the subscript dimension and have a third index.
An objective for such planner is to have the minimum number of bus trips on the network as they cost money. This will be constrained by available budget and maximum level of total green house gas emissions (GHGs) among others.
For freight trips, the planner may be more concerned about the deterioration of the roads from the number of trips that tractor trailers moving freight produce. The number of trips is out of the control of the planner (as opposed to the allocation of buses which are commonly operated by the city). A possible objective for the planner is to maximize road condition by allocating preventive interventions (overlays, crack-sealing, etc.). One possible constraint is the annual budget. The problem could be turned around, and the cost change into an objective, meanwhile the road network condition could be transformed into a constraint by requiring a minimum average network level of condition every year for the coming decade.
A decision maker who has analysed the problem and obtained a solution should now consider how his simplification of the world may affect his choice of answers. In this sense, the planner that identified 100 million dollars per year as required expenditure to achieve required levels of service must consider that 1% of the raw materials are moved outside the region, and should adjust his model accordingly (possibly the adjustment would not make a difference), but if the percentage is large (say 20%), then the consequences should be considered and the model fine-tuned. How to do that will be discussed in the subsequent chapters.
FIGURE 1.4
Freight trips to intermediate producers on other regions.
TABLE 1.5
Explanation of Trips’ Purpose or Nature
Assumption |
Detailed Explanation |
1 |
All commuting trips from suburbs to downtown |
2 |
All raw materials to be transformed within the region |
3 |
Intermediate products produce intra- and inter-region trips |
4 |
All industries of the same type aggregated to one big company |
5 |
Aggregation of trips from one zone to the other |
1. ConcreteMixer, Inc. was contracted by Infradevelopper, Inc. to produce Portland concrete class III, which is a high-resistance waterproof concrete. What are the objective(s) and constraint(s) of each company?
2. A steel re-bar company is contracted by InfrasRoad, Inc. to produce 100,000 re-bars, type 45M of 6 m long. For this task, they need to use their machines, raw iron and labour. What is/are the objective(s)? Constraints?
3. You are hired to design a house for a wealthy customer. He wants 10 rooms, 10 bathrooms, a cinema room, a gym, an indoor pool, a garage for 15 cars, 2 kitchens and at least 3 terraces. The house must look like a castle from the outside but be modern from the inside. He is not concerned about the cost, but cares about having a smart home with voice control for blinds, lights, temperature control, ambient music and electric devices. Controlling each possible aspect is requested. What is your objective? Constraint(s)?
4. A structural engineer is asked to design the new Champlain Bridge connecting Montreal and Brossard regions. What could be the objective and constraints?
5. A transportation engineer is asked to design the new Champlain Bridge. What could be the objective and constraints?
6. A road maintenance engineer is asked to reduce the amount of gas emissions produced by the annual maintenance and rehabilitation of the pavements within a metropolitan area. For this, the planner has some control over the maintenance and rehabilitation treatments employed to rehabilitate pavements. What could be the objective and the constraints?
7. A water planner wants to make sure there is enough water coming to town through the pipeline that feeds in the river and brings water into the water treatment plant. What would be his objective?
Now, try to think what elements would condition or constrain this objective that actually push the decision maker to move in the direction contrary to that of the objective.
8. What is the objective of a structural engineer dimensioning beams and columns for a high-rise building? Which ones would be his or her constraints? Think of the fact that this engineer follows codes such as the building codes and the seismic codes, which guide the designer to allocate certain amounts of reinforcement to the concrete elements and to use certain strength for the concrete itself.
9. Consider the position of a manager who is in charge of making sure there is no flooding in town; hence, the manager must replace pipes in order to increase their capacity and make sure there is no standing water during a period of intense rain. What is the objective and what are the constraints?
10. What is the objective of a project manager in charge of the construction of a new building in downtown Montreal? Formulate the objective and the constraints and then modify your formulation by converting a constraint in the new objective and the old objective in a new constraint.
11. An engineer is being asked to design a dam for a hydroelectric company. What would be the various possible combinations of objectives and constraints?
12. The city hall has received thousands of complaints regarding the improper functioning of the mass transportation system (buses, metro, trains) in the city, and 90% of the people complaining are travellers going to work, while the rest are students going to school. What should be the objective and what constraints can you identify?
13. A student is trying to pass a certain class at school. What is her objective and her constraints?
14. A foundation engineer is hired to conduct soil explorations in order to design the foundations of a building. The idea is to have a good idea of the bearing capacity of the soil; the more exploration the engineer conducts, the more accurate will be the characterization of the bearing capacity. However, this is also expensive and time consuming. Identify possible objective-constraint pairs for this problem.
15. As airport manager you perceive that the airport needs to go through a rehabilitation. This requires soil exploration to determine where the weak segments of the pavement are. This also requires a measurement of the thickness of the pavement in order to make sure the strength is adequate.
These two elements can be tackled through sampling with boreholes. Finally, you need to measure the surface skid resistance to ensure safety. You know your maximum budget is one million dollars for getting the job done. What could be your objective and constraints?
16. You have to travel to Miami for a conference. The university gives you $1000 for such purpose. Enunciate your objective and constraints.
17. Consider now a business executive that needs to travel every week. Given the company pays for his plane ticket, what would be possible objectives and constraints?
18. Let us twist the previous example and let us think of the poor student trying to travel home for vacations. She pays for everything from her pocket. What would be her objective and constraints?
19. What is the objective of a driver whose company pays for the rental, the fuel and the food involved in a road trip?
20. What is the objective and constraints of a driver using his own car to travel during the long weekend for vacations to New York?
Answers
1. Holcim’s objective is to minimize cost and constraint is that concrete characteristics are adequate. SNC Lavalin’s objective is to acquire the maximum concrete strength and waterproof possible while not spending more than the given budget.
2. Possible objectives: Minimize cost of production or maximize productivity. Constraints: Number of re-bars each machine produces per hour, number of hours employees work per day (or per week).
3. As a professional engineer, you must satisfy the customer’s expectations. So the objective is to maximize number/capability of technological features. The constraint is the type of technology that is able to meet the client’s requirements. Budget is not a constraint in this case as the customer is a rich millionaire who does not care!
4. Objectives: Minimize cost or minimize re-bar size and amount of concrete. Constraint: Achieve sufficient structural capacity to comply with steel/concrete codes.
5. Objective: Maximize the bridge’s traffic capacity (i.e. number of vehicles that can use the bridge). Constraint: Budget.
6. The objective is to minimize the total annual amount of gas emissions (or you can also do it for another period of time such as a semester or a month, but the typical choice of a year is to match the annual operation and budget cycle).
The constraints are the level of condition and the overall quality of the roads. As you can imagine without this constraint, the optimal solution would be to do no maintenance and rehabilitation activities because that results in zero gas emission.
We need a minimum level of quality on the condition of the roads to push in the opposite direction to the minimization of gas emissions (i.e. minimization of rehabilitation and maintenance treatments).
7. The objective is to maximize the amount of water coming into the water treatment plant. The problem is the constraints. For instance, there is a budget that will restrict the ability to have a very big pipe, so pipe diameter will be conditioned by budget: the bigger the pipe, the more expensive it is.
Another constraint comes from the fact that the water treatment plant has a restricted capacity as well. So it is pointless to have a lot of water if it cannot be treated.
8. The engineer will try to have a design that complies with codes; codes commonly provide you with minimum strength, dimensions, separation, reinforcement (re-bars), etc.
The problem is that the customer has a budget and often there is a conflict between the client and the designer because the design implies a large amount of money. So the objective is to have a safe design and to maximize the structural adequacy of the building.
The constraints are not only the budget but also the minimums required by the code. This puts the engineer in a complicated situation wherein sometimes element spacing, type of materials and location of columns and beams may need to be revised in an attempt to reduce the cost while still warranting an adequate design.
9. The manager attempts to maximize total network capacity for the pipes in the system. This implies replacements, and replacements are limited by not only the budget, and they are also limited by the season of the year.
10. One of the many possible objectives is to minimize construction time; in this case, the budget and the quality of the construction will become constraints.
Alternatively, one can use the cost as an objective and state a minimization of cost while constraint by a time budget (no more than 12 months for the completion per instance) and a quality of construction constraint (no less than 9 in overall quality score).
One can also make the quality an objective and state a maximization of construction quality while restricted by budget and time constraints.
11. The dam must be safe, so you may want to maximize structural integrity while constrained by a money budget.
This can be changed to minimize budget while constrained by a minimum level of safety on the design.
12. The objective for the city planner would be to minimize total travel time for all passengers on the network. The constraints in this case would be the total budget available for changes and the number of operators and vehicles available for the movement of people.
Another possible objective could be to minimize cost while constrained by a maximum travel time. The establishment of such travel time is a complicated matter we will try to tackle in Chapter 7.
13. The student may use as objective to maximize her grades and her constraints would be total time to study, total budget for books and other support materials.
A possible alternation would be to have as objective to minimize total cost and effort in time used to study, and in this case, the constraint will be to obtain at least a B-grade.
14. The foundation engineer’s objective could be to maximize certainty for the characterization of the soil’s bearing capacity and the constraint will be the budget available for soil exploration.
A possible objective could be to minimize cost while having 80% confidence that the soil characterization is correct.
15. The airport manager would want to minimize total cost, and in this case, the constraints will be to make sure the strength of the pavement is at least superior to some minimum value. The other constraint will come from the skid resistance of the surface to make sure you warrant certain level of safety for the planes that are landing or taking off.
A possible alternation of this objective is maximizing the strength of the pavement, and the skid resistance and budget become objectives. Alternatively, you can have maximizing skid resistance as objective while constrained by a money budget and minimum overall strength.
16. The objective is to minimize cost (because that means money in your pocket) the constraint is to arrive to your destination.
17. The business executive wants to maximize his comfort–defined as legroom, space for his own, amenities and features such as having a meal on the plane, enjoying entertainment through the availability of films, music, games, etc. In addition, the ability to have a flat-bed seat on long-haul flights, the space separation to the next passenger (unless he enjoys somebody’s elbows over his seat space).
So in summary, the objective is to maximize comfort. The constraints are arriving at the destination within a reasonable amount of time and under the given budget given by the company to pay for the ticket.
18. The poor traveller who pays for her ticket wants to minimize cost; of course, she also enjoys the amenities of entertainment and meals and the comfort of the legroom, overall seat width and if she can get into a business class seat she will, but all these elements will be part of the constraints. She will establish the minimum required amount of features in that regard.
19. The traveller will rent the best car he can, so he will maximize the luxury of the vehicle while restrained by a certain budget.
20. The student travelling to New York on a road trip using his own vehicle wants to minimize travel cost, reducing fuel consumption and overall travel expenditures. This traveller will pack home-made sandwiches, roll the car downhill and will not stop to rest unless strictly necessary (consider when you stop, you expend more fuel given where you have to go through a cycle of lower shifts). The constraints will be the level of comfort; he is not going to travel without food or a place to sleep at night.