© Springer-Verlag GmbH Deutschland, ein Teil von Springer Nature 2022
S. Boblest et al.Spezielle und allgemeine Relativitätstheoriehttps://doi.org/10.1007/978-3-662-63352-6_4

4. Physikalische Folgen der Lorentz-Invarianz

Sebastian Boblest1  , Thomas Müller2   und Günter Wunner3  
(1)
Dürnau, Deutschland
(2)
Max-Planck-Institut für Astronomie, Haus der Astronomie, Heidelberg, Deutschland
(3)
Universität Stuttgart, 1. Institut für Theoretische Physik, Stuttgart, Deutschland
 

Die Lorentz-Invarianz der physikalischen Gesetze führt zu einer Vielzahl von Phänomenen, die in der nichtrelativistischen, durch die Galilei-Transformation bestimmten Physik nicht auftreten. Praktisch alle diese Konsequenzen der SRT widersprechen unserem Alltagsverständnis, weil sie erst bei hohen Geschwindigkeiten große Effekte aufweisen.

4.1 Verlust der Gleichzeitigkeit

Wir haben alle ein elementares Verständnis, was es bedeutet, wenn zwei Ereignisse „gleichzeitig“ stattfinden. Praktisch jeder von uns besitzt heute mindestens eine sehr genau gehende Uhr und wir müssen nur die jeweiligen Uhrzeiten vergleichen, die z. B. zwei Beobachter an unterschiedlichen Orten bei bestimmten Ereignissen gemessen haben, und können dann entscheiden, ob diese beiden Ereignisse, innerhalb der Messgenauigkeit, gleichzeitig stattgefunden haben.

Woher wissen wir aber, dass beide Uhren wirklich synchron gehen? Bei den Genauigkeiten, die im Alltag wichtig sind, ist diese Frage nebensächlich, wir können die beiden Uhren einfach zusammenbringen und vergleichen. Auf einer fundamentaleren Ebene ist diese Frage aber überhaupt nicht trivial, denn um die beiden Uhren zusammenzuführen, muss mindestens eine aus ihrem Ruhsystem herausbewegt werden, dabei transformieren sich ihre Koordinaten entsprechend der Lorentz-Transformation. Weil dabei die Zeit mittransformiert wird, zerstört dieser Vorgang tatsächlich die Synchronität.

Eine Möglichkeit zwei Uhren an unterschiedlichen Orten zu synchronisieren ist in Abb. 4.1 gezeigt. Die beiden Uhren sollen in einem Abstand d ruhen. Eine Apparatur in der Mitte sendet gleichzeitig einen Lichtstrahl zu beiden Uhren aus. Beide Uhren werden dann auf t = 0 gestellt, wenn der Lichtstrahl sie erreicht. Nach einem ähnlichen Prinzip funktionieren auch Funkuhren, die ihren Gang regelmäßig mit einem Zeitzeichensender abgleichen. Die Ungenauigkeit aufgrund der unterschiedlichen Abstände zum Sender wird in diesem Fall vernachlässigt, ließe sich aber für ein genaueres Ergebnis auch nachträglich korrigieren.
Abb. 4.1

Schema zur Uhrensynchronisation. Zwei Uhren im Abstand d werden genau dann auf t = 0 gestellt, wenn der Lichtstrahl, der in der Mitte gleichzeitig zu beiden Uhren ausgesendet wurde, sie erreicht

Wir möchten jetzt untersuchen, wie sich die Gleichzeitigkeit von Ereignissen in verschiedenen Bezugssystemen darstellt. Dazu betrachten wir zwei Systeme S und Sʹ, wobei sich Sʹ relativ zu S mit der Geschwindigkeit β > 0 entlang der x-Achse bewegt. In Sʹ sollen zwei Ereignisse E1 („Uhr 1 zeigt $$ {t}_1^{\prime }=3 $$“) und E2 („Uhr 2 zeigt $$ {t}_2^{\prime }=3 $$“) gleichzeitig an verschiedenen Orten stattfinden. Es gilt also
$$ {E}_1:\left(c{t}_1^{\prime },{x}_1^{\prime}\right)\quad \mathrm{und}\quad {E}_2:\left(c{t}_2^{\prime },{x}_2^{\prime}\right)\quad \mathrm{mit}\quad {x}_1^{\prime}\ne {x}_2^{\prime }. $$
(4.1)
Uns interessieren die Zeitkoordinaten der beiden Ereignisse bezogen auf das System S. Dazu verwenden wir die inverse Lorentz-Transformation
$$ ct=\gamma \left( ct^{\prime }+\beta x^{\prime}\right),\quad x=\gamma \left(x^{\prime }+\beta ct^{\prime}\right), $$
(4.2)
Aus der Differenz der Zeitkoordinaten in S,
$$ c{t}_2-c{t}_1=\gamma \left(c{t}_2^{\prime }+\beta {x}_2^{\prime }-c{t}_1^{\prime }-\beta {x}_1^{\prime}\right)=\gamma \beta \left({x}_2^{\prime }-{x}_1^{\prime}\right) $$
(4.3)
folgt wegen $$ {t}_1^{\prime }={t}_2^{\prime } $$ und $$ {x}_1^{\prime}\ne {x}_2^{\prime } $$, dass t2 ≠ t1 ist. Im System S finden die beiden Ereignisse also nicht gleichzeitig statt (s. Abb. 4.2).
Abb. 4.2

Das System Sʹ bewege sich mit der Geschwindigkeit β = 0,5 relativ zu S. Zwei Ereignisse E1 und E2, die im System Sʹ zur gleichen Zeit, aber an unterschiedlichen Orten stattfinden, finden im System S nicht gleichzeitig statt. Die grauen, gestrichelten Linien geben Orte gleicher Zeit in Sʹ an, wohingegen die schwarzen, gepunkteten Linien Orte gleicher Zeit in S bestimmen

Wenn die Gleichzeitigkeit von Ereignissen vom Inertialsystem abhängt, so kann auch die zeitliche Abfolge von Ereignissen in unterschiedlichen Systemen verschieden sein. Auf den ersten Blick erscheint das unphysikalisch, denn eine willkürliche zeitliche Abfolge von Ereignissen scheint das Kausalitätsprinzip von Ursache und Wirkung zu verletzen. Die Lösung für dieses Problem liegt darin, dass die hier betrachteten Punkte jeweils raumartige Intervalle bilden. Zwei in einem Inertialsystem zur gleichen Zeit an verschiedenen Orten stattfindende Ereignisse sind nicht kausal verbunden. Die Abfolge zeitartiger, d. h. möglicherweise kausal verknüpfter, Ereignisse dagegen ist in jedem Inertialsystem gleich, auch wenn hier verschiedene Zeitdifferenzen möglich sind.

4.2 Lorentz-Kontraktion bewegter Maßstäbe

Der Effekt der Lorentz-Kontraktion ist mit dem Verlust der Gleichzeitigkeit aus dem vorherigen Abschnitt eng verbunden. Betrachten wir wieder ein System Sʹ, welches sich mit der Geschwindigkeit β > 0 bezüglich S bewege. Ein Stab mit der Länge $$ l^{\prime }=\mid {x}_B^{\prime }-{x}_A^{\prime}\mid $$ ruhe in Sʹ. Seine beiden Endpunkte werden durch die Weltlinien $$ {\mathcal{W}}_A $$ und $$ {\mathcal{W}}_B $$ beschrieben (s. Abb. 4.3). Betrachten wir den Stab zur Zeit ctʹ = 0, so stellen wir fest, dass die beiden Ereignisse an den Endpunkten des Stabes, die wir zur Längenmessung verwenden, bezogen auf S nicht gleichzeitig stattfinden. Nun bedeutet aber eine Längenmessung, dass wir die Orte der Endpunkte zur gleichen Zeit bestimmen müssen, um aus deren Differenz die Länge ermitteln zu können. Für die Längenmessung in S heißt das, dass wir zwei Beobachter OA und OB finden müssen, die sich zur Zeit ct0 an den jeweiligen Endpunkten des Stabes befinden. Aus deren räumlichen Abstand erhalten wir dann die gemessene Länge l = |xB − xA| in S.
Abb. 4.3

Längenkontraktion eines in Sʹ ruhenden Stabes der Länge lʹ. Die in S ruhenden Beobachter OA und OB messen zur Zeit ct0 die Länge l. Sʹ bewegt sich gegenüber S mit β = 0,5

Um den Zusammenhang zwischen der Ruhelänge lʹ und der in S gemessenen Länge l herzustellen, benötigen wir zunächst die Weltlinien $$ {\mathcal{W}}_A $$ und $$ {\mathcal{W}}_B $$ der beiden Endpunkte, die wir jeweils mit Hilfe der Koordinatenzeit $$ {t}_A^{\prime } $$ beziehungsweise $$ {t}_B^{\prime } $$ parametrisieren,
$$ {\mathcal{W}}_A:c{t}_A=\gamma \left(c{t}_A^{\prime }+\beta {x}_A^{\prime}\right),{x}_A=\gamma \left({x}_A^{\prime }+\beta c{t}_A^{\prime}\right), $$
(4.4)
$$ {\mathcal{W}}_B:c{t}_B=\gamma \left(c{t}_B^{\prime }+\beta {x}_B^{\prime}\right),{x}_B=\gamma \left({x}_B^{\prime }+\beta c{t}_B^{\prime}\right). $$
(4.5)
Die Längenmessung erfolgt gleichzeitig in S, was uns zu tA = tB = t0 führt. Damit können wir die Zeiten $$ {t}_A^{\prime } $$ und $$ {t}_B^{\prime } $$ ermitteln und in die Gleichungen für die Orte xA und xB einsetzen. Deren Differenz führt uns auf
$$ l=\mid {x}_B-{x}_A\mid =\frac{\left|{x}_B^{\prime }+\beta {t}_0-{x}_A^{\prime }-\beta {t}_0\right|}{\gamma }=\frac{\left|{x}_B^{\prime }-{x}_A^{\prime}\right|}{\gamma }=\frac{l^{\prime }}{\gamma }. $$
(4.6)
Da γ > 1 für β > 0 ist, ist die in S gemessene Länge l stets kürzer als die Ruhelänge lʹ.

Wir betrachten später noch genauer, was die Lorentz-Kontraktion für die Beobachtung schnell bewegter Körper bedeutet. Dabei wird durch unterschiedliche Lichtlaufzeit von verschiedenen Punkten eines Objektes die Lorentz-Kontraktion nicht direkt beobachtbar.

4.3 Bewegte Uhren: Zeitdilatation

Der Verlust der Gleichzeitigkeit, den wir in Abschn. 4.1 besprochen haben, widerspricht unserer alltäglichen Erfahrung vom Ablauf der Zeit. Noch unverständlicher wird es, wenn wir Zeitdifferenzen von unterschiedlichen Bezugssystemen aus untersuchen.

Dazu positionieren wir zwei baugleiche Uhren in den Koordinatenursprüngen von S und Sʹ, die jeweils in ihrem System ruhen. Das System Sʹ bewege sich wieder mit der Geschwindigkeit β > 0 bezüglich S. Betrachten wir nun die in Sʹ ruhende Uhr, deren Weltlinie der ctʹ-Achse entspricht (s. Abb. 4.4).
Abb. 4.4

Die Uhr, die im Koordinatenursprung des Systems S′ ruht, zeigt eine Zeitdifferenz cΔt′ an. Im System S entspricht das einer Zeitdifferenz cΔt

Bezogen auf das System S hat ihre Weltlinie die Koordinaten (ct = γctʹ, x = γβctʹ). Dann können wir eine Zeitdifferenz $$ c\Delta t^{\prime }=c\left({t}_2^{\prime }-{t}_1^{\prime}\right) $$ in eine Zeitdifferenz bezogen auf S umrechnen,
$$ c\Delta t=c{t}_2-c{t}_1=\gamma c{t}_2^{\prime }-\gamma c{t}_1^{\prime }=\gamma c\Delta t^{\prime }. $$
(4.7)
Das heißt aber, dass wir im bewegten System Sʹ eine kleinere Zeitdifferenz messen als im System S.

Ohne weitere Anmerkungen würden wir mit dem bisher Gesagten in ein Paradoxon laufen, denn wir könnten die Situation auch so betrachten, dass Sʹ ruht und S sich bewegt, was aufgrund des Relativitätsprinzips vollkommen legitim wäre. Dann würde aber die Zeitdifferenz im System S kürzer dauern als in Sʹ und wir hätten einen Widerspruch. Der entscheidende Punkt ist, dass wir die Zeitdifferenz in S nicht vom Ort der Uhr im Ursprung beurteilen können. Tatsächlich brauchen wir, wie im Beispiel der Lorentz-Kontraktion, mindestens zwei synchronisierte, ruhende Uhren in S, die an den Orten $$ {x}_1=\gamma \beta c{t}_1^{\prime } $$ und $$ {x}_2=\gamma \beta c{t}_2^{\prime } $$ die jeweilige Zeit $$ c{t}_1^{\prime } $$ und $$ c{t}_2^{\prime } $$ der bewegten Uhr ablesen.

Der Effekt der Zeitdilatation kann sehr gut bei kurzlebigen Elementarteilchen nachgewiesen werden. Beim Auftreffen der kosmischen Strahlung auf die Atmosphäre entstehen z. B. sich mit sehr hoher Geschwindigkeit bewegende Myonen. Diese haben eine mittlere Lebensdauer Δt ≈ 2 · 10−6 s.

Rossi und Hall [5] haben 1941 diese Myonen benutzt, um erstmals die relativistische Zeitdilatation zu messen (s. Abb. 4.5). Ohne Zeitdilatation ergäbe sich aus der mittleren Lebensdauer der Myonen eine mittlere Reichweite von
$$ L<\beta \Delta t\approx 600\ \mathrm{m}. $$
(4.8)
Da die Myonen in einer Höhe von etwa 9 − 12 km entstehen, sollten also praktisch keine dieser Teilchen auf dem Erdboden ankommen. Aufgrund der Zeitdilatation verlängert sich aus dem Ruhsystem der Erde aus gesehen aber die Lebenszeit der Myonen, und die mittlere Reichweite steigt auf
$$ L=\beta \frac{\Delta t}{\gamma }. $$
(4.9)
Bei einer Geschwindigkeit β = 0,995 ergibt das etwa 6000 m, genug, damit ein merklicher Anteil der Myonen den Erdboden erreichen kann. Rossi und Hall haben die Abhängigkeit der Lebensdauer von der Geschwindigkeit ausgenutzt, um die Zeitdilatation nachzuweisen. Dazu haben sie an zwei Punkten mit unterschiedlicher Meereshöhe gemessen, wieviele Myonen bei ihnen ankommen. Zum einen in Denver auf einer Höhe von 1616 m und zum anderen beim nicht weit entfernten Echo Lake auf einer Höhe von 3240 m. Aufgrund der größeren Höhe sollten dort mehr Myonen gemessen werden, was auch tatsächlich gefunden wurde. Um noch weitere Informationen zu gewinnen, wurden bei einigen Messreihen Eisenplatten vor die Detektoren gesetzt, die nur Myonen mit genügend hoher Geschwindigkeit durchqueren konnten. Durch den Vergleich der Abnahme der Zahl der Myonen mit unterschiedlichen Geschwindigkeiten konnten die beiden mit der speziell-relativistischen Vorhersage vergleichen. Ähnliche Versuche wurden später mit erhöhter Genauigkeit durchgeführt und bestätigten die Vorhersagen der SRT sehr gut, siehe z. B. [2]. Eine kompakte Apparatur zur Bestimmung der Lebenszeit von Myonen wird auch in [1] beschrieben.
Abb. 4.5

Skizze zum Experiment von Rossi und Hall [5]. Beim Auftreffen der kosmischen Strahlung auf die Atmosphäre entstehen kurzlebige Myonen (μ−) mit einer Lebensdauer von etwa 2 · 10−6 s. Je nach Meereshöhe eines Beobachtungspunktes erreichen unterschiedlich viele dieser Teilchen den Erdboden

Ein sehr schöner Versuch mit echten Uhren wurde 1972 von Hafele und Keating [3, 4] durchgeführt. Sie schickten Atomuhren in Linienflügen um die Welt einmal in Ost- und einmal in Westrichtung. Bei diesem Versuch treten auch allgemein-relativistische Effekte aufgrund der Erdgravitation auf (s. Abschn. 13.​4.​6).

4.4 Paradoxa der SRT

Die Eigenschaften der Lorentz-Invarianz führen sehr leicht zu scheinbaren Widersprüchen. Widersprüchliche Vorhersagen würden die SRT aber „ad absurdum“ führen, d. h. als physikalische Theorie unbrauchbar machen.

Die SRT ist vermutlich diejenige Theorie, in der die größte Anzahl solcher Paradoxa diskutiert wird. In diesem Abschnitt besprechen wir einige solcher scheinbaren Widersprüche. Mit den gerade diskutierten Problemstellungen sind wir aber gut gerüstet, diese aufzulösen.

4.4.1 Das Stab-Rahmen-Paradoxon

Wir betrachten einen bewegten Stab der Länge l und einen ruhenden Rahmen mit derselben Länge l. Wegen der Längenkontraktion hat der Stab im Ruhsystem des Rahmens die Länge l∕γ und passt daher bequem in den Rahmen. Wir sehen jedoch sofort einen scheinbaren Widerspruch:

„Im Ruhsystem des Rahmens erfährt der Stab eine Längenkontraktion und passt in den Rahmen. Im Ruhsystem des Stabes dagegen erfährt der Rahmen eine Längenkontraktion. Der Stab passt nicht in den Rahmen.“

Um dieses Paradoxon aufzulösen müssen wir präzise darlegen, was die Sprechweise „passt in den Rahmen“ bedeutet. Wir verstehen darunter, dass sich Anfangs- und Endpunkt gleichzeitig innerhalb des Rahmens befinden. Wie wir gesehen haben ist aber Gleichzeitigkeit eine inertialsystemabhängige Eigenschaft. Darin liegt der Schlüssel zur Auflösung unseres Problems.

Im Folgenden soll sich der Stab mit der Geschwindigkeit β relativ zum Ruhsystem S des Rahmens in positive x-Richtung bewegen. Dementsprechend bewegt sich der Rahmen, bezogen auf das Ruhsystem Sʹ des Stabes, mit der Geschwindigkeit − β in negative xʹ-Richtung. Die Randpunkte des Rahmens werden in dessen Ruhsystem S durch die Weltlinien
$$ {\mathcal{R}}_l:\left(c{t}_{rl},{x}_{rl}\left({t}_{rl}\right)={r}_l=\mathrm{const}\right)\quad \mathrm{bzw}.\quad {\mathcal{R}}_r:\left(c{t}_{rr},{x}_{rr}\left({t}_{rr}\right)={r}_r=\mathrm{const}\right) $$
(4.10)
parametrisiert, wobei der erste Index der Koordinaten für „Rahmen“ und der zweite Index für „links“ bzw. „rechts“ steht. Die entsprechende Parametrisierung bezogen auf das Ruhsystem des Stabes erhalten wir durch eine Lorentz-Transformation zu
$$ {\mathcal{R}}_l:\left(c{t}_{rl}^{\prime },{x}_{rl}^{\prime}\left({t}_{rl}^{\prime}\right)=\frac{r_l}{\gamma }-\beta c{t}_{rl}^{\prime}\right)\quad \mathrm{bzw}.\quad {\mathcal{R}}_r:\left(c{t}_{rr}^{\prime },{x}_{rr}^{\prime}\left({t}_{rr}^{\prime}\right)=\frac{r_r}{\gamma }-\beta c{t}_{rr}^{\prime}\right) $$
(4.11)
mit $$ c{t}_{rl}^{\prime }=\gamma \left(c{t}_{rl}-\beta {r}_l\right) $$ und $$ c{t}_{rr}^{\prime }=\gamma \left(c{t}_{rr}-\beta {r}_r\right) $$. Für die Endpunkte des Stabes erhalten wir analog die Weltlinien
$$ {\mathcal{S}}_l:\left(c{t}_{sl}^{\prime },{x}_{sl}^{\prime}\left({t}_{sl}^{\prime}\right)={s}_l^{\prime }=\mathrm{const}\right)\quad \mathrm{bzw}.\quad {\mathcal{S}}_r:\left(c{t}_{sr}^{\prime },{x}_{sr}^{\prime}\left({t}_{sr}^{\prime}\right)={s}_r^{\prime }=\mathrm{const}\right) $$
(4.12)
bezogen auf dessen Ruhsystem Sʹ. Die inverse Transformation von Sʹ nach S liefert
$$ {\mathcal{S}}_l:\left(c{t}_{sl},{x}_{sl}\left({t}_{sl}\right)=\frac{s_l^{\prime }}{\gamma }+\beta c{t}_{sl}\right)\quad \mathrm{bzw}.\quad {\mathcal{S}}_r:\left(c{t}_{sr},{x}_{sr}\left({t}_{sr}\right)=\frac{s_r^{\prime }}{\gamma }+\beta c{t}_{sr}\right) $$
(4.13)
mit $$ c{t}_{sl}=\gamma \left(c{t}_{sl}^{\prime }+\beta {s}_l^{\prime}\right) $$ und $$ c{t}_{sr}=\gamma \left(c{t}_{sr}^{\prime }+\beta {s}_r^{\prime}\right) $$.
Abb. 4.6 zeigt das Minkowski-Diagramm der Situation aus Sicht des Ruhsystems des Rahmens mit den zugehörigen Weltlinien $$ {\mathcal{R}}_l $$ und $$ {\mathcal{R}}_r $$ der Randpunkte. $$ {\mathcal{S}}_l $$ und $$ {\mathcal{S}}_r $$ beschreiben die Weltlinien der beiden Stabenden. Die Länge $$ \Delta s^{\prime }=\mid {s}_r^{\prime }-{s}_l^{\prime}\mid $$ des Stabes gemessen in Sʹ ist gleich dem Abstand Δr = |rr − rl| zwischen den Rändern des Rahmens gemessen in S; wir setzen daher Δr = Δsʹ =: ℓ. Wie wir aus Abschn. 4.2 wissen, bedeutet messen, dass wir die Endpunkte des Stabes zur gleichen Zeit feststellen müssen. Dies hat zur Folge, dass im Ruhsystem des Rahmens der Stab eine gemessene Länge Δs = Δsʹ∕γ = ℓ∕γ besitzt und daher bequem in den Rahmen hineinpasst.
Abb. 4.6

Stab-Rahmen-Paradoxon aus Sicht des Ruhsystems S des Rahmens. Die Weltlinien $$ {\mathcal{R}}_l $$ und $$ {\mathcal{R}}_r $$ kennzeichnen die Randpunkte des Rahmens, wohingegen die Weltlinien $$ {\mathcal{S}}_l $$ und $$ {\mathcal{S}}_r $$ die Endpunkte des Stabes angeben

Die Ereignisse ①–④ in Abb. 4.6 kennzeichnen die vier wesentlichen Stationen der Bewegung. In ① trifft die rechte Seite des Stabes (dunkelgrauer Balken) den linken Rand des Rahmens. Zwischen den Ereignissen ② und ③ „befindet“ sich der Stab innerhalb des Rahmens. In ④ hat der Stab den Rahmen komplett verlassen. Die zugehörigen Zeitpunkte können direkt durch Schnitt der jeweiligen Weltlinien des Stabes mit denen des Rahmens ermittelt werden. Für die Zeiten erhalten wir
$$ c{t}_1=\frac{r_l}{\beta }-\frac{s_r^{\prime }}{\beta \gamma},\quad c{t}_2=\frac{r_l}{\beta }-\frac{s_l^{\prime }}{\beta \gamma},\quad c{t}_3=\frac{r_r}{\beta }-\frac{s_r^{\prime }}{\beta \gamma},\quad c{t}_4=\frac{r_r}{\beta }-\frac{s_l^{\prime }}{\beta \gamma}. $$
(4.14)
Zu jedem Ereignis zeigen die hellgrauen Balken die Lage des Stabs an wo er sich bezogen auf sein Ruhsystem Sʹ befindet. Das heißt zum Beispiel, wenn der rechte Endpunkt des Stabes im Ereignis ③ den rechten Rand des Rahmens berührt, so befindet sich sein linker Rand noch gar nicht im Rahmen. Dieser scheinbare Widerspruch ist dadurch begründet, dass Gleichzeitigkeit abhängig vom System ist. Aus Sicht des Rahmensystems befindet sich der Stab zur Zeit ct3 vollständig innerhalb des Rahmens. Bezogen auf das Ruhsystems des Stabes werden dessen Endpunkte jedoch zu unterschiedlichen Zeiten gemessen.
Abb. 4.7 zeigt die Situation aus Sicht des ruhenden Stabs mit den identischen Ereignissen ①-④. Deren Koordinaten folgen aus der Lorentz-Transformation vom System S in das System Sʹ,
$$ c{t}_1^{\prime }=\frac{r_l}{\beta \gamma}-\frac{s_r^{\prime }}{\beta },\quad c{t}_2^{\prime }=\frac{r_l}{\beta \gamma}-\frac{s_l^{\prime }}{\beta },\quad c{t}_3^{\prime }=\frac{r_r}{\beta \gamma}-\frac{s_r^{\prime }}{\beta },\quad c{t}_4^{\prime }=\frac{r_r}{\beta \gamma}-\frac{s_l^{\prime }}{\beta }. $$
(4.15)
Wieder kennzeichnet Ereignis ①, wann das rechte Stabende den linken Rand des Rahmens trifft. Die hellgrauen waagrechten Balken geben die Lage des Stabs in dessen Ruhsystem wieder, wohingegen die dunkelgrauen schrägen Balken dessen Position beschreiben, wie sie im Ruhsystem des Rahmens gemessen werden.
Abb. 4.7

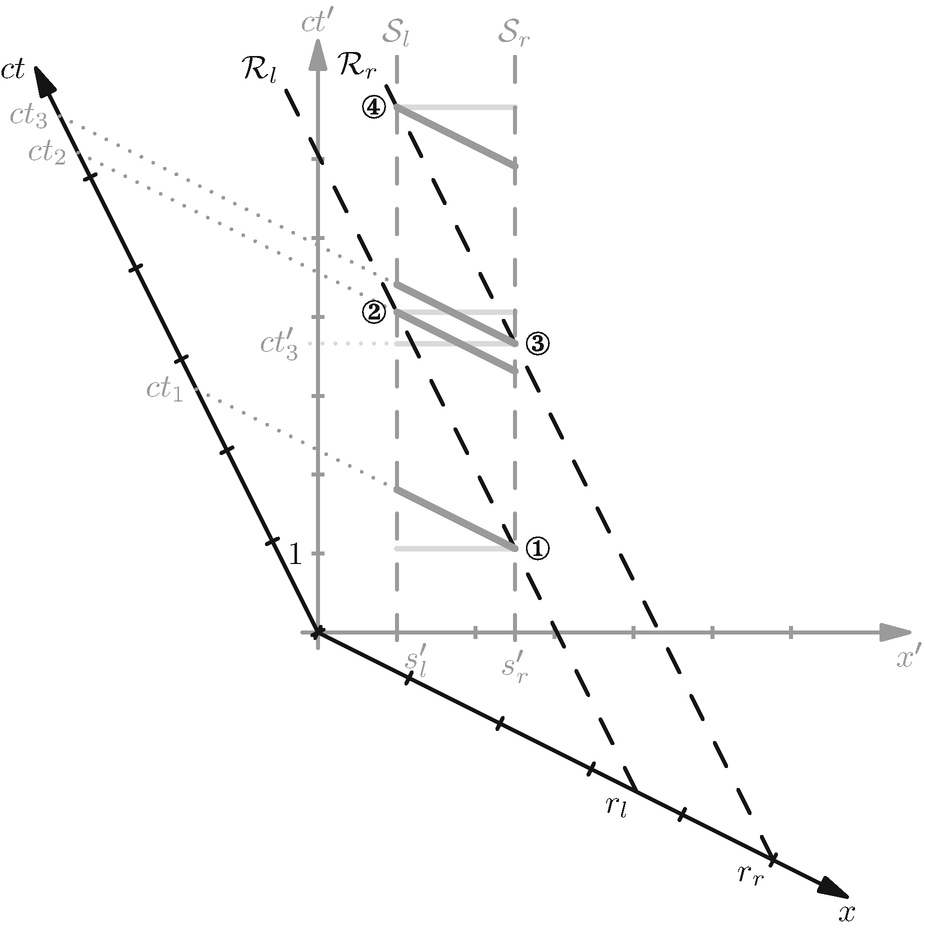
Stab-Rahmen-Paradoxon aus Sicht des Ruhsystems S′ des Stabes

Bei den Ereignissen ② und ③ fällt sofort auf, dass sie zeitlich vertauscht sind und Ereignis ③ vor ② stattfindet. Dies lässt sich auch sofort aus den Zeitdifferenzen mit Hilfe der Beziehungen (4.14) und (4.15) herleiten,
$$ c\Delta {t}_{3,2}=c{t}_3-c{t}_2=\frac{\ell }{\beta}\left(1-\frac{1}{\gamma}\right)>0 $$
(4.16)
und
$$ c\Delta {t}_{3,2}^{\prime }=c{t}_3^{\prime }-c{t}_2^{\prime }=\frac{\ell }{\beta}\left(\frac{1}{\gamma }-1\right)<0. $$
(4.17)
Das heißt, das rechte Ende des Stabes trifft zuerst den rechten Rand des Rahmens in ③ bevor das linke Ende des Stabes auf den linken Rand des Rahmens in ② trifft. Diese Abfolge konnten wir jedoch schon in Abb. 4.6 anhand der hellgrauen Balken beobachten.

Das scheinbare Paradoxon zeigt sich nun darin, dass der Stab länger ist als der gemessene Abstand zwischen den Rändern des Rahmens, zum Beispiel zur Zeit $$ c{t}_3^{\prime } $$ und daher nicht hineinpasst. Um dieses Paradoxon zu lösen, verabschieden wir uns zunächst von der Vorstellung eines starren Stabes und eines soliden Rahmens und betrachten die jeweiligen Endpunkte und Randpunkte als Punktereignisse. Dies ist schon allein deshalb notwendig, da wir nur eine räumlich eindimensionale Bewegung betrachten und daher ein solider Rahmen schon bei der ersten Berührung unseren Stab aufhalten würde.

Die anfängliche Problematik des Paradoxons, ob der Stab nun durch den Rahmen „passt“ oder nicht, können wir wie folgt auflösen. Aus Sicht des Rahmensystems S „passt“ der Stab räumlich durch den Rahmen, da die Stabenden innerhalb der Ereignisse ② und ③ den Rahmen passieren. Aus Sicht des Stabsystems Sʹ „passt“ der Stab zeitlich durch den Rahmen, da wiederum seine Stabenden innerhalb der Ereignisse ② und ③ den Rahmen passieren.

4.4.2 Das Uhrenparadoxon

Betrachten wir zwei baugleiche Uhren. Die erste Uhr befinde sich im System S und die zweite im System Sʹ. Beide Uhren seien in ihrem jeweiligen Bezugssystem in Ruhe. Das System Sʹ bewege sich mit der Geschwindigkeit β entlang der positiven x-Achse des Systems S. Die gängige Aussage lautet nun, dass die zweite Uhr aufgrund der Zeitdilatation langsamer läuft, da sie sich, im Gegensatz zur ersten Uhr, bewegt. Der scheinbare Widerspruch ergibt sich hier, wenn wir die Situation im Ruhsystem der zweiten Uhr betrachten. Dort bewegt sich die erste Uhr und erfährt eine Zeitdilatation. Welche Uhr geht nun langsamer, die erste oder die zweite?

Zuerst müssen wir uns klar machen, dass wir nicht allein mit der ersten Uhr feststellen können, dass die zweite langsamer geht. Wir können nur zu dem Zeitpunkt, an dem sich die zweite Uhr am Ort der ersten befindet, ihre Uhrzeit ablesen. Um ein Zeitintervall messen zu können, müssen wir noch mit einer anderen Uhr vergleichen, die sich im System S an einem anderen Ort befindet. Wir führen also noch eine weitere Uhr im System S ein. Um die Situation in beiden Systemen gleichwertig diskutieren zu können, soll es auch noch eine weitere Uhr im System Sʹ geben. In beiden Systemen sollen die jeweils dort ruhenden Uhren synchronisiert sein und den gleichen Abstand voneinander haben. Unter diesen Voraussetzungen können wir die Ergebnisse des letzten Abschnittes verwenden, wobei $$ \mid {s}_r^{\prime }-{s}_l^{\prime}\mid =\mid {r}_r-{r}_l\mid =: \ell $$ Wir denken uns dazu an beiden Enden von Rahmen und Stab jeweils eine Uhr befestigt.

Abb. 4.8 zeigt das Minkowski-Diagramm für das Uhrenparadoxon aus der Sicht des Ruhsystems S mit den beiden Weltlinien $$ {\mathcal{S}}_l $$ und $$ {\mathcal{S}}_r $$ der Uhren, die in Sʹ in Ruhe sind, sich aber relativ zu S in positiver x-Richtung bewegen. Um die verstrichene Zeit für die bewegte Uhr auf der Weltlinie $$ {\mathcal{S}}_r $$ zu ermitteln, bestimmen wir die Zeitdifferenz zwischen den Ereignissen ① und ③ einmal aus Sicht der bewegten Uhr und einmal aus dem Vergleich der ruhenden Uhren an den Orten x = rl und x = rr. Da die Ereignisse hier mit denen aus dem vorherigen Abschnitt übereinstimmen, können wir unmittelbar die Zeiten aus den Beziehungen (4.14) und (4.15) verwenden. So folgt für die Zeitdifferenzen
$$ c\Delta {t}_{1,3}=c{t}_3-c{t}_1=\frac{r_r-{r}_l}{\beta }=\frac{\ell }{\beta}\quad \mathrm{und}\quad c\Delta {t}_{1,3}^{\prime }=c{t}_3^{\prime }-c{t}_1^{\prime }=\frac{r_r-{r}_l}{\beta \gamma}=\frac{\ell }{\beta \gamma}. $$
(4.18)
Auch wenn die Strecke zwischen ① und ③ im Minkowski-Diagramm länger erscheint als der vertikale Abstand, so müssen wir die Skalierung der Zeitachsen berücksichtigen. Es gilt daher $$ c\Delta {t}_{1,3}^{\prime }<c\Delta {t}_{1,3} $$ und folglich vergeht die Zeit in Sʹ langsamer als in S. Das gleiche Ergebnis erhalten wir auch für die Uhr auf der Weltlinie $$ {\mathcal{S}}_l $$.
Abb. 4.8

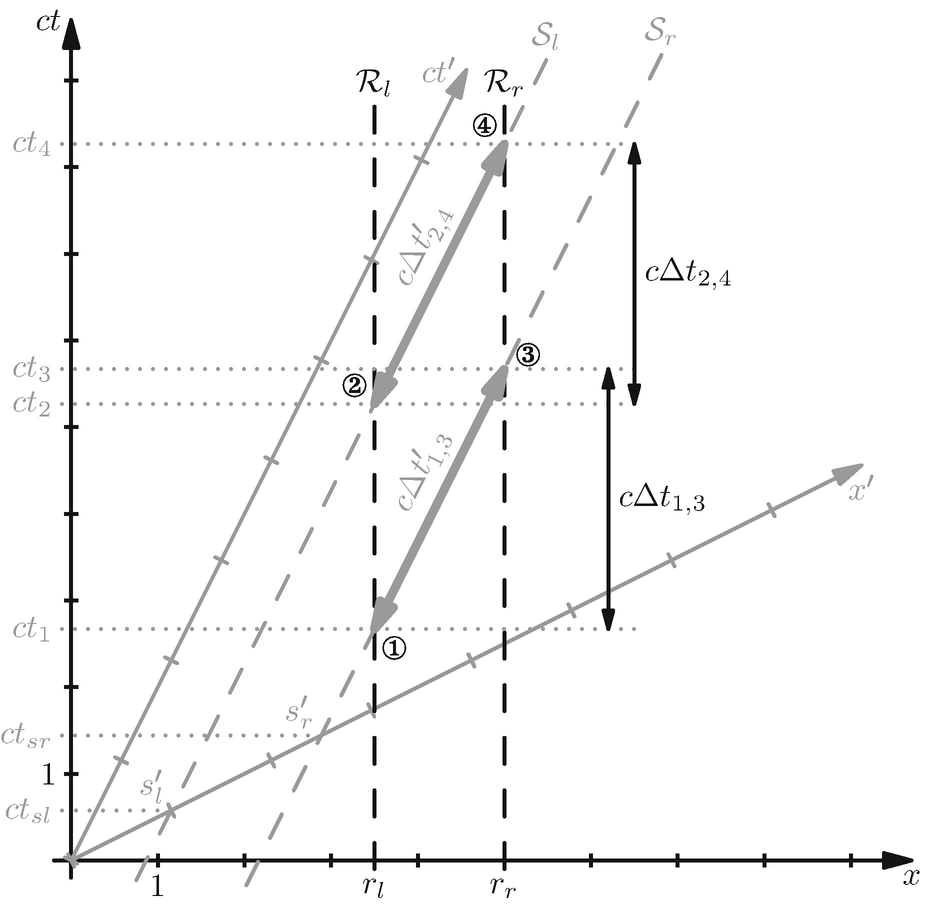
Uhrenparadoxon aus Sicht des Ruhsystems S. Die ruhenden Uhren in S folgen den Weltlinien $$ {\mathcal{R}}_l $$ und $$ {\mathcal{R}}_r $$. Die sich zu S relativ bewegenden Uhren sind durch die Weltlinien $$ {\mathcal{S}}_l $$ und $$ {\mathcal{S}}_r $$ gekennzeichnet

Aus der Sicht des Systems Sʹ (s. Abb. 4.9) müssen wir jetzt die Zeitdifferenz der bewegten Uhr entlang der Weltlinie $$ {\mathcal{R}}_l $$ mit Hilfe der Ereignisse ① und ② berechnen. Aus den Beziehungen (4.14) und (4.15) folgt,
$$ c\Delta {t}_{1,2}=c{t}_2-c{t}_1=\frac{s_r^{\prime }-{s}_l^{\prime }}{\beta \gamma}=\frac{\ell }{\beta \gamma}\quad \mathrm{und}\quad c\Delta {t}_{1,2}^{\prime }=c{t}_2^{\prime }-c{t}_1^{\prime }=\frac{s_r^{\prime }-{s}_l^{\prime }}{\beta }=\frac{\ell }{\beta }. $$
(4.19)
Da hier $$ c\Delta {t}_{1,2}<c\Delta {t}_{1,2}^{\prime } $$ ist, vergeht die Zeit im System S langsamer als im System Sʹ. Das scheint aber im direkten Widerspruch zur vorherigen Aussage zu sein, dass die Zeit in Sʹ langsamer als in S vergeht.
Abb. 4.9

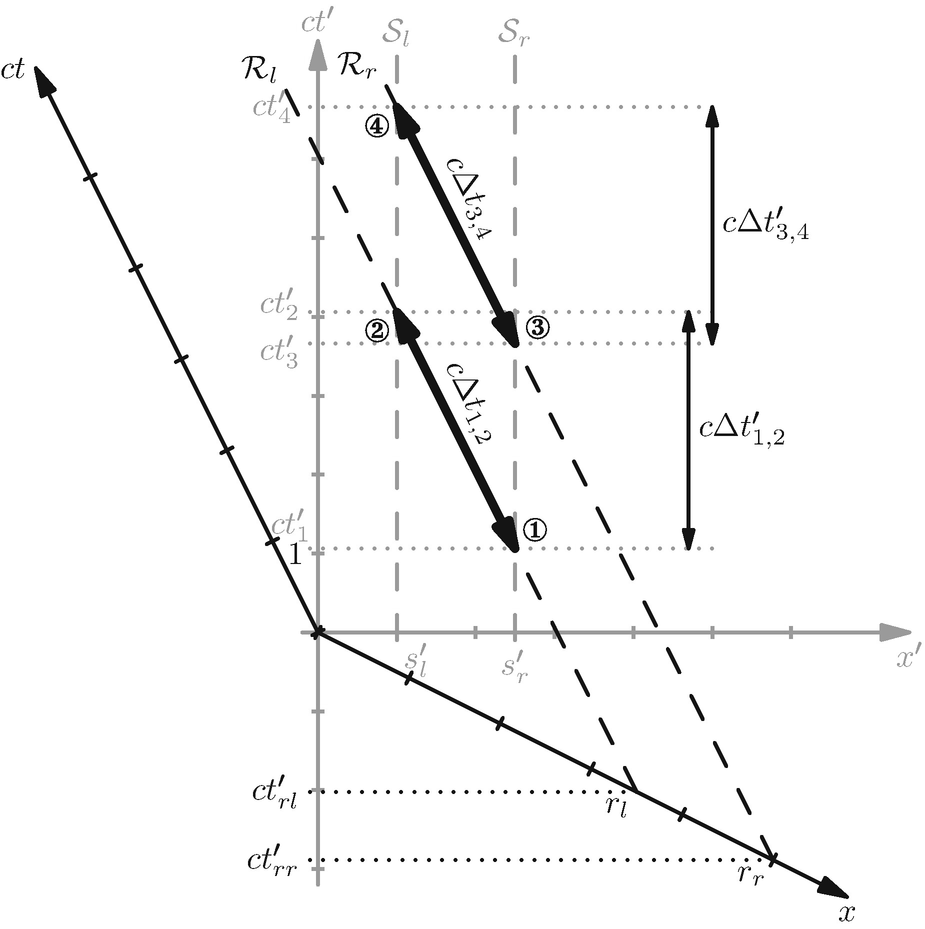
Uhrenparadoxon aus Sicht des Ruhsystems S′. Hier bewegen sich die beiden Uhren des Systems S entlang der Weltlinien $$ {\mathcal{R}}_l $$ und $$ {\mathcal{R}}_r $$

Die Ursache dieser Diskrepanz liegt in der Definition von Gleichzeitigkeit in beiden Systemen. Die beiden Uhren im System S, die sich an den Orten x = rl und x = rr befinden, werden auf ctrl = ctrr = 0 synchronisiert. Unter Zuhilfenahme der Lorentz-Transformationen können wir die Zeiten dieser beiden Uhren bezogen auf das System Sʹ angeben. Es gilt
$$ c{t}_{rl}^{\prime}\left(c{t}_{rl}=0\right)=-\gamma \beta {r}_l\quad \mathrm{und}\quad c{t}_{rr}^{\prime}\left(c{t}_{rr}=0\right)=-\gamma \beta {r}_r. $$
(4.20)
Mit rr > rl folgt daraus, dass $$ c{t}_{rr}^{\prime }<c{t}_{rl}^{\prime }<0 $$ ist (s. a. Abb. 4.9). Aus Sicht des Systems Sʹ laufen die beiden Uhren nicht synchron.
Andererseits sind die beiden Uhren im System S, die sich an den Orten $$ x^{\prime }={s}_l^{\prime } $$ und $$ x^{\prime }={s}_r^{\prime } $$ befinden, auf $$ c{t}_{sl}^{\prime }=c{t}_{sr}^{\prime }=0 $$ synchronisiert. Bezogen auf das System S sind die Uhrzeiten zum Zeitpunkt der Synchronisierung jedoch unterschiedlich,
$$ c{t}_{sl}\left(c{t}_{sl}^{\prime }=0\right)=\gamma \beta {s}_l^{\prime}\quad \mathrm{und}\quad c{t}_{sr}\left(c{t}_{sr}^{\prime }=0\right)=\gamma \beta {s}_r^{\prime }. $$
(4.21)
Mit $$ {s}_r^{\prime }>{s}_l^{\prime } $$ folgt daraus, dass ctsr > ctsl > 0 ist (s. a. Abb. 4.8).

Das Uhrenparadoxon gründet sich alleine darauf, dass sich die beiden Systeme S und Sʹ nicht über eine gemeinsame Zeitsynchronisierung einigen können. Welche Uhr langsamer geht, hängt also davon ab, mit welchem Bezugssystem wir Zeitdifferenzen bestimmen.

4.4.3 Das Zwillingsparadoxon

Dies ist wahrscheinlich das bekannteste Paradoxon der SRT. Betrachtet wird ein Zwillingspaar. Einer der Zwillinge bleibt auf der Erde, der andere reist mit hoher Geschwindigkeit und kehrt zur Erde zurück. Auf der Erde ist aufgrund der Zeitdilatation mehr Zeit vergangen als im Raumschiff. Das Paradoxon bei dieser Situation ergibt sich, wenn man sie aus der Sicht des anderen Zwillings betrachtet. Von dort aus betrachtet bewegt sich der Zwilling auf der Erde mit hoher Geschwindigkeit, es sollte also zu einer Zeitdilatation auf der Erde kommen.

Tatsächlich sind das Ruhsystems des Zwillings auf der Erde und das System des reisenden Zwillings in diesem Fall aber nicht gleichberechtigt. Der reisende Zwilling ist nicht während der gesamten Reise im gleichen Inertialsystem, da er, um zurückzukehren, beschleunigen muss. Aufgrund der dabei wirkenden Kraft ist es eindeutig, welcher der beiden Zwillinge sich bewegt und welcher während der gesamten Zeit ruht. Wir betrachten das Zwillingsparadoxon nochmals quantitativ am Ende von Kap. 6 im Rahmen der relativistischen Mechanik.

4.5 Übungsaufgaben

4.5.1 Das „Myonenparadoxon“

Wenn wir nochmal zu den Myonen zurückkommen, können wir ein scheinbares Problem bemerken. Im Ruhsystem der Myonen haben diese die Lebensdauer τ ≈ 2 · 10−6 s, denn dort geht ihre Uhr ja nicht langsamer. Warum können sie dann trotzdem die Erde erreichen?