
![$$ {x}^{\mu}\left[t\left(\tau \right)\right]=\left(\begin{array}{l}\hfill ct\left(\tau \right)\hfill \\ {}\hfill \boldsymbol{r}\left[t\left(\tau \right)\right]\hfill \end{array}\right) $$](../images/331389_2_De_6_Chapter/331389_2_De_6_Chapter_TeX_Equ2.png)
Unser Ziel ist es, die anderen, in der klassischen Mechanik auftretenden Größen Geschwindigkeit, Beschleunigung, Impuls und Energie kovariant zu formulieren, um uns den so gewonnenen Formalismus dann an Beispielen klar zu machen. Eine wirklich umfassende Darstellung der relativistischen Mechanik werden wir aber nicht vornehmen, so werden wir z. B. die Verallgemeinerung des Drehimpulses nicht diskutieren. Weitere Details findet der interessierte Leser z. B. in [3].
6.1 Vierergeschwindigkeit


 sowie
sowie  erhalten wir
erhalten wir

6.2 Viererbeschleunigung

![$$ {b}^{\mu }=\gamma \frac{\mathrm{d}{u}^{\mu }}{\mathrm{d}t}=\gamma \frac{\mathrm{d}}{\mathrm{d}t}\left[\gamma \left(\begin{array}{c}c\\ {}\dot{\boldsymbol{r}}\end{array}\right)\right]=\gamma \dot{\gamma}\left(\begin{array}{c}c\\ {}\dot{\boldsymbol{r}}\end{array}\right)+{\gamma}^2\left(\begin{array}{c}0\\ {}\ddot{\boldsymbol{r}}\end{array}\right). $$](../images/331389_2_De_6_Chapter/331389_2_De_6_Chapter_TeX_Equ8.png)


 nicht auf. Man erkennt deshalb leicht, dass
nicht auf. Man erkennt deshalb leicht, dass
6.3 Viererimpuls

An dieser Stelle ist ein Hinweis angebracht: Man findet in der Literatur oft die Aussage, dass die Masse eines Teilchens geschwindigkeitsabhängig über m(γ) = m0γ sei. Tatsächlich kann man mit dieser Definition oft gut arbeiten. Streng genommen gehört der Faktor γ in (6.12) aber zur Vierergeschwindigkeit und nicht zur Masse. Die Ruhemasse eines Teilchens ist ein Lorentz-Skalar und nicht geschwindigkeitsabhängig.
6.4 Viererkraft






6.5 Kräftefreie Bewegung
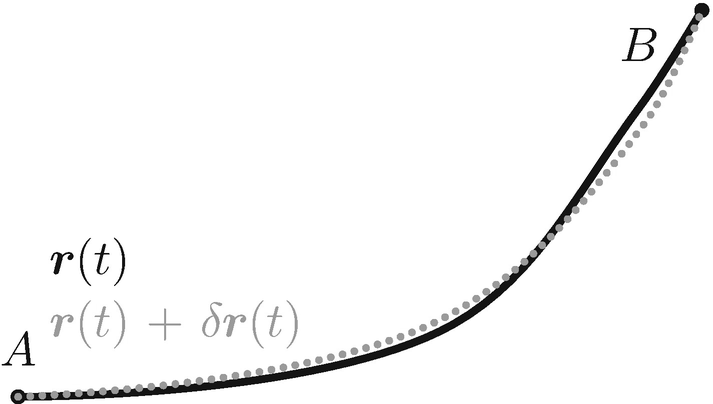
Variation des Weges. Betrachtet werden kleine Variationen δr(t) des Weges r(t) von Ereignis A zu Ereignis B, mit der Bedingung, dass δr(tA) = δr(tB) = 0



![$$ \mathrm{d}p=\left[\frac{\mathrm{d}}{\mathrm{d}t}\frac{\dot{\boldsymbol{r}}}{\sqrt{c^2-{\dot{\boldsymbol{r}}}^2}}\right]\, \mathrm{d}t\quad \mathrm{und}\quad q=\delta \boldsymbol{r}. $$](../images/331389_2_De_6_Chapter/331389_2_De_6_Chapter_TeX_Equ22.png)

![$$ {\left.-\frac{\dot{\boldsymbol{r}}}{\sqrt{c^2-{\dot{\boldsymbol{r}}}^2}}\cdotp \delta \boldsymbol{r}\right|}_A^B+\underset{A}{\overset{B}{\int }}\delta \boldsymbol{r}(t)\left[\frac{\mathrm{d}}{\mathrm{d}t}\frac{\dot{\boldsymbol{r}}}{\sqrt{c^2-{\dot{\boldsymbol{r}}}^2}}\right]\, \mathrm{d}t=0. $$](../images/331389_2_De_6_Chapter/331389_2_De_6_Chapter_TeX_Equ24.png)
![$$ \underset{A}{\overset{B}{\int }}\delta \boldsymbol{r}(t)\left[\frac{\mathrm{d}}{\mathrm{d}t}\frac{\dot{\boldsymbol{r}}}{\sqrt{c^2-{\dot{\boldsymbol{r}}}^2}}\right]\, \mathrm{d}t=0\quad \mathrm{f}\ddot{\mathrm{u}}\mathrm{r}\ \mathrm{beliebige}\quad \delta \boldsymbol{r}(t). $$](../images/331389_2_De_6_Chapter/331389_2_De_6_Chapter_TeX_Equ25.png)
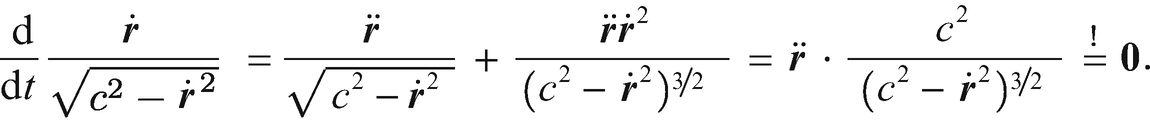
 bzw.
bzw.  . Durch Multiplikation von (6.26) mit der Masse m0 erhalten wir
. Durch Multiplikation von (6.26) mit der Masse m0 erhalten wir
 eingesetzt. Dies ist die Gleichung für den relativistischen Impuls für den Fall, dass eine kräftefreie Bewegung vorliegt. Er ist dann eine Erhaltungsgröße.
eingesetzt. Dies ist die Gleichung für den relativistischen Impuls für den Fall, dass eine kräftefreie Bewegung vorliegt. Er ist dann eine Erhaltungsgröße.6.6 Relativistische Energie
 aus (6.18)
an. Für die 0-te Komponente gilt:
aus (6.18)
an. Für die 0-te Komponente gilt:



6.6.1 Äquivalenz von Masse und Energie

Es ist alles andere als trivial, den Zusammenhang (6.31) theoretisch abzuleiten, Einstein selbst widmete diesem Problem eine ganze Reihe von Arbeiten, ohne wirklich vollständig erfolgreich zu sein. Eine Übersicht über seine Versuche gibt ein Artikel von Hecht [4].







 . Allgemein ist die relativistische Energie die Summe der kinetischen Energie und der Ruheenergie. Das muss insbesondere beim Vergleich mit der nichtrelativistischen kinetischen Energie berücksichtigt werden.
. Allgemein ist die relativistische Energie die Summe der kinetischen Energie und der Ruheenergie. Das muss insbesondere beim Vergleich mit der nichtrelativistischen kinetischen Energie berücksichtigt werden.

 und damit über 4000-mal so groß wie seine Ruheenergie! Im Large Hadron Collider, dem momentan weltgrößten Teilchenbeschleuniger, treffen Protonen genau mit einer solchen Energie aufeinander, d. h. bei zwei gleich schnellen Protonen entspricht dies einem Stoß bei 8 TeV. Abb. 6.2 zeigt die relativistische Energie im Vergleich zur Newton'schen kinetischen Energie für ein Proton.
und damit über 4000-mal so groß wie seine Ruheenergie! Im Large Hadron Collider, dem momentan weltgrößten Teilchenbeschleuniger, treffen Protonen genau mit einer solchen Energie aufeinander, d. h. bei zwei gleich schnellen Protonen entspricht dies einem Stoß bei 8 TeV. Abb. 6.2 zeigt die relativistische Energie im Vergleich zur Newton'schen kinetischen Energie für ein Proton.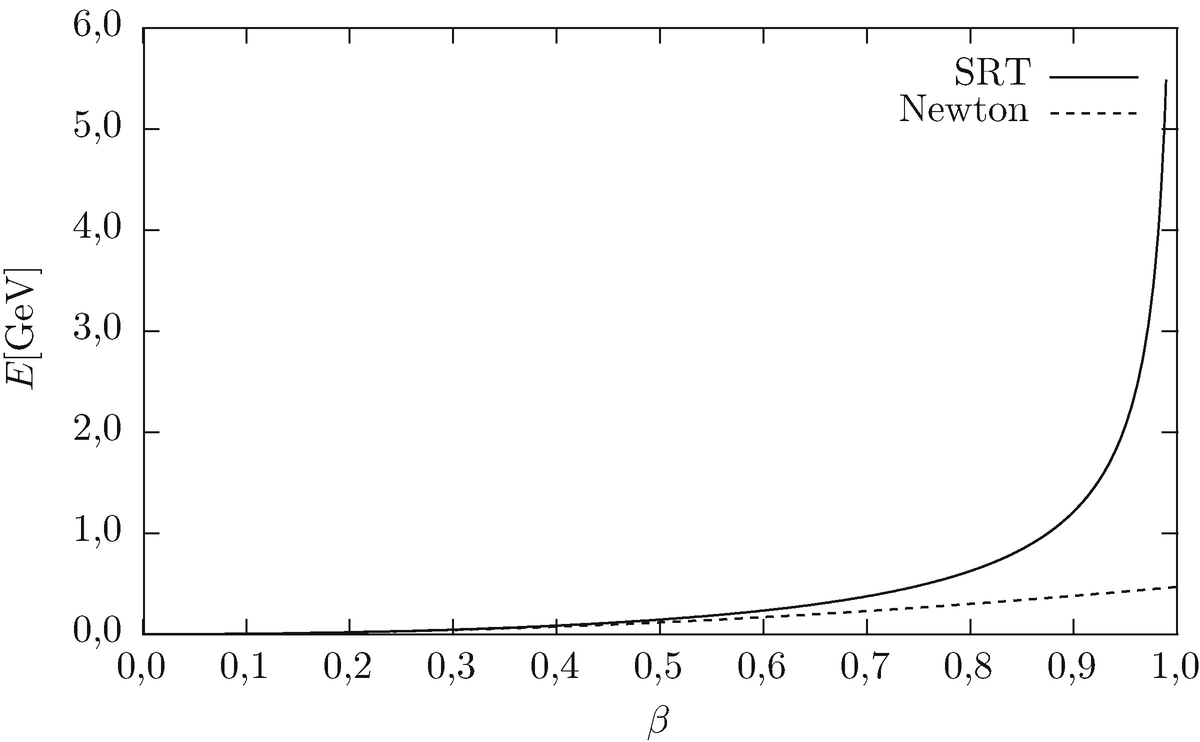
Vergleich zwischen relativistischer und Newton'scher kinetischer Energie für ein Proton. Beim relativistischen Ausdruck ist die Ruheenergie abgezogen. Für β → 1 divergiert der relativistische Energieausdruck
6.6.2 Photonen und der Compton-Effekt

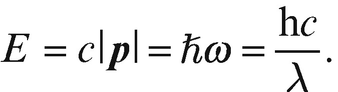
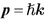 und
und  zwischen Impuls und Wellenvektor, bzw. Energie und Frequenz für Photonen haben wir dann
zwischen Impuls und Wellenvektor, bzw. Energie und Frequenz für Photonen haben wir dann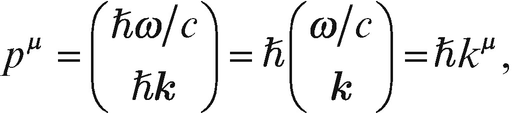

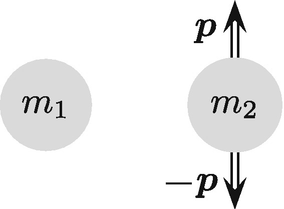
Zur Äquivalenz von Masse und Energie: Ein Teilchen, das 2 Photonen gleicher Energie in entgegengesetzte Richtungen emittiert, ändert seinen Impuls und entsprechend auch seine kinetische Energie nicht, es muss also seine Ruhemasse verringern



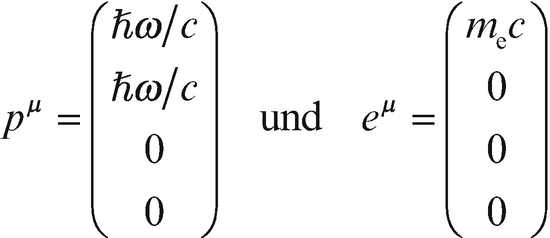


 und nutzen den Zusammenhang
und nutzen den Zusammenhang  aus. Dann ist
aus. Dann ist







6.6.3 Weitere Beispiele
- 1.
Angeregte Atome oder Moleküle sind schwerer als Atome oder Moleküle im Grundzustand. Betrachten wir das Wasserstoffatom, so wird die Bindungsenergie von
 frei, wenn sich aus einem Proton und einem Elektron ein Wasserstoffatom bildet. Die Masse des Wasserstoffatoms ist also kleiner als die Masse von Proton plus Elektron. Man spricht vom Massendefekt
, hier verursacht von der negativen Bindungsenergie von Elektron und Proton. Für das Wasserstoffatom ist dieser Effekt relativ klein, da die Protonenmasse in (6.41) etwa 70 Millionen mal größer ist als die Bindungsenergie.
frei, wenn sich aus einem Proton und einem Elektron ein Wasserstoffatom bildet. Die Masse des Wasserstoffatoms ist also kleiner als die Masse von Proton plus Elektron. Man spricht vom Massendefekt
, hier verursacht von der negativen Bindungsenergie von Elektron und Proton. Für das Wasserstoffatom ist dieser Effekt relativ klein, da die Protonenmasse in (6.41) etwa 70 Millionen mal größer ist als die Bindungsenergie. - 2.Atomkerne zeigen, wie bereits kurz angesprochen, ebenfalls einen Massendefekt. Die Gesamtmasse von Atomkernen ist kleiner als die Summe der Massen der Protonen und Neutronen. Der Massendefekt ergibt sich aus der Bindungsenergie EB∕c2 aufgrund der starken Wechselwirkung. Die Masse des Atomkernes ist also
 (6.60)wobei EB < 0 ist. Wir betrachten als Beispiel das Nuklid 12C. Hier ist A = 12 und Z = 6. Die atomare Masseneinheit ist
(6.60)wobei EB < 0 ist. Wir betrachten als Beispiel das Nuklid 12C. Hier ist A = 12 und Z = 6. Die atomare Masseneinheit ist (6.61)Im Vergleich zur Masse der einzelnen Bestandteile ergibt sich
(6.61)Im Vergleich zur Masse der einzelnen Bestandteile ergibt sich (6.62)mit der Neutronenmasse
(6.62)mit der Neutronenmasse (6.63)und der Elektronenmasse
(6.63)und der Elektronenmasse (6.64)
(6.64)Das heißt etwa 0,8% der Masse der Protonen und Neutronen geht in die Bindungsenergie.
- 3.
Bei Kernspaltungs- und Kernfusionsreaktionen kann eine große Menge an Energie freiwerden. In Kap. 19 werden wir sehen, dass Sterne ihre Leuchtenergie aus Fusionsprozessen gewinnen.
- 4.Teilchen und Antiteilchen können paarweise erzeugt oder vernichtet werden, z. B. in der Reaktion
 (6.65)Aus Elektron und Positron entstehen also zwei Photonen. Der Elektronenmasse entspricht ein Energieäquivalent von etwa
(6.65)Aus Elektron und Positron entstehen also zwei Photonen. Der Elektronenmasse entspricht ein Energieäquivalent von etwa Daher gilt
Daher gilt (6.66)
(6.66)Hier werden 100 % der Masse in Energie umgewandelt. Die Ruheenergie der Elektronen ist eine untere Grenze für die freiwerdende Energie, da die Elektronen auch kinetische Energie besitzen.
6.7 Reise mit konstanter Beschleunigung
Als Anwendung der gerade hergeleiteten Zusammenhänge betrachten wir einen Raumfahrer, dessen Raumfahrzeug in seinem Ruhsystem konstant mit a = g = 9,81 ms−2 in x-Richtung beschleunigt wird.
6.7.1 Bewegungsgleichungen





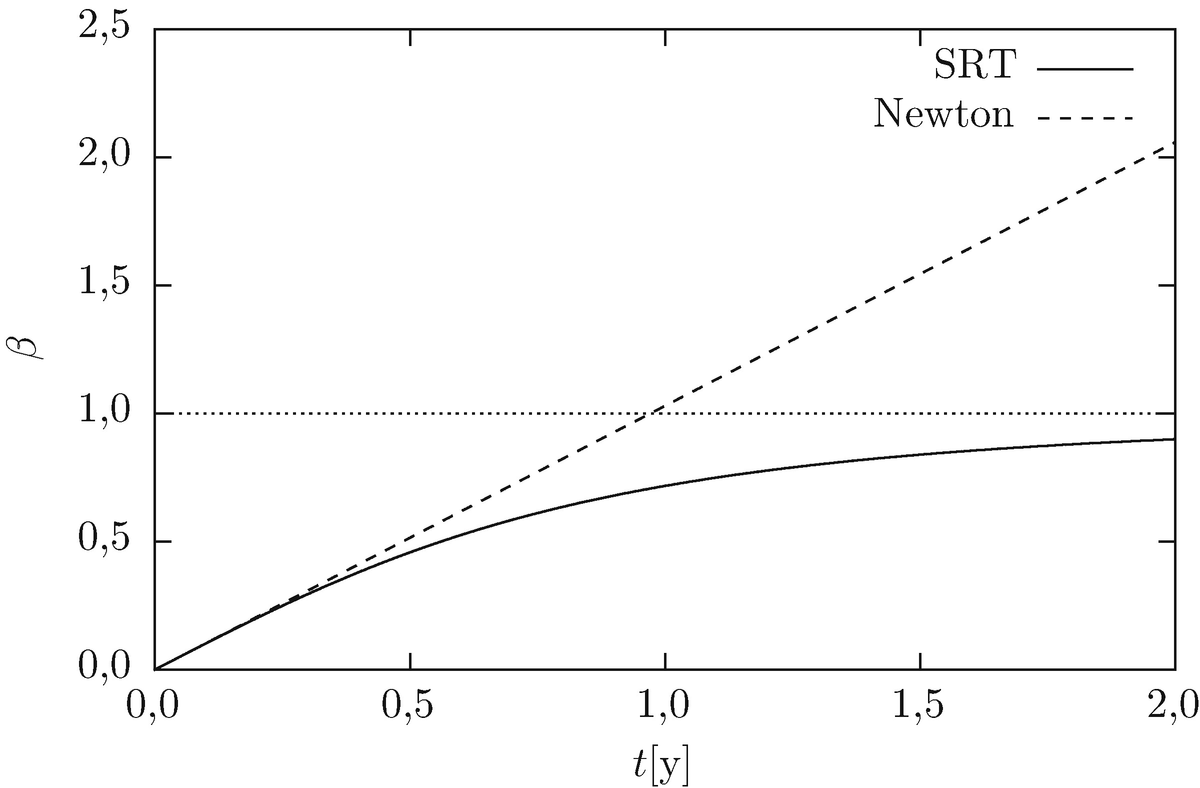
Entwicklung der Geschwindigkeit bei konstanter Beschleunigung. Während in der Newton'schen Mechanik die Geschwindigkeit der Rakete über alle Grenzen wächst (gestrichelte Linie), ist in der SRT die Lichtgeschwindigkeit β = 1 die obere Schranke (durchgezogene Linie)
![$$ x(t)\ =\underset{0}{\overset{t}{\int }}v\left(t^{\prime}\right)\, \mathrm{d}t^{\prime }={\left.c\sqrt{t^{\prime 2}+\frac{c^2}{g^2}}\right|}_0^t=\frac{c^2}{g}\left[\sqrt{1+{\left(\frac{gt}{c}\right)}^2}-1\right]. $$](../images/331389_2_De_6_Chapter/331389_2_De_6_Chapter_TeX_Equ72.png)
 wie in der Newtonʼschen Mechanik. Für große Zeiten dagegen ist x(t) ≈ ct, unabhängig vom Wert der Beschleunigung (s. Abb. 6.5).
wie in der Newtonʼschen Mechanik. Für große Zeiten dagegen ist x(t) ≈ ct, unabhängig vom Wert der Beschleunigung (s. Abb. 6.5).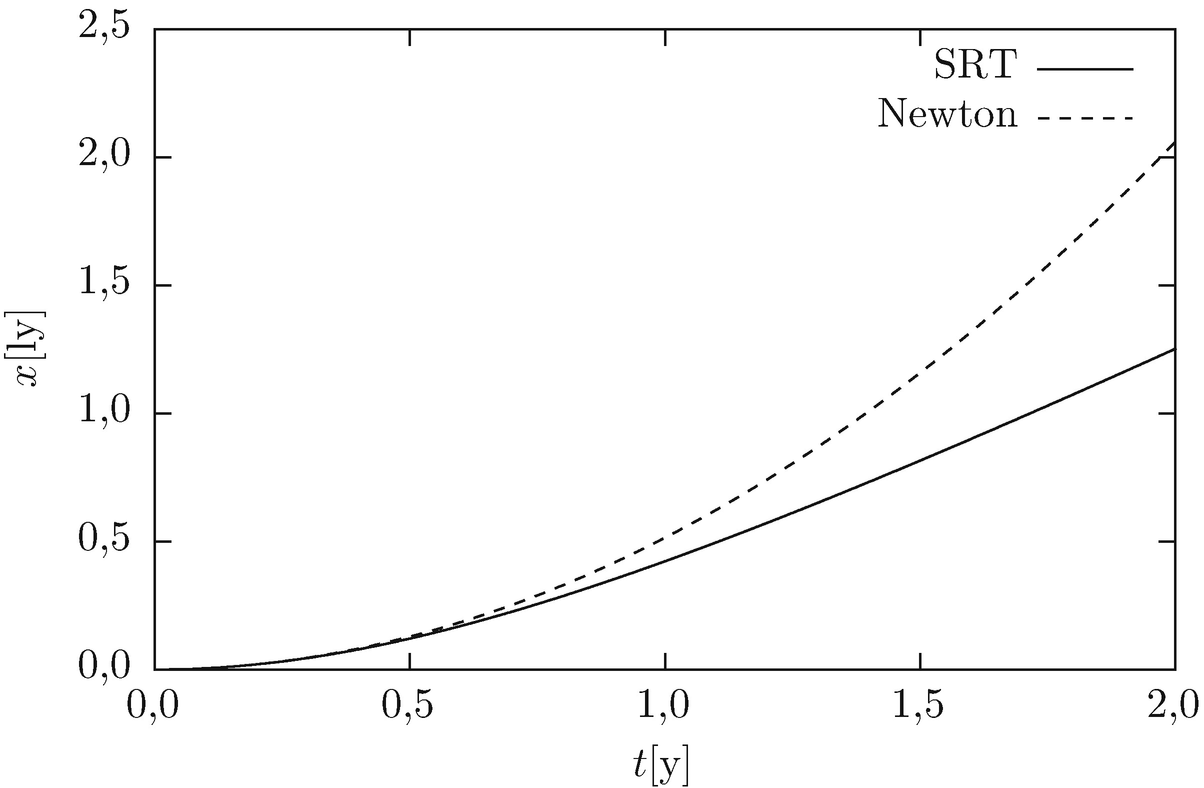
Relativistische Bewegungsgleichung der Rakete: Während in der Newton'schen Mechanik der zurückgelegte Weg für alle Zeit mit gt2∕2 pro Zeit t zunimmt (gestrichelte Linie), ändert er sich in der SRT für große t proportional zu ct, unabhängig von der Beschleunigung g
Betrachtung aus Sicht des Raumfahrers

![$$ \tau =\underset{0}{\overset{t}{\int }}\sqrt{1-\frac{g^2{t}^{\prime 2}}{c^2+{g}^2{t}^{\prime 2}}}\, \mathrm{d}t^{\prime }=\frac{c}{g}\ln \left[\frac{gt}{c}+\sqrt{1+{\left(\frac{gt}{c}\right)}^2}\right]=\frac{c}{g}\mathrm{arsinh}\left(\frac{gt}{c}\right). $$](../images/331389_2_De_6_Chapter/331389_2_De_6_Chapter_TeX_Equ74.png)

![$$ x\left(\tau \right)=\frac{c^2}{g}\left[\cosh \left(\frac{g}{c}\tau \right)-1\right]. $$](../images/331389_2_De_6_Chapter/331389_2_De_6_Chapter_TeX_Equ76.png)
Wegen des exponentiellen Zusammenhangs zwischen vergangener Eigenzeit und zurückgelegter Strecke könnte ein Raumfahrer, der lediglich mit Erdbeschleunigung konstant beschleunigt, während relativ kurzer Zeitdauern sehr weit entfernte Punkte im Universum erreichen. Gegen die tatsächliche Durchführung einer solchen Reise spricht aber, neben vielen technischen Problemen, der immense Energiebedarf, um die Beschleunigung dauerhaft aufrechtzuerhalten.
6.7.2 Anwendung auf das Zwillingsparadoxon

Abschnitte der Rundreise im Zwillingsparadoxon. In Abschnitt ① beschleunigt der Raumfahrer auf sein Reiseziel hin. In Abschnitt ② bremst er auf dem Hinweg ab, in Abschnitt ③ beschleunigt er wieder auf die Erde zu, und in Abschnitt ④ bremst er schließlich ab, um bei der Erde anzuhalten
![$$ {t}_{\mathrm{Zw}}\left(\tau \right)=\frac{c}{g}\left\{\begin{array}{ll}\sinh \left(\frac{g}{c}\tau \right)& \mathrm{f}\ddot{\mathrm{u}}\mathrm{r}\, \tau \le {\tau}_1,\\ {}\sinh \left[\frac{g}{c}\left(\tau -2{\tau}_1\right)\right]+2\sinh \left(\frac{g}{c}{\tau}_1\right)& \mathrm{f}\ddot{\mathrm{u}}\mathrm{r}\, {\tau}_1<\tau \le 3{\tau}_1,\\ {}\sinh \left[\frac{g}{c}\left(\tau -4{\tau}_1\right)\right]+4\sinh \left(\frac{g}{c}{\tau}_1\right)& \mathrm{f}\ddot{\mathrm{u}}\mathrm{r}\, 3{\tau}_1<\tau \le 4{\tau}_1\end{array}\right. $$](../images/331389_2_De_6_Chapter/331389_2_De_6_Chapter_TeX_Equ77.png)
![$$ {x}_{\mathrm{Zw}}\left(\tau \right)=\frac{c^2}{g}\left\{\begin{array}{ll}\cosh \left(\frac{g}{c}\tau \right)-1& \mathrm{f}\ddot{\mathrm{u}}\mathrm{r}\, \tau \le {\tau}_1,\\ {}2\cosh \left(\frac{g}{c}{\tau}_1\right)-\cosh \left[\frac{g}{c}\left(\tau -2{\tau}_1\right)\right]-1,& \mathrm{f}\ddot{\mathrm{u}}\mathrm{r}\, {\tau}_1<\tau \le 3{\tau}_1,\\ {}\cosh \left[\frac{g}{c}\left(\tau -4{\tau}_1\right)\right]-1& \mathrm{f}\ddot{\mathrm{u}}\mathrm{r}\, 3{\tau}_1<\tau \le 4{\tau}_1.\end{array}\right. $$](../images/331389_2_De_6_Chapter/331389_2_De_6_Chapter_TeX_Equ78.png)

 ergibt das
ergibt das![$$ {\beta}_{\mathrm{Zw}}\left(\tau \right)=\left\{\begin{array}{ll}\tanh \left(\frac{g}{c}\tau \right)& \mathrm{f}\ddot{\mathrm{u}}\mathrm{r}\, \tau \le {\tau}_1,\\ {}-\tanh \left[\frac{g}{c}\left(\tau -2{\tau}_1\right)\right],& \mathrm{f}\ddot{\mathrm{u}}\mathrm{r}\, {\tau}_1<\tau \le 3{\tau}_1,\\ {}\tanh \left[\frac{g}{c}\left(\tau -4{\tau}_1\right)\right]& \mathrm{f}\ddot{\mathrm{u}}\mathrm{r}\, 3{\tau}_1<\tau \le 4{\tau}_1.\end{array}\right. $$](../images/331389_2_De_6_Chapter/331389_2_De_6_Chapter_TeX_Equ80.png)
 sehen wir daran wieder, dass die Geschwindigkeit immer kleiner als die Lichtgeschwindigkeit ist.
sehen wir daran wieder, dass die Geschwindigkeit immer kleiner als die Lichtgeschwindigkeit ist.




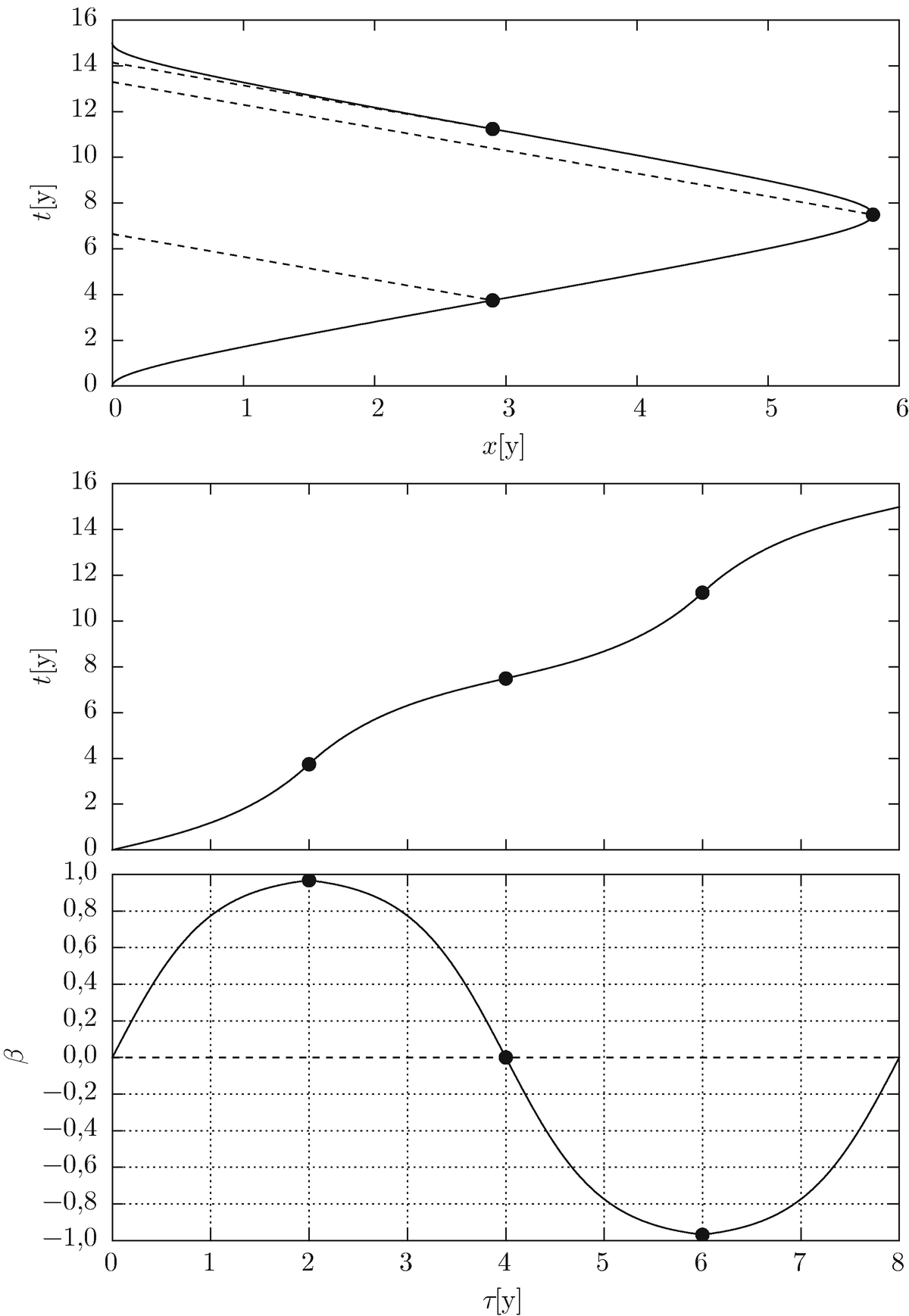
Weltlinie x(t) (oben), Koordinatenzeit t(τ) (Mitte) und Geschwindigkeit β(τ) (unten) des reisenden Zwillings. Bei der Weltlinie sind zusätzlich Lichtsignale an die Erde für die Zeiten t = τ1, 2τ1 und 3τ1 eingezeichnet
Vergleich der Reisen zu verschiedenen Zielen im klassischen Zwillingsparadoxon. Aufgelistet sind die vergangene Eigenzeit τf des Raumfahrers und die vergangene Koordinatenzeit t(τf) am Ende der Reise, sowie die maximal erreichte Geschwindigkeit βmax und der maximale Lorentz-Faktor. Betrachtet werden typische Entfernungen zu nahen Sternen, eine Reise zum Andromedanebel, der etwa zwei Millionen Lichtjahre entfernt ist, und zum Ende des sichtbaren Universums; siehe auch [5]
Entfernung [ly] | τf [y] | t(τf) [y] | βmax | γmax |
|---|---|---|---|---|
5 | 7,55 | 13,32 | 0,9602 | 3,582 |
100 | 18,03 | 203,84 | 0,9998 | 52,64 |
2,00 · 106 | 56,31 | 4,00 · 106 | 1 − 4,69 · 10−13 | 1,033 · 106 |
1,3784 · 1010 | 90,54 | 2,76 · 1010 | 1 − 9,87 · 10−21 | 7,12 · 109 |
Aufgrund der extremen Zeitdilatation könnte ein Raumfahrer in seiner Lebenszeit selbst extremste Entfernungen im Bereich von Milliarden von Lichtjahren zurücklegen. Wir werden in der Kosmologie aber sehen, dass unser Universum keine statische Raumzeit wie die Minkowski-Raumzeit ist, sondern als expandierender Raum beschrieben werden kann. In einer solchen Raumzeit ergeben sich für das Zwillingsparadoxon noch weitere Aspekte, da sich die Raumzeit, insbesondere während einer sehr langen Reise, ausdehnt. Man benötigt für diesen Fall dann ein Konzept der konstanten Beschleunigung in einer gekrümmten Raumzeit, das in [8] diskutiert wird. Wir möchten diesen Fall aber nicht behandeln. Außerdem wäre er erst nach der Behandlung der ART und der entsprechenden Gleichungen der Kosmologie verständlich. Eine entsprechende Diskussion findet der interessierte Leser in [1].
Ein weiteres Problem ist die unglaubliche Energiemenge, die für eine solche Reise nötig wäre. Die relativistische Energie in (6.30) ergibt sich als Lorentz-Faktor mal der Ruheenergie. Wenn also auf einer Reise Lorentz-Faktoren im Bereich 106 und höher auftreten, bräuchte man genug Treibstoff, um ein millionenfaches der Ruheenergie des Raumschiffes zu erzeugen. Selbst wenn man direkt Materie und Antimaterie zerstrahlen könnte, hätte man ein Last zu Treibstoffverhältnis von weit über Eins zu einer Million, da der Treibstoff für spätere Reisephasen anfangs ja auch noch beschleunigt werden muss.
6.8 Relativistische Kreisbahn
Als kleine Ergänzung möchten wir noch den Fall einer gleichförmigen Bewegung auf einer Kreisbahn ansprechen. In diesem Fall ist die Beschleunigung betragsmäßig immer noch konstant, zeigt aber stets senkrecht zur Bewegungsrichtung.
Wir wollen unser Koordinatensystem so wählen, dass die Bewegung in der xy-Ebene verläuft. Zur Zeit τ = t = 0 soll sich unser Massepunkt bei den Koordinaten x = R, y = z = 0 befinden, wobei wir im Folgenden die z-Koordinate weglassen. Dabei bezeichnet R den Radius der Kreisbahn. Wie bisher wollen wir den Betrag der Viererbeschleunigung a = g wählen. Außerdem soll der Betrag der Geschwindigkeit entlang der Kurve konstant bleiben.





 setzen. Zusammen mit den Beziehungen (6.89) und (6.90) erhalten wir direkt
setzen. Zusammen mit den Beziehungen (6.89) und (6.90) erhalten wir direkt


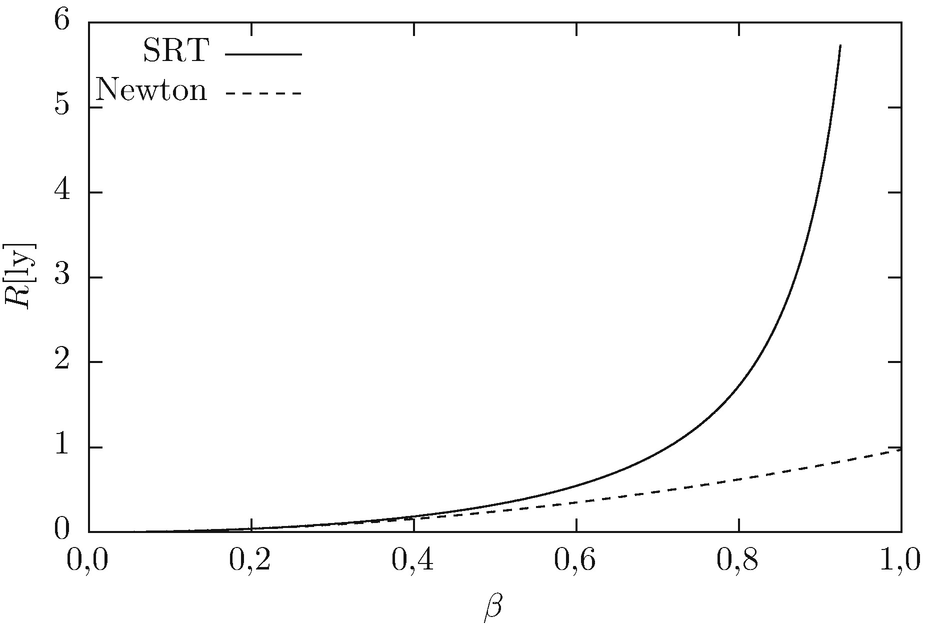
Radius R(β) einer Kreisbahn bei relativistischen Geschwindigkeiten und konstanter Beschleunigung a = g. Der Kreisradius in relativistischer Rechnung (durchgezogene Linie) divergiert bei β = 1, der Radius in Newton'scher Mechanik (gestrichelte Linie) steigt quadratisch mit der Geschwindigkeit. Das relativistische Ergebnis geht für kleine Geschwindigkeiten v ≪ c in das nichtrelativistische über
Es muss allerdings angemerkt werden, dass bei dieser Situation noch ein zusätzlicher Effekt auftritt, den wir in diesem Rahmen nicht behandeln wollen, nämlich die Thomas-Präzession3 des Bezugssystems des Raumfahrers. Diese führt dazu, dass nach einem vollständigen Umlauf das Bezugssystem des Raumfahrers nicht mehr parallel zum ursprünglichen Bezugssystem ist, es sei denn, der Raumfahrer korrigiert dies durch zusätzliche Navigation. Die Thomas-Präzession [9] ist auch als relativistische Korrektur zur Spin-Bahn-Kopplung in der Atomphysik von Bedeutung.
6.9 Übungsaufgaben
6.9.1 Rundreise auf Kreisbahn (für motivierte Rechner)
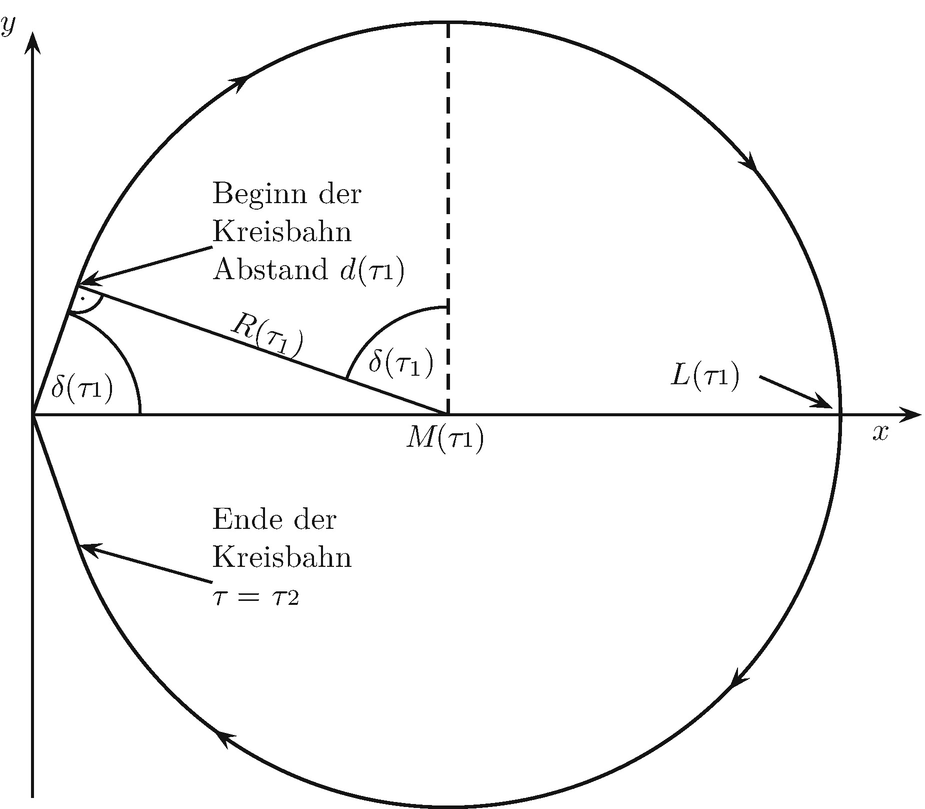
Skizze zum wendenden Raumfahrer
![$$ \left(\begin{array}{l}\hfill x\left(\tau \right)\hfill \\ {}\hfill y\left(\tau \right)\hfill \end{array}\right)=d\left(\tau \right)\left(\begin{array}{l}\hfill \cos \left[\delta \left({\tau}_1\right)\right]\hfill \\ {}\hfill \sin \left[\delta \left({\tau}_1\right)\right]\hfill \end{array}\right). $$](../images/331389_2_De_6_Chapter/331389_2_De_6_Chapter_TeX_Equ94.png)
- (a)
Bestimmen Sie die mathematische Darstellung der gesamten Weltlinie des Raumfahrers.
- (b)
Ermitteln Sie, welche Entfernungen der Raumfahrer für gegebene Beschleunigungsdauern τ1 jetzt erreichen kann.
- (c)
Bestimmen Sie dann die benötigte Beschleunigungsdauer für eine gegebene Entfernung und berechnen Sie die Gesamtreisedauer für den Raumfahrer und für einen auf der Erde verbleibenden Beobachter. Welche Unterschiede ergeben sich zur geradlinigen Reise?
6.9.2 Relativistische Beschleunigung
Berechnen Sie die beiden Skalarprodukte uμbμ und bμbμ und diskutieren Sie die Ergebnisse.