© Springer-Verlag GmbH Deutschland, ein Teil von Springer Nature 2022
S. Boblest et al.Spezielle und allgemeine Relativitätstheoriehttps://doi.org/10.1007/978-3-662-63352-6_19

19. Energieproduktion in Sternen

Sebastian Boblest1  , Thomas Müller2 und Günter Wunner3  
(1)
Dürnau, Deutschland
(2)
Max-Planck-Institut für Astronomie, Haus der Astronomie, Heidelberg, Deutschland
(3)
Universität Stuttgart, 1. Institut für Theoretische Physik, Stuttgart, Deutschland
 

In diesem Kapitel befassen wir uns mit den physikalischen Prozessen, mit deren Hilfe Sterne Energie gewinnen. Wir haben bereits in Abschn. 1.​5.​1 einen Eindruck von den unglaublichen Energiemengen erhalten, die Sterne freisetzen. So hat die Sonne nach (1.​58) eine Leuchtkraft von etwa L⊙  ≈ 4 · 1026 W. Um im Gleichgewicht zu bleiben, muss sie also mit gleicher Leistung Energie freisetzen.

Heute wissen wir, dass Sterne diese Energie durch Kernfusionsprozesse gewinnen, die in ihrem Inneren ablaufen. Eine erste quantitative Untersuchung dieser Vorgänge wurde in den 1930er Jahren durch Weizsäcker1 und Bethe2 [6] vorgenommen. 1957 veröffentlichten Burbidge,3 Burbidge,4 Fowler5 und Hoyle6 eine umfassende Untersuchung der Fusionsprozesse in Sternen [7]. Entsprechend der Autorennamen wird diese Veröffentlichung auch als B2HF-Paper bezeichnet. Dabei ist das Verständnis dieser Prozesse nicht nur bedeutsam, um den Aufbau und die Entwicklung von Sternen zu verstehen, sondern vor allem auch um die Entstehung und die Häufigkeit der verschiedenen in der Natur vorkommenden Elemente zu erklären.

Wir beginnen unsere Diskussion mit grundlegenden Überlegungen zu den Bedingungen, unter denen Kernfusionsprozesse ablaufen und warum bei ihnen Energie freigesetzt werden kann, bevor wir dann einige wichtige Reaktionen detaillierter betrachten.

19.1 Kernfusion als Energiequelle

Sterne wie die Sonne leuchten für mehrere Milliarden Jahre mit fast konstanter Leuchtkraft. Sie müssen die dafür nötige Energie also aus einem sehr großen Reservoir beziehen. Wie wir gleich sehen werden, ist die bei Kernfusionsreaktionen freiwerdende Energiemenge viel größer als etwa bei chemischen Reaktionen. Zum Vergleich: Bei der Verbrennung von 1 kg Steinkohle wird beispielsweise eine Energiemenge E ≈ 2,9 · 107 J = 1 SKE (eine Steinkohleeinheit) frei. Wenn die ganze Sonne aus Steinkohle bestünde, ergäbe das bei ihrer jetzigen Leuchtkraft genug Energie, um etwa 4600 Jahre zu leuchten, also viel zu kurz im Vergleich zu ihrem Alter von etwa 4,6 · 109 y [5].

Im 19. Jahrhundert war Kernfusion noch unbekannt und dementsprechend die Frage nach der Energiequelle der Sonne ein ungelöstes Problem. Wir können das besser verstehen, wenn wir untersuchen, wie lange die Sonne ihre Energie aus anderen Energiequellen beziehen könnte. Chemische Reaktionen sind nach dem gerade gesehenen Beispiel ungeeignet. Eine weitere naheliegende Energiequelle ist die gravitative Bindungsenergie. Wir haben in Abschn. 1.​4.​3 hergeleitet, dass eine homogene Vollkugel mit Masse M und Radius R die gravitative Bindungsenergie Em = −(3∕5)GM2∕R besitzt, die beim Kollaps freigeworden sein muss. Für die Sonne ergibt dies mit R⊙ ≈ 7 · 108 km und M⊙ = 2 · 1030 kg (s. (1.​55) und (1.​54)) eine während des Kollapses freigewordene Energie von
$$ {E}_{\mathrm{m}}^{\odot}\approx 2,29\cdotp 1{0}^{41}\, \mathrm{J}. $$
(19.1)
Diese Energiemenge wäre ausreichend, damit die Sonne mit ihrer gegenwärtigen Leistung für einen Zeitraum
$$ {\tau}_{\mathrm{KH}}=\frac{E_{\mathrm{m}}}{L_{\odot }}\approx 5,9\cdotp 1{0}^{14}\, \mathrm{s}\approx 1,88\cdotp 1{0}^7\mathrm{y} $$
(19.2)
leuchten könnte. Das Verhältnis τKH von Gravitationsbindungsenergie zu Leuchtkraft heißt Kelvin-Helmholtz-Zeitskala7,8 .

Als reiner Gravitationseffekt ergäbe sich also eine Lebensdauer für Sterne im Bereich von einigen zehn Millionen Jahren. Das ist deutlich länger als es mit chemischen Reaktionen möglich wäre, aber immer noch viel zu kurz um das geschätzte Alter der Sonne von etwa 4,57 · 109 y zu erklären. Tatsächlich gewinnen aber Protosterne, wie wir gesehen haben, ihre Energie aus diesem Reservoir, bevor sie heiß genug werden, dass Fusionsprozesse beginnen können. Im 19. Jahrhundert war kein größeres Energiereservoir bekannt, aus dem die Sonne ihre Strahlungsenergie beziehen könnte. Das sich ergebende Sonnenalter war aber unverträglich mit geologischen Erkenntnissen zum Alter der Erde und Darwins Untersuchungen zur Evolution.

Wie lässt sich aber nun mit Kernfusion Energie gewinnen? Abb. 19.1 zeigt die Bindungsenergie pro Nukleon für Atomkerne mit verschiedenen Massenzahlen A, wobei für jedes A der am stärksten gebundene Kern ausgewählt wurde. Da der Wasserstoffkern nur aus einem Proton besteht, ist seine Bindungsenergie natürlich Null. Dagegen weist der doppelt magische 4He-Kern pro Nukleon eine Bindungsenergie von etwa $$ 7\, \mathrm{MeV} $$ auf. Wenn man also vier Protonen zu einem Heliumkern fusioniert, wobei zwei Protonen in Neutronen umgewandelt werden müssen, so kann man mit einer freiwerdenden Energie in der Größenordnung von $$ 28\, \mathrm{MeV} $$ rechnen. Der tatsächliche Wert liegt etwas niedriger, weil die bei der Fusion freiwerdenden Neutrinos nicht mit der Sternmaterie wechselwirken und so einen Teil der Energie abführen. Außerdem sind mehrere Reaktionswege von den 4 Protonen zum Heliumkern möglich, die eine leicht unterschiedliche Energiebilanz aufweisen. Wir nehmen für die folgenden Überlegungen deshalb eine freiwerdende Energie von $$ 26\, \mathrm{MeV} $$ an.
Abb. 19.1

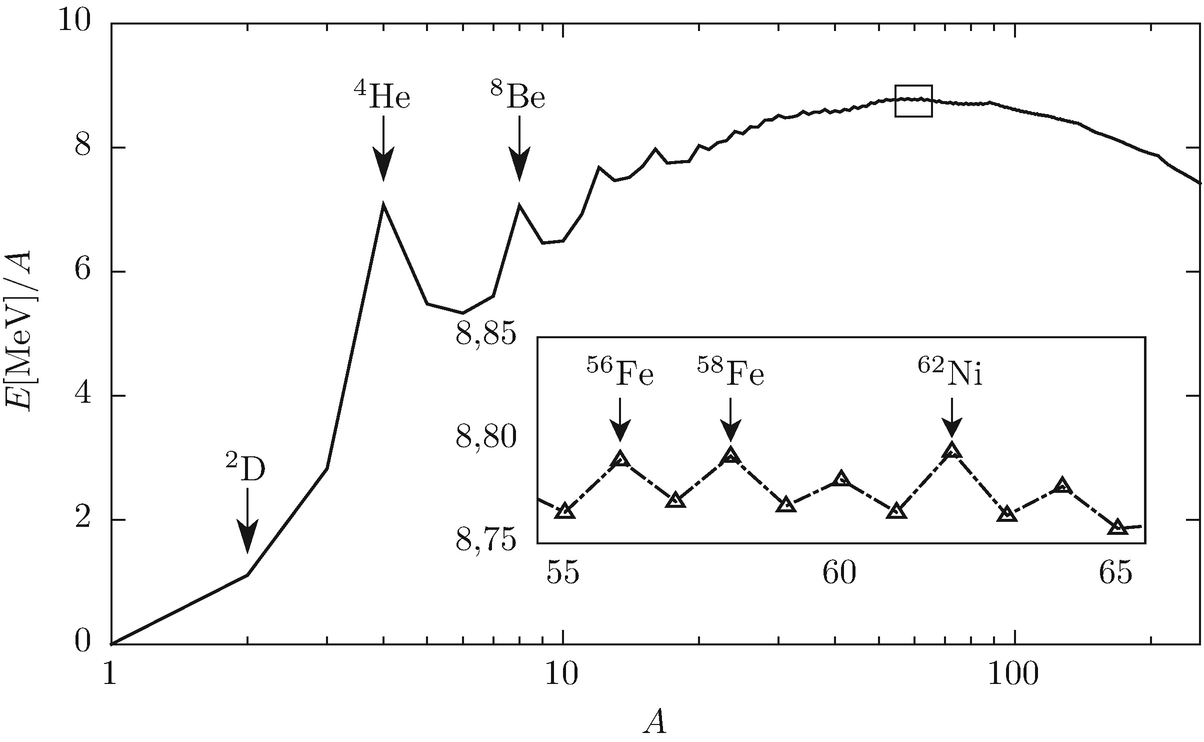
Bindungsenergie pro Nukleon für Nuklide mit verschiedenen Massenzahlen A. Für jede Massenzahl ist jeweils das Nuklid mit der höchsten Bindungsenergie gewählt. Der Ausschnitt zeigt den Bereich von A = 55–65 mit den drei am stärksten gebundenen Nukliden 62Ni, 58Fe und 56Fe. Die Daten für die Abbildung stammen aus [3]

Wenn wir von einem anfänglichen Wasserstoffanteil der Sonne von 70 % ausgehen und weiter die Leuchtkraft L⊙ = 3,86 · 1026 W als konstant annehmen, so können wir berechnen, wie lange die Sonne durch Wasserstofffusion strahlen kann.

Umgerechnet in Joule ergibt sich die freiwerdende Energie $$ {E}_{4\mathrm{p}\to \mathrm{He}}=26\, \mathrm{MeV}=4,2\cdotp 1{0}^{-12}\, \mathrm{J} $$ pro entstehendem Heliumkern. Pro Sekunde müssen also
$$ {N}_{\mathrm{s}}=3,86\cdotp 1{0}^{26}\, \mathrm{J}/ {E}_{4\mathrm{p}\to \mathrm{He}}=9,3\cdotp 1{0}^{37} $$
(19.3)
solcher Reaktionen stattfinden, um den Strahlungsverlust auszugleichen. Die maximal mögliche Anzahl solcher Reaktionen ist ungefähr
$$ {N}_{4\mathrm{p}\to \mathrm{He}}=\frac{0,7{M}_{\odot }}{4{m}_{\mathrm{p}}}=2,1\cdotp 1{0}^{56}. $$
(19.4)
Das führt auf die grobe Abschätzung
$$ {t}_{\mathrm{H}}=\frac{N_{\mathrm{s}}}{N_{4\mathrm{p}\to \mathrm{He}}}\mathrm{s}\approx 7,1\cdotp 1{0}^{10}\mathrm{y}. $$
(19.5)
Die Sonne könnte also bei gleichbleibender Leuchtkraft für etwa 71 Milliarden Jahre ihren Energiebedarf aus der Wasserstofffusion decken. Die tatsächliche Lebensdauer der Sonne ist um etwa einen Faktor 7 geringer, weil Sterne nur etwa 10 % ihres Wasserstoffs fusionieren, entscheidend ist aber das im Vergleich zur Gravitationsenergie um ein Vielfaches größere Energiereservoir der Kernfusion.

Anhand von Abb. 19.1 sehen wir aber auch, dass bei der Fusion von Wasserstoff zu Helium mit großem Abstand mehr Energie pro Nukleon frei wird, als bei der Fusion schwererer Elemente, etwa Helium zu Kohlenstoff. Solche Reaktionen finden statt, wenn ein Stern seinen Wasserstoffvorrat im Zentrum im Wesentlichen verbraucht hat. Aufgrund der viel kleineren Energieausbeute reicht der Energievorrat dieser Reaktionen aber nur für sehr viel kürzere Zeiträume. Auf diese Aspekte gehen wir etwas ausführlicher in Abschn. 19.5 ein.

Zuvor möchten wir aber analysieren, welche Voraussetzungen gegeben sein müssen, damit Fusionsreaktionen überhaupt stattfinden können.

19.2 Voraussetzungen für Fusionsprozesse

In der Sonne herrschen Temperaturen in der Größenordnung von T ∼ 107 K (s. (18.​22)). Dies entspricht einer thermischen Energie $$ E\gtrsim 800–900\, \mathrm{eV} $$ also weit über der Ionisierungsenergie von Wasserstoff. Die leichten Atome werden in Sternen also ionisiert vorliegen. Protonen stoßen sich aber aufgrund der elektromagnetischen Wechselwirkung ab. Nähert sich ein Proton einem anderen, so muss es den Coulomb-Wall überwinden, d. h. die beiden Protonen müssen sich so nahe kommen, dass die kurzreichweitige starke Wechselwirkung zur Kernreaktion führen kann.

Um abzuschätzen, wie groß der Coulomb-Wall ist, nehmen wir für den Radius eines Protons etwa rp ≃ 10−15 m an, was für eine Abschätzung völlig ausreichend mit aktuellen Werten übereinstimmt [2].

Bei ,,Berührung“ der Protonen haben die Mittelpunkte einen Abstand von 2rp. Damit ergibt sich für die potentielle Energie
$$ V\left(2{r}_{\mathrm{p}}\right)=\frac{e^2}{4\pi {\varepsilon}_0}\frac{1}{2{r}_{\mathrm{p}}}. $$
(19.6)
Wir wollen diese Energie mit der Bindungsenergie des Wasserstoffatoms vergleichen. Dazu drücken wir den Protonenradius rp durch den Bohr-Radius aB ≃ 0,529 · 10−10 m aus (7.​56) aus.
Es ist also rp ≃ 2aB · 10−5 und wir erhalten
$$ V\left(2{r}_{\mathrm{p}}\right)=\frac{e^2}{4\pi {\varepsilon}_0}\frac{1}{2{a}_{\mathrm{B}}}\frac{1}{2}\cdotp 1{0}^5=\frac{\alpha^2}{2}{m}_{\mathrm{e}}{c}^2\frac{1}{2}\cdotp 1{0}^5=\frac{1}{2}{E}_{\mathrm{Ry}}\cdotp 1{0}^5 $$
(19.7)
mit der Rydberg-Energie9
$$ {E}_{\mathrm{Ry}}={\alpha}^2{m}_{\mathrm{e}}{c}^2/\, 2=13,60569253(30)\, \mathrm{eV} $$
(19.8)
und der Feinstrukturkonstante α in (1.​18). Der Coulomb-Wall beträgt also etwa $$ V\left(2{r}_{\mathrm{p}}\right)=6,8\cdotp 1{0}^5\, \mathrm{eV} $$ und ist demnach viel größer als die thermischen Energien im Bereich von $$ 1\, \mathrm{keV} $$.

Dass dennoch Fusionsprozesse stattfinden, hat zwei Gründe. Zum einen haben nicht alle Protonen bzw. Atomkerne die gleiche Geschwindigkeit, sondern es liegt eine Geschwindigkeitsverteilung vor. Zum anderen kann es durch den quantenmechanischen Tunneleffekt auch zu Fusionsprozessen kommen, wenn die Energie dafür klassisch nicht ausreichend wäre.

19.2.1 Geschwindigkeitsverteilung der Nukleonen

Wir haben bereits diskutiert, dass die Materie in einem Stern in guter Näherung als ideales Gas beschrieben werden kann. Dementsprechend gehorchen die auftretenden Geschwindigkeiten der Maxwell-Boltzmann-Verteilung und für die Beträge der Geschwindigkeiten ergibt sich deshalb die Wahrscheinlichkeitsdichte
$$ \mathcal{P}(v)\, \mathrm{d}v=4\pi {\left(\frac{m}{2\pi {k}_{\mathrm{B}}T}\right)}^{3/ 2}{v}^2\exp \left(-\frac{m{v}^2}{2{k}_{\mathrm{B}}T}\right)\, \mathrm{d}v. $$
(19.9)
Für Fusionsprozesse sind nicht die Geschwindigkeiten der Teilchen im Ruhsystem, sondern die Relativgeschwindigkeiten im Schwerpunktsystem relevant, die aber ebenfalls einer Maxwell-Verteilung gehorchen. Wir müssen lediglich den Übergang von der Masse m zur reduzierten Masse
$$ {m}_{\mathrm{r}}=\frac{m_{\mathrm{A}}{m}_{\mathrm{B}}}{m_{\mathrm{A}}+{m}_{\mathrm{B}}} $$
(19.10)
vornehmen. Weil wir uns mit Atomkernen beschäftigen, ist es zweckmäßig, die reduzierte Masse über die Massenzahlen auszudrücken. Mit mA,B = AA,Bmu, wobei mu die atomare Masseneinheit aus (18.​59) bezeichnet, ergibt sich
$$ {m}_{\mathrm{r}}=\frac{A_{\mathrm{A}}{A}_{\mathrm{B}}}{A_{\mathrm{A}}+{A}_{\mathrm{B}}}{m}_{\mathrm{u}}={A}_{\mathrm{r}}{m}_{\mathrm{u}}. $$
(19.11)
Außerdem ist es von Vorteil, die Maxwell-Verteilung auf die Energie umzuformulieren, wobei wir hier den nichtrelativistischen Zusammenhang E = p2∕2mr verwenden. Wir erhalten dann
$$ \mathcal{P}(E)\, \mathrm{d}E=2\sqrt{\frac{E}{\pi {k}_{\mathrm{B}}^3{T}^3}}\exp \left(-\frac{E}{k_{\mathrm{B}}T}\right)\, \mathrm{d}E. $$
(19.12)
Der Anteil hochenergetischer Teilchen nimmt exponentiell mit der Energie ab, es gibt aber immer einen kleinen Anteil an Teilchen, mit sehr hoher Energie. In Abb. 19.2 ist die Maxwell-Energieverteilung skizziert. Eine kleine Randbemerkung ist hier angebracht: Die Maxwell-Verteilung (19.9) ist nichtrelativistisch, sie erlaubt auch Geschwindigkeiten v > c. Bei nicht zu hohen Temperaturen ist der Anteil hoher Geschwindigkeiten verschwindend klein und diese Abweichung spielt keine Rolle. Bei den hohen Temperaturen in Sternen ist diese Annahme allerdings unter Umständen problematisch. Für unsere qualitative Diskussion ist die nichtrelativistische Betrachtung aber sicherlich ausreichend. Für eine einführende Diskussion über die Vereinheitlichung von Relativitätstheorie und Thermodynamik verweisen wir interessierte Leser auf [8].
Abb. 19.2

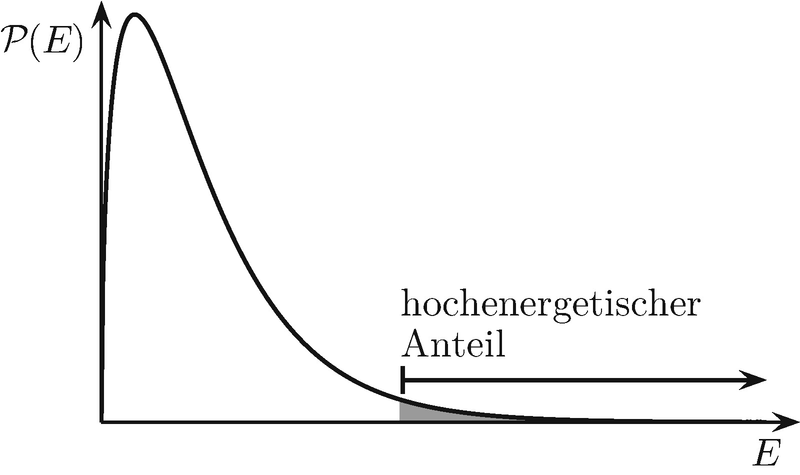
Skizze der Maxwell-Energieverteilung. Auch wenn die thermische Energie viel kleiner als der Coulomb-Wall ist, existiert immer ein kleiner Anteil von Teilchen mit sehr hoher Energie, die dann fusionieren können

19.2.2 Tunneleffekt

In der klassischen Physik ist es einem Teilchen nur möglich, einen Potentialwall der Höhe V zu überwinden, wenn seine kinetische Energie größer ist als V. In der Quantenmechanik gilt diese Einschränkung nicht mehr, mit einer kleinen Wahrscheinlichkeit kann hier ein Teilchen durch den Potentialwall tunneln. Sowohl bei Kernzerfällen als auch bei Kernfusion spielen diese Tunnelprozesse eine zentrale Rolle.

Die erste quantitative Untersuchung des Tunneleffektes bei Prozessen im Atomkern führte Gamow 1928 durch [9]. Er studierte den radioaktiven α-Zerfall, bei dem ein 4He-Kern den Kern verlässt. Wir betrachten hier Fusionsprozesse und damit genau den gegenteiligen Ablauf, aber die entsprechenden Ergebnisse zum Tunneleffekt bleiben auch in umgekehrter Richtung gültig.

Ein einfaches eindimensionales Beispielsystem in der Quantenmechanik ist ein freies Teilchen mit Energie E und ein Rechteckpotential mit V > E. Im Bereich des Potentials lautet die Schrödingergleichung dann
(19.13)
mit der Lösung
(19.14)
Die Amplitude der Wellenfunktion nimmt also exponentiell ab, und zwar umso schneller, je größer die Differenz V − E ist. Der Faktor ψ0 muss so bestimmt werden, dass ψ normiert ist, aber das spielt für uns keine Rolle. Entscheidend ist, dass die Wahrscheinlichkeit, das Teilchen im Intervall [x, x + dx] zu finden durch |ψ(x)|2dx gegeben ist. Wenn sich das Rechteckpotential von x1 bis x2 erstreckt, ergibt sich dann die Tunnelwahrscheinlichkeit zu
(19.15)
Die Tunnelwahrscheinlichkeit sinkt also zum einen mit der Höhe des Potentials V − E über der Energie und zum anderen mit der Breite x2 − x1.
Wenn wir diese einfache Betrachtung auf die Fusion zweier geladener Teilchen übertragen möchten, so müssen wir das Rechteckpotential durch das Coulomb-Potential
$$ V(r)=\frac{Z_{\mathrm{A}}{Z}_{\mathrm{B}}}{4\pi {\varepsilon}_0}\frac{e^2}{r} $$
(19.16)
ersetzen (s. Abb. 19.3). Dabei sind ZA und ZB die Ladungen der beiden Teilchen. Aufgrund des nichtkonstanten Potentials können wir nicht so einfach wie in (19.14) die Schrödingergleichung lösen, inbesondere kennen wir den genauen Potentialverlauf in Kernnähe nicht.
Abb. 19.3

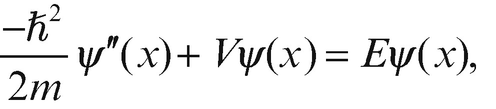
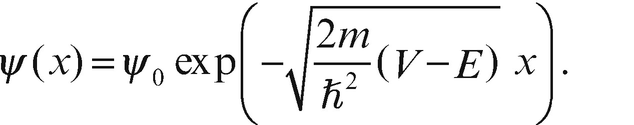
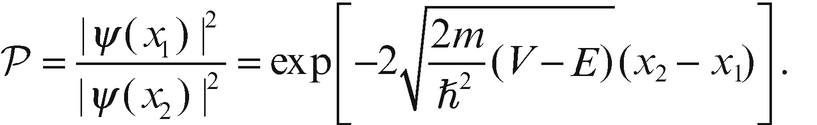
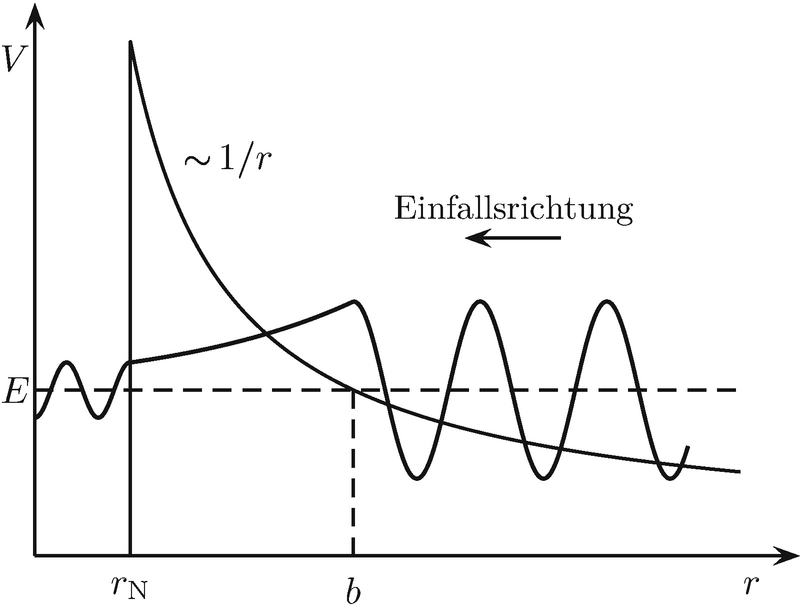
Der Tunneleffekt bei Fusionsprozessen. Mit einer gewissen Wahrscheinlichkeit kann ein einfallendes Teilchen durch den Coulomb-Wall des Zielteilchens tunneln, in den Einflussbereich der starken Wechselwirkung gelangen und die beiden Teilchen können fusionieren. Der Potentialverlauf ist in dieser Skizze vereinfacht dargestellt

Die detaillierte Rechnung ergibt [13]
$$ {\mathcal{P}}_{\mathrm{T}}\approx \exp \left(-\sqrt{E_{\mathrm{G}}/ E}\right), $$
(19.17)
mit der Gamow-Energie
$$ {E}_{\mathrm{G}}=2{\pi}^2{\alpha}^2{m}_{\mathrm{u}}{c}^2{A}_{\mathrm{r}}{Z}_{\mathrm{A}}^2{Z}_{\mathrm{B}}^2=979\, \mathrm{keV}\cdotp {A}_{\mathrm{r}}{Z}_{\mathrm{A}}^2{Z}_{\mathrm{B}}^2, $$
(19.18)
wobei wir Ar aus (19.11) verwendet haben. Oft wird in der astrophysikalischen Literatur auch die Notation $$ 2\pi \eta =\sqrt{E_{\mathrm{G}}/ E} $$ eingeführt. Wir folgen dieser Konvention hier allerdings nicht. Bei der Fusion zweier Protonen ist Ar = 1∕2 und ZA = ZB = 1 und man erhält $$ {E}_{\mathrm{G},\mathrm{pp}}\simeq 489,6\, \mathrm{keV} $$. Im Zentrum der Sonne bei der Temperatur Tz aus (18.​22) liegt die thermische Energie bei etwa $$ E\approx {k}_{\mathrm{B}}{T}_{\mathrm{z}}\approx 1,3\, \mathrm{keV} $$. Sie ist also um ein Vielfaches kleiner als die Gamow-Energie. Damit ist $$ {\mathcal{P}}_{\mathrm{T}}\approx \exp \left(-19,2\right)\approx 4,8\cdotp 1{0}^{-9} $$. Die Wahrscheinlichkeit für ein Durchtunneln der Coulomb-Barriere ist also sehr klein.

Die Gamow-Energie steigt mit der Ladungszahl der beteiligten Reaktionspartner, dementsprechend sinkt die Tunnelwahrscheinlichkeit stark. Bei der Fusion zweier 4He-Kerne ist die Gamow-Energie wegen ZA = ZB = 2 und weiter Ar = 1∕2 bereits 16-mal so hoch wie bei zwei Protonen. Damit dennoch Fusionsreaktionen höher geladener Teilchen möglich werden, muss deshalb die mittlere Teilchenenergie und damit die Temperatur in entsprechenden Sternen viel höher sein.

19.3 Bestimmung von Reaktionsraten

Die Diskussion in den letzten beiden Abschnitten hat aufgezeigt, dass in Sternen Fusionsprozesse ablaufen können. Entscheidend ist aber, mit welcher Rate bestimmte Fusionsreaktionen ablaufen. Bei der Untersuchung der Fusionsraten orientieren wir uns an der Abhandlung in [13].

In der Physik charakterisiert man die Reaktionswahrscheinlichkeit bei Streuprozessen über den Wirkungsquerschnitt σ. Im vorliegenden Fall muss dieser proportional zu $$ {\mathcal{P}}_{\mathrm{T}} $$ in (19.17) sein. Daneben spielen aber noch die genauen kernphysikalischen Abläufe bei der jeweiligen Fusionsreaktion eine Rolle. Diese werden in einem Faktor S(E) zusammengefasst, der in einer Kombination von Experiment und Theorie bestimmt werden muss, da die Bedingungen im Inneren von Sternen kaum im Labor realisiert werden können und daher Laborergebnisse aufgrund theoretischer Überlegungen extrapoliert werden.

In vielen Fällen ändert sich S(E) nur schwach mit der Energie und kann dann über weite Energiebereiche als konstant angesehen werden. Ausnahmen von dieser Regel sind Energien, die angeregten Niveaus in den beteiligten Kernen entsprechen. Die Werte von S(E) für verschiedene Reaktionen sind umfangreich tabelliert [1]. In der angegebenen Referenz findet sich auch eine umfassende Diskussion der Bestimmungsmethoden und der Unsicherheiten in den jeweiligen Werten. Insgesamt fasst man diese Größen dann im Wirkungsquerschnitt
$$ \sigma (E)=\frac{S(E)}{E}\exp \left[-{\left(\frac{E_{\mathrm{G}}}{E}\right)}^{1/ 2}\right] $$
(19.19)
zusammen.
Die Rate RAB, mit der Fusionen zwischen Teilchen der Sorten A und B stattfinden, wird aber nicht nur durch den Wirkungsquerschnitt bestimmt, sondern auch durch die Häufigkeit, mit der sich zwei solche Teilchen nahe kommen. Diese Rate ist umso größer, je höher die jeweiligen Teilchendichten sind und je höher die relativen Geschwindigkeiten der Teilchen zueinander sind, d. h.
$$ {R}_{\mathrm{A}\mathrm{B}}\sim {n}_{\mathrm{A}}{n}_{\mathrm{B}}\sigma {v}_{\mathrm{r}}. $$
(19.20)
Wie die Geschwindigkeiten der Teilchen gehorchen auch die Relativgeschwindigkeiten und damit die Energien einer Maxwell-Verteilung. Um einen Ausdruck für die Reaktionsrate pro Einheitsvolumen zu erhalten müssen wir den Ausdruck σvr also entsprechend mitteln. Da wir den Wirkungsquerschnitt als Funktion der Energie erhalten haben, drücken wir die Geschwindigkeit über $$ {v}_{\mathrm{r}}=\sqrt{2E/ {m}_{\mathrm{r}}} $$ über die Energie aus und verwenden die Energieform (19.12) der Maxwell-Verteilung. Dann haben wir
$$ {\displaystyle \begin{array}{rll}\left\langle \sigma {v}_{\mathrm{r}}(E)\right\rangle & ={\left(\frac{8}{\pi {m}_{\mathrm{r}}{k}_{\mathrm{B}}^3{T}^3}\right)}^{1/ 2}\underset{0}{\overset{\infty }{\int }}\sigma (E)E\exp \left(-\frac{E}{k_{\mathrm{B}}T}\right)\, \mathrm{d}E& \\ {}& ={\left(\frac{8}{\pi {m}_{\mathrm{r}}{k}_{\mathrm{B}}^3{T}^3}\right)}^{1/ 2}\underset{0}{\overset{\infty }{\int }}S(E)\exp \left[-\frac{E}{k_{\mathrm{B}}T}-{\left(\frac{E_{\mathrm{G}}}{E}\right)}^{1/ 2}\right]\, \mathrm{d}E.\end{array}} $$
(19.21)
Selbst wenn wir S(E) als konstant annehmen, können wir dieses Integral nicht direkt berechnen. Wir suchen deshalb nach einer geeigneten Näherung. Im Argument der Exponentialfunktion in der zweiten Zeile treten zwei Terme auf, zum einen − E∕kBT aus der Maxwell-Verteilung und zum anderen −(EG∕E)1∕2 aus der Tunnelwahrscheinlichkeit. Der Maxwell-Anteil divergiert für große Energien gegen minus Unendlich, der Tunnelanteil geht gegen Null, bei kleinen Energien ist das Verhalten genau umgekehrt. Das führt dazu, dass der Integrand in (19.21) nur in einem begrenzten Energiebereich einen relevanten Beitrag liefert. Physikalisch bedeutet dies, dass der Anteil von Teilchen mit einer sehr großen Energie sehr klein ist und dass auf der anderen Seite die Tunnelwahrscheinlichkeit für Teilchen mit kleiner Energie sehr gering ist.
Das Maximum des Exponenten liegt bei
$$ {E}_{\mathrm{P}}={\left[{E}_{\mathrm{G}}{\left(\frac{k_{\mathrm{B}}T}{2}\right)}^2\right]}^{1/ 3}, $$
(19.22)
mit dem Funktionswert
$$ \exp \left({E}_{\mathrm{P}}\right)=\exp \left[-3{\left(\frac{E_{\mathrm{G}}}{4{k}_{\mathrm{B}}T}\right)}^{1/ 3}\right]. $$
(19.23)
Dieses Maximum heißt Gamow-Peak . Wir entwickeln den Exponenten um das Maximum und finden
$$ \frac{E}{k_{\mathrm{B}}T}+{\left(\frac{E_{\mathrm{G}}}{E}\right)}^{1/ 2}\approx 3{\left(\frac{E_{\mathrm{G}}}{4{k}_{\mathrm{B}}T}\right)}^{1/ 3}+3{\left(\frac{1}{16{E}_{\mathrm{G}}{\left({k}_{\mathrm{B}}T\right)}^5}\right)}^{1/ 3}{\left(E-{E}_{\mathrm{P}}\right)}^2. $$
(19.24)
Wenn wir diesen Ausdruck wieder in die Exponentialfunktion einsetzen und etwas umformen, ergibt sich ein konstanter Beitrag multipliziert mit einer Gauß-Funktion, d. h.
$$ {\displaystyle \begin{array}{rll}\left\langle \sigma {v}_{\mathrm{r}}(E)\right\rangle \approx {\left(\frac{8}{\pi {m}_{\mathrm{r}}{k}_{\mathrm{B}}^3{T}^3}\right)}^{1/ 2}\underset{0}{\overset{\infty }{\int }}& S(E)\exp \left[-3{\left(\frac{E_{\mathrm{G}}}{4{k}_{\mathrm{B}}T}\right)}^{1/ 3}\right]& \\ {}& \cdotp \exp \left[-\frac{1}{2}{\left(\frac{E-{E}_{\mathrm{P}}}{\sigma_{\mathrm{G}}}\right)}^2\right]\, \mathrm{d}E,\end{array}} $$
(19.25)
dabei ist die Varianz gegeben über
$$ {\sigma}_{\mathrm{G}}={3}^{-1/ 2}{\left[2{E}_{\mathrm{G}}{\left({k}_{\mathrm{B}}T\right)}^5\right]}^{1/ 6}. $$
(19.26)
Der Energiebereich E ∈ [EP ± ΔG∕2], in dem die Exponentialfunktion mindestens einen Funktionswert größer als 1∕e des Maximalwertes annimmt, wird als Gamow-Fenster bezeichnet. Aus der Definition der Gauß-Funktion sieht man, dass $$ {\Delta}_{\mathrm{G}}=2\sqrt{2}{\sigma}_{\mathrm{G}} $$ gilt. In diesem Energieintervall findet der dominante Anteil der Fusionsreaktionen statt. In Abb. 19.4 sind diese Zusammenhänge skizziert.
Abb. 19.4

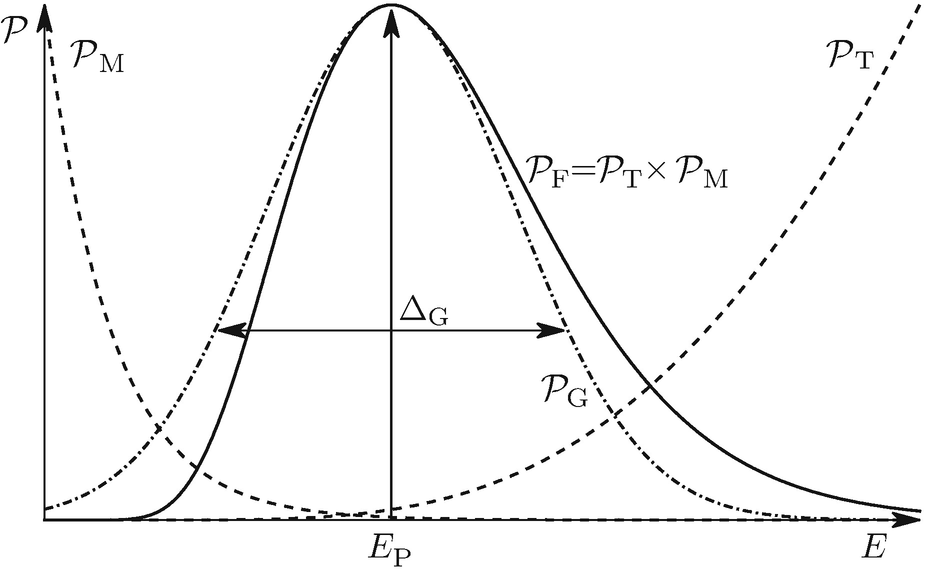
Die allermeisten Fusionsreaktionen finden in einem relativ kleinen Energiefenster um den Gamow-Peak bei E = EP statt, da aufgrund der Maxwell-Verteilung $$ {\mathcal{P}}_{\mathrm{M}} $$ nur sehr wenige sehr energiereiche Teilchen vorhanden sind und bei niedrigen Energien die Tunnelwahrscheinlichkeit $$ {\mathcal{P}}_{\mathrm{T}} $$ extrem klein wird. Zur quantitativen Auswertung wird das Produkt $$ {\mathcal{P}}_{\mathrm{F}} $$ um das Maximum herum als Gauß-Funktion entwickelt. In dieser Skizze ist $$ {\mathcal{P}}_{\mathrm{F}} $$ skaliert dargestellt

An dieser Stelle verwenden wir jetzt die schwache Energieabhängigkeit des S-Faktors und setzen S(E) ≈ S(EP). Dann können wir diesen Ausdruck zusammen mit der ersten Exponentialfunktion, die nicht von E abhängt, vor das Integral ziehen. Die Integration ist dann nur noch über eine reine Gauß-Funktion auszuführen und wir erhalten
$$ {\displaystyle \begin{array}{rll}\left\langle \sigma {v}_{\mathrm{r}}(E)\right\rangle \approx & {\left(\frac{4}{m_{\mathrm{r}}{k}_{\mathrm{B}}^3{T}^3}\right)}^{1/ 2}S\left({E}_{\mathrm{P}}\right)\exp \left[-3{\left(\frac{E_{\mathrm{G}}}{4{k}_{\mathrm{B}}T}\right)}^{1/ 3}\right]& \\ {}& \cdotp {\sigma}_{\mathrm{G}}\left[1+\operatorname{erf}\left(\frac{E_{\mathrm{P}}}{\sqrt{2}{\sigma}_{\mathrm{G}}}\right)\right].\end{array}} $$
(19.27)
Für das Argument der Fehlerfunktion $$ \operatorname{erf}(x) $$ finden wir mit (19.22) und (19.26) $$ {E}_{\mathrm{P}}/ \left(\sqrt{2}{\sigma}_{\mathrm{G}}\right)\approx 0,69{\left({E}_{\mathrm{G}}/ {k}_{\mathrm{B}}T\right)}^{1/ 6}\approx 1,93 $$ für unsere oben berechneten Werte $$ {E}_{\mathrm{G}}\simeq 490\, \mathrm{keV} $$ und $$ {k}_{\mathrm{B}}{T}_{\mathrm{z}}\simeq 1,3\, \mathrm{keV} $$. Insgesamt führt das dann auf $$ \operatorname{erf}\left({E}_{\mathrm{P}}/ \left(\sqrt{2}{\sigma}_{\mathrm{G}}\right)\right)\simeq 0,99\approx 1 $$. Wegen der Potenz 1∕6 ändert sich dieses Verhältnis mit dem Verhältnis von Gamow-Energie zu thermischer Energie nur sehr schwach und wir können in einem sehr weiten Bereich unsere Näherung verwenden.
Um den restlichen Ausdruck übersichtlicher darstellen zu können, erweitern wir mit (EG∕EG)1∕2. Zusammen mit dem Faktor $$ {E}_{\mathrm{G}}^{1/ 6} $$ aus σG erhalten wir dann für EG wie für kBT die Potenz 2∕3. Den verbleibenden Faktor $$ {E}_{\mathrm{G}}^{-1/ 2} $$ fassen wir mit $$ {m}_{\mathrm{r}}^{-1/ 2} $$ zusammen über $$ {\left({m}_{\mathrm{r}}{E}_{\mathrm{G}}\right)}^{1/ 2}=\sqrt{2}\pi {m}_{\mathrm{r}} c\alpha {Z}_{\mathrm{A}}{Z}_{\mathrm{B}} $$ und drücken im nächsten Schritt mr wieder über mr = Armu aus. Um tabellierte Werte für S verwenden zu können, müssen wir noch von den SI-Einheiten [S] = J m2 auf die dort üblichen Einheiten $$ \left[S\right]=\mathrm{keV}\, \mathrm{b} $$ umrechnen, wobei 1 b = 1barn = 10−28 m2, d. h. SSI = 1,60 · 10−44 Stab. Unter Berücksichtigung aller Zahlenfaktoren inklusive der Zahlenwerte von c, mu und α ergibt sich schlussendlich
$$ \left\langle \sigma {v}_{\mathrm{r}}(E)\right\rangle \simeq \frac{6,48\cdotp 1{0}^{-24}}{A_{\mathrm{r}}{Z}_{\mathrm{A}}{Z}_{\mathrm{B}}}{\left(\frac{E_{\mathrm{G}}}{4{k}_{\mathrm{B}}T}\right)}^{2/\, 3}\exp \left[-3{\left(\frac{E_{\mathrm{G}}}{4{k}_{\mathrm{B}}T}\right)}^{1/\, 3}\right]\frac{S_{\mathrm{tab}}\left({E}_{\mathrm{P}}\right)}{\mathrm{keV}\, \mathrm{b}}\, {\mathrm{m}}^3{\mathrm{s}}^{-1}. $$
(19.28)
Mit diesem Ausdruck ist dann die Reaktionsrate gegeben durch
$$ {R}_{\mathrm{A}\mathrm{B}}=\frac{n_{\mathrm{A}}{n}_{\mathrm{B}}}{1+{\delta}_{\mathrm{A}\mathrm{B}}}\left\langle \sigma {v}_{\mathrm{r}}(E)\right\rangle . $$
(19.29)
In (19.29) ist über das Kronecker-Delta δAB auch der Fall der Fusion gleicher Teilchen berücksichtigt. In diesem Fall wird aus nAnB der Ausdruck $$ {n}_{\mathrm{A}}^2/ 2 $$, da sonst die Reaktion von Teilchen ① mit Teilchen ② doppelt gezählt würde, einmal als ① + ② und einmal als ② + ①.

Um die Rate für eine bestimmte Reaktion zu berechnen, müssen wir neben der Temperatur die Teilchendichten der beteiligten Nuklide kennen. Als Beispiel betrachten wir die Fusion zweier Protonen im Zentrum der Sonne. Mit den oben berechneten Werten für die thermische Energie und die Gamow-Energie ist EG,pp∕4kBTz ≃ 94. Wir brauchen jetzt noch die Teilchendichte np im Zentrum der Sonne. Dazu müssen wir den Massenanteil des Wasserstoffs dort kennen. In der astrophysikalischen Literatur wird der Wasserstoffmassenanteil üblicherweise mit X bezeichnet, entsprechend bezeichnen Y den Heliumanteil und Z den aller anderen Elemente.

Da die Sonne bereits seit etwa 5 Milliarden Jahren Wasserstoff verbrennt, ist der Wasserstoffanteil im Zentrum im Vergleich zur Oberfläche kleiner. Abb. 19.5 zeigt die Entwicklung der Massenanteile von Wasserstoff und Helium in Abhängigkeit von der Radialposition in der Sonne entsprechend dem Sonnenmodell aus [5]. Im Zentrum der Sonne liegt der Wasserstoffanteil demnach heute bei etwa 36 %. Mit der Dichte im Sonnenzentrum $$ {\rho}_{\mathrm{z}}^{\odot }=1,502\cdotp 1{0}^5\, \mathrm{kg}\, {\mathrm{m}}^{-3} $$ in (18.​23) ergibt sich dann np = ρzXz∕mp ≃ 3,27 · 1031 m−3. Weiter verwenden wir den Tabellenwert [1]
Abb. 19.5

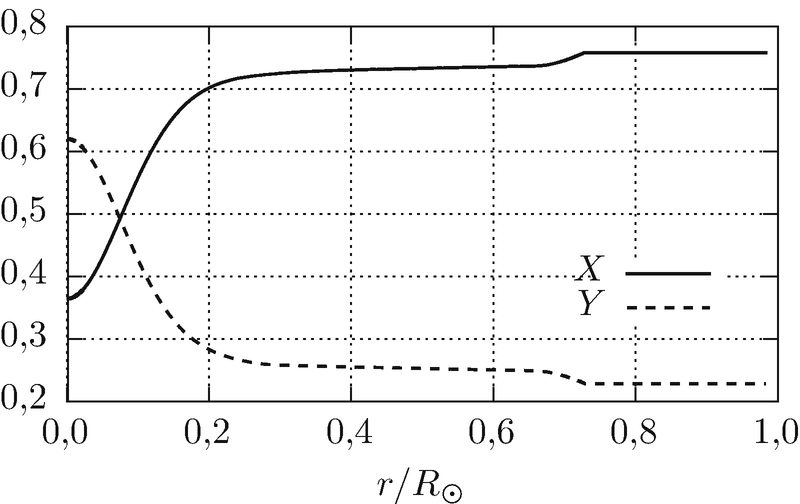
Massenanteil von Wasserstoff X und Helium Y bei verschiedenen Abständen zum Sonnenmittelpunkt. Im Zentrum ist der Wasserstoffanteil bereits auf etwa 36 % abgefallen. Die Daten für die Abbildung stammen aus [5]

$$ {S}_{\mathrm{pp}}=\left(4,01\pm 0,04\right)\cdotp 1{0}^{-22}\, \mathrm{keV}\, \mathrm{b}, $$
(19.30)
und finden
$$ {R}_{\mathrm{pp}}\simeq 6,83\cdotp 1{0}^{13}\, {\mathrm{m}}^{-3}\, {\mathrm{s}}^{-1}. $$
(19.31)
Dieser Wert von etwa 7 · 1013 Fusionsreaktionen pro Kubikmeter und Sekunde erscheint auf den ersten Blick sehr groß, muss aber mit den etwa 3 · 1031 Protonen pro Kubikmeter verglichen werden. Die Wahrscheinlichkeit für ein Proton in einem bestimmten Zeitraum an einer Fusionsreaktion beteiligt zu sein ist also tatsächlich sehr klein. Das konnten wir erwarten, da wir bereits abgeschätzt haben, dass die Sonne ihren Energiebedarf für viele Milliarden Jahre durch Wasserstoffbrennen decken kann. Wenn wir berücksichtigen, dass pro Fusionsreaktion zwei Protonen verbraucht werden, so ergibt sich die mittlere Protonenlebensdauer bezüglich der Proton-Proton-Reaktion zu
$$ {t}_{\mathrm{p}\mathrm{p}}=\frac{n_{\mathrm{p}}}{2{R}_{\mathrm{p}\mathrm{p}}}\simeq 7,6\cdotp 1{0}^9\, \mathrm{y}, $$
(19.32)
wobei die Reaktionsrate über diesen langen Zeitraum natürlich nicht konstant sein wird.

19.4 Fusion von Wasserstoff

Wir wissen bereits, dass die Fusion von Wasserstoff zu Helium für mehrere Milliarden Jahre die von der Sonne abgestrahlte Energie liefern kann. Tatsächlich gewinnen alle Sterne während des größten Teils ihres Lebens ihre Energie aus der Fusion von Wasserstoff zu Helium.

Bereits vor der eigentlichen Wasserstofffusion kommt es zu einer weiteren Reaktion, dem Deuteriumbrennen ab einer Temperatur von etwa T ~ 6 · 106 K. Dabei wird über die Reaktion
$$ {}^2\mathrm{D}+{}^1\mathrm{H}\to {\quad\quad }^3\mathrm{He}+\gamma $$
(19.33)
das im Stern vorhandene Deuterium zu Helium verbrannt. Diese Reaktion kann auch in sehr kleinen Sternen mit etwa M ≃ 0,012M⊙ stattfinden [11], die in ihrem Inneren keine ausreichende Temperatur für die weiteren Fusionsreaktionen erzeugen können. Solche Sterne, die nicht über die Deuteriumbrennphase hinauskommen, werden als braune Zwerge bezeichnet. Der Grund dafür, dass in braunen Zwergen die Dichte nicht hoch genug wird, damit die Wasserstofffusion zünden kann, ist das Einsetzen der Elektronenentartung. Der Entartungsdruck der Elektronen in (18.​64) ist temperaturunabhängig und verhindert, dass die Temperatur hoch genug wird. Die Konkurrenz zwischen Entartungsdruck und Gasdruck spielt auch bei der weiteren Entwicklung zu späteren Brennphasen eine wichtige Rolle, wie wir weiter unten sehen werden.

In Sternen, die für die Wasserstofffusion zu Helium heiß genug werden, sind dann zwei verschiedene Prozesse wichtig: Die Proton-Proton-Kette und der CNO-Zyklus.

19.4.1 Proton-Proton-Kette

Leichte Sterne wie die Sonne fusionieren Wasserstoff überwiegend über die Proton-Proton-Kette oder kurz pp-Kette. Dabei werden über verschiedene Zwischenstufen vier Protonen zu einem Heliumkern verschmolzen. Es gibt zwei Ausgangsreaktionen für diese Kette, die um ein Vielfaches bedeutendere ist die direkte Fusion zweier Protonen
$$ {}^1\mathrm{H}+{}^1\mathrm{H}\to {\quad\quad }^2\mathrm{D}+{\mathrm{e}}^{+}+{\nu}_{\mathrm{e}}. $$
(19.34)
Für diese Reaktion haben wir die Reaktionsrate bereits besprochen, in der Sonne findet diese mit einem Anteil von 99,76 % statt. In sehr viel kleinerem Umfang von 0,24 % findet eine weitere Reaktion statt, bei der ein Elektron beteiligt ist und entsprechend kein Positron entsteht:
$$ {}^1\mathrm{H}+{\mathrm{e}}^{-}+{}^1\mathrm{H}\to {\quad\quad }^2\mathrm{D}+{\nu}_{\mathrm{e}}. $$
(19.35)
In beiden Reaktionen entsteht ein Deuteriumkern. Dieser kann jetzt wieder über die Reaktion (19.33) zu einem 3He-Kern weiterreagieren.
An dieser Stelle gibt es drei mögliche Folgereaktionen, die wieder sehr unterschiedliche relative Häufigkeiten haben (s. a. Abb. 19.6). Bei der Proton-Proton-Reaktion I (ppI) fusionieren mit einer Lebensdauer, d. h. der mittleren Zeit, bis ein 3He-Kern an dieser Reaktion teilnimmt, von etwa 106 Jahren, zwei 3He-Kerne zu 4He über
$$ {}^3\mathrm{He}+{}^3\mathrm{He}\to {\quad\quad }^4\mathrm{He}+{}^1\mathrm{H}+{}^1\mathrm{H}. $$
(19.36)
Dieser Prozess ist in der Sonne dominant. Die zweite Möglichkeit (ppII) ist eine dreistufige Reaktionskette. Hier wird mit einem als Katalysator wirkenden 4He-Kern ein weiterer 4He-Kern erzeugt:
$$ {}^3\mathrm{He}+{}^4\mathrm{He}\quad\quad \hspace{0.5em}\to {\quad\quad }^7\mathrm{Be}+\gamma, \, $$
(19.37a)
$$ {}^7\mathrm{Be}+{\mathrm{e}}^{-}\quad\quad \hspace{1.25em}\to {\quad\quad }^7\mathrm{Li}+{\nu}_{\mathrm{e}}, $$
(19.37b)
$$ {}^7\mathrm{Li}+{}^1\mathrm{H}\quad\quad \hspace{1.5em}\to {\quad\quad }^4\mathrm{He}+{}^4\mathrm{He}. $$
(19.37c)
Diese Reaktionskette läuft in der Sonne etwa 6-mal weniger häufig ab als ppI. Alternativ kann nach dem ersten Teilschritt von ppII der entstandene 7Be-Kern mit einem weiteren Proton zu 8B fusionieren. Diese ppIII-Reaktionskette ist
$$ {}^3\mathrm{He}+{}^4\mathrm{He}\quad\quad \hspace{0.5em}\to {\quad\quad }^7\mathrm{Be}+\gamma, \, $$
(19.38a)
$$ {}^7\mathrm{Be}+{}^1\mathrm{H}\quad\quad \hspace{1em}\to {\quad\quad }^8\mathrm{B}+\gamma, $$
(19.38b)
$$ {}^8\mathrm{B}\quad\quad \hspace{0.5em}\to {\quad\quad }^8\mathrm{B}\mathrm{e}+{\mathrm{e}}^{+}+{\nu}_{\mathrm{e}}, $$
(19.38c)
$$ {}^8\mathrm{Be}\quad\quad \hspace{0.5em}\to {\quad\quad }^4\mathrm{He}+{}^4\mathrm{He}. $$
(19.38d)
Beryllium hat die Kernladungszahl 4, die Gamow-Energie für diese Reaktion ist deshalb sehr hoch im Vergleich zu den anderen Reaktionen. Deshalb findet die ppIII-Reaktionskette nur mit einem sehr kleinen Anteil statt, sie wird bei höheren Temperaturen aber bedeutend. Der entstandene 8B-Kern ist instabil und zerfällt nach (19.38c) über inversen Betazerfall zu 8Be.
Abb. 19.6

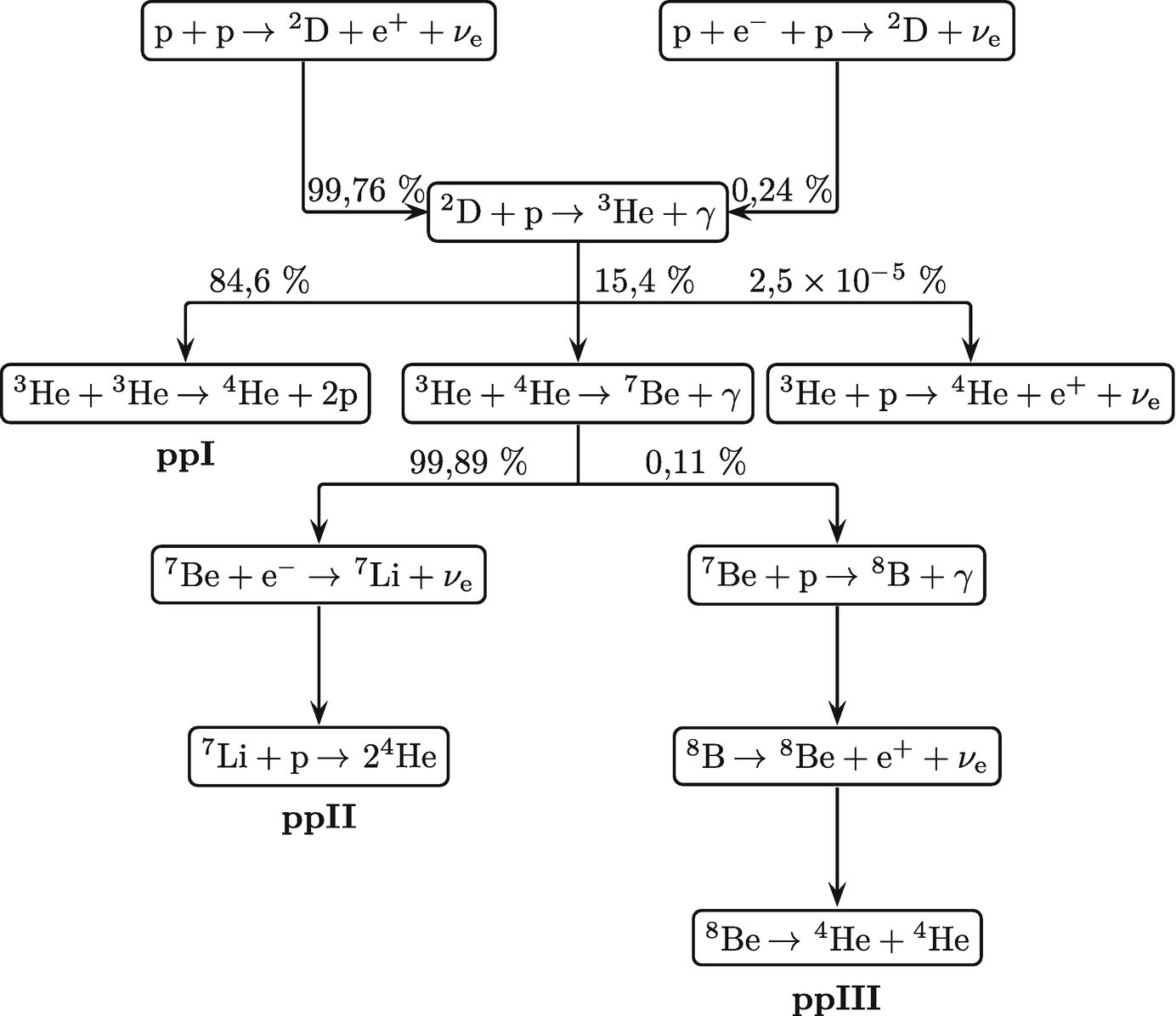
Die verschiedenen Untertypen der pp-Reaktionskette (ppI-ppIII) mit ihren jeweiligen Anteilen in der Sonne. Die Angaben wurden aus [10] entnommen. Die Reaktion eines 3He-Kerns mit einem Proton zu einem 4He-Kern hat einen so kleinen Anteil, dass sie nicht zur eigentlichen pp-Kette gezählt wird

Im letzten Teilschritt (19.38d) zerfällt der 8Be-Kern mit einer mittleren Lebensdauer von 6,7 · 10−17 s in zwei 4He-Kerne. Wäre die Masse des 8Be-Kerns nur um den Bruchteil 1 : 10−5 kleiner und dieser Kern damit stärker gebunden, so wäre dieser Zerfall nicht möglich. Dies hätte weitreichende Folgen, denn dann könnten in Sternen während der Wasserstofffusion, aber auch schon nach dem Urknall, schwerere Elemente gebildet werden und die heutige Elementzusammensetzung des Universums sähe völlig anders aus. Dieser Zusammenhang trägt den Namen Berylliumbarriere. Da 8Be instabil ist, können in Sternen und auch in der Frühphase des Universums nur Elemente bis Lithium erbrütet werden. Erst am Ende seines Lebens, wenn einem Stern der Wasserstoffvorrat im Zentrum langsam zur Neige geht, kann die Fusion schwerer Elemente bis Eisen bzw. vor allem in Supernovae auch darüberhinaus stattfinden (s. Abschn. 19.6).

19.4.2 Bethe-Weizsäcker-Zyklus

Neben der gerade besprochenen Reaktionskette gibt es noch einen weiteren bedeutenden Zyklus, der schwerere Elemente als Katalysator mit einschließt. Da wegen der Berylliumbarriere in Sternen nur Elemente bis einschließlich Lithium entstehen können, müssen diese schwereren Elemente bei der Entstehung des Sterns bereits vorhanden sein, um den Bethe-Weizsäcker-Zyklus zu ermöglichen. Das ist möglich, wenn der entsprechende Stern Supernovareste eines vorher explodierten Sterns enthält. Diese Reaktionskette kann also bei den ersten Sternen im Universum, die nur aus H und He bestanden, nicht stattgefunden haben. Des Weiteren können Reaktionen von 4He mit 1H nicht stattfinden, da kein Nuklid mit Massenzahl A = 5 mit ausreichender Lebensdauer existiert. So zerfällt 5He durch Neutronenemission in etwa 8 · 10−22 s wieder zu 4He und 5Li innerhalb von 3 · 10−22 s unter Emission eines Protons ebenfalls zu 4He und das Wasserstoffisotop 5H zerfällt noch schneller.

Die Reaktionen von Protonen mit Deuterium, Lithium, Beryllium und Bor laufen alle sehr schnell ab und verbrauchen die Reaktionspartner daher in kurzer Zeit. Aus diesem Grund sind diese Elemente sowohl in der Sonne als auch auf der Erde relativ selten. Kohlenstoff dagegen ist ein relativ häufiges Element und hat einen Anteil von etwa 1 % an neu gebildeten Sternen. Der Grund dafür ist die Existenz eines Zyklus, bei dem Kohlenstoff als Katalysator für die Fusion von Protonen zu Helium wirkt:
$$ {}^{12}\mathrm{C}+{}^1\mathrm{H}\quad\quad \hspace{0.5em}\to {\quad\quad }^{13}\mathrm{N},\, $$
(19.39a)
$$ {}^{13}\mathrm{N}\quad\quad \hspace{0.5em}\to {\quad\quad }^{13}\mathrm{C}+{\mathrm{e}}^{+}+{\nu}_{\mathrm{e}}, $$
(19.39b)
$$ {}^{13}\mathrm{C}+{}^1\mathrm{H}\quad\quad \hspace{0.5em}\to {\quad\quad }^{14}\mathrm{N}+\gamma, \, $$
(19.39c)
$$ {}^{14}\mathrm{N}+{}^1\mathrm{H}\quad\quad \hspace{0.5em}\to {\quad\quad }^{15}\mathrm{O}+\gamma, $$
(19.39d)
$$ {}^{15}\mathrm{O}\quad\quad \hspace{0.5em}\to {\quad\quad }^{15}\mathrm{N}+{\mathrm{e}}^{+}+{\nu}_{\mathrm{e}}, $$
(19.39e)
$$ {}^{15}\mathrm{N}+{}^1\mathrm{H}\quad\quad \hspace{0.5em}\to {\quad\quad }^{12}\mathrm{C}+{}^4\mathrm{He}.\, $$
(19.39f)
Diese Reaktionskette wird als Bethe-Weizsäcker-Zyklus oder nach den beteiligten Elementen als CNO-Zyklus bezeichnet. Alle an dieser Reaktion beteiligten Nuklide werden periodisch erzeugt und vernichtet. Allerdings sind die Reaktionsraten der einzelnen Reaktionen sehr unterschiedlich. Hat sich aber eine Gleichgewichtssituation eingestellt, so bleiben die Teilchendichten der schweren Nuklide konstant. Für die Fusionsreaktionen der Stickstoff- bzw. Kohlenstoffkerne mit einem Proton ist die Gamow-Energie viel höher als bei den Reaktionen der pp-Kette. In der Sonne ist dieser Zyklus deshalb nur sehr gering an der Energiefreisetzung beteiligt. Allerdings sind die Temperaturabhängigkeiten der pp-Reaktionen und des CNO-Zyklus sehr unterschiedlich, so gilt Rpp ~ T4 und RCNO ~ T16−20 [13]. Wenn die Temperatur nur etwas steigt, nimmt der Anteil der CNO-Reaktionen daher stark zu. Im Verlauf der weiteren Entwicklung wird auch die Temperatur im Zentrum der Sonne steigen und der Anteil des CNO-Zyklus an der Energieproduktion auf etwa 20 % anwachsen [4]. Abb. 19.7 fasst die Reaktionen des CNO-Zyklus zusammen. Hier wird die periodische Abfolge der Reaktionen besonders deutlich. Massereichere Sterne erreichen in ihrem Zentrum höhere Temperaturen. Der Anteil des CNO-Zyklus wird wegen seiner stärkeren Temperaturabhängigkeit daher mit steigender Sternmasse sehr schnell dominant gegenüber den pp-Reaktionen. Der Ablauf der Wasserstofffusion unterscheidet sich daher in massearmen und massereichen Sternen grundlegend.
Abb. 19.7

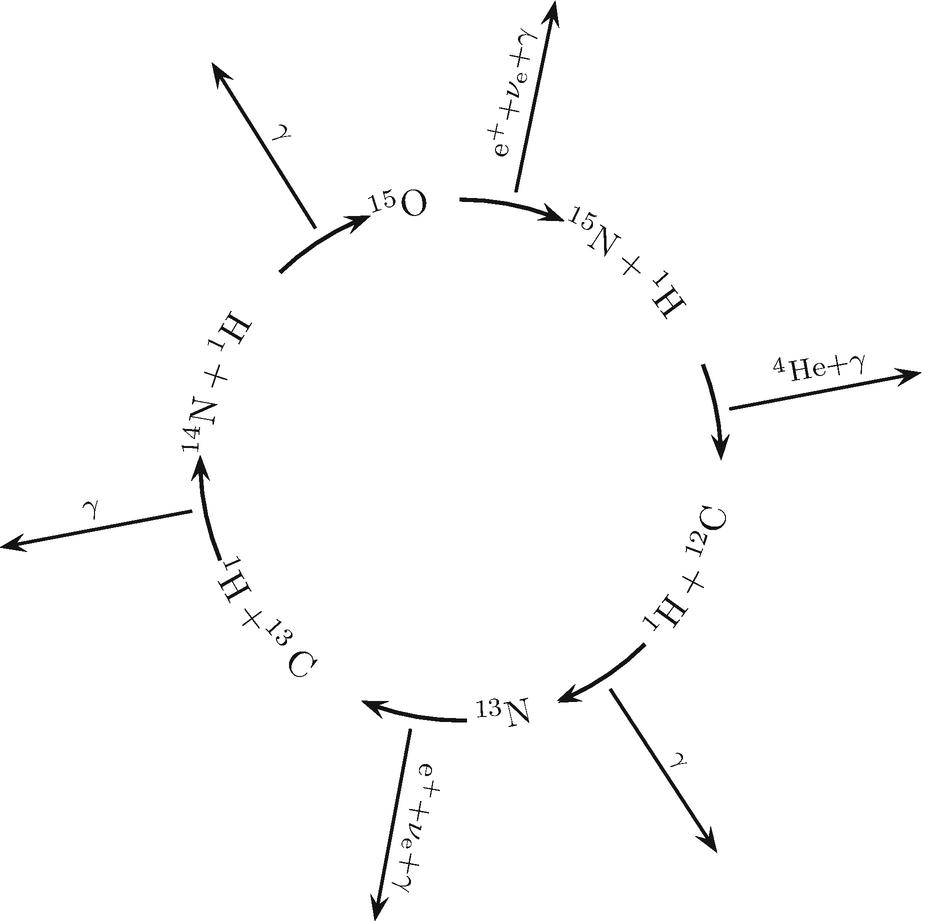
Der Bethe-Weizsäcker-Zyklus. Unter Verwendung von Kohlenstoff, Stickstoff und Sauerstoff als Katalysatoren werden effektiv 4 Protonen zu einem 4He-Kern fusioniert. Wegen der hohen Kernladungszahlen der beteiligten Nuklide läuft dieser Prozess erst bei höheren Temperaturen als die pp-Kette effektiv ab

19.4.3 Dauer der Wasserstoffbrennphase

Die starke Temperaturabhängigkeit der bei der Wasserstofffusion auftretenden Reaktionen führt zu verschiedenen Zeitdauern der Wasserstoffbrennphase für unterschiedlich massereiche Sterne. Abb. 19.8 zeigt die Dauer der Wasserstoffbrennphase tH normiert auf die Dauer $$ {t}_{\mathrm{H}}^{\odot } $$ bei der Sonne. Bereits für Sterne, die nur 10 % masseärmer als die Sonne sind, dauert die Wasserstoffbrennphase länger als das Alter des Universums von etwa 13,8 Milliarden Jahren. Dagegen durchläuft ein Stern mit M = 10M⊙ diese Phase in nur etwa 18 Millionen Jahren.
Abb. 19.8

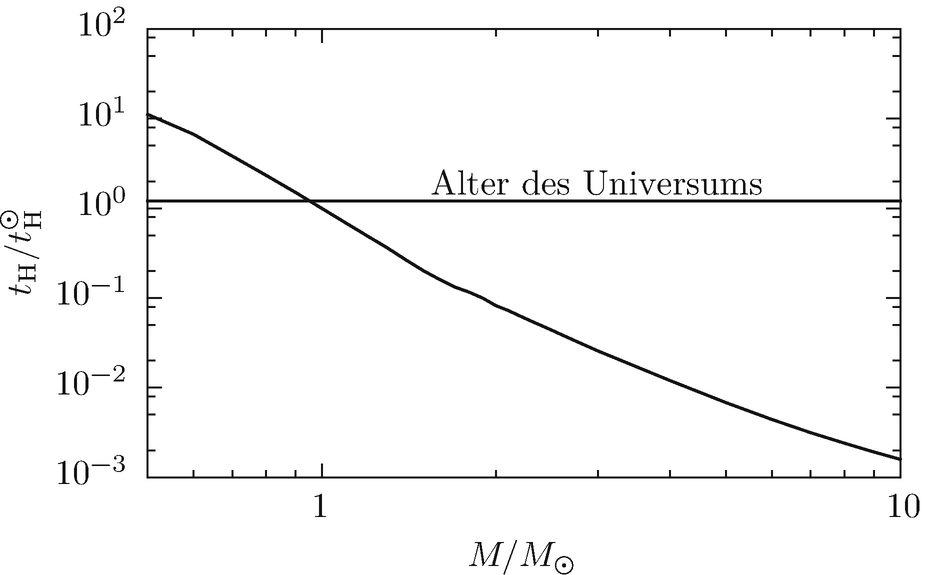
Dauer des Wasserstoffbrennens in Abhängigkeit von der Sternmasse im Vergleich zum Wert für die Sonne $$ {t}_{\mathrm{H}}^{\odot}\approx 1,15\cdotp 1{0}^{10}\mathrm{y} $$ für Sternmodelle mit chemischer Zusammensetzung wie die Sonne. Die Dauer dieser Phase ist bereits für Sterne mit $$ M\lesssim 0,9\, {\mathrm{M}}_{\odot } $$ länger als das Alter des Universums von etwa 13,8 · 109 y [12], während massereichere Sterne diese Phase sehr viel schneller durchleben. Die Daten für die Abbildung stammen aus [17]

19.5 Kernfusion nach dem Wasserstoffbrennen

Wenn einem Stern der Wasserstoff im Kern zur Neige geht, findet, je nach Masse, eine Abfolge weiterer Fusionsreaktionen statt, die wir jetzt kurz diskutieren wollen.

19.5.1 Heliumbrennphase

Durch die fortlaufende Fusion von Wasserstoff steigt der Heliumanteil im Zentrum eines Sterns immer weiter und es bildet sich schließlich ein Sternkern aus Helium. Dort steigen die Dichte und die Temperatur so lange, bis Heliumnuklide zu Kohlenstoff fusionieren können. Voraussetzung dafür ist wie für das Einsetzen der Wasserstofffusion, dass die Temperatur im Kern des Sterns hoch genug wird, bevor der Elektronenentartungsdruck eine weitere Kontraktion und damit Temperaturerhöhung unmöglich macht. Da für die Fusion von Helium höhere Temperaturen nötig sind als bei Wasserstoff, ist auch die Mindestmasse höher und liegt bei etwa M ≂ 0,5M⊙. Leichtere Sterne können kein Helium fusionieren. Allerdings wird aus Abb. 19.8 klar, dass so leichte Sterne in unserem Universum noch für sehr lange Zeit in der Wasserstoffbrennphase sind. Lediglich wenn ein Stern während seiner Entwicklung Materie verliert, etwa an einen Begleiter, ist diese Begrenzung daher bisher relevant. Allerdings spielt auch bei Sternen im Massenbereich der Sonne der Elektronenentartungsdruck beim Übergang zum Heliumbrennen bereits eine wichtige Rolle. Wenn im teilweise entarteten Heliumkern des Sterns die Kernfusion einsetzt und die Temperatur steigt, so erhöht dies den Fermi-Druck nicht, da dieser nur dichteabhängig ist. Gleichzeitig erhöht sich mit der Temperatur aber die Reaktionsrate und damit wieder die Temperatur. Diese Kettenreaktion führt zu einer Folge von kurzen extremen Anstiegen der Luminosität des Sternzentrums, man spricht vom Heliumflash. Bei jedem dieser Flashes steigt die Temperatur in einer Schale um den Kern so weit, dass die Elektronenentartung wieder keine Rolle mehr spielt und am Ende der Flashphase ist sie aufgehoben. Durch die Flashes ändert sich nicht die von außen gesehene Leuchtkraft des Sterns, aber diese Phase hat großen Einfluss auf die Sternentwicklung. Wir werden in Abschn. 20.​4 sehen, wie weiße Zwerge, die Überreste massearmer Sterne, aufgrund eines ähnlichen Prozesses explodieren können.

Die Fusion von Helium wird auch als Triple-α-Prozess bezeichnet und läuft in zwei Schritten ab:
$$ {}^4\mathrm{He}+{}^4\mathrm{He}\quad\quad \hspace{0.5em}\to {\quad\quad }^8\mathrm{Be},\, $$
(19.40a)
$$ {}^8\mathrm{Be}+{}^4\mathrm{He}\quad\quad \hspace{0.5em}\to {\quad\quad }^{12}{\mathrm{C}}^{\ast },\, $$
(19.40b)
$$ {}^{12}{\mathrm{C}}^{\ast}\quad\quad \hspace{0.5em}\to {\quad\quad }^{12}\mathrm{C}+2\gamma . $$
(19.40c)
Dabei ist (19.40a), die Fusion zweier Heliumkerne zu Beryllium, genau die Umkehrung des letzten Schrittes der ppIII-Kette in (19.38d). Dieser Schritt ist endotherm und benötigt etwa $$ 92\, \mathrm{keV} $$ Energie. Da der 8Be-Kern innerhalb von 6,7 · 10−17 s zerfällt, muss die Folgereaktion (19.40b) praktisch gleichzeitig erfolgen, effektiv fusionieren also drei Heliumkerne gleichzeitig zu Kohlenstoff [16]. Das Kohlenstoffnuklid entsteht in einem angeregten Zustand und zerfällt meistens direkt wieder, nur in wenigen Fällen erfolgt die Abregung in den Grundzustand unter Abgabe von Gammastrahlung wie in (19.40c).
Neben dem Triple-α Prozess laufen in der Heliumbrennphase auch noch weitere Reaktionen ab, in denen der entstandene Kohlenstoff mit einem weiteren Heliumkern weiter fusioniert:
$$ {}^{12}\mathrm{C}+{}^4\mathrm{He}\quad\quad \hspace{0.5em}\to {\quad\quad }^{16}\mathrm{O}+\gamma, \, $$
(19.41a)
$$ {}^{16}\mathrm{O}+{}^4\mathrm{He}\quad\quad \hspace{0.6em}\to {\quad\quad }^{20}\mathrm{Ne}+\gamma, $$
(19.41b)
$$ {}^{16}\mathrm{Ne}+{}^4\mathrm{He}\to {\quad\quad }^{24}\mathrm{Mg}+\gamma, $$
(19.41c)
$$ {}^{16}\mathrm{Mg}+{}^4\mathrm{He}\to {\quad\quad }^{28}\mathrm{Si}+\gamma . $$
(19.41d)
Insbesondere die Reaktion (19.41a) ist von großer Bedeutung, denn durch sie ändert sich das Verhältnis von Kohlenstoff zu Sauerstoff im Stern, das großen Einfluss auf die weitere Entwicklung hat. Gleichzeitig ist für diese Reaktion die Bestimmung des S-Faktors aber relativ schwierig [16].

19.5.2 Spätere Fusionsphasen

Je größer die Kernladung der zu fusionierenden Elemente ist, desto massereicher muss der entsprechende Stern sein, um die dafür nötige Temperatur in seinem Inneren erzeugen zu können. Im Anschluss an das Heliumbrennen kann die Fusion von Kohlenstoff einsetzen, wenn der Stern die dafür nötigen Temperaturen von T ≂ 5 · 108 K erzeugen kann. Dafür muss er etwa eine Masse von 8 M⊙ besitzen. In diesem Fall verschmelzen zwei Kohlenstoffkerne zu einem hochangeregten 24Mg-Kern, der dann in verschiedene leichtere Nuklide zerfällt:
$$ {}^{12}\mathrm{C}+{}^{12}\mathrm{C}\to {\quad\quad }^{24}\mathrm{Mg}\to \left\{\begin{array}{l}{}^{23}\mathrm{Mg}+\mathrm{n},\\ {}{}^{20}\mathrm{Ne}+{}^4\mathrm{He},\\ {}{}^{23}\mathrm{Na}+\mathrm{p}.\end{array}\right. $$
(19.42)
Bei noch höheren Temperaturen T ≂ 109 K in Sternen mit M ≳ 10 M⊙ kann das entstandene Neon durch Gammastrahlung aufgespalten werden, dies nennt man Photodesintegration :
$$ {}^{20}\mathrm{Ne}+\gamma \to {\quad\quad }^{16}\mathrm{O}+{}^4\mathrm{He}. $$
(19.43)
Das entstandene Helium und auch freie Neutronen können dann mit weiteren Nukliden reagieren:
$$ {}^{20}\mathrm{Ne}+{}^4\mathrm{He}\to {\quad\quad }^{24}\mathrm{Mg}+\gamma, $$
(19.44a)
$$ {}^{20}\mathrm{Ne}+\mathrm{n}\to {\quad\quad }^{21}\mathrm{Ne}+\gamma, $$
(19.44b)
$$ {}^{21}\mathrm{Ne}+{}^4\mathrm{He}\to {\quad\quad }^{24}\mathrm{Mg}+\mathrm{n}. $$
(19.44c)
Es schließen sich die Phasen des Sauerstoff- und des Siliziumbrennens an. Dabei fusionieren zuerst Sauerstoffkerne zu schwereren Nukliden über
$$ {}^{16}\mathrm{O}+{}^{16}\mathrm{O}\to {\quad\quad }^{32}\mathrm{S}\to \left\{\begin{array}{l}{}^{31}\mathrm{S}+\mathrm{n},\\ {}{}^{31}\mathrm{P}+\mathrm{p},\\ {}{}^{30}\mathrm{P}+{}^2\mathrm{D},\\ {}{}^{28}\mathrm{S}\mathrm{i}+{}^4\mathrm{He}.\end{array}\right. $$
(19.45)
Nach der Fusion von zwei Siliziumkernen in der Reaktion
$$ {}^{28}\mathrm{Si}+{}^{28}\mathrm{Si}\to {\quad\quad }^{56}\mathrm{Ni}+\gamma $$
(19.46)
und den möglichen Photodesintegrationen
$$ {}^{28}\mathrm{Si}+\gamma \to {\quad\quad }^{27}\mathrm{Al}+{}^1\mathrm{H}, $$
(19.47a)
$$ {}^{28}\mathrm{Si}+\gamma \to {\quad\quad }^{24}\mathrm{Mg}+{}^4\mathrm{He}, $$
(19.47b)
bzw. den β+-Zerfällen
$$ {}^{56}\mathrm{Ni}\quad\quad \hspace{0.5em}\to {\quad\quad }^{56}\mathrm{Co}+{\mathrm{e}}^{+}+{\nu}_{\mathrm{e}},\, $$
(19.48a)
$$ {}^{56}\mathrm{Co}\quad\quad \hspace{0.5em}\to {\quad\quad }^{56}\mathrm{Fe}+{\mathrm{e}}^{+}+{\nu}_{\mathrm{e}}\, $$
(19.48b)
entsteht im Stern schließlich der hochgebundene 56Fe-Kern, einer der stabilsten Kerne, wie wir in Abb. 19.1 gesehen haben. An diesem Punkt kann durch Fusion keine weitere Energie freigesetzt werden. Was dann passiert, werden wir in Kap. 21 besprechen. Generell setzen die späteren Brennphasen viel weniger Energie frei als die Fusion von Wasserstoff. Die Zeiträume dieser Fusionsphasen sind deshalb viel kürzer als die des Wasserstoffbrennens. In Tab. 19.1 sind die Brenndauern der einzelnen Phasen für unterschiedlich massive Sterne aufgelistet. Ein Stern mit etwa einer Sonnenmasse fusioniert also nach der etwa 11 Milliarden Jahre dauernden H-Brennphase etwa weitere 100 Millionen Jahre Helium, wobei er sich etwa auf den zehnfachen Radius aufbläht.
Tab. 19.1

Überblick über die verschiedenen Fusionsphasen für Sterne mit Anfangsmassen von 1M⊙–75M⊙. Gezeigt sind in allen Fällen die Temperatur in der Brennphase, die Sternmasse am Anfang der Brennphase, die aufgrund von Masseverlusten kleiner sein kann als die Anfangsmasse, sowie die Dauer der jeweiligen Phase. Das mit ∗ gekennzeichnete Modell ist ein sehr metallarmer Stern mit 0, 01 % des Gehalts schwererer Elemente der Sonne. (Die Daten für die Tabelle stammen aus [20])

Minit [M⊙]

T [K]

M [M⊙]

τ

T [K]

M [M⊙]

τ

 

H-Brennphase

He-Brennphase

1

1,57 · 107

1,00

1,10 · 1010 y

1,25 · 108

0,71

1,10 · 108 y

13

3,44 · 107

12,9

1,35 · 107 y

1,72 · 108

12,4

2,67 · 106 y

25

3,81 · 107

24,5

6,70 · 106 y

1,96 · 108

19,6

8,39 · 105 y

75

4,26 · 107

67,3

3,16 · 107 y

2,10 · 108

16,1

4,78 · 105 y

75∗

7,60 · 107

75,0

3,44 · 107 y

2,25 · 108

74,4

3,32 · 105 y

 

C-Brennphase

Ne-Brennphase

13

8,15 · 108

11,4

2,82 · 103 y

1,69 · 109

11,4

0,341 y

25

8,41 · 108

12,5

5,22 · 102 y

1,57 · 109

12,5

0,891 y

75

8,68 · 108

6,37

1,07 · 103 y

1,62 · 109

6,36

0,569 y

75∗

10,4 · 108

74,4

2,7 · 101 y

1,57 · 109

74

0,026 y

 

O-Brennphase

Si-Brennphase

13

1,89 · 109

11,4

4,77 y

3,28 · 109

11,4

17,8 d

25

2,09 · 109

12,5

0,402 y

3,65 · 109

12,5

0,733 d

75

2,04 · 109

6,36

0,908 y

3,55 · 109

6,36

2,09 d

75∗

2,39 · 109

74

0,010 y

3,82 · 109

74

0,209 d

Die noch späteren Brennphasen bei massereicheren Sternen spielen sich in noch deutlich kürzeren Zeiträumen ab. Die Dauer des Siliziumbrennens liegt in der Größenordnung von Tagen.

19.6 Entstehung schwerer Elemente

Wir haben gerade gesehen, dass bei der Fusion in Sternen nur Elemente bis etwa Eisen und Nickel entstehen können. Schwerere Elemente werden bei der Fusion nicht produziert, da dabei keine Energie frei wird. Außerdem ist für entsprechende Reaktionen die Gamow-Energie aus (19.18) und damit die Coulomb-Barriere sehr hoch und die Wahrscheinlichkeit für Tunnelprozesse entsprechend sehr klein.

Da aber dennoch Elemente mit sehr viel höheren Kernladungszahlen in nicht vernachlässigbaren Mengen existieren, müssen diese durch andere Prozesse entstehen, und zwar hauptsächlich durch den Einfang von freien Neutronen. Da Neutronen ungeladen sind, müssen sie keine Coulomb-Barriere durchtunneln, und sie können daher auch mit schweren Kernen reagieren.

Wenn ein Isotop $$ {}_Z^AX $$ ein Neutron einfängt, so entsteht dabei allerdings ein schwereres Isotop des gleichen Elementes in der Reaktion
$$ {}_Z^AX+\mathrm{n}\to {\quad\quad }_Z^{A+1}X+\gamma . $$
(19.49)
Das entstehende Isotop $$ {}_Z^{A+1}X $$ ist dabei oft hochangeregt und emittiert deshalb Gammastrahlung, um in den Grundzustand zu gelangen. Auf diese Weise ist also noch kein neues Element entstanden. Allerdings sind Isotope mit sehr hohem Neutronenüberschuss, d. h. solche, die sehr viel mehr Neutronen besitzen als Protonen, instabil gegen β−-Zerfall:
$$ {}_Z^AX\to {\quad\quad }_{Z+1}^AY+{\mathrm{e}}^{-}+{\bar{\nu}}_{\mathrm{e}}. $$
(19.50)
Wenn durch Neutroneneinfang ein solches radioaktives Isotop entsteht, kann daraus also ein Isotop eines schwereren Elementes entstehen.

Man kategorisiert diese Einfangsprozesse in zwei Unterkategorien.

19.6.1 s-Prozess

Wenn die mittlere Zeitdauer zwischen Neutroneneinfangreaktionen sehr viel größer ist als die mittlere Zerfallszeit für den β−-Zerfall, d. h. $$ {\tau}_{\mathrm{n}}\gg {\tau}_{\beta^{-}} $$ so spricht man vom s-Prozess (s für slow).

In diesem Fall haben Isotope, die β−-instabil sind, nicht genug Zeit, weitere Neutronen einzufangen, bevor sie zerfallen. Abb. 19.9 zeigt eine mögliche Reaktionskette im s-Prozess vom 56Fe-Isotop aus. Die Eisenisotope 57Fe und 58Fe sind ebenfalls stabil und können daher weiter Neutronen einfangen. Das Isotop 59Fe ist aber instabil und zerfällt zu 59Co, das wiederum stabil ist. Wenn dieses Isotop dann ein Neutron einfängt, entsteht der instabile Kern 60Co, der dann zu 60Ni zerfällt. Auf diese Weise können immer schwerere Isotope erzeugt werden. Allerdings können auf diese Weise keine Isotope entstehen, für die ein stabiles Isobar existiert, d. h. ein Isotop eines leichteren Elementes mit gleicher Massenzahl. In Abb. 19.9 trifft dies auf 58Ni und 74Se zu. Ebenso führt der s-Prozess nicht zu stabilen Isotopen, bei denen es ein leichteres β−-instabiles Isotop gibt, da dieses vorher zum um 1 höherwertigen Isobar zerfällt. Dieser Fall entspricht 80Se. Solche Isotope sind gegenüber dem s-Prozess abgeschirmt.
Abb. 19.9

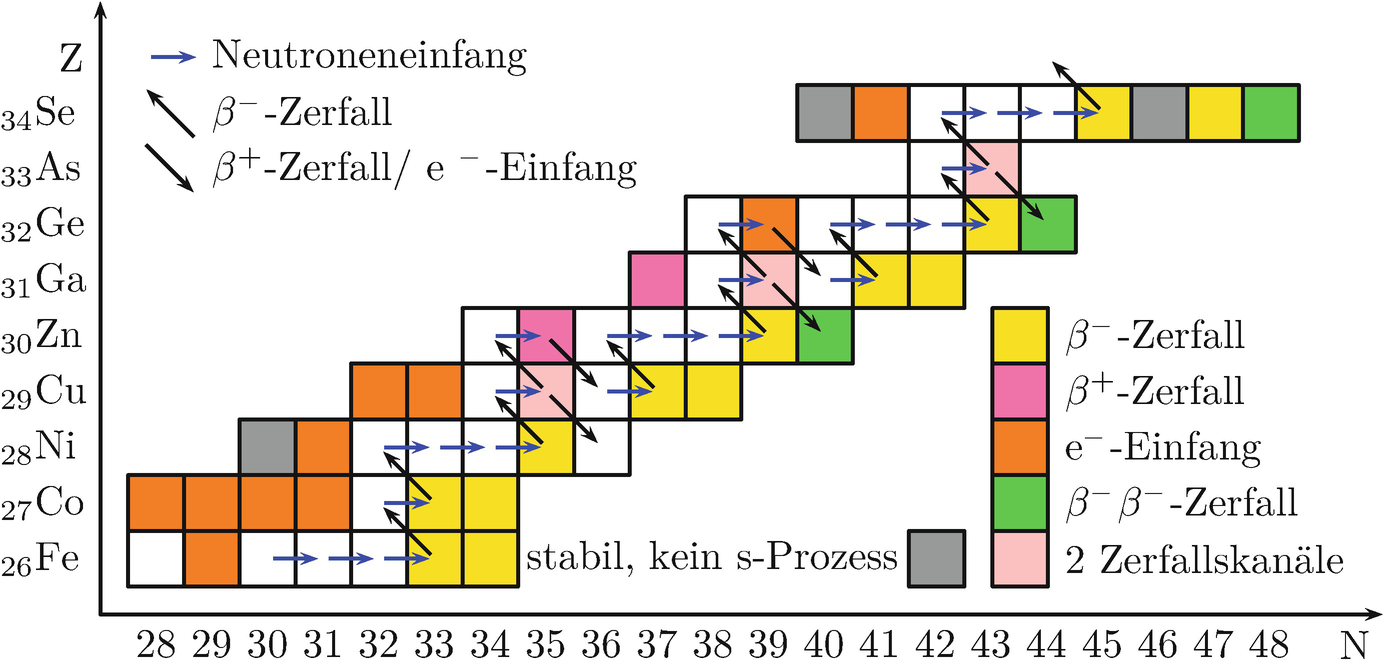
Der s-Prozess ausgehend vom 56Fe-Isotop

Abb. 19.9 zeigt der Vollständigkeit halber auch Isotope mit anderen Zerfallskanälen. Isotope mit einem Protonenüberschuss zerfallen über β+-Zerfall
$$ {}_Z^AX\to {\quad\quad }_{Z-1}^AY+{\mathrm{e}}^{+}+{\bar{\nu}}_{\mathrm{e}} $$
(19.51)
oder durch Elektroneneinfang
$$ {}_Z^AX+{\mathrm{e}}^{-}\to {\quad\quad }_{Z-1}^AY+{\nu}_{\mathrm{e}}. $$
(19.52)
Für einige neutronenreiche Elemente ist der einfache Betazerfall energetisch verboten, weil das nächsthöherwertige Isobar eine niedrigere Bindungsenergie hat. Solche Elemente können doppelten Betazerfall zeigen, bei dem sie direkt in das übernächste Isobar übergehen. Diese Reaktion ist allerdings sehr unwahrscheinlich, und diese Isotope haben daher sehr lange Halbwertszeiten im Bereich 1020 y und können daher selbst für den s-Prozess als stabil betrachtet werden.
Dazu noch eine Randbemerkung: Interessant ist der doppelte Betazerfall insbesondere, weil man hofft, sogenannten neutrinolosen doppelten Betazerfall nachweisen zu können, d. h. statt der Reaktion
$$ {}_Z^AX\to {\quad\quad }_{Z+2}^AZ+2{\mathrm{e}}^{-}+2{\bar{\nu}}_{\mathrm{e}} $$
(19.53)
die Reaktion
$$ {}_Z^AX\to {\quad\quad }_{Z+2}^AZ+2{\mathrm{e}}^{-}, $$
(19.54)
die nur möglich ist, wenn Neutrinos ihre eigenen Antiteilchen sind. Der Nachweis des neutrinolosen doppelten Betazerfalls wäre ein Hinweis auf Physik jenseits des Standardmodells.

19.6.2 r-Prozess

Wenn die mittlere Zeitdauer zwischen Neutroneneinfangreaktionen dagegen sehr viel kleiner ist als die mittlere Zerfallszeit für den β−-Zerfall, d. h. $$ {\tau}_{\mathrm{n}}\ll {\tau}_{\beta^{-}} $$, so spricht man vom r-Prozess (r für rapid).

In diesem Fall können β−-instabile Isotope weitere Neutronen einfangen, bevor sie zerfallen, und es entstehen Isotope mit noch höherem Neutronenüberschuss, die dann zu höherwertigen Elementen zerfallen, wenn etwa der Neutronenfluss sinkt. Abb. 19.10 skizziert diesen Fall. Auch gegen den r-Prozess sind Isotope mit stabilen Isobaren niederwertigerer Elemente abgeschirmt, in der Abbildung z. B. 86Sr.
Abb. 19.10

Der r-Prozess. Die Legende ist analog zu Abb. 19.9. Grau markierte Isotope sind in diesem Fall durch andere stabile oder sehr langlebige Isotope abgeschirmt. Das braun markierte Isotop $$ {}_{37}^{87}\mathrm{Rb} $$ zerfällt zwar über β−-Zerfall aber mit einer sehr hohen Halbwertszeit von 4,81 · 1010 y und kann deshalb $$ {}_{38}^{87}\mathrm{Sr} $$ abschirmen

Welcher dieser beiden Extremfälle abläuft, hängt letztlich von der Anzahl freier Neutronen ab, die die Reaktionsrate nach (19.29) bestimmt. Der s-Prozess findet in Sternen in späten Brennphasen statt. Dort entstehen freie Neutronen, etwa in den von uns diskutierten Reaktionen (19.42), (19.44c) und (19.45), aber vor allem auch in anderen Reaktionen, die wir nicht besprochen haben, siehe z. B. [15]. Freie Neutronen sind allerdings selbst instabil und zerfallen mit eine Halbwertszeit von ungefähr 10 Minuten:
$$ \mathrm{n}\to \mathrm{p}+{\mathrm{e}}^{-}+{\bar{\nu}}_{\mathrm{e}}. $$
(19.55)
Der r-Prozess findet vermutlich in Supernovae statt, die wir in den Kap. 20 und 21 kurz besprechen. Durch den r-Prozess frisch synthetisierte Elemente konnten in den Spektren der beim Verschmelzen zweier Neutronensterne gebildeten Kilonova AT2017gfo nachgewiesen werden, wie wir in Abschn. 15.​5.​4 bereits diskutiert haben.

19.7 Neutrinooszillationen

Die bei den pp-Reaktionen freiwerdenden Elektronneutrinos können in umfangreichen Experimenten, vornehmlich dem Sudbury Neutrino Observatory [18] in Kanada und dem Super-Kamiokande-Detektor [19] in Japan, auf der Erde nachgewiesen werden. Dabei stellte sich heraus, dass nur etwa ein Drittel des erwarteten Elektronneutrinostroms auf der Erde ankommt. Der Grund dafür sind die sogenannten Neutrinooszillationen . Im Standardmodell der Teilchenphysik sind die drei Neutrinoarten νe, νμ und ντ masselos, in vielen Ansätzen für eine Erweiterung der Standardmodells ergeben sich aber kleine von Null verschiedene Neutrinomassen. Bei Prozessen der schwachen Wechselwirkung wie den oben beschriebenen Fusionsreaktionen entstehen die Neutrinos in einem der Flavoreigenzustände {νe, νμ, ντ}. Ihre Propagation durch den Raum erfolgt aber in Eigenzuständen mit definierter Masse, die nicht mit den Flavoreigenzuständen übereinstimmen. Ein auf der Sonne entstehendes Elektronneutrino oszilliert daher während des Fluges zur Erde zwischen den Flavorzuständen hin und her und kann hier auch als Myon- oder Tauneutrino im Detektor nachgewiesen werden. Neutrinooszillationen werden im Wesentlichen über die drei Mischungswinkel θ12, θ13 und θ23 und die entsprechenden quadrierten Massendifferenzen beschrieben. Die genaue Messung dieser Größen ermöglicht daher zum einen Untersuchungen von Physik jenseits des Standardmodells und zum anderen ein verbessertes Verständnis der Fusionsprozesse in Sternen. Referenz [10] ist ein aktueller Übersichtsartikel zu diesem Thema.

Für die Entdeckung der Neutrinooszillationen wurden die Leiter der kanadischen und der japanischen Arbeitsgruppe, A. B. McDonald10 und T. Kajita,11 2015 mit dem Nobelpreis für Physik ausgezeichnet [21].