© Springer-Verlag GmbH Deutschland, ein Teil von Springer Nature 2022
S. Boblest et al.Spezielle und allgemeine Relativitätstheoriehttps://doi.org/10.1007/978-3-662-63352-6_18

18. Innere Struktur von Sternen

Sebastian Boblest1  , Thomas Müller2   und Günter Wunner3  
(1)
Dürnau, Deutschland
(2)
Max-Planck-Institut für Astronomie, Haus der Astronomie, Heidelberg, Deutschland
(3)
Universität Stuttgart, 1. Institut für Theoretische Physik, Stuttgart, Deutschland
 
 
Sebastian Boblest (Korrespondenzautor)
Email: sebastian.boblest@googlemail.com
 
Thomas Müller
Email: tmueller@mpia.de
 
Günter Wunner
Email: wunner@itp1.uni-stuttgart.de

In diesem Kapitel möchten wir die Eigenschaften der Materie im Inneren von Sternen untersuchen. Dabei werden wir einen Satz von Gleichungen herleiten, mit denen eine ganze Vielzahl unterschiedlicher Sterntypen beschrieben werden kann.

18.1 Hydrostatisches Gleichgewicht

Wenn eine Gaswolke unter ihrer Eigengravitation kollabiert, muss es auch eine Bedingung geben, die dafür sorgt, dass der Kollaps schließlich stoppt. Damit dies passieren kann, ist ein Druckgradient nötig, sodass jede einzelne Kugelschale des Sterns davon getragen wird. Wenn dieser Zustand erreicht ist, befindet sich der Stern im hydrostatischen Gleichgewicht . Zur Herleitung der Gleichgewichtsbedingung betrachten wir eine Kugelschale des Sterns mit Dicke dr (s. Abb. 18.1). Dabei nehmen wir dann automatisch Kugelsymmetrie für das Problem an. Das macht Sinn, denn aufgrund der Radialsymmetrie ist für uns nur der in radialer Richtung wirkende Druck entscheidend, zum einen der Druck p(r) am unteren Rand der Kugelschale, zum anderen der Druck p(r + dr) oben. Zusätzlich wirkt noch die Gewichtskraft der Kugelschale, diese ergibt sich zu
$$ {\boldsymbol{F}}_{\mathrm{m}}=-G\frac{M(r)\delta m}{r^2}{\mathbf{e}}_r, $$
(18.1)
Abb. 18.1

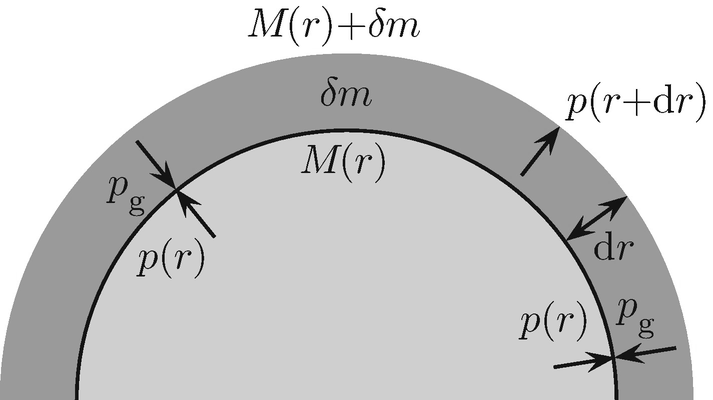
Skizze zur Herleitung der Bedingung für hydrostatisches Gleichgewicht. Der Gravitationsdruck pm jeder Kugelschale mit Masse δm muss durch einen Gegendruck p der weiter innen liegenden Schichten kompensiert werden, damit der Stern sich im Gleichgewicht befindet

mit der von der Kugel mit Radius r umschlossenen Masse M(r) und der Masse der Kugelschale δm = ρm4πr 2 dr, wobei 4πr 2 die Oberfläche der Kugelschale ist. Der Gravitationsdruck ist also
$$ {p}_{\mathrm{m}}=G\frac{M(r)\delta m}{r^2}. $$
(18.2)
Aufgrund der Druckdifferenz zwischen Innenseite und Außenseite der Kugelschale ergibt sich eine nach außen wirkende resultierende Kraft
$$ {\boldsymbol{F}}_{\Delta p}=\left[p(r)-p\left(r+\mathrm{d}r\right)\right]A\, {\mathbf{e}}_r. $$
(18.3)
Im Gleichgewicht müssen sich diese beiden Kräfte aufheben, d. h.
$$ {\boldsymbol{F}}_{\mathrm{m}}+{\boldsymbol{F}}_{\Delta p}=\mathbf{0.} $$
(18.4)
Wir linearisieren den Ausdruck für p(r) und erhalten
$$ {\left.p\left(r+\mathrm{d}r\right)=p(r)+\frac{\mathrm{d}p}{\mathrm{d}r}\right|}_r\, \mathrm{d}r+\mathcal{O}\left(\mathrm{d}{r}^2\right). $$
(18.5)
Wir setzen diesen Ausdruck in (18.3) ein und ersetzen A dr durch δm∕ρ. Dann haben wir
$$ {\boldsymbol{F}}_{\Delta p}=-\frac{\mathrm{d}p}{\mathrm{d}r}{\left|{}_r\, A\, \mathrm{d}r\, {\mathbf{e}}_r=-\frac{\mathrm{d}p}{\mathrm{d}r}\right|}_r\, \frac{\delta m}{\rho_{\mathrm{m}}(r)}{\mathbf{e}}_r. $$
(18.6)
Einsetzen in die Bedingung (18.4) führt schließlich auf
$$ \frac{\mathrm{d}p}{\mathrm{d}r}=-G\frac{\rho_{\mathrm{m}}(r)M(r)}{r^2}. $$
(18.7)
Damit haben wir einen Ausdruck für den Druckgradienten bezüglich des jeweiligen Radius in Abhängigkeit von der Dichte und der umschlossenen Masse gefunden. Durch diesen Druckgradienten wird der Stern stabilisiert. Für M(r) gilt außerdem wegen $$ M=\int {\rho}_{\mathrm{m}}\left(\boldsymbol{r}\right)\mathrm{d}V $$ in einem sphärisch-symmetrischen Stern
$$ \frac{\mathrm{d}M(r)}{\mathrm{d}r}={\rho}_{\mathrm{m}}(r)4\pi {r}^2. $$
(18.8)
Mit Hilfe der Bedingung für hydrostatisches Gleichgewicht können wir eine Größenordnung des Drucks im Zentrum eines Sterns gewinnen. Da wir die Funktion ρm(r) nicht kennen, können wir aus (18.8) die bis zum Radius r umschlossene Masse nicht bestimmen und (18.7) nicht direkt integrieren. Wir behelfen uns deshalb mit einer Abschätzung des Druckgradienten. Auf der Oberfläche des Sterns gilt, abgesehen vom Atmosphärendruck, den wir vernachlässigen, p(R) = 0. Den Druck im Zentrum bezeichnen wir mit pz. Wir nehmen jetzt einen linearen Druckabfall mit dem Radius an, d. h.
$$ \frac{\mathrm{d}p}{\mathrm{d}r}=-\frac{p_{\mathrm{z}}}{R}, $$
(18.9)
bzw.
$$ p(r)={p}_{\mathrm{z}}\left(1-\frac{r}{R}\right). $$
(18.10)
Gl. (18.10) erfüllt offensichtlich unsere beiden Bedingungen p(0) = pz und p(R) = 0. Den Ausdruck auf der rechten Seite von (18.9) vergleichen wir mit der rechten Seite von (18.7), wobei wir die Gesamtmasse M statt M(r) und die mittlere Dichte $$ \left\langle {\rho}_{\mathrm{m}}\right\rangle $$ statt ρm(r) verwenden, und finden
$$ \frac{p_{\mathrm{z}}}{R}=G\frac{\left\langle {\rho}_{\mathrm{m}}\right\rangle M}{R^2}. $$
(18.11)
Mit $$ \left\langle {\rho}_{\mathrm{m}}\right\rangle =M/ \left[\left(4/ 3\right)\pi {R}^3\right] $$ ist dann
$$ {p}_{\mathrm{z}}\sim \frac{3}{4\pi }G\frac{M^2}{R^4}. $$
(18.12)
Mit den Werten für die Sonne aus (1.​54) und (1.​55) finden wir
$$ {p}_{\mathrm{z},\, \mathrm{Sch}\ddot{\mathrm{a}} \mathrm{tzung}}^{\odot}\gtrsim 2,7\cdotp 1{0}^{14}\mathrm{Pa}=2,6\cdotp 1{0}^9\mathrm{atm}, $$
(18.13)
wobei eine Atmosphäre (1atm = 101.325 Pa) etwa der mittlere Luftdruck auf Meereshöhe ist. Wir werden sehen, dass der reale Wert für pz um ein Vielfaches höher liegt.
Wir kommen trotz der enthaltenen relativ groben Näherungen nochmals auf den Ausdruck (18.12) zurück. Wenn wir die mittlere Dichte dort wieder einführen und den verbleibenden Term M wieder durch den Schwarzschild-Radius rs = 2GM∕c 2 aus (1.​38) ersetzen, ergibt sich bei Vernachlässigung von Vorfaktoren
$$ {p}_{\mathrm{z}}\gtrsim {c}^2\left\langle {\rho}_{\mathrm{m}}\right\rangle \frac{r_{\mathrm{s}}}{R}. $$
(18.14)
Größenordnungsmäßig ergibt sich damit der Zusammenhang
$$ \frac{\left\langle p\right\rangle }{\left\langle {\rho}_{\mathrm{m}}\right\rangle {c}^2}\approx \frac{r_{\mathrm{s}}}{R}. $$
(18.15)
Dabei ist $$ \left\langle p\right\rangle $$ der mittlere Druck und $$ \left\langle {\rho}_{\mathrm{m}}\right\rangle {c}^2 $$ die mittlere Ruheenergiedichte. Gleichung (18.15) verknüpft den mittleren Druck und die mittlere Dichte im Stern miteinander. Allgemein bezeichnen wir Relationen zwischen den Größen, die den Zustand der Materie in einem gegebenen System beschreiben, im Allgemeinen sind dies etwa Druck, Temperatur, Dichte, aber auch die chemische Zusammensetzung, als Zustandsgleichungen. Zustandsgleichungen wie in (18.15) werden oft in Form einer dimensionslosen Funktion f der beschreibenden Größen als
$$ f\left({\rho}_{\mathrm{m}},T,\dots \, \right)\equiv \frac{p\left({\rho}_{\mathrm{m}},T,\dots \, \right)}{\rho_{\mathrm{m}}{c}^2} $$
(18.16)
dargestellt. Gleichung (18.15) ist eine stark vereinfachte Form einer solchen Zustandsgleichung, da sie gemittelte Größen miteinander verknüpft. In den Abschn. 18.3 und 18.4 werden wir Zustandsgleichungen für ganz unterschiedliche Situationen detailliert betrachten.

Der Zusammenhang (18.7) ist außerdem nur gültig, solange die Dichte und der Druck so klein sind, dass allgemein-relativistische Effekte vernachlässigbar sind. Für sehr massive Objekte gilt er daher nicht. In Abschn. 21.​4.​1 behandeln wir das hydrostatische Gleichgewicht daher noch einmal im Rahmen der ART.

18.2 Physikalische Bedingungen in Sternen

Die physikalischen Parameter, die einen Stern beschreiben, sind seine Masse M, die Leuchtkraft L, sein Radius R, Druck p und Temperatur T und seine chemische Zusammensetzung. Diese Größen sind nicht unabhängig voneinander, sondern durch mathematische Relationen miteinander verknüpft. Mit der Bedingung für hydrostatisches Gleichgewicht in (18.7) und der Massenerhaltung (18.8) haben wir bereits die ersten dieser Relationen kennengelernt. Sterne sind in guter Näherung schwarze Körper. Diese Feststellung klingt zunächst völlig unplausibel, aber ein schwarzer Körper ist eben nicht dadurch gekennzeichnet, dass er schwarz ist, sondern dadurch, dass auf ihn treffende elektromagnetische Strahlung vollständig absorbiert wird und die von ihm emittierte Strahlung ein Schwarzkörperspektrum aufweist. Diese Eigenschaften gelten für Sterne relativ gut. Für einen schwarzen Körper gibt das Stefan-Boltzmann-Gesetz 1 den Zusammenhang L = AσT 4 zwischen abgestrahlter Leistung L, Oberfläche A und der Temperatur an. Der Zahlenwert der Stefan-Boltzmann-Konstanten ist
$$ \sigma =5,670373(21)\cdotp 1{0}^{-8}\mathrm{W}\, {\mathrm{m}}^{-2}\, {\mathrm{K}}^{-4}. $$
(18.17)
Dementsprechend gilt für die Leuchtkraft eines Sterns
$$ L=4\pi {R}^2\sigma {T}_{\mathrm{eff}}^4. $$
(18.18)
Dabei hätte ein schwarzer Körper mit der effektiven Temperatur Teff die gleiche Leuchtkraft wie der jeweilige Stern. Für die Sonne ist Teff ≈ 5800 K. Die Sonne hält ihre Temperatur im Wesentlichen konstant, obwohl sie entsprechend (18.18) kontinuierlich Energie abstrahlt. Das ist nur möglich, wenn die Sonne im Inneren diese Strahlungsverluste aus einem Energiereservoir heraus kompensiert. Wir bezeichnen mit L(r) den Anteil der Leuchtkraft, der bis zum Radius r produziert wird, analog zur umschlossenen Masse M(r). Völlig analog zu (18.8) für den Gradienten für M(r) gilt dann die Relation
$$ \frac{\mathrm{d}L(r)}{\mathrm{d}r}=4\pi {r}^2\varepsilon (r). $$
(18.19)
Dabei ist ε(r) die Energieerzeugungsrate. In Kap. 19 zeigen wir, dass Sterne mit Hilfe von Kernfusion Energie produzieren.

Wir werden sehen, dass die Fusionsrate R und damit ε(r) von der Dichte der beteiligten Reaktionspartner und der Temperatur abhängt. Dadurch ist (18.19) an die anderen Größen im Sterninneren gekoppelt. Die Dichte und Temperatur und damit die Energieerzeugungsrate sind im Inneren des Sterns am höchsten. Die erzeugte Energie muss dann aus dem Inneren des Sterns nach außen transportiert werden.

Ein möglicher Prozess für den Wärmetransport ist Diffusion. Voraussetzung dafür ist ein Temperaturgradient. Unter Annahme eines diffusiven Wärmetransports ergibt sich für diesen die Bestimmungsgleichung
$$ \frac{\mathrm{d}T(r)}{\mathrm{d}r}=-\frac{3\kappa (r){\rho}_{\mathrm{m}}(r)}{16\sigma {T}^3(r)}\frac{L(r)}{4\pi {r}^2}. $$
(18.20)
Die Herleitung dieser Beziehung findet sich z. B. in [6]. Wir sehen, dass der Temperaturgradient wie der Druckgradient negativ ist, d. h. die Temperatur nimmt nach innen zu. Es ist anschaulich klar, dass diese Bedingung für Wärmetransport von innen nach außen notwendig ist.

Ein weiterer Mechanismus für die Wärmeleitung in Gasen und Flüssigkeiten ist Konvektion. Auch in Sternen spielt dieser eine wichtige Rolle, eine quantitative Behandlung des Wärmetransports ist daher allein mit (18.20) nicht möglich. Wir sehen aber, wie die verschiedenen Parameter, die die Sternmaterie beschreiben, durch verschiedene Gleichungen miteinander verknüpft sind und dementsprechend gemeinsam behandelt werden müssen.

In (18.20) taucht noch eine weitere Größe auf, die Opazität κ(r). Sie gibt an, wie durchlässig das Material im Stern für Strahlung ist. Für massearme Sterne gibt es die Abschätzung κ(r) ~ ρm(r)T(r)−3,5, für massereiche Sterne κ(r) ~ const [5]. Um detaillierte Sternmodelle zu entwickeln, sind aber numerische Berechnungen der Opazität nötig.

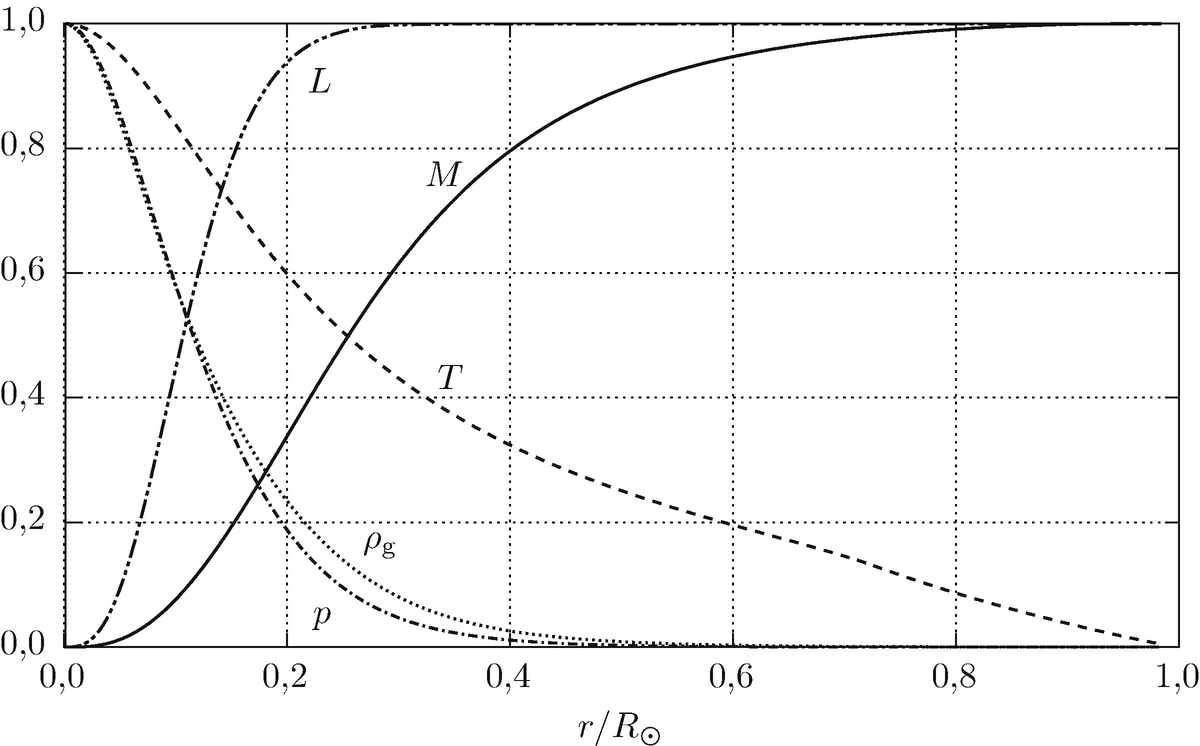
Abb. 18.2 zeigt die Ergebnisse quantitativer Rechnungen für die Sonne [1]. Dargestellt sind die Entwicklung von Druck, Temperatur und Dichte in Abhängigkeit von der radialen Position in diesem Modell, sowie der beim jeweiligen Radius umschlossene Anteil M(r) der Gesamtmasse und der bis zum Radius r erzeugte Anteil der Leuchtkraft L(r). In (18.13) haben wir für den Druck im Zentrum der Sonne eine Abschätzung pz ~ 3 · 109 atm gefunden. Die genaue Berechnung ergibt einen deutlich höheren Wert von
Abb. 18.2

Zustandsgrößen im Inneren der Sonne normiert auf den Maximalwert in Abhängigkeit von der radialen Position normiert auf den Sonnenradius. Die Kurve M gibt den bis r umschlossenen Anteil an der Gesamtmasse an, die Kurve L den bis dorthin produzierten Anteil der Gesamtleuchtkraft [2]

$$ {p}_{\mathrm{z}}^{\odot }=2,34\cdotp 1{0}^{16}\mathrm{Pa}=2,31\cdotp 1{0}^{11}\mathrm{atm}, $$
(18.21)
d. h. etwa 231 Milliarden mal der Luftdruck auf der Erdoberfläche. Aus diesen Rechnungen folgen weiter die Werte
$$ {T}_{\mathrm{z}}^{\odot }=1,548\cdotp 1{0}^7\mathrm{K} $$
(18.22)
und
$$ {\rho}_{\mathrm{z}}^{\odot }=1,502\cdotp 1{0}^5\mathrm{kg}\, {\mathrm{m}}^{-3} $$
(18.23)
für Temperatur und Dichte im Zentrum der Sonne.

Man erkennt in Abb. 18.2, dass Druck und Temperatur nach außen hin sehr stark abfallen, damit ist die Annahme eines linearen Druckgradienten in (18.9) sehr ungenau. Das ist der Grund dafür, dass die Abschätzung (18.13) nur eine grobe untere Schranke liefert.

Da die Dichte im Zentrum der Sonne viel größer ist als in äußeren Schichten, befindet sich ein großer Anteil an der Gesamtmasse im Zentrum der Sonne, z. B. enthält die innere Kugel mit r ≈ 0,25 R⊙ bereits etwa 50 % der Gesamtmasse. Ebenso wird der allergrößte Teil der von der Sonne abgestrahlten Leistung im Zentrum erzeugt.

18.3 Zustandsgleichung für Sternmaterie

Mit (18.15) haben wir bereits eine einfache Abschätzung für die Zustandsgleichung für Sternmaterie hergeleitet. Jetzt betrachten wir diese noch etwas detaillierter.

Aufgrund der hohen Temperatur im Sterninneren ist in vielen Fällen die Wechselwirkungsenergie der Teilchen untereinander sehr klein gegen die kinetische Energie und kann daher vernachlässigt werden. In diesem Fall ist die Beschreibung als ideales Gas eine sehr gute Näherung. Dessen Zustandsgleichung lautet
$$ pV=N{k}_{\mathrm{B}}T $$
(18.24)
mit der Anzahl N an Gasteilchen. Wir dividieren durch N und erweitern über $$ V/ N=\left(V/ M\right)\left(M/ N\right)=\left\langle m\right\rangle / {\rho}_m $$ . Dabei bezeichnet $$ \left\langle m\right\rangle $$ die mittlere Masse pro Gasteilchen. Gl. (18.24) wird dann zu
$$ p(r)=\frac{\rho_{\mathrm{m}}(r)}{\left\langle m\right\rangle }{k}_{\mathrm{B}}T(r). $$
(18.25)
Dabei haben wir wieder die Abhängigkeit vom Radius explizit eingesetzt. Die mittlere Teilchenmasse $$ \left\langle m\right\rangle $$ kann sich natürlich streng genommen auch an verschiedenen Orten innerhalb des Sterns unterscheiden und dann auch eine radiusabhängige Funktion sein. So besteht die Sonne etwa in ihren äußeren Schichten überwiegend aus Wasserstoff, während im Zentrum der Anteil von Helium überwiegt (s. Abb. 19.​5).
Wir können prüfen, wie genau das Innere der Sonne durch (18.25) beschrieben wird, indem wir die Werte für Druck, Temperatur und Dichte aus (18.21) bis (18.23) einsetzen. Aufgelöst ergibt sich dann
$$ \left\langle m\right\rangle =\frac{k_{\mathrm{B}}{T}_{\mathrm{z}}^{\odot }{\rho}_{\mathrm{z}}^{\odot }}{p_{\mathrm{z}}^{\odot }}\approx 1,37\cdotp 1{0}^{-27}\, \mathrm{kg}. $$
(18.26)
Das ist etwas weniger als die Masse des Protons und damit zumindest in der korrekten Größenordnung für ein Gemisch aus Wasserstoff und Helium.
Für einen Stern in der Wasserstofffusionsphase (s. Abschn. 19.​4) ist es eine akzeptable Näherung, für die mittlere Teilchenmasse die Masse des Wasserstoffatoms einzusetzen. Mit dem Druck aus (18.25) wird die Zustandsgleichung (18.16) des vorhergehenden Abschnittes dann zu
$$ f\left[{\rho}_{\mathrm{m}}(r),T(r)\right]=\frac{p(r)}{\rho_{\mathrm{m}}(r){c}^2}=\frac{k_{\mathrm{B}}T(r)}{m_{\mathrm{H}}{c}^2}. $$
(18.27)
Diese Zustandsgleichung ist nur von der Temperatur T(r) abhängig. Wenn wir in (18.27) die gemittelte Temperatur $$ \left\langle T\right\rangle $$ einsetzen und den Zusammenhang f ≈ rs ∕R aus (18.15) verwenden, erhalten wir die Abschätzung
$$ f(T)=\frac{k_{\mathrm{B}}T}{m_{\mathrm{H}}{c}^2}\approx \frac{r_{\mathrm{s}}}{R}. $$
(18.28)
Radius und Temperatur sind also im Gleichgewicht über T ~ 1∕R miteinander verknüpft. Wir sehen außerdem, dass das Verhältnis von kinetischer Energie kB T zu Ruheenergie mH c 2 der Atome den Radius des Sterns bestimmt. Bei einem Hauptreihenstern, der Energie aus der Fusion von Wasserstoff gewinnt, haben wir etwa eine Temperatur von T ≈ 1,5 · 107 K, was einer thermischen Energie $$ {k}_{\mathrm{B}}T\approx 1,3\, \mathrm{ke}\ \mathrm{V} $$ entspricht. Außerdem beträgt die Ruheenergie von Protonen und Neutronen etwa $$ {m}_{\mathrm{p}}{c}^2\approx {m}_{\mathrm{n}}{c}^2\approx 1\, \mathrm{Ge}\ \mathrm{V} $$ . Dann ergibt sich für das Verhältnis (18.28)
$$ f(T)\approx \frac{1,3\mathrm{ke}\ \mathrm{V}}{1\mathrm{Ge}\ \mathrm{V}}\approx \frac{1{0}^3}{1{0}^9}=1{0}^{-6}. $$
(18.29)
Für die Sonne ist $$ {r}_{\mathrm{s}}^{\odot}\approx 3\mathrm{km} $$ und R ≈ 7 · 105 km. Damit haben wir f⊙ ≈ 4,3 · 10−6. Die Sonne erfüllt (18.29) also ziemlich gut.

18.4 Entartetes Elektronengas

Die zweite Zustandsgleichung, die wir besprechen wollen, kommt ins Spiel, wenn die Dichte der Materie sehr hoch wird. Wir haben bereits in Abb. 18.2 gesehen, dass im Inneren der Sonne die Dichte sehr viel größer als in äußeren Schichten ist. Zwar ist in der Sonne durchgehend eine Beschreibung als ideales Gas angebracht, in anderen Sternen ist es aber möglich, dass für die inneren Bereiche diese Beschreibung nicht mehr zutrifft.

Hier können die Elektronen aufgrund ihrer quantenmechanischen Eigenschaften einen Druck aufbauen. Der entscheidende Punkt wird sein, dass dieser Druck unabhängig von der Temperatur ist, d. h. auch bei T ≈ 0 verhindert dieser Entartungsdruck der Elektronen einen weiteren Kollaps. Bevor wir uns diesem Zustand quantitativ nähern, wollen wir die Entstehung des Entartungsdrucks in einem anschaulichen Bild besser verstehen.

18.4.1 Anschauliche Interpretation des Entartungsdrucks

Durch die hohe Dichte überlappen an einem bestimmten Punkt die Wellenfunktionen der Elektronen (s. Abb. 18.3) . Dieser Zustand entspricht einer globalen Wellenfunktion und ist dem der Valenzelektronen in einem Metall ähnlich. Die frei beweglichen Elektronen lassen eine Behandlung des Gases als freies Elektronengas oder Fermi-Gas, analog zu der Situation in Metallen, zu. Elektronen sind Fermionen, für sie gilt das Pauli-Prinzip,2 d. h. es können nicht zwei Elektronen im gleichen Quantenzustand sein. Allgemein spricht man bei Materie, die so hohe Dichte aufweist, dass sie aufgrund von quantenmechanischen Effekten stabilisiert wird, von entarteter Materie .
Abb. 18.3

Delokalisierung der Elektronen zu einem Fermigas beim Kollaps eines Sterns für sehr kleine Atomabstände d durch die Überlappung der Elektronenhüllen

Die Eigenschaft der Fermionen, einen Gegendruck gegen die Gravitation aufzubauen, lässt sich in einer Modellbetrachtung qualitativ verstehen. In einem Stern steht den Elektronen als möglicher Aufenthaltsort nur das Sternvolumen zur Verfügung. Wie im einfachen Modell des Potentialtopfes sind dadurch die möglichen Energieniveaus der Fermionen diskret.

Wir können die grundlegenden Eigenschaften der entarteten Materie deshalb bei der Betrachtung von quantenmechanischen Teilchen in einem dreidimensionalen Kastenpotential der Breite L ableiten (s. Abb. 18.4). Die Vorgehensweise in diesem Abschnitt wird oft völlig analog auch in der Festkörperphysik bei der Behandlung des freien Elektronengases verwendet, siehe z. B. [3]. Die Lösung der Schrödingergleichung für diesen Fall führt zu den Eigenfunktionen
Abb. 18.4

Die Entstehung des Fermi-Drucks lässt sich stark vereinfacht im Potentialtopfmodell für die Elektronen (schwarz) verstehen, wobei die Breite R des Topfes mit dem Radius der entarteten Region im Stern verknüpft ist. Sinkt der Radius, so steigt die Energie der Niveaus im Topf an. Es muss also Energie aufgebracht werden, um den Stern zu kontrahieren

$$ {\varPsi}_{\boldsymbol{k}}\left(\boldsymbol{r}\right)=\exp \left(\mathrm{i}\boldsymbol{k}\cdotp \boldsymbol{r}\right), $$
(18.30)
also zu ebenen Wellen. Für die Komponenten des Wellenvektors gelten periodische Randbedingungen, d. h.
$$ {k}_i=\frac{2\pi }{L}n,\quad \mathrm{mit}\quad n\in \mathbb{\mathbb{Z}}\quad \mathrm{und}\quad i\in \left\{x,y,z\right\}. $$
(18.31)
Durch die Randbedingung an die Komponenten des Wellenvektors kann sichergestellt werden, dass die Wellenfunktionen an den Rändern des Kastenpotentials verschwinden. Als ebene Wellen sind die Ψk auch Eigenfunktionen des Impulsoperators mit den als Vektor darstellbaren Eigenwerten
(18.32)
Die von Teilchen besetzten Zustände lassen sich am anschaulichsten im Impulsraum darstellen. Dort liegen diese Zustände alle innerhalb einer Kugel mit Radius R = | pF |, der Fermi-Kugel (s. Abb. 18.5). Der Fermi-Impuls pF ist dabei der zum höchsten besetzten Zustand gehörende Impuls. Aufgrund der Bedingung ki = 2πn∕L in (18.31) und des Zusammenhangs (18.32) zwischen Wellenvektor und Impuls nimmt jeder erlaubte Zustand ein Volumen (h∕L)3 im Impulsraum ein. Wegen des Pauli-Prinzips können nur jeweils zwei Fermionen mit unterschiedlichem Spin einen solchen Zustand besetzen. Sind alle Zustände mit gegebenem Impuls besetzt, so müssen die weiteren Teilchen Zustände mit höherem Impuls belegen. 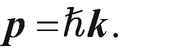In einer Kugel mit Volumen $$ V=4\pi {p}_{\mathrm{F}}^3/ 3 $$ liegen demnach
Abb. 18.5

Alle Zustände mit p < pF liegen in einer Kugel mit Radius R = pF im Impulsraum. Zur einfacheren Darstellung ist die Skizze auf Zustände mit pi ≥ 0 beschränkt

$$ N=2\frac{4\pi {p}_{\mathrm{F}}^3/ 3}{{\left(\frac{h}{L}\right)}^3}=\frac{8}{3}\pi \frac{V}{h^3}{p}_{\mathrm{F}}^3 $$
(18.33)
Zustände. Im zweiten Schritt haben wir dabei das Volumen V = L 3 des Kastens eingesetzt. Wir lösen nach dem Fermi-Impuls auf und erhalten
$$ {p}_{\mathrm{F}}={\left(\frac{3N}{8\pi}\frac{h^3}{V}\right)}^{1/ 3}. $$
(18.34)
Die Fermi-Energie ist über die relativistische Energie-Impuls-Beziehung
$$ {E}_{\mathrm{F}}=\sqrt{m^2{c}^4+{c}^2{p}_{\mathrm{F}}^2}, $$
(18.35)
die wir in Abschn. 6.​6 diskutiert haben, mit dem Fermi-Impuls verknüpft. Steigt der Fermi-Impuls, so steigt auch die Fermi-Energie. Um die entarteten Elektronen weiter zu komprimieren, muss also Energie aufgebracht werden.

18.4.2 Voll entartetes ideales Fermigas

In diesem Abschnitt folgen wir der Argumentation in [7]. Da in diesem Abschnitt Druck und Impuls gleichzeitig vorkommen und wir für beide das Symbol p verwenden, schreiben wir in diesem Abschnitt den Druck immer als pe. Wir knüpfen an das oben Gesagte an und betrachten jetzt die Anzahldichte $$ \mathrm{d}\mathcal{R}/ \left({\mathrm{d}}^3r\, {\mathrm{d}}^3p\right) $$ der Fermionen im Phasenraum. Diese ist verknüpft mit einer Verteilungsfunktion f(r, p, t) definiert über
$$ \frac{\mathrm{d}\mathcal{R}}{{\mathrm{d}}^3r\, {\mathrm{d}}^3p}=\frac{2}{h^3}f. $$
(18.36)
Dabei ist h 3 das bereits eingeführte Volumen einer Zelle im Phasenraum, der Faktor zwei resultiert aus den beiden möglichen Spineinstellungen für Elektronen. Für f kennen wir bereits einen Ausdruck, denn für Fermionen gilt die Fermi-Dirac-Statistik,3 d. h.
$$ f(E)=\frac{1}{\exp \left(\frac{E-\mu }{k_{\mathrm{B}}T}\right)+1}, $$
(18.37)
dabei ist μ das chemische Potential. Es gibt an, um welchen Betrag sich die Energie ändert, wenn ein Fermion aus dem System entfernt wird. Im entarteten Fall können wir deshalb μ ≈ EF setzen. Je kleiner die Temperatur wird, desto größer wird der Faktor 1∕(kB T) in der Exponentialfunktion in (18.37). Die Funktion f nähert sich dadurch immer mehr einer Stufenfunktion an. Im Grenzfall völlig entarteter Fermionen (T → 0, μ∕kB T → ∞) gilt schließlich
$$ f(E)=\left\{\begin{array}{ll}1,&amp; E\le {E}_{\mathrm{F}},\\ {}0,&amp; E&gt;{E}_{\mathrm{F}},\end{array}\right. $$
(18.38)
d. h. alle Zustände mit E < EF sind besetzt und alle Zustände mit E > EF sind unbesetzt (s. Abb. 18.6).
Abb. 18.6

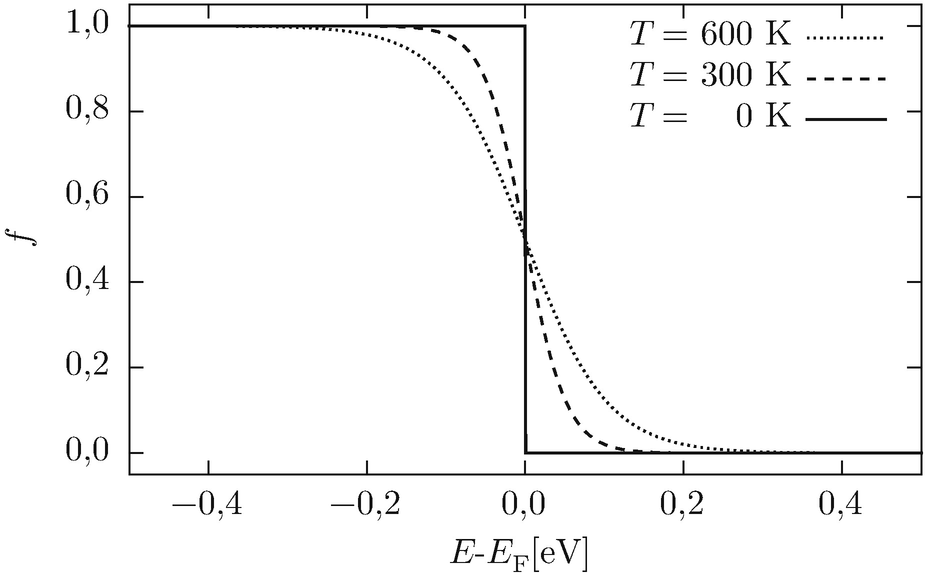
Fermi-Dirac-Verteilungsfunktion für verschiedene Temperaturen. Je kleiner die Temperatur wird, desto mehr nähert sich f einer Stufenfunktion an. Für T → 0 K sind alle Zustände mit E < EF besetzt und alle Zustände mit E > EF unbesetzt

Für die Anzahldichte der Fermionen gilt
$$ n=\int \frac{\mathrm{d}\mathcal{R}}{{\mathrm{d}}^3r\, {\mathrm{d}}^3p}{\mathrm{d}}^3p. $$
(18.39)
Für den Druck in einem System mit isotrop verteilten Impulsen ist weiter
$$ {p}_{\mathrm{e}}=\frac{1}{3}\int pv\frac{\mathrm{d}\mathcal{R}}{{\mathrm{d}}^3r\, {\mathrm{d}}^3p}{\mathrm{d}}^3p. $$
(18.40)
Der Faktor 1∕3 folgt dabei aus der Isotropie und für die Geschwindigkeit können wir wegen p = mγv und E = mγc 2 (s. (6.​35))
$$ v=p{c}^2/ E $$
(18.41)
schreiben.
Mit (18.38) und (18.39) ist die Elektronendichte gegeben über
$$ {n}_{\mathrm{e}}=\int \frac{\mathrm{d}\mathcal{R}}{{\mathrm{d}}^3r\, {\mathrm{d}}^3p}{\mathrm{d}}^3p=\underset{0}{\overset{p_{\mathrm{F}}}{\int }}\frac{2}{h^3}f(E){\mathrm{d}}^3p=\underset{0}{\overset{p_{\mathrm{F}}}{\int }}\frac{2}{h^3}4\pi {p}^2\mathrm{d}p=\frac{8\pi }{3{h}^3}{p}_{\mathrm{F}}^3. $$
(18.42)
Aus (18.38) folgt dabei die obere Integrationsgrenze pF, da Zustände mit größerem Impuls nicht besetzt sind. Wenn der Fermi-Impuls der Elektronen sehr groß wird, dann verhalten sich die Elektronen relativistisch. Um die Stärke relativistischer Einflüsse zu charakterisieren, führt man einen dimensionslosen Relativitätsparameter
$$ x=\frac{p_{\mathrm{F}}}{m_{\mathrm{e}}c} $$
(18.43)
ein. Dieser gibt den Fermi-Impuls in Einheiten des nichtrelativistischen Impulses eines Elektrons, das sich mit Lichtgeschwindigkeit bewegt, an. Damit ist
(18.44)
In dieser Gleichung haben wir die reduzierte Compton-Wellenlänge des Elektrons
(18.45)
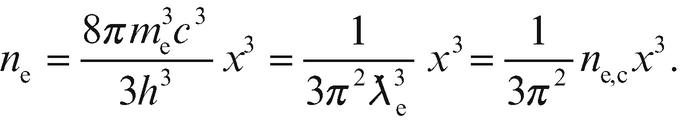
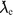eingeführt. Sie unterscheidet sich nur um einen Faktor 2π von der Compton-Wellenlänge, die wir in (6.​59) kennengelernt haben. Die Größe heißt reduziert, weil in ihrer Definition 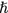statt h steht, analog zu den beiden Formen des Planck'schen Wirkungsquantums. Im Folgenden sprechen wir einfach von der Compton-Wellenlänge. Wir sehen daran, dass wir die Anzahldichte ne in Einheiten einer charakteristischen Anzahldichte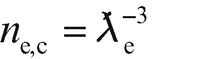
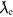(18.46)
messen, die einem Elektron in einem Würfel mit Kantenlänge entspricht. Zu ne,c gehören eine entsprechende charakteristische Massendichte und Energiedichte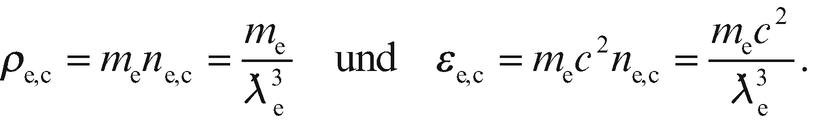
(18.47)
Mit den jetzt eingeführten Größen können wir den Druck auswerten. Mit dem Impuls p = yme c ergibt sich aus (18.40) zusammen mit (18.41) der Ausdruck
$$ {p}_{\mathrm{e}}=\frac{1}{3}\frac{2}{h^3}\underset{0}{\overset{p_{\mathrm{F}}}{\int }}p\, \frac{p}{\sqrt{p^2{c}^2+{m}_{\mathrm{e}}^2{c}^4}}\, 4\pi {p}^2\, \mathrm{d}p=\frac{\varepsilon_{\mathrm{e},\mathrm{c}}}{3{\pi}^2}\underset{0}{\overset{x}{\int }}\frac{y^4\, \mathrm{d}y}{\sqrt{1+{y}^2}}. $$
(18.48)
Das in diesem Ausdruck vorkommende Integral ist analytisch lösbar. Man findet
$$ \phi (x)\equiv \frac{1}{3{\pi}^2}\underset{0}{\overset{x}{\int }}\frac{y^4\, \mathrm{d}y}{\sqrt{1+{y}^2}}=\frac{1}{8{\pi}^2}\left[x\sqrt{1+{x}^2}\left(\frac{2}{3}{x}^2-1\right)+\mathrm{arsinh}(x)\right]. $$
(18.49)
Den Vorfaktor 1∕(3π 2) haben wir mit in die Funktion ϕ(x) gezogen, denn dann ist
$$ {p}_{\mathrm{e}}={\varepsilon}_{\mathrm{e},\mathrm{c}}\phi (x). $$
(18.50)
Wir sind mit diesem Ausdruck allerdings noch nicht ganz am Ziel, denn wir möchten einen Ausdruck pe(ρm). Wir können zwar x mit Hilfe von (18.46) und (18.47) in Abhängigkeit von der Elektronendichte ρe ausdrücken. In Sternmaterie liefert diese aber nicht den dominanten Beitrag zur Gesamtmassendichte, sondern im Gegenteil einen nahezu vernachlässigbaren Anteil. Selbst wenn der Druck also fast ausschließlich von den entarteten Elektronen verursacht wird, dominiert die Dichte der Ruhemasse der Ionen die Gesamtdichte
$$ {\rho}_{\mathrm{ges}}=\sum \limits_i{n}_i{m}_i. $$
(18.51)
In diesem Ausdruck sind ni und mi die Anzahldichte und Masse der Ionen vom Typ i. Bereits an dieser Stelle sehen wir, dass die Eigenschaften entarteter Materie von der chemischen Zusammensetzung abhängen, denn die Anzahl an Kernbausteinen pro Ion und die Ionendichte zusammen legen die Gesamtdichte fest. Um (18.51) geschickt zu formulieren, führen wir die mittlere Baryonenmasse
$$ {m}_{\mathrm{Bar}}=\frac{1}{n_{\mathrm{Bar}}}\sum \limits_i{n}_i{m}_i $$
(18.52)
ein. Dabei ist die Baryonendichte
$$ {n}_{\mathrm{Bar}}=\sum \limits_i{n}_i{A}_i $$
(18.53)
über die Anzahldichten ni und Massenzahlen Ai der einzelnen Bestandteile der Materie definiert. Die Gesamtdichte ist jetzt einfach
$$ {\rho}_{\mathrm{ges}}={n}_{\mathrm{Bar}}{m}_{\mathrm{Bar}}. $$
(18.54)
Um jetzt diesen Ausdruck wieder mit der Elektronendichte zu verknüpfen, führen wir die mittlere Elektronenzahl pro Baryon Ye ein. Mit nBar = ne Ye erhalten wir dann
$$ {\rho}_{\mathrm{ges}}=\frac{n_{\mathrm{e}}}{Y_{\mathrm{e}}}{m}_{\mathrm{Bar}}. $$
(18.55)
Mit ne aus (18.44) führt das auf
$$ {\rho}_{\mathrm{ges}}(x)={\rho}_{\mathrm{c}}{x}^3, $$
(18.56)
wobei wir die kritische Massendichte
(18.57)
eingeführt und im zweiten Schritt (18.46) eingesetzt haben. Damit können wir
$$ x={\left(\frac{\rho_{\mathrm{ges}}}{\rho_{\mathrm{c}}}\right)}^{1/ 3} $$
(18.58)
schreiben. Für die Baryonenmasse können wir ohne nennenswerten Fehler die atomare Masseneinheit [4]
$$ {m}_{\mathrm{u}}=1,660538921(73)\cdotp 1{0}^{-27}\, \mathrm{kg} $$
(18.59)
einsetzen. Für jedes Isotop eines Elementes mit Kernladung Z und Massenzahl A ist die mittlere Elektronenzahl pro Baryon gegeben über Ye = Z∕A. Für eine Vielzahl an Isotopen, z. B. 4He, 6C und 8O, ist A = 2Z und daher Ye = 1∕2. Gegenbeispiele sind etwa der in Sternen dominant vorhandene Wasserstoff 1H mit Ye = 1 und 56Fe mit Ye = 0,46, das als Fusionsendprodukt sehr massereicher Sterne in Abschn. 19.​5.​2 eine wichtige Rolle spielt. Tatsächlich sind aber die drei genannten Isotope von Helium, Kohlenstoff und Sauerstoff diejenigen, die in entarteter Materie die wichtigste Rolle spielen. Wir können daher in (18.56) Ye = 0,5 setzen. Wie wir außerdem am Beispiel von Eisen sehen, ist dieser Zahlenwert außer für Wasserstoff auch für die meisten anderen Isotope relativ genau.
Es ergibt sich dann
$$ {\rho}_{\mathrm{c}}=1,94786\cdotp 1{0}^9\mathrm{kg}\, {\mathrm{m}}^{-3}. $$
(18.60)
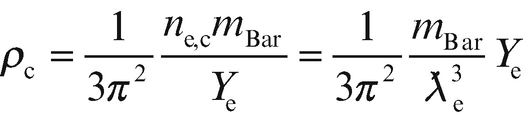
Um ein Gefühl für die Größe von ρc zu bekommen, vergleichen wir mit der Dichte $$ {\rho}_{\mathrm{z}}^{\odot } $$ im Zentrum der Sonne in (18.23). Es ist $$ {\rho}_{\mathrm{c}}\simeq 1,3\cdotp 1{0}^4{\rho}_{\mathrm{z}}^{\odot } $$ .

Die Gl. (18.50) und (18.56) sind die gesuchte Zustandsgleichung in parametrischer Form, wobei wir natürlich den Ausdruck für x in (18.58) in pe einsetzen können und dann direkt die gesuchte Formel pe(ρm) erhalten. Aufgrund der relativ komplizierten Funktion ϕ(x) aus (18.49) ergibt sich aber ein unschöner Ausdruck.

Wir können für die beiden Grenzfälle x ≪ 1, d. h. nichtrelativistische Elektronen, und x ≫ 1, d. h. hochrelativistische Elektronen, aber sehr einfache Ausdrücke erhalten, wenn wir ϕ(x) für diese Fälle nähern. Im ersten Fall ergibt eine einfache Taylorreihe um x = 0
$$ \phi (x)\approx \frac{x^5}{15{\pi}^2}\quad \mathrm{f}\ddot{\mathrm{u}}\mathrm{r}\quad x\ll 1. $$
(18.61)
Um eine Näherung für den hochrelativistischen Grenzfall zu erhalten, verwenden wir $$ \sqrt{1+{x}^2}\approx x $$ für große x. Da außerdem der $$ \mathrm{arsinh}(x) $$ für große x ungefähr wie $$ \ln (2x) $$ läuft, können wir diesen Beitrag vernachlässigen und finden den dominanten Term
$$ \phi (x)\approx \frac{x^4}{12{\pi}^2}\quad \mathrm{f}\ddot{\mathrm{u}}\mathrm{r}\quad x\gg 1. $$
(18.62)
Das führt dann insgesamt auf
$$ {p}_{\mathrm{e}}(x)=\frac{\varepsilon_{\mathrm{e},\mathrm{c}}}{3{\pi}^2}\cdotp \left\{\begin{array}{ll}\frac{x^5}{5}&amp; \mathrm{f}\ddot{\mathrm{u}}\mathrm{r}\, x\ll 1,\\ {}\frac{x^4}{4}&amp; \mathrm{f}\ddot{\mathrm{u}}\mathrm{r}\, x\gg 1.\end{array}\right. $$
(18.63)
Wenn wir schließlich die Definition (18.58) einsetzen, finden wir
$$ {p}_{\mathrm{e}}\left({\rho}_{\mathrm{m}}\right)=\frac{\varepsilon_{\mathrm{e},\mathrm{c}}}{3{\pi}^2}\cdotp \left\{\begin{array}{ll}\frac{1}{5}{\left(\frac{\rho_{\mathrm{m}}}{\rho_{\mathrm{c}}}\right)}^{5/ 3}&amp; \mathrm{f}\ddot{\mathrm{u}}\mathrm{r}\, {\rho}_{\mathrm{m}}\ll {\rho}_{\mathrm{c}},\\ {}\frac{1}{4}{\left(\frac{\rho_{\mathrm{m}}}{\rho_{\mathrm{c}}}\right)}^{4/ 3}&amp; \mathrm{f}\ddot{\mathrm{u}}\mathrm{r}\, {\rho}_{\mathrm{m}}\gg {\rho}_{\mathrm{c}}.\end{array}\right. $$
(18.64)
Zustandsgleichungen der Form
$$ {p}_{\mathrm{e}}\sim {\rho}^{\varGamma },\quad \mathrm{d}.\, \mathrm{h}.\quad {p}_{\mathrm{e}}{V}^{-\varGamma }=\mathrm{const} $$
(18.65)
werden in der Thermodynamik als polytrope Zustandsgleichungen bezeichnet und dieser Begriff wird deshalb für die Form (18.64) ebenfalls verwendet. Grundsätzlich muss mit steigender Dichte der Druck eines Sterns steigen, ansonsten wäre er instabil. Gl. (18.64) erfüllt diese Bedingung, aber der funktionale Zusammenhang zwischen Druck und Dichte ist nicht in beiden Grenzfällen gleich. Man bezeichnet Zustandsgleichungen, bei denen der Druck mit der Dichte stark steigt als hart, und solche, bei denen er langsam steigt, als weich. Die Zustandsgleichung für den hochrelativistischen Grenzfall ist also weicher als im nichtrelativistischen Grenzfall. Diese Aussage gilt natürlich auch für die ungenäherte Gleichung und spielt eine entscheidende Rolle für weiße Zwerge: Sternreste, die durch den Entartungsdruck der Elektronen stabilisiert werden und die wir in Kap. 20 besprechen. Dort führt das ,,relativistische Aufweichen“ der Zustandsgleichung dazu, dass diese Sterne nicht beliebig massiv werden können.
In Zahlenwerten ergibt (18.64)
$$ {p}_{\mathrm{e}}\left({\rho}_{\mathrm{m}}\right)=\left\{\begin{array}{l}3,16\cdotp 1{0}^6{\rho}_{\mathrm{m}}^{4/ 3}\, \left[\mathrm{kg}\, {\mathrm{m}}^{-3}\right]\mathrm{Pa},\\ {}4,93\cdotp 1{0}^9{\rho}_{\mathrm{m}}^{5/ 3}\, \left[\mathrm{kg}\, {\mathrm{m}}^{-3}\right]\mathrm{Pa}.\end{array}\right. $$
(18.66)
Wenn wir in (18.66) wieder den Wert der Dichte im Zentrum der Sonne aus (18.23) in die nichtrelativistische Näherung einsetzen, so finden wir
$$ {p}_{\mathrm{e}}\left({\rho}_{\mathrm{z}}^{\odot}\right)\approx 0,06{p}_{\mathrm{z}}^{\odot }, $$
(18.67)
mit dem Druck $$ {p}_{\mathrm{z}}^{\odot } $$ im Sonneninneren aus (18.21). Aus dieser einfachen Abschätzung wird klar, dass der Druck im Inneren der Sonne nicht vom Entartungsdruck der Elektronen, sondern vom Gasdruck entsprechend (18.25) verursacht wird.
Abschließend geben wir noch den Ausdruck für die Zustandsgleichungsfunktion f = pe∕(ρm c 2) im genäherten Fall an. Wir verknüpfen den Faktor 1∕c 2 mit der Energiedichte im Vorfaktor und finden dann
$$ f\left({\rho}_{\mathrm{m}}\right)=\frac{1}{3{\pi}^2}\cdotp \left\{\begin{array}{ll}\frac{1}{5}{\left(\frac{\rho_{\mathrm{m}}}{\rho_{\mathrm{c}}}\right)}^{2/ 3}&amp; \mathrm{f}\ddot{\mathrm{u}}\mathrm{r}\, {\rho}_{\mathrm{m}}\ll {\rho}_{\mathrm{c}},\\ {}\frac{1}{4}{\left(\frac{\rho_{\mathrm{m}}}{\rho_{\mathrm{c}}}\right)}^{1/ 3}&amp; \mathrm{f}\ddot{\mathrm{u}}\mathrm{r}\, {\rho}_{\mathrm{m}}\gg {\rho}_{\mathrm{c}}.\end{array}\right. $$
(18.68)

18.5 Zusammenfassung

Mit (18.27) für das ideale Gas und (18.64) für das entartete Elektronengas haben wir zwei völlig unterschiedliche Zustandsgleichungen für Sternmaterie gefunden. Es fällt sofort ein wesentlicher Unterschied auf: Während f in (18.27) nur eine Funktion der Temperatur ist, hängt (18.64) nur von der Dichte ab. Dieser Unterschied bleibt natürlich auch gültig, wenn wir in (18.64) den allgemeinen Ausdruck für den Druck einsetzen.

Die Entwicklung eines Sterns hängt von der jeweiligen Stärke der beiden Drücke p ~ ρm T in (18.25) und $$ p\sim {\rho}_{\mathrm{m}}^{n/ 3} $$ in (18.64) ab. Ein kontrahierender, nicht entarteter Stern wird entsprechend (18.25) solange seine Temperatur erhöhen, bis dadurch Fusionsprozesse in Gang kommen und einen weiteren Kollaps verhindern. Wenn allerdings der Entartungsdruck so groß wird, dass er einen weiteren Kollaps verhindern kann, bevor die Temperatur für einen bestimmten Fusionsprozess hoch genug ist, so kann es zu diesem nicht kommen. Im Wesentlichen entscheidet die Masse eines Sterns darüber, welche dieser beiden Möglichkeiten stattfindet. In Kap. 19 kommen wir auf dieses Thema bei der Diskussion der Energieproduktion in Sternen zurück.