S. Boblest et al.Spezielle und allgemeine Relativitätstheoriehttps://doi.org/10.1007/978-3-662-63352-6_7

7. Kovariante Formulierung der Elektrodynamik

Sebastian Boblest¹, Thomas Müller² und Günter Wunner³

(1)

Dürnau, Deutschland

(2)

Max-Planck-Institut für Astronomie, Haus der Astronomie, Heidelberg, Deutschland

(3)

Universität Stuttgart, 1. Institut für Theoretische Physik, Stuttgart, Deutschland

Die Newton‘sche Mechanik ist Galilei-invariant. Deshalb mussten wir im vorherigen Kapitel eine kovariante Formulierung für eine relativistische Mechanik finden. Dies führte zu einer Modifikation der klassischen Bewegungsgleichungen.

Im Gegensatz dazu ist die Elektrodynamik, d. h. die Maxwell'schen Gleichungen, bereits Lorentz-invariant. Dies kommt jedoch bei der Formulierung mit elektrischem Feld E, magnetischer Flussdichte B, elektrischen Strömen j und Ladungsdichten ρ_el nicht explizit zum Ausdruck. Insbesondere sind E, B und j keine Vierervektoren und ρ_el kein Lorentz-Skalar. In diesem Kapitel wollen wir daher die Maxwell'schen Gleichungen in einer kovarianten Formulierung darstellen. Dies wird es uns ermöglichen, direkt zu sehen, wie sich die elektrischen und magnetischen Felder, sowie Ladungen und Ströme transformieren.

7.1 Potentiale in der klassischen Elektrodynamik

In Abschn. 1.3 haben wir die Elektrodynamik bereits kurz angesprochen. Jetzt ergänzen wir diesen Abschnitt um einige weitere Details. Wir kennen bereits die Maxwell-Gleichungen. Diese haben wir unterteilt in die homogenen Maxwell-Gleichungen

$\nabla \times \boldsymbol{E}+\dot{\boldsymbol{B}}=\mathbf{0}$

(1.5a)

und

$\nabla \cdotp \boldsymbol{B}=0$

(1.5b)

und die inhomogenen Maxwell-Gleichungen

$\nabla \times \boldsymbol{B}={\mu}_0\left(\boldsymbol{j}+{\varepsilon}_0\dot{\boldsymbol{E}}\right),$

(1.5c)

und

$\nabla \cdotp \boldsymbol{E}=\frac{\rho_{\mathrm{el}}}{\varepsilon_0}.$

(1.5d)

Aus (1.5a) ergibt sich durch Integration über eine Fläche F und unter Verwendung des Stokes'schen Satzes das Induktionsgesetz

$\underset{F}{\int}\left(\nabla \times \boldsymbol{E}\right)\, \mathrm{d}\boldsymbol{f}=\underset{\partial F}{\int}\boldsymbol{E}\cdotp \mathrm{d}\boldsymbol{s}={U}_{\mathrm{ind}}=-\underset{F}{\int}\dot{\boldsymbol{B}}\cdotp \mathrm{d}\boldsymbol{f}=-\dot{\varPhi}.$

(7.1)

mit dem magnetischen Fluss

$\varPhi =\underset{F}{\int}\boldsymbol{B}\cdotp \mathrm{d}\boldsymbol{f}$

(7.2)

durch F. Gl. (1.5b) besagt, dass es keine magnetischen Monopole gibt. Mit Hilfe der Vektoranalysis folgt, dass B als Rotation eines Vektorpotentials darstellbar ist, also

$\boldsymbol{B}=\nabla \times \boldsymbol{A}.$

(7.3)

Damit folgt aus (1.5a)

$\nabla \times \boldsymbol{E}+\nabla \times \dot{\boldsymbol{A}}=\nabla \times \left(\boldsymbol{E}+\dot{\boldsymbol{A}}\right)=\mathbf{0.}$

(7.4)

Das Vektorfeld $\boldsymbol{E}+\dot{\boldsymbol{A}}$ ist also wirbelfrei. In der Vektoranalysis wird weiter gezeigt, dass sich ein Vektorfeld als Gradient eines skalaren Feldes darstellen lässt, falls seine Rotation (auf einem einfach zusammenhängenden Gebiet) verschwindet. Also können wir schreiben

$\boldsymbol{E}+\dot{\boldsymbol{A}}=-\mathbf{\nabla}\varphi,$

(7.5)

mit dem elektrodynamischen Potential φ. Aufgelöst nach dem elektrischen Feld ergibt sich

$\boldsymbol{E}=-\mathbf{\nabla}\varphi -\dot{\boldsymbol{A}}.$

(7.6)

Das skalare Potential und das Vektorpotential sind nicht eindeutig, man spricht in diesem Zusammenhang von Eichfreiheit . Setzt man etwa Aʹ = A + ∇χ, mit einer beliebigen skalaren Funktion χ(r, t), so folgt daraus

(7.7)

weil die Rotation des Gradienten einer beliebigen skalaren Funktion verschwindet. Für das elektrische Feld ergibt sich dann

$\boldsymbol{E}=-\mathbf{\nabla}\varphi -\dot{\boldsymbol{A}}^{\prime }+\mathbf{\nabla}\dot{\chi }=-\mathbf{\nabla}\varphi^{\prime }-\dot{\boldsymbol{A}}^{\prime }$

(7.8)

mit

$\varphi^{\prime }=\varphi -\dot{\chi}.$

(7.9)

Man nennt χ(r, t) Eichfunktion und die Operation (A, φ) ↦ (Aʹ, φʹ) heißt Eichtransformation .

7.2 Formulierung mit Viererpotential

Wenn wir in (1.5c) und (1.5d) die Potentiale einsetzen und umformen, finden wir unter Verwendung von μ₀ε₀ = 1∕c² aus (1.8)

$\nabla \times \left(\nabla \times \boldsymbol{A}\right)+\frac{1}{c^2}\left(\mathbf{\nabla}\dot{\varphi }+\ddot{\boldsymbol{A}}\right)={\mu}_0\boldsymbol{j}$

(7.10a)

und

$\nabla \cdotp \left(-\mathbf{\nabla}\varphi -\dot{\boldsymbol{A}}\right)=\frac{\rho_{\mathrm{el}}}{\varepsilon_0}.$

(7.10b)

Mit der Relation a × (b × c) = b(a · c) − c(a · b) kann (7.10a) weiter umgeformt werden zu

$\mathbf{\nabla}\left(\nabla \cdotp \boldsymbol{A}\right)-\Delta \boldsymbol{A}+\frac{1}{c^2}\left(\mathbf{\nabla}\dot{\varphi }+\ddot{\boldsymbol{A}}\right)={\mu}_0\boldsymbol{j}.$

(7.11)

Nutzt man nun die Eichfreiheit aus, so können die Potentiale so gewählt werden, dass

$\frac{\dot{\varphi}}{c^2}+\nabla \cdotp \boldsymbol{A}=0$

(7.12)

gilt, d. h. der erste Term und der erste Term in der Klammer in (7.11) heben sich weg und es bleibt nur

$-\Delta \boldsymbol{A}+\frac{\ddot{\boldsymbol{A}}}{c^2}=\square \boldsymbol{A}={\mu}_0\boldsymbol{j}.$

(7.13)

In dieser Gleichung haben wir den d‘Alembert-Operator¹

${\partial}_{\mu }{\partial}^{\mu }=-\frac{1}{c^2}\frac{\partial^2}{\partial {t}^2}+\Delta =-\square$

(7.14)

unter Verwendung der Differentialoperatoren ∂_μ und ∂^μ aus (5.32) eingeführt.

Die gerade verwendete Eichung heißt Lorenz-Eichung.² Die Eichfunktion χ(r, t) ist hier Lösung der Differentialgleichung

$\frac{1}{c^2}\ddot{\chi}-\Delta \chi =\frac{1}{c^2}\dot{\varphi}+\nabla \cdotp \boldsymbol{A}.$

(7.15)

Wir schauen uns die Bedingung (7.12) nochmals minimal umgeformt an:

$\frac{1}{c}\frac{\partial }{\partial t}\frac{\varphi }{c}+\nabla \cdotp \boldsymbol{A}=0.$

(7.16)

In dieser Form können wir erkennen, dass diese Gleichung der Bedingung entspricht, dass die kovariante Ableitung ∂_μ angewendet auf den Vierervektor

${A}^{\mu }=\left(\begin{array}{c}\varphi /c\\ {}\boldsymbol{A}\end{array}\right)$

(7.17)

Null ergeben soll. Wir nennen A^μ Viererpotential. Die Bedingungsgleichung der Lorenz-Eichung lässt sich dann als

${\partial}_{\mu }{A}^{\mu }=0$

(7.18)

schreiben. Die Lorenz-Eichung kann in jedem Bezugssystem gewählt werden. Damit ist ∂_μA^μ ein Lorentz-Skalar. Dementsprechend ist A^μ ein kontravarianter Lorentz-Tensor 1. Stufe, transformiert sich also wie die Koordinaten mit der Lorentz-Transformation.

Aus (7.10b) folgt

$-\nabla \cdotp \dot{\boldsymbol{A}}-\Delta \varphi =\frac{\rho_{\mathrm{el}}}{\varepsilon_0}.$

(7.19)

Aus ∂_μA^μ = 0 folgt durch Zeitableitung weiter

$\frac{1}{c^2}\ddot{\varphi}=-\nabla \cdotp \dot{\boldsymbol{A}}.$

(7.20)

Unter Verwendung der Gl. (7.19) und (7.20) finden wir schließlich

$\frac{1}{c^2}\frac{\partial^2}{\partial {t}^2}\frac{\varphi }{c}-\Delta \frac{\varphi }{c}=-{\partial}_{\mu }{\partial}^{\mu}\frac{\varphi }{c}=\square \frac{\varphi }{c}=\frac{1}{c}\frac{\rho_{\mathrm{el}}}{\varepsilon_0}=\sqrt{\frac{\mu_0}{\varepsilon_0}}{\rho}_{\mathrm{el}}.$

(7.21)

Im letzten Schritt haben wir dabei wieder c² = 1∕μ₀ε₀ aus (1.8) eingesetzt. Kombinieren wir (7.13) mit (7.21), so folgt daraus

$\square {A}^{\mu }=\left(\begin{array}{l}\hfill \sqrt{\frac{\mu_0}{\varepsilon_0}}{\rho}_{\mathrm{el}}\hfill \\ {}\hfill {\mu}_0\cdotp \boldsymbol{j}\hfill \end{array}\right)={\mu}_0\left(\begin{array}{l}\hfill c{\rho}_{\mathrm{el}}\hfill \\ {}\hfill \boldsymbol{j}\hfill \end{array}\right)={\mu}_0{j}^{\mu },$

(7.22)

mit dem Viererstrom j^μ, der ein kontravarianter Tensor 1. Stufe ist. Daraus ergibt sich weiter, dass

${\partial}_{\mu }{j}^{\mu }={\dot{\rho}}_{\mathrm{el}}+\nabla \cdotp \boldsymbol{j}$

(7.23)

ein Lorentz-Skalar ist. Wir können noch weitere Informationen über diesen Ausdruck gewinnen. Dazu bilden wir die Divergenz von (1.5c). Mit dem Wissen, dass ein reines Wirbelfeld stets quellenfrei ist, ergibt das

$\nabla \cdotp \left(\nabla \times \boldsymbol{B}\right)=0={\mu}_0\left(\nabla \cdotp \boldsymbol{j}+{\varepsilon}_0\nabla \cdotp \dot{\boldsymbol{E}}\right)={\mu}_0\left(\nabla \cdotp \boldsymbol{j}+{\dot{\rho}}_{\mathrm{el}}\right).$

(7.24)

Da der hintere Teil von (7.24) ein Lorentz-Skalar ist, muss diese Gleichung in allen Bezugssystemen gelten. Damit ist die Kontinuitätsgleichung

${\partial}_{\mu }{j}^{\mu }={\dot{\rho}}_{\mathrm{el}}+\nabla \cdotp \boldsymbol{j}=0$

(7.25)

begründet, die in allen Inertialsystemen gilt.

7.2.1 Wellengleichung

Wir betrachten (7.22) jetzt für den Fall, dass wir uns im Vakuum befinden. Dann gilt j^μ = 0 und damit ergibt sich die Wellengleichung

$\square {A}^{\nu }=0,$

(7.26)

deren Lösung eine Superposition ebener Wellen der Form

$f\left({x}^{\mu}\right)={\mathrm{e}}^{\left(-\mathrm{i}{k}_{\mu }{x}^{\mu}\right)}={\mathrm{e}}^{\mathrm{i}\left(\boldsymbol{k}\cdotp \boldsymbol{x}-\omega t\right)}$

(7.27)

ist. Hier tritt wieder der Viererwellenvektor aus (6.44) auf, diesmal in der kovarianten Form

${k}_{\mu }=\left(\begin{array}{c}-\omega /c\\ {}\boldsymbol{k}\end{array}\right).$

(7.28)

Damit ergibt sich für f die Gleichung:

(7.29)

Um diese Bedingung zu erfüllen, muss

$\omega =c\mid \boldsymbol{k}\mid$

(7.30)

gelten. Wir wissen das bereits aus (6.45) und auch, dass k_μ ein lichtartiger Vektor ist. Hier sehen wir, dass die Lichtartigkeit von k^μ notwendig ist, damit Photonen die für sie geltende Wellengleichung erfüllen. Es folgt dann

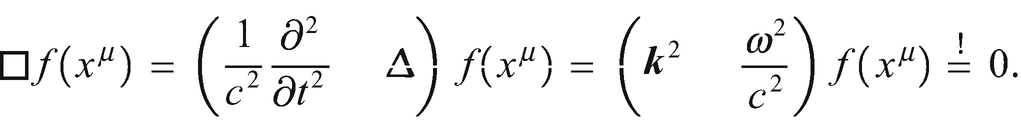
${A}^{\nu}\left({x}^{\mu}\right)=\underset{{{\mathbb{R}}}^{1,3}}{\int }{{\tilde{A}}^{\nu}}\left({k}^{\mu}\right)\delta \left[{\left({k}^0\right)}^2-{\boldsymbol{k}}^2\right]{\mathrm{e}}^{-\mathrm{i}{k}_{\mu }{x}^{\mu }}{\mathrm{d}}^4k$

(7.31)

wobei ${\tilde{A}}^{\nu}\left({k}^{\mu}\right)$ frei wählbar ist.

7.3 Formulierung mit dem Feldstärketensor

Das elektrische Feld und das Magnetfeld sind wie bereits diskutiert nicht Lorentz-kovariant. Mit (7.22) haben wir eine zu den Maxwell-Gleichungen äquivalente Beziehung gefunden, bei der die Lorentz-Kovarianz direkt ersichtlich ist. Allerdings ist sie für das Viererpotential formuliert und nicht für das elektrische und magnetische Feld. Wenn wir genauer verstehen möchten, wie sich diese in der SRT transformieren, wäre eine Formulierung, in der sie direkt auftauchen, vorteilhaft. Eine solche Formulierung werden wir uns jetzt erarbeiten.

7.3.1 Feldstärketensor

Die zentrale Größe zur kovarianten Formulierung der Elektrodynamik ist der Feldstärketensor . Um ihn zu erhalten, bilden wir die Viererrotation des Viererpotentials:

${F}_{\mu \nu}={\partial}_{\mu }{A}_{\nu }-{\partial}_{\nu }{A}_{\mu }.$

(7.32)

F_μν ist also ein antisymmetrischer kovarianter Lorentz-Tensor 2. Stufe, wobei

${A}_{\nu }={\eta}_{\mu \nu}{A}^{\mu }=\left(\begin{array}{l}\hfill -\frac{\varphi }{c}\hfill \\ {}\hfill \boldsymbol{A}\hfill \end{array}\right)$

(7.33)

gilt. Wir werten (7.32) für alle Komponenten aus. Da die Viererrotation antisymmetrisch ist, verschwinden alle Diagonalelemente

${F}_{00}={F}_{11}={F}_{22}={F}_{33}=0.$

(7.34a)

Als nächstes betrachten wir die Komponenten mit Zeit- und Raumanteil. Es ist mit (7.6)

${F}_{i0}={\partial}_i{A}_0-{\partial}_0{A}_i=-\frac{1}{c}\frac{\partial \varphi }{\partial {x}^i}-\frac{1}{c}{\dot{A}}_i=\frac{1}{c}{E}_i=-{F}_{0i}.$

(7.34b)

Für die reinen Raumkomponenten schließlich ergibt sich

${F}_{12}\ =\frac{\partial {A}_y}{\partial {x}^1}-\frac{\partial {A}_x}{\partial {x}^2}={B}_z=-{F}_{21},\$

(7.34c)

${F}_{13}\ =-{B}_y=-{F}_{31},\$

(7.34d)

${F}_{23}\ ={B}_x=-{F}_{32}.\$

(7.34e)

Als Matrix ausgeschrieben haben wir damit

${F}_{\mu \nu}=\left(\begin{array}{cccc}0& -{E}_x/c& -{E}_y/c& -{E}_z/c\\ {}{E}_x/c& 0& {B}_z& -{B}_y\\ {}{E}_y/c& -{B}_z& 0& {B}_x\\ {}{E}_z/c& {B}_y& -{B}_x& 0\end{array}\right).$

(7.35)

Weiter lässt sich der kontravariante Feldstärketensor über den allgemeinen Zusammenhang zwischen ko- und kontravarianten Tensoren definieren:

${F}^{\mu \nu}={\eta}^{\mu \alpha}{\eta}^{\nu \beta}{F}_{\alpha \beta}=\left(\begin{array}{cccc}0& {E}_x/c& {E}_y/c& {E}_z/c\\ {}-{E}_x/c& 0& {B}_z& -{B}_y\\ {}-{E}_y/c& -{B}_z& 0& {B}_x\\ {}-{E}_z/c& {B}_y& -{B}_x& 0\end{array}\right).$

(7.36)

Jetzt wo uns die ko- und kontravariante Form des Feldstärketensors zur Verfügung stehen, können wir durch Kontraktion auch wieder einen Lorentz-Skalar erhalten. Wir finden

${F}_{\mu \nu}{F}^{\mu \nu}=\frac{2}{c^2}\left({c}^2{\boldsymbol{B}}^2-{\boldsymbol{E}}^2\right).$

(7.37)

Wir verwenden dieses Ergebnis gleich weiter.

7.3.2 Dualer Feldstärketensor

Wir führen noch einen weiteren Tensor ein, um die Maxwell-Gleichungen möglichst kompakt formulieren zu können. Dazu definieren wir zunächst den total antisymmetrischen Levi-Civita-Tensor:³

(7.38)

Der Levi-Civita-Tensor ist ein Pseudotensor 4. Stufe. Bei einem Koordinatenwechsel gilt also wie üblich

${\varLambda^{\alpha}}_{\kappa }{\varLambda^{\beta}}_{\lambda }{\varLambda^{\gamma}}_{\mu }{\varLambda^{\delta}}_{\nu }{\varepsilon}^{\kappa \lambda \mu \nu}={\varepsilon}^{\alpha \beta \gamma \delta}.$

(7.39)

Mit Hilfe des Levi-Civita-Tensors können wir zusätzlich den dualen Feldstärketensor definieren als

${\hat{F}}^{\mu \nu}=\frac{1}{2}{\varepsilon}^{\mu \nu \alpha \beta}{F}_{\alpha \beta}=\left(\begin{array}{cccc}0& {B}_x& {B}_y& {B}_z\\ {}-{B}_x& 0& -{E}_z/c& {E}_y/c\\ {}-{B}_y& {E}_z/c& 0& -{E}_x/c\\ {}-{B}_z& -{E}_y/c& {E}_x/c& 0\end{array}\right).$

(7.40)

${\hat{F}}^{\mu \nu}$ ist auch ein Pseudotensor, hat also einen Vorzeichenwechsel bei Raumspiegelungen. Aus der Kontraktion von ${\hat{F}}^{\mu \nu}$ mit F_μν können wir noch einen Pseudoskalar gewinnen. Es ist nämlich

${F}_{\mu \nu}{\hat{F}}^{\mu \nu}=-\frac{4}{c}\boldsymbol{B}\cdotp \boldsymbol{E}.$

(7.41)

7.3.3 Erste Schlussfolgerungen

Unter Verwendung des Lorentz-Skalars in (7.37) und des Pseudo-Skalars in (7.41) können wir wichtige Informationen darüber gewinnen, wie sich elektrische und magnetische Felder transformieren, einfach aus der Tatsache, dass Lorentz-Skalare in allen Bezugssystemen den gleichen Zahlenwert haben. Daraus können wir direkt folgende Ergebnisse ableiten:

1.
Gilt E · B = 0, bzw. E ⊥ B in einem Inertialsystem, dann ist E · B = 0, bzw. E ⊥ B in allen Inertialsystemen.
2.
Gilt außerdem E² − c²B² > 0, dann gibt es ein System mit B' = 0, d. h. in einem bestimmten System gibt es nur ein elektrisches Feld, das Magnetfeld lässt sich wegtransformieren. Gilt dagegen E² − c²B² < 0, dann gibt es ein System mit E' = 0, d. h. in einem bestimmten System gibt es nur ein magnetisches und das elektrische Feld lässt sich wegtransformieren.
3.
Gilt E · B ≠ 0 in einem System, dann gilt es in allen Systemen, d. h. keines der Felder lässt sich wegtransformieren.
4.
Gilt E² − c²B² = 0 in einem System, dann ist |E| = c|B| in allen Systemen. Gilt zusätzlich E · B = 0, dann bilden E, B und k ein Orthogonalsystem.

7.3.4 Kovariante Form der Maxwell-Gleichungen

Mit den bisherigen Vorbereitungen haben wir nun alles zusammen, um die Maxwell-Gleichungen in kovarianter Form für die Felder zu schreiben. So lässt sich mit Hilfe des Feldstärketensors

${\partial}_{\nu }{F}^{\mu \nu}={\mu}_0{j}^{\mu }$

(7.42)

schreiben. Wir prüfen nach, dass diese Gleichung erfüllt ist.

Für μ = 0 haben wir

${\partial}_i{F}^{0i}=-\frac{1}{c}\nabla \cdotp \boldsymbol{E}={\mu}_0{j}^0={\mu}_0c{\rho}_{\mathrm{el}},\quad \mathrm{bzw}.\quad \nabla \cdotp \boldsymbol{E}=\frac{\rho_{\mathrm{el}}}{\varepsilon_0}.$

(7.43a)

Für μ = 1 ergibt sich

${\partial}_{\nu }{F}^{1\nu }=-\frac{1}{c^2}\dot{E_x}+\left(\frac{\partial {B}_z}{\partial y}-\frac{\partial {B}_y}{\partial z}\right)=-\frac{1}{c^2}\dot{E_x}+{\left(\nabla \times \boldsymbol{B}\right)}_x,$

(7.43b)

und insgesamt für μ = i ≠ 0

${\partial}_{\nu }{F}^{i\nu}=-\frac{1}{c^2}\dot{\boldsymbol{E}}+\left(\nabla \times \boldsymbol{B}\right)={\mu}_0\boldsymbol{j},\quad \mathrm{bzw}.\quad \frac{1}{\mu_0}\nabla \times \boldsymbol{B}-{\varepsilon}_0\dot{\boldsymbol{E}}=\boldsymbol{j}.$

(7.43c)

Die Gleichung ∂_νF^μν = μ₀j^μ ist also die kovariante Form der beiden Erregungsgleichungen (1.5c) und (1.5d).

Weiter lassen sich die inneren Feldgleichungen nun als

${\partial}_{\nu }{\hat{F}}^{\mu \nu}=0$

(7.44)

schreiben. Wir betrachten auch diese Gleichung im Einzelnen:

Für μ = 0 ergibt sich

${\partial}_{\nu }{\hat{F}}^{0\nu }=\nabla \cdotp \boldsymbol{B}=0.$

(7.45a)

Für μ = 1 haben wir

${\partial}_{\nu }{\hat{F}}^{1\nu }=-\frac{1}{c}\dot{B_x}+\frac{1}{c}\left(\frac{\partial {E}_y}{\partial z}-\frac{\partial {E}_z}{\partial y}\right)=-\frac{1}{c}\left[\dot{B_x}+{\left(\nabla \times \boldsymbol{E}\right)}_x\right]$

(7.45b)

und insgesamt für μ = i ≠ 0:

${\partial}_{\nu }{\hat{F}}^{i\nu}=-\frac{1}{c}\left(\dot{\boldsymbol{B}}+\nabla \times \boldsymbol{E}\right)=\mathbf{0.}$

(7.45c)

Die Gleichung ${\partial}_{\nu }{\hat{F}}^{\mu \nu}=0$ ist also die kovariante Form der beiden homogenen Maxwell-Gleichungen (1.5a) und (1.5b).

Man kann die homogenen Maxwell-Gleichungen auch mit dem normalen Feldstärketensor formulieren, muss dann aber den etwas längeren Ausdruck

${\partial}_{\lambda }{F}_{\mu \nu}+{\partial}_{\mu }{F}_{\nu \lambda}+{\partial}_{\nu }{F}_{\lambda \mu}=0$

(7.46)

in Kauf nehmen.

7.4 Wechsel des Bezugssystems

Die Transformation des Feldstärketensors erfolgt über die inverse Lorentz-Transformation:

${F}_{\mu \nu}^{\prime }={\varLambda_{\mu}}^{\alpha }{\varLambda_{\nu}}^{\beta }{F}_{\alpha \beta}.$

(7.47)

Möchte man (7.47) auswerten, so ist es praktisch, sie analog zu (5.13) in der Form F' = ΛFΛ^T zu schreiben. Beim Wechsel zwischen Bezugssystemen (Inertialsystemen) transformieren sich also die elektrischen und die magnetischen Felder zusammen. Eine getrennte Betrachtung ist daher nicht sinnvoll.

Wir betrachten als Beispiel hier wieder den Boost in ein System, das sich in x-Richtung bewegt und dessen Achsen parallel zum aktuellen System sind. Aus (7.47) ergibt sich dann

$\begin{array}{rll}& {F}_{\mu \nu}^{\prime }=& \\ {}& \left(\begin{array}{cccc}0& -{E}_x/c& -\gamma \left({E}_y/c-\beta {B}_z\right)& -\gamma \left({E}_z/c+\beta {B}_y\right)\\ {}{E}_x/c& 0& \gamma \left(-\beta {E}_y/c+{B}_z\right)& -\gamma \left(\beta {E}_z/c+\beta {B}_y\right)\\ {}\gamma \left({E}_y/c-\beta {B}_z\right)\quad & -\gamma \left(-\beta {E}_y/c+{B}_z\right)& 0& {B}_x\\ {}\gamma \left({E}_z/c+\beta {B}_y\right)& \gamma \left(\beta {E}_z/c+{B}_y\right)& -{B}_x& \quad 0\\ {}\end{array}\right)\, .\end{array}$

(7.48)

Wenn wir mit F_μν in (7.35) vergleichen, finden wir damit die Beziehungen

$\begin{array}{rllllll}{E}_x^{\prime }& ={E}_x,& {E}_y^{\prime }& =\gamma \left({E}_y- c\beta {B}_z\right),& {E}_z^{\prime }& =\gamma \left({E}_z+ c\beta {B}_y\right),& \\ {}{B}_x^{\prime }& ={B}_x,& {B}_y^{\prime }& =\gamma \left(\beta {E}_z/ c+{B}_y\right),& {B}_z^{\prime }& =\gamma \left(-\beta {E}_y/ c+{B}_z\right).\end{array}$

(7.49)

Die x-Komponenten der Felder bleiben invariant, aber die y- und z-Komponenten der Felder mischen untereinander. Auch für einen allgemeinen Boost lässt sich ein sehr kompakter Ausdruck für die transformierten Felder finden (s. Übung 7.8.1).

7.5 Feld einer bewegten Punktladung

Die gerade gewonnenen Relationen verwenden wir jetzt, um, angelehnt an [1], das Feld einer schnell bewegten Punktladung Q im System S' vom Laborsystem S aus zu untersuchen. S und Sʹ sollen sich dabei in Standardkonfiguration zueinander befinden, d. h. die Punktladung ruhe im Ursprung von Sʹ und soll sich mit Geschwindigkeit β entlang der x-Achse bewegen und die Ursprünge von S und Sʹ sollen bei t = tʹ = 0 zusammenfallen. Im Ruhsystem der Punktladung existiert nur ein statisches elektrisches Feld der Form

$\boldsymbol{E}^{\prime}\left(\boldsymbol{r}^{\prime },t^{\prime}\right)=\frac{Q}{4\pi {\varepsilon}_0}\frac{\boldsymbol{r}^{\prime }}{r^{\prime 3}}$

(7.50)

und kein Magnetfeld. Wenn wir dieses Feld jetzt im Laborsystem S untersuchen möchten, müssen wir berücksichtigen, dass sich unser Beobachtungspunkt P, der in S ruht, sich in Sʹ mit Geschwindigkeit − β bewegt, d. h. wir betrachten zwar ein zeitunveränderliches Feld aber der Beobachtungspunkt hängt von der Zeit ab.

Würden wir unseren Beobachtungspunkt im Ursprung von S wählen, so würde die Punktladung sich direkt hindurch bewegen. Um das zu vermeiden wählen wir die Bahnkurve von P in Sʹ zu

${\boldsymbol{r}}_P^{\prime}\left(t^{\prime}\right)={\left(-\beta ct\prime, b\prime, 0\right)}^{\mathrm{T}}.$

(7.51)

Aus (7.50) und (7.51) folgt $r^{\prime }=\sqrt{\beta^2{c}^2{t}^{\prime 2}+{b}^{\prime 2}}$ und damit für die Komponenten des Eʹ-Feldes

$\begin{array}{rll}{E}_x^{\prime }& =\frac{Q}{4\pi {\varepsilon}_0}\frac{-\beta ct^{\prime }}{r^{\prime 3}},& \\ {}{E}_y^{\prime }& =\frac{Q}{4\pi {\varepsilon}_0}\frac{b^{\prime }}{r^{\prime 3}},\\ {}{E}_z^{\prime }& =0.\end{array}$

(7.52)

Aus Symmetriegründen kann das elektrische Feld in P in beiden Systemen keinen z-Anteil haben. Wir können jetzt (7.49) mit der Ersetzung β ↦ − β verwenden, um ins Laborsystem umzurechnen. Da nur ${E}_x^{\prime }$ und ${E}_y^{\prime }$ nicht verschwinden, ergibt sich einfach

$\begin{array}{rllllll}{E}_x& ={E}_x^{\prime },& {E}_y& =\gamma {E}_y^{\prime },& {E}_z& =\gamma {E}_z^{\prime },& \\ {}{B}_x^{\prime }& =0,& {B}_y^{\prime }& =0,& {B}_z& =\gamma \beta {E}_y^{\prime}/ c=\beta {E}_y/ c.\end{array}$

(7.53)

Damit sind wir aber noch nicht am Ziel, denn die Komponenten des Eʹ-Feldes hängen von den Koordinaten von Sʹ ab. Wir müssen also auch diese noch transformieren über die inzwischen wohlbekannten Relationen

$\begin{array}{rll} ct^{\prime }& =\gamma \left( ct-\beta x\right)=\gamma ct,& \\ {}x^{\prime }& =\gamma \left(-\beta ct+x\right)=-\gamma \beta ct,\\ {}b& =b^{\prime }.\end{array}$

(7.54)

Damit finden wir $r^{\prime }=\sqrt{\gamma^2{\beta}^2{c}^2{t}^2+{b}^2}$ und

$\begin{array}{rll}{E}_x& =-\frac{Q}{4\pi {\varepsilon}_0}\frac{\gamma \beta ct}{{\left({\gamma}^2{\beta}^2{c}^2{t}^2+{b}^2\right)}^{3/ 2}},& \\ {}{E}_y& =\frac{Q}{4\pi {\varepsilon}_0}\frac{\gamma b}{{\left({\gamma}^2{\beta}^2{c}^2{t}^2+{b}^2\right)}^{3/ 2}},\\ {}{B}_z& =\gamma \beta {E}_y^{\prime}/ c=\beta {E}_y/ c.\end{array}$

(7.55)

Abb. 7.1 zeigt beispielhaft das elektrische Feld eines bewegten Elektrons mit b = 1a_B. Die Zeit ist in Einheiten von a_B∕c ≈ 1,77 · 10⁻¹⁹ s angegeben, d. h. der Zeit, die ein Photon benötigt, um eine Strecke der Länge des Bohr-Radius⁴

(7.56)

zu durchqueren. Wir können die Darstellung des elektrischen Feldes noch umformulieren, sodass seine Struktur deutlicher wird. Dazu berücksichtigen wir zuerst, dass der Vektor von der Punktladung zum Beobachtungspunkt im Laborsystem

$\boldsymbol{r}=\left(\begin{array}{c}-\beta ct\\ {}b\\ {}0\end{array}\right)\quad \mathrm{mit}\quad r=\sqrt{\beta^2{c}^2{t}^2+{b}^2}$

(7.57)

ist. Wir sehen daran erstens, dass

$\frac{E_x}{E_y}=\frac{r_x}{r_y}$

(7.58)

gilt, d. h. das E-Feld zeigt von der Ladung aus gesehen in r-Richtung, ist also weiter ein Radialfeld. Außerdem gilt

$b=r\sin \left(\varphi \right),$

(7.59)

wenn φ der Winkel zwischen Bewegungsrichtung der Ladung und dem Vektor zum Aufpunkt ist. Zweitens können wir mit diesem Wissen nun

$\begin{array}{rll}{r}^{\prime 2}& ={\gamma}^2{r}^2+{r}^2{\sin}^2\left(\varphi \right)\left(1-{\gamma}^2\right)={\gamma}^2{r}^2\left(1+\frac{1-{\gamma}^2}{\gamma^2}{\sin}^2\left(\varphi \right)\right)& \\ {}& ={\gamma}^2{r}^2\left(1-{\beta}^2{\sin}^2\left(\varphi \right)\right)\end{array}$

(7.60)

schreiben. Wir setzen diesen Ausdruck in die E-Feldkomponenten in (7.55) ein und es ergibt sich

$\boldsymbol{E}\left(\boldsymbol{r}\right)=-\frac{Q}{4\pi {\varepsilon}_0}\frac{{\mathrm{e}}_r}{r^2{\gamma}^2{\left(1-{\beta}^2{\sin}^2\left(\varphi \right)\right)}^{3/ 2}}.$

(7.61)

Dieser Ausdruck beschreibt das elektrische Feld mit der bewegten Punktladung als Zentrum. Dem normalen Abfall mit 1∕r² ist eine Winkelabhängigkeit überlagert. In und entgegen der Bewegungsrichtung verschwindet der Sinus-Term. Das Feld entspricht dem einer ruhenden Punktladung, abgeschwächt um den Faktor 1∕γ². Transversal zur Bewegungsrichtung ist ${\left(1-{\beta}^2{\sin}^2\left(\varphi \right)\right)}^{3/ 2}=1/ {\gamma}^3$ und das Feld ist um einen Faktor γ verstärkt im Vergleich zur ruhenden Ladung. Abb. 7.2 zeigt die zugehörigen Linien konstanter Feldstärke für verschiedene Geschwindigkeiten.

Abb. 7.1
Verlauf der Feldstärke für ein bewegtes Elektron und einen festen Beobachtungspunkt mit b = 1a_B in Einheiten der Feldstärke ${E}_{1{\mathrm{a}}_{\mathrm{B}}}={E}_0/ \left(4\pi {\varepsilon}_0{a}_{\mathrm{B}}^2\right)$

$$ {E}_{1{\mathrm{a}}_{\mathrm{B}}}={E}_0/ \left(4\pi {\varepsilon}_0{a}_{\mathrm{B}}^2\right) $$ — Abb. 7.1
Verlauf der Feldstärke für ein bewegtes Elektron und einen festen Beobachtungspunkt mit b = 1a_B in Einheiten der Feldstärke ${E}_{1{\mathrm{a}}_{\mathrm{B}}}={E}_0/ \left(4\pi {\varepsilon}_0{a}_{\mathrm{B}}^2\right)$

Abb. 7.2
Linien konstanter Feldstärke für ein gleichförmig bewegtes Elektron. Dargestellt sind Isolinien für die Feldstärken in Abständen von ein bis vier Bohr-Radien bezüglich des ruhenden Elektrons. In Bewegungsrichtung wird das Feld gestaucht, senkrecht zur Bewegungsrichtung wird es gedehnt. Alle Längenangaben sind ebenfalls in Bohr-Radien gegeben

Betrachten wir noch kurz das Magnetfeld. Der Ausdruck für B_z ist nichts anderes als das Biot-Savart'sche Gesetz.⁵^,⁶ Für das Magnetfeld einer bewegten Punktladung ergibt sich

$\boldsymbol{B}=\frac{\mu_0}{4\pi }Q\frac{\boldsymbol{v}\times \boldsymbol{r}}{r^2},$

(7.62)

d. h. hier

${B}_z=\frac{\mu_0}{4\pi }Q\frac{c\beta b}{{\left({\beta}^2{c}^2{t}^2+{b}^2\right)}^{3/ 2}}.$

(7.63)

Das entspricht bis auf relativistische Korrekturen unserem Wert

${B}_z=\frac{\mu_0}{4\pi }Q\frac{c\gamma \beta b}{{\left({\gamma}^2{\beta}^2{c}^2{t}^2+{b}^2\right)}^{3/ 2}}.$

(7.64)

7.6 Kovariante Form der Lorentz-Kraft

Mit dem Feldstärketensor lässt sich die Lorentz-Kraft kovariant formulieren:

$\frac{\mathrm{d}}{\mathrm{d}\tau }{p}_{\mu }=q{F}_{\mu \nu}{u}^{\nu }.$

(7.65)

Wir betrachten diese Gleichung genauer. Für μ = i ∈ {1, 2, 3} ergibt sich

$\frac{\mathrm{d}}{\mathrm{d}\tau }{p}_i=\gamma \frac{\mathrm{d}}{\mathrm{d}t}{p}_i=\gamma q\left(\boldsymbol{E}+\boldsymbol{v}\times \boldsymbol{B}\right)=\frac{\mathrm{d}}{\mathrm{d}\tau }{p}^i,$

(7.66a)

und für μ = 0

$\frac{\mathrm{d}}{\mathrm{d}\tau }{p}_0=-\frac{\mathrm{d}}{\mathrm{d}\tau}\left( m\gamma c\right)=-\gamma \frac{q}{c}\boldsymbol{E}\cdotp \boldsymbol{v}=-\frac{\mathrm{d}}{\mathrm{d}\tau }{p}^0,$

(7.66b)

bzw.

$\frac{\mathrm{d}}{\mathrm{d}t}\left(\gamma m{c}^2\right)=q\boldsymbol{E}\cdotp \boldsymbol{v}=\frac{\mathrm{d}W}{\mathrm{d}t}=q\boldsymbol{E}\cdotp \frac{\mathrm{d}\boldsymbol{s}}{\mathrm{d}t}.$

Es gilt also

$\mathrm{d}W=q\boldsymbol{E}\cdotp \mathrm{d}\boldsymbol{s},$

(7.67)

d. h. der Energiezuwachs ist gleich der vom elektrischen Feld geleisteten Arbeit. Alternativ lässt sich schreiben

$\frac{\mathrm{d}}{\mathrm{d}\tau }{p}^{\mu }={F}^{\mu }=q{\eta}^{\mu \alpha}{F}_{\alpha \nu}{u}^{\nu },$

(7.68)

mit der Minkowski-Kraft F^μ. Wir definieren zusätzlich die Minkowski-Kraft-Dichte f^μ, indem wir die Ersetzungen q ↦ ρ_el, qu^ν ↦ ρ_elu^ν = j^ν vornehmen. Wir erhalten dann

${f}^{\mu}\equiv {\eta}^{\mu \alpha}{F}_{\alpha \nu}{j}^{\nu }=\left(\begin{array}{c}\frac{1}{c}\boldsymbol{j}\cdotp \boldsymbol{E}\\ {}{\rho}_{\mathrm{el}}\boldsymbol{E}+\boldsymbol{j}\times \boldsymbol{B}\end{array}\right).$

(7.69)

7.7 Energie-Impuls-Tensor des elektromagnetischen Feldes

Aus der klassischen Elektrodynamik ist bekannt, dass elektromagnetische Felder, ähnlich wie das Gravitationsfeld, einen Energieinhalt haben. Zur Beschreibung dieser Energie führen wir jetzt den Energie-Impuls-Tensor ein.

7.7.1 Einführung des Energie-Impuls-Tensors

In der klassischen Elektrodynamik sind die nicht Lorentz-kovarianten Größen Feldenergie w als

$w=\frac{1}{2}\left({\varepsilon}_0{\boldsymbol{E}}^2+\frac{1}{\mu_0}{\boldsymbol{B}}^2\right)$

(7.70)

und der Poynting-Vektor (Energiestrom) S als

$\boldsymbol{S}=\frac{1}{\mu_0}\boldsymbol{E}\times \boldsymbol{B}$

(7.71)

definiert. Als entsprechende Lorentz-kovariante Größe definieren wir den Energie-Impuls-Tensor über

${T}^{\mu \nu}=\frac{1}{\mu_0}\left({\eta}^{\mu \beta}{F}_{\beta \alpha}{F}^{\alpha \nu}+\frac{1}{4}{\eta}^{\mu \nu}{F}_{\alpha \beta}{F}^{\alpha \beta}\right).$

(7.72)

Dabei ist ${F}_{\alpha \beta}{F}^{\alpha \beta}=2\left({\boldsymbol{B}}^2-{\boldsymbol{E}}^2/ {c}^2\right)$ nach (7.37). Wir werden diese Form gleich motivieren. Vorher betrachten wir die einzelnen Komponenten dieses Tensors aber genauer. Dazu werten wir die Komponenten von F_μαF^αν aus.

Für μ = ν = 0 ergibt sich einfach

${F}_{0\alpha }{F}^{\alpha 0}=\frac{{\boldsymbol{E}}^2}{c^2},$

(7.73a)

für μ = 0, ν = i

${F}_{0\alpha }{F}^{\alpha i}=\frac{1}{c}{\left(\boldsymbol{E}\times \boldsymbol{B}\right)}_i=\frac{\mu_0}{c}{S}_i$

(7.73b)

und für μ = i, ν = j

${F}_{i\alpha}{F}^{\alpha j}=\frac{E_i{E}_j}{c^2}+{B}_i{B}_j-{\delta}_i^j{\boldsymbol{B}}^2.$

(7.73c)

Mit diesen Ergebnissen können wir nun die Komponenten von T_μ^ν bestimmen:

${T_0}^0\ =\frac{1}{\mu_0}\left[-\frac{1}{c^2}{\boldsymbol{E}}^2-\frac{1}{2}\left({\boldsymbol{B}}^2-\frac{{\boldsymbol{E}}^2}{c^2}\right)\right]=-\frac{1}{2{\mu}_0}\left(\frac{{\boldsymbol{E}}^2}{c^2}+{\boldsymbol{B}}^2\right)=-w,\$

(7.74a)

${T}^{0i}\ =-\frac{1}{c}{S}_i={T}^{i0},\$

(7.74b)

${T}^{ij}\ ={G}^{ij}.\$

(7.74c)

Dabei ist G^ij der Maxwell'sche Spannungstensor mit

${G}^{ij}=\frac{E_i{E}_j}{c^2}+{B}_i{B}_j-\frac{1}{2}{\delta}^{ij}\left({\boldsymbol{B}}^2+\frac{{\boldsymbol{E}}^2}{c^2}\right).$

(7.75)

Insgesamt erhalten wir in Matrixschreibweise:

${T}^{\mu \nu}=\left(\begin{array}{cc}-w& -{\boldsymbol{S}}^{\mathrm{T}}/c\\ {}-\boldsymbol{S}/c& {G}^{ij}\end{array}\right).$

(7.76)

7.7.2 Interpretation des Energie-Impuls-Tensors

Um die Bedeutung des Energie-Impuls-Tensors klar zu machen, betrachten wir einen kleinen Quader in einer elektromagnetischen Welle, die sich in x-Richtung ausbreitet, d. h. für den Poynting-Vektor ergibt sich S = S_xe_x. Dann gilt:

(7.77a)

bzw.

$\frac{F_x}{\Delta A}={p}_S=\frac{1}{c}{S}_x=\frac{\Delta {p}_x}{\Delta \mathrm{A}\Delta \mathrm{t}}=c\frac{\Delta {p}_x}{\Delta V},$

(7.77b)

wobei p_S den Strahlungsdruck bezeichnet. Weiter gilt

$\frac{\Delta {p}_x}{\Delta V}={\varPi}_x,$

(7.78)

mit der Impulsdichtekomponente Π_x. Allgemein ist die Impulsdichte definiert über

$\boldsymbol{\varPi} =\frac{1}{c^2}\boldsymbol{S}.$

(7.79)

Der Maxwell'sche Spannungstensor G^ij bestimmt den Druck, den eine elektromagnetische Kraft auf ein Volumenelement, hier den kleinen Quader, ausübt:

$\frac{\boldsymbol{F}}{\Delta A}=-\boldsymbol{G}\cdotp \boldsymbol{n},$

(7.80)

mit dem Normalenvektor n senkrecht zum Flächenelement Δ A. Daraus folgt

$\mathrm{d}\boldsymbol{F}=-\boldsymbol{G}\mathrm{d}\boldsymbol{f},$

(7.81)

mit df = ndA. Die Diagonalelemente von G^ij sind Drücke bzw. Zugspannungen, die Nebendiagonalelemente sind Scherspannungen (s. Abb. 7.3). Die Dimension von T^μν ist also gleich Energie durch Volumen, bzw. Kraft pro Fläche also Druck.

Abb. 7.3
Interpretation des Maxwell'schen Spannungstensors. G^ij ist die Spannung, d. h. die Kraft pro Fläche, in Richtung e_j auf die Fläche mit Normalenrichtung e_i. Die Diagonalelemente sind Drücke, bzw. Zugspannungen, die Nebendiagonalelemente sind Scherspannungen

Der Energie-Impuls-Tensor hängt eng mit der Minkowski-Kraft-Dichte zusammen. Um das zu sehen, verwenden wir (7.42) um (7.69) als

${f}^{\mu }=\frac{1}{\mu_0}{\eta}^{\mu \alpha}{F}_{\alpha \nu}{\partial}_{\lambda }{F}^{\nu \lambda}$

(7.82)

umzuschreiben. Als nächstes ziehen wir die Ableitung ∂_λ vor F_αν und ziehen den dann aufgrund der Produktregel neu auftauchenden Term wieder ab:

${f}^{\mu }=\frac{1}{\mu_0}{\eta}^{\mu \alpha}{\partial}_{\lambda}\left({F}_{\alpha \nu}{F}^{\nu \lambda}\right)-\frac{1}{\mu_0}{\eta}^{\mu \alpha}{\partial}_{\lambda}\left({F}_{\alpha \nu}\right){F}^{\nu \lambda}.$

(7.83)

Den zweiten Term können wir weiter umformen. Dazu verwenden wir die Antisymmetrie des Feldstärketensors und schreiben

$\begin{array}{rll}\frac{1}{\mu_0}{\eta}^{\mu \alpha}{\partial}_{\lambda}\left({F}_{\alpha \nu}\right){F}^{\nu \lambda}& =\frac{1}{2{\mu}_0}{\eta}^{\mu \alpha}\left({F}^{\nu \lambda}{\partial}_{\lambda }{F}_{\alpha \nu}+{F}^{\lambda \nu}{\partial}_{\nu }{F}_{\alpha \lambda}\right)& \\ {}& =\frac{1}{2{\mu}_0}{\eta}^{\mu \alpha}{F}^{\nu \lambda}\left({\partial}_{\lambda }{F}_{\alpha \nu}+{\partial}_{\nu }{F}_{\lambda \alpha}\right).\end{array}$

(7.84)

Unter Verwendung von (7.46) können wir den Klammerausdruck ersetzen und erhalten

$\begin{array}{rll}\frac{1}{2{\mu}_0}{\eta}^{\mu \alpha}{F}^{\nu \lambda}\left({\partial}_{\lambda }{F}_{\alpha \nu}+{\partial}_{\nu }{F}_{\lambda \alpha}\right)& =-\frac{1}{2{\mu}_0}{\eta}^{\mu \alpha}{F}^{\nu \lambda}{\partial}_{\alpha }{F}_{\nu \lambda}& \\ {}& =-\frac{1}{4{\mu}_0}{\eta}^{\mu \alpha}{\partial}_{\alpha}\left({F}^{\nu \lambda}{F}_{\nu \lambda}\right).\end{array}$

(7.85)

Im zweiten Schritt haben wir dabei wieder die Produktregel berücksichtigt. Damit haben wir jetzt insgesamt

$\begin{array}{rll}{f}^{\mu }& =\frac{1}{\mu_0}{\eta}^{\mu \alpha}\left[{\partial}_{\lambda}\left({F}_{\alpha \nu}{F}^{\nu \lambda}\right)+\frac{1}{4}{\partial}_{\alpha}\left({F}^{\nu \lambda}{F}_{\nu \lambda}\right)\right]& \\ {}& =\frac{1}{\mu_0}{\eta}^{\mu \alpha}\left[{\partial}_{\lambda}\left({F}_{\alpha \nu}{F}^{\nu \lambda}\right)+\frac{1}{4}{\delta}_{\alpha}^{\lambda }{\partial}_{\lambda}\left({F}^{\nu \kappa}{F}_{\nu \kappa}\right)\right]\\ {}& =\frac{1}{\mu_0}{\partial}_{\lambda}\left({\eta}^{\mu \alpha}{F}_{\alpha \nu}{F}^{\nu \lambda}+\frac{1}{4}{\eta}^{\mu \lambda}{F}^{\nu \kappa}{F}_{\nu \kappa}\right)\end{array}$

(7.86)

bei Verwendung von ${\eta}^{\mu \alpha}{\delta}_{\alpha}^{\lambda }={\eta}^{\mu \lambda}$ Durch Vergleich mit (7.72) erkennen wir die Relation

${f}^{\mu }={\partial}_{\lambda }{T}^{\mu \lambda},$

(7.87)

mit dem Vierergradienten ∂_λ aus (5.40). Die Minkowski-Kraft-Dichte ist also die Divergenz des Energie-Impuls-Tensors. Um die Bedeutung dieses Zusammenhanges zu verstehen, betrachten wir ihn wieder komponentenweise.

$\frac{\partial w}{\partial t}+\nabla \cdotp \boldsymbol{S}\ =-\boldsymbol{j}\cdotp \boldsymbol{E}\ \mathrm{f}\ddot{\mathrm{u}}\mathrm{r}\, \mu =0,\quad$

(7.88a)

$\frac{1}{c^2}\frac{\partial {S}_i}{\partial t}+\nabla \cdotp {\boldsymbol{G}}_i\ ={\rho}_{\mathrm{el}}{E}_i+{\left(\boldsymbol{j}\times \boldsymbol{B}\right)}_i\ \mathrm{f}\ddot{\mathrm{u}}\mathrm{r}\, \mu =i.\quad$

(7.88b)

Dabei steht der Index i in G_i für die entsprechende Zeile und in den anderen Ausdrücken für die jeweilige Komponente.

Betrachtung im Vakuum

Im Vakuum ist j^μ = 0, also auch f^μ = 0 und daher ∂_νT^μν = 0. Es existieren dann insgesamt vier Kontinuitätsgleichungen:

$\begin{array}{rll}& \frac{\partial \omega }{\partial t}+\nabla \cdotp \boldsymbol{S}=0,& \\ {}& \frac{1}{c^2}\frac{\partial {S}_i}{\partial t}+\nabla \cdotp {\boldsymbol{G}}^i=0,\end{array}$

(7.89)

mit (1∕c²)∂S_i∕∂t = ∂Π_i∕∂t. G^ij beschreibt also eine Impulsstromdichte.

Ausblick auf die ART

In der ART spielt der Energie-Impuls-Tensor für uns eine viel wichtigere Rolle als in der SRT. Allerdings geht es uns dort nicht um den Energie-Impuls-Tensor der Elektrodynamik, sondern um einen analogen Tensor für die Gravitation. In Situationen, in denen sowohl Elektrodynamik als auch Gravitation wichtig sind, kann man T^μν aufspalten über

${T}^{\mu \nu}={T}_{\mathrm{em}}^{\mu \nu}+{T}_{\mathrm{mat}}^{\mu \nu},$

(7.90)

wobei ${T}_{\mathrm{em}}^{\mu \nu}$ nur elektromagnetische Felder beschreibt und ${T}_{\mathrm{mat}}^{\mu \nu}$ Materie, also Ladungen und Ströme und auch andere Beiträge, etwa Teilchenfelder und Gravitationsfelder. Solche Fälle werden wir allerdings nicht betrachten.

Wir können uns für die ART aber dennoch bereits die grundlegende Struktur von Energie-Impuls-Tensoren merken. Es ist stets

$\boldsymbol{T}=\left(\begin{array}{ll}\hfill \mathrm{Energiedichte}\hfill & \hfill \mathrm{Str}\ddot{\mathrm{o}} \mathrm{me}\hfill \\ {}\hfill \mathrm{Str}\ddot{\mathrm{o}} \mathrm{me}\hfill & \hfill \mathrm{Druck}\ \mathrm{und}\ \mathrm{Scherspannungen}\hfill \end{array}\right).$

(7.91)

Dabei bemerken wir, dass Energiedichten und Drücke die gleichen physikalischen Einheiten haben, was uns an verschiedenen Stellen immer wieder begegnen wird.

7.8 Übungsaufgaben

7.8.1 Feldtransformation bei allgemeinem Boost

Zeigen Sie, dass für einen allgemeinen Boost aus (3.31) die transformierten Felder

$\boldsymbol{E}^{\prime }=\gamma \left(\boldsymbol{E}+c\boldsymbol{\beta} \times \boldsymbol{B}\right)-\frac{\gamma^2}{\gamma +1}\boldsymbol{\beta} \left(\boldsymbol{\beta} \cdotp \boldsymbol{E}\right)$

(7.92a)

und

$\boldsymbol{B}^{\prime }=\gamma \left(\boldsymbol{B}-\boldsymbol{\beta} \times \boldsymbol{E}/ c\right)-\frac{\gamma^2}{\gamma +1}\boldsymbol{\beta} \left(\boldsymbol{\beta} \cdotp \boldsymbol{B}\right)$

(7.92b)

resultieren.