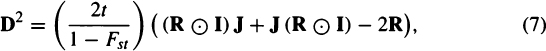263Chapter 10
A Post-Neumann History of Biological and Genetic Distance Studies in Bioarchaeology
Lyle W. Konigsberg
I. INTRODUCTION
This chapter reviews briefly the circumstances surrounding the shift from “varietal thinking” to population genetic-based approaches to archaeological skeletal samples. It then turns to the meat of the chapter—a history of biological distance analysis within bioarchaeology in the last half of the previous century. Before starting this adventure, I should lay some preliminary ground rules and sketch the focus and a broad outline for this chapter.
As concerns rules, I will, whenever possible, cite only published works, avoiding the many dissertations, theses, and other unpublished documents that are difficult for many readers to obtain. I make no claim that the history I give here is uniform in focus and degree of coverage. My personal bias (through experience) has been toward eastern U.S. bioarchaeology and, as a consequence, my coverage of other areas often borders on the paltry. I can only apologize at the outset for what may appear as a slight to researchers who work in other areas. As one of these researchers (Jantz, 1973) is just a few doors down the hall from me, I can assure him and the many others that any exclusions are born of my own ignorance. They are not comments on the quality of the work. While on the subject of focus, I should also make a few comments about the level of mathematical sophistication assumed for this chapter. History and mathematics are not often 264a comfortable mix, and I have tried to avoid the use of mathematical concepts here. That said, I must admit that biological distance analysis and paleodemography are probably the two most mathematical branches of bioarchaeology, and it simply is not possible to discuss the history of either without some recourse to equations. I have learned over the years that equations are best left to “boxed text” that the reader can choose to ignore. This is not a textbook, and as such the “box” is not an option. I do provide a very brief appendix both to correct my own previous errors (of which, sadly, there are more than I might care to admit) and to provide in one place some information that may be of use to those who do biodistance analysis using archaeological skeletal material.
II. THE END OF THE BEGINNING
As described elsewhere, Della Collins Cook discussed the development of the “biological distance” concept within American bioarchaeology up through the 1950s and 1960s. As she points out, the period following World War II was epitomized by the work of Georg K. Neumann on “varieties” among American Indians. Although his seminal work on American Indian variation (Neumann, 1952) was titled “Archaeology and Race in the American Indian,” it is clear that Neumann viewed Native American prehistoric biological variation as reflecting genetic “types” rather than “races.” While Neumann’s understanding of the works of Fisher, Haldane, and Wright on population genetic theory was clearly extremely limited, Neumann did attempt to objectively classify prehistoric Native American skeletal remains. Neumann’s background in multivariate statistical analysis was also limited to nonexistent, and it was on this front that his work would ultimately fall out of favor. The seeds of discontent were also sowed by the development of the “New Archaeology,” especially the “New Physical Anthropology” (Washburn, 1951).
A mere 14 years after the publication of Neumann’s seminal work, Joseph K. Long (1966) published a devastating statistical critique of Neumann’s typological views on Native American prehistoric biological variation. Specifically, Long applied a multiple discriminant analysis to craniometric data from 151 male adults from archaeological contexts. Long attempted to reclassify the crania into Neumann’s “Lenapid,” “Walcolid,” “Iswanid,” and “Otamid” types, but found that overall the classification was rather poor and was in part driven by whether crania bore artificial cranial “deformation.” To quote from Long (1966:462): “Nothing here supports Neumann’s (1952) explanation of subgroups based on large-scale migrations into the area.” Long (1966:463) argued for using discriminant function analysis on a more regional level, stating that “this approach assumes a rejection of the simplistic picture of race and culture in North America.”
265Neumann and his students generally reacted to Long’s (1966) article by either dismissing its results in a sentence or two or by outright ignoring its existence. In her monograph on the Oneota, Elizabeth Glenn (1974) wrote that “one of the lines of procedure in this analysis will be to test the cranial data of the different Oneota foci to determine to what extent they coincide with Neumann’s varietal groupings of the area.” One hundred and forty pages later, on the last page of her text, Glenn (1974:141) notes: “It might be added that one might wonder about the utility of the varietal approach, as such, with this population. Not only do the varieties not ‘describe’ all segments of the Oneota population, but also, the key traits associated with the differentiation of these varieties have not been the critical discriminants in these analyses.” But she then continues that “… the value of the populations on which the varieties are based … are unquestionably valuable to the consideration of this [the Oneota] population.” Curiously, Glenn chose not to cite Long (1966), despite the fact that her 1974 monograph is based on her 1971 doctoral dissertation written under Neumann at a time when Long’s work was well known and easily available. Robbins and Neumann (1972), in a lengthy tome (the bulk of which is taken up by 285 tables) on the Fort Ancient Culture dispatch with Long’s work in one sentence that ignores the results of his work: “In testing the validity of Neumann’s varietal typology, Long (1966:235) uses multiple discriminant analyses of specific measurements and indices to establish a metrical classification of the varietal groupings.” This is the sole reference to Long’s article in Robbins and Neumann (1972).
While it is not on the surface clear how Neumann and his students could simply choose to ignore Long’s article, it is important to realize that Neumann was an established researcher, while Long was just beginning his own anthropological career. Long’s publication was based on his M.A. thesis from the University of Kentucky, written in 1964 under Dr. Charles E. Snow. Snow himself, as a student of Hooton’s, initially subscribed to a “varietal” classification of prehistoric human skeletal remains from the eastern U.S. By the 1970s, when Snow published his last monograph (Snow, 1974) he had clearly rejected a Neumann-type approach, but at the time that Long was writing his thesis there is no particular reason to suspect that Snow had departed from typological thinking. Long continued his career in anthropology after his discriminant function analyses, but he obtained his Ph.D. in medical anthropology at UNC–Chapel Hill (Long, 1973) and never returned to skeletal biology/bioarchaeology. He is probably best remembered as the founder of the Society for the Anthropology of Consciousness. Regardless of Neumann and his student’s reaction (or lack thereof) to Long’s publication, with the advent of the “New Archaeology” the time was ripe for change at the end of the 1960s. By the beginning of the next decade there were a host of dissertations that used biological distance analysis within archaeological contexts to address issues of past population structure. These studies were radical departures from their predecessors, which had addressed issues of mass migration and 266definition of “varietal types” and “races.” Buikstra (1979:226) summarized this shift specifically within Hopewell (U.S. midwestern Middle Woodland) archaeology in a section she titled “Georg Neumann/Charles Snow: The End of an Era.” Although our discussion until this point has focused on the eastern United States, and consequently on Georg Neumann, this shift occurred for other regions of the world [see, e.g., Van Gerven et al. (1973) for Nubia and Rightmire (1970) for South Africa]. In a curious attempt to rewrite history, Armelagos and Van Gerven (2003:58) argued that within skeletal biology “typology continues despite our understanding of adaptation and the processes of morphological change.” They thus appear to reject the idea that the legacy of Neumann has ended. As should be clear from the remainder of this chapter, I disagree with Armelagos and Van Gerven’s view of the recent history of biological distance studies.
III. THE RISE OF MULTIVARIATE ANALYSIS: IN SITU DEVELOPMENT OR MIGRATION OF PEOPLE?
Following on the heels of “varietal” and “racial” approaches, many biodistance studies were undertaken in the 1970s to determine whether archaeologically or ethnohistorically defined cultures arose by in situ development or by external migration into the region of interest. Unlike the earlier “varietal” studies, which had used only rudimentary statistical approaches, these more modern studies tended to use multivariate approaches—either discriminant function analysis (i.e., canonical variates or Mahalanobis distance analysis) for metric traits or (typically) Smith’s Mean Measure of Divergence (MMD) for discrete traits. Overwhelmingly, the osteological evidence presented was in favor of local continuity of archaeologically defined cultures (Bennett, 1973a; Buikstra, 1976, 1977; Droessler, 1981; El-Najjar, 1978; Jacobs, 1993; Mackey, 1977; Molto, 1983; Reichs, 1984; Sciulli and Mahaney, 1986; Suchey, 1975; Van Gerven et al., 1973; Wolf, 1977). This was not, however, an absolutely universal finding. Turner (1980:26) noted that the results of his analysis of discrete traits “clearly support the notion that the development of the Mississippian culture period in northern Alabama involved the movement of people into the area, either replacing, displacing, or hybridizing the descendants of previous inhabitants.” Berryman (1980:12) similarly cited craniometric evidence for a “migration of Middle Tennessee people into the eastern Tennessee area” at or prior to the emergence of Mississippian. And in areas where there was well-documented archaeological or ethnohistoric evidence for migration, such as the Tiwanaku “colonization” in Peru (Blom et al., 1998), the spread of Zapotecans during the formative period (Christensen, 1998), and the intrusion of the Oneota into central Illinois (Steadman, 1998), bioarchaeologists have cited biodistance evidence to 267support these large-scale migrations. Further, as Adams and colleagues (1978) note in “a world tour of migration theories” (which curiously lacks Oceania) “migration theory obviously has a higher probability value in island environments than elsewhere, for here diffusion over any distance must necessarily also involve migration.” As a consequence, biodistance studies focused on Oceania [amply reviewed in Pietrusewsky’s (2000) chapter] have always been framed around various migration hypotheses.
From a historical standpoint, it is particularly interesting to look at the accumulation of biodistance evidence against large-scale migrations during the 1970s and 1980s. As Adams et al. (1978) note, migration “theories” were largely on the wane by the 1970s. They view this development as a logical result of, among other things, the rise of positivist thought (and decline of specific historicity) in archaeology that came with the advent of the “New Archaeology.” They go on to write (p. 516) “archaeology’s retreat from migrationism has had a profound impact on current trends in Amerindian craniometry” and (p. 523) “whether one views physical anthropology as a ‘handmaiden to human history’ or worries that ‘we have somehow drifted farther and farther away from prehistory,’ our views of history continue to effect the methods and goals of our research.” At the end of their review Adams and co-workers (1978) sketch “the beginnings of scientific migrationism,” but in truth interest in any form of a migration resurrection has remained tepid, at best, until Anthony’s (1990) sounding of the waters a decade ago. It seems almost inconceivable that the biodistance studies of the 1970s and 1980s could, as a group, have come to wrong answers to the migration versus in situ development question. However, aside from any platitudes about “statistics never telling lies,” what is very curious about these many studies is that they never established any particular methodology or guidelines for using biodistance data to answer questions about migration. Although the studies often appealed to population genetic analyses of living groups, there were no methodological or theoretical developments along the lines now presented in the modern human origins debate (Cole, 1996; Konigsberg et al., 1994; Relethford, 2001; Relethford and Harpending, 1994; Rogers, 1995; Waddle, 1994a,b), and the studies were often unclear on whether they had provided necessary (or simply sufficient) evidence for biological continuity of archaeological cultures. With the advent of direct genetic assays for prehistoric skeletal remains [see O’Rourke et al. (2000), Stone (2000), and later], we are beginning to return to the old migration questions, and there is likely to be an increase in such studies over the foreseeable future. Clearly, from a modeling/statistical standpoint there is a need to return to the question of in situ development versus long-range migration. This is made quite clear in Alan Rogers’ (1995) article “How Much Can Fossils Tell Us about Regional Continuity?” Rogers surmises that it would be very difficult in a statistical sense to provide evidence from fossil material for regional continuity. If this is the case, then why were bioarchaeological studies from the 1970s 268and 1980s so successful in demonstrating (repeatedly) that there was regional continuity? Sampling issues alone, a hoary issue in paleoanthropology, do not appear to explain this divergence.
IV. EXAMINING LOCAL MIGRATION
While the discussion over in situ development versus migration was playing out in the literature, a new bioarchaeological focus arose during the early 1970s. With the publication of Lane and Sublett’s (1972) “Osteology of Social Organization: Residence Pattern” article in American Antiquity, the study of short-distance migration (Anthony, 1990), more specifically mating/residence practices, became a legitimate domain of study. Lane and Sublett argued that cranial discrete traits could be used to test for post-“marital” residence pattern by comparing biological distances across cemeteries within males and within females. Specifically, they stated that if residence patterns were female–female based (i.e., uxorilocal), they would expect cemeteries to be heterogeneous in female comparisons and homogeneous in male comparisons. Alternatively, if residence patterns were male–male based (i.e., virilocal), they would expect cemeteries to be heterogeneous in male comparisons and homogeneous in female comparisons. In either case (uxorilocal or virilocal), they predicted that within cemetery comparisons of males with females would demonstrate heterogeneity. Although these postulates could have been motivated through population genetic theory and models [and indeed were in Lane’s (1977) dissertation], Lane and Sublett chose to support their suggested patterns by analogy to expected material culture distributions in archaeological data [see, e.g., Longacre (1964) and Deetz (1968)]. As they were publishing in American Antiquity this was a fairly logical choice for citation. The Lane and Sublett model was ultimately based on the idea that if one looked only at skeletons from adults, then if males had a higher migration rate than females this would homogenize males across sites (because any cemetery would include migrant males). As an interesting historical sidebar, it should be mentioned that Corruccini (1972), in the same year as Lane and Sublett, published an analysis of prehistoric and historic Pueblo skeletal material that used the same logic as the Lane–Sublett model. To quote from Corruccini:
… the Pueblo female samples are more tightly bound by a considerable margin than the males. The Pueblo sex differences … point to a proportionality between amount of genetic differentiation and amount of mating and residence flexibility, the latter factor being connected with the matrilocal patterns mentioned earlier. (Corruccini, 1972:386)
Following quickly on Lane and Sublett’s publication there were additional extensions given in the literature. Spence (1974a) extended the Lane–Sublett model by also considering the effect of migration on within-sample variation in 269discrete traits by sex. He suggested that within a single cemetery male homogeneity would be expected if residence were based virilocally, whereas the opposite (female homogeneity) would be expected if residence were based uxorilocally. Like Lane and Sublett, Spence also motivated his model by analogy to the distribution of archaeological artifacts. In the same year, he (Spence, 1974b) also published a test case using within-sample variances by sex for craniometric data. Buikstra (1980) drew explicitly on the Lane–Sublett model, but also added an additional layer. She looked at discrete trait biodistances between mounds by sex within a single site (Pete Klunk mounds). Addition of the between mound component allowed her to contrast expectations depending on whether the mounds were used contemporaneously or in serial fashion. Other authors (Birkby, 1982; Bondioli et al., 1986; Droessler, 1981; Kennedy, 1981) also drew on the Lane–Sublett model, or its logic, to make statements about past residential patterns.
It is interesting to note that the Lane–Sublett model grew out of analogy to the archaeological record. Like the antimigrationist paradigm of the 1970s and 1980s in bioarchaeology, which came fairly directly from the “New Archaeology,” the focus of the Lane–Sublett model on short-distance migration was also born of the “New Archaeology.” Like the antimigrationist paradigm, the Lane–Sublett model could also be critiqued on the grounds that it had little supporting theory. It was, as well, belabored by a host of implicit but unstated assumptions. Brenda Kennedy (1981) first pointed out a potential shortcoming of the Lane–Sublett model in that the predictions were ambiguous in certain settings. For example, in discussing a patrilocal (really, virilocal) pattern Kennedy wrote that:
It may be assumed that the hypothetical “first group of men to engage in these marriage practices” formed a relatively homogenous group, since up to this point no exogamic unions had occurred. However, what of the second, third, and fourth generations of males taking part in these customs? Given the input into the male gene pool of the genes of their mothers who have come from a variety of sources, do the males remain a relatively homogenous group? (Kennedy, 1981:28)
The answer to this ambiguity lay in reformulating the predictions of the Lane–Sublett model on the basis of population genetic models (Konigsberg, 1988), a subject taken up in the Appendix. The conundrum in the Lane–Sublett model is that the effects of differential migration by sex are only displayed in the current postmigration generation because autosomal alleles are assigned randomly to the sexes in the next generation. The stability of the Lane–Sublett model was also challenged by an influential article by Cadien et al. (1974) in which they argued that the time depth represented within skeletal series could affect interpretations adversely. More recently, the simple-minded approaches I took in the late 1980s to the Lane–Sublett model have been rightly critiqued by others (Aguiar and Neves, 1991; Williams-Blangero and Blangero, 1990). Among these critiques, I do not include Tyrrell’s (2000:299), who has referred to my dissertation as 270“a self-defeating exercise.” He objected to my eliminating discrete traits that appeared to be dependent on sex of the individual as “artificially skewing the frequency differences.” He apparently did not read my dissertation particularly closely, as I wrote:
Clearly, only traits which are genetically or physiologically dependent on age or sex should be eliminated, and it may therefore be desirable in some instances to form grand samples across populations in order to reduce the effect of extraneous variation due to residential practices. (Konigsberg, 1987:113)
V. EXAMINING TEMPORAL VARIATION
Many studies have attempted to correlate biological variation with the passage of time in archaeological contexts. By and large, these studies have started from the premise that the local temporal sequences represent in situ development. Consequently, long-range migration is assumed to have occurred at a trivial or nonexistent rate. Often this assumption is tested in some way, but in other analyses it stands as a tacit assumption. For example, Larsen (1982) has compared bone biomechanical properties for preagricultural and postagricultural groups from the Georgia Bight and writes (Larsen and Ruff, 1991) that “given the well-established record of cultural continuity in prehistoric Georgia coastal populations, especially during prehistory (see discussion in Larsen, 1982), it is appropriate to suggest that biological change in this region did not likely result from population replacement.” This is taken as an untested assumption (to my knowledge, there are no biological distance or ancient DNA studies for the prehistoric Georgia Bight), and the skeletal material is then used to document what are generally viewed as plastic responses to environmental change rather than the result of directional evolutionary forces (such as gene flow or selection). Larsen (1997) gives numerous examples of bioarchaeological studies that have suggested plastic responses of bones through temporal sequences, with the prime mover usually being the adoption of agriculture. I will not comment on the history of such studies here, as they are outside the direct purview of biological distance analysis.
There are two research topics where temporal variation has, pretty much by necessity, been explained in evolutionary terms. First, in geographic areas such as parts of the American Great Plains, where there is no clear evidence for short-term environmental change, gene flow or other evolutionary arguments have taken priority (Jantz, 1973; Jantz and Willey, 1983; Key, 1983; Key and Jantz, 1981). Second, changes in dental size (typically dental reduction) usually must be explained using some form of evolutionary mechanism, as tooth size is unlikely to exhibit plastic responses to environmental change. Guagliardo (1982) suggested that tooth size could be modulated by interuterine stress and 271that differential mortality associated with the stress could then lead to different average tooth size across age classes. As a consequence, differences in adult tooth size across age cohorts could be interpreted either as a result of selection (Perzigian, 1975) or, following Guagliardo, as evidence for interuterine stress followed by differential mortality. Although Guagliardo’s argument could be extended to suggest some form of plastic response in dental size, if there is a nonzero genetic correlation between stress-induced mortality and stress-induced interuterine dental size reduction, then the appropriate quantitative genetic model would be one of evolution by natural selection on correlated characters. In this case, the direct selection operates through stress-induced mortality, whereas selection for reduced dental size comes as a correlated response. Less complicated selection models have been given to explain the almost universal reduction in dental size over the course of human history and prehistory; these are reviewed briefly in Larsen (1997:245). One of these models, the “probable mutation effect” (Brace, 1964), has been a source of long-term debate, which is discussed next.
VI. POPULATION GENETICS AND BIODISTANCE
It is exceedingly difficult to pinpoint when population and quantitative genetic theory first made their entrada into bioarchaeology. As sketched out earlier, many of the methods and debates in biodistance analysis of the 1970s and 1980s were motivated by developments from the “New Archaeology.” As such, they did not make explicit use of genetic theory. Much as I might like to claim some historical priority from my dissertation work (Konigsberg, 1987), the roots of genetic theory in biodistance analysis run much deeper. While it was resoundingly criticized in some quarters, McKee’s (1984) deterministic computer simulation of dental size reduction via the probable mutation effect represents an early explicit use of models from the great population geneticist of the last century, Sewall Wright. But there are earlier threads than this.
I would trace the incorporation of population genetic theory to three influences from the literature. First, the publication of Cadien et al.’s (1974) influential article on “Biological Lineages, Skeletal Populations, and Microevolution” set the stage for incorporation of population genetic theory. In truth, they did little other than critique skeletal biologists for treating samples (or “lineages”) with considerable time depth as if they were single snapshots of a biological population. However, Cadien and colleagues (1974) at least explicitly referred to and cited the relevant evolutionary works of Fisher, Haldane, and Wright and focused attention on the diachronic nature of skeletal samples. The lemons that Cadien and colleagues saw would eventually become lemonade for others (e.g., Konigsberg, 1990b; Owsley and Jantz, 1978; Owsley et al., 1982), but their 272article stands as an important historical piece and one that was almost always cited before embarking on a biodistance study using archaeological human skeletal material. A second historical influence, although sadly one with relatively little impact, was the completion of Rebecca Lane’s dissertation in 1977. While Lane and Sublett’s (1972) American Antiquity article greatly overshadowed Lane’s later dissertation, Rebecca Lane’s dissertation is a remarkable study that unfortunately was never published. As she was working with historic Allegany Seneca Indian cemeteries that were relocated, she was able to collect both osteological information and genealogical information. Individuals within cemeteries were not identified, but she was still able to calculate kinship coefficients between cemeteries from the genealogical information associated with cemeteries and to compare this with biological distances from cranial discrete traits. Based on her empirical regression work, she suggested that a biological distance measure she derived to measure between cemetery divergence (the “standard effective divergence”) was a hyperbolic function of the average kinship between cemeteries. So far as I can tell from the literature, this was the first (and for many years the only) attempt to directly relate biodistance to genetic kinship in archaeological samples. The final historical thread was an increasing emphasis on “The Use of Quantitative Traits in the Study of Human Population Structure,” to quote directly from the title of Relethford and Lees’ (1982) seminal paper. This emphasis led to a resurgence of interest in quantitative traits [see, e.g., the brief review in Williams-Blangero et al. (1990)], an area that had been pushed aside for many years. The near abandonment had come as a result of increasing interest in physical anthropology on single locus genetic markers and the dissatisfaction with metric approaches that appeared to be “non-genetic” or, worse, racist [see Washburn’s (1951) review of the “old physical anthropology”].
As Rebecca Lane’s (1977) dissertation does represent the earliest use of explicit population genetic theory in bioarchaeology, I will start this brief history in 1977. As mentioned earlier, Lane suggested that a measure of biological distance she derived was inversely related to the average genetic kinship between groups. As genetic kinship is a measure of similarity, it makes sense that distance measures should have some form of monotonic decrease with increasing genetic kinship. Indeed, Morton (1975) had given the relationship in the literature, and the relationship between Mahalanobis squared distances (or any squared Euclidean distance measure) and average kinship is now well known [see the Appendix, Eq. (7)]. In this regard, it is unfortunate that Smith’s MMD, a nonlinear distance measure often used for discrete skeletal traits (see review in Tyrell, 2000), has persisted. John Blangero derived a threshold trait distance that is analogous to the Mahalanobis distance commonly used with metric traits (see Pietrusewsky, 2000), and consequently its relationship to genetic kinship is known. A number of authors have now used Blangero’s generalization of the Mahalanobis distance 273(Ishida and Dodo, 1997; Konigsberg, 1990b; Konigsberg et al., 1993) in analyses of cranial discrete traits.
The ability to frame skeletal biodistance analyses within population genetic frameworks depended on advancements in quantitative trait theory. Although most of the foundations for these advancements were laid initially outside of anthropology (Crow and Denniston, 1974; Jacquard, 1974; Morton, 1973), the publication of Crawford and Workman’s (1973) edited volume on “Methods and Theories of Anthropological Genetics” brought these foundations to the anthropological forefront. Relethford and Lees’ (1982) review of quantitative trait analyses began to spark interest among skeletal biologists, who had a very long history of analyzing quantitative traits and a short to nonexistent history of incorporating quantitative and population genetic models in their analyses. At the time I was writing my dissertation in the mid-1980s there was already a considerable number of dissertations on biodistance analysis using archaeological human skeletal samples, and many of these appealed at least indirectly to population genetic theory and models. In this sense, many of these earlier works could be considered to fit within Relethford and Lees’ category of “model-free” analyses. There were, however, few previous works that could be categorized as falling into Relethford and Lees’ category of “model-bound” analyses. Rebecca Lane’s dissertation was probably the only example of an explicit use of population genetic theory in skeletal analysis. In truth, while I attempted to use population and quantitative genetic models in my dissertation, most of my work there should be classified as “model-free.” Although I used population and quantitative genetic models, I did not attempt to directly estimate population genetic parameters.
An interesting area of analysis that has grown directly out of the quantitative genetics literature (Lande, 1976; Lande and Arnold, 1983; Lofsvold, 1988) is the assessment of natural selection as versus genetic drift to explain temporal sequences (Sciulli and Mahaney, 1991). While this may sound like an esoteric area that could little inform us about our prehistoric past, the magnitude of genetic drift is fairly directly related to population size and migration. Consequently, if it is the case that natural selection does not account for some short-term changes, whereas drift does, then we may be in a position to make estimates of past population sizes. Conversely, the drift explanation may require population sizes that are so small that only natural selection remains as a probable explanation for the observed temporal pattern. In Sciulli and Mahaney’s (1991) study of tooth size reduction between Late Archaic and Hopewell samples from Ohio they found that the population sizes necessary to get the observed amount of change by drift were so small that natural selection provides the best explanation.
Another area that has seen expanding application is the Relethford–Blangero model (Relethford and Blangero, 1990). Relethford and Blangero extended the Harpending–Ward (Harpending and Ward, 1982) model, which was given for allele frequencies to cover the case of multivariate quantitative traits. In the 274Relethford–Blangero model an R matrix (see Appendix) is estimated for a number of populations using quantitative traits. The diagonal of the matrix gives a standardized distance for each population to the centroid (the hypothetical group that would exist if the populations were not divided from one another). In the Harpending–Ward model each population has an observed level of heterozygosity, which is replaced in the Relethford–Blangero model with a summary measure of additive genetic variance. In either model, the variance (heterozygosity is a measure of variance) is related to the distance to centroid in a negative fashion. Populations that are near the centroid tend to have considerable internal variation, whereas populations far from the centroid tend to have very little internal variation. This is true because drift and low migration in isolated populations move the populations away from the centroid and homogenize them. If all populations receive long-range migrants (migrants external to the considered populations) at the same rate, then the regression of within-group variance on distance to the centroid should be negative. Populations that have greater long-range gene flow than the average should fall above the regression line, whereas populations with less long-range gene flow than expected should fall below the regression line. Steadman (1998) has applied such an analysis for west-central Illinois. It is possible to apply the Relethford–Blangero model to published distance analyses (see Appendix), although this requires within-group variance–covariance matrices, which are rarely published. These matrices are necessary to obtain the observed within-group variances, while only a distance matrix is necessary to obtain the R matrix.
The theoretical relationship of prehistoric biological distances to time and space (simultaneously) is an area that is rather poorly developed. This is at the core of the Cadien et al. (1974) article, but has received relatively little attention. Konigsberg (1990a,b) provided some simple rudimentary models, while Epperson (1993) has given much more sophisticated models. Interestingly, space–time models for biological distances have begun to appear in the modern human origins debate (Relethford, 1999). This shows that these old problems with which we have dealt (migration versus in situ development) are now common fodder on the more global scale of the origins debate. As Relethford has pointed out repeatedly, the issue of documenting continuity versus replacement is complicated greatly by the fact that unequal population sizes can distort our interpretations. As mentioned previously, Rogers (1995), however, asks the question “how much can fossils tell us about regional continuity?” and answers “not much.” If Rogers is correct in this statement, then the numerous “demonstrations” of regional continuity cited earlier for 1970s and 1980s biodistance analyses must fall by the wayside. However, Rogers takes as requisite evidence for regional continuity the demonstration of a nonzero temporal correlation within regions. This discards the between region synchronic relationships, as well as the cross time–space relationships. While there is certainly no agreement on how these relationships 275should be analyzed (Cole, 1996; Konigsberg, 1997; Konigsberg et al., 1994; Sokal et al., 1997; Waddle, 1994a,b), most authors do support looking beyond the within-region sequences.
VII. THE RESHAPING OF MULTIVARIATE ANALYSIS AND THE DAWN OF ANCIENT DNA
Any history of biodistance analysis at the turn of the millennium would be incomplete without at least briefly mentioning two fairly recent developments. First, there has been “a revolution in morphometrics” (Rohlf and Marcus, 1993) within the previous decade based on analyzing three-dimensional coordinate data. Benfer (1975) first described a caliper-based method for “digitizing” the human skull, but because of the awkwardness (and high error rate?), routine analysis of three-dimensional coordinate data had to await the development of relatively inexpensive, reliable, and transportable three-dimensional digitizers. To date, the “new morphometry” has been applied to problems in the analysis of human cranial sexual dimorphism and growth, but there has been only one study whose focus was biodistance analysis among archaeological human skeletal samples (McKeown, 2000). The other development that stands to radically transform biodistance analysis, and possibly replace it with genetic distance analysis, in the future is the new area of ancient DNA (aDNA) analysis. There have been three excellent reviews of aDNA (Kaestle and Horsburgh, 2003; O’Rourke et al., 2000; Stone, 2000). As I have “successfully” dropped an open Eppendorf containing DNA samples into a buffer reservoir on more than one occasion, I refer the interested reader to the literature for a historical review of the expanding field of aDNA analysis.276
277Appendix
I. FROM MARITAL MIGRATION TO UNEQUAL VARIANCES BY SEX
Konigsberg (1988) gave a population genetic model for the effects of differential migration on genetic variances within the sexes (both across sites and between sites). While the basic results in this article were correct (e.g., equation 7 from that article), the logic of the derivation was not. Consequently, I correct here that derivation.
In the island model (Wright, 1969) there are an infinite number of subpopulations, all of size N, that exchange migrants with rate m. A standardized genetic variance between the islands, symbolized as Fst can be used to characterize the effects of genetic drift and migration. Wright (1969:294) defined Fst as “the correlation between random gametes within subdivisions, relative to gametes of the total population,” but I will use an equivalent definition as the probability of identity by descent within subdivisions (see Hartl and Clark, 1997). The probability of identity by descent within subdivisions is just the probability on sampling two alleles (with replacement) that they will be the same allele because they derive from a common ancestor. The recurrence relationship for
(1) |
Assuming an equal sex ratio but different migration rates by sex, we can write Fst statistics for males, females, and males with females. The Fst for males is the probability of sampling identical by descent alleles within males within subdivisions (similarly for females), whereas the Fst for males with females is the probability of sampling identical by descent alleles from a male paired randomly 278with a female from within subdivisions. These Fst values and the total Fst are
|
|
(2) |
|
|
|
|
where triangles and circles are used to represent male and female. The ratio of male to female Fst values is then
(3) |
as in Konigsberg (1988). Equation (3) can be used with a quantitative genetic model to specify the ratio of male to female within-group genetic variances or the ratio of between-group variances (see Konigsberg, 1988). Wood (1986) gives a migration matrix method for calculating the equilibrium R matrix (see next section for definition of the R matrix) that could be used to find separate male and female matrices.
II. FROM D2 TO “R” AND BACK AGAIN
We will first look at how to use a Mahalanobis (or any squared Euclidean) distance matrix to estimate an R matrix. The R matrix is a standardized variance-covariance matrix. As Relethford and Harpending (1994) note: “R matrices have certain properties that make them useful for studying genetic relationships among populations.” They enumerate a number of important properties of R matrices, some of which are exploited in the Relethford-Blangero (1990) model that Steadman (1998) used in a bioarchaeological context. As the literature often provides D2 matrices for archaeological skeletal samples, it is useful to have a way to convert these to R matrices without requiring raw data.
To find the R matrix we first need to calculate what is known as a “codivergence” matrix, usually written as C. The codivergence matrix measures the variance around the centroid. A population’s codivergence with itself is just the squared distance from a population’s multivariate means to the centroid. Codivergences between two populations can be zero (if they are both at the centroid), 279positive if they are both “on the same side” of the centroid, or negative if they are on “opposite sides.” The C matrix is given as
(4) |
where I is a g by g identity matrix (g being the number of groups), 1 is a g by one column vector of ones, D2 is the matrix of squared distances (calculated on t traits), and w is a g by one column vector of relative census sizes. By definition we have 1w’ = 1. Using results from Relethford and Harpending (1994), we can calculate Fst (see earlier) as
(5) |
where diag {C} is an operator that places the diagonal of a matrix into a column vector. The R matrix is then
(6) |
From Williams-Blangero and Blangero (1989) (their equation 7) we can write the original D2 matrix as
where J is a g by g matrix of ones and  represents a Hadamard product.
represents a Hadamard product.
Written without the first parenthetical term of 2t/(1 – Fst), Eq. (7) represents a standardized distance often used in human population genetics studies. As another definition for the R matrix is as a matrix of average kinship coefficients between populations (off the diagonal) and within populations (on the diagonal), Eq. (7) shows that there is a direct relationship between biological distance and average kinship. However, this relationship only holds for Euclidean distance measures (such as Mahalanobis distances). Consequently, it is not possible using Eqs. (2) and (5) to estimate Fst or the R matrix from nonlinear distances, such as Smith’s MMD. The R matrix method given earlier can be applied to discrete traits using Blangero’s generalization of the Mahalanobis distance for threshold traits. Tyrell and Chamberlain (1998) attempted to estimate Fst and “effective genetic distances” from cranial discrete traits, but they used a model appropriate for diploid genetic markers, not for threshold traits. Where they refer to the “heterogeneity” of a trait they are actually using the formula for heterozygosity at a biallelic locus.280