
227Chapter 9
A Brief History of Paleodemography from Hooton to Hazards Analysis
Susan R. Frankenberg and Lyle W. Konigsberg
I. INTRODUCTION
Paleodemography, or the study of past population dynamics, should be and often has been an important component of bioarchaeology. Studies of population structure provide ways to evaluate the contributions and impacts of past behaviors, social structure, economics, and environment on human life and well being, with the relationships between past behavior and biology being a principal concern of bioarchaeology. The application of paleodemography in bioarchaeological studies has not been consistent through time, however, for a number of reasons. These reasons include the facts that many demographic methods have not been easy to translate to archaeological skeletal samples and that many bioarchaeologists have been ignorant of available methodologies. This chapter traces the history of paleodemography within bioarchaeology, identifying first and continued uses of various demographic techniques and tracing the underlying mathematical threads common to diverse approaches. This history also seeks to evaluate criticisms of and continuing problems in paleodemography from both outside and within the field.
The first clear use of paleodemographic concepts and methods on the American scene began in the 1920s-1930s with Hooton’s work on Madisonville and Pecos Pueblo. Hooton was concerned with estimating living population size and evaluating survivorship from cemetery samples, but apparently was unaware of then-common formal demographic methods that could assist in these endeavors. 228Little new was published in paleodemography after Hooton until Angel’s work in the late 1940s through 1960s. In contrast to Hooton, Angel was aware of work in formal demography, but rejected life table methods in favor of his own obtuse calculations. The number of paleodemographic methods and applications exploded in the 1970s, beginning with use of formal life table methods and the development of life tables for anthropological populations. By the 1980s, when calculation of life tables was standard procedure in skeletal studies, paleodemography came under attack both within and outside the field. The principal criticisms of paleodemographic methods at that time were that demographic reconstructions implied unrealistic rates of survival and other parameters, that paleodemographic life tables often were more informative about fertility than about mortality, and that methods of age estimation were too imprecise to allow meaningful demographic analyses.
The mid-1980s to the present time has been a period of mixed results and varied successes. Dissatisfied with the discrete age nature of life tables and the limitations mentioned earlier, numerous scholars have moved on to hazards analysis as a means of modeling paleodemographic processes more realistically. These types of studies have addressed interval-censored data and nonzero growth rates and are beginning to build uncertainty of age estimation into the models. Some scholars also have moved on to identify the diverse sampling, measurement, and analytical issues in paleodemography that must be addressed in order to understand past population processes successfully (for examples, see Milner et al., 2000). While a small number of researchers continue to reject paleodemography as viable and others continue to follow methodologies now shown to be unrealistic and inaccurate, we believe we can expect more from paleodemography in the future. This chapter presents a brief history of the accomplishments and pitfalls of paleodemography beginning with Hooton and ending with current and future directions of study.
II. THE HOOTONIAN PALEODEMOGRAPHIC LEGACY
Hooton’s (1920) paleodemographic analysis in his monograph on the “Indian Village Site and Cemetery Near Madisonville, Ohio,” like much of his bioarchaeological work, was decades ahead of its time. In a few brief pages, Hooton (1920:20) compared rather deficient skeletal age-at-death data from Madisonville to age-at-death data from European populations in order to estimate a reasonable crude death rate. This step presaged Weiss’ (1973) far more elaborate development of model life tables for anthropology and Coale and Demeny’s (1966) models for broader applications. Hooton also applied the central relationship between death rate, length of cemetery use, and number of burials in order to 229estimate living population. He wrote “assuming the total number of burials in the cemetery to have been about 1350 and the annual death rate to have been about 3 per hundred, a village of 450 to 500 inhabitants would have been sufficient to fill this cemetery in a century” (Hooton, 1920:27). Symbolically, we have
(1) |
where N is the number of skeletons, T is the length of time for which a cemetery is used, and d is the death rate per annum. Many years later Ubelaker (1974) used this same relationship to estimate population size from an ossuary sample. In a similar vein, Konigsberg (1985) treated N and d as known in order to logarithmically plot population size against length of cemetery use. A semilogarithmic plot for estimating T and P using Hooton’s data from Madisonville (Hooton, 1920) is shown in Fig. 1.
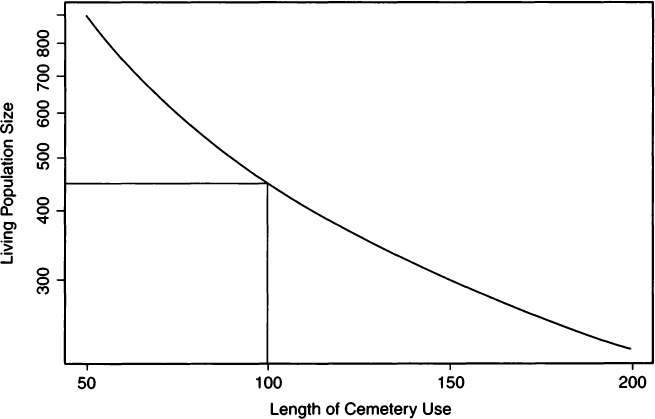
Figure 1 Semilogarithmic plot of living population size (P) and length of cemetery use (T) for the Madisonville site based on the number of skeletons (N) and annual death rate (d). Straight lines show that a living population of roughly 450 individuals could generate the observed cemetery size over a period of 100 years.
230Ten years after his work on the Madisonville site, Hooton (1930) published a monograph on The Indians of Pecos Pueblo that also included a paleodemographic analysis ahead of its time in bioarchaeology. Compared to formal demography, however, his analysis of the Pecos Pueblo population was quite primitive. For example, Lotka (1922) had published the underpinnings of stable population theory 8 years earlier, and the use of life tables in mortality analysis had occurred considerably earlier [see Newell (1988) and Smith and Keyfitz (1977) for reviews and collected papers]. Hooton used a rather ad hoc survivorship graph (Hooton, 1930:335) to drive his analysis and attempted to find the number of skeletons that would be produced by a stationary population with a particular population size over a 100-year period. We have reproduced his figure here using a slightly different format (see Fig. 2). Hooton’s graph is discussed in detail, as it allows us to point out the refinements that come from (later) use of formal life tables.
The logic underlying Hooton’s calculation of the number of deaths in a 100-year period was as follows. Suppose that the living population size is constant at 1000 individuals, with survivorship such that 0.5 of the population survives until age 33.33, 0.1 survives until age 66.67, and all are dead by age 100. Hooton divided a 100-year span into three cohorts of 33.33 years each. The first cohort, which is represented with vertical hatching in Fig. 2, consists of 1000 individuals, all of whom die within the 100-year interval, generating 1000 deaths. 231By 33.33 years into the 100 span, a second cohort (diagonal hatching) would have been born. This second cohort includes 500 individuals, which, with the remaining 500 individuals from the first cohort, totals a population of 1000 individuals. Of these 500 individuals in the second cohort, 90% would have died within the following 66.67 years, generating 450 deaths. The final cohort (horizontal hatching) consists of 650 individuals, again bringing the total population to 1000 individuals alive at time 66.67 years. These 650 individuals augment the 100 individuals still alive from the first cohort and the 250 individuals still alive from the second cohort. Of the third cohort, 50% will have died by the end of the 100-year span, yielding 325 deaths. Summing the deaths from the three cohorts we have 1000 + 450 + 325 = 1775 deaths, which is the value Hooton gave near the top of his page 336. Hooton (1930:336) recognized that his graph was a bit unrealistic, noting that he had assumed “that all of the population at the beginning of the century are young, whereas at least 10 percent are very old persons left over from the preceding century.” He consequently suggested adding an additional 100 (10% of 1000) individuals, bringing the total number of deaths to 1875. This was a completely ad hoc, and in fact, logically inconsistent adjustment. Based on this adjustment, there should have been 1100 people alive at the beginning of the century, except that Hooton took great pains in the rest of his graph to assure that births accrued such that the population size stayed constant at 1000.
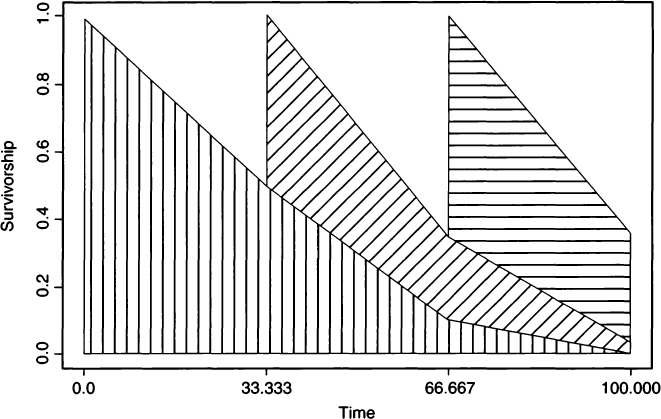
Figure 2 Survivorship of three cohorts over 100 years at Pecos Pueblo based on Hooton’s (1930) Figure XI-2.
There are a number of unsupported assumptions that Hooton used to draw his figure and that conspire to lead us to the wrong answer. As Hooton noted, there should be some individuals who enter the century at age 66.67 years, but he curiously neglected to mention that there also should be individuals who enter the century at age 33.33. If there are three cohorts, then they all should be represented at any one point in time. This is not the case in Hooton’s figure and our reproduction because the population starts far from its stable age distribution (i.e., the characteristic age distribution that follows from a fixed regime of age specific mortality and a fixed growth rate). The concept of a stable age distribution was well known to demographers in Hooton’s time (e.g., Sharpe and Lotka, 1911), although the available mathematical form was better suited to continuous time problems than to the three age-class model Hooton used. Had Hooton understood the mathematics behind life table analysis he could have found the stable age distribution directly, and because he assumed that the population was stationary, the stable age distribution would have remained constant in both proportions and raw numbers. One way to find the stationary age distribution is to iterate through Hooton’s figure many times, something that was not particularly feasible in the 1920s with paper and pencil. Doing this we find that the population stabilizes at 625 0–33.33 year olds, 312.5 33.34–66.66 year olds, and 62.5 66.67–100 year olds. Applying Hooton’s logic, we start the century with 1000 individuals, all of whom will be dead by the end of the century, at 33.33 years into the century 232we pick up 625 new individuals by births, of whom 90% will die by the end of the century, and at 66.67 years we pick up an additional 625 individuals, 50% of whom will die within the next 33.33 years. Consequently, there should be 1000 + 1.4 × 625 = 1875 skeletons, the number Hooton actually estimated, but for the wrong reasons!
If we calculate a life table using Hooton’s Pecos Pueblo data, we find that the number of skeletons that should accrue in one century is actually much greater than Hooton’s estimate (Hooton, 1930), totaling about 2727 individuals instead of 1875. The reason for Hooton’s underestimate is that although his graph implies a linear decline in survivorship (the usual assumption in a life table), his calculations treat survivorship as a step function. In other words, his mathematical modeling implies that everyone who is born survives until 33.33 years, at which age half of the cohort immediately dies. Then the remainder of the cohort lives until exactly 66.67 years, at which age 80% of the cohort promptly dies. The remaining 10% then live until 100 years, at which age they all die. In fact, what Hooton clearly intended from his graph was a continuous birth and death process, for which he needed to apply a life table. Table I gives a rather abbreviated life table to show these calculations. The first column (X) gives the age, the second column [l(x)] gives the survivorship from Hooton, and the third column [d(x)], although not in Hooton (1930), is calculated directly from survivorship. For example, d(33.33) = l(33.33) – l(66.67) = 0.4. The next three columns [L(x), T(x), and c(x)] are calculated first assuming a linear decrease in l(x) across the age category and then assuming a step function for survivorship. The fourth (and seventh) column [L(x)] is one of the least simple to understand and is, in fact, the source of Hooton’s underestimate. We consequently explain L(x) in some detail.
L(x) is a column that is specific to life tables, and that has no analog in the hazard models presented here. Technically, L(x) represents the person-years lived within an age interval. If we make the age intervals infinitesimally small, 233as is the case in hazard models, then L(x) simply becomes l(x). However, in life tables the width of an age category can be rather large, as are Hooton’s age categories, which are 33.33 years long. To find L(x), we might proceed by adding together the l(x) values year by year or, in the continuous case, we would use calculus to integrate l(x) across the age category. The usual assumption in a life table is that l(x) decreases linearly across the age category, as in Hooton’s graph but not in his math. Following standard procedures, we use the trapezoid rule to find that L(x) is the average of l(x) at the beginning and end of the age category multiplied by the width of the age category. Thus, L(33.33) = (0.5 × l(33.33) + 0.5 × l(66.67)) × 33.33 as shown under “usual life table” in Table I. In contrast, adopting Hooton’s assumption of a step function for l(x), we integrate across a rectangle so that L(x) is simply l(x) times the age width. This is shown in Table I under the section labeled “Hooton’s method.”
Pecos Pueblo Life Table Calculated from Hooton’s (1930) Dataa
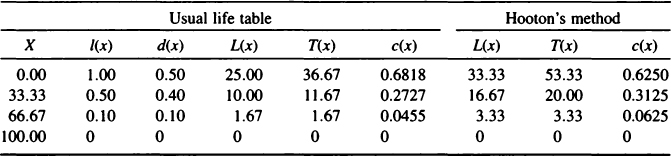
aThe “usual life table” L(x), T(x), and c(x) are calculated assuming a linear decrease in l(x) across the age category, whereas “Hooton’s method” values are calculated assuming a step function for survivorship.
The fifth and eighth columns in Table I, T(x), represent the people years to be lived in age category X and in all subsequent age categories. Since the value of T(x) is calculated by subtracting the L(x) of the previous category from the T(x) of that category, the overestimation of L(x) using Hooton’s method compared to usual life table calculations also results in overestimation of T(x). The sixth and final columns, c(x), show the living age distribution, which is calculated as L(x)/T(x). The final column in Table I gives the age distribution implied by Hooton’s method, while the sixth column gives the slightly different age distribution that arises from a traditional life table analysis. Differences in the stable age distributions between the usual life table and Hooton’s method do not appear great enough to have much effect on the predicted number of skeletons. Instead, Hooton’s substantial underestimation of total population size is a product of the discrete nature of his step function survivorship. Because of the step function in survivorship, the birth of 625 individuals in Hooton’s model only occurs every 33.33 years at a single point in time. Consequently, he does not account for a substantial number of individuals who were moving into the population by birth and out of the population by death. We need a continuous time birth and death model, which the life table can provide, albeit with linear survivorship through age intervals. In a stationary population, T(x)/l(x) is the average age-at-death, and its inverse is equal to the crude birth and death rates. The crude death rate is the proportion of the population that dies per annum. Using these facts, we find that the number of deaths from a stationary population of 1000 individuals across a century is 1/36.67 × 1000 × 100 = 2727 using the correct life table approach and 1/53.33 × 1000 × 100 = 1875 using Hooton’s step function survivorship.
There are additional complications that we could address here, including the fact that Pecos Pueblo is known to have been in a population decline so that a stationary model is inappropriate. In the interest of following a historical thread, we will forestall discussion of nonstationary models until later in this chapter, 234but for the moment we move from “Hooton to hazards” within the context of the Pecos Pueblo example. We argue that the linear decline of survivorship is an unappealing aspect of the usual life table approach. Indeed, it is common to make different assumptions about the shape of survivorship within the very young (Coale and Demeny, 1966:20). In hazards analysis we replace the piecewise linear survivorship function with a smooth curve. For our example here we will fit a Gompertz model to the survivorship values that Hooton used. The Gompertz model survivorship is
(2) |
The numbering of the parameters in this equation keeps this model in line with the Siler model (Gage, 1988). We estimate the parameters a3 and b3 using the method of maximum likelihood (see Appendix) and find for Hooton’s Pecos Pueblo example that a3 = 0.01265 and b3 = 0.02693. Figure 3 compares the linear survivorship from a life table approach to the Gompertz model. 235We can integrate Eq. (2) (see Appendix) to arrive at the stationary population mean age-at-death of 35.5 years, which is close to the value we found from the life table. As shown later, hazards analysis has a number of advantages over life table approaches. For now, we simply take solace in the fact that hazards analysis is not giving us a radically different answer from the life table approach.
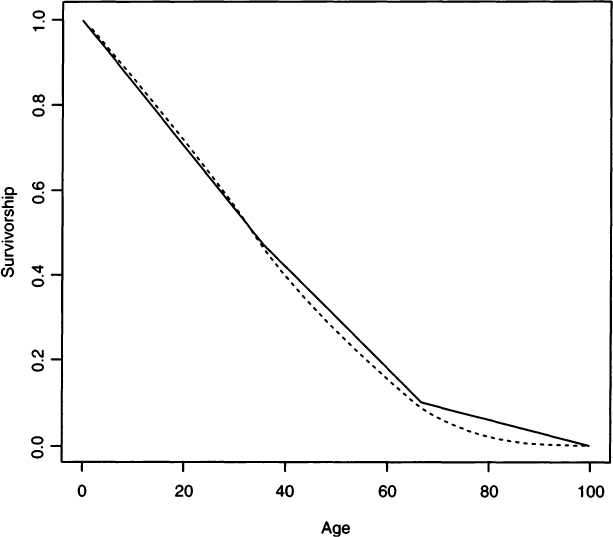
Figure 3 Linear survivorship calculated from a life table (solid line) and from a Gompertz model (dashed line) using Hooton’s Peco Pueblo data (see Table I).
III. THE DOLDRUMS PRIOR TO THE ADOPTION OF LIFE TABLES IN PALEODEMOGRAPHY
While Hooton may or may not have known how to calculate a life table, his student Larry Angel, whose 1969 article (Angel, 1969) is frequently cited as a cornerstone of paleodemographic research, rejected the use of life tables in bioarchaeology. Angel’s (1947) first major publication in paleodemography on “the length of life in ancient Greece” cites a number of then standard demographic and life table works (e.g., Dublin and Lotka, 1936), but he chose not to present life tables for ancient Greece. Instead, Angel presented a frequency analysis of crania in broad age classes (his Table 1), a frequency analysis based on a more refined categorization of suture closure (his Table 2), and average ages at death from the first two tables and from a finer 5-year categorization (his Table 3). In his Figure 1, Angel presented a graph of life expectancy against age, which was calculated by forming successive samples prior to averaging ages at death, and then subtracting the floor of the interval. For example, life expectancy at age 35 would be the average ages at death for those who die past age 35 years, minus 35 years. While this gives results identical to those that would come from a life table, the life table provides additional measures (e.g., age-specific probability of death) that apparently were of no interest to Angel.
Angel’s 1947 article is not the work for which he is best known in paleodemographic circles. Instead, his 1969 article “The Bases of Paleodemography” is widely cited in historical accounts. In this latter work Angel took an outwardly hostile approach toward life tables, writing that “one can construct a model life table (including life expectancy) from ancient cemetery data (Angel, 1947, 1953), but this falsifies biological fact to a greater or lesser degree . . .” (Angel, 1969:428). In lieu of calculating life tables, Angel presented a rather bizarre analysis that, among other errors, assumed that the age distribution of the living was equal to the age distribution of the dead. We can see examples of this in such statements as “There are 74 ‘living’ children per 62+ adults in the 18 to 34 age range = 2.4 per couple” (Angel, 1969:433). The count of 74 “living” children comes from a method we have never been able to understand, as it involves a prorating of deaths and Angel never gave any instruction on how deaths were supposed to be apportioned. The 62+ adults in the 18 to 34 age range is also a 236bit mysterious, although we know that it is based on the observed distribution of deaths.
Angel closed his article with the statement that:
The ultimate bases for paleodemography are accurate identification of each individual (sex, age, disease, fecundity, fertility, family relationship) from his or her skeleton and accurate counting of an adequate sample of such individuals collected by meticulous excavation techniques. The key is close collaboration between archaeologist and physical anthropologist. (Angel, 1969:434)
His work is probably best remembered for this message of collaboration between archaeology and biological anthropology, the battle cry of the bioarchaeologist. While Angel’s work frequently is cited in paleodemographic contexts, it is really his mentor Hooton who deserves the greater credit.
Other physical anthropologists and bioarchaeologists contemporaneous with Angel also attempted to evaluate past population structure without formally using life table analysis. For example, Howells (1960) judged past population sizes for various archaeological groups based on the age structure of skeletal samples informally combined with information on settlement patterns and other sociocultural information. In the same volume, Vallois (1960) tabulated the age structure of archaeological and fossil skeletal samples and compared these groups both among themselves and with early historical (i.e., Roman period) documents in an effort to assess both the representativeness of various archaeological samples and temporal trends in mortality. Similarly, in a reassessment of age and sex at Indian Knoll, Johnston and Snow (1961) graphically compared the age structure of this archaeological sample with both fossil and more recent archaeological samples worldwide. Some bioarchaeologists continued to follow into the next decade the same approach of tabulating skeletal samples by age classes, taking percents and then graphing the “mortality profiles.” For example, Blakely (1971) compared Indian Knoll to archaeological samples from Illinois Archaic, Hopewell, and Middle Mississippian sites in this way, although he did attempt to formalize his comparisons of mortality using χ2.
IV. LIONIZATION OF THE LIFE TABLE
It is not entirely clear to us who should claim credit for the first application of life tables in paleodemography. In their 1976 treatment of paleodemography, Swedlund and Armelagos cited Hooton and Angel’s work as the beginning of paleodemography in physical anthropology. However, they went on to note that “the application of demographic principles has not been an important aspect of skeletal studies until the last decade” (Swedlund and Armelagos, 1976:34). Acsádi and Nemeskéri’s (1970) monograph on the “History of Human Life Span and Mortality” was certainly one of the first major treatments in paleodemography 237to fully exploit life table calculations. Swedlund and Armelagos’ book contained an entire chapter on paleodemography, and the publication of Ken Weiss’ (1973) “Demographic Models for Anthropology” brought life tables to the attention of both archaeologists and biological anthropologists. Ubelaker’s (1974) study of ossuary paleodemography provided detailed information on how to construct life tables, as did Buikstra’s (1976) demographic analysis of Illinois Middle Woodland. David Asch’s monograph, again on Illinois Middle Woodland, brought a level of mathematical sophistication to paleodemography that was decades ahead of its time, as it required an intimate knowledge of stable population theory (Asch, 1976). By the mid-1970s, life tables clearly had become fairly commonplace in bioarchaeology. This is all the more remarkable when we consider that Angel, in 1969, wrote his “bases of paleodemography” without ever using life tables per se.
As there have been so many descriptions in the literature of how to construct life tables we will not give a description here (for reviews, see Meindl and Russell, 1998; Milner et al., 2000). The all-too familiar columns are age, dx or proportions of deaths in age classes, lx, or survivorship, qx or age-specific probability of death, Lx or people-years lived in age intervals, Tx or people-years to be lived, ex or life expectancy, and cx or proportion of the living population in the age class. Only the last column may be unfamiliar; it is equal to Lx/ex. One of the best accounts for constructing paleodemographic life tables is given by Moore and colleagues (1975) who give a detailed description of how to adjust a life table for populations with nonzero growth rates and also indicate the effects of underenumeration on various life table columns. We will hold off on the discussion of nonzero growth rates until the following section. Concerning the effects of underenumeration, Moore and colleagues (1975) note that a deficit of infants, a common occurrence in archaeological samples, will affect dx and lx throughout, but will have no effect on qx and ex beyond the first age interval. This is true because these latter two parameters are conditioned on survival past infancy for values beyond qx and ex.
V. THE PROBLEM OF NONZERO GROWTH RATES
If human populations grow exponentially, then the population size at time t (Nt) is a function of the population size at time 0 (N0), as follows:
(3) |
Here r is the population growth rate, which is 0 for a stationary population, negative for a declining population, and positive for an increasing population. Moore and colleagues (1975) used the slightly different equation:
(4) |
238but Eq. (3) is generally preferred to Eq. (4) because the former uses continuous compounding, whereas the latter compounds annually.
It is quite rare to have information on growth rate in a paleodemographic setting. In the case of Pecos Pueblo, some estimates of population size were available from the historic period, although the site extended well into the prehistoric period from which there are no population estimates. Hooton (1930:332) provided what was known about historic population sizes for Pecos Pueblo, which we have plotted as a semilogarithmic plot in Fig. 4. If the growth rate were constant, then the points should fall along a straight line, which they obviously do not. We have drawn in the least-squares regression line for didactic purposes; this line has a slope of about –0.015. In the following calculations, it is assumed that the growth rate for Pecos Pueblo throughout its history and prehistory was –0.015. This is a value that is clearly unrealistic, as Pecos Pueblo was inhabited for about 1000 years, and to reach its historically known population size after 1000 years of population decline (at r = –0.015) the founding population size would have to have been well into the millions. In all likelihood, the population was stationary through the prehistoric period and only entered population decline in the historic period. Furthermore, the rate of decline accelerated through the historic period, as seen in the nonlinearity in Fig. 4.
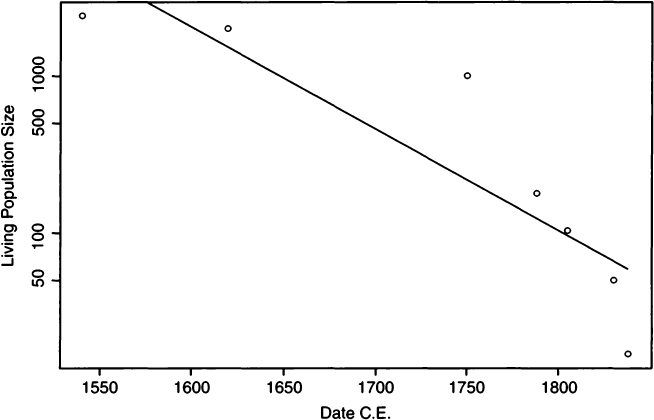
Figure 4 Semilogarithmic plot of living population sizes at specific dates reported by Hooton (1930:332). Points represent recorded population sizes, whereas the straight line is a least-squares regression line with a slope of roughly –0.015.
239The method for calculating a life table from skeletal samples derived from growing or declining populations has been given in a number of different paleodemographic sources (Asch, 1976; Bennett, 1973b; Moore et al., 1975; Weiss, 1973). The logic is as follows. For our current example with a growth rate of –0.015, individuals who die at exactly age 50 come from a birth cohort that was larger than the current birth cohort. Specifically, the birth cohort for those who die at age 50 years was exp(0.015 × 50) = 2.117 times larger than the current birth cohort. Note that this expression is exp(–rt), where t is the exact age-at-death and r is the growth rate. As a consequence, the number of deaths that occur at exactly age 50 need to be adjusted down by dividing by 2.117 in order to set them to the same cohort size as those who die at exactly age zero. Dividing the number of deaths by exp(–rt) is the same as multiplying the deaths by exp(rt), which is the correction given in the aforementioned sources and is equivalent to the annualized correction of (1 + r)t.
As an example of calculating a life table corrected for growth we will continue with the Pecos Pueblo example, using the more detailed tabulation of ages from Palkovich (1983). There has been considerable discussion of Hooton’s original age assessments on which Palkovich’s figures are based (Mobley, 1980; Palkovich, 1983; Ruff, 1981). While Ruff has reexamined many of Hooton’s age assessments, any new paleodemographic analysis should proceed from scorings of age indicators in both a reference sample and the archaeological sample of interest, as noted later. As the Pecos Pueblo skeletons have now been reburied (Tarpy, 2000), any such reanalysis will have to rely on archival data. Table II lists Palkovich’s original life table with r = 0 and our recalculated life table with r = –0.015. The adjustments to number of deaths shown here are found using 240the midpoint of each age interval, as is common practice. In Palkovich’s original table the life expectancy at birth assuming a stationary population is 28.18 years so the crude birth and death rates equal 1/28.18 = 0.035. In our recalculation under an unreasonable growth rate of –0.015, the birth rate is 0.032 and the death rate is 0.047. The calculation of birth rate from a nonstationary life table is rather complicated, involving an adjusted column
Pecos Pueblo Life Table Under Zero Population Growth (r = 0) and Population Decline (r = –0.015)a
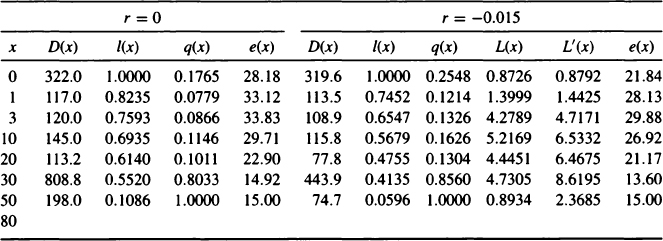
aAge data are from Palkovich (1983). L(x) are years lived in the age interval, and L′(x) is L(x) adjusted by e–ra.
VI. ADIEU TO PALEODEMOGRAPHY?
By the mid-1970s the scope of paleodemography came to cover the routine calculation of life tables, usually under the assumption of zero population growth (Lallo et al., 1980; Lovejoy et al., 1977; Owsley and Bass, 1979; Owsley et al., 1977; Ubelaker, 1974). During this period of numerous publications in paleodemography, there were occasional lapses that demonstrated that authors did not understand the basics of stable population theory. For example, Blakely (1988a:22), in commenting on his graph of the percentage dead in age categories (his Figure 2), noted that “[t]he Dickson Mounds curve is pyramidal, indicating age stability.” His comments are based on a misreading of Weiss (1973:65), where Weiss notes that the living age distribution from a census should be pyramidal if the population was stable. In skeletal samples, the living age distribution must be calculated from survivorship, and as a consequence it is always pyramidal if age intervals are of equal width. The reason Blakely (1988a:22) found that the King site did not have a pyramidal distribution is because he was using dx instead of cx. With this and a few other minor exceptions, bioarchaeologists by the early 1980s had become fairly facile at calculating and interpreting life tables.
Also by the early 1980s the status quo in paleodemography had come under serious attack. The first scathing critique of paleodemography came from William Petersen (1975). Petersen came to his discussion as an outsider, a social demographer, and his critique was largely leveled at older literature in archaeological demography. In fact, his only references to specific paleodemographic studies that we have cited so far are Hooton, Acsádi and Nemeskéri, and Weiss (Acsádi and Nemeskéri, 1970; Hooton, 1930; Weiss, 1973). Petersen criticized Hooton (1930) for his comparison of Pecos Pueblo mortality to modern European national data, while he mentioned Acsádi and Nemeskéri (1970) only in passing in his discussion of the accuracy of sex determination. Weiss (1973) was the recipient of the greatest amount of abuse by far:
. . . Weiss’s contribution shows the typical faults of a pioneer. In a paper addressed to an audience generally poorly versed in mathematics, he uses an unnecessarily 241cumbersome notation. More important, he displays an ignorance of fundamentals (or, at best, a carelessness in presenting them) that contrasts sharply with his technical pretentiousness. Weiss’s work differs from the norm in archaeology and anthropology mainly in that it makes some genuine effort to assimilate the elements of demography. (Petersen, 1975:228)
Weiss (commenting in Petersen (1975:240)] responded: “a great deal of needless confusion comes from the author’s fixation upon the basic traditions and concepts of his own field along with an inevitably spotty knowledge of the literature of the other.” As an outsider, and one clearly unfamiliar with then current work in paleodemography, Petersen’s critique did not stick.
The same cannot be said for comments that were published in 1982 and 1983 (Bocquet-Appel and Masset, 1982; Howell, 1982; Sattenspiel and Harpending, 1983). The comments by Howell and by Sattenspiel and Harpending came from anthropologists who were quite familiar with anthropological demography. Bocquet-Appel and Masset’s “Farewell to Paleodemography” was written by practitioners who had actively worked with prehistoric skeletal material. These criticisms from within the field are summarized briefly here as they relate to historical developments in paleodemography. For fuller treatment and reponses to these criticisms, we refer the reader to the original exchanges (e.g., Bocquet-Appel, 1986; Bocquet-Appel and Masset, 1985, 1996; Buikstra and Konigsberg, 1985; Greene et al., 1986; Konigsberg and Frankenberg, 1992, 1994; Masset, 1993; Masset and Parzysz, 1985; Piontek and Weber, 1990; Van Gerven and Armelagos, 1983). In a nutshell, Howell (1982) critiqued Lovejoy and colleagues’ (1977) demographic reconstruction for the Libben site, noting that it implied an unrealistically low rate of survival into mid- and old-adulthood. Sattenspiel and Harpending (1983) showed that the inverse of the mean age-at-death is approximately equal to the crude birth rate in a nonstationary population (when the growth rate is unknown), but is relatively unrelated to the crude death rate. They (Sattenspiel and Harpending, 1983) consequently suggested that paleodemographic data were more informative about fertility than about mortality, a viewpoint that was rather foreign to a generation of paleodemographers who had grown up with life table analysis as an indicator of mortality. Finally, Bocquet-Appel and Masset (1982) argued that methods of age estimation were too imprecise and biased to produce usable results for demographic analyses.
VII. HAZARDS ANALYSIS: THE DEATH OF THE LIFE TABLE IN PALEODEMOGRAPHY?
By the mid-1980s there was growing dissatisfaction with the discrete age nature of the life table, as well as with the limitations summarized earlier. 242A number of authors (Gage, 1988; Gage and Dyke, 1986; Wood et al., 1992) suggested the application of hazard models as a logical alternative to life tables, and as shown in subsequent sections, there are many practical advantages to hazards analysis. The most detailed account to date of hazard models for anthropology is by Wood and colleagues (1992). In hazards analysis, the little l(x) column of the life table is replaced with a survivorship function, usually written as S(a) or S(t) which is the probability of survival to exact age a or t. The little d(x) is replaced with a smooth function, usually written as f(a), which is the probability density function for age-at-death. The age-specific probability of death, q(x), is replaced with the hazard rate, h(a). Wood and colleagues (1992) give the relationships among the hazard rate, probability density function for age-at-death, and survivorship in their equations 5–8.
One practical benefit of hazards analysis is that it allows us to deal with the different age ranges that might be assigned to individual skeletons. For example, in the Pecos Pueblo sample there were 51 skeletons that could be aged no more precisely than 20 to 80 years old at time of death. While Palkovich (1983) apportioned these skeletons to the adult age classes based on the age distribution of the other adult skeletons, hazards analysis allows us to treat these individuals as interval censored. In fact, all skeletons could be treated as interval censored data, with the interval lengths varying from skeleton to skeleton. Thus, the arbitrary binning into traditional age classes is unnecessary. We fit survivorship to Pecos Pueblo data using a four-parameter model:
(5) |
where the first exponential is a negative Gompertz function representing juvenile survivorship and the second exponential is the Gompertz function from Eq. (2) that represents adult survivorship (Gage, 1988). Figure 5a compares the survivorship fit by this four-parameter hazard model to the survivorship values that Palkovich calculated from a life table. Figure 5b compares Palkovich’s d(x) to the probability density function for age-at-death calculated from the hazard model. Details of the fitting procedure are given in the Appendix, and values for the hazard parameters are given in Table III.
If there is some estimate of the growth rate, then the hazards analysis can be adjusted for growth rate. We define a new survivorship
(6) |
which can be obtained from Asch (1976:72) or from Milner and colleagues’ (2000) with an additional integration in the numerator. This adjusted survivorship is used to fit against the unadjusted deaths, as shown in the Appendix. Figure 6a gives the fitted survivorship curve at r = –0.015 for Pecos Pueblo, the hazard model survivorship curve at r = 0, and plotted interval-wise survivorships calculated from the life table at r = –0.015 (from Table II). Figure 6b shows the probability of death functions and Fig. 6c shows the conditional probability of death functions for both stationary and nonzero growth rate hazard models. As seen from Fig. 6a, a negative growth rate lowers the survivorship from what we would calculate if we assumed a stationary population. Similarly, under a positive growth rate the survivorship would be elevated over what we would calculate if we assumed a stationary population. In a figure caption, Milner and colleagues (2000: Figure 16.1) appear to say the opposite, when they write that “positive values of r make it appear as if survival is lower at each age, whereas negative values have the opposite effect.” However, they are talking about the effect of fitting a stationary model to a positive growth population, whereas we are talking about fitting a growth model to a stationary population. From the hazard model fit with r = –0.015, we find crude birth and death rates of 0.0342 and 0.0492 (see Appendix), which agree well with the values of 0.032 and 0.047 from the nonstationary life table.
243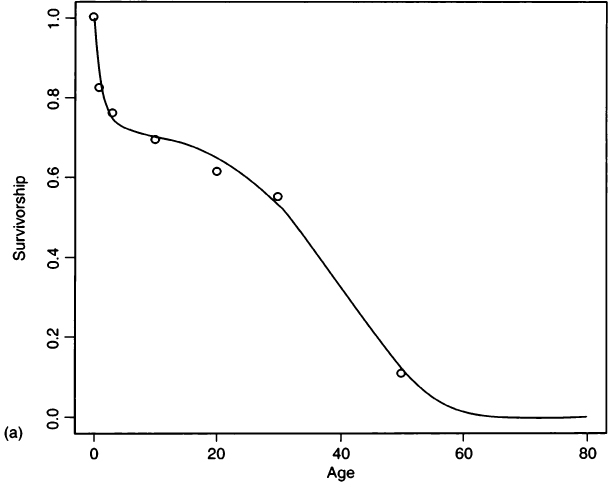
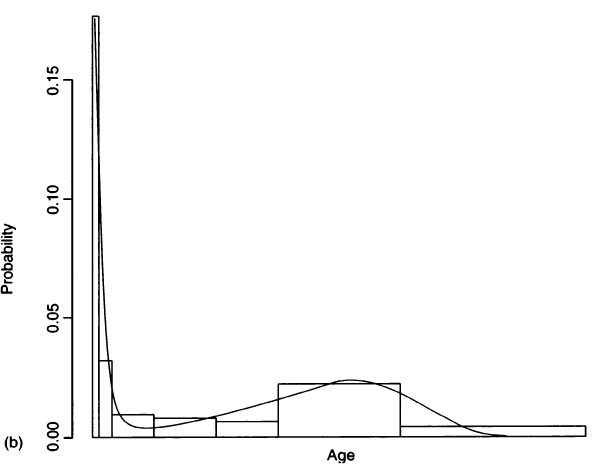
Figure 5 A comparison of Palkovich’s life table data with a four-parameter hazard model for Pecos Pueblo. (a) Life table survivorship values (open circles) compared with survivorship fit by the hazard model (solid line). (b) Palkovich’s d(x) (open bars) compared with the probability density function for age-at-death calculated from the hazard model (solid line).
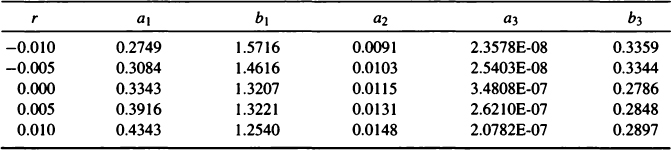
Hazard Parameters Estimated for Pecos Pueblo under Zero Growth, a High Rate of Population Decline (r = –0.015), and a Low Rate of Population Decline (r = –0.003)a
|
r = 0 |
r = –0.015 |
r = –0.003 |
a1 |
0.2398 |
0.3529 |
0.2628 |
b1 |
0.7519 |
0.7156 |
0.7564 |
a3 |
0.0024 |
0.0039 |
0.0028 |
b3 |
0.0832 |
0.0746 |
0.0804 |
Birth rate |
0.0366 |
0.0342 |
0.0362 |
Death rate |
0.0366 |
0.0492 |
0.0392 |
MAL |
20.61 |
22.22 |
20.85 |
MAD |
27.29 |
27.09 |
27.10 |
aAlso shown for each model are the crude birth and death rates, mean age in the living (MAL), and mean age-at-death (MAD).
244We also can generalize Eq. (1) to give the size of a founding population that would generate the observed number of skeletons in a nonstationary setting. Following Asch’s (1976) equation B-5 on his page 72, the size of the founding population (P0) is estimated as
(7) |
245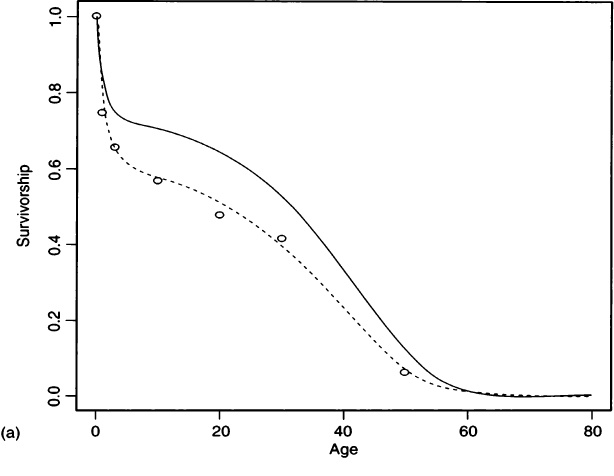
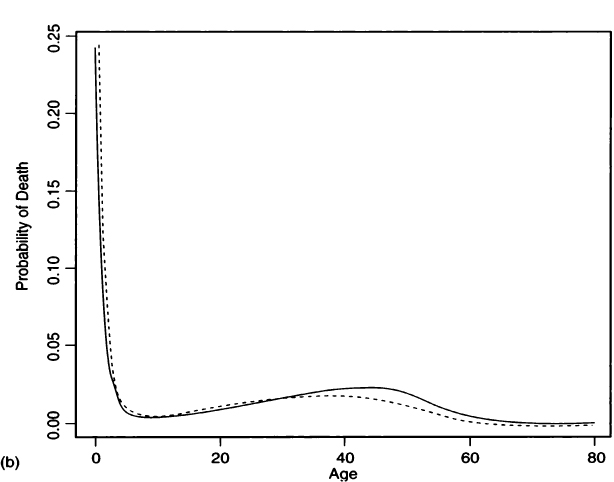
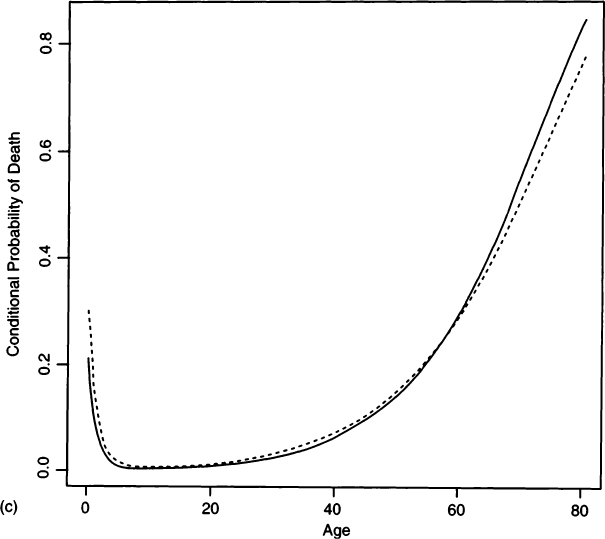
Figure 6 A comparison of hazard models for Pecos Pueblo assuming stationarity (r = 0.0, solid line) and population decline (r = –0.015, dashed line). (a) Survivorships fit by both hazard models and life table survivorship values (open circles) calculated for r = –0.015. (b) Probability of death functions for the two hazard models. (c) Conditional probability of death functions under both stationary and nonzero growth rates.
246where T is the length of the time interval and N is the number of skeletons. In the stationary case, d = b, the first integral equals T, the second integral equals 1.0, and P0 is simply P. Equation (1) is consequently a special case of Eq. (7). We use Eq. (7) and information from Hooton (1930) to try to estimate the number of deaths that should have occurred between 1500 and 1700 CE at Pecos Pueblo. Hooton (1930:336) used historical accounts and interpolation to suggest that the population sizes for 1500, 1533, 1566, 1600, 1633, 1666, and 1700 were 2600, 2440, 2280, 2120, 1920, 1640, and 1400 individuals, respectively. These population sizes imply a growth rate of about –0.003 per annum. Using this growth rate, assuming a “founding population” of 2600 people, and reestimating the hazard model over a 200-year time span (see Table III), we find that there should have been slightly more than 15,000 deaths during this 200-year span. This number of deaths is almost twice what Hooton (1930:337) estimated. The primary reason for his underestimate was that he did not accrue deaths continuously [as the integrals in Eq. (7) do], but instead treated Pecos as a series of 33-year-long birth cohorts.
247VIII. IS MEAN AGE-AT-DEATH A MEASURE OF MORTALITY IN NONSTATIONARY POPULATIONS?
In their 1983 article, Sattenspiel and Harpending raised the near heretical notion that when a paleodemographic life table from a nonstationary population is treated as if it were stationary, it will yield a mean age-at-death that is nearly the inverse of the crude birth rate. They then noted that the inverse of the mean age-at-death in such a setting is not a particularly good indicator of the crude death rate (Sattenspiel and Harpending, 1983). As their argument is based on continuous age rather than the discrete ages approximated by life tables, hazards analysis is an appropriate mechanism for exploring their argument. From the Pecos Pueblo example, we found a mean age-at-death of 27.29 when we fit a stationary model. If the population truly were stationary, then this figure is also the life expectancy at birth and the inverse of the crude birth and death rates, which would equal 0.037. In the nonstationary hazard model we found a mean age-at-death of 27.10, a mean age in the living of 22.22 years, a birth rate of 0.034, and a death rate of 0.049. Note that if we use a stationary model when the population was actually in a decline with r = –0.015, we would overestimate the crude death rate by about 24.5%, but we would underestimate the crude birth rate by only 8.8%. In the appendix to their paper, Sattenspiel and Harpending (1983:497) derived the relationship between mean age-at-death (āD), mean age in the living (āL), growth rate (r), and crude death rate (d) as
(8) |
In a later publication, Horowitz and Armelagos (1988:191) note after a rather lengthy derivation riddled with typos that “on close reading of the appendix to Sattenspiel and Harpending (1983) one does find a similar formula . . .” to the one Horowitz and Armelagos present. The equation given by Horowitz and Armelagos (their equation 9) is
(9) |
248which actually is identical with Sattenspiel and Harpending’s equation. Equation (8) can be rewritten as
(10) |
Equation (10) shows that when the growth rate is zero, the inverse of the mean age-at-death equals the crude birth and death rates. In a nonstationary population the ratio of the mean age of the living to the mean age-at-death is a critical element in determining whether crude birth rate or crude death rate would be better estimated by the inverse of the mean age-at-death. As the ratio of mean age in the living to mean age-at-death is generally in the vicinity of 1, we can see that the inverse of the mean age-at-death is typically a better estimator for the birth rate than for the death rate. When the mean age in the living and the mean age-at-death are equal, the birth rate will be equal to the inverse of the mean age-at-death, while the crude death rate will be misestimated by a factor of r.
An issue related to the relationship between birth rate and mean age-at-death is the claim that the error in fitting stationary models to growing populations can be isolated in certain more complex models. Gage (1988) suggests that in the Siler model [a model identical to Eq. (5) but with the addition of a constant baseline hazard parameter called a2] the error involved in fitting a stationary model to nonstationary data is entirely subsumed under one parameter (a2). The Appendix shows that there are different ways to apply the associative law to rewrite the Siler model and that the growth rate affects different parameters depending on how the model is rewritten. We also show by example that changes in growth rate affect all the parameter estimates (see Table IV) and that Gage’s claim consequently is incorrect. Hazard models, in and of themselves, do not allow us to circumvent the nonstationarity problem.
Example of the Effect of Various Growth Rates on Estimation of the Five Parameters in a Siler Model (see Appendix)
249IX. CAN WE EXPECT MORE FROM PALEODEMOGRAPHY?
The central criticism from Bocquet-Appel and Masset (1982) was that age determination methods and methods of paleodemographic reconstruction are so crude and inexact that paleodemography simply is not worth studying. They have continued to write prolifically about this topic (Bocquet-Appel, 1986, 1994; Bocquet-Appel and Masset, 1985, 1996; Masset, 1989, 1993), usually to maintain their critique, but on rare occasions to revisit that which they dismissed previously. Obviously, if raw data on which paleodemographers base their analyses are so tragically flawed and unfixable, then we must end our history in 1982 with the farewell from these authors. However, we believe that since 1982 there have been very hopeful developments in paleodemography, and we intend to end our history on this more upbeat note. A large number of salvos followed quickly on the heels of Bocquet-Appel and Masset’s critique and continued for a few years (Buikstra and Konigsberg, 1985; Greene et al., 1986; Lanphear, 1989; Piontek and Weber, 1990; Van Gerven and Armelagos, 1983). Although one of us was involved in this initial response, it was not until 10 years after the original Bocquet-Appel and Masset “farewell” that we published what we thought might end the debate (Konigsberg and Frankenberg, 1992). We were wrong in thinking this, and consequently we need to examine the full history of events over the last two decades.
We started working earnestly on the statistical use of age estimators in paleodemography in 1988. A publication in the journal Biometrics during the previous year (Kimura and Chikuni, 1987) entirely drove our way of thinking at that time. The authors of that article, both of whom worked in fisheries departments, had iteratively applied what is known as an “age-length key” in the fisheries literature. The age-length key is a tabulation of age classes against fish length developed using fish of known age as determined by counting otolith rings. As Kimura and Chikuni pointed out (1987), iterative application of the age-length key constitutes what is known as an EM algorithm (Dempster et al., 1977) and consequently is a maximum likelihood method. We also found in looking through the fisheries literature that the problem of “age mimicry” (Mensforth, 1990) that Bocquet-Appel and Masset described in 1982 had been described about 5 years earlier in the fisheries literature (Kimura, 1977; Westrheim and Ricker, 1978). Kimura (1977:318) wrote “the age-length key will give biased results if applied to a population where the age composition differs from that of the population from which the age-length key was drawn.”
The age-length key without iteration is a Bayesian method, and as such it uses age distribution of the reference sample as an informative prior when determining ages in a target sample. We knew this, fisheries workers certainly knew this, and Bocquet-Appel and Masset must have known this since they said as much 250in their 1982 article. Where we differed from Bocquet-Appel and Masset was that we felt, as did people in fisheries research, that this was not an insurmountable problem and that maximum likelihood estimation was the answer. It has continued to befuddle us through the years that Bocquet-Appel and Masset have so tenaciously argued against almost everything we have tried to do, when at the same time we have seen no “Farewell to Fisheries Demography” in the fisheries literature. We suspect that as fisheries science has a much greater economic impact than paleodemography, any abandonment of fish demography would have to come after considerable scientific and emotional expense. Granted, some of the methodological problems in paleodemography may be more difficult than those faced in fisheries science, but at least incorrect answers to paleodemographic questions are unlikely to have the drastic management effects that could arise from misestimates of fish stock.
We will not make a point-by-point response to Bocquet-Appel and Masset’s (1996) most recent critique, as this is not the appropriate place. Some of our differences seem to be simply based on misreading each other’s work. For example, in their 1996 paper, Bocquet-Appel and Masset discuss the idea of conditioning the reference sample on age, which has the effect of making age in the reference sample distributed uniformly. Bocquet-Apel and Masset (1996:573) then wrote: “This is where the idea to construct a uniform reference sample comes from, which was unfortunately interpreted as discarding data by Konigsberg and Frankenberg!” The reference they make to us is in regard to the following quote:
Bocquet-Appel (1986) suggested that if the reference sample has a uniform age distribution, then the target sample age distribution will be estimated independent of the reference. . . . While this solution does consequently remove the problem of dependence between the target and the reference age distributions, it is not in general a useful way to proceed. The chief problem with selecting a reference sample with a uniform age distribution is that this requires discarding data, which certainly cannot be an efficient way to proceed. (Konigsberg and Frankenberg, 1992:239)
The passage we were referring to from Bocquet-Appel was the following:
The only acceptable strategy for avoiding the influence of a particular reference population is to use a reference population in which the distribution is truly randomly distributed over the ages and, in this particular case an a priori uniform distribution . . . . (Bocquet-Appel, 1986:127)
A decade later Bocquet-Appel and Masset (1996:573) appear to have reinterpreted this passage to imply that one should condition on age in order to get the probability of being in a particular indicator state (their “simple technical trick”). If this was the intended message from Bocquet-Appel’s earlier article (Bocquet-Appel, 1986), then it is curious that he never indicated in that article how to use these sets of conditional probabilities in order to estimate the age-at-death structure for the target. That would await the 1996 publication.
251What we presented in 1992 was essentially the use of maximum likelihood methods in order to estimate the age-at-death structure for a paleodemographic sample using aging information from a reference sample (Konigsberg and Frankenberg, 1992). This was not an especially novel concept, as Boldsen (1988), Paine (1989), and Siven (1991) had already discussed likelihood applications in paleodemography. Bocquet-Appel and Masset’s 1996 article was a claim for historical priority, as well as an argument that only the mean age-at-death can be estimated reliably using what we would call contingency table paleodemography (see the Appendix; Konigsberg and Frankenberg, 2002). They did not feel that the actual age structure (i.e., distribution of age-at-death within categories) could be determined accurately. Bocquet-Appel and Masset (1996) tried to demonstrate their point using simulation studies, arguing that their method, which they refer to as iterative proportional fitting, differed from what we presented in 1992 (Konigsberg and Frankenberg, 1992), which they refer to as iterative Bayesian. We are disinclined to trust their simulations because they managed to demonstrate differences between two methods that are identical (i.e., if you start both methods with the same data, each steps through the parameter space in the same way and thus gives identical results, as shown in the Appendix).
There have been other suggested methods for determining adult age-at-death within paleodemography. Jackes (1985) suggested using normal distributions of age within pubic symphyseal phases in order to get smooth distributions of age for target samples and has continued to apply this method (Jackes, 2000). The chief problem with this method is that the resultant age distributions for the target are in part dependent on the reference sample, a problem that was specifically noted in Bocquet-Appel and Masset’s (1982) original critique. Jackes (2000:435) also has tried using the contingency table paleodemographic approach, finding that the method “is shown to be completely ineffective in replicating the real age-at-death distribution.” However, she was attempting to fit a life table with 17 age categories using a six-phase indicator, and her solution has many age categories estimated with zero frequencies. This represents a solution on a boundary of the parameter space, and as such there is no unique likelihood solution (Fienberg, 1977:132). In other words, as stated by Clark (1981:299), “If I < J (i.e., the number of length intervals is less than the number of age-groups with distinct length distributions), there will usually be a multiplicity of algebraic solutions and therefore no useful estimates.”
An additional topic from Bocquet-Appel and Masset (1996) is the use of what they have called a “juvenility index” (or JI). The JI is a ratio of “the number of dead from 5 to 14 and the number of dead after 20 (D5–14/D20–ω)” (Bocquet-Appel and Masset, 1996:580). Bocquet-Appel and Masset first introduced this index in 1977 in order to estimate mean age-at-death for samples that had underenumeration of 0–5 year olds and where age-at-death estimates might be highly questionable (Bocquet and Masset, 1977). They then used 40 paleodemographic 252life tables and regressed mean age-at-death on the JI (Bocquet-Appel and Masset, 1982). By 1996 they had elaborated these regressions to include nonstationary growth rates (Bocquet-Appel and Masset, 1996). Buikstra and colleagues (1986) took a similar approach, but calculated the proportion of deaths over age 30 out of deaths over age 5 (D30–ω/D5–ω). Proportions have slightly simpler statistical properties than ratios [compare Buikstra et al. (1986) to Masset and Paryzysz (1985)], which is the reason Buikstra and colleagues used the former. Buikstra et al. (1986) then used regressions of crude birth rate and crude death rate on their death proportion in nonstationary models drawn from Coale and Demeny (1966). Using these regressions, they showed [following Sattenspiel and Harpending’s (1983) suggestion] that the birth rate was more highly correlated with the death proportion than the crude death rate. However, Buikstra and colleagues (1986) cautioned against using the regressions to estimate crude birth rate and instead used a direct comparison of death proportions across time in west central Illinois to suggest an increased birth rate with the development of Mississippian culture. Storey (1992:174) has since applied such an analysis to Tlajinga-33, and there has been extensive discussion of using death ratios and proportions in the literature (Corruccini et al., 1989; Hoppa, 1996; Konigsberg et al., 1989; Paine and Harpending, 1998).
Near the end of our 1992 paper we spelled out future directions for paleodemography that included both reworking of then-current approaches and development of new methods. For example, we suggested switching to appropriate methods for age structure estimation, understanding reference samples, evaluating the efficiency of parameter estimators, developing methods for comparing different anthropological or paleodemographic samples, and incorporating uncertainty of age estimates into reduced parameterizations of life table functions (Konigsberg and Frankenberg, 1992). The incorporation of age estimation within hazard models is one direction that others and we have taken (Konigsberg and Holman, 1999; Milner et al., 2000; Müller et al., 2002; O’Connor, 1995) and is a cornerstone of the “Rostock Manifesto” (Hoppa and Vaupel, 2002). An additional area we did not consider at the time was the use of ordinal parametric models such as logistic and probit regression to describe the development of age indicators that are phase- or stage-based. Boldsen (Skytthe and Boldsen, 1993) pioneered this approach in paleodemography, referring to it as transition analysis because it models the age-to-transition between phases (see also Milner et al., 2000; Boldsen et al., 2002). As a consequence of the developments since 1992 we have almost completely abandoned contingency table approaches to paleodemography because they do not make good use of the ordinal nature of stage data or the continuous nature of age-at-death. Contingency table type approaches are still found within paleodemographic analyses (Gowland and Chamberlain, 2002; Jackes, 2003), but we suspect that they will eventually decrease in popularity.
253Another direction since our 1992 paper that we did not anticipate was the growth of Bayesian methods in age estimation (Di Bacco et al., 1999; Lucy, 1997; Lucy et al., 1996). Although we (Konigsberg and Frankenberg, 1994; Konigsberg et al., 1998) and others (e.g., Milner et al., 2000) have found Bayesian logic and terminology useful, we are uncomfortable with the wholesale implementation of Bayesian methods in paleodemography. Lucy (1997) and Lucy et al. (1996) used the reference sample age distribution for their informative prior, which returns us to the original Bocquet-Appel and Masset (1982) critique. Di Bacco et al. (1999) have presented a Bayesian solution where they take vague priors for hazard parameters and then update these with information from the reference and target samples. This is a more hopeful method, although we have not yet seen an implementation or example of this type of analysis in the literature.
It seems clear to us that the statistical issues currently swirling around paleodemographic analysis will settle in the near future. A good sign that some consensus is being reached is the publication of “Palaeodemography: Age Distributions from Skeletal Samples” coedited by Rob Hoppa and Jim Vaupel (2002). That volume shows a fairly united front shared by both North American and European researchers and codified in the so-called “Rostock Manifesto.” Consensus does not, however, mean the solution to all our problems. Cultural and archaeological sampling issues remain a considerable problem (Hoppa, 1999), as does the issue of Howell’s (1976) “uniformitarian assumption” regarding rates of aging. Hoppa’s (2000) publication of different rates of aging for the pubic symphysis is a disturbing message, although we suspect that the differences between reported samples reflect interobserver differences, not intersample differences in aging. If this is indeed the case, then there is a strong argument for standardization of observation methods and for interobserver error studies conducted on the same samples. Ultimately, the “uniformitarian assumption” is just that, an untestable assumption. However, the calibration literature (Brown, 1993; Brown and Sundberg, 1987, 1989; Konigsberg et al., 1998), which has been rather widely ignored in paleodemography (exceptions are Aykroyd et al., 1996, 1997) could be applied in this context. In multivariate calibration there is a “consistency diagnostic” that can be calculated for samples of unknown age-at-death. This diagnostic tests for whether aging rates in the unknown age sample are discordant when compared to the reference sample.
The history of paleodemography is far from over, as researchers continue to refine both measurement and analytical methods and to address the issues described earlier (e.g., Chamberlain, 2000; Meindl and Russell, 1998; Milner et al., 2000; Paine, 2000). It is hoped that paleodemographic studies are now moving into an evaluation phase. By evaluation we mean systematically critiquing the strength, applicability, and reliability of age estimation techniques and developing models that realistically reflect paleodemographic processes and measure the impacts upon them. Evaluation also means using statistically sound, 254anthropologically pertinent measures to assess what is being measured and to enable researchers to assign confidence limits to their results. The refinement of paleodemographic methods, the solution of measurement and analytical issues, and the development of consensus among some paleodemographers will play only minor roles in the future of paleodemography, however, unless bioarchaeology as a field adopts current methods and contributes to this evaluation.
ACKNOWLEDGMENT
Order of authorship was determined by a draw of straws.
255Appendix
I. INTRODUCTION
This appendix makes extensive use of the general statistical, mathematical, and graphics package known as “R.” “R” is an S-like free software package initially developed by Robert Gentleman and Ross Ihaka in the Statistics Department at the University of Auckland and added to by numerous members of a working group. It is available under Free Software Foundation’s GNU General Public License for a number of computing platforms and operating systems, UNIX, FreeBSD, Linux, and Windows 9x/NT/2000. We strongly recommend that readers of this chapter download “R” so that they can work through some of the examples given. Additional information on “R” is available on the Internet at http://www.r-project.org/.
II. MAXIMUM LIKELIHOOD ESTIMATION OF HAZARD MODEL PARAMETERS
In the maximum likelihood estimation method we form a parametric model to describe observed data. The parametric model is characterized by its parameters, and once we establish particular values for the parameters, we can find the log probability (up to an additive constant) of obtaining observed data. If we maximize this log probability by searching through the parameter space (i.e., trying different values for the parameters), then we will have found the most likely parameter values to have generated observed data; hence, the name maximum likelihood estimate. In a hazard model we have a parametric description for survivorship to exact age t. The probability of death between two exact ages is the difference between survivorship at the beginning and at the end of the age interval. The log-likelihood is defined as the sum across intervals of the products of the observed count of deaths in each interval with the estimated log probability of death in that interval. The “R” function calculates the log likelihood for the Gompertz model using the Pecos Pueblo example where 0.5 of the deaths fall between 0 and 33.33 years of age, 0.4 fall between 33.33 and 66.67 years of age, and 0.1 fall between 66.67 and 100.0 years of age.256
function(x) {
a <- x[1] # put x vector in a & b
b <- x[2]
t<-c(0,100/3,200/3,100) # ages are 0, 33.33, 66.67,
& 100
l<-exp(a/b*(1-exp(b*t))) # Gompertz survivorship
at ages
d<-l [1:3]-1[2:4] # difference 1(t) to get d(x)
obs<-c(.5,.4,.1) # observed d(x) for Pecos
Pueblo
lnlk<-obs%*% log(d) # form the log-likelihood
return(lnlk) # return log-likelihood
}
Now the “optim” function in “R” can be called in order to maximize the log likelihood. We call “optim” with starting values of 10–6 for a and b, assume that the aforementioned function is stored as “Gompertz,” and set “fnscale” to a negative value in order to maximize, instead of minimize, the log likelihood.
optim(c(1E-6,1E-6), Gompertz, control=list (fnscale=-1))
We can also fit more complicated hazard models by maximum likelihood. For example, we fit a four-parameter model to Pecos Pueblo data. The model is
(1) |
Data are in a file called “pecos,” which looks like the following:
[,1] [,2] [,3]
[1,] 0 1 322
[2,] 1 3 117
[3,] 3 10 120
[4,] 10 20 145
[5,] 20 30 108
[6,] 30 50 772
[7,] 50 80 189
[8,] 20 80 51
The first column ([,1]) is the beginning of an age interval, the second column ([,2]) is the end of that age interval, and the third column ([,3]) is the number of skeletons in the interval (from Palkovich, 1983). The eighth row ([8,]) contains 25751 individuals who can be aged no more precisely than as adults between 20 and 80 years old. The likelihood function can be calculated with the following “R” function:
function(x,deaths=pecos) {
al <- x[1]
bl <- x[2]
a3 <- x[3]
b3 <- x[4]
t<-deaths[,1:2]
l<-exp(-a1/b1*(1-exp(-b1*t)))*exp(a3/b3*(1-exp(b3*t)))
d<-l[,1]-l[,2]
obs<-deaths[,3]
lnlk<-crossprod(obs,log(d))
return(lnlk)
}
As with the Gompertz model, this function also can be maximized using “optim.”
III. EXTRACTING SUMMARY MEASURES FROM HAZARD MODELS
Most summary measures from hazard models, such as mean age-at-death, birth rate, and death rate, require numerical integration. This can be done using the add-on library “integrate” in “R.” For example, to find the mean age-at-death in a Gompertz model we would integrate survivorship from age 0 to the maximum (we assume 100 years), which in “R” could be written as
integrate(function(t,a=.01265,b=.02693)
{exp(a/b*(1-exp(b*t)))},0,100)
This call would return the value 35.52587, which is rounded to the nearest first decimal place in the text of the chapter.
258IV. FITTING A HAZARD MODEL WITH A KNOWN NONZERO GROWTH RATE
To fit a nonzero growth rate hazard model we have to include integration within the likelihood equation [see Equation (6) in the text of the chapter]. An “R” function for calculating the likelihood is given. As with the preceding functions, this function can be called by “optim” in order to maximize the function, but this call should be made only after fitting the stationary model to get good starting values.
function(x,r=-.015,deaths=pecos) {
al <- x[1]
bl <- x[2]
a3 <- x[3]
b3 <- x[4]
t<-deaths[1:7,1]
ipdf<- function(t) {
1<-exp(-a1/b1*(1-exp(-b1*t)))*exp(a3/b3*(1-exp(b3*t)))
*exp(-r*t)*(a1*exp(-b1*t)+a3*exp(b3*t))
}
for(i in 1:7){
L[i]<-integrate(ipdf,t[i],80)$value
}
L<-L/L[1]
d<-L[1:6]-L[2:7]
d<-c(d,L[7],1-d[1]-d[2]-d[3])
obs<-deaths[,3]
lnlk<-crossprod(obs,log(d))
return(lnlk)
}
V. EFFECT OF AN UNKNOWN GROWTH RATE ON ESTIMATION OF HAZARD PARAMETERS
Gage has suggested that for a five-parameter Siler model:
. . . the effect of applying the stationary model to a population that is growing or declining will cause misestimation of a2 equal to the magnitude of the intrinsic rate of increase. On the other hand, the remaining parameters are unaffected and can be compared across populations without restriction. . . . (Gage, 1988:440)
259However, his statement is based on an erroneous derivation. He notes that when fitting survivorship to a stable age distribution, the frequency of individuals exactly age t years old is
(2) |
where Nt is the number of individuals t years old and B is the number of births. He then uses the associative property of multiplication to rewrite Eq. (2) as
(3) |
which gives the appearance that the growth rate is “absorbed” onto the a2 parameter. However, there are many other ways to apply the associative law, such as
(4) |
which gives the impression that the growth rate only affects estimation of the two parameters in the juvenile component of mortality.
Table IV tabulated estimates of the five parameters in a Siler model starting with a stationary model, adjusting the deaths to follow a nonstationary model, and then estimating the Siler model assuming a stationary population. It is clear from Table IV that, at least for this mortality pattern, changes in growth rate affect all of the parameter estimates.
VI. CONTINGENCY TABLE PALEODEMOGRAPHY
Konigsberg and Frankenberg (1992) and Bocquet-Appel and Masset (1996) have presented what we would refer to as “contingency table paleodemography.” In contingency table demography, a reference sample is cross-tabulated by age and an age indicator, and tabulation of the indicator in a target sample is used to estimate the (unobserved) marginal distribution of age in the target. 260As an example of such an approach we use reference and target data taken from Bocquet-Appel and Bacro (1997), as follows:
Stage
I II III IV V VI
Age
23-29 8 19 30 7 1 0
30-39 2 18 43 25 1 0
40-49 0 6 29 27 5 1
50-59 0 2 26 37 13 0
60-69 0 0 9 28 9 1
70-79 0 0 7 28 10 3
80-89 0 0 2 10 10 5
Target 2 8 31.5 40.5 12 2
We have written two “R” functions, the first after Konigsberg and Frankenberg (1992) following Kimura and Chikuni (1987), and the second after Bocquet-Appel and Masset (1996). In each function “n1” is the reference sample data given as age by indicator (as shown earlier), and “n2” is the target vector. These are rather Spartan routines (e.g., they have the number of iterations “hard-wired,” with no convergence check) that show the simplicity of the algorithms.
function (nl=nij1,n2=nj 2,niter=200) # Konigsberg and
Frankenberg
{
nrc-NROW(n1)
nc<-NCOL(n1)
pia<-nl/apply(n1,1,sum) # pia from reference
N<-sum(n2)
da<-rep(N*1/nr,nr) # Start from uniform da
for (iter in 1:niter) {
pai<-(da%o%rep(1,nc)*pia)/ # K&F eqn. 9
(rep(1,nr)%o%
(apply(da%o%rep(1,nc)
*pia,2,sum)))
da<-as.vector(t(n2)%*%t(pai)) # K&F eqn. 10
}
return(da)
}
function (nl=nij1,n2=nj2,niter=200) # Bocquet-Appel and
Masset
{
nr<-NROW(n1)
nc<-NCOL(n1)
ma<-rep(sum(nj2)/nr,nr)
fia<-(n1)/((n1%*% rep(1,nc)) # fia from reference
%*%rep(1,nc))
fi<-apply(fia,2,sum) # fi from reference
for (i in 1:niter) {
fai<-fia/(rep(1,nr)%*%t(fi)) # B-A&P eqn 1.
ma2<-fai%*%n2 # B-A&P eqn 2.
fia<-fia*(ma2/ma)%*%rep(1,nc) # B-A&P eqn 3.
fi<-apply(fia,2,sum) # B-A&P eqn 4.
ma<-ma2
}
return(as.vector(ma))
}
261After 200 iterations the estimated age distribution from either function is 13.556024, 11.238048, 16.889118, 20.163258, 18.448143, 12.991268, and 2.714141, while after 20,000 iterations the age distribution is 15.851453, 2.182010, 27.973884, 17.821325, 14.883364, 15.727492, and 1.560473. We also have fit the age distribution by numerically maximizing the log-likelihood (in “optim”), which gives an age distribution of 17.761260, 2.902435, 30.032820, 22.258262, 12.926188, 20.902711, and 1.216324. While the mle converged properly, the standard errors on the estimated parameters are enormous. None of the standard errors is less than 100, whereas the parameters are all proportions between 0 and 1. This is a clear indication that there is insufficient information in the data, a result of fitting more age categories than there are indicator states. Other examples we have tried [e.g., Hoenig and Heisey’s (1987) example at the bottom of their page 242] do converge properly with reasonable standard errors.262