CHAPTER 2
Phases of Matter
Every day you encounter substances that exist in different phases—the air you breathe, the water you drink, and your mom’s wooden cooking spoon. This chapter will take a closer look at the phases of matter and the changes in phase that matter can undergo.
Gases
The basic properties of gases are these:
• Gases have no definite volume and can be compressed.
• Gases have no definite shape and take the shape of their container.
• Gas molecules are spread far apart.
In addition to these basic properties, there are a number of theories and laws that tell more about how gases behave. These are the major focus of this chapter.
Kinetic Molecular Theory
The behavior of gases can further be explained with Kinetic Molecular Theory, or KMT. KMT tells the following:
• Gas molecules are individual particles that travel in a straight-line random motion. This will continue until they collide or are acted upon by another force.
• Gas molecules continuously collide and transfer energy during these collisions. In an isolated sample of gas the net energy is conserved.
• The volume of the individual gas molecules is negligible compared to the volume they occupy.
• No forces of attraction are considered to exist between the gas molecules.
Pressure
Gases exert a pressure on other objects as they collide. This pressure exerted by a gas can be defined as the amount of force exerted on an area. Anyone who has watched or listened to a weather report can recall hearing about the barometric pressure or atmospheric pressure. These pressures can differ as high and low pressure systems move across a particular region. There are two devices used to measure pressure exerted by gases, the mercury barometer and the manometer. Both devices can be useful depending upon the situation.
The mercury barometer (see Figure 2.1) uses a glass column filled with mercury that is inverted into a container filled with mercury. As you move to higher altitudes the level of the mercury in the glass column drops because there is less air present at the higher altitude. On average, the height of the mercury in the column is 760 millimeters higher than the level of mercury in the container. This average pressure is called standard pressure or normal barometric pressure.
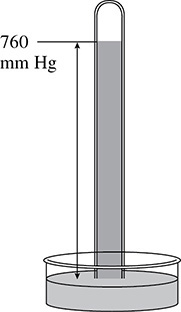
Figure 2.1 A Mercury Barometer
There are a number of units that can be used to measure barometric pressure. For example, millimeters can be converted into inches; thus, a standard pressure of 760 mm Hg can also be recorded as 30.0 inches of mercury. Inches of mercury are the units used for weather reports in the United States. Three other very common units that correspond to 760 mm Hg are:
• 1.0 atmospheres (atm)
• 760 torr (after Evangelista Torricelli)
• 101.3 kilopascals (kPa)
One final unit encountered in measuring pressure is pounds per square inch (psi). This unit is usually reserved for measuring the air pressure in a car’s tires at gas stations in the United States.
A manometer is used to determine the pressure of a gas that is confined in a vessel. The shape and opening at the top of the manometer allow a certain amount of mercury to be shifted depending upon the atmospheric pressure and the pressure of the gas in the vessel. There are three situations to consider when using a manometer: gas pressure being equal to the atmospheric pressure, gas pressure being greater than the atmospheric pressure. and gas pressure being less than the atmospheric pressure. These situations can be seen in Figure 2.2.
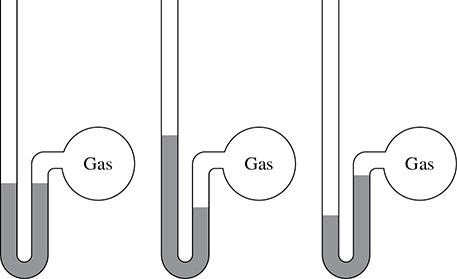
Figure 2.2 Three Manometers
Boyle’s Law
Robert Boyle performed experiments to see how varying the pressure on a gas would affect the volume of the gas. His experiments showed that as the pressure on a gas was increased, the volume that the gas occupied decreased. In Figure 2.3, the diagram on the left shows a piston that is not putting much pressure on a sample of a gas. The diagram in the center shows that the piston has been pressed downward, increasing the pressure on the gas. In response to the increase in pressure, the volume of the gas has decreased.
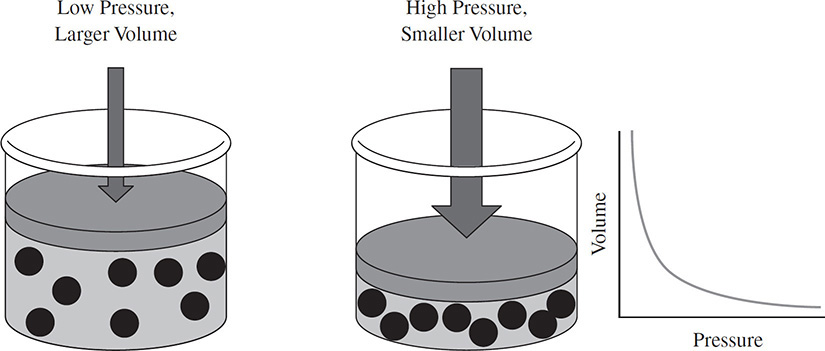
Figure 2.3 Boyle’s Law
Boyle was able to determine that, at a constant temperature, there was an inverse relationship between pressure and volume. That is, as the value of one factor increased, the value of the other factor decreased. The graph in Figure 2.3 shows the mathematical relationship between pressure and volume. The equation P1V1 = P2V2 can be used to perform calculations using Boyle’s Law to determine the final volume of a gas after it has undergone a change in pressure.
Problem:
A gas that occupies 22.4 liters has the pressure on it increased from 760 torr to 1520 torr. What is the new volume? Why does your answer make sense?
Solution: The initial volume of the gas is 22.4 liters (V1) at an initial pressure of 760 torr (P1). The new pressure is 1520 torr (P2).
Using the equation P1V1 = P2V2 we rearrange to solve for the new volume so that the equation looks like P1V1/P2 = V2.
Substituting we have:
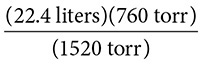
The value of the new volume is 11.20 liters.
Does the answer make sense? Yes. The pressure was increased/doubled; therefore, the volume must decrease/be halved. The answer clearly shows a volume that is less than that of the original 22.4 liters.
THINK ABOUT THIS 
Charles’ Law
Jacques Charles did quantitative experiments involving the effect of temperature changes on the volume of gases. Through various experiments, he was able to quantify the relationship between temperature and volume. This relationship, unlike the relationship expressed by Boyle’s Law, was found to be a direct relationship. That is, as the temperature of a gas increased, so did the volume of the gas. The graph in Figure 2.4 demonstrates a direct relationship:
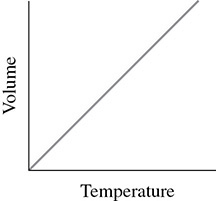
Figure 2.4 Charles’ Law
It is important to examine the topic of temperature before attempting to calculate using Charles’ Law:
THINK ABOUT THIS
Problem:
A sample of a gas at STP occupies 11.2 liters. The temperature of the gas is changed to 273°C. What is the new volume of the gas? Does your answer make sense?
Solution: First we will need to convert the temperatures to Kelvin. The initial temperature of the sample (T1) is 273 K. The new temperature is (T2) K = 273 + 273 = 546 K. The initial volume (V1) is 11.2 liters. Using Charles’ Law and substituting we get:
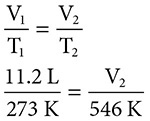
Solving gives us an answer of 22.4 liters. Did we do this right? Yes, an increase/doubling in the temperature resulted in an increase/doubling in the volume of the gas.
Temperature
Temperature is defined as the average kinetic energy of a sample. What does temperature really measure? Many people confuse temperature with heat. Temperature measures motion, hence the definition “average kinetic energy.” There are two important temperature scales to know in chemistry, Celsius and Kelvin. The Celsius scale is based upon the freezing points and boiling points of water, 0°C and 100°C respectively. The Kelvin scale is based upon the lowest temperature that can be achieved, 0 K, or absolute zero. It is believed that, at absolute zero, all motion of molecules stops. The relationship between Celsius and Kelvin is K = C + 273. The Kelvin scale is used when solving problems because, unlike the Celsius scale, the Kelvin scale does not result in a negative number or a zero to multiply or divide by.
Problem:
What are the boiling and freezing points of water on the Kelvin scale?
Solution: The boiling point of water is 100°C. Because K = C + 273, 100 + 273 = 373 K. Using the same equation, the freezing point of water will be 273 K.
Standard Temperature and Pressure
Because experiments can involve a wide range of conditions that can affect the experiment’s outcome, a standard needs to be set to create a common set of conditions. Standard temperature and pressure, or STP, is defined as 0°C and 1 atm (273 K and 760 torr).
Average Kinetic Energy of Gases
Even though an increase in temperature results in an increase in the average kinetic energy, not all of the gas molecules will have the same amount of kinetic energy. This is why the term “average kinetic energy” is used. The two curves in Figure 2.5 show the distribution of molecular speeds of a gas at two different temperatures. Notice that at a higher temperature the gas molecules are moving with more kinetic energy.
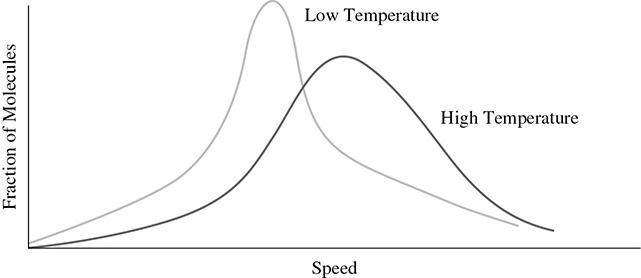
Figure 2.5 Kinetic Energy
Combined Gas Law
Charles’ and Boyle’s Laws are used when the pressure and temperature of a system are held constant, respectively. What happens if pressure, temperature, and volume are all changed in a problem? The Combined Gas Law, 
, combines the laws of Charles and Boyle. Notice that if you cover the T’s with your finger, Boyle’s equation remains. Likewise, if you cover the P’s, Charles’ equation remains. Rather than memorizing both equations for Charles’ and Boyle’s Laws, it is much easier to just remember the Combined Gas Law and “cover” the variables that are being held constant.
Problem:
A 5.6 liter sample of neon gas is at STP. If the temperature is increased to 298 K and the pressure changed to 600 torr, what will the new volume of the gas sample be?
Solution: The problem starts at STP, meaning that P1 = 760 torr and T1 = 273 K. The initial volume is 5.6 liters, so V1 = 5.6 L. The final pressure P2 is 600 torr and the final temperature is 298 K.
Next, use the Combined Gas Law:
Substitution gives: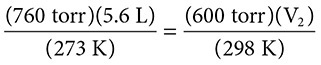 
Cross-multiply and divide to solve for the new volume:
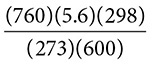= 7.7 liters. Ask yourself, Does the answer make sense?
The temperature was increased and the pressure was decreased, therefore the volume should be greater than the original 5.6 liters.
Dalton’s Law of Partial Pressures
Dalton discovered that when gases are mixed in the same container and they have the same temperature, the total pressure exerted by the gases is equal to the sum of the pressures exerted by the individual gases. This can be seen in the equation: Ptotal = Pgas1 + Pgas2 + Pgas3. . . . Consider a container that has a mixture of nitrogen and oxygen gas. If the pressure of the oxygen gas is 400 torr and the pressure of the nitrogen gas is 360 torr, what is the total pressure? Using Dalton’s Law of Partial Pressures, the total pressure is the sum of these individual pressures, 760 torr.
Problem:
Refer to the example given above. Write an equation for the partial pressures of nitrogen and oxygen. If the total pressure in the container is 900 torr and the partial pressure of the oxygen gas is 560 torr, what is the partial pressure of the nitrogen gas?
Solution: The equation is Ptotal = PO2 + PN2. The total pressure of 900 torr minus the partial pressure of the oxygen gas, 560 torr, gives the pressure of the nitrogen gas, 340 torr.
Avogadro’s Law
Avogadro’s work will be examined in greater detail in Chapter 6. For now just learn this rule: Equal volumes of gases will contribute to the total pressure equally. For example, suppose a container is filled with 50% neon gas and 50% argon gas and the total pressure of the gases is 760 torr. The pressure of each gas would be 380 torr. If the volumes of the gases are not equal, the percentage of the volume that each gas occupies will contribute an equal percentage to the total volume.
Problem:
A container has three gases mixed together at STP. The container has (by volume) 10% He, 40% neon, and 50% argon. What is the partial pressure of the three gases?
Solution: Because this mixture of gases is at STP, the total pressure will be standard pressure, 760 torr. Because of the percentages of the gases have been given, we can set up the following:
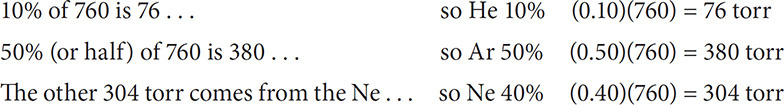
Check your work. Does the sum of the partial pressures equal the total pressure of 760 torr?
Graham’s Law of Diffusion/Effusion and Density of Gases
Have you ever walked into a room and noticed the odor of an open bottle of perfume? If the open bottle of perfume is on one side of the room, why can you smell it on the other side of the room? Gases travel with great speeds and they can spread out or diffuse. According to Graham’s Law, at the same temperature and pressure, gases diffuse at a rate inversely proportional to the square roots of their molecular masses. This can be seen in the equation:
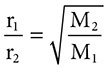
Even though this may seem a bit difficult to digest, it can be simply put as “lighter, less dense gases will travel at greater speeds.”
Because gases are light, you need a larger sample of gas to measure the mass of a given sample. For convenience, you can assume a 22.4-liter sample
(for reasons to be discussed later) and use the equation: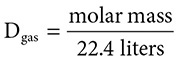 
Problem:
Calculate the effusion rate of nitrogen gas to oxygen gas. How does this compare to the density of the gases?
Solution:
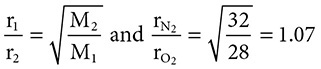
Because the value of the ratio of the rates is greater than 1.00, the numerator, the rate for N2, had a greater value. Because the nitrogen gas is lighter in mass, it should travel at faster speeds. Calculating the densities of these gases,
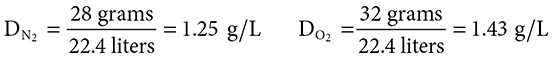
you can see that density and rate of effusion are inversely proportional, N2 has a greater rate of effusion and a lower density.
THINK ABOUT THIS
Ideal Gas Law—Relating Pressure, Volume, Temperature, and Moles
The Ideal Gas Law is derived from Kinetic Molecular Theory. Now that you have examined some gas laws, you can rephrase KMT and realize that ideally, gas molecules:
• Should be as far apart as possible (low pressures and high temperatures are best for this condition)
• Should have as little mass as possible (like H2 or He)
• Should have no attraction for each other (we will discuss nonpolar molecules and forces of attraction later in the book)
It should be noted that gases do deviate from ideality, and there are equations that can adjust calculations to compensate for nonideal situations. These equations, however, are complex and are beyond the focus of this review.
By definition, an ideal gas obeys the equation PV = nRT. You will notice two new variables in this equation, n and R. The variable n stands for the number of moles of the gas and R is a constant. Before you can use this equation you must first become familiar with the mole and what it stands for.
If you buy a dozen eggs you expect to open the carton and find 12 eggs inside. The term “dozen” is used as a substitute for the word “twelve.” The same idea applies when using the term “mole.” A mole of “something” is equal to 6.02 × 1023 of those “things.” For example a mole of carbon atoms is 6.02 × 1023 carbon atoms. The number 6.02 × 1023 is also known as Avogadro’s Number.
As for the constant, R, the value of this constant depends upon the units being used for pressure, temperature, and volume. When you use the conventional units of liters, atmospheres, and Kelvin, the value and units are 0.0820 (L•atm)/(mol•K).
Problem:
How many molecules of H2 gas are present in a 11.2 liter sample at 273 K and a pressure of 760 mm Hg?
Solution: The pressure is 760 mm Hg; this is equal to 1.0 atm. The volume of the gas is 11.2 liters and the temperature is 273 K. From the above you know that R = 0.0820 (L•atm)/(mol•K). The Ideal Gas Law is PV = nRT. Substituting gives: (1.0 atm)(11.2 L) = (n)(0.0820L•atm)/(mol•K)(273 K).
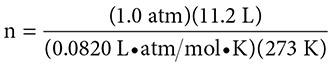
Solving gives an answer of 0.50 moles of H2 gas. Because one mole of a gas contains 6.02 × 1023 molecules of the gas, 0.50 moles of the gas will contain half of Avogadro’s number, or 3.01 × 1023 molecules of H2 gas.
Liquids
Liquids are characterized by their definite volume. Unlike gases, liquids (for the most part) cannot be compressed. Liquids, like gases, do not have a definite shape and will take the shape of the container they are placed in. The molecules of a liquid are constantly touching one another because of the forces that exist between them and hold them together. These forces are not strong enough to hold the molecules in a fixed position as is the case for solids.
Liquids are constantly evaporating at their surface. That is, the molecules at the surface of the liquid can achieve enough kinetic energy to overcome the forces between them and they can move into the gas phase. This process is called vaporization, or evaporation. As the molecules of the liquid enter the gas phase, they leave the liquid phase with a certain amount of force. This amount of force is called the vapor pressure. Vapor pressure depends upon the temperature of the liquid. Think about a pot of water that is being heated in preparation for dinner. The water starts out cold and you do not see any steam. As the temperature of the water increases you begin to see more steam. As the temperature of the water molecules increases, the molecules have more kinetic energy, which allows them to leave the liquid phase with more force and pressure. You can then conclude that as the temperature of a liquid increases, the vapor pressure increases as well. This is a direct relationship.
Boiling Point
As mentioned earlier, the boiling point of water is 100°C or 373 K. Why does this phenomenon occur at this temperature? Does it always occur at this temperature? Is it true that water will boil at 100°C or 373 K provided that the atmospheric pressure is 760 torr? A temperature of 100°C or 373 K is what is referred to as the normal boiling point of water, the temperature at which water will boil when the atmospheric pressure is 760 torr. But why does water boil at this temperature? When water is heated to 373 K, the vapor pressure of the water molecules is 760 torr, a vapor pressure that is exactly the same as the atmospheric pressure! That answers the question: A liquid boils when the atmospheric pressure is equal to the vapor pressure of the liquid.
Does water always boil at 100°C? No, it does not, because atmospheric pressure can change. If a low pressure system is over the region where you live, atmospheric pressure is lower and water will boil at a temperature below 100°C because a lower temperature is needed to achieve the lower required vapor pressure.
THINK ABOUT THIS
Solids
Solids are characterized by their definite shape and volume. The atoms in a solid have a rigid, fixed, regular geometric pattern. These properties result from the fact that atoms in a solid constantly vibrate, but vibrate in place. When solids are heated to high enough temperatures, they have enough kinetic energy to undergo the process of melting and turning into a liquid. The melting point of a solid is the temperature at which this occurs. When a liquid changes into a solid, the process is called freezing. It should be pointed out that the melting and freezing points of a solid are the exact same temperature. For example, ice melts at 273 K and water freezes at 273 K. This is why solids and liquids are listed together in the phase change diagrams that follow.
Sublimation and Deposition
Why is it that when you buy ice cream from a vendor in a park on a hot summer day, the ice cream wrapper is not soaked with water from the “ice” that is used to keep it cold? Is the vendor using ice at all? “Dry ice” is the term for solid carbon dioxide. Dry ice can change from the solid phase right to a gas phase, without any apparent liquid phase in between. This process is called sublimation. Some other substances that can sublime are mothballs (naphthalene) and solid iodine. Deposition can be thought of being “the opposite of” sublimation. In this process a gas will form a solid, again without any apparent liquid phase in between.
Phase Changes
Matter can exist in three phases: solid, liquid, and gas. Figure 2.6 summarizes the names of the changes that phases can undergo.
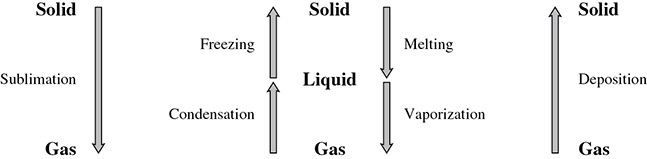
Figure 2.6 Phase Change Comparison
A heating curve is also helpful in looking at phase changes over time. Figure 2.7 is an example of a heating curve, specifically a heating curve for water.
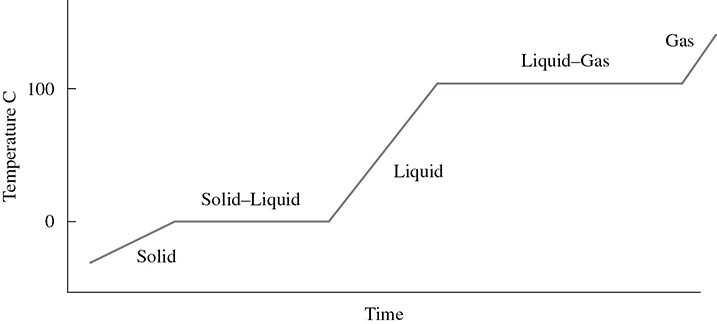
Figure 2.7 Heating Curve for Water
In this diagram, heat is being applied to a sample of ice. The temperature of the ice will increase until it reaches 0°C. At this point the solid and liquid phases exist at the same time. Notice that there is no change in the average kinetic energy during the phase change. If heat is being added and there is no change in the average kinetic energy, then the sample must be gaining potential energy. After all of the ice has become water, the temperature (average kinetic energy) will rise again until it reaches the boiling point. Again, there is a phase change and the sample is gaining potential energy while the phase change occurs.
A phase diagram is helpful when looking at the effects of temperature and pressure on a substance. Because pressure can have an effect on the volume of gases and the boiling points of liquids, it is important not to overlook pressure when examining changes in the phase. A general phase diagram is shown in Figure 2.8.
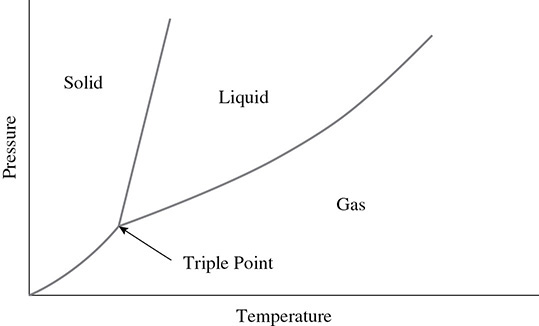
Figure 2.8 Phase Diagram
The point where the solid, liquid, and gas phases can all exist at the same time, given a specific temperature and pressure, is called the triple point. For H2O, the triple point exists when the pressure is 4.57 atm and the temperature is 0.01°C.
REVIEW QUESTIONS
1. Which gas under a high temperature and a low pressure behaves most like an ideal gas?
(A) He
(B) O2
(C) NH3
(D) CO2
(E) Ne
2. Which sample demonstrates particles arranged in a regular geometric pattern?
(A) CO2(g)
(B) CO2(s)
(C) CO2(l)
(D) CO2(aq)
(E) None of the above
3. At which temperature does a water sample have the highest average kinetic energy?
(A) 0 degrees Celsius
(B) 100 degrees Celsius
(C) 0 K
(D) 100 K
(E) 273 K
4. A liquid will boil when
(A) its freezing point is equal to its melting point
(B) a salt has been added to the liquid
(C) its vapor pressure is equal to the melting point
(D) it is heated to a temperature that is below the boiling point
(E) its vapor pressure is equal to the surrounding pressure
5. Which gas is expected to have the highest rate of effusion?
(A) O2
(B) F2
(C) H2O
(D) He
(E) CH4
6. Which phase change is described correctly?
(A) Solid to gas is called deposition.
(B) Gas to solid is called sublimation.
(C) Liquid to solid is called freezing.
(D) Solid to liquid is called vaporization.
(E) Liquid to gas is called condensation.
7. A solid, liquid, and gas can exist together at the
(A) sublimation point
(B) triple point
(C) boiling point
(D) freezing point
(E) melting point
8. A mixture of gases exists in a sealed container with the following percentages:
helium 40%, neon 50%, and argon 10%
If the total pressure of the gases is 1100 torr, then which of the following is true about these gases?
(A) Volume and temperature have an inversely proportional relationship.
(B) Volume and pressure have a direct relationship.
(C) The partial pressure of the neon gas is 550 torr.
(D) The partial pressure of the argon gas is 100 torr.
(E) The partial pressures of the gases cannot be calculated with the given information.
9. Which of the following gases is expected to have the lowest density at STP?
(A) SO2
(B) CO2
(C) Cl2
(D) Xe
(E) Ar
10. An ideal gas at STP occupies 22.4 liters. If the pressure on the gas is increased to 1000 torr and the temperature of the gas is reduced to 250 K, what can be said about the gas?
(A) The number of moles of the gas has changed.
(B) The volume of the gas has increased.
(C) The volume of the gas has decreased.
(D) The pressure and the temperature have an inversely proportional relationship.
(E) None of the above.
11. Which is inconsistent with the Kinetic Molecular Theory?
(A) Gas molecules have forces of attraction for each other.
(B) Gas molecules move in a random, straight-line motion.
(C) Gas molecules have a negligible volume compared to the volume they occupy.
(D) Collisions between gas molecules lead to a transfer of energy that is conserved.
(E) All of the above statements are correct.
12. Refer to the following choices:
I. Boyle’s Law
II. Charles’ Law
III. Combined Gas Law
Which of the above can be used to calculate changes in volume with changes in pressure at constant temperature?
(A) I only
(B) II only
(C) II and III only
(D) I and III only
(E) I and II only
13. Referring to the heating curve in Figure 2.7, which of the following is not associated with the heating curve for water?
(A) Addition of heat energy
(B) Melting
(C) Boiling
(D) Increase in kinetic energy
(E) Sublimation
ANSWERS AND EXPLANATIONS
1. (A) The smaller the gas, the more ideal it will behave. Also, gases behave most ideal when far apart. This occurs under low pressure and high temperature.
2. (B) A regular geometric pattern best describes a solid.
3. (B) Average Kinetic Energy is the term that describes temperature. The highest temperature present in these samples is 100 degrees Celsius, which is 373 Kelvin.
4. (E) A liquid will boil when the vapor pressure of the liquid is equal to the atmospheric pressure around it. Because atmospheric pressure can change, so can the boiling point of a liquid.
5. (D) The lightest gas will have the lowest density and highest rate of effusion. Of the choices, helium is the lightest gas listed.
6. (C) The freezing of a liquid will form a solid.
7. (B) The triple point combines the right conditions of pressure and temperature so that a substance can exist in the gas, liquid, and solid phases all at the same time.
8. (C) Neon makes up 50% of the gas atoms present. Neon will also contribute to 50% of the total pressure. (1100 torr)(0.50) = 550 torr.
9. (E) The density of a gas is the molar mass of the gas divided by 22.4L. For argon this will be 39.95g/22.4L = 1.78 g/L. Remember that no calculator is needed. Because argon is the lightest gas present, it will have the lowest density.
10. (C) In this problem the pressure changes from 760 torr to 1000 torr. The temperature changes from 273 K to 250 K. Both changes in conditions point toward a decrease in volume. When the Combined Gas Law is used, the volume will decrease from 22.4 L to 15.6 L.
11. (A) Ideally, gas molecules need to be far apart and with no attraction for each other. Also, small gases like hydrogen and helium are ideal.
12. (D) Both Boyle’s Law and the Combined Gas Law have the variables for pressure and volume. Charles’ Law looks only at the changes in volume with changes in temperature.
13. (E) The heating curve for a substance will not show when a substance sublimes. However, sublimation can be indicated in the curve that includes the triple point.
14. (T, T, CE) Gases are compressible and will occupy a smaller volume when the pressure on them is increased.