CHAPTER 6
Stoichiometry and Solution Chemistry
Stoichiometry is the branch of chemistry that deals with the amounts of products produced from certain amounts of reactants. Most of the chemistry discussed so far in this book has dealt with what is present (qualitative chemistry). The next step is to examine how much is present (quantitative chemistry). You may want to refer to Appendix 1, Mathematical Skills Review, in the back of this book.
Chemical Formulas
Chemical formulas not only tell which elements are present in a compound but also how much of each element is present. There are three different types of chemical formulas that need to be examined. The chart below shows the major differences between them.
THINK ABOUT THIS 
Problem:
A compound has an empirical formula of CH2 and a molar mass of 70 grams/mole. What is the molecular formula of this compound?
Solution: The empirical formula CH2 has a mass of 14. Divide 70 by 14 to find that there are five units of CH2 in this compound. This means that the molecular formula is C5H10.
Balancing Chemical Equations
Balancing a chemical equation requires an understanding of the Law of Conservation of Mass, which says that mass cannot be created or destroyed. The amount of mass in the reactants will be the amount of mass in the products. The credit for this discovery is given to Antoine Lavoisier, who took very careful measurements of the quantities of chemicals and equipment that he used. Conservation of mass also holds true when balancing equations. The number of atoms of each element in the reactants will be equal to the number of atoms of each element in the products. A useful mnemonic device for conservation of mass is “What goes in, must come out.”
The two most important rules to remember when balancing equations are:
• You may change only the coefficients.
• You must use the lowest whole number coefficients.
Now add one more unofficial rule to those listed above:
• Leave the simplest substance until last.
Step by step you can now balance an equation. Try this example:
Al + O2 → Al2O3
Inspection shows that you should leave the reactant Al for last because it is the “simplest” and not bonded to any other elements. Inspection also shows that two oxygen atoms enter the reaction and three leave the reaction. The numbers two and three are factors of the number six. Therefore you can alter the coefficients that are before the substances containing oxygen and get:
Al + 3O2 → 2Al2O3
This now shows a total of six oxygen atoms as reactants and six oxygen atoms as products. The coefficients are multipliers and not only modify the number of oxygen atoms, but modify the number of aluminum atoms as well in aluminum oxide. Now you have four atoms of aluminum on the right side of the equation. To balance this, place a coefficient of 4 before the Al on the reactant side and get:
4Al + 3O2 → 2Al2O3
Does it all add up? Four aluminum atoms and six oxygen atoms are on the reactant side of the equation and four aluminum and six oxygen atoms are on the product side of the equation.
Problem:
Balance the following chemical equations:
1. Zn + HCl → H2 + ZnCl2
2. SiO2 + HF → SiF4 + H2O
3. SiCl4 + Mg → Si + MgCl2
4. H2 + N2 → NH3
5. SO3 → S + O2
Solutions:
1. Zn + 2HCl → H2 + ZnCl2
2. SiO2 + 4HF → SiF4 + 2H2O
3. SiCl4 + 2Mg → Si + 2MgCl2
4. 3H2 + N2 → 2NH3
5. 2SO3 → 2S + 3O2
In addition to balancing chemical equations, you can also classify the types of reactions that occur. There are four types of reactions: synthesis, decomposition, single replacement, and double replacement. Explanations and examples of each are as follows:
• In a synthesis reaction, many substances come together to form one compound:
A + B → AB
• In a decomposition reaction, one compound breaks down into many substances:
YZ → Y + Z
• In a single replacement reaction, one element replaces one other element.
AB + C → CB + A
• In a double replacement reaction, two elements “switch partners”:
AB + XY → AY + XB
Problems:
Classify the five balanced equations above as single replacement, double replacement, synthesis, or decomposition.
Solutions:
1. Single Replacement
2. Double Replacement
3. Single Replacement
4. Synthesis
5. Decomposition
Mole Ratios
A mole ratio is the ratio of the number of moles of one substance to the number of moles of another substance. Because coefficients can represent moles, molecules, or atoms, you can think of a mole ratio as a “coefficient ratio.” For example, look at the equation for aluminum oxide, 4Al + 3O2 → 2Al2O3. You can pick any two substances from the equation and determine their mole ratio. The mole ratio of Al to Al2O3 is 4:2 or 2:1, while the mole ratio of O2 to Al2O3 is 3:2. This leads to another type of problem that you might encounter. Suppose you were asked to produce 1,000 moles of Al2O3 for a big chemical company. How much aluminum and oxygen would you need to purchase?
Start with the balanced equation: 4Al + 3O2 → 2Al2O3.
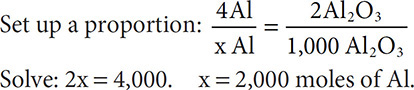
To solve for the number of moles of oxygen gas, use a dimensional analysis:
Problem:
The Haber process is a method for making ammonia according to the equation 3H2 + N2 → 2NH3. How many moles of nitrogen gas and hydrogen gas are needed to produce 700 moles of ammonia?
Solution: Start with the balanced equation: 3H2 + N2 → 2NH3.
Doing the same for N2 via a dimensional analysis reveals that 350 moles of N2 are required too:
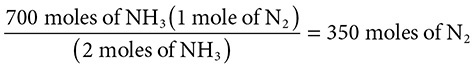
Moles, Mass, Volumes, and Molecules
You have already encountered problems involving moles, molecules, and molar masses earlier in this book. There is still one other relationship that needs to be connected with the mole and that is molar volume. Once you make a connection between moles and volume, mass, and molecules you will be able to solve problems easily. One very helpful mnemonic device to use is the Mole-Go-Round. Some think of this method as a way of “cheating the system,” but because the SAT II exam does not require you to show work, the Mole-Go-Round is a perfectly acceptable method for achieving better results.
So what is this Mole-Go-Round? It is a simple diagram that shows a pattern between the relationship of moles and other factors. The Mole-Go-Round is shown in Figure 6.1.
Figure 6.1 The Mole-Go-Round
Moles are in the middle as they should be because once you know how many moles there are of a sample, then you can make conversions to find out other quantities. Note these two things:
1. When converting to moles the mathematical operation is division, while “eXiting” moles requires the operation to be multiplication. (The letter “X” has been emphasized so that you remember to multiply.)
2. The factor between grams and molar mass will differ depending upon the molar mass of the compound in question.
Problem:
Given a 22.0-gram sample of CO2(g) at STP, how many liters will this sample occupy? How many molecules are present?
Solution: This problem starts out in the “mass” portion of the Mole-Go-Round. You have 22.0 grams of CO2. (Notice how a number [22.0], units [gram], and substance [CO2] are carefully recorded in each step of the problem.) The next step is to convert to moles by dividing by the molar mass. The molar mass for CO2 is 44.0 grams/mole. This gives 0.50 moles of CO2 as shown in Figure 6.2.
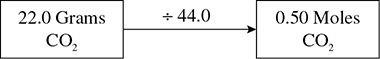
Figure 6.2 Converting Grams to Moles
The next step is to convert the 0.50 moles of CO2 to molar volume and to the number of molecules. This is done by multiplying 0.50 moles by 22.4 liters and then multiplying 0.50 moles by 6.02 × 1023 as shown in Figure 6.3.
Figure 6.3 Converting Moles to Volume and Number of Molecules
Mass and Volume Problems
Knowing how to convert moles to mass and to volume opens up a range of other types of problems that can be solved. Earlier in this chapter, you looked at how many moles of reactants it would take to produce a certain number of products. But you might also be asked to produce a certain amount of product in grams instead of moles or to find the amounts of reactants needed in grams as well. This type of problem is called a mass-mass problem, and it can be solved with the help of the Mole-Go-Round and three simple steps.
Consider the following: C(s) + O2(g) → CO2(g). How many grams of carbon dioxide can be formed from the burning of 120 grams of carbon? Assume an abundant amount of oxygen.
1. 120 grams of C is converted to moles by dividing by the atomic mass of carbon. 120 grams divided by 12 is 10 moles of C(s).
2. Use the mole ratio from the balanced equation and substitute the new amount of reactants:
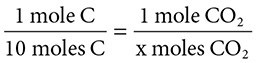
10 moles of carbon dioxide are produced because for everyone one mole of carbon used, one mole of carbon dioxide is produced.
3. Convert 10 moles of CO2 to grams, as called for in the problem. To convert moles to mass, the number of moles is multiplied by the molar mass (44 grams/mole). 440 grams of carbon dioxide will be produced.
Problem:
How many grams of NaCl can be produced from the reaction of 46 grams of Na with enough Cl2 according to the equation 2Na(s) + Cl2(g) → 2NaCl(s)?
Solution: Convert given grams to moles. 46 grams Na ÷ 23 grams/mole = 2.0 moles Na.
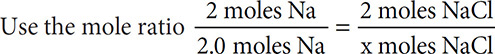
and find that an equal number, 2.0 moles, of NaCl are produced.
Convert 2.0 moles of NaCl to grams of NaCl by multiplying by the molar mass of 58.5 grams/mole = 117 grams of NaCl.
Coefficients can indicate still another quantity: volume. When reactions contain gases, provided that the conditions are the same (temperature and pressure), the coefficients can indicate the number of “volumes” of a gas that are present. Look at the burning of methane gas: CH4(g) + 2O2(g) → 2H2O(g) + CO2(g). The mole ratio for these gases is also their volume ratio. Let’s consider the production of the famous greenhouse gas CO2. How many liters of CO2 can be produced from the burning of 50 liters of CH4? Set up a proportion and solve:
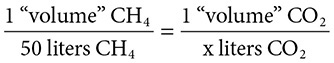
The proportion set up above dictates that 50 liters of carbon dioxide gas are produced.
Problem:
Given the reaction: C3H8(g) + O2(g) → CO2(g) + H2O(g), balance the equation. If 100 liters of C3H8 are burned, how many liters of CO2 are produced?
Solution: The balanced equation is C3H8(g) + 5O2(g) → 3CO2(g) + 4H2O(g). (Did you place the coefficient for O2 in the last step in balancing the equation?) Next, set up the volume proportion:
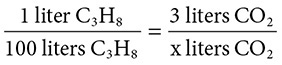
and find that 300 liters of CO2 are produced.
Limiting and Excess Reagents
Atoms and molecules react in specific ratios and amounts as shown throughout this chapter. At the heart of the proportions and ratios is the mole. What happens when reactants aren’t measured out in specific amounts but are simply “thrown together”? Will all of the reactants react? This is not the case with chemical reactions. Reactants react in certain proportions and ratios and, at times, there will be excess reagents left over.
Consider the baloney sandwiches made for your lunch when you went to elementary school. Let’s say that your favorite sandwich had two slices of bread and three slices of baloney. In the refrigerator there are four slices of bread and seven slices of baloney. You are in luck because now you can make two sandwiches from four slices of bread and six slices of baloney. But one of the original slices of baloney is now left over. One slice of baloney is in excess. The “leftovers” in a chemical reaction are called excess reagents. The substances that are used up completely are called limiting reagents. The limiting reagent for your lunch was the bread.
Consider the following reaction: HCl + NaOH → NaCl + H2O. The HCl and NaOH are consumed in a 1:1 ratio. If two moles of HCl reacted with one mole of NaOH, one mole of HCl is in excess because only one mole was needed to react with one mole of NaOH. Now consider the following: 2H2 + O2 → 2H2O. How many grams of water can be made from 8.0 grams of H2 and 96.0 grams of O2? Start by converting to moles because the balanced equation shows a mole ratio and not a gram ratio.
1. 8.0 grams of H2 ÷ 2 grams/mole = 4.0 moles H2.
2. 96.0 grams of O2 ÷ 32 grams/mole = 3.0 moles O2.
In order to react 4.0 moles of H2 you need 2.0 moles of O2 because, as dictated by the balanced equation, two moles of hydrogen gas react with one mole of oxygen gas, a 2:1 ratio. Because 3.0 moles of oxygen gas are present and only 2.0 moles are needed, oxygen gas is in excess and the hydrogen gas is the limiting reagent. Here is another way to look at it: in order to react all 3.0 moles of oxygen gas, you would need 6.0 moles of hydrogen gas, an amount that is not available and again labels hydrogen gas as the limiting reagent.
Problem:
Potassium and bromine will react according to the equation: 2K + Br2 → 2KBr. If 117 grams of potassium are reacted with 160 grams of bromine, how many moles of KBr can be produced?
Solution: Convert the known masses from grams to moles:
117 grams of K ÷ 39 grams/mole = 3.0 moles of K
160 grams of Br2 ÷ 160 grams/mole = 1.0 mole Br2
By inspection you see that three moles of K would require 1.5 moles of Br2 because, according to the balanced equation 2K + Br2 → 2KBr, the ratio of K to Br2 is 2:1. The amount of bromine present is just 1.0 mole and this would make the bromine the limiting reagent. Because only 1.0 mole of Br2 can react, only 2.0 moles of the potassium will be used. This would yield only 2.0 moles of KBr, as dictated by the balanced equation.
Percent Composition
Percent composition, also called percent by mass, is a useful piece of data to obtain when looking at the composition of certain substances. In percent composition problems you are asked to find the percent of the mass of an element in a compound as compared to the molar mass of the compound. A simple ratio will suffice and the result is multiplied by 100%. For CaCl2, for example, what percent of this compound is made up of chlorine? The total mass is
(1 Ca atom × 40 = 40) + (2 Cl atoms × 35.5 = 71) = 111 grams/mol
The percent by mass of chlorine is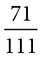 
× 100% = 64% chlorine.
Problem:
Find the percent by mass of each element in the compound C6H12O6 (molar mass = 180).
Solution:
The percent carbon is (72/180) × 100% = 40%
The percent hydrogen is (12/180) × 100% = 6.7%
The percent oxygen is (96/180) × 100% = 53.3%
Empirical Formulas from Percent Composition
In the previous section the problems presented a chemical formula and asked for the percent composition. There is a method for going from percent composition to chemical formula; however, you will obtain only the empirical formula from this. The three steps in determining the empirical formula of a compound from the percent composition are as follows:
1. Assume a 100-gram sample. This will allow the percent signs to be written as “grams.”
2. Convert the number of grams of each element into moles of each element.
3. Divide the number of moles of each element by the number of moles that is the smallest of all the numbers.
Let’s put theory into practice: A sample is found to contain 58.80% Ba, 13.75% S, and 27.45% O. What is the empirical formula of this substance?
1. Assume a 100-gram sample. This allows the percent signs to become “grams” and leaves us with 58.80 grams of Ba, 13.75 grams of S, and 27.45 grams of O.
2. Convert grams to moles:
58.80 grams of Ba ÷ 137.34 grams/mole = 0.43 moles of Ba
13.75 grams of S ÷ 32 grams/mole = 0.43 moles of S
27.45 grams of O ÷ 16 grams/mole = 1.72 moles of O
3. As of now the compound looks like Ba0.43 S0.43 O1.72. This is an absurd way of writing an empirical formula! So now the numbers of moles are divided by the lowest number of moles, 0.43. This leaves the empirical formula as BaSO4.
Problem:
A compound is 14.6% C and 85.4% Cl by mass. This compound also has a molar mass of 166 grams/mole. What are the empirical and molecular formulas of this compound?
Solution: First find the empirical formula:
1. You were given 14.6% C and 85.4% Cl; assuming a 100-gram sample, you have 14.6 grams of C and 85.4 grams of Cl.
2. 14.6 grams of C ÷ 12 grams/mole = 1.22 moles of C. 85.4 grams of Cl ÷ 35.5 grams/mole = 2.41 moles of Cl.
3. Divide by the lowest number of moles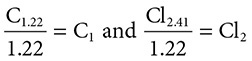 
The empirical formula is CCl2.
4. The mass of empirical formula CCl2 is 83 grams/mole. This compound has a molar mass of 166 grams/mole. Dividing 166 by 83 tells that there are 2 units of the empirical formula CCl2. The molecular formula of this compound is C2Cl4.
Concentration and Dilutions
Two cups of tea are presented to two individuals who are enjoying their time together. Person A has ordered one cup (8 ounces) of tea with one lump of sugar. Person B has ordered a “double” and gets a cup of tea that is twice as large (16 ounces). Person B drops two lumps of sugar into the larger cup of tea. An argument ensues over whose tea is sweeter. Person B believes that the larger cup of tea is sweeter because it has twice as many lumps of sugar in it. What should Person A say to Person B?
Concentration can be expressed in many different ways. No matter which way concentration is expressed, it always has one thing in common. It is a ratio of solute to solvent. A solute is a substance that changes phase when dissolved; for example, NaCl(s) becomes NaCl(aq) when dissolved in water. The solvent does not change phase when something is dissolved in it.
The most common way of expressing concentration in chemistry is molarity. Molarity is the ratio of moles of solute to total liters of solution:
Notice the term “total liters of solution.” This does not mean the volume of the solvent as the denominator considers the total volume of the solute and solvent together.
Problem:
What is the molarity of a solution that is made by dissolving 117 grams of NaCl in enough water to make 1,000 mL of solution?
Solution:
1. Convert the grams of NaCl to moles by dividing by the molar mass of NaCl, 58.5 g/mol.
117 grams ÷ 58.5 grams/mole = 2.00 moles of NaCl
2. The 1,000 mL of solution need to be expressed in liters so we convert:
1,000 mL (1 liter /1000 mL) = 1.000 liters
3. Solve:
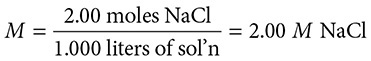
Now let’s take the 2.00 M NaCl solution made above and add water to the solution. Will the concentration be changed? By adding water, we have altered the denominator and have increased its value. Larger denominator means a lower overall value, and the molarity should decrease.
Let’s say 0.250 liter of water were added to make the total volume 1.250 liters of solution. What is the new molarity? We can use the equation M1V1 = M2V2 to solve for the new molarity of a solution that has been diluted. The original molarity was 2.00 M (M1), the original volume was 1.000 L (V1), and the new volume is 1.250 L (V2). The new molarity should decrease because of the addition of the water. So, M1V1 = M2V2 and substitution gives:
(2.00 M)(1.000 L) = (M2)(1.250 L)
Solving gives a new molarity = 1.60 M NaCl. The concentration has decreased as predicted.
Think about it, even without a calculator this is feasible: 1.000 L is 80% of 1.250 L. Therefore, 80% of 2.00 M is 1.60 M.
Problem:
A 1.00-liter solution of 0.50 M HCl is diluted to make 2.0 liters of solution. What is the new molarity of this solution?
Solution: Using the equation: M1V1 = M2V2 we substitute and get:
(0.50 M)(1.00 L) = (M2)(2.0 L)
The final molarity is 0.25 M HCl.
Colligative Properties
The directions for cooking pasta sometimes call for adding salt to the water in which the pasta is cooked. Adding a solute to a solvent changes the properties of the solvent. Some of the properties that change are boiling points, freezing points, and vapor pressure. The degree of change that can be brought about depends upon the concentration of the particles in solution. This way of expressing concentration is called molality.
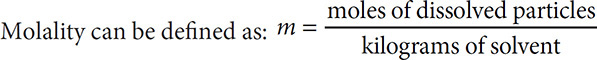
Notice that the equation calls for “moles of dissolved particles.” Ionic compounds can dissociate in solution and form a number of particles in solution. For example, if a 1.0-molal solution of NaCl were prepared, it would “act” as if it were 2.0 molal in nature. This is because every one mole of NaCl releases two moles of ions (Na+ and Cl−). This is a huge difference from a compound like glucose, C6H12O6, where the atoms are covalently bonded and will not dissociate in solution. That means a 1.0-molal solution of glucose will be one molal in particles even though one mole of glucose has more atoms than one mole of NaCl has ions.
Problem:
222 grams of CaCl2 are dissolved in 2.00 kg of water. What is the resulting molality of this solution?
Solution: First convert the grams of CaCl2 to moles by dividing by the molar mass (molar mass = 111). This yields 2.0 moles of CaCl2. Dividing by 2.00 kg of water we get:
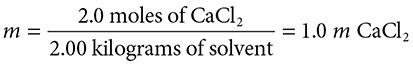
However, because the calcium chloride yields three moles of ions per mole of salt, the solution will behave as if it were 3.0 m in nature. Therefore, for further calculations below, we will treat this solution as it were 3.0 m in particles.
Now that the molality of solution can be calculated, we can further examine how much a colligative property can be changed once a certain amount of particles have been dissolved in solution. When looking at the effects on boiling point and freezing points one should remember the following mnemonic device: “The rich get richer and the poor get poorer” meaning that the boiling point elevates while the freezing point depresses.
The boiling point of water will increase by a constant of 0.52°C for every 1 m of solute dissolved in solution. Let us reexamine the 3.0 m particles solution made earlier. What will the boiling point be for this solution? A simple multiplication tells us that:
3.0 m (0.52°C/1 m) = 1.56°C as the increase.
We have not yet found the new boiling point of the solution. Remember that the original boiling point was 100°C. Now the boiling point is 1.56°C higher than 100°C and has become 101.56°C.
The freezing point of water will decrease by a constant of 1.86°C for every 1 m of solute dissolved in solution. To calculate the change in freezing point we set up the following and multiply:
3.0 m particles (1.86°C/1 m) = 5.58°C lower freezing point.
Because the original freezing point was 0°C, the new freezing point is −5.58°C.
THINK ABOUT THIS
Problem:
400 grams of AlCl3 are dissolved in 1.0 kilogram of water. Find the molality of this solution. What is the boiling point of the solution?
Solution: Convert 400 grams of AlCl3 to moles by dividing by the molar mass of 133.5 grams/mole. This gives 3.00 moles (close enough) of AlCl3.
To find the molality we set up m = (3.00 moles/1.0 kg) = 3.00 m AlCl3. However, because there are 4 ions per mole, the solution behaves as if it were 12.00 m particles.
To find the increase in boiling point multiply the molality by the constant:
12.00 m (0.52°C/1m) = about 6°C.
The new boiling point will be 100°C + 6°C = 106.00°C or 106.24° (actual).
Solubility of Compounds
Even though it may seem like a good idea to use any salt to melt ice or change the boiling point of water, not every salt can be dissolved completely in water. One of the salts that will not dissociate 100% into its ions is AgCl. Just how much AgCl can dissolve in water will be examined later when we examine solubility products in Chapter 8. You should also know that the temperature and amount of solvent used to dissolve a salt also alter how much of the salt can be dissolved. Because different amounts of solvent can be used, a standard of 100 grams of water has been set as the norm on solubility curves. The maximum amount of a solute that can dissolve in 100 grams of water is called the solute’s solubility. This amount is what makes a solution saturated. If 100 grams of a solvent have less than the maximum amount of solute dissolved, the solution is said to be unsaturated. If the solvent can be “tricked” into dissolving more solute than what it takes to make the solution saturated, then the solution is said to be supersaturated.
Gases and solids show different trends in solubility as the temperature of solution changes. In general, solids increase in solubility as temperature increases and gases decrease in solubility as temperature increases. The graph in Figure 6.4 shows the solubility of KCl and Pb(NO3)2 as the temperature of the 100-gram sample of water is heated from 0°C to 100°C.
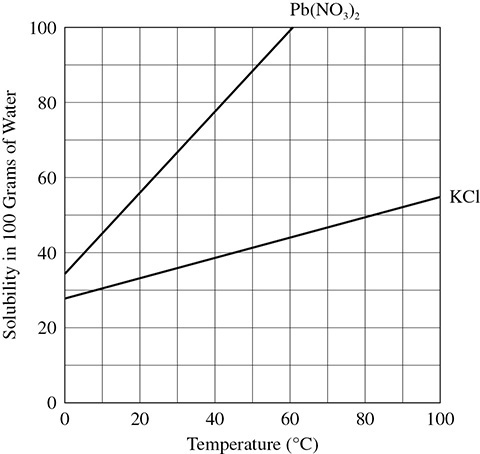
Figure 6.4 Solubility Curve
THINK ABOUT THIS
While solubility curves can be quite detailed, there are some general rules that can be used to help determine if a solute is soluble in water. These rules are outlined below.
The rules listed in the table can help identify the insoluble salts that form during a chemical reaction. These salts that “settle out” of the solution are called precipitates.
Problem:
Given the reaction in water: 2KI + Pb(NO3)2 → PbI2 + 2KNO3, which of these substances would be labeled as aqueous (aq) or solid precipitates (s)?
Solution: KI is soluble in water; the halogen is not bonded to Hg, Pb, or Ag. Pb(NO3)2 is soluble because all nitrates are soluble. PbI2 is not soluble in water because the iodide ion is bonded to Pb. Finally, KNO3 is soluble because all nitrates are soluble. The final equation should look like this:
2KI(aq) + Pb(NO3)2(aq)→ PbI2(s) + 2KNO3(aq)
Net Ionic Equations
Now that you know the rules for solubility, you can take a look at exactly which substances take part in a reaction. While reactions are written to show the reactants and products in the overall reaction, not every substance plays a part in the reaction. These nonparticipating substances are called spectators. Consider the equation: 2KI(aq) + Pb(NO3)2(aq)→ PbI2(s) + 2KNO3(aq). There is a substance in this reaction that is a spectator, and you can find it if you know the solubility rules and how to write a net ionic equation.
When writing a net ionic equation, first write out all soluble substances as ions in solution. Substances that are not soluble or do not dissociate into ions completely are written as shown in the overall equation. Return to the equation: 2KI(aq) + Pb(NO3)2(aq)→ PbI2(s) + 2KNO3(aq). First write out the soluble substances as ions in solution:
2K1+(aq) 2I1−(aq) + Pb2+(aq) + 2NO31−(aq) → PbI2(s) + 2K1+(aq) + 2NO31−(aq)
Next, find the substances that appear on both sides of the equation in equal amounts. This would be the potassium ions and nitrate ions. These ions appear exactly the same on both sides of the equation and they are the spectator ions in the reaction. These will cancel out and the net ionic reaction remains:
2I1−(aq) + Pb2+(aq) → PbI2(s)
Problem:
Give the net ionic reactions for the following reaction:
AgNO3(aq) + NaCl(aq) → AgCl(s) + NaNO3(aq)
Solution: First we write out all of the aqueous ions in solution for the soluble substances:
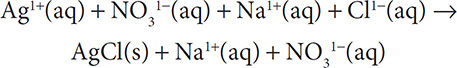
Next we see that the sodium and nitrate ions appear on both sides of the equation so they will cancel out and we get a net ionic equation that looks like: Ag1+(aq) + Cl1−(aq) → AgCl(s).
Problem:
Give the net ionic equations for the following reaction:
2(NH4)3PO4(aq)+ 3CaCl2(aq) → 6NH4Cl(aq) + Ca3(PO4)2(s)
Solution: Although this looks complicated, the steps are still the same as in the previous two examples. Taking it one step at a time will ensure a correct answer. First write out the ions that are dissolved in solution:
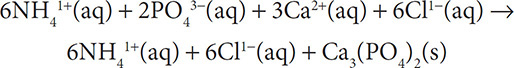
The ions that are spectators are the ammonium and chloride ions. They will not appear in the net ionic equation: 2PO43−(aq) + 3Ca2+(aq) → Ca3(PO4)2(s).
Percent Yield
Sometimes, even though we measure out our reactants carefully, we do not get the full amount of product expected. For example, examine the reaction 2H2 + O2 → 2H2O. If we reacted 4 grams of H2(g) (2 moles of hydrogen gas) with 32 grams of O2(g) (one mole of oxygen gas) we would expect to get 36 grams of water (2 moles of water). This is clearly dictated by the balanced reaction. But, upon collecting the water formed, we find that just, for example, 34 grams of water are formed. We can now look at the percent yield for this reaction:
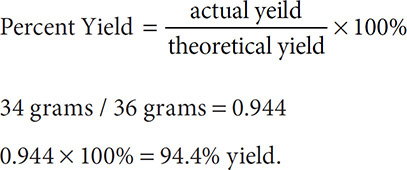
REVIEW QUESTIONS
1. What is the mass of 3.0 × 1023 atoms of neon gas?
(A) 0.50 grams
(B) 1.0 grams
(C) 5.0 grams
(D) 40.0 grams
(E) 10.0 grams
2. According to the reaction Pb(s) + S(s) → PbS(s), when 207 grams of lead are reacted with 64 grams of sulfur,
(A) there will be an excess of 207 grams of lead
(B) the sulfur will be in excess by 32 grams
(C) the lead and sulfur will react completely without any excess reactants
(D) the sulfur will be the limiting factor in the reaction
(E) there will be an excess of 103.5 grams of lead
3. What is the total number of atoms represented in one molecule of (CH3)2NH?
(A) 5
(B) 8
(C) 9
(D) 10
(E) 12
4. A hydrocarbon has the empirical formula CH3. A probable molecular formula for this compound could be
(A) C3H3
(B) C2H6
(C) C3H8
(D) C4H8
(E) C5H10
5. The chemical symbol Ar could stand for
(A) one mole of argon
(B) one atom of argon
(C) both a mole or an atom of argon
(D) neither a mole or an atom of argon
(E) one molecule of argon
6. Which salt has a solubility that is different from the other four?
(A) AgCl
(B) PbBr2
(C) Ca3(PO4)2
(D) Na2CO3
(E) Al(OH)3
7. A solution of a salt and 100 grams of water that can still dissolve more solute at a given temperature is classified as
(A) unsaturated
(B) supersaturated
(C) saturated
(D) anhydrous
(E) hypertonic
8. The net ionic equation for the reaction between CaCl2 and Na2CO3 to form calcium carbonate and sodium chloride would include all of the following except:
(A) Ca2+
(B) CO32–
(C) 2Na1+
(D) CaCO3
(E) All of the substances above would be in the net ionic equation.
9. Which solution listed below is going to have the highest boiling point?
(A) 1.5 m NaCl
(B) 1.5 m AgCl
(C) 2.0 m C6H12O6
(D) 2.0 m CaCl2
(E) 1.0 m Al2(SO4)3
10. Which equation is correctly balanced?
(A) Na + Cl2 → 2NaCl
(B) CH4 + 3O2 → CO2 + H2O
(C) 2KI + Pb(NO3)2 → 2KNO3 + PbI2
(D) H2SO4 + KOH → K2SO4 + H2O
(E) C6H12O6 + 6O2 → 6CO2 + H2O
11. 110 grams of KF are dissolved in water to make 850 ml of solution. What is the molarity of the solution?
(A) 0.129 M
(B) 0.620 M
(C) 0.002 M
(D) 0.068 M
(E) 2.23 M
12. Given one mole of CH4(g) as STP. Which statements are true?
I. There are 6.02 × 1023 molecules present.
II. The sample will occupy 22.4 L.
III. The sample will weigh 16 g.
(A) I only.
(B) II only.
(C) I and III only.
(D) II and III only.
(E) I, II, and III.
Questions 13–14 refer to the following:
(A)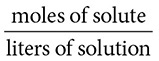 
(B) 
(C)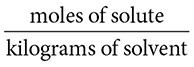 
(D) 
(E) 
13. Is used to find the molarity of a solution
14. Is used to find the molality of a solution
ANSWERS AND EXPLANATIONS
1. (E) The question shows that we have half of a mole of atoms of neon. This means that we have half of the gram atomic mass of neon. Using the periodic table, we see that the gram atomic mass is 20.0 g/mol. The answer is 10.0 grams.
2. (B) 207 grams of Pb is one mole of Pb. This requires just one mole (32 grams) of S. Because 64 grams of S are present, the S will be in excess by 32 grams.
3. (D) In this sample we have 2 carbon atoms, 7 hydrogen atoms, and 1 nitrogen atom.
4. (B) The empirical formula is the lowest ratio of the elements in the compound. Choice B is the only choice that follows this proportion.
5. (C) When a chemical symbol is written in a chemical equation it could mean one mole or one atom of the element.
6. (D) All of the compounds are insoluble except for the sodium carbonate. All sodium compounds are soluble in water while the other choices all follow the rules for being insoluble in water.
7. (A) A solution that can hold more solute is classified as unsaturated. If the solvent is holding as much solute as possible, it is saturated. If the solution is “tricked” into holding more solute than a saturated solution then it is supersaturated.
8. (C) Because sodium salts are always soluble their ions will appear on both sides of the equation. This will make the spectator sodium ions cancel out and not appear in the net ionic equation.
9. (D) Multiplying the molality by the number of particles formed by the substance will give the molality of the ions present in solution. Both the glucose and silver chloride will not form ions. The sodium chloride solution will be 3 molal in effect while the aluminum sulfate solution will be 5 molal in effect. The greatest impact on the boiling point of water will come from the calcium chloride solution that is 6 molal in effect.
10. (C) The number of atoms of each element as a reactant must be equal to the number of atoms of each element as a product.
11. (E) The GFM of KF is 58.1. Dividing 110/58.1 gives 1.89 moles of KF. Dividing the number of moles by 0.850 liters of solution gives a molarity of about 2.23 molar KF solution. You don’t need a calculator. You have approximately 2 moles of KF and you are dividing by a number that is lower than 1.0. This gives an answer that is bigger than 2.0. The only choice that comes close is E.
12. (E) One mole of any gas will have one mole of molecules present. One mole of methane gas will weigh 16.0 grams (the GFM) and will also occupy one molar volume (22.4 L).
13. (A) Molarity is found by diving the moles of solute by the total liters of solution formed.
14. (C) Molality is found by dividing the moles of solute by the number of kilograms of solvent used to make the solution.
15. (F, F) Water is 89% oxygen by mass and 11% hydrogen by mass.
16. (F, F) Gases become less soluble in water with an increase in temperature because the water molecules are moving further apart.
17 (F, T) Calcium phosphate is insoluble in water while salts which have a group I ion present are soluble in water.