COROLLARY.   Let Q be a quadratic form on an n-dimensional vector space V over a field F of characteristic not two such that the associated bilinear form is non-degenerate. Then C(V, Q) is a tensor product of quaternion algebras if n is even and is a tensor product of quaternion algebras and its center if n is odd. Moreover, the center C is two-dimensional of the form F(c) where c² = (− 1 )^v 2 ^{− n}δ1, δ a discriminant, and C is afield or a direct sum of two copies of F according as (− 1)^v(2δ) is not or is a square in F.

Proof.   The first statement follows by induction on the dimensionality and the factorization lemma (Lemma 5). To determine the center in the odd dimensional case, we choose an orthogonal base (u₁, u₂,…, u_n) where n = 2v + 1. Then u_iu_j = − u_ju_i for i ≠ j, which implies that the element c = u₁u₂ … u_n commutes with every u_i Hence c is in the center and since c F 1 and the center is two-dimensional, the center is F[c]. We have

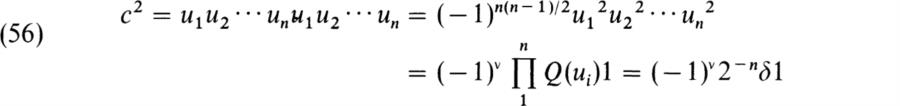
where δ is the discriminant determined by the base (u_l, u₂,…, u_n). Then F[c] is a field or a direct sum of two copies of F according as (− 1)^v2^{− n}δ is not or is a square. Since n = 2v + 1, this holds if and only if (− 1)^v2δ is not or is a square.

In the remainder of this section, we shall give a brief indication of some applications of Clifford algebras to the study of orthogonal groups. For this purpose, we need to introduce the even (or second) Clifford algebra C⁺(V, Q) defined to be the subalgebra of C(V, Q) generated by all of the products uv, u,v ∈ V (that is, by V²). We recall that a vector u is called non-isotropic if Q(u) ≠ 0. If is non-isotropic, then

Hence

which shows that C⁺ = C⁺ (V, Q) is generated by the elements u₁u, u ∈ V. Now we can write V = Fu₁ + (Fu₁) and u = αu₁ + v where α ∈ F and v u₁ Then u₁u = αQ(u₁)l + u₁v. It follows that C⁺ is generated by the n− 1 dimensional subspace V₁ = u₁(Fu₁). We have

and the restriction of − Q(u₁)Q to (Fu₁) is a quadratic form Q₁ with nondegenerate bilinear form B₁. Hence we have a surjective homomorphism of C((Fu₁), Q₁) onto C⁺. On the other hand, if (u₁,…, u_n) is a base for V, then 1, u_i1 … u_ir, i₁ < … < i_r is a base for C(V, Q). Then the elements 1 and u_i1 … u_ir with even r are contained in C⁺ and there are 2^{n − 1} of these. Thus dim C⁺ ≥ 2^{n − 1}, while dim C((Fu₁), Q₁) = 2^{n − 1}. It follows that C⁺ ≅ C((Fu₁), Q₁). This proves the first statement in

THEOREM 4.14.   Let B be non-degenerate and char F ≠ 2. Then the even Clifford algebras C ⁺ (V, Q) ≅ C((Fu₁), Q₁) where u₁ is any non-isotropic vector and Q₁ is the restriction of − Q(u₁)Q to F (u₁). C ⁺ (V, Q) is central simple if the dimensionality n of V is odd and is a tensor product of a central simple algebra and a two-dimensional algebra D, which is either a field or a direct sum of two copies of F if n = 2v. The two alternatives for D correspond respectively to the following: (− l)^vδ is not or is a square in F, where δ is a discriminant of B₁.

Proof.   The second assertion is an immediate consequence of the first and Theorem 4.13. Now assume n is even and let c = u₁u₂ … u_n where (u₁, u₂,…, u_n) is an orthogonal base for V. Then c ∈ C⁺ and u_ic = −cu_i and u_iu_jC = cu_iu_j. Hence c is in the center of C⁺ and c F1. Hence the center of C ⁺ is F[c]. As in (56) we have

where β = 2^{− v} and F[c] is a field or a direct sum of two copies of F according as (− 1)^v β²δ and hence (− 1)^vδ is not or is a square.

In both the even and the odd dimensional case, the subspace Fc, where c = u₁u₂ … u_n and (u₁, u₂,…, u_n) is an orthogonal base, is independent of the choice of this base. For F[c] is either the center of C(V, Q) or the center of C(V, Q) ⁺. Moreover, c F1 and c² ∈ F1 It is clear that these conditions characterize the set of non-zero elements of Fc.

Now let f be an orthogonal transformation in V. Then f(x)² = Q(f(x)) 1 = Q(x) 1. Hence the universal map property of C(V, Q) implies that f has a unique extension to an automorphism g of C(V,Q). Now g stabilizes C(V, Q)⁺ and it stabilizes the center of C(V, Q) and of C(V, Q)⁺. Since one of these centers is F[c], g stabilizes F[c]. It follows from the characterization we have given of the set of non-zero elements of Fc that g(c) = αc, α ≠ 0 in F. Since g(c)² = g(c²), we have α = ± 1 so g(c) = ±c. Now we can write g(u_i) = f(u_i) = ∑α_iju_j, α_ij ∈ F, where the matrix (α_ij) is orthogonal. Then

Since u_iu_j = − u_ju_i if i ≠ j, and u_i² = Q(u_i)1, it is clear from the definition of determinants that the sum can be written as det(α_ij)u_lu₂ … u_n+ a linear combination of elements u_i1u_i2 … u_ir, i₁ < i₂ < … < i_r with r < n (cf. BAI, p.416). Since these elements together with u₁u₂ … u_n constitute a base and since g(c) = ±c, we have g(c) = det(α_iJ)c. Hence g(c) = c if f is a rotation and g(c) = − c otherwise.

We now observe that any automorphism g of a finite dimensional semisimple algebra A that fixes the elements of the center C of A is inner. For, if where the A_i are the simple components of A, then 1 = 1₁ + 1₂+ … + 1_s where 1_i is the unit of A_i and and . Hence g(l_i) = 1_i so g stabilizes every A_i and g fixes the elements of the center C1_i of A_i. By the Skolem-Noether theorem, there exists an element u_i invertible in A_i such that the restriction of g to A_i is the inner automorphism determined by u_i. Then g is the inner automorphism determined by u = ∑u_i.

We can apply this to the foregoing situation. Then we see that if the given orthogonal transformation f is a rotation, there exists an invertible element u ∈ C(V, Q) such that

These considerations lead to the introduction of the following groups.

DEFINITION 4.6.   The Clifford group Γ(V, Q) is the subgroup of invertible elements u ∈ C(V, Q) such that uxu^−l ∈ V for all x ∈ V. Clearly this is a subgroup of the multiplicative group of invertible elements of C(V, Q). The even Clifford group is Γ ⁺ (V, Q) = Γ(V, Q) ∩ C ⁺ (V, Q).

If x ∈ V and u ∈ Γ = Γ(V, Q), then uxu^{− 1} ∈ V and (uxu^{− 1})² = ux²u^{− l} = Q(x)l. Hence the linear transformation x uxu^{− l} of V is in the orthogonal group 0(V, Q). The map , where (u) is x uxu ^{− 1}, x ∈ V, is a homomorphism of Γ(V, Q) into 0(V, Q) called the vector representation of the Clifford group.

Let v ∈ V be non-isotropic. Then v is invertible in C(V, Q) and for x ∈ V we have

Since vxv^{− 1} = vxvv^{− 2} = Q(v)^{− 1}vxv, this gives

Thus v ∈ Γ. We recall that a map of the form

is orthogonal and is called the symmetry S_v associated with the non-isotropic v (BAI, p. 363). Evidently S_xv = S_v if α ≠ 0 in F. We recall also that any orthogonal transformation is a product of symmetries and any rotation is a product of an even number of symmetries. The formula (59) now reads

Now it is clear that if the v_i are non-isotropic, then v₁ … v_r ∈ Γ(V, Q) and this element is in Γ⁺(V, Q) if r is even. It is clear also that Γ⁺(V, Q) contains the group F* of non-zero elements of F. We can now prove

THEOREM 4.15.   The even Clifford group Γ⁺ coincides with the set of products v₁ … v_2r, v_i non-isotropic in V. We have the exact sequence

where the second map is the injection of F*.

Proof.   Let u ∈ Γ⁺. Then the automorphism a uau^{– 1} of C(V, Q) fixes the element c = u₁u₂…u_n where (u₁, u₂, …, u_n) is an orthogonal base for V. Then, as above, χ(u) ∈ O⁺ (V, Q). On the other hand, let f ∈ O⁺ (V, Q) and write f = S_vl … S_v2r where the v_i are non-isotropic vectors in V. Then v₁… v_2r ∈ Γ⁺ and χ(v₁ …v_2r) = S_v1 … S_v2r, by (61). Thus χ(Γ⁺ ) = O⁺. The kernel of χ restricted to Γ⁺ is the intersection of Γ⁺ with the center of C(V, Q). Since either C(V, Q) or C(V, Q)⁺ is central simple, it is clear that this intersection is F*. This completes the proof of the exactness of (62). Moreover, if u ∈ Γ⁺ then χ(u)∈ O⁺ , so there exists an element v₁ … v_2r such that χ(v₁ … v_2r) = χ(u). Then u = αv₁ … v_2r, α ∈ F*, and hence u = (αv_l)v₂ … v_2r. This proves the first statement of the theorem.    

Let C^op be the opposite algebra of C = C(V, Q). We have x² = Q(x)l for x ∈ V ⊂ C^op. Hence we have a unique homomorphism of C into C^op sending x x. This means that we have an anti-homomorphism i of C into C such that x x. Then i² is a homomorphism fixing every x ∈ V, so i² = 1. Thus i is an involution in C, that is, an anti-automorphism satisfying i² = 1. This can be characterized as the involution of C fixing all of the elements of V. We call i the main involution of C. Evidently C⁺ is stabilized by i, so the restriction i|C⁺ is an involution in C⁺.

Now let u ∈ Γ⁺ and write u = v₁ … v_2r. Then

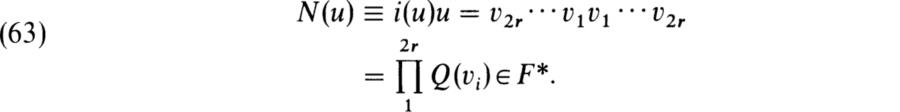
If u' ∈ Γ⁺ , we have

Hence u N(u) is a homomorphism of Γ⁺ into F*. It is clear from (63) that N (Γ⁺) is the set of products where the v_i are non-isotropic in V and this contains F*², the set of squares of elements of F*. If f is any rotation, there exists a u ∈ Γ⁺ such that χ(u) = f and u is determined up to a factor in F*. Hence the coset N(u)F*² in the group F*/F*² is determined by f. We now give the following definition, which ties together these concepts.

DEFINITION 4.7.   The kernel of the homomorphism N of Γ⁺; into F* is called the spin group Spin (V, Q). Its image O'(V, Q) under the vector representation χ is called the reduced orthogonal group. If f is any rotation and χ(u) = f, then N(u)F*² is called the spinorial norm of f

The spinorial norm map is also a homomorphism (of O⁺ (V, Q) into F*/F*²). The spinorial norm of a rotation can be defined directly, without the intervention of the Clifford algebra. If f is a given rotation, then we can write f = S_V1 … S_v2r and we can simply define the spinorial norm of f to be the coset . Since χ(v₁ … v_2r) = f and , this is the same element of F*/F*², which we have called the spinorial norm. The difficulty with the direct definition is that it is not apparent that the spinorial norm is well defined, since there are many ways of writing a rotation as product of symmetries. The definition using the Clifford algebra shows that we get the same elements of F*/F*² no matter what factorization of f as product of symmetries is used.

Now the reduced orthogonal group can also be defined as the kernel of the spinorial norm map. For, if f ∈ O' = O'(V, Q), then there exists a u ∈ Spin (V, Q) such that χ(u) =f. Then the spinorial norm of f is N(u)F*² = F*². Conversely, if the spinorial norm of the rotation f is F*², then f = S_vl … S_v2r and , β ≠ 0. Replacing v₁ by β^{– 1} v₁ we may assume . Then χ(v₁ … v_2r) = f and N(v₁ … v_2r) = 1, so the spinorial norm of f is F*².

The reduced orthogonal group contains the commutator subgroup Ω of 0, since any commutator can be written in the form

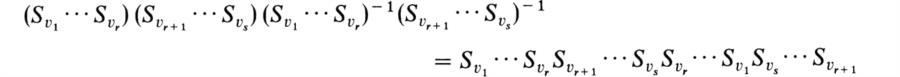
from which it is clear that the spinorial norm is F*². Thus we have the following inclusions among the various subgroups of O = O(V, Q) that we have defined:

and such that O⁺/O' is isomorphic to the subgroup of F*/F*² of cosets of the form βF*² where β has the form , v_i non-isotropic. We can say considerably more in the case in which Q is of positive Witt index (BAI, p. 369).

THEOREM 4.16.   Let Q be of positive Witt index. Then the reduced orthogonal group O'(V, Q) coincides with the commutator subgroup Ω of O(V, Q) and .

Proof. Since Q is of positive Witt index, there exists a subspace U of V that is a hyperbolic plane, so we have V = U and U has a base (u, v) such that Q(u) = 0 = Q(v) and B(u, v) = 1. The orthogonal transformations that stabilize U and act as the identity map on form a subgroup O₁ isomorphic to the orthogonal group in U. is the set of linear maps f_α such that u αu, v α^{– 1}v, w w for w ∈ where α ∈ F* (BAI, pp. 365366). We have f_α = S_{u – v}S_{u – αv}, so that the spinorial norm of f_α is Q(u – v)Q(u – αv) = (– 1)( – α) = α. Since α can be taken to be any element of F*, this proves that . Next let y be any nonisotropic vector in V and let Q(y) = α. Then Q(u + αv) = α = Q(y). Hence by Witt’s theorem there is an orthogonal transformation g such that g(u + αv) = y (BAI, p. 351). Then . Let f ∈ O' and write f = S_vl … S_v2r where α_i = Q(v_i) and hence . Then we have orthogonal transformations g_i such that . Then . Since O(V, Q)/Ω is abelian,

so to prove that f ∈ Ω, it suffices to prove that h ∈ Ω. Now f ∈ O' and since Ω ⊂ O', h ∈ O'. Hence h ⊂ O⁺₁, so h =f_α = S _{u– c}S_{u – αv}, as above, and α = β². Then .    

The main structure theorem on orthogonal groups, which we derived in BAI, states that if Q has positive Witt index and n ≥ 3, then Ω/(Ω ∩ {1, – 1}) is simple except in the cases n = 4, Witt index 2 and n = 3, |F| = 3. An interesting question is, when does – 1 ∈ Ω? This can happen only for even n. In this case we have

PROPOSITION 4.11.   Let n be even and let Q be of positive Witt index. Then – 1 ∈ Ω if and only if the discriminant is a square.

Proof. Let (u_l, u₂, …, u_n) be an orthogonal base. Then the discriminant obtained from this base is 2^–n and this is a square if and only if is a square. On the other hand – 1 = S_ul S_u2 … S_un so the spinorial norm of – 1 is . Hence by Theorem 4.15, – 1 ∈ Ω if and only if is a square.    

EXERCISES

        1. Show that any central simple algebra of degree two (p. 222) over a field F of characteristic ≠ 2 is a quaternion algebra as defined on p. 232 and that any such algebra is isomorphic to a Clifford algebra C(V, Q) where dim V = 2.

In exercises 2–9, Q is a quadratic form with non-degenerate bilinear form B on an n- dimensional vector space V over F of characteristic ≠ 2.

        2. Let n be even and (u₁, u₂, …, u_n) an orthogonal base for V over F so Q(u_i) = γ_i ≠ 0. Obtain an explicit formula

where v = n/2 and (α, β) denotes the algebra with base (1, i, j, k) such that i² = α1, j² = β1, ij = k = –ji

        3. Use exercise 2 to show that C(V, Q) ~ 1 if Q has maximal Witt index ( = v, see p. 370 of BAI).

        4. Let n be odd, but otherwise let the notations be as in 2. Obtain a formula like (66) tensored with the center for C(V, Q) and a formula like (66) for C⁺ (V, Q).

        5. Apply exercise 4 to obtain the structure of C(V, Q) and C⁺ (V, Q) if n is odd and Q has maximal Witt index.

        6. Let n = 4, F = . Obtain the structure of C(V, Q) for the following cases in which (u₁, u₂, u₃, u₄) is an orthogonal base for V and the matrix diag {Q(u₁), Q(u₂), Q(u₃), Q(u₄)} is respectively

        7. Note that a ^ta (the transpose of a) is an involution in M_n(F). Use the Skolem-Noether theorem to show that any involution in M_n(F) has the form

where ^ts = ±s. Let Sym J_s be the subspace of M_n(F) of J_s-symmetric elements, that is, satisfying J_s(a) = a. Show that dim J_s = n(n + 1)/2 if ^ts = s and dim J_s = n(n – 1 )/2 if ^ts = – s.

        8. Let A be a finite dimensional central simple algebra over F, E a splitting field for A. Show that if A is viewed as contained in A_E ≅ M_n(E), then any involution J in A has a unique extension to an involution J_E of A_E over E. Then J_E = J_s for some s ∈ M_n(E) such that ^ts = ± s. Call J of orthogonal or symplectic type according as s is symmetric or skew. Show that J is of orthogonal (symplectic) type if and only if dim Sym J = n(n + 1)/2 (n(n – 1)/2).

        9. Determine the type of the main involution in C(V, Q) for n even and the type of the involution induced in C⁺ (V, Q) by the main involution if n is odd.

If J and K are involutions in A and B respectively then we write (A, J) ≅ (B, K) if there exists an isomorphism η to A onto B such that ηJ = Kη.

     10. Prove the following extension of Lemma 5: If U is a 2v-dimensional subspace of V on which the restriction of B is non-degenerate, then C(V, Q) ≅ C(U, Q′) C(U, – δ′Q″) and (C(V, Q), i) ≅ (C(U, Q') C(U, – δ′Q″), i i) if v is even. (Here i is the main involution.)

     11. Let c denote the conjugation a in and s the standard involution a in . Show that , and .

The next three exercises concern isomorphisms for (C(V, Q), l) where V is a finite dimensional vector space over and Q is a positive definite quadratic form on V.

     12. Show that

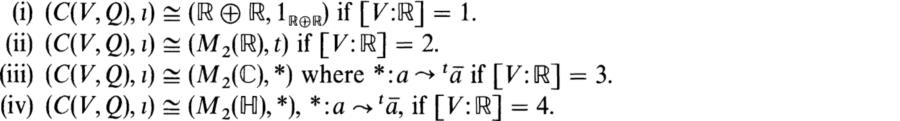
     13. Show that if n = 2v, then

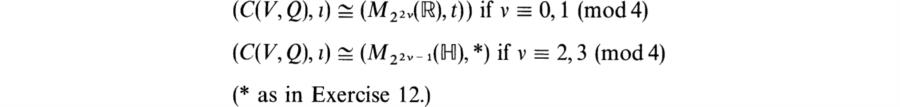
     14. Show that if n = 2v – 1 then

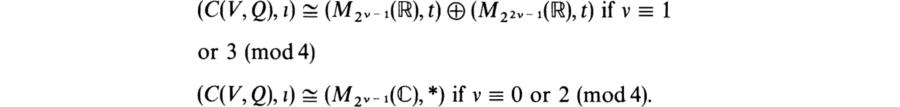
Exercises 15–18 sketch a derivation of the main structure theorem for Clifford algebras for arbitrary fields including characteristic two.

     15. Define a quaternion algebra over an arbitrary field F to be an algebra generated by two elements i, j such that

Show that any such algebra is four-dimensional central simple. Show that this definition is equivalent to the one given in the text if char F ≠ 2.

   Now let V be an n-dimensional vector space equipped with a quadratic form Q with non-degenerate bilinear form. Note that if char F = 2, then B is an alternate form and hence n is even.

     16. Show that if n = 2, then C(V, Q) is a quaternion algebra.

     17. Show that Lemma 5 is valid for arbitrary F. (Hint: Let (u, v) be any base for U and let . Use this in place of the one used in the proof given in the text to extend the proof to arbitrary F.)

     18. Prove Theorem 4.13 for B non-degenerate and F arbitrary. Note that the proof of dim C(V, Q) = 2ⁿ given in the text by reduction to the non-degenerate case carries over to arbitrary F.

In exercises 19–21 we assume that char F = 2.

     19. Define C⁺ = C⁺ (V, Q) as for char F ≠ 2: the subalgebra generated by all products uv, u, v ∈ V. Show that dim C⁺ = 2^{n – 1} and C⁺ is generated by the elements u₁v for any non-isotropic u₁. Show that the subalgebra C' of C⁺ generated by the u₁v such that Q(u₁) ≠ 0 and is isomorphic to a Clifford algebra determined by an (n – 2)-dimensional vector space and that this algebra is central simple of dimension 2^{n – 2}. Let (u₁, v₁, …, u_v, v_v) be a symplectic base (that is, . Show that is in the center of C⁺, that c F1, and that . Hence conclude that and F[c] is the center of C⁺. Show that F[c] is a field or a direct sum of two copies of F according as is not or is of the form β² + β, β ∈ F. Thus conclude that C⁺ is simple or a direct sum of two isomorphic central simple algebras according as .

     20. Let F^[2] denote the set of elements of the form β² + β, β ∈ F. Show that F^[2] is a subgroup of the additive group of F and put G = F/F^[2]. Let (u_l, v_l, …, u_v, v_v) be a symplectic base for V and define

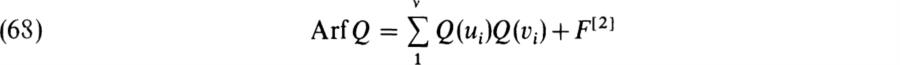
in G. Show that this is independent of the choice of the symplectic base. Arf Q is called the Arf invariant of Q. Note that the last result in exercise 14 can be stated as the following: C⁺ (V, Q) is simple if and only if Arf Q ≠ 0.

     21. Show that there exists a unique derivation D in C = C(V, Q) such that Dx = x for x ∈ V. Show that C⁺ (V, Q) is the subalgebra of D-constants ( = elements a such that Da = 0).

Historical Note

Clifford algebras defined by means of generators and relations were introduced by W. K. Clifford in a paper published in 1878 in the first volume of the American Journal of Mathematics. In this paper Clifford gave a tensor factorization of his algebras into quaternion algebras and the center. The first application of Clifford algebras to orthogonal groups was given by R. Lipschitz in 1884. Clifford algebras were rediscovered in the case n = 4 by the physicist P. A. M. Dirac, who used these in his theory of electron spin. This explains the terminology spin group and spinorial norm. The spin group for orthogonal groups over are simply connected covering groups for the proper orthogonal groups. As in the theory of functions of a complex variable, multiple-valued representations of the orthogonal group become single-valued for the spin group. Such representations occurred in Dirac’s theory. This was taken up in more or less general form by R. Brauer and H. Weyl (1935) and by E. Cartan (1938) and in complete generality by C. Chevalley (1954).

REFERENCES

N. Jacobson, Structure of Rings, American Mathematical Society Colloquium Publication XXXVII, Providence 1956, rev. ed., 1964.

I. Herstein, Noncommutative Rings, Carus Mathematical Monograph, No. 15, Mathematical Association of America, John Wiley, New York, 1968.

C. Faith, Algebra II. Ring Theory, Springer, New York, 1976.

For Clifford algebras:

C. Chevalley, The Algebraic Theory of Spinors; Columbia University Press, New York, 1954.