4

Basic Structure Theory of Rings

The structure theory of rings, which we shall consider in this chapter, is an outgrowth of the structure theory of finite-dimensional algebras over a field that was developed during the latter part of the nineteenth century and the early part of this century. The discovery of quaternions by Hamilton in 1843 led to the construction of other “hypercomplex number systems,” that is, finite dimensional algebras over and , including some non-associative ones (e.g., the octonions of Cayley and Graves). The problem of classifying such systems was studied intensively during the second half of the nineteenth century by a number of mathematicians: Molien, Frobenius, Cartan, and others. Their results constituted a very satisfactory theory for algebras over and , which included a complete classification of an important subclass, the semi-simple algebras. This structure theory was extended to finite dimensional algebras over an arbitrary field by Wedderburn in 1908. In 1927, Artin, stimulated by Emmy Noether’s earlier strikingly successful simplification of ideal theory of commutative rings by the introduction of chain conditions, and motivated by the needs of arithmetic in finite dimensional algebras, extended the Wedderburn theory to rings satisfying chain conditions for one-sided ideals. In 1945 this author developed a structure theory of rings without finiteness assumptions. The principal ingredients of this theory were a new definition of a radical, the concepts of primitivity and semi-primitivity (formerly called semisimplicity), and a density theorem (due independently to Chevalley) that constituted an extensive generalization of a classical theorem of Burnside.

In this chapter we shall reverse the historical order of development by first giving an account of the general theory and then specializing successively to Artin’s theory and to Wedderburn’s theory of finite-dimensional algebras over fields. The Wedderburn structure theorem for simple algebras reduces the classification of these algebras to division algebras. The proper vehicle for studying these is the Brauer group of algebra classes with composition defined by tensor products. We shall give an introduction to the study of these groups and related results on central simple algebras. At the end of the chapter we shall apply the results to the study of Clifford algebras. These are needed to round out the structure theory of orthogonal groups that was presented in Chapter 6 of BAI. Further applications of the theory to representation theory of finite groups will be given in the next chapter.

4.1   PRIMITIVITY AND SEMI-PRIMITIVITY

In the development of ring theory that we shall give, rings of endomorphisms of abelian groups and concretizations of rings as rings of endomorphisms play a predominant role. We recall that if M is an abelian group (written additively), the set of endomorphisms of M has a natural structure of a ring. Thus we obtain End M (or End M), the ring of endomorphisms of M. By a ring of endomorphisms we mean a subring of End M for some abelian group M. We define a representation ρ of a ring R to be a homomorphism of R into a ring End M of endomorphisms of an additive abelian group M. A representation ρ of R acting on M (that is, with codomain End M) defines a left R-module structure on M by specifying that the action of R on M is given through ρ:

for a ∈ R, x ∈ M. Equation (1) defines a left module action since ρ(a) is an endomorphism and a ρ(a) is a ring homomorphism. Conversely, if M is a left module for the ring R, then M is an abelian group and M affords a representation ρ = ρ_M of R by defining a_M for a ∈ R to be the endomorphism

Then ρ : a a_M is a homomorphism of R into End M, hence a representation of R.

By an irreducible representation of a ring we shall mean a representation ρ for which the associated module M (as just defined) is irreducible: M ≠ 0 and M and 0 are the only submodules of M. The structure theory that we shall develop is based on two articles of faith: irreducible representations are the best kinds of representations and the best behaved rings are those that have enough irreducible representations to distinguish between elements of the ring, that is, given a pair of distinct elements a, b of R, there exists an irreducible representation ρ such that ρ(a) ≠ ρ(b). Evidently this is equivalent to the simpler condition that given any a ≠ 0 in R there exists an irreducible representation ρ of R such that ρ(a) ≠ 0.

Before we proceed to the main definitions, it will be useful to collect some elementary facts on representations and modules. Because of the connection between representations and left modules that we have noted, we give preference in this chapter to left modules. Accordingly, in this chapter the unadorned term “module” will always mean left module.

If ρ is a representation of the ring R acting in M, the kernel of ρ is evidently the ideal

(bx = ρ(b)x). We shall call the representation ρ (and occasionally the module M) faithful if ker ρ = 0. For any x ∈ M we have the order ideal or annihilator of x, ann_Rx = {b ∈ R|bx = 0}. This is a left ideal and the cyclic submodule Rx generated by x is isomorphic to R/ann_Rx where R is regarded as left R-module in the natural way. It is evident that

If f is a homomorphism of a ring S into R and ρ is a representation of R acting on M, then ρf is a representation of S acting on M. The corresponding module action of S on M is given by

for b ∈ S. As in the last chapter, the notations _SM and _RM serve to distinguish M as S-module from M as R-module (as well as to indicate that the action is on the left). In most cases, it will be clear from the context which of these is intended and “M” will be an adequate notation. It is clear that

where, of course, f⁻¹( ) denotes the inverse image under f. If the representation ρ of R is faithful, then ann_SM = f⁻¹(0) = kerf

Let B be an ideal of R contained in ann_RM. Then M becomes an = R/B module by defining the action of the coset a + B on x ∈ M by

Since bx = 0 for every b ∈ B, x ∈ M, it is clear that (6) is a well-defined action. It is immediate also that this is a module action of on M and it is clear that a subset N of M is an R-submodule if and only if it is an -submodule. In other words, _RM and have the same lattice of submodules. The relation between the kernels of the representations of R and of is given by the formula

We now proceed to introduce two of our main definitions.

DEFINITION 4.1.   A ring R is called primitive if it has a faithful irreducible representation. R is called semi-primitive if for any a ≠ 0 in R there exists an irreducible representation ρ such that ρ(a) ≠ 0

We shall be interested also in representations that are completely reducible in the sense that the corresponding module M is completely reducible, that is, M = ∑M_α where the M_α are irreducible submodules. We establish first two characterizations of semi-primitivity in the following

PROPOSITION 4.1.   The following conditions on a ring R are equivalent: (1) R is semi-primitive. (2) R has a faithful completely reducible representation. (3) R is a subdirect product of primitive rings (see p. 69).

Proof. (1) (2). For each a ≠ 0 in R let M_a be an irreducible module such that for the representation ρ_Ma we have ρ _Ma(a) ≠ 0. Form M = _a≠0M_a. This is a completely reducible module and it is clear that

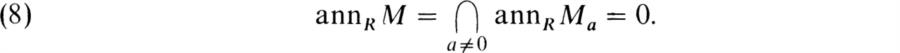
Hence ρ_M is a faithful completely reducible representation for R.

(2) (3). Suppose ρ is a faithful completely reducible representation for R so M = ∑M_α, M_α irreducible, for the corresponding module M. We have 0 = ann_RM = _αann_RM_α, and ann_RM_α is an ideal in R. Hence R is a subdirect product of the rings R_α = R/ann_RM_α. On the other hand, since (ann_RM_α)M_α = 0, M_α can be regarded as an irreducible module for R and the representation of R_α defined by M_α is faithful. Hence R_α is primitive and R is a subdirect product of primitive rings.

(3) (1). Let R be a subdirect product of the primitive rings R_α. For each R_α let ρ_α be a faithful irreducible representation of R_α. We have the canonical homomorphism π_α of R onto R_α and _α ker π_α = 0. We have the irreducible representation ρ_απ_α of R whose kernel is ker π_α. Accordingly, we have a family of irreducible representations {ρ_απ_α} of R such that _α ker ρ_απ_α = 0. Then R is semi-primitive.

The definitions we have given thus far involve objects (representations and modules) that are external to the ring R. It is easy and useful to replace the definitions by internal characterizations. Let I be a left ideal of the ring R. We define

It is clear that if we put M = R/I and regard this as a left R-module then

It follows from this or directly from (9) that (I : R) is an ideal. Moreover, by(9), (I : R) ⊂ I and (I : R) contains every ideal of R contained in I. In other words, (I : R) is the (unique) largest ideal of R contained in I. We can now give the following characterization of primitivity and semi-primitivity.

PROPOSITION 4.2. A ring R is primitive if and only if R contains a maximal left ideal I that contains no non-zero ideal of R. A ring R is semi-primitive if and only if R ≠ 0 and _I(I : R) = 0 where the intersection is taken over all maximal left ideals I of R.

Proof.   If R is primitive, we have an irreducible module M such that ann_RM = 0. Now M R/I for a maximal left ideal I (p. 117). Then (I : R) = ann_RR/I = ann_RM = 0. Thus I is a maximal left ideal containing no non-zero ideal of R. Conversely, if the condition holds, we have a maximal left ideal I such that (I : R) = 0. Then M = R/I provides a faithful irreducible representation of R, so R is primitive.

Now let R be semi-primitive and let {ρ_α} be a set of irreducible representations of R that is adequate for distinguishing the elements of R. Then ker ρ_α = 0. If M_a is the module for ρ_α then M_α R/I_α, I_α a maximal left ideal in R. Hence (I_α : R) = ann_RM_α = ker ρ_α and _α(I_α : R) = 0. A fortiori, (I : R) taken over all of the maximal left ideals of R is 0. The converse follows by retracing the steps.

The internal characterizations of primitivity and semi-primitivity have some important consequences that we shall now record. The first of these is

COROLLARY 1.   Any simple ring (≠0) is primitive.

Proof.   Any ring R ≠ 0 contains a maximal left ideal I (p. 68). If R is simple, (I : R) = 0. Hence R is primitive.

Next we obtain characterizations of primitive and semi-primitive commutative rings.

COROLLARY 2.   Let R be a commutative ring. Then R is primitive if and only if R is a field and R is semi-primitive if and only if it is a subdirect product of fields.

Proof.   If R is a commutative primitive ring, R contains a maximal left ideal I containing no ideal ≠0 of R. Since R is commutative, I is an ideal. Hence I = 0. Then 0 is a maximal ideal in R, which means that R ≠ 0 and 0 and R are the only ideals in the commutative ring R. Then R is a field. Conversely, it is clear that any field satisfies the first condition of Proposition 4.2. Hence any field is primitive. It now follows from Proposition 4.1.3 that R is semi-primitive if and only if it is a subdirect product of fields.

We shall now give some examples of primitive and semi-primitive rings. A convenient way of constructing examples of rings is as rings of endomorphisms of abelian groups. If R is a ring of endomorphisms of an abelian group M, then M is an R-module in the natural way in which the action ax, a ∈ R, x ∈ M is the image of x under a. Obviously, the corresponding representation is the injection of R into End M and so this is faithful. Hence if R acts irreducibly on M ≠ 0 in the sense that there is no subgroup of M other than 0 and M that is stabilized by R, then R is a primitive ring. Several of the following examples are of this type.

EXAMPLES

1. The ring L of linear transformations of a finite dimensional vector space over a division ring is simple (p. 171). Hence L is primitive.

2. Let V be a vector space over a division ring Δ that need not be finite dimensional. We claim that the ring L of linear transformations in V over Δ acts irreducibly on V and hence is a primitive ring. To prove irreducibility, we have to show that if x is any non-zero vector and y is any vector, there exists an l ∈ L such that Ix = y. Now this is clear, since we can take x to be an element in a base (eα for V over Δ, and given any base (e_α) and corresponding elements f_α for every e_α, then there exists a linear transformation l such that le_α = f_α. If V is infinite dimensional, the subset F of transformations l with finite dimensional range (l(V) finite dimensional) is a non-zero ideal in L. Since 1 F, F ≠ L. Hence L is not simple, so this is an example of a primitive ring that is not simple. If the dimensionality of V is countably infinite, it is easy to see that F is the only proper non-zero ideal of L. Hence L/F is simple and thus primitive.

3. If (x₁,x₂,x₃,…) is a base for a vector space V over a division ring Δ, then a linear transformation l is determined by its action on the base. We can write

where the λ_ij∈ Δ and for a given i only a finite number of the λ_ij are ≠0. Thus l can be described by a matrix = (λ_ij), which is row finite in the sense that there are only a finite number of non-zero entries in each row. The set of row-finite matrices with entries in Δ is a ring under the usual matrix addition and multiplication, and the map I where is the matrix of l relative to the base (x_i) is an anti-isomorphism. Now let R be the set of linear transformations whose matrices relative to the given base have the form

where Φ is a finite square block and λ ∈ Δ. The set of matrices of the form (12) is a subring of the ring of row-finite matrices. Hence R is a subring of the ring of linear transformations L. R acts irreducibly on V. For, if x is a non-zero vector and y is any vector, then we can write x = ξ₁x₁ +… + ξ_nx_n, y = η₁x₁ + … + η_nx_n for some n where the ξ_l, η_i ∈ Δ. Thus x and y are contained in a finite dimensional subspace V′ of V. There exists a linear transformation l′ of V′ into itself such that l′x = y and l′ can be extended to a linear transformation l of V contained in R (for example, by specifying that lx_i = 0 if i > n). Then lx = y. Hence V is irreducible as R-module and so R is primitive.

4. Let V be as in example 3 with Δ = F, a field, and let p and q be the linear transformations in V over F such that

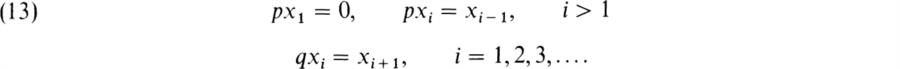
Then pqx_i = x_i for all i and qpx₁ = 0, qpx_i = x_i for i > 1. Hence

Let R be the set of linear transformations

where the α_ij ∈ x. The first relation in (14) implies that R is closed under multiplication, so R is a ring of endomorphisms of V. Now put

The matrix of e_ij has a 1 in the (j,i)-position, 0’s elsewhere. It follows that the matrix ring corresponding to R includes all the matrices (12). Thus R contains the ring given in example 3 as a subring. Hence the present R acts irreducibly on V, so R is primitive.

5. For any ring R we have the regular representation ρ_R whose module is the additive group of R on which the ring R acts by left multiplication (see BAI, pp. 422–426). This representation is faithful and the submodules of R are the left ideals. Now let A be an algebra over the field F. Then the regular representation ρ_A of A provides a monomorphism of A into the algebra L of linear transformations of the vector space A/F. Thus any algebra over a field can be imbedded in a primitive ring. We shall now show that A is also a homomorphic image of a primitive ring. Since A is an arbitrary algebra over a field, this will show that there is not much that can be said about homomorphic images of primitive rings. For our construction we take V = A, a direct sum of a countably infinite number of copies of the vector space A. Let A act on V in the obvious way and identify A with the corresponding algebra of linear transformations in V. For n = 1, 2, 3,… let V_n be the subspace of V of elements of the form (x₁,x₂,…,x_n,0, 0,…), x_i ∈ A, and let L_n be the set of linear transformations that map V_n into itself and annihilate all of the elements (0,…,0,x_{n+ 1},x_{n+ 2},…). Then L₁ ⊂ L₂ ⊂^…. Put L = L_i and let R be the ring of linear transformations generated by A and L. Then R acts irreducibly on V, so R is primitive. Moreover, R = A+L, A ∩ L = 0, and L is an ideal in R. Then R/L A, so the given algebra A is a homomorphic image of the primitive algebra R.

6. The ring is semi-primitive since _pprime(p) = 0 and /(p) is a field. Hence is a subdirect product of fields, so is semi-primitive. Similarly any p.i.d. with an infinite number of primes is semi-primitive.

EXERCISES

        1. Let F{x,y} be the free algebra generated by x and y, and let K be the ideal in F{x,y} generated by xy – 1. Show that F{x,y}/K is isomorphic to the algebra R defined in example 4 above.

        2. (Samuel.) Let V,F be as in example 4 and let S be the algebra of linear transformations generated by p as in example 4 and the linear transformation r such that rx_i = x_{i² + 1}. Show that S is primitive and S is isomorphic to the free algebra F{x,y}.

        3. Let F{x,y} be as in exercise 1 and let K be the ideal generated by xy – yx – x. Assume that F is of characteristic 0. Show that R = F{x,y}/K is primitive.

        4. Let R be a ring containing an ideal N ≠ 0 that is nilpotent in the sense that there exists an integer m such that N^m = 0 (that is, the product of any m elements of N is 0). Show that R is not semi-primitive.

        5. Show that if R is primitive then the matrix ring M_n(R) is primitive.

        6. Show that if R is primitive and e is an idempotent element ≠0 in R, then the ring eRe (with unit e) is primitive.

        7. Show that if R and R′ are Morita similar (p. 179), then R is primitive if and only if R′ is primitive.

        8. Let F be a field, P = F[t₁,…, t_n], the ring of polynomials in n indeterminates with coefficients in F. Show that for any i = 1, 2,…,n, there exists a unique derivation D_i of P such that

(see exercise 11, p. 147). For f ∈ P let denote the multiplication g fg in P. Show that if D is a derivation in P and f ∈ P, then D is a derivation in P. Show that the derivations of P into P are the maps where D_i is as above and f_l ∈ P. Let R be the ring of endomorphisms of the additive group of P generated by the derivations and the multiplications of P. Show that if F is of characteristic 0, then R is an irreducible ring of endomorphisms and hence R is primitive.

        9. Let F be a field of characteristic 0 and F{x_l,…, x_n, y₁,…, y_n} the free algebra over F determined by the 2n elements x_l,…, x_n, y_l,…, y_n. Let I be the ideal in F{x_l,…, x_n,…, y_l,…, y_n} generated by the elements

1 ≤ i,j ≤ n. The algebra W_n = F{x_l,…, x_n, y_l,…, y_n}/I is called a Weyl algebra. Show that if P and R are as in exercise 8, then the homomorphism η of F{x₁,…,x_n, y₁,…,y_n} into R such that x_{i i}, y_t D_l, 1 ≤ i ≤ n, is surjective and ker η = l Hence conclude that W_n is primitive.

     10. Show that W_n is simple. (Suggestion: First treat the case in which n = 1.)

4.2   THE RADICAL OF A RING

From the point of view that we took in the previous section, the purpose of defining the radical of a ring is to isolate that part of the ring whose elements are mapped into 0 by every irreducible representation of the ring. Accordingly, we introduce the following

DEFINITION 4.2.   The (Jacobson) radical of a ring is the intersection of the kernels of the irreducible representations of the ring.

Evidently, the radical, rad R, of the ring R is an ideal in R.

We shall call an ideal P of R primitive (in R) if R/P is a primitive ring. Let l be a maximal left ideal of R and let P = (I : R). Then M = R/I is an irreducible module for R whose annihilator is P. Hence M can be regarded as an = R/P-module by (6) and M is irreducible as -module. By (7), annM = ann_RM/P = P/P = 0. Hence M is a faithful irreducible module for and so is primitive. Then, by definition, P is a primitive ideal in R. Conversely, let P be a primitive ideal in R. Then we have an irreducible module M for = R/P such that the associated representation is faithful. Regarding M as R-module via (4) we see that M is an irreducible R-module such that ann_RM = P (see(5). Now M R/I where I is a maximal left ideal of R and hence ann_RR/I = P. Since ann_RR/I = (I : R), we have P = (I: R). We therefore have the

LEMMA 1.   An ideal P of R is primitive in R if and only if P = (I : R) for some maximal left ideal I of R.

We can now give our first internal characterization of the radical.

PROPOSITION 4.3. (1) rad R is the intersection of the primitive ideals of R. (2) rad R is the intersection of the maximal left ideals of R.

Proof. (1) By definition,

where {M} is the class of irreducible modules of R. Since M R/I and ann R/I = (I : R), we have

where I runs over the maximal left ideals of R. By the lemma, this can be written also as

where P runs over the primitive ideals in R. This proves (1). To prove (2), we recall that for any module M we have ann_RM = _x∈M ann_Rx = _{x ≠ 0} ann_Rx. If M is irreducible, this expresses ann_RM as an intersection of maximal left ideals. Hence, by (17), rad R is an intersection of maximal left ideals, so rad R ⊃ I where I ranges over the maximal left ideals of R. On the other hand, since I ⊃ (I: R), I ⊃ (I : R) = rad R so

where the intersection is taken over the set of maximal left ideals of R.

We prove next

PROPOSITION 4.4. (1) R is semi-primitive if and only if rad R = 0. (2) If R ≠ 0, then R/rad R is semi-primitive and rad R is contained in every ideal B of R such that R/B is semi-primitive.

Proof. (1) If rad R = 0, then P = 0 for the primitive ideals of R. Then R is a subdirect product of the primitive rings R/P and R is semi-primitive by Proposition 4.1. Conversely, if R is semi-primitive, R is a subdirect product of primitive rings and so there exists a set of primitive ideals whose intersection is 0. Then rad R = P = 0 if P runs over the set of primitive ideals of R.

(2) If B is an ideal of R, then any ideal of = R/B has the form P/B where P is an ideal of R containing B. Since R/P / where = P/B, it is clear that is primitive in if and only if P is primitive in R. Since is semiprimitive if and only if = 0, primitive in , it follows that is semiprimitive if and only if B is the intersection of all of the primitive ideals of R containing B. Then B ⊃ rad R, by (18′). If B = radR, (18′) implies that B is an intersection of primitive ideals. Then R/B = R/rad R is semi-primitive. This proves (2).

We shall give next an important element characterization of the radical. For this purpose, we introduce a number of definitions. First, we call an element z of a ring R left (right) quasi-regular in R if 1 — z has a left (right) inverse in R. Evidently, left (right) quasi-regularity is equivalent to the following: the principal left (right) ideal R(1 — z) ((1 — z)R) = R. If z is both left and right quasi-regular, then z is called quasi-regular. A left (right) ideal I is called quasiregular if all of its elements are left (right) quasi-regular.

If z is left quasi-regular, 1 — z has a left inverse that we can write as 1 — z′. Then (1 — z′) (í — z) = 1 gives the relation

The binary product z′ O z = z + z′ — z′z defines the circle composition O in the ring R. Let σ denote the map x 1 — x in R. Then σ² = 1, so σ is bijective. We have

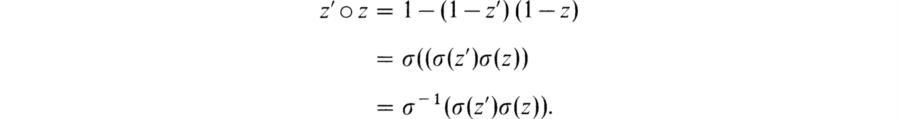
This implies that the circle composition is associative. Also since σ(0) = 1, 0oz = z = zo0. Thus (R,o,0) is a monoid.

LEMMA 2. (1) If I is a quasi-regular left (right) ideal, then I is a subgroup of (R, o, 0). (2) Nilpotent elements are quasi-regular.

Proof. (1) Let z ∈ l. Then we have a z′ ∈ R such that z′ Ο z = 0. Then z + z′ — z′z = 0 and z′ = z′z — z ∈ I. Hence there exists a z″ such that z″ O z′ = 0. Since (R,O,0) is a monoid, the equations z′ O z = 0 = z″ O z′ imply that z″ = z, so z′ is the inverse of z in (R, O, 0) and z′ ∈ I. Since I is closed under O and contains 0, statement (1) is clear.

(2) If zⁿ = 0, then (1 — z) (1 + z + z² + … + zⁿ⁻¹) = 1 = (1 + z + z² + … + zⁿ⁻¹) (1 — z). Hence z is quasi-regular.

An ideal (left, right ideal) is called nil if all of its elements are nilpotent. The second part of Lemma 2 shows that any nil left (right) ideal is quasi-regular.

We can now give the following element characterizations of rad R.

PROPOSITION 4.5. (1) radR is a quasi-regular left ideal that contains every quasi-regular left ideal of R. (2) rad R is the set of elements z such that az is left quasi-regular for every a ∈ R.

Proof. (1) Suppose z ∈ rad R is not left quasi-regular. Then R(l —z) ≠ R, so this left ideal can be imbedded in a maximal left ideal I. Since rad R is the intersection of the maximal left ideals of R, z ∈ I. But 1 – z ∈ R(1 – z) ⊂ I, so 1 = 1 – z + z ∈ I contrary to I R. This contradiction shows that every z ∈ rad R is left quasi-regular, so it proves that rad R is a quasi-regular left ideal. Now let Z be any quasi-regular left ideal of R. If Z z rad R, then there exists a maximal left ideal I such that Z I. Then I + Z I and so I + Z = R. Then 1 = b + z for some b ∈ I, z ∈ Z, and 1 = (1 — z)⁻¹b ∈ I contrary to I R. Thus Z ⊂ R and part (1) is proved.

(2) If z ∈ rad R, then az ∈ rad R for any a in R, so az is left quasi-regular. Conversely, suppose z satisfies this condition. Then Rz is a quasi-regular left ideal. Hence Rz ⊂ rad R by (1) and z ∈ rad R.

The concept of primitivity of a ring and of an ideal in a ring is not left-right symmetric. For, there exist primitive rings that are not right primitive in the sense that they have no irreducible right modules M′ such that the associated anti-representation ρ′ :a ρ′(a), where ρ′(a)x = xa, is monic. The first examples of such rings were given by George Bergman. In spite of this lack of symmetry in the concept of primitivity, the concepts of the radical and semi-primitivity are symmetric. Evidently, everything we have done can be carried over to antirepresentations, right modules, and right ideals. Suppose we denote the corresponding right radical as rad′ R. Then we have the analogue of Proposition 4.5 for rad′ R. On the other hand, by Lemma 2, the elements of rad R and rad′ R are quasi-invertible. Hence, by Proposition 4.5 and its analogue for right ideals, we have rad′ R ⊂ rad R and rad R ⊂ rad′ R. Thus rad R = rad′ R. This permits us to give a number of additional characterizations of rad R. We give these and summarize the ones we obtained before in

THEOREM 4.1.   We have the following characterizations of the radical of a ring: radR is

            1. the intersection of the primitive ideals of R,

            2. the intersection of the maximal left ideals of R,

            3. the intersection of the right primitive ideals of R,

            4. the intersection of the maximal right ideals of R,

            5. a quasi-regular left ideal containing every quasi-regular left ideal,

            6. the set of elements z such that az is left quasi-regular for every a ∈ R,

            7. a quasi-regular right ideal containing every quasi-regular right ideal,

            8. the set of elements z such that za is right quasi-regular for every a ∈ R.

It is clear also that rad R contains every nil right ideal as well as every nil left ideal of R. Moreover, since right semi-primitivity (defined in the obvious way) is equivalent to rad′R = 0, it is clear that a ring is semi-primitive if and only if it has a faithful completely reducible anti-representation and if and only if it is a subdirect product of right primitive rings. Another way of putting the left-right symmetry is that if we regard R and R^op as the same sets, then rad R = rad R^op and if R is semi-primitive, then so is R^op.

EXERCISES

        1. Show that a ring R is a local ring (p. 111) if and only if R/rad R is a division ring and that if this is the case, then rad R is the ideal of non-units of R.

        2. Determine the radical of /(n), n ≥ 0.

        3. (McCrimmon.) Show that z ∈ rad R if and only if for every a ∈ R there exists a w such that z + w = waz = zaw.

        4. Show that ab is quasi-regular if and only if ba is quasi-regular.

        5. Call an element a of a ring R von Neumann regular if there exists a b such that aba = a. Show that the only element in rad R having this property is 0. (A ring is called von Neumann regular if all of its elements are von Neumann regular. Hence this exercise implies that such rings are semi-primitive.)

        6. Let R be a ring such that for any a ∈ R there is an integer n(a) > 1 such that a^n(a) = a. Show that R is semi-primitive.

        7. Let e be a non-zero idempotent in a ring R. Show that rad eRe = e(rad R)e = eRe ∩ rad R. (Sketch of proof: Show that every element of e(rad R)e is quasiregular in eRe, so e(rad R)e ⊂ rad eRe. Next let z ∈ rad eRe and let a ∈ R. Write a = eae + ea(1 – e) + (1 – e)ae + (1 – e)a(1 – e) (the two-sided Peirce decomposition). Then za = zeae + zea( 1 –e) and zeae has a quasi-inverse z′ in eRe. Then za O z′ = zea(1 – e), which is nilpotent, thus quasi-regular. Hence za is right quasiregular. Hence z ∈ rad R ∩ eRe and rad eRe ⊂ e(rad R)e.)

        8. Show that for any ring R, rad M_n(R) = M_n(rad R). (Sketch of proof: We have a 1–1 correspondence B M_n(B) of the set of ideals of R onto the set of ideals of M_n(R) (see exercise 1, p. 171). Let {e_i|1 ≤ i, j ≤ n} be a set of matrix units for M_n(R). We have the isomorphism r (r1)e₁₁ of R onto e₁₁ M_n(R)e₁₁. Under this the image of rad R is rade₁₁M_n(R)e₁₁ = e₁₁ radM_n(R)e₁₁ (by exercise 7) = e₁₁M_n(B)e₁₁. It follows that B = rad R.)

        9. Show that if R and R′ are (Morita) similar, then in any correspondence between the ideals of R and R′ given by Morita I, the radicals of R and R′ are paired.

     10. Prove that any ultraproduct of semi-primitive (primitive) rings is semi-primitive (primitive).

4.3   DENSITY THEOREMS

If V is a vector space over a division ring Δ, then a set S of linear transformations in V is called dense if for any given finite set of linearly independent vectors x₁,x₂, …, x_n and corresponding vectors y₁, y₂, …, y_n there exists an l ∈ S such that lx_i = y_i 1 ≤ i ≤ n. If V is finite dimensional, then we can take the x_i to be a base and y_i = ax_i for any given linear transformation a. Then we have an l ∈ S such that lx_i = ax_i 1 ≤ i ≤ n, from which it follows that l = a. Hence the only dense set of linear transformations in a finite dimensional vector space is the complete set of linear transformations.

In this section we shall prove a basic theorem that permits the identification of any primitive ring with a dense ring of linear transformations. We consider first a more general situation in which we have an arbitrary ring R and a completely reducible (left) module M for R. Let R′ = End_RM, R″ = End_R.M where M is regarded in the natural way as a left R′-module. We shall prove first the

DENSITY THEOREM FOR COMPLETELY REDUCIBLE MODULES.   Let M be a completely reducible module for a ring R. Let R′ = End_R M, R″ = End_R M. Let {x_u,…, x_n} be a finite subset of M, a″ an element of R″. Then there exists an a ∈ R such that ax_i = a″x_i, 1 ≤ i ≤ n.

The proof we shall give is due to Bourbaki and is based on the following pair of lemmas.

LEMMA 1.   Any R-submodule N of M is an R″-submodule.

Proof.   Since M is completely reducible as R-module, we can write M = N P where P is a second submodule (p. 121). Let e be the projection on N determined by this decomposition. Then e ∈ R′ and N = e(M). Hence if a″ ∈ R″, then a″(N) = a″e(M) = ea″(M) ⊂ N. Thus N is a submodule of _R″ M.

LEMMA 2.   Let M be a module, M⁽ⁿ⁾ the direct sum of n copies of M, n = 1, 2,… Then End_RM⁽ⁿ⁾ is the set of maps (u_l, u₂, …, u_n) (v₁ v₂, …, v_n) where v_l = ∑, a′_iju_j, a′_ij ∈ R′ = End_RM. Moreover, for any a″ ∈ R″ = End_RM, the map (u_l, u₂, …, u_n)(a″u₁, a″u₂, …, a″u_n) is contained in the ring of endomorphisms of M⁽ⁿ⁾ regarded as a left End_RMⁿ-module.

Proof.     Let l ∈ End_RM⁽ⁿ⁾, and consider the action of I on the element (0, …, 0, u_i, 0, …, 0) where u_i is in the ith place. We have 1(0,…, 0, u_i0, …, 0) = (u_1i, u_2i, …, u_ni), which defines the map u_i u_ji, 1 ≤ j ≤ n. This is contained in End_RM. Denoting this map as a′_ji we obtain l(u₁, …, u_n) = . It is clear also that any map of this form is contained in End_RM⁽ⁿ⁾. This proves the first assertion. The second follows, since for any a″ ∈ R″ the map (u₁, u₂, …, u_n) (a″u₁, a″u₂, …, a″u_n) commutes with every map (u₁, u₂, …, u_n) , a′_ji ∈ R′.

We can now give the

Proof of the theorem. Suppose first that n = 1. Then N = Rx₁ is an R -submodule, hence an R″ -submodule. Since x₁ ∈ N, a″x₁ ∈ N = Rx₁. Hence we have an a ∈ R such that ax₁ = a″x₁. Now suppose n is arbitrary. Consider M⁽ⁿ⁾ the direct sum of n copies of the R-module M. The complete reducibility of M implies that M⁽ⁿ⁾ is completely reducible. By Lemma 2, if a″ ∈ R″, the map (u_l, u₂, …, u_n) (a″u₁, a″u₂, …, a″u_n) is in the ring of endomorphisms of M⁽ⁿ⁾, regarded as left End_RM⁽ⁿ⁾ module. We apply the result established for n = 1 to this endomorphism and the element x = (x₁, …, x_n) of M⁽ⁿ⁾. This gives an element a ∈ R such that ax = (a″x_l, …, a″x_n). Then ax_i = a″x_i, 1 ≤ i ≤ n, as required.

There is a good deal more that can be done at the level of completely reducible modules (see the exercises below). However, for the sake of simplicity, we shall now specialize to the case that is of primary interest for the structure theory: a faithful irreducible representation of a ring. In this case we have the

DENSITY THEOREM FOR PRIMITIVE RINGS.   A ring R is primitive if and only if it is isomorphic to a dense ring of linear transformations in a vector space over a division ring.

Proof.   Suppose R is a primitive ring, so R has a faithful irreducible representation ρ acting in M. By Schur’s lemma, Δ = End_RM is a division ring. Since ρ is faithful, R is isomorphic to ρ(R), which is a ring of linear transformations in M regarded as a vector space over Δ. Now let x₁, …, x_n be linearly independent vectors in M, y₁, …, y_n arbitrary vectors. Since the x’s can be taken to be part of a base, there exists a linear transformation l such that lx_i = y_i, 1 ≤ i ≤ n. Since l ∈ End_ΔM and Δ = End_RM, it follows from the previous theorem that there exists an a ∈ R such that ax_i = lx_i = y_i, 1 ≤ i ≤ n. Then ρ(R) is a dense ring of linear transformations in M over Δ. Conversely, suppose R is isomorphic to a dense ring of linear transformations in a vector space M over a division ring Δ. If ρ is the given isomorphism, then putting ax = ρ(a)x for a ∈ R, x ∈ M, makes M an R-module. Moreover, this is irreducible since if x ≠ 0 and y is arbitrary, we have an a ∈ R such that ax = y. Hence ρ is a faithful irreducible representation of R and so R is primitive.

For some applications it is important to have an internal description of the division ring Δ in the foregoing theorem. This can be obtained by identifying an irreducible R-module with an isomorphic one of the form R/I where I is a maximal left ideal of R. We need to determine End_R(R/I). We shall do this for any left ideal I or, equivalently, for any cyclic module. We define the idealizer of I in R by

It is clear that this is a subring of R containing I as an ideal and, in fact, B contains every subring of R having this property. We have

PROPOSITION 4.6.   If I is a left ideal in R, then End_R(R/I) is anti-isomorphic to B/I where B is the idealizer of I in R.

Proof.   Since 1 + I is a generator of R/I, f ∈ End_R(R/I) is determined by f(1 + I) = b + I = b(1 + l) as the map

If a ∈ l, a + I = I = 0 in R/I and hence its image ab + I = I. Then ab ∈ l. Thus b ∈ the idealizer B of I. Conversely, let b ∈ B and consider the homomorphism of the free R-module R into R/I sending 1 b + I. Any d ∈ l is mapped into db + l = l by this homomorphism. Hence we have an induced homomorphism of R/I into R/I sending 1 + I b + I. Thus any b ∈ B determines an endomorphism of R/I given by (22). Denote the correspondence between elements of B and endomorphisms of R/I determined in this way by g. Evidently g is additive and g(1) = 1. Also if b₁, b₂ ∈ B, we have g(b₁b₂)(1 + l) = b₁b₂ + I and g(b₂)g(b₁) (1 + l) = g(b₂)(b₁ + l) = b₁b₂ + I. Hence g is an antihomomorphism of B onto End_R(R/I). The ideal in B of elements mapped into 0 by this map is l. Hence B/I and End_R(R/I) are anti-isomorphic.

The reader should be warned that in spite of this nice determination of the division ring Δ in the density theorem, given by Proposition 4.6, this division ring is not an invariant of the primitive ring. A given primitive ring may have non-isomorphic irreducible modules giving faithful representations and even some irreducible modules whose endomorphism division rings are not isomorphic. There are important cases in which the division ring is an invariant of the primitive ring. For example, as we shall show in the next section, this is the case for artinian primitive rings. Our next theorem gives the structure of these rings.

THEOREM 4.2.   The following conditions on a ring R are equivalent:

            (1) R is simple, left artinian, and non-zero.

            (2) R is primitive and left artinian.

            (3) R is isomorphic to a ring End_ΔM where M is a finite dimensional vector space over a division ring Δ

Proof.   (1) (2) is clear.

(2) (3). Let M be a faithful irreducible module for R, Δ = End_RM. We claim that M is finite dimensional over Δ. Otherwise, we have an infinite linearly independent set of elements {x_i|i = 1, 2, 3,…} in M. Let I_j = ann_Rx_j so I_j is a left ideal. Evidently, is the subset of R of elements annihilating x₁,…, x_n. By the density theorem there exists an a ∈ R such that ax₁ = ^… = ax_n = 0, ax_{n + l} ≠ 0. Hence Then

is an infinite properly descending sequence of left ideals in R contrary to the artinian property of R. Thus M is finite dimensional over Δ and if we let (x₁, x₂, …, x_n) be a base for M over Δ, the density property implies that for any y₁, …, y_n there exists an a ∈ R such that ax_i = y_i, 1 ≤ i ≤ n. Hence if ρ is the representation determined by M, ρ(R) = End_ΔM so R is isomorphic to the ring of linear transformations in the finite dimensional vector space M over Δ.

(3) (1). This has been proved in proving the Wedderburn-Artin theorem (p. 171). It can also be seen directly by using the anti-isomorphism of End_ΔM with M_n(Δ) and recalling that if R is any ring, the map B M_n(B) is an isomorphism of the lattice of ideals of R with the lattice of ideals of M_n(R) (exercise 8, p. 103 of BAI; or exercise 1, p. 171). The result then follows from the simplicity of Δ.

EXERCISES

        1. Let R be a primitive ring, M a faithful irreducible module for R, Δ = End_RM. Show that either R M_k(Δ) for some n or for any k = 1, 2, 3,…, R contains a subring having M_k(Δ) as a homomorphic image.

        2. Use exercise 1 to show that if R is a primitive ring such that for any a ∈ R there exists an integer n(a) > 1 such that a^n(a) = a, then R is a division ring.

        3. Call a set S of linear transformations k-fold transitive if for any l ≤ k linearly independent vectors x₁,…, x_l and arbitrary vectors y₁,…, y_l there exists an a ∈ S such that ax_i = y_i 1 ≤ i ≤ l. Show that a ring of linear transformations that is two-fold transitive is dense.

In the next three exercises, M = _RM is completely reducible, R′ = End_RM, R″ = End_R′ M.

        4. Show that any homomorphism of a submodule _RN of _RM into _RM can be extended to an endomorphism of _RM (an element of R′) and that if _RN is irreducible, any non-zero homomorphism of _RN into _RM can be extended to an automorphism of _RM.

        5. Show that if x ≠ 0 is an element of an irreducible submodule _RN of _RM, then R′x is an irreducible submodule of _R′ M. (Hint: Let y = a′x ≠ 0, a′ ∈ R′, and consider the map u a′u of _RN = Rx into _RM.)

        6. Show that _R′ M is completely reducible and that its dimensionality (defined on p. 125) is finite if R is left artinian. Show also that in this case R″ = ρ(R) where ρ is the representation defined by M.

        7. Let M be a completely reducible R-module, B an ideal in R. Show that the following conditions are equivalent: (i) BM = M. (ii) If x ∈ M satisfies Bx = 0, then x = 0. (iii) For any x, x ∈ Bx.

        8. Prove the following extension of the density theorem for completely reducible modules: If R, M, and B are as in exercise 7 and B satisfies (i), (ii), (iii), then for any a″ ∈ R″ and x₁,…, x_n ∈ M there exists a b ∈ B such that bx_i = a″ x_i, 1 ≤ i ≤ n.

        9. Use exercise 8 to prove the simplicity of the ring of linear transformations in a finite dimensional vector space over a division ring.

4.4   ARTINIAN RINGS

In this section we shall derive the classical results on structure and representations of (left) artinian rings. We shall show first that the radical of such a ring is nilpotent. We recall that if B and C are ideals of a ring R, then BC = . This is an ideal in R. Also, if D is another ideal, then (BC)D = B(CD). We define B^k inductively by B¹ = B, Bⁱ = B^{i − 1} B and B is called nilpotent if B^k = 0 for some k. This is equivalent to the following: the product of any k elements of B is 0. In particular, b^k = 0 for every B. Hence B nilpotent implies that B is a nil ideal. On the other hand, it is easy to give examples of nil ideals that are not nilpotent (exercise 1, at the end of this section).

THEOREM 4.3.   The radical of a (left) artinian ring is nilpotent.

Proof.   Let N = rad R, R artinian. By induction, N ⊃ N² ⊃ N³ ⊃ …. Since these are left ideals, there is a k such that P ≡ N^k = N^{k + 1} = …. Then P = P² = N^2k. N is nilpotent if and only if P = 0. Suppose this is not the case and consider the set S of left ideals I of R such that (1) I ⊂ P and (2) PI ≠ 0. Since P has these properties, S is not vacuous, and since R is artinian, S contains a minimal element I. Evidently, I contains an element b such that Pb ≠ 0. Then Pb is a left ideal contained in I and in P and P(Pb) = P²b = Pb ≠ 0. Hence Pb = I by the minimality of I in S. Since b ∈ I, we have a z ∈ P such that zb = b or (1 − z)b = 0. Since z ∈ P ⊂ rad R, z is quasi-regular. Hence (1 − z)⁻¹ exists and b = (1 − z)⁻¹(l − z)b = 0. This contradicts Pb ≠ 0 and proves (rad R)^k = P = 0.

We recall that the radical of any ring contains all quasi-regular one-sided ideals, hence all nil one-sided ideals of the ring. The foregoing result implies that all such ideals in an artinian ring are nilpotent. We shall now derive the main result on the structure of semi-primitive artinian rings. For the proof we shall need the

LEMMA.   Let M be an artinian module that is a subdirect product of irreducible modules. Then M is a direct sum of a finite number of irreducible submodules.

Proof.   The second hypothesis is equivalent to the following: M contains a set of submodules {N_α} such that ∩N_α = 0 and every M_α = M/N_α is irreducible. Consider the set of finite intersections of . The artinian condition on M implies that there exists a minimal element in this set, say, N₁ ∩ … ∩ N_m. Then for any N_α, N_α ∩ (N₁ ∩ … ∩ N_m) = N₁∩ … ∩ N_m so N_α ⊃ N₁ ∩ … ∩ N_m. Since N_α = 0, we have N_l ∩ … ∩ N_m = 0. Then we have a monomorphism of M into . Thus M is isomorphic to a submodule of the completely reducible module M_i. Then M is completely reducible and is a direct sum of irreducible modules isomorphic to some of the M_i.

We shall now call a ring semi-simple if it is a subdirect product of simple rings. We have the following easy consequence of the preceding lemma.

PROPOSITION 4.7.   If R is semi-simple and R satisfies the minimum condition for two-sided ideals, then R is a direct sum ⁿ₁R_i of simple rings R_i.

Proof.   Let M(R) be the ring of endomorphisms of the additive group of R generated by the left and the right multiplications x ax and x xa. This ring is called the multiplication ring of R. The additive group R can be regarded in the natural way as M(R)-module and when this is done, the submodules of _M(R)R are the ideals of the ring R. The hypothesis that R is semi-simple is equivalent to the following: R as M(R)-module is a subdirect product of irreducible M(R)-modules. The other hypothesis of the lemma is also fulfilled. The conclusion then follows from the lemma.

We can now prove the main

STRUCTURE THEOREM FOR SEMI-PRIMITIVE ARTINIAN RINGS.   The following conditions on a ring R are equivalent:

            (1) R is artinian and contains no nilpotent ideals ≠ 0.

            (2) R is semi-primitive and artinian.

            (3) R is semi-simple and artinian.

            (4) _RR is a completely reducible R-module.

            (5) R is a direct sum of a finite number of rings R_i each of which is isomorphic to the ring of linear transformations of a finite dimensional vector space over a division ring.

The implication (1) (5) is called the Wedderburn-Artin theorem.

Proof. (1) (2). This is clear, since the radical of an artinian ring is a nilpotent ideal containing all nilpotent ideals and rad R = 0 is equivalent to semi-primitivity.

(2) (3) is clear from Theorem 4.2, which establishes the equivalence of simplicity and primitivity for artinian rings.

(2) ⇒ (4). Since rad R is the intersection of the maximal left ideals, semi-primitivity of R implies that _RR is a subdirect product of irreducible modules. Then (4) follows from the lemma.

(4) ⇒ (2). The semi-primitivity is clear, since the representation determined by _RR is faithful and completely reducible. Also we have R = ∑Iα, Iα a minimal left ideal. Then . Then for a∈R, we have a = a1 = and hence R = I₁ I₂ … I_l for a subset of the I_j. Then it is clear that

is a composition series for _RR. The existence of such a series implies that R is artinian and noetherian. Then (2) holds.

(3) (5). Evidently the artinian property implies that R satisfies the minimum condition for two-sided ideals. Hence, by Proposition 4.7, R is a direct sum of simple rings. Thus where the R_i are ideals and are simple rings. Then for i ≠ j, R_iR_j ⊂ R_i ∩ R_j = 0. It follows that any left ideal of R_i is a left ideal of R; hence, each R_i is artinian. Then R_i is isomorphic to the ring of linear transformations of a finite dimensional vector space over a division ring. Hence (5) holds.

(5) (2). If where the R_i are ideals and R_i is isomorphic to End_Δl M_i, M_i a finite dimensional vector space over the division ring Δ_l, then R_l is primitive artinian by Theorem 4.2, and R is a subdirect product of primitive rings, so R is semi-primitive. Since R_i is a submodule of _RR and the R-submodules of R_i are left ideals, _RR_i is artinian. Hence R is artinian. Thus (2) holds. This completes the proof.

Let R be any ring and suppose R = R₁ … R_S where the R_i are ideals that are indecomposable in the sense that if ideals, then either R′. = 0 or R″ = 0. Now let B be any ideal in R. Then B = B1 = BR = BR₁ +…+ BR_S and since BR_i ⊂ R_i, we have B = BR₁ … BR_S. Also BR_i is an ideal of R, so if B is indecomposable then we have BR_l = B for some i. Similarly, we have B = R_jB for some j and since R_i ∩ R_j = 0 if i ≠ j, we have B = R_iB. It follows that if is a second decomposition of R as a direct sum of indecomposible ideals, then s = t and the R′_j are, apart from order, the same as the R_i. This applies in particular to the decomposition of a semi-simple artinian ring as direct sum of ideals that are simple rings. We see that there is only one such decomposition. Accordingly, we call the terms R_i of the decomposition the simple components of R.

The structure theorem for semi-primitive artinian rings (or Theorem 4.2) shows that if R is simple artinian, then R End_ΔM, M a finite dimensional vector space over the division ring Δ. We now consider the question of uniqueness of M and Δ. The problem can be posed in the following way: Suppose End_Δ1M₁ and End_Δ2M₂ are isomorphic for two finite dimensional vector spaces M_i over Δ_i; what does this imply about the relations between the two spaces? We shall see that the vector spaces are semi-linearly isomorphic. We recall that if σ is an isomorphism of Δ₁ onto Δ₂, then a map s : M₁ → M₂ is called a a-semi-linear map if

for x,y ∈ M₁ δ ∈ Δ₁ (BAI, p. 469). It is immediately apparent that if s is bijective, then s^–1 is a σ^{‒ 1} -semi-linear map of M₂ onto M₁. We shall say that M₁ and M₂ are semi-linearly isomorphic if there exists a semi-linear isomorphism ( = bijective semi-linear map) of M₁ onto M₂. This assumes tacitly that the underlying division rings Δ₁ and Δ₂ are isomorphic. Moreover, if {x_α} is a base for M₁ over Δ₁ and s is a semi-linear isomorphism of M_l onto M₂, then {Sxα} is a base for M₂ over Δ₂. Hence the spaces have the same dimensionality. Conversely, let M₁ over Δ₁ and M₂ over Δ₂ have the same dimensionality and assume that Δ₁ and Δ₂ are isomorphic. Let {x_α}, {y_α} be bases for M₁ and M₂ respectively, indexed by the same set, and let σ be an isomorphism of Δ₁ onto Δ₂. Define the map s of M₁ into M₂ by

One checks directly that s is σ-semi-linear and bijective. Hence we see that M₁ over Δ₁ and M₂ over Δ₂ are semi-linearly isomorphic if and only if they have the same dimensionality and Δ₁ and Δ₂ are isomorphic.

The key result for the isomorphism theorem (and for representation theory as well) is the following

LEMMA 1.   Any two irreducible modules for a simple artinian ring are isomorphic.

Proof.   We choose a minimal left ideal I of R, so I is an irreducible R-module. The result will follow by showing that any irreducible module M for R is isomorphic to I. Since R is simple, the representation of R given by M is faithful. Hence, since I ≠ 0, there exists an x ∈ M such that Ix ≠ 0. We have the homomorphism b bx of I into M. Since Ix ≠ 0, the homomorphism is not 0. By Schur’s lemma, it is an isomorphism

We shall require also the following

LEMMA 2.   Let M be a vector space over a division ring Δ, R = End_ΔM the ring of linear transformations of M over Δ. Then the centralizer of R in the ring of endomorphisms End M of M as abelian group is the set of maps δ′ :u δu, δ ∈ Δ. Moreover, δ δ′ is an isomorphism of Δ onto this centralizer.

Proof.   Since M is a completely reducible Δ-module, the first statement is a special case of the density theorem. We can also give a simple direct proof of this result: Let d be an endomorphism of (M, + ,0) that centralizes End_ΔM. Let x ≠ 0 in M. Then dx ∈ Δx. Otherwise, x and dx are linearly independent, and hence there is an l ∈ End_ΔM such that Ix = 0 and l(dx) ≠ 0. Since l(dx) = d(lx) = 0, this is impossible. Hence for any x ≠ 0 we have a δ_x ∈ Δ such that dx = δ_xx. Let y be a second non-zero element of M and choose l ∈ End_ΔM such that lx = y. Then δ_yy = dy = dlx = ldx = lδ_xx = δ_xlx = δ_xy. Hence δ_x = δ_y for all non-zero x and y, which implies that d has the form δ′ : u δu. It is clear that δ δ′ is an isomorphism.

We can now prove the

ISOMORPHISM THEOREM FOR SIMPLE ARTINIAN RINGS.   Let M_ibe a finite dimensional vector space over a division ring Δ_i, i = 1, 2, and let g be an isomorphism of R₁ = End_Δ1M₁ onto R₂ = End_Δ2M₂. Then there exists a semi-linear isomorphism s of M_l onto M₂ such that

for all a ∈ R₁.

Proof.   We consider M₁ as R₁ = End_ΔiM₁ module in the natural way and regard M₂ as R₁-module by defining ay = g(a)y for a ∈ R₁, y ∈M₂. These two modules for the simple artinian ring R₁ are irreducible. Hence they are isomorphic. Accordingly, we have a group isomorphism s of M₁ onto M₂ such that for any x ∈ M₁, a ∈ R₁ we have s(ax) = a(sx). Since ay = g(a)y, y ∈ M₂, this gives the operator relation g(a) = sas⁻¹ which is (25).

Since S is an isomorphism of M₁ onto M₂, the map b sbs^{− 1}, _b ∈ End M_l is an isomorphism of the endomorphism ring End M₁ of the abelian group M₁ onto the endomorphism ring End M₂ of the abelian group M₂. Since this maps End_Δ1 M₁ onto End_Δ2M₂, its restriction to the centralizer of End _Δ1 M₁ in End M₁ is an isomorphism of this centralizer onto the centralizer of End_Δ2M₂ in End M₂. By Lemma 2, the two centralizers are isomorphic respectively to Δ₁ and Δ₂ under the maps sending δ_i ∈ Δ_i into the endomorphism δ′ : u_i δ_iu_i. Hence we have an isomorphism σ of Δ₁ onto Δ₂ that is the composite of with the inverse of δ₂ δ′₂. Thus we have sδ′₁s^{− 1} = (σδ₁)′ and hence for any x ∈ M₁ we have . This shows that s is a σ-semi-linear isomorphism of M₁ onto M₂.

An immediate consequence of this theorem is that if End_Δ1M₁ and End_Δ2M₂ are isomorphic, then M₁ and M₂ are semi-linearly isomorphic. Conversely, if s is a semi-linear isomorphism of M₁ onto M₂ then sas^{− 1} ∈ End,_Δ2 M₂ for any a ∈ End_Δ1M₁ and it is immediate that a sas′^{− 1} is an isomorphism of End_Δ1M₁ onto End_Δ2M₂. We have seen that M₁ and M₂ are semi-linearly isomorphic if and only if M₁ and M₂ have the same dimensionality and Δ₁ and Δ₂ are isomorphic. This shows that a simple artinian ring is determined up to isomorphism by an integer n, the dimensionality of M, and the isomorphism class of a division ring Δ.

The isomorphism theorem for simple artinian rings also gives a determination of the automorphism group of such a ring. If we take R = End_ΔM where M is a finite dimensional vector space over the division ring Δ, then the isomorphism theorem applied to End_ΔM and End_ΔM states that the automorphisms of R are the maps

where s ∈ G, the group of bijective semi-linear transformations of the vector space M. Denoting the map in (26) as I_s, we have the epimorphism s I_s of G onto Aut R, the group of automorphisms of R. The kernel of this epimorphism is the set of bijective semi-linear transformations s such that sas⁻¹ = a for every a ∈ R = End_ΔM. By Lemma 2, any such map has the form δ′ : x δx, δ ∈ Δ. We note also that if δ ≠ 0, then δ′ is a semi-linear automorphism of M whose associated automorphism of Δ is the inner automorphism i_δ: α δαδ⁻¹.This follows from

Thus the kernel of s I_s is the group Δ^*′ of multiplications x δx determined by the non-zero elements δ of Δ. Evidently, our results on automorphisms can be stated in the following way.

COROLLARY.   We have an exact sequence

where Δ* is the multiplicative group of non-zero elements of Δ, G is the multiplicative group of bijective semi-linear transformations of the vector space M, Aut R is the group of automorphisms of R = End _ΔM, i is the map δ δ′, and I is the map s I_s.

Of course, this implies that Aut R G/Δ*′.

A reader who is familiar with the fundamental theorem of projective geometry (see BAI, pp. 468–473) should compare the results obtained here on isomorphisms and automorphisms of simple artinian rings with the fundamental theorem and its consequences. We remark that the present results could be derived from the geometric theorem. However, it would be somewhat roundabout to do so.

We shall derive next the main result on representations of artinian rings. This is the following

THEOREM 4.4.   Any module for a semi-simple artinian ring R is completely reducible and there is a 1−1 correspondence between the isomorphism classes of irreducible modules for R and the simple components of the ring. More precisely, if where the R_j are the simple components and I_j is a minimal left ideal in R_j, then {I₁,…,I_S} is a set of representatives of the isomorphism classes of irreducible R-modules.

Proof.   Write each simple component as a sum of minimal left ideals of R. This gives R = ∑I_k where I_k is a minimal left ideal of R contained in a simple component. Now let M be an R-module and let x be any non-zero element of M. Then x = 1x ∈ Rx = ∑I_kx. By Schur’s lemma, either I_kx = 0 or I_kx is an irreducible module isomorphic to I_k. Now and this shows that M is a sum of irreducible submodules that are isomorphic to minimal left ideals of the simple components of R. Hence M is completely reducible and if M is irreducible, it is isomorphic to a minimal left ideal I of a simple component of R. To complete the proof, we need to show that if I is a minimal left ideal in Rj and I′ is a minimal left ideal in R_j′, then I I′ as R-modules if and only if j = j′. Suppose first that j = j′. Then I and I′ are R_j-isomorphic by Lemma 1 on p. 205. Since R_kI = 0 = R_kI′ for k ≠ j′, it follows that I and I′ are R-isomorphic. Next assume j ≠ j′. Then R_jI = I and R_jI = 0; hence I and I′ are not isomorphic as R-modules.

We also have a definitive result on irreducible representations for arbitrary (left) artinian rings. This is

THEOREM 4.5.   Let R be (left) artinian, N = rad R, and where the _i are the simple components. For each j, , let _j be a minimal left ideal of _j. Then _j is an irreducible module for R, (as R-modules) if j ≠ j′, and any irreducible R-module is isomorphic to one of the _j.

Proof.   Any irreducible R-module M is annihilated by N, so it can be regarded as an irreducible -module. Conversely, any irreducible -module is an irreducible R-module. It is clear also that irreducible R-modules are isomorphic if and only if they are isomorphic as -modules. Hence the theorem is an immediate consequence of Theorem 4.4.

EXERCISES

        1. If z is a nilpotent element of a ring, then the index of nilpotency is the smallest t such that z^t = 0, z^t−1 ≠ 0. A similar definition applies to nilpotent ideals. Note that if N is a nilpotent ideal, then the indices of nilpotency of the elements of N are bounded. Use this to construct an example of a nil ideal that is not nilpotent.

        2. Prove that the center of any simple ring is a field.

        3. Show that if where the R_i are simple, then the center C of R is where C_i = C ∩ R_i is the center of R_i. Hence C is a commutative semi-simple artinian ring. Note that the R_i are determined by the simple components C_i of C since R_i = C_lR.

        4. Let R be left artinian, N = rad R, and assume that N^t = 0, N^t−1 ≠ 0. Show that R/N and N^l/N^{i + 1}, 1 ≤ i ≤ t − 1, are completely reducible modules for R of finite dimensionality. Use this to prove that _RR has a composition series and hence that R is left noetherian.

The next four exercises are designed to give conditions for anti-isomorphism of simple artinian rings and to determine the anti-isomorphisms and involutions of such rings.

        5. Let V be a vector space over a division ring Δ that has an anti-automorphism j:δ . A sesquilinear form on V (relative to j) is a map f of V × V into Δ such that

for x,y ∈ V, δ ∈ Δ. Call f non-degenerate if f (z,y) = 0 for all y implies z = 0 and f (x, z) = 0 for all x implies z = 0. Show that if V is finite dimensional and f is non-degenerate, then for a linear transformation l in V over Δ there exists a (left) adjoint relative to f defined to be a linear transformation l′ such that f(lx, y) = f(x, I′y) for all x,y. Show that l l′ is an anti-isomorphism and that this is an involution if f is hermitian in the sense that f(y,x) = f for all x,y or anti-hermitian: f (y,x) = − f.

        6. Let V and Δ be as in exercise 5 and let V* be the dual space hom_Δ(V,Δ). This is a right vector space over Δ, hence a left vector space over Δ^op. If l is a linear transformation of V over Δ, let l* be the transposed linear transformation in V*. Show that 1 l* is an anti-isomorphism of End_ΔV onto End V*_Δ. Hence show that if V_i,i = 1, 2, is a finite dimensional vector space over a division ring Δ_i then End_Δ1V₁ and End_Δ2V₂ are anti-isomorphic if and only if Δ₁ and Δ₂ are antiisomorphic and V₁ and V₂ have the same dimensionality.

        7. Let V be a finite dimensional vector space over a division ring Δ and assume End_ΔV has an anti-automorphism J. Note that J(l) l* is an isomorphism of End_ΔV onto End_Δ^opV* where V* is regarded in the usual way as left vector space over Δ^op (αx* = x*a). Hence there exists a semi-linear isomorphism s of V over Δ onto V* over Δ^op such that

for l ∈ End_Δ V. If x, y ∈ V, define

Show that f is a non-degenerate sesquilinear form on V corresponding to the antiautomorphism σ that is the isomorphism of Δ onto Δ^op associated with s and that J is the adjoint map relative to f.

        8. (Continuation of exercise 7.) Show that if J is an involution (J² = 1), then either f is skew hermitian or f can be replaced by ρf, ρ ≠ 0, in Δ so that pf is hermitian and J is the adjoint map relative to ρf (Sketch: Note that for any v ∈ V, the map x σ^−lf (v, x) is a linear function, so there exists a v′ ∈ V such that f(v,x) = , x ∈ V. Show that for any u ∈ V the map l:x f(x,u)v is in End_ΔV and its adjoint relative to f is y σ⁻¹f(v,y)u = f(y,v′)u. Conclude from J²(l) = l that there exists a δ ≠ 0 in Δ such that for all x,y ∈ V. Show that = δ⁻¹ and if δ ≠ − 1, then ρf for ρ = δ + 1 is hermitian and J is the adjoint map relative to ρf.)

        9. Note that the Wedderburn-Artin theorem for simple rings has the following matrix form: Any simple artinian ring is isomorphic to a matrix ring M_n(Δ′), Δ′ a division ring (Δ′ ≅ Δ^op if Δ is as in the statement of the theorem). Note that the isomorphism theorem implies that if Δ′₁ and Δ′₂ are division rings, then M_n1(Δ′₁) ≅ M_n2(Δ′₂) implies that n₁ = n₂ and Δ′₁ ≅ Δ′₂. Show that the isomorphism theorem implies also that the automorphisms of M_n(Δ′) have the form A S(^σA)S⁻¹ where S ∈ M_n(Δ′), σ is an automorphism of Δ, and ^σA = (σ(α_ij)) for A = (α_ij).

     10. Formulate the results of exercises 6–8 in matrix form.

4.5   STRUCTURE THEORY OF ALGEBRAS

In this section we shall extend the structure theory of rings that we developed in sections 1–4 to algebras over commutative rings. We shall then specialize to the case of finite dimensional algebras over a field.

We recall that an algebra A over a commutative ring K is a (left) K-module and a ring such that the module A and the ring A have the same additive group (A, + ,0) and the following relations connecting the K-action and ring multiplication hold:

for a, b ∈ A, k ∈ K (p. 44). We have the ring homomorphism

of K into A (p. 138). The image under ε is K1 = {Kl |k ∈ K}. This is contained in the center of A, and ka for k ∈ K, a ∈ A, coincides with (k1)a = a(k1). Conversely, given a ring R and a subring K of the center of R, R becomes a K- algebra by defining ka for k ∈ K, a ∈ R, to be the ring product ka. We remark also that rings are -algebras in which na for n ∈ , a ∈ R, is the nth multiple of a. Hence the theory of rings is a special case of that of algebras.

The prime examples of K-algebras are the algebras End_KM where M is a K- module for the commutative ring K. Here kf for k ∈ K,f ∈ End_kM, is defined by (kf) (x) = kf(x) =f(kx), x ∈ M (p. 139). If A is an arbitrary K-algebra, then we define a representation of A to be a (K-algebra) homomorphism of A into an algebra End_KM. If ρ is a representation of A acting in the K-module M, then we define ax = ρ(a)x, a ∈ A, x ∈ M, to make M an A-module as well as a K- module. Since ρ(ka) = kρ(a), k ∈ K, and ρ(a) is a K-endomorphism, we have

for k ∈ K, a ∈ A, x ∈ M. We now give the following

DEFINITION 4.3.   If A is an algebra over the commutative ring K, a (left) A- module is an abelian group written additively that is both a (left) K-module and a (left) A-module such that (30) holds for all k ∈ K, a ∈ A, x ∈ M.

If M is a module for A, we obtain a representation ρ_M of A by defining ρ_M(a) for a ∈ A to be the map x ax. This is contained in End_kM, and a ρ_M(a) is an algebra homomorphism. It follows from (30) that kx = (kl)x. Hence, if M and N are modules for the algebra A, then any homomorphism f of M into N regarded as modules for the ring A is also a K-homomorphism. It is clear also that any A-submodule is also a K-submodule and this gives rise to a factor module M/N for the algebra A in the sense of Definition 4.3. We remark also that if M is a ring A-module, then M is a K-module in which kx = (k1)x, and (30) holds; hence, this is an algebra A-module. The algebra A itself is an A-module in which the action of A is left multiplication and the action of K is the one given in the definition of A. The submodules are the left ideals. These are the same as the left ideals of A as ring. If k ∈ K and f ∈ hom_A(M,N) where M and N are modules for A, then kf is defined by (kf)(x) = kf(x), x ∈ M. This is contained in hom _A(M, N), and this action of K on hom_A(M,N) is a module action. It is immediate that End_AM is an algebra over K.

We can now carry over the definitions and results on the radical, primitivity, and semi-primitivity to algebras. An algebra is called primitive if it has a faithful irreducible representation, semi-primitive if there are enough irreducible representations to distinguish elements. The radical is defined to be the intersection of the kernels of the irreducible representations of the algebra. The results we proved for rings carry over word for word to algebras. We have observed that if A is an algebra over K, then the left ideals of A as ring are also left ideals of A as algebra and, of course, the converse holds. Since the radical of A as algebra or as ring is the intersection of the maximal left ideals, it is clear that rad A is the same set with the same addition and multiplication whether A is regarded as ring or as algebra. Similarly, A is primitive (semiprimitive) as algebra if and only if it is primitive (semi-primitive) as ring.

The structure and representation theory of artinian rings carries over to algebras. In particular, the theory is applicable to algebras that are finite dimensional over fields, since any left ideal in such an algebra is a subspace and the descending chain condition for subspaces is satisfied. For the remainder of this section, except in some exercises, we consider this classical case: A a finite dimensional algebra over a field F. Then rad A is a nilpotent ideal containing every nil one-sided ideal of A. If rad A = 0, then A where the A_i are ideals that are simple algebras. If A is simple, then A is isomorphic to the algebra of linear transformations in a finite dimensional vector space M over a division algebra Δ. Here M is any irreducible module for A and Δ is the division algebra End_AM given by Schur’s lemma. We recall also that M can be taken to be A/I where I is a maximal left ideal of A and Δ is anti-isomorphic to B/I where B is the idealizer of I (Proposition 4.7, p. 203). Hence Δ is a finite dimensional division algebra over F. Since End_ΔM for M n-dimensional over Δ is anti-isomorphic to M_n(Δ) and M_n(Δ) is anti-isomorphic to M_n(Δ^op), it is clear that A is a finite dimensional simple algebra over F if and only if it is isomorphic to an algebra M_n(Δ′), Δ′ a finite dimensional division algebra. These results were proved by Wedderburn in 1908.

In BAI, pp. 451–454, we determined the finite dimensional division algebras over algebraically closed, real closed, and finite fields. We showed that if F is algebraically closed, then F is the only finite dimensional division algebra over F and if F is real closed, then there are three possibilities for finite dimensional algebras over F: (1) F, (2) F(), and (3) the quaternion algebra over F with base (1,i,j,k) such that i² = − 1 = j² and ij = k = −ji. If F is finite, then one has Wedderburn’s theorem that the finite dimensional algebras over F are fields. There is one of these for every finite dimensionality and any two of the same (finite) dimensionality are isomorphic (see BAI, pp. 287–290). Combining these results with the structure theorems, one obtains a complete determination of the finite dimensional semi-simple algebras over algebraically closed, real closed, or finite fields.

The results on representations of artinian rings are also applicable to finite dimensional algebras over fields. Thus if A over F is semi-simple, then any representation of A is completely reducible and we have a 1−1 correspondence between the isomorphism classes of irreducible modules and the simple components of the algebra.

One can apply the theory of algebras to the study of arbitrary sets of linear transformations in a finite dimensional vector space V over a field F. If S is such a set, we let Env S denote the subalgebra of End_F V generated by S. We call this the enveloping algebra of S. Evidently, Env S consists of the linear combinations of 1 and the products s₁s₂…s_r, s_i ∈ S, and the dimensionality dim Env S≤ n² where n = dim V. The injection map into End_FV is a representation of Env S. The theory of algebras is applicable to the study of S via this representation. We shall now apply this method and the density theorem to obtain a classical theorem of the representation theory of groups. This is

BURNSIDE’S THEOREM.   Let G be a monoid of linear transformations in a finite dimensional vector space V over an algebraically closed field F that acts irreducibly on V in the sense that the only subspaces stabilized by G are V and 0. Then G contains a base for End_F V over F.

Proof.   The hypothesis is that G contains 1 and G is closed under multiplication. Then Env G = FG, the set of F-linear combinations of the elements of G. Then V is an irreducible module for A = Env G and A′ = End _A V is a division algebra by Schur’s lemma. Evidently, A′ is the centralizer of A in End_F V, so A′ is a finite dimensional algebra over F. Since F is algebraically closed, we have A′ = F1. By the density theorem, End_A′V = A. Hence A = FG = End_FV. Evidently this implies that G contains a base for End_FV.

If S is an arbitrary set of linear transformations in V over F that acts irreducibly, then Burnside’s theorem can be applied to the submonoid G generated by S. The result one obtains is that there exists a base for End_FV consisting of 1 and certain products of the elements of S.

EXERCISES

In these exercises A is an algebra over a field F. In exercises 1–5, A may be infinite dimensional; thereafter all vector spaces are finite dimensional.

        1. Let a ∈ A and let α₁, …, α_m be elements of F such that a − α_l,l is invertible in A. Show that either a is algebraic over F or the elements (a − α_i,1)⁻¹, 1 ≤ i ≤ m, are linearly independent over F.

        2. Let A be a division algebra with a countable base over an uncountable algebraically closed field F (e.g., F = ). Show that A = F.

        3. Let A be finitely generated over an uncountable algebraically closed field F and let M be an irreducible A-module. Show that End_AM = F.

        4. Show that the elements of rad A are either nilpotent or transcendental over F.

        5. Let A be finitely generated over an uncountable field F. Show that rad A is a nil ideal.

        6. Assume F contains n distinct nth roots of 1 and let ε be a primitive one of these. Let s and t be the linear transformations of the vector space V/F with base (x₁, x₂, …, x_n) whose matrices relative to this base are respectively

Verify that

and that Env {s, t} = End_F V. Let u and v be linear transformations of a vector space W/F such that uⁿ = 1 = vⁿ, uv = εvu. Apply the representation theory of simple algebras to show that dim W = r dim V and there exists a base for W over F such that the matrices of u and v relative to this base are respectively diag {σ, σ,…, σ} and diag {τ, τ, …, τ} .

        7. If a is a linear transformation in a vector space V over F with base (x₁, …, x_n) and ax_i = ∑α_ijx_j, then the trace of a, tr a = ∑α_ii, is independent of the choice of the base (BAI, p. 196). Moreover, tv a is the sum of the characteristic roots of a. Let

Show that t(a,b) is a non-degenerate symmetric bilinear form on End_F V (BAI, p. 346).

        8. Let G, V, F be as in Burnside’s theorem. Suppose tr G = {tr a|a ∈ G} is a finite set. Show that G is finite and |G| ≤ |tr G|ⁿ², n = dim V. (Hint: G contains a base (a₁,…, a_n²) for End_FV by Burnside’s theorem. Consider the map a (t(a, a₁), t(a, a₂,…, t(a, a_n²)) where t(a, b) = tr ab as in exercise 7.)

        9. A linear transformation is called unipotent if it has the form 1 + z where z is nilpotent. Let G be a monoid of unipotent linear transformations in a finite dimensional vector space V over an algebraically closed field F. Prove Kolchins theorem that V has a base relative to which the matrix of every a ∈ G has the form

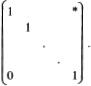
(Hint: Let V = V₁ ⊃ V₂ ⊃ … ⊃ V_{s + 1} = 0 be a composition series for V as A = FG-module and apply exercise 7 to the induced transformations in the irreducible modules V_i/V_{i + 1}.) Extend the theorem to arbitrary base fields F.

     10. (Burnside.) Let G be a group of linear transformations in a finite dimensional vector space V over an algebraically closed field F such that there exists an integer m not divisible by the characteristic of F such that a^m = 1 for all a ∈ G. Prove that G is finite. (Hint: If G acts irreducibly, the theorem follows from exercise 8. Otherwise, we have a subspace U ≠ 0, ≠ V stabilized by G. Use induction on the dimensionality to conclude that the induced groups of transformations in U and in V/U are finite. Let K₁ and K₂ be the kernels of the homomorphisms of G onto the induced groups in U and V/U. Then K₁ and K₂ and hence K₁ ∩ K₂ are of finite index in G. Finally, show that K₁ ∩ K₂ = 1.)

4.6   FINITE DIMENSIONAL CENTRAL SIMPLE ALGEBRAS

An algebra A over a field F is called central if its center C = F1 = {α1|α ∈ F}. If A is a finite dimensional simple algebra over A, then A ≅ M_n(Δ) where Δ is a finite dimensional division algebra over Δ. The center C of A is isomorphic to the center of Δ and hence C is a field (cf. exercise 2, p. 209). Now A can be regarded as an algebra over C. When this is done, A becomes finite dimensional central simple over C. As we shall see in this section and the next, the class of finite dimensional central simple algebras has some remarkable properties. To facilitate their derivation it will be useful to collect first some simple results on tensor products of modules and algebras over fields that will be needed in the main part of our discussion.

We note first that since any F-module ( = vector space over F) is free, it is projective and thus flat (p. 154). Hence if we have an injective linear map i: V′ → V of F-modules, then i 1 and 1 i are injective maps of V′ U → V U and of U V′ into U V respectively for any F-module U. If {x_z|α ∈ I} is a base for V/F, then any element of U V can be written in one and only one way as a finite sum . The fact that it is such a sum is clear since any element of U V has the form . The uniqueness follows from the isomorphism of (Proposition 3.3, p. 131), which implies that if , then every . Then the isomorphisms imply that a_α x_α = 0 if and only if a_z = 0. Similarly, if {y_β|β ∈ J} is a base for U, then every element of U V can be written in one and only one way as . It is clear also that if {xz|α ∈ I} is a base for V and {y_β|β} ∈ J} is a base for U, then {y_β x_z|β ∈ j,α ∈ I} is a base for U V. Hence the dimensionality [U V : F] = [U : F][V : F].

If A and B are algebras over the field F, then A B contains the subalgebras 1 B = {1 b|b ∈ B} and A 1 = {a 1|a ∈ A}. These are isomorphic to B and A respectively under the maps b 1 b and a a 1. Hence we can identify B with the subalgebra 1 B and A with the subalgebra A 1 of A B. If we write a for a 1 and b for 1 b, then we have ab = ba and A B = AB = BA.

We shall now prove the following result, which in effect gives internal characterizations of tensor products of algebras over a field.

PROPOSITION 4.8.   If A and B are subalgebras of an algebra D over a field F, then D ≅A _FB if the following conditions are satisfied:

            (1) ab = ba for all a ∈ A,b ∈ B.

            (2) There exists a base (x_α) for A such that every element of D can be written in one and only one way as .

If D is finite dimensional, then condition (2) can be replaced by

            (2′) D = AB and [D: F] = [A: F] [B: F].

Proof.   The first condition implies that we have an algebra homomorphism of A B into D such that a b ab, a ∈ A, b ∈ B (p. 144). The second condition insures that this is bijective, hence, an isomorphism. It is immediate that (2′) (2) if D is finite dimensional.

As a first application of this criterion, we prove

PROPOSITION 4.9.   If B is an algebra over F, then M_n(B) ≅ M_n(F)_FB.

Proof.   This follows by applying the criterion to the subalgebras M_n(F) and B1 = {bl|b ∈ B} where

If {e_ij|1 ≤ i, j ≤ n} is the usual base of matrix units for M_n(F), then (b1)e_ij = e_ij(b1). Hence condition (1) holds. Moreover, (b1)e_ij is the matrix that has b in the (i,j)-position and 0’s elsewhere. This implies condition (2).

Next we prove

PROPOSITION 4.10.   M_m(F)M_n(F) ≅ M_mn(F).

Proof.   This follows by applying the criterion to the subalgebras consisting of the matrices

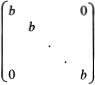
where b ∈ M_m(F), and of the matrices

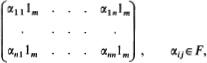
respectively. We leave the details to the reader.

If A is any algebra, we define A^e = A _FA^op and we call this the enveloping algebra of A. If A is a subalgebra of another algebra B, then we have a natural module action of A^e on B defined by

where the a_i ∈ A, b_i ∈ A^op, y ∈ B. It is clear from the universal property of the tensor product that we have a homomorphism of A^e into B such that Hence (31) is well-defined. Direct verification shows that it is a module action. In particular, we have a module action of A^e on A. The submodules of A as A^e-module are the ideals of A. Hence if A is simple, then A is A^e-irreducible. We recall that the endomorphisms of A regarded as left (right) A-module in the natural way are the right (left) multiplications x xa (x ax). It follows that End_A^eA is the set of maps that are both left and right multiplications x cx = xd. Putting x = 1, we obtain d = c; hence End_A^eA is the set of maps x cx, c in the center. If A is central, this is the set of maps x (α1)x = αx, α ∈ F. We shall now apply this to prove our first main theorem on finite dimensional central simple algebras.

THEOREM 4.6.   If A is a finite dimensional central simple algebra over a field F, then where n = dim A.

Proof.   We regard A as A^e-module as above. Then A is irreducible and End_A^eA = F. Also A is finite dimensional over F. Hence by the density theorem A^e maps onto End_FA. Since both A^e and End_FA have dimensionality n², we have an isomorphism of A^e onto End_FA. Since End_FA ≅ M_n(F), the result follows.

We consider next how a finite dimensional central simple algebra A sits in any algebra B (not necessarily finite dimensional) containing A as subalgebra. The result is

THEOREM 4.7.   Let A be a finite dimensional central simple subalgebra of an algebra B. Then B ≅ A _FC where C is the centralizer of A in B. The map I AI is a bijection of the set of ideals of C with the set of ideals of B. Moreover, the center of B coincides with the center of C.

Proof.   We regard B as A^e-module as above. By the preceding theorem, A^e is simple. Hence B is a direct sum of A^e-irreducible modules all of which are isomorphic to A (since A is A^e-irreducible and any two irreducible A^e-modules are isomorphic). Now observe that the generator 1 of A as A^e-module satisfies (a 1)1 = a1 = 1a = (l a)1 and (a 1)1 = 0 implies a = 0. Hence in any irreducible A^e-module, we can choose a c such that (a 1)c = (1 a)c and (a 1)c = 0 implies a = 0. Applying this to B as A^e-module, we see that we can write B = Ac_α where ac_α = c_αa for all a ∈ A and ac_α = 0 implies a = 0. Then c_α ∈ C and any element of B can be written in one and only one way as a finite sum ∑a_αc_α, a_α ∈ A.If c ∈ Cwe have c = ∑a_αc_α and ac = ca implies a_αa = aa_α. It follows that every a_α ∈ F1 and c ∈ ∑Fc_α. This implies that C = ∑Fc_α and {c_α} is a base for C. It is now clear from Proposition 4.8 that A _FC ≅ B.

Now let I be an ideal in C. Then Al is an ideal in B = AC. Moreover, AI ∩ C = I. For, if (x₁ = l, x₂,…, x_n) is a base for A, then the canonical isomorphism of A _FC onto B (p. 144) implies that any element of B can be written in one and only one way as . Then the elements of AI have the form ∑d_ix_i, d_i ∈ I, and if such an element is in C, it also has the form c₁x₁, c₁ ∈ C. It follows that C ∩ Al is the set of elements d₁x₁ = d₁ ∈ I. Thus C ∩ AI = I, which implies that the map I AI of the ideals of C into ideals of B is injective. To see that it is surjective, let I′ be any ideal of B. Then I′ is a submodule of B as A^e-module. Hence I′ = ∑Ad_β where d_β ∈ I = I′ ∩ C, which implies that I′ = AI Thus the map I Al is also surjective.

It remains to prove that the center of B is the center of C. Since the center of B is contained in C, it is contained in the center of C. On the other hand, if c is contained in the center of C, it commutes with every element of B = AC and so it is in the center of B.

It follows from the preceding theorem that B is simple if and only if C is simple and B is central if and only if C is central. The theorem can be applied to tensor products in which one of the factors is finite dimensional central simple. Thus let B = A _FC where A is finite dimensional central simple. We identify A and C with the corresponding subalgebras A 1 and 1 C of A C. Now we claim that C is the centralizer of A in B. For, let {y_β} be a base for C over F. Then any element of B can be written in one and only one way as b = ∑a_βy_β, a_β ∈ A, and ab = ba for a ∈ A is equivalent to aa_β = a_βa for every a_β. This implies that b commutes with every a ∈ A if and only if b = ∑α_βy_β α_β ∈ F, that is, if and only if b ∈ C. We can now apply Theorem 4.7 to obtain the

COROLLARY 1.   Let A be a finite dimensional central simple algebra over F, C an arbitrary algebra over F. Then the map I A _FI is a bijection of the set of ideals of C with the set of ideals of B = A _FC. Moreover, the center of B coincides with the center of C (identified with the corresponding subalgebra of B).

An important special case of this result is

COROLLARY 2.   Let A be a finite dimensional central simple algebra over F, C any algebra over F. Then A _FC is simple if C is simple and A _FC is central if C is central.

Iteration of Corollary 2 has the following consequence.

COROLLARY 3.   The tensor product A_{1 F}A_{2 F}…_FA_rof a finite number of finite dimensional central simple algebras is finite dimensional central simple.

Of particular interest are tensor products in which one of the factors is an extension field E of the base field F. If A is any algebra over F, then A _FE can be regarded as an algebra over E. This algebra over E is denoted as A_E and is called the algebra obtained from A by extending the base field to E (see exercise 13, p. 148). If (x_α) is a base for A over F, then by identifying A with A 1 in A_E we can say that (xα) is a base for A_E over E. Hence the dimensionality of A over F is the same as that of A_E over E. It follows also that if K is an extension field of E, then (A_E)_K ≅ A_K. If B is a second algebra over F with base (y_β), then A _FB has the base (x_αy_β) ( = (x_α y_β)) over F and this is also a base for (A _FB)_E over E and A_{E E}B_E over E. It follows that (A _FB)_E ≅ A_{E E}B_E. (More general results are indicated in exercise 13, p. 148.)

If A is finite dimensional central simple over F, then Corollary 2 to Theorem 4.7 shows that A_E is finite dimensional central simple over E. We recall also that M_n(F) is finite dimensional central simple over F. These are the simplest examples of central simple algebras. We now give

DEFINITION 4.4.   The matrix algebra M_n(F) is called a split central simple algebra over F. If A is finite dimensional central simple over F, then an extension field E of F is called a splitting field for A if A_E is split over E (A_E ≅ M_n(E)for some n).

Evidently any extension field of F is a splitting field of M_n(F) and if E is a splitting field for A and B, then E is a splitting field for the central simple algebra A _FB. This follows since A_E ≅ M_n(E) and B_E ≅ M_m(E) imply (A _FB)_E ≅ A_{E E}B_E ≅ M_n(E) _EM_m(E) ≅ M_nm(E). We note also that if E is a splitting field for A, then it is a splitting field for A^op. For, (A^op)_E = (A_E)^op ≅ M_n(E)^op, and since M_n(E) has an anti-automorphism, M_n(E)^op ≅ M_n(E). If A ≅ M_r(B) where B is central simple over F then E is a splitting field for A if and only if it is a splitting field for B. We have A_E ≅ M_r(B_E) since M_r(B) ≅ M_r(F) _FB and M_r(B)_E ≅ M_r(F)_{E E}B_E ≅ M_r(B_E). Now B_E ≅ M_s(Δ) where Δ is a central division algebra over E. Then A_E ≅ M_rs(Δ). If E splits A (that is, is a splitting field for A) then A_E ≅ M_n(E) and hence M_n(E) ≅ M_rs(Δ) which implies that rs = n and Δ = E. Then B_E ≅ M_S(E) and E splits B. The converse is clear from Proposition 4.10. In particular, if A ≅ M_r(Δ) where Δ is a central division algebra over F then E splits A if and only if E splits Δ. Thus it suffices to consider splitting fields for central division algebras. We remark finally that any extension field K of a splitting field is a splitting field. This is clear since (A_E)_K ≅ A_K and M_n(E)_K ≅ M_n(K).

If E is an algebraically closed extension field of F, then the only finite dimensional simple algebras over E are the algebras M_n(E) (p. 213). Accordingly, any algebraically closed extension field E of F is a splitting field for every finite dimensional central simple algebra over F. We shall see later that every field can be imbedded in an algebraically closed field (section 8.1). When this result is available, it proves the existence of splitting fields for finite dimensional central simple algebras.

We shall now prove the existence of finite dimensional splitting fields for any finite dimensional central simple algebra A. Writing A = M_n(Δ) where Δ is a finite dimensional central division algebra, we shall show that any maximal subfield of Δ is a splitting field. This will follow from the following result (which we shall improve in Theorem 4.12).

THEOREM 4.8.   If Δ is a finite dimensional central division algebra over F, then a finite dimensional extension field E of F is a splitting field for Δ if and only if E is a subfield of an algebra A = M_r(Δ) such that the centralizer C_A(E) = E.

Proof.   Suppose the condition holds: E is a subfield of A = M_r(Δ) such that C_A(E) = E. We can identify A with End_Δ′V where V is an r-dimensional vector space over Δ′ = Δ^op. Then V is a Δ′ _FE module such that (d e)x = dex = edx for d ∈ Δ′, e ∈ E ⊂ A. Since Δ′ _FE is simple, the representation of Δ′ _FE in V is faithful and we can identify Δ′ _FE with the corresponding ring of endomorphisms in V. Since Δ′ _FE is finite dimensional simple over F, V is completely reducible as Δ′ _FE module and so we can apply the density theorem. Now End_ΔV = A so End_{Δ′ E}V is the centralizer of E in A. By hypothesis, this is E. Now V is finite dimensional over F since it is finite dimensional over Δ′ and Δ′ is finite dimensional over F. Thus V is finite dimensional over E. Hence, by the density theorem, Δ′ _FE is isomorphic to the complete algebra of linear transformations in V over E. If the dimensionality [V : E] = n, then Δ′ _FE ≅ M_n(E). Thus E is a splitting field for Δ′ over F and hence of Δ over F.

Conversely, suppose Δ _FE M_n(E). Then also Δ′ _FE = M_n(E). Let V be an irreducible module for Δ′ _FE. Since Δ′ _FE ≅ M_n(E), V is an n-dimensional vector space over E and Δ′ _FE can be identified with End_EV. Also V is a vector space over Δ′ and if [V : Δ′] = r, then since E centralizes Δ′, E ⊂ End_Δ′V. The centralizer of E in End_Δ′ V is contained in the centralizer of Δ′ E in End_EV. Since Δ′ E = End_EV, this is E. Hence C_EndΔ′V(E) = E and C_Mn(Δ)(E) = E.

The existence of a maximal subfield of Δ is clear since [Δ : F] < ∞. We now have the following corollary, which proves the existence of finite dimensional splitting fields for any finite dimensional central simple algebra.

COROLLARY.   Let A be finite dimensional central simple over F and let A M_r(Δ) where Δ is a division algebra. Then any maximal subfield E of Δ is a splitting field for A.

Proof. It suffices to show that E is a splitting field for Δ. Let E′ = C_Δ(E). Then E′ ⊃ E and if E′ ≠ E, we can choose c ∈ E′ E. The division algebra generated by E and c is commutative, hence this is a subfield of Δ properly containing E, contrary to the maximality of E. Thus C_Δ(E) = E. Hence Theorem 4.8 with A = Δ shows that E is a splitting field.

If E is a splitting field for A so that A_E ≅ M_n(E), then [A : F] = [A_E : E] = [M_n(E) : E] = n². Thus we see that the dimensionality of any central simple algebra is a square. The square root n of this dimensionality is called the degree of A.

We shall prove next an important theorem on extension of homomorphisms:

THEOREM 4.9.   Let A be a simple subalgebra of a finite dimensional central simple algebra B. Then any homomorphism of A into B can be extended to an inner automorphism of B.

Proof.   We form the algebra E = A _FB^op, which is finite dimensional and simple. Any module for E is completely reducible and any two irreducible E-modules are isomorphic. It follows that any two E-modules of the same finite dimensionality over F are isomorphic. We now make B into an E-module in two ways. In the first, the action is (∑a_i b_i)x = ∑a_ixb_i and in the second it is where f is the given homomorphism of A into B. Clearly these are module actions and the two modules are isomorphic. Hence there exists a bijective linear transformation l of B over F such that

for all a_i ∈ A, x,b_i ∈ B. In particular, l(x)b = l(xb) for all x,b ∈ B. It follows that l has the form x dx where d is an invertible element of B. We have also al(x) = l(f(a)x) for all a ∈ A, x ∈ B. Then adx = df(a)x. Putting x = 1 we obtain f(a) = d^{− l}ad. Hence f can be extended to the inner automorphism b d⁻¹bd in B.

If we take A = F1 in Theorem 4.9 we obtain the important

COROLLARY (Skolem-Noether). Any automorphism of a finite dimensional central simple algebra is inner.

We prove next an important double centralizer theorem for central simple algebras.

THEOREM 4.10.   Let A be a semi-simple subalgebra of a finite dimensional central simple algebra B. Then the double centralizer C_B(C_B(A)) = A.

Proof. Consider the algebra B B^op and its subalgebra A B^op. If we identify B with B 1, then it is easily seen as in the proof of Theorem 4.7 that B ∩ (A B^op) = A. Now regard B as B B^op-module in the usual way. By the proof of Theorem 4.6, the algebra B B^op is isomorphic to the algebra of linear transformations of B over F of the form x ∑b_ixb′_i where b_i,b′_i ∈ B. Then the result that B ∩ (A B^op) = A implies that if a linear transformation of B is simultaneously of the form x ∑a_ixb_i where a_i ∈ A, b_i ∈ B, and of the form x bx, b ∈ B, then b = a ∈ A. We now consider the algebra A B^op. We claim that this is semi-simple. To see this we write A = A₁ … A_S where the A_i are simple ideals. Then A B^op = (A₁ B^op) … (A_s B^op) and A_i B^op is an ideal in A B^op. Since A_i is simple and B^op is finite dimensional central simple, A_i B^op is simple by Corollary 2, p. 219. Thus A B^op is a direct sum of ideals that are simple algebras. Hence A B^op is semi-simple. Now regard B as A B^op-module by restricting the action of B B^op to the subalgebra A B^op. Since A B^op is semi-simple, B is completely reducible as E = A B^op -module. Now consider E′ = End_EB. If we use the fact that Ihe endomorphisms of B as right B-module are the left multiplications, we see that E′ is the set of maps x cx, c ∈ C_B(A). Since B is finite dimensional over F and B is completely reducible as A B^op-module, it follows from the density theorem that End_E′B is the set of maps Now let c′ ∈ C_B(C_B(A)). Then x c′x commutes with x cx for c ∈ C_B(A) and with x xb for b ∈ B. It follows that x c′x is in End_E′B. Hence x c′x also has the form x ∑a_ixb_i, a_i ∈ A, b_i ∈ B. We have seen that this implies that c′ ∈ A. Thus we have proved that C_B(C_B(A)) ⊂ A. Since A ⊂ C_B(C_B(A)) is clear, we have C_B(C_B(A)) = A.

The foregoing result does not give us any information on the structures of the various algebras involved in the proof or on their relations. We shall now look at this question and for the sake of simplicity, we confine our attention to the most interesting case in which A is a simple subalgebra of the central simple algebra B. The extension to A semi-simple is readily made and will be indicated in the exercises.

Assume A simple. Then E = A B^op is simple, so E M_r(Δ) where Δ is a division algebra. Let d = [Δ : F]. Then we have

If {e_ij |1 ≤ i,j ≤ r} is the usual set of matrix units for M_r(Δ), then it is clear that Δ ≅ e₁₁M_r(Δ)e₁₁ which is just the set of matrices with (1, l)-entry in Δ and other entries 0. Also, M_r(Δ) is a direct sum of the r minimal left ideals M_r(Δ)e_ii and these are isomorphic modules for the algebra M_r(Δ). Each of these irreducible modules has dimensionality r²d/r = rd over F. Now consider B as E = A B^op-module. Since E is simple, B as E-module is a direct sum of, say, s irreducible submodules all of which are isomorphic to minimal left ideals of E. Since E ≅ M_r(Δ), the dimensionality over F of any irreducible E-module is rd. Hence we have

By (33) and (34) we see that s|r and

Now consider C_B(A) ≅ E′ = End_EB. Since B is a direct sum of s irreducible E-modules and these are isomorphic to minimal left ideals Ee, e² = e, of E, we can determine the structure of End_EB, hence of C_B(A), by using the following

LEMMA.   Let e be a non-zero idempotent in an algebra E, I = Ee, I^(s) the direct sum of s copies of I. Then End_EI^(s) is isomorphic to M_s((eEe)^op).

Proof.   By Lemma 2, p. 198, End_EI^(s) consists of the maps (u₁,…, u_s) (v₁,…, v_s) where v_i = ∑_ja′_iju_j and a′_ij ∈ End_EI. This gives a map (a′_ij) η(a′_ij) of M_s(End_EI) into End_EI^(s). Direct verification shows that this is an isomorphism. Next we consider End_EI = End_EEe. As in the proof of Lemma (1), p. 180, End_EEe is the set of maps ae aebe, a, b ∈ E. In this way we obtain a map of eEe into End_EEe such that ebe η(ebe):ae aebe. Direct verification shows that this is an anti-isomorphism. Hence End_EI ≅ (eEe)^op and End_EI^(s) ≅ M_s((eEe)^op).

Applying this lemma to B as E-module, we see that End_EB ≅ M_s((e₁₁M_r(Δ)e₁₁)^op) ≅ M_s(Δ^op). Hence C_B(A) ≅ M_s(Δ^op) and

Then

We summarize these results in

THEOREM 4.11.   Let A be a simple subalgebra of a finite dimensional central simple algebra B. Then [B : f] = [A : F] [C_B(A) : F] and A B^op ≅ M_r(Δ), Δ a division algebra, and C_B(A) ≅ M_S(A^op). Moreover, s|r, [B : F] = rsd where d = [Δ : F] and [A : F] = r/s.

The relation [B : F] = [A : F][C_B(A) : F] shows that if A is a field, then C_B(A) = A [B : F] = [A : F]². This gives the following precise determination of the finite dimensional splitting fields of a central division algebra.

THEOREM 4.12.   A finite dimensional extension field E of F is a splitting field for a central division algebra Δ if and only if [E : F] = nr where n is the degree of Δ, and E is isomorphic to a subfield of M_r(Δ).

EXERCISES

        1. Let Δ be a finite dimensional central division algebra over F, E a maximal subfield of Δ. Show that [Δ : F] = [E : F]².

        2. (Proof of Wedderburn’s theorem on finite division rings.) Let Δ be a finite division ring, F the center of Δ so Δ is a central division algebra over F. Show that if E1 and E₂ are maximal subfields of Δ, then these are conjugates in the sense that there exists an s ∈ Δ such that E₂ = sE₁s⁻¹. Conclude from this that the multiplicative group Δ* of non-zero elements of Δ is a union of conjugates of the subgroup E₁*. Hence conclude that Δ = E₁ = F is commutative (see exercise 7, p. 77 of BAI).

        3. (Proof of Frobenius’ theorem on real division algebras.) Let Δ be a finite dimensional division algebra over . If Δ is commutative, then either Δ = or Δ = . If Δ is not commutative, its center is either or ; is ruled out since it is algebraically closed and so has no finite dimensional division algebras over it. Now suppose Δ is central over and Δ . Then Δ contains an element i such that i² = − 1 and since = (i) has an automorphism such that i − i, there exists a j in Δ such that ji = − ij. Show that the subalgebra generated by i and j is Hamilton’s quaternion algebra . Use exercise 1 to prove that [Δ : ] =4 and that Δ = .

        4. Let E be a cyclic field over F, [E : F] = n, Gal E/F, the Galois group of E/F, = . Let (E,s,γ) be the subalgebra of M_n(E) generated by all of the diagonal matrices

b ∈ E, and the matrix

where γ is a non-zero element of F. Note that b is a monomorphism and identify b with . Then we have the relations

and every element of (E,s,γ) can be written in one and only one way in the form

where the b_l ∈ E. Prove that (E, s, γ) is central simple and [E, s, γ) : F] = n².

        5. Let E,F,G,s be as in exercise 4. Note that s ∈ End_FE and for any b ∈ E, x bx is in End_FE. Identifying this with b, we have sb = s(b)s. Show that the algebra L of linear transformations in E over F generated by the multiplications b ∈ E and s is isomorphic to the algebra (E, s, 1) of exercise 4. Hence conclude that L = End_FE and (E, s, 1) ≅ M_n(F).

        6. Prove that (E, s, γ) ≅ M_n(F) if and only if γ is the norm of an element of E. (Hint: Use Theorem 4.9, p. 222). Hence show that if n = p is a prime and γ is not a norm in E, then (E, s, γ) is a division algebra.

        7. Let E = (r) where r is a root of x³ + x² − 2x − 1. Srhow that E/ is cyclic (see BAI, p. 236, exercise 1). Show that if γ is an integer not divisible by 8, then γ is not a norm of any element of E. Hence conclude from exercise 6 that (E, s, γ) is a division algebra.

        8. Let A be an algebra over F with base (u₁,…, u_n) and let a ρ(a) be the regular matrix representation determined by this base. Put N(a) = det ρ(a) (see BAI, p. 403). Show that A is a division algebra if and only if N(a) ≠ 0 for every a ≠ 0 in A. Use this criterion to show that if t is an indeterminate, then A is a division algebra if and only if A_F(t) is a division algebra. Generalize to show that if t₁,…,t_r are indeterminates, then A_{F(t1,…, tl)} is a division algebra if and only if A is a division algebra.

        9. Show that if Δ₁ and Δ₂ are finite dimensional division algebras over F and Δ₁ is central, then Δ_{1 F} Δ₂ = M_r(E) where E is a division algebra and r|[Δ_i : F], i = 1, 2. Hence show that Δ₁ Δ₂ is a division algebra if ([Δ₁ : F], [Δ₂ : F]) = 1.

     10. If A is a subalgebra of an algebra B, a linear map D of A into B is called a derivation of A into B if

for a_i ∈ A. Form B⁽²⁾ and define

for a ∈ A, (x,y) ∈ B⁽²⁾. Verify that B⁽²⁾ is an A-module with this action. Show that B⁽²⁾ is an A B^op-module in which

     11. A derivation of B into B is called a derivation in B. If d ∈ B, the map x [d, x] = dx − xd is a derivation in B called the inner derivation determined by d. Prove that if A is a semi-simple subalgebra of a finite dimensional central simple algebra B, then any derivation of A into B can be extended to an inner derivation of B.

     12. Let A be a semi-simple subalgebra of a finite dimensional central simple algebra B. Show that C_B(A) is semi-simple and investigate the relation between the structure of A, A B^op and C_B(A).

4.7   THE BRAUER GROUP

The results on tensor products of finite dimensional central simple algebras given in the previous section lead to the introduction of an important group that was first defined by R. Brauer in 1929. The elements of this group are similarity classes of finite dimensional central simple algebras. If A and B are such algebras, we say that A is similar to B (A ∼ B) if there exist positive integers m and n such that M_m(A) ≅ M_n(B) or, equivalently, M_m(F) A ≅ M_n(F) B. The relation of similarity is evidently reflexive and symmetric. It is also transitive since if

and

then

Note that we have used associativity and commutativity of tensor multiplication as well as the formula M_n(F) M_m(F) = M_mn(F), which was established in Proposition 4.10, p. 217. We now see that ∼ is an equivalence relation. Let [A] denote the similarity class of A, that is, the equivalence class of finite dimensional central simple algebras similar to A. Suppose A ∼ A′ and B ∼ B′ so we have positive integers m, m′, n, n′ such that A M_n(F) ≅ A′ M_n′(F) and B M_m(F) ≅ B′ M_m′(F). Then A B M_nm(F) ≅ A′ B′ M_n′m′,(F). Hence A B ∼ A′ B′. Thus we have a well-defined binary composition of similarity classes given by

Evidently this is associative and commutative. Moreover, the set of matrix algebras M_n(F) constitutes a similarity class 1 and this acts as unit since A ∼ A M_n(F). We have seen in Theorem 4.6, p. 218, that A A^op ∼ 1. Hence [A][A^op] = 1 = [A^op][A].

If A is finite dimensional central simple over F, we can write A ≅ Mn(F) Δ for Δ, a finite dimensional central division algebra. Conversely, if Δ is as indicated, then M_n(F) Δ is finite dimensional central simple over F. We recall that the isomorphism theorem for simple artinian rings (p. 206) implies that if M_n(Δ) ≅ M_m(Δ′) for division algebras Δ and Δ′, then m = n and Δ ≅ Δ′. It follows that the division algebra Δ in the formula A ≅ M_n(F) Δ is determined up to isomorphism by A. Hence a similarity class [A] contains a single isomorphism class of finite dimensional central division algebras and distinct similarity classes are associated with non-isomorphic division algebras. Now the class of subalgebras of the matrix algebras M_n(F), n = 1, 2, 3,… is a set and every algebra over F is isomorphic to a member of this set. Hence the isomorphism classes of algebras over F constitute a set. This set has as subset the isomorphism classes of central division algebras over F. Hence the similarity classes of central simple algebras over F is a set. Our results show that this set is a group under the composition defined by (44). This group is denoted as Br(F) and is called the Brauer group of the field F. It is clear that the determination of Br(F) for a field F is equivalent to a complete classification of the finite dimensional central division algebras over F.

If F is algebraically closed or is a finite field, then Br(F) = 1. If F = , then Br(F) is a cyclic group of order two by Frobenius’ theorem. We shall determine Br(F) for F a p-adic field in Chapter 9 (section 9.14). One of the most important achievements of algebra and number theory in the 1930’s was the determination of Br() and, more generally, Br(F) for F a number field (that is, a finite dimensional extension field of ). This involves some deep arithmetic results.

Let E be an extension field of F. If A is finite dimensional central simple over F, then A_E is finite dimensional central simple over E. We have (A _FB)_E ≅ A_{E E}B_E and M_n(F)_E ≅ M_n(E). This implies that we have a homomorphism of Br(F) into Br(E) sending [A] into [A_E]. The kernel, which we shall denote as Br(E/F) is the set of classes [A] such that A_E ∼ 1 (1 for F is customary here), that is, the [A] such that A is split by E. We shall consider this group in Chapter 8 for the case in which E is a finite dimensional Galois extension field of F.

EXERCISE

        1. Use Theorem 4.11 (p. 224) to show that if A is finite dimensional central simple over F and E is a subfield of A/F, then C_A(E) ∼ A_E (in Br(E)).

4.8   CLIFFORD ALGEBRAS

In this section we apply some of the results on central simple algebras to the study of certain algebras—the Clifford algebras—defined by quadratic forms. These algebras play an important role in the study of quadratic forms and orthogonal groups. The results on these matters that we require can be found in BAI, Chapter 6.

Let V be a finite dimensional vector space over a field F equipped with a quadratic form Q. We recall the definition: Q is a map of V into the base field F such that

            1. Q(αx) = α²Q(x), α ∈ F, x ∈ V.

            2. B(x, y) ≡ Q(x + y)−Q(x)−Q(y) is bilinear.

Evidently, B(x, y) is symmetric, that is, B(y,x) = B(x, y) and B(x, x) = 2Q(x). We use Q to define an algebra in the following manner.

DEFINITION 4.5.   Let V be a vector space over a field F, Q a quadratic form on V. Let be the tensor algebra defined by V (p. 140) and let K_Q be the ideal in T(V) generated by all of the elements of the form

Then we define the Clifford algebra of the quadratic form Q to be the algebra

If a ∈ T(V), we write and we have the map i : x of V into C(V,Q). Since V generates T(V), i(V) generates the Clifford algebra. We have . Moreover, we claim that we have the following universality of the map i: If f is a linear map of V into an algebra A such that

then there exists a unique algebra homomorphism g of C(V,Q) into A such that

is commutative. To see this, we recall the basic property of the tensor algebra that any linear map f of V into an algebra has a unique extension to an algebra homomorphism f′ of T(V) into A (see p. 140). Now for the given f, the kernel, ker f′, contains every element x x − Q(x)1, x ∈ V, since . Hence the ideal K_Q ⊂ ker f′ and so we have the induced homomorphism . In particular, g() = f′ (x) = f(x), which is the commutativity of (46). The uniqueness of g is clear since the generate C(V,Q).

The ideal K_Q defining C(V,Q) contains every

Since we see that

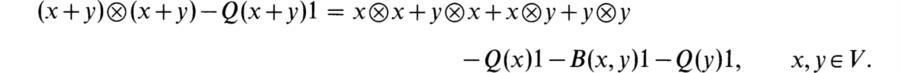
Equivalently, we have the relations

in C(V,Q) as well as ² = Q(x)1. We can use these to prove

LEMMA 1.   If the elements u_l, u₂,…, u_n span the vector space V over F, then the elements

span the vector space C(V,Q) over F.

Proof.   Since T(V) is generated by V and the u_i span V, it is clear that the u_i generate T(V), so every element of T(V) is a linear combination of 1 and monomials in the u_i of positive degree. We now call 1 and the monomials standard. Let S be the set of these. We proceed to prove by induction on i and on the degree of u ∈ S that u_iu is congruent modulo the ideal K_Q to a linear combination of standard monomials of degree ≤deg u + 1. This is clear if deg u = 0. Now suppose u = u_i1u_i2 … u_ir, r ≥ 1. If i = 1, the result is clear if i₁ > 1 and if i_l = 1, then (mod K_Q). Now let i > 1. If i ≤ i₁ the result follows as in the case i = 1. Hence assume i > i₁. Then, by (47)

By the degree induction, u_iu_i2 … u_ir is congruent modulo K_Q to a linear combination of standard monomials of degree ≤r. Then induction on the subscript i implies that u_i1u_iu_i2 … u_ir and hence u_iu_i1u_i2 … u_ir is congruent modulo K_Q to a linear combination of standard monomials of degree ≤ r + 1. The result we have proved implies that if C′ is the subspace of C(V, Q) spanned by the elements then . This implies that C′C′ ⊂ C′ so C′ is a subalgebra of C(V,Q). Since C′ contains = {| x ∈ V} and generates C(V, Q), we have C′ = C(V, Q).

Evidently, the lemma implies that if dim V = n, then dim C(V, Q) ≤ 2ⁿ, which is the number of standard monomials in the u_i.

For the sake of simplicity, we assume in the remainder of the text of this section that char F ≠ 2. The extension of the results to the characteristic two case will be indicated in the exercises. We assume first that B is non-degenerate and we separate off the lowest dimensional cases n = 1, 2.

n = 1. We have dim C(V, Q) ≤ 2 and if V = Fu, then u⁻² = Q(u)1 and Q(u) ≠ 0, since B is non-degenerate. Let A = F[t]/(t² − Q(u)1) where t is an indeterminate. Then A has the base (1, ) where = t + (t² − Q(u) 1). Then ² = Q(u) 1, which implies that the linear map f of V into A such that f(u) = satisfies f(x)² = Q(x). Hence we have a homomorphism of C(V, Q) into A such that . This is surjective. Since dim A = 2 and dim C(V,Q) ≤ 2, we have dim C(V,Q) = 2 and our homomorphism is an isomorphism. If Q(u) is not a square in F, then t² − Q(u) 1 is irreducible in F[t] and C(V, Q) is a field. If Q(u) = β², β ∈ F, then satisfies

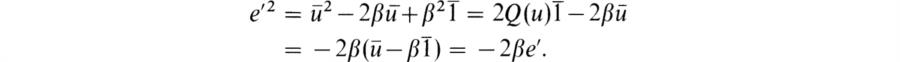
Hence e = −(2β)⁻¹e′ is an idempotent ≠ 0, 1 in C(V,Q). Then C(V, Q) = Fe F(1 − e), a direct sum of two copies of F. Hence we have the following lemma.

LEMMA 2.   If B(x, y) ,is non-degenerate and n = 1, then dim C(V, Q) = 2 and if V = Fu, then C(V, Q) is afield or a direct sum of two copies of F according as Q(u) is not or is a square in F.

n = 2. Choose an orthogonal base (u,v) for V. Then Q(u)Q(v) ≠ 0. Let C′ be the Clifford algebra of Fu relative to the restriction Q′ of Q to Fu. Then C′ has a base (1, ) where ² = Q(u) 1. Now consider the matrices

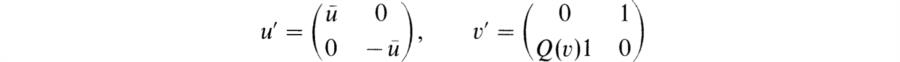
in M₂(C′). We have

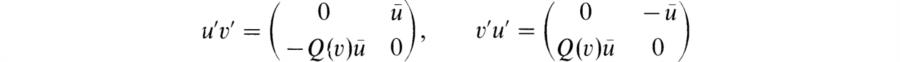
so u′v′ + v′u′ = 0. Also u′² = Q(u) 1, v′² = Q(v) 1. It follows that A = F1 + Fu′ + Fv′ + Fu′ v′ is a subalgebra of M₂(C′). It is clear from the form of the matrices that 1, u′ v′, u′v′ are linearly independent. Hence dim A = 4. The relations on u′ and v′ imply that the linear map f of V into A such that u u′, v v′ satisfies f(x)² = Q(x) 1, x ∈ V. Hence we have a homomorphism g of C(V, Q) into A such that g() = u′, g() = v′. Then g is surjective and since dim C(V, Q)≤4 and dim A = 4, it follows that g is an isomorphism and dim C(V, Q) = 4.

An algebra A over a field F of characteristic ≠2 is called a (generalized) quaternion algebra if A is generated by two elements i and j such that

where α, β ∈ F. We denote this algebra as (α, β) or (α, β)/F if we need to call attention to the base field F. We now prove

LEMMA 3.   Any quaternion algebra is four-dimensional central simple over F.

Proof.   The relations (49) imply that any element of A is a linear combination of the elements 1, i, j, ij. Now suppose λl + μi + vj + ρij = 0 for λ, μ, v, ρ ∈ F. If we multiply this relation on the left by i and on the right by i⁻¹ = α⁻¹i, we obtain λ1 + μi − vj − ρij = 0. Then λ1 + μi = 0 and vj + ρij = 0. Multiplication of these on the left by j and on the right by j⁻¹ = β⁻¹ j then gives λ1 − μi = 0 and vj − ρij = 0. Then λ1 = μi = vj = ρij = 0 and λ = μ = v = ρ = 0. Hence the elements 1, i, j, ij are linearly independent and so these constitute a base for A. Hence dim.A = 4. Now let I be an ideal ≠ A in A and let = 1 + I, = i + I, = j + I. Then . Hence A/I is a quaternion algebra and so dim A/I = 4. Then I = 0 and hence A is simple. It remains to show that the center of A is F1. Let center of A. Then ci = ic implies that v = ρ = 0. The fact that λ1 + μi commutes with j implies that μ = 0. Hence c = λ1 and the center is F1.

The result we obtained before on C(V, Q) in the case n = 2 can now be stated in the following way.

LEMMA 4.   If B(x, y) is non-degenerate and n = 2, then C(V, Q) is a quaternion algebra.

Proof.   We had an isomorphism of C(V, Q) with the algebra A generated by u′ and v′ such that u′² = Q(u) 1 ≠ 0, v′² = Q(v) 1 ≠ 0, and u′v′ = − v′u′. Then A and, hence, C(V, Q) are quaternion algebras.

We recall that if B(x, y) is a symmetric bilinear form on a vector space V and (u₁, u₂,…, u_n) is a base for V, then δ = det (B(u_i, u_j)) is called a discriminant of B. A change of base replaces δ by δβ² where β ≠ 0 is the determinant of the matrix giving the change of base. B is non-degenerate if and only if δ ≠ 0. We recall also that if U is a subspace of V on which the restriction of B to U is non-degenerate, then V = U U. Moreover, the restriction of B to U is nondegenerate.

We shall now prove the following factorization property.

LEMMA 5.   Let B(x, y) be non-degenerate and dim V ≥ 3. Let U be a twodimensional subspace of V on which the restriction of B to U is non-degenerate. Write V = U U and let Q′ and Q″ denote the restrictions of Q to U and U respectively. Then

where δ′ is a discriminant of the restriction of B to U.

Proof.   We shall prove (50) by using two universal map properties to produce inverse isomorphisms between C(V, Q) and the right-hand side of (50). We denote the canonical maps of U into C(U, Q′) and of U into C(U, − δ′Q″) as i′ : y y′ and i′ : z z″ respectively. Let (u, v) be an orthogonal base for U and put (in C(V, Q)). We have , so where δ′ is the discriminant of the restriction of B to U defined by the base (u, v)). Also if y ∈ U and z ∈ U, then hence

Since y⁻² = Q(y) 1 and , the universal map property of Clifford algebras implies that we have homomorphisms of C(U, Q′) and C(U, − δ′Q″) into C(V, Q) sending respectively. The elements and generate the images under the homomorphisms and, by (51), these elements commute. Hence the images under our homomorphisms centralize each other, so by the universal map property of tensor products, we have a homomorphism h of into C(V, Q) such that

Now consider the element d′ = 2u′v′ in C(U, Q′). The calculations made before show that d′y′ = −y′d′ and d′² = −δ′ 1, so d′ is invertible in C(U, Q′). Next consider the element . We have

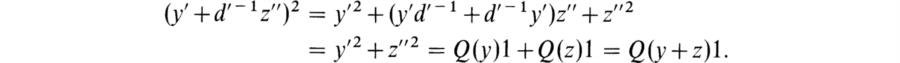
Hence by the universal map property of C(V, Q) we have a homomorphism g of C(V, Q) into such that

Checking on generators, by (52) and (53), we see that gh = 1 on and hg = 1 on C(V, Q). Hence C(V, Q) ≅ .

We are now ready to prove the main theorem on the structure of Clifford algebras.

THEOREM 4.13.   Let Q be a quadratic form of an n-dimensional vector space over afield F of characteristic ≠2. Then

        (1) dim C(V, Q) = 2ⁿ and if (u₁, u₂,…, u_n) is a base for V, the elements

constitute a base for C(V, Q) over F.

        (2) The canonical map i : x of V into C(V, Q) is injective.

        (3) If the bilinear form B associated with Q is non-degenerate, then C(V, Q) is central simple if n is even and if n = 2v + 1, v ∈ , then C(V, Q) is either simple with a two-dimensional field as center or is a direct sum of two isomorphic central simple algebras according as (−1)′ 2δ, δ a discriminant of B, is not or is a square in F.

Proof.   We note first that the second statement in (1) and statement (2) are consequences of the dimensionality relation dim C(V, Q) = 2ⁿ. For, by Lemma 1, the elements in (54) span C(V, Q). Since the number of these elements is ≤ 2ⁿ, if dim C(V, Q) = 2ⁿ, their number is 2ⁿ (that is, they are distinct) and they form a base. This implies also that the _i, 1 ≤ i ≤ n, are linearly independent and hence the linear map i : x is injective.

Next we prove the dimensionality relation and (3) in the non-degenerate case. If n = 1, the results follow from Lemma 2 and if n = 2, they follow from Lemmas 3 and 4. Now assume n > 2. Then we can pick a two-dimensional subspace U on which the restriction of B is non-degenerate. Then V = U U and the restriction of B to U is non-degenerate. By Lemma 5, C(V, Q) ≅ C(U, Q′) C(U, − δ′Q″) where δ′ is a discriminant of the restriction of B to U. Moreover, C(U, Q′) is a quaternion algebra, hence, is fourdimensional central simple. Using induction on the dimensionality, we may assume the results for the quadratic form −δ′Q″ on U. Then dim C(U, − δ′Q″) = 2^{n − 2} and this algebra is central simple if n − 2 is even. Hence dim C(V, Q) = 2²2^{n − 2} = 2ⁿ, and by Corollary 2 to Theorem 4.7, p. 219, this algebra is central simple if n is even. If n = 2v + 1, n − 2 = 2(v − 1) + 1 and the induction hypothesis implies that if δ″ is a discriminant of the restriction of B to U, then C(U, − δ′Q″) is simple with two-dimensional center or is a direct sum of two isomorphic central simple algebras according as (− l)^{v − 1} 2( − δ′)^{n − 2} δ″ is not or is a square in F. Accordingly, C(V, Q) is simple with two-dimensional center or is a direct sum of two isomorphic central simple algebras according as (− l)^{v − 1} 2( − δ)^{n − 2} δ″ is not or is a square. Now

and since n − 3 is even this is a square if and only if (− 1)^v 2δ is a square. This proves (3).

It remains to prove the dimensionality formula in the degenerate case. For this purpose, we shall imbed V in a finite dimensional space W with a quadratic form that has a non-degenerate associated bilinear form and is an extension of Q. To do this we write V = V U for some subspace U. Then the restriction of B to U is non-degenerate. Now put W = V U (V)* where (V)* is the space of linear functions on V. Let x = z + y + f where z ∈ V ,y ∈ U, and f ∈ (V)* and define

It is readily seen that is a quadratic form on W whose associated symmetric bilinear form is non-degenerate. Let x be the canonical map of W into C(W, ). It follows from the universal property of C(V, Q) that we have a homomorphism of C(V, Q) into C(W, ) such that for x ∈ V. Let (u₁,…, u_n, u_{n + 1},…, u_q) be a base for W such that (u₁,…, u_n) is a base for V. Since is non-degenerate, the elements , are distinct and linearly independent. Then this holds also for the elements . Since the homomorphism of C(V, Q) into C(W, ) maps _i1 … _ir into _i1 … _ir, the elements _i1 … _ir, i₁ < … < i_r, 1 ≤ r ≤ n, are linearly independent. Hence dim C(V, Q) = 2ⁿ.

Since the map i : x of V into C(V, Q) is injective, we can identify V with the corresponding subspace of C(V, Q). Hence from now on we assume V ⊂ C(V, Q). If U is a subspace of V, then the subalgebra of C(V, Q) generated by U can be identified with C(U, Q′) where Q′ is the restriction of Q to U. This is clear from the last part of the proof of Theorem 4.13. For, if (u₁…u_ir) is a base for U over F, then the argument shows that the elements 1, u_i1, … ,u_ir, i1 < i2 < … < i_r, 1 ≤ r ≤ m, are linearly independent and this implies that the canonical homomorphism of C(U, Q′) into C(V, Q) is a monomorphism.

It is clear from the definitions that if Q = 0, then C(V, Q) is the exterior algebra E(V) defined by V (p. 141). The results (1) and (2) of Theorem 4.13 give another proof of properties of E(V) that were derived in BAI, pp. 411–414.

We remark finally that the proof of statement (3) in Theorem 4.13 yields a stronger result than we stated in this theorem. We state this as the following