We have y = (β₀, β₁,…, β_{m – 2}, f(x)), f(x)∈ E'[x], and since (β₀, β₁,…, β_{m – 2},x) = (ρ₀^p, ρ₁^p,…, ρ_{m – 2}, x^p,) it follows from (50) that x^p – f(x) + x + y when y ∈ E'. Thus f(x) = x^p – x – γ and if we choose p_{m – 1} g so that f(p_{m – 1}) = 0, then the derivative argument shows that E'(ρ_{m – 1}) is separable over E'. Hence E = F(ρ₀, ρ₀, …, ρ_{m – 1}) is separable over F. The formulas show that if ρ = (ρ₀,ρ₁,…, ρ_{m – 1} is then ρ = (β₀, β₁…, β_{m – 1}).

We can now prove

THEOREM 8.31.   Let Q be a subgroup of (W_m(F), +) containing W_m(F) such that Q/W_m(F) is finite. Then there exists an abelian p-extension E of F such that the exponent of the Galois group of E/F is p^e, e ≤ m, and QW_m(E) = Q.

Proof.   Let β⁽¹⁾, β⁽²⁾…, β^(r) be elements of Q such that the cosets β⁽ⁱ⁾ + W_m(F) generate Q/W_m(F). By Lemma 2, contains a field E that is finite dimensional separable over F and is generated by elements ρ_v^(di) 1 ≤ i ≤ r, 0 ≤ v ≤ m – 1 such that (ρ₀⁽ⁱ⁾,…, ρ_{m – 1}⁽ⁱ⁾) = (β₀⁽ⁱ⁾,…, ρ_{m – 1}⁽ⁱ⁾) in W_m(E). Let E' be the normal closure of E in so E' is a finite dimensional Galois extension of F containing E. We form W_m(E') and let the Galois group G of E'/F act on W_m(E') as before. If s ∈ G and ρ⁽ⁱ⁾ = (ρ₀⁽ⁱ⁾,ρ_{m – 1}⁽ⁱ⁾), then ρ⁽ⁱ⁾ = (β⁽ⁱ⁾ gives (sρ⁽ⁱ⁾ = β⁽ⁱ⁾. Hence (sρ⁽ⁱ⁾ – ρ⁽ⁱ⁾) = 0, so sρ⁽ⁱ⁾ – ρ⁽ⁱ⁾ is in the prime ring of W_m(E'). This implies that sE ⊂ E, s ∈ G. It follows that E is Galois over F and hence E' = E. If s, t ∈ G, then sρ⁽ⁱ⁾ = ρ⁽ⁱ⁾ + γ⁽ⁱ⁾, tρ⁽ⁱ⁾ = ρ⁽ⁱ⁾ + δ⁽ⁱ⁾ where γ⁽ⁱ⁾ + δ⁽ⁱ⁾ ∈ W_m(F). Hence tsρ⁽ⁱ⁾ = ρ⁽ⁱ⁾ + γ⁽ⁱ⁾ + δ⁽ⁱ⁾ = stρ⁽ⁱ⁾, which implies that G is abelian. Also s^kρ⁽ⁱ⁾ = ρ⁽ⁱ⁾ + γ⁽ⁱ⁾. Since W_m(E) is of characteristic p^m, this implies that s^pm = 1 hence G has order p^q and exponent p^e with e ≤ m. Let χi be the character of G defined by ρ⁽ⁱ⁾ : χ_i(s) = sρ⁽ⁱ⁾ – ρ⁽ⁱ⁾. Then it is clear that χi(s) = 1, 1 ≤ i ≤ r, implies that s = 1. It follows that the χi generate . Hence, if ρ is any element of W_m(E) such that ρ ∈ W_m(F) then x_P = ∏x_i^m. This implies that ρ = ∑ m_ip⁽ⁱ⁾ + β, β ∈ W_m(F) m_i integers. Then (ρ) = ∑,m_iβ⁽ⁱ⁾ + (β) ∈ Q. Since ρ is any element of SW_m(E) this shows that Q(W_m(E)) ⊂ Q. The converse is clear so the proof is complete.

The results we have obtained are analogous to the main results on Kummer extensions. They establish a 1– 1 correspondence between the abelian p-extensions whose Galois groups have exponent p^e, e ≤ m, with the subgroups Q of (W_m(F) +) containing W_m,(F) as subgroup of finite index.

We shall now consider the special case of cyclic p-extensions. We observe first that the original Artin-Schreier theorem is an immediate consequence of the general theory: Any p-dimensional cyclic extension of F has the form F(ρ) where p = ρ^p – ρ = β ∈ F and β is an element such that there exists no α ∈ F satisfying α = β. We shall now prove a result that if such an extension exists, then there exist cyclic extensions of F of any dimension p^m, m ≥ 1. For this purpose we require

LEMMA 3.   If β = (β₀,β₁,…, β_{m – 1}) ∈ W_m(F), then p^{m – 1}) ∈ W_m(F) p^{m – 1} β ∈ W_m(F) if and only if β₀ ∈ F.

Proof.   We note first that by iteration of the formula (66) we obtain p^{m – 1} β = (0,…, 0, β₀^{pm – 1}). Next we write

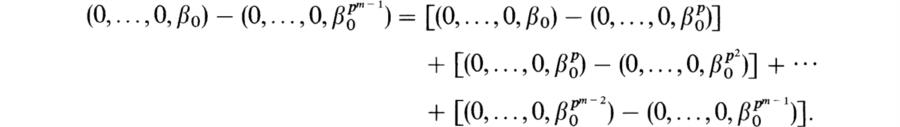
Evidently the right-hand side is contained in W_m(F). Hence p^{m – 1}β = (0,… ,0,β₀^{pm – 1})∈W_m(F) if and only if (0,…0,β₀)∈W_m(F). Suppose that this is the case, say, (0,…, 0, β₀) = ρa – α for α = (α₀, α₁,…, α_{m – 1})∈ W_m(F). Applying R to this relation gives PR_α – Rα = 0 where Rα = (α₀,…, α_{m – 2}). Hence if γ = (α₀,α₁,…,α_{m – 2},0), then P_γ = γ and if δ = α – γ, then Pδ – δ = (0,…,0,γ₀). Moreover, since Rδ = Rα – Rδ = 0, δ = (0,…, 0, δ_{m – 1}). Then the formula (50) applied to Pδ = δ = (0,…, 0, β₀) implies that δ_{m – 1} = α₀, so β₀ ∈ F. Conversely, if this condition holds, then δ = (0,…, 0, β₀) for δ = (0,…, 0, δ_{m – 1}) and hence p^{m – 1}β ∈ W_m(F).

We can now prove

THEOREM 8.32.   Let F be a field of characteristic p ≠ 0. Then there exist cyclic extensions of p^m dimensions, m ≥ 1, over F if and only if there exist such extensions of P dimensions. The condition for this is F ≠ F.

Proof.   We have seen that there exists a cyclic extension of p dimensions over F if and only if F ≠ F. Suppose that this conditions holds and choose β₀ ∈ F, β₀ ∈ F. Let β = (β₀, β₂…, α_{m – 1}) where the β_i, i > 0, are any elements of F. By Lemma 3, p^{m – 1} β ∉ W_m(F). This implies that the subgroup Q of (W_m(F) +) generated by β and W_m(F) has the property that Q/W_m(F) is cyclic of order p^m. By Theorem 8.31, Q = QW_m(E) for an abelian p-extension E/F. Moreover, we have seen that the Galois group G of E/F is isomorphic to Q/W_m(F). Hence this is cyclic of order p^m and E/F is cyclic of p^m dimensions.

EXERCISE

        1. Show that if β ∈ W_m(F) satisfies p^{m – 1} β ∈ W_m(F), then there exists a η ∈ W_m(F) such that pγ = β(W_m(F)). Use this to prove that any cyclic extension of p^{m – 1} dimensions over F can be embedded in a cyclic extension of p^m dimensions over F.

8.12   TRANSCENDENCY BASES

A finite subset {a₁…, a_n}, n ≥ 1, of an extension field E/F is called algebraically dependent over F if the homomorphism

of the polynomial algebra F[x₁,…, x_n], x_i indeterminates, into E has a nonzero kernel. In other words, there exists a non-zero polynomial F(x₁,…,x_n) such that F(a₁, …, a_n) = 0. Evidently if {a₁…, a_n}, 1 ≤ m ≤ n, is algebraically dependent, then so is {a₁…,a_n}. We shall now say that an arbitrary non-vacuous subset of E is algebraically dependent over F if some finite subset has this property. We have the following criterion.

THEOREM 8.33. A non-vacuous subset s of an extension field E/F is algebraically dependent over F if and only if there exists an a∈S that is algebraic over F(S – {a}).

Proof.   If T is a subset of E and a is algebraic over F(T), then a is algebraic over F(U) for some finite subset U of T. It follows that it suffices to prove the theorem for S finite, say, S = {a_l,… a_n}. Suppose first that S is algebraically dependent. We shall prove by induction on n that there exists a_i a_i such that a_i is algebraic over F(S_i), S_i = S – {a_i}. This is clear from the definitions if n = 1, so we assume that n > 1. We may assume also that {a₁,…, a_{n– 1}} is algebraically independent (= not algebraically dependent). Then we have a polynomial f(x₁…, x_n) ≠ 0 such that f(a₁…, a_n) = 0. Write f(x₁,…,x_n) = f₀(x₁,…,x_n) ≠ 0 such that f(a₁,…,a_n) = 0. Write f(x₁,…,x_n) = f₀(x₁,…,x_{n– 1})x_n^m + f₁(x₁,…,x_{n– 1})x_n^{m – 1} + … + f_m f_m(x₁,…,x_{n– 1}) with f₀(x₁,…,x_{n– 1}) ≠ 0. Then f₀(a₁,…,a_{n – 1}) ≠ 0. so g(x) = f₀(a₁,…, a_{n – 1})x_n^m + f₁(a₁,…, a_{n – 1}) ≠ 0. Then f₀(a₁,…, a_{n – 1}) so g(x) = f₀(a₁,…, a_{n – 1})x_n^m + f₁(a₁,…, a_{n – 1})s_n^{m – 1} + … + f_m(a₁,…,a_{n – 1}) is non-zero polynomial in F(a₁…, a_{n – 1})[x] such that g(a_n) = 0. Hence a_n is algebraic over F(a₁,…, a_{n – 1}).

Conversely, suppose one of the a_i is algebraic over S_i = s – {a_i}. We may assume that i = n. Then we have elements b₁,…, b_m ∈ F(a_l,… a_{n – 1}) such that g(a_n) = 0 for g(x) = x^m + b₁x^{m – 1} + … b_m ∈ F(a₁ …, a_{n – 1})[x]. There exist polynomials f₀(x₁…, x_{n – 1}), f₁(x₁…, x_{n – 1}),…,f_m(x₁,…, x_{n – 1}) ∈ F [x₁,…, x_{n – 1}] with f₀(a₁…, a_{n – 1})≠ 0 such that b_i = f_i(a₁,…, a_{n – 1}) f₀(a₁,…, a_{n – 1})^{– 1}. Then if we put

we shall have F(x₁,…, x_n) ≠ 0 and f(a₁,…, a_n) = 0. Thus S is algebraically dependent over F.

We shall now introduce a correspondence from the set E to the set (E) of subsets of E, which will turn out to be a dependence relation on E in the sense defined on pp. 122–123. This is given in

DEFINITION 8.1.   An element a of E is called algebraically dependent over F on the subset S (which may be vacuous) if a is algebraic over F(s). In this case we write a S.

Using this definition, Theorem 8.33 states that a non-vacuous subset S is algebraically dependent over F if and only if there exists an a ∈ S that is alge-braically dependent over F on S – {a}. We shall now show that the correspondence between elements of E and subsets of E satisfies the axioms for a dependence relation, that is, we have

THEOREM 8.34 The correspondence of E to (E) given in Definition 8.1 is a dependence relation.

Proof.   The axioms we have to verify are the following: (i) If a ∈ S, then a S. (ii) If a S, then a U for some finite subset U of S. (iii) If a S and every b ∈ S satisfies b T, then a T. (iv) If a S and a S – {b} for some b in S, then b (S – {b}) ∪ {a}. Axiom (i) is clear and (ii) was noted in the proof of Theorem 8.33. To prove (iii) let A be the subfield of E of elements algebraic over F(T). Then S ⊂ A and if a S, then a is algebraic over A. Hence a ∈ A, which means that a T. To prove (iv) let a S, a S – {b} where b ∈ S. Put K = F(T) where T = s – {b}. Then a is transcendental over K and algebraic over K(b). Hence, by Theorem 8.33, {a, b} is algebraically dependent over K, so there exists a polynomial f(x, y) ≠ 0 in indeterminates x, y with coefficients in K such that f(a, b) = 0. We can write f(x, y) = a₀(x)y^m + a₁(x)y^{m – 1} + … + a_m(x) with a_i(x) ∈ K[x] and a₀(x) ≠ 0. Then a₀(a) ≠ 0, so f(a, y) ≠ 0 in K[y], and f(a, b) = 0 shows that b is algebraic over K(a) = F(T ∪ {a}). Hence b T ∪ {a} as required.

We can now apply the results that we derived on dependence relations to algebraic dependence. The concept of a base becomes that of a transcendency base, which we define in

DEFINITION 8.2.   If E is an extension field of F, a subset B of E is called a transcendency base of E over F if(1) B is algebraically independent, and (2) every a ∈ E is algebraically dependent on B.

The two results we proved in the general case now give

THEOREM 8.35.   E/F has a transcendency base and any two such bases have the same cardinality.

It should be remarked that B may be vacuous. This is the case if and only if E is algebraic over F. The cardinality |B| is called the transcendency degree (tr deg) of E/F. A field E is called purely transcendental over F if it has a transcendency base B such that E = F(B).

EXERCISES

        1. Let E ⊃ K ⊃ F. Show that tr deg E/F = tr deg E/K + tr deg K/F.

        2. Show that if char F ≠ 3 and E = F(a, b) where a is transcendental over F and a³ + b³ = 1, then E is not purely transcendental over F.

        3. Let be the field of complex numbers, the rationals. Show that tr deg = ||. Show that if B is a transcendency base of /, then any bijective map of B onto itself can be extended to an automorphism of /. Hence conclude that there are as many automorphisms of / as bijective maps of onto .

        4. Show that any subfield of a finitely generated E/F is finitely generated.

        5. Let E = F(x₁…, x_m) where the x_i are algebraically independent. Call a rational expression f = gh ^{– 1} homogeneous of degree m (∈) if g is a homogeneous polynomial of degree r, h is a homogeneous polynomial of degree s, and r – s = m. Show that the set E₀ of homogeneous rational expressions of degree 0 is a subfield of E that is purely transcendental of transcendency degree m – 1 over F. Show that E is a simple transcendental extension of E₀.

8.13   TRANSCENDENCY BASES FOR DOMAINS. AFFINE ALGEBRAS

Let D be a commutative domain that is an algebra over a field F, E, the field of fractions of D, so F ⊂ D ⊂ E. Evidently, since F(D) is a subfield of E containing D, F(D) = E and hence D contains a transcendency base for E/F (see the comment (ii) on bases on p. 124). We call trdeg E/F the transcendency degree of D/F. This is an important concept for studying homomorphisms of domains that are algebras over the same field F. For, we have the following

THEOREM 8.36. (i) Let D/F and D'/F be domains and suppose there exists a surjective homomorphism η of D/F onto D'/F. Then tr deg D/F ≥ tr deg D'/F. (ii) Moreover, if tr deg D/F = tr deg D'/F = m < ∞ then η is an isomorphism.

Proof. (i) Let B' be a transcendency base for D'/F. For each x' ∈ B' choose an x ∈ D such that ηx = x'. Then C = {x} is an algebraically independent subset of D. Hence, C can be augmented to a base B for E/F, E the field of fractions of D (see comment (i) on p. 124). Hence

(ii) Now let B' = {x'₁,…, x'_m}, C = {x₁,…, x_m} where ηx_i = x'_i. Since C is an algebraically independent set of cardinality tr deg E/F, B = C is a transcendency base for D/F. Let a be a non-zero element of D. Then a is algebraic over F(x₁,…, x_m). Let m(λ) = λⁿ – α₁λ^{n – 1} + … + α_n, α_i ∈ F(x₁ …, x_m) be the minimum polynomial of a over F(x₁…, x_m). Since a ≠ 0, α_n ≠ 0. We can write α_i = g_i(x₁,…, x_m)g₀(x₁,…,x_m)^{– 1} where g_i(x₁,…, x_m), g₀(x₁… x_m) ∈ F[x₁…, x_m]. Then we have

and hence

Since a_n ≠ 0, g_n(x_l,…, x_m) ≠ 0 and since the x'_i are algebraically independent g_n(x'₁,…, x'_m) = 0. Then by (77), ηa ≠ 0. Thus a ≠ 0 ⇒ ηa ≠ 0 and η is an isomorphism.

We prove next the important

NOETHER NORMALIZATION THEOREM.   Let D be a domain which is finitely generated over a field F, say, D = F[u_l,…,u_m]. Let tr deg D = r ≤ m. Then there exists a transcendency base {v_i} such that D is integral over F[u₁,…, u_r].

Proof.   The result is trivial if m = r so suppose m > r. Then the u_i are algebraically dependent. Hence there exists a non-zero polynomial

in indeterminates x_i with coefficients in F such that f(u₁…, u_m) = 0. Let X be the set of monomials x₁^j₁… x_m^j_m; occurring in F (with non-zero coefficients). With each such monomial x₁^j₁ … x_m^j_m we associate the polynomial j₁ + j₂t + … + j_mt^{m – 1} ∈ [t], t an indeterminate. The polynomials obtained in this way from the monomials in X are distinct. Since a polynomial of degree n in one indeterminate with coefficients in a field has at most n zeros in the field, it follows that there exists an integer d ≥ 0 such that the integers j₁ + j₂d + … + j_md^{m – 1} obtained from the monomials in X are distinct. Now consider the polynomial f(x₁, x₁^d + y₂,…, x₁^{dm – 1} + y_m) where y₂,…, y_m are indeterminates. We have

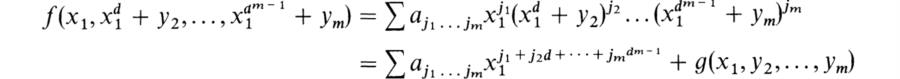
where the degree of g in x₁ is less than that of ∑a_j1…jmx₁^{j₁ + J₂d + … + j_mdm – 1}. Hence for a suitable β ∈ F*, β f(x₁, x₁^d + y₂…,x₁^{dm – 1} + y_m) is monic as a polynomial in x₁ with coefficients in F[y₂,…, y_m]. If we put w_i = u_i – u₁^{di – 1}, 2 ≤ i ≤ m we have ηf(u_l, u₁^d + w₂,…, u^{dm – 1} + w_m) = 0 which implies that u₁ is integral over D' = F[w₂,…, w_m]. By induction on the number of generators, D' has a transcendency base {v_i} such that D' is integral over F[v₁…, v_r]. Then D is integral over F[v₁…, v_r] by the transitivity of integral dependence.

A commutative algebra that is finitely generated over a field is called an affine algebra. Such an algebra is Noetherian (Corollary to the Hilbert basis theorem, p. 421). We recall that the Krull dimension of a Noetherian ring is defined to be Sup s for chains of prime ideals P₀ P₁ … P_s in R. We are now in a position to prove the following theorem on dimension of an affine domain.

THEOREM 8.37.   Let D be an affine domain of transcendency degree r over F. Then the Krull dimension dim D ≥ r and dim D = r if F is algebraically closed.

Proof.   By Noether’s normalization theorem we may write D = F[u₁,…, u_r, u_{r + 1},…, u_m] where the u_i. 1 ≤ i ≤ r, constitute a transcendency base and the remaining u_j are integral over F[u₁,…, u_r]. Then F[u₁,…, u_r] is factorial and hence is integrally closed in its field of fractions. Under these circumstances we can apply the “going-down” Theorem 7.1 to show that dim D = dim F[u₁,…,u_r]. First, let p₀ p₁ … p_s be a strictly descending chain of prime ideals in F[u₁…, u_r. By the lying-over Theorem 7.5, there exists a prime ideal P₀ in D such that P^c₀ = P₀ ∩ F[u₁,…,u_r] = p₀. By Theorem 7.6, there exists a prime ideal P₁ in D such that P_i = F[u₁ and u_r] P_x. Then P₀ P₁. Then by induction we obtain a chain of prime ideals P₀ P₁ … P_s such that P_i, ∩ F[u₁,…,u_r] = p_i 0 ≤ i ≤ s. This implies that dim D ≥ dim F[u₁…, u_r]. Next let P₀ P₁ …P_s, for prime ideals P_i in D. Then, by Corollary 2 to Proposition 7.17 (p. 410), p₀ p₁ … p_s, p_i = P^c₁ is a properly descending chain of prime ideals in F[u₁…, u_r]. It follows that dim F[u₁…,u_r] ≥ dim D. Hence dim D = dim F[u₁,…,u_r]. Now we have the chain of prime ideals

in F[u₁…, u_r]. Hence dim D = dim F[u₁…, u _r] ≥ r = tr deg D/F. On the other hand, we have shown earlier (p. 453) that if F is algebraically closed then dim F[u₁,…, u_r] for algebraically independent u_i is r. This concludes the proof.

EXERCISE

        1. Use the Noether normalization theorem to prove the Corollary to Theorem 7.15 (p. 426). {Sketch of proof. Let m be a maximal ideal in F[x₁,…, x_n], x_i indeterminates, F algebraically closed. Then F[x₁,…, x_n]/M is a field that is an affine algebra F[_l,…, _n], _i = x_i + M. By the Noether normalization theorem and Proposition 7.17, tr deg F[x₁,…, x_n]/M = 0. Since F is algebraically closed, F[x₁,…, x_n]/M = F. Then _i = a_i ∈ F, 1 ≤ i ≤ n, and M = (x₁ – a_l,…, x_n – a_n)}.

8.14   LUROTH'S THEOREM

The purely transcendental extension fields E/F, especially those having a finite transcendency degree, appear to be the simplest type of extension fields. It is clear that such a field is isomorphic to the field of fractions F(x₁,…, x_n) of the polynomial ring F[x₁…,x_n] in indeterminates x₁,…,x_n. Even though these fields look quite innocent, as noted in BAI (p. 270), there are difficult and unsolved problems particularly on the nature of the subfields of F(x₁,…,x_n)/F. A problem of the type mentioned in BAI, which, as far as we know remains unsolved (although it was stated as an exercise in the first edition of the author’s Lectures in Abstract Algebra vol. III (1964), p. 160), is the following: Let the alternating group a_n operate on F(x₁,…x_n) by automorphisms of this field over F so that π x_i = x_π(i), 1 ≤ i ≤ n, for π ∈ A_n and let Inv A_n be the subfield of fixed points under this action. Is Inv A_n purely transcendental over F?

The one case where the situation is quite simple is that in which F has transcendency degree one. We consider this case.

Let E = F(t), t transcendental, and let u ∈ E, ∉ F. We can write u = f(t)g(t)^{– 1} where f(t), g(t) ∈ F[t] and (f(t), g(t))= 1. If n is the larger of the degrees of F(t) and g(t) then we can write

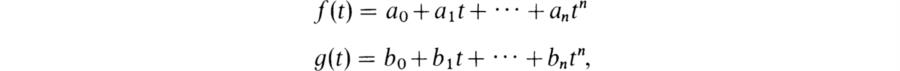
a_i, b_i ∈ F, and either a_n or b_n ≠ 0. We have f(t) – ug(t) = 0, so

and a_n – ub_n ≠ 0 since either a_n ≠ or b_n ≠ 0 and u ∉ F. Thus (78) shows that t is algebraic over F(u) and [F(t):F(u)] ≤ n. We shall now prove the following more precise result.

THEOREM 8.38.   Let E = F(t), t transcendental over F, and let u ∈ F(t), ∉ F. Write u = (f(t)g(t) ^{– 1} = 1 where (f(t),g(t)) = 1, and let n = max (deg F(t), deg g(t)). Then u is transcendental over F, t is algebraic over F(u), and [F(t): F(u)] = n. Moreover, the minimum polynomial of t over F(u) is a multiple in F(u) of f (x, u) = f(x) – ug(x).

Proof. Put f(x, y) = f(x) – yg(x) ∈ F[x, y], x, y indeterminates. This polynomial in x and y is of first degree in y and it has no factor h(x) of positive degree since (f(x),g(x))= 1. Hence it is irreducible in F[x, y]. Now t is algebraic over F(u) so if u were algebraic over F, then t would be algebraic over F, contrary to the hypothesis. Hence u is transcendental over F. Then F[x, u] ≅ F[x, y] under the isomorphism over F fixing x and mapping u into y and hence f(x,u) is irreducible in F[x, u]. It follows that F(x, u) is irreducible in F(u)[x] (BAI, p. 153). Since f(t, u) = F(t) – ug(t) = 0, it follows that F(x, u) is a multiple in F(u) of the minimum polynomial of t over F(u). Hence [F(t):F(u)] is the degree in x of F(x, u). This degree is n, so the proof is complete.

A first consequence of this theorem is that it enables us to determine the elements u that generate F(t). These have the form u = F(t)g(t)^{– 1} where f(t) and g(t) have degree 1 or 0, (f(t), g(t)) = 1, and either f(t) or g(t) ∉ F. Then

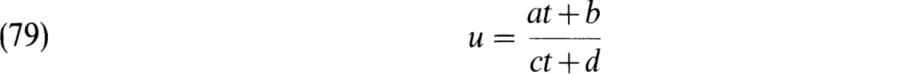
where a, b, c, d ∈ F, either a ≠ 0 or c ≠ 0, and at + b and ct + d have no common factor of positive degree. It is easily seen that this set of conditions is equivalent to the single condition

Now if F(u) = F(t), then we have a uniquely determined automorphism of F(t)/F such that t u and every automorphism is obtained in this way.

The condition (80) holds for the matrix

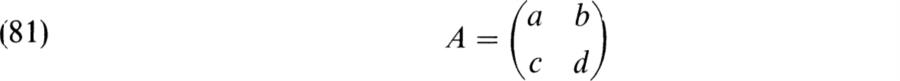
if and only if A is invertible. Now consider the linear group GL₂(F) of these matrices (BAI, p. 375). Any matrix A ∈ GL₂(F) as in (81) determines a generator u = (at + b)/(ct + d) of F(t) and hence determines the automorphism η(A) of F(t)/F such that

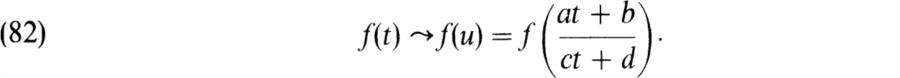
If

∈ GL₂(F), then

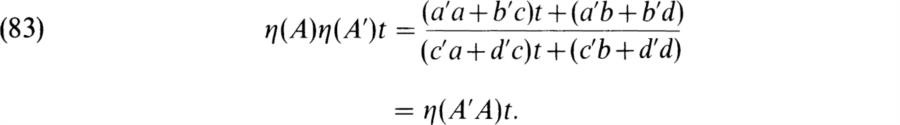
Since any automorphism of F(t)/F sends t into a generator, η is surjective. Hence by (83), η is an anti-homomorphism of GL₂(F) onto Gal F(t)/F. The kernel consists of the matrices A as in (81) such that ((at + b)(ct + d)^{– 1} = t or at + b = ct² + dt. This gives c = b = 0 and a = d. Hence the kernel is the set of scalar matrices a₁, a ≠ 0. The factor group GL₂(F)/F*1 is called a projective linear group and is denoted as PGL₂(F). Hence Gal F(t)/F is anti-isomorphic to PGL₂(F) and since any group is anti-isomorphic to itself (under g g^{– 1}), we also have Gal F(t)/F ≅ PGL₂(F).

One can determine all of the subfields of E/F for E = F(t), t transcendental: These have the form F(u) for some u. This important result is called

LUROTH’S THEOREM.   If E = F(t), t transcendental over F, then any subfield k of E/F, K ≠ F, has the form F(u), u transcendental over F.

Proof.   Let v ∈ K, ∉ F. Then we have seen that t is algebraic over F(v). Hence t is algebraic over K. Let f(x) = xⁿ + k₁x^{n – 1} + … + k_n be the minimum polynomial of t over K, so the k_i ∈ K and n = [F(t):K]. Since t is not algebraic over F, some k_j ∉ F. We shall show that K = F(u), u = k_j. We can write u = g(t)h(t)^{– 1} where g[t], h(t) ∈ F[t], (g(t), h(t)) = 1, and m = max (deg h, deg g) > 0. Then, as we showed in Theorem 8.38, [E : F(u)] = m. Since K ⊃ F(u) and [E : K] = n, we evidently have m ≥ n and equality holds if and only if K = F(u). Now t is a root of the polynomial g(x) – uh(x) ∈ K[x]. Hence we have a q(x) ∈ K[x] such that

The coefficient k_i of f(x) is in F(t) so there exists a non-zero polynomial c₀(t) of least degree such that c₀(t)k_i = c_i(t) ∈ F[t] for 1 ≤ i ≤ n. Then c₀(t)f(x) = f(x, t) = c₀(t)xⁿ + c₁(t)x^{n – 1} + … + c_n(t) ∈ F[x, t], and f(x, t) is primitive as a polynomial in x, that is, the c_i(t) are relatively prime. The x-degree of f(x, t) is n and since k_j = g(t)h(t)^{– 1} with (g(t), h(t) = = 1, the t-degree of f(x, t) is ≥ m. Now replace u in (84) by g(t)h(t)^{– l} and the coefficients of q(x) by their expressions in t. Then (84) shows that f(x, t) divides g(x)h(t) – g(t)h(x) in F(t)[x]. Since f(x, t) and g(x)h(t) – g(t)h(x) ∈ F[x, t] and f(x, t) is primitive as a polynomial in x, it follows that there exists a polynomial q(x, t) ∈ F[x, t] such that

Since the t-degree of the left-hand side is ≤ m and that of F(x, t) is ≥ m, it follows that this degree is m and q(x, t) = q(x) ∈ F[x]. Then the right-hand side is primitive as a polynomial in x and so is the left-hand side. By symmetry the left-hand side is primitive as a polynomial in t also. Hence q(x) = q ∈ F. Then F(x, t) has the same x-degree and t-degree so m = n, which implies that K = F(u).

We shall now indicate some of the results that are presently known on subfields of purely transcendental extensions of transcendency degree greater than one. We use the algebraic geometric terminology in which a purely transcendental extension E/F is called a rational extension and a subfield of such an E/F is called unirational. In BAI (p. 270) we have noted some results and given some references on unirational fields of the form Inv G where G is a finite group of automorphisms of a field F(x₁…, x_n)/F where the x_i are indeterminates that are permuted by G. Further results on the rationality and non-rationality of fields of the form Inv G are given in a survey article by D. J. Saltman, “Groups acting on fields: Noether’s problem” in Contemporary Mathematics vol. 43, 1985, pp. 267–277.

An old result on subfields of rational extensions of transcendency degree two is the theorem of Castelnuovo-Zariski: if F is algebraically closed of characteristic 0 then any subfield L of a rational extension F(x₁,x₂) such that F(x₁,x₂) is affine over L is rational. The result does not always hold for characteristic p ≠ 0. (See R. Hartshorne’s Algebraic Geometry, Springer-Verlag, New York, 1977, p. 422.)

Examples of non-rational subfields of rational extensions of transcendency degree 3 over are given in the following papers:

            1. M. Artin and D. Mumford, “Some elementary examples of unirational varieties that are not rational,” Proc. London Math. Soc. vol. 25, 3rd ser. (1972), pp. 75–95.

            2. C. H. Clemens and P. A. Griffiths, “The intermediate jacobian of the cubic threefold,” Annals of Math. (2) vol. 95 (1972), pp. 281–356.

            3. V. A. Iskovkikh and J. Manin, “Three dimensional quartics and counterexamples to the Luroth problem,” Math. Sbornik, vol. 86 (1971), pp. 140–166.

A. Beauville, J. L. Colliot-Thelene, J. J. Sansuc, and Sir P. Swinnerton-Dyer in “Varietes stablement rationelles non rationelle,” Annals of Math. (2) vol. 121, pp. 283–318 have given an example of an extension K/ of transcendency degree three such that a purely transcendental extension of transcendency degree three over K is purely transcendental of transcendency degree six over but K is not rational over .

EXERCISES

        1. Let F_q be a field of q elements and let K be the subfield of fixed elements of F_q(t), t transcendental, under Gal F_q(t)/F_q. Determine an element u such that K = F_q(u).

        2. Let E = F[t, v] where t is transcendental over F and v² + t² = 1. Show that E is purely transcendental over F.

The following two exercises sketch proofs due to Mowaffag Hajja (to appear in Algebras, Groups, and Geometries) that Im A₃ and Inv A₄ are rational. This improves results of Burnside published in Messenger of Mathematics, vol. 37 (1908), p. 165. We mention also that it has been proved recently by Takashi Maeda (to appear in the J. of Algebra) that Inv A₅ for the base field is rational. The situation for Im A_n with n > 5 is still unsettled.

        3. Show that InvA₃ in K = F(x_l, x₂, x₃) is rational.

   (Sketch of Proof: We distinguish three cases:

               i. F contains a primitive cube root of 1, which implies char F ≠ 3.

            ii. char F ≠ 3 but F contains no primitive cube root of 1.

   iii. char F = 3.

In all cases A₃ is the group of automorphisms of K/F generated by the automorphism σ such that x₁ x₂, x₂ x₃, x₃ x₁. Also Gal K/Inv A₃ = A₃ and [K:Inv A₃] = |A₃| = 3. In case i we put x_j = x₁ + w^jx₂ + w^2jx₃ where w³ = 1, w ≠ 1. Then σx_j = w^{– j}X_j and K = F(X₁, X₂, X₃). Now put Y₁ = X₁²/X₂, Y₂ = X²₂/x₁, Y₃ = xX₃. Then σY_j = Y_j so F(Y₁, Y₂, Y₃) ⊂ Inv A₃. On the other hand, X₁³ = Y₁²Y₂ and K = F(X₁, X₂, X₃) = F(Y₁, Y₂, Y₃,X₁). Hence [K: F(Y₁, Y₂, Y₃)] ≤ 3. Then Inv A₃ = F(Y₁, Y₂, Y₃). In case ii we adjoin a primitive cube root of unity w to K to obtain k' = K(w) = F'(x₁, x₂, x₃) for F' = F(w). We have w² + w + 1 = 0, (w, w²) is a base for k'/ K and for F'/F and we have an automorphism τ of k'/K such that w w². As in case i, we define X_j = x_l + w^jx₂ + w^2jx₃, j = 1, 2, 3, Y₁ = X²₁/x₂, Y₂ = X²₂/x₁, Y₃ = X₃ = x_l + x₂ + x₃. Then Inv A₃ = F'(Y₁, Y₂, Y₃). We have τY₁ = Y₂, ΓY₂ = Y₁ ΓY₃ =Y₃∈K Hence if Y₂ = wZ₁ + w²Z₂ where Z_i∈K then Y₂ = w²Z₁ + wZ₂ and Y₂ = Y₂ implies σZ_i = Z_i and Inv a₃ = F(Z₁,Z₂,Z₃). In case iii we let = σ – 1 and U_} = A^Jx₁ j = 0, 1, 2. Then K = F(U₀, U₁, U₂) and σU₀ = U₀ + U₁ σU₁ = U₁ + U₂ σU₂ = U₂. Let U = U₀U₂ + U₁² − U₁U₂ Then K = F(U, U₁, U₂), σU = U, σU₁ = U₁ + U₂ and σU₂ = U₂. Hence (σ((U³₁ - U₁U₂U²) and Inv a₃ ⊃ F(U, U₂, ₁³ - U₁U₂²). Since [K:F(U, U₂, U₁³ - U₁U₂²).≤ 3 it follows that Inv a₃ = F(U, U₂, U₁³ - U₁U₂²). (Cf. exercise 1, p. 271 of BAI.))

        4. Show that Inv A₄ inK = F(x₁, x₂, x₃, x₄) is rational.

   (Sketch of Proof: It is clear that A₄ is generated by the automorphisms α, β, σ of K/F such that . If char F ≠ 2 we define

Then K = F(s, z₁, z₂, z₃). The action of α, β, σ on (s, z₁, z₂, z₃) is given by the following table

Put Y₁ = Z₁z₃/z₂, Y₂ = σY₁ = z₂z₃/z₁, Y₃ = σ²y₁ = Z₁z₂/z₃. Then F(s, Y₁, Y₂, Y₃) ⊂ Inv H where H = Since , and | H | = 4, it follows as before that Inv H = F(s, Y₁, Y₂, Y₃). Since σs₁ = s₁ and σY₁ = Y₂, σY₂ = Y₃, ΓY₃ = Y₁, the result of exercise 3 shows that Inv in F(s, Y₁, Y₂, Y₃) is rational over F(s). It follows that Inv A₄ in K is rational over F. Now suppose char F = 2. Put x = x₁, y = x₁ + x₃, z = x₁ + x₂, s = x₁ + x₂ + x₃ + x₄, X = xs + yz = x_jx₄ + x₂x₃. Then K = F(x,y,z,s) = F(X, y, z, s) and αX = X, αy = y + s, az = z, αs = s, βX = X, βy = y, ftz = z + s, βs = s. It follows that Inv H in K = F(X, s, y (y + s), z(z + 5)). Then Inv H = F(X,s,y(y + s), z(z + s)). If we put , then Hence. Inv H = F(X₁, X₂, X₃, s). Then the rationality of Inv A₄ follows from exercise 3 since αs = s, αX₁ = X₂, αX₂ = X₃, αX₃ = X₁)

8.15   SEPARABILITY FOR ARBITRARY EXTENSION FIELDS

In this section we shall introduce a concept of separability for arbitrary extension fields that generalizes this notion for algebraic extensions. This is based on the concept of linear disjointness, which we now define.

DEFINITION 8.3.   Let E be an extension field of F, A, and B subalgebras of E/F. Then A and B are said to be linearly disjoint over F if the canonical homomorphism of A _FB into E sending a b into ab, a ∈ A, b ∈ B, is a monomorphism.

It is clear that if A and B satisfy this condition and A' and B' are subalgebras of A and B respectively, then A' and B' satisfy the condition. Let K and L be the subfields of E/F generated by A and B respectively. Then A and B are linearly disjoint over F if and only if K and L are linearly disjoint over F. To prove this it suffices to show that if k₁…,K_m are F-linearly independent elements of K and l₁…,l_n are F-linearly independent elements of L, then the elements k_il_j, 1 ≤ i ≤ m, 1 ≤ j ≤ n, are linearly independent over F. This follows from the linear disjointness over F of A and B by writing k_t = a_i = a_i a^{– 1}, a_i, a ∈ A, 1 ≤ i ≤ m, l_j = b_jb^{– 1} = b_j, b ∈ B, 1 ≤ j ≤ n. Conversely, the linear disjointness of K and L over F implies that of A and B.

The following result permits establishment of linear disjointness in stages.

LEMMA 1.   Let E₁ and E₂ be subfields of E/F, a subfield of E₁/F. Then E₁ and E₂ are linearly disjoint over F if and only if the following two conditions hold: (1) K₁ and E₂ are linearly disjoint over F and (2) K₁(E₂) and E₁ are linearly disjoint over K₁.

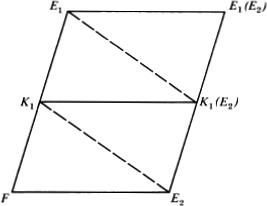
Proof.   Assume the two conditions. Let (u_a) be a base for E₂/F. By (1) these elements are linearly independent over and, since they are contained in K₁(E₂), they are linearly independent over E_u by (2). Hence E₁ and E₂ are linearly disjoint over F. Conversely assume that E₁ and E₂ are linearly disjoint over F. Then (1) is clear since K₁ ⊂ E₁. Let (u_x) be a base for E₁/K₁ (v_β) a base for K₁/F, (w_γ) a base for E₂/F. Then (u_αv_β) is a base for E₁/F and since E₁ and E₂ are linearly disjoint over F, the set of elements {uαVβWγ.} is linearly independent. This implies that the only relations of the form ∑d_iu_x = 0 with d_i in the subalgebra K₁E₂ generated by K₁ and E₂ are the trivial ones in which every d_i = 0. Since K₁E₂ is the set of elements cd^{– 1}, c, d ∈ K₁E₂, it follows that (u_α) is a set of elements that is linearly independent over K₁(E₂). Then (2) holds.

We now assume that the characteristic is p ≠ 0 and we imbed E in its algebraic closure . If e > 0, we denote the subset of of elements a such that a^pe ∈ F by F^{p– e}. This is a subfield and F ⊂ F^{p – 1} ⊂ F^{p– 2} ⊂ … Hence F^{p– ∪} ≡ _{e ≥ 1} F^{p – e} is a subfield. Since linear disjointness is a property of finite subsets, it is clear that F^{p– ∞} and E are linearly disjoint over F if and only if F^{p ∈} and E are linearly disjoint over F for every e. A result on separable algebraic extensions that we proved before can now be reformulated as

LEMMA 2.   If E/F is separable algebraic, then E and F^{p – ∞} are linearly disjoint over F.

Proof.   It suffices to show that if a₁…, a_m are F-independent elements of E, then these are linearly independent over F^{p – e} for every e. This is equivalent to the following: a₁^pe,…, a_m^pe are F-independent, which is a property of separable algebraic extensions proved on p. 489. Hence F and F^p are linearly disjoint over F.

We prove next

LEMMA 3.   If E is purely transcendental over F, then E/F and F^{p – ∞} are linearly disjoint over F.

Proof.   It suffices to prove the result for F = F(x₁…, x_n) where the x_i are algebraically independent. Moreover, the result will follow in this case if we can show that F[x₁,…,x_n] and F^{p – e} are linearly disjoint over F for every e > 0. We have a base for F[x₁,…, x_n]/F consisting of all of the monomials x^k_1¹…x^k_nⁿ, k_i ≥ 0. The map m m^pe for the set of monomials is injective onto a subset. Hence if (m_a) is the base of monomials, then the set {m_α^pe} is linearly independent over F. It follows that {m_α} is linearly independent over F^{p – e} and hence F[x_i …, x_n] and F^{p – e} are linearly disjoint over F.

An extension E/F is said to be separably generated over F if E has a transcendency base B such that E is separable algebraic over F(B). In this case B is called a separating transcendency base for E/F. The example of E inseparable algebraic over F shows that E/F may not be separably generated. The example of B = {x^p} in F(x), x transcendental, shows that even if E is separably generated over F, not every transcendency base has the property that F is separable algebraic over F(B).

We can now prove our main result.

THEOREM 8.39.   Let E be an extension field of a field of characteristic p > 0. Then the following properties of E/F are equivalent:

            (1) Every finitely generated subfield of E/F is separably generated.

            (2) E and F^{p – ∞} are linearly disjoint over F.

            (3) E and F^{p – 1} are linearly disjoint over F.

Proof.   (1)⇒(2). To prove this we suppose that E is separable algebraic over F(B), B a transcendency base of E/F. By Lemma 3, F^p-∞ and F(B) are linearly disjoint over F. By Lemma 2, E and F(B)^{P x} are linearly disjoint over F(B). Since F(B)^P-∞ ⊃ F^p-∞ (B) it follows that F^P-∞(B) and E are linearly disjoint over F (B). Then, by Lemma 1, E and F^{p – i} are linearly disjoint over F. Since this is a property of finite subsets, the result proved shows that (l)⇔(2).

(2) ⇒ (3) obviously.

(3) ⇒ (1). Assume that E and F^{p – i} are linearly disjoint over F and let K = F(a₁…,a_n) be a finitely generated subfield of E/F. We prove by induction on n that we can extract from the given set of generators a transcendency base a_i,…,a_i, (where r is 0 if all the a_i are algebraic over F) such that K is separable algebraic over F(ai₁,…, a_i). The result is clear if n = 0, so we assume n > 0. The result is clear also if a₁…, a_n are algebraically independent. Hence we assume that a₁,…,a_r, 0 ≤ r < n, is a transcendency base for K/F. Then a₁ …, a_{r + 1} are algebraically dependent over F, so we can choose a polynomial F(x₁,…,x_{r + 1}) ≠ 0 ∈ F[x₁,…,x_{r + 1}] of least degree such that f(a₁ … a_{r + 1} = 0. Then f(x₁,…,x_{r + 1}) is irreducible. We claim that f does not have the form g(x₁^p,…,x^p_{r + 1}), g ∈ F[x₁,…,x_{r + 1}]. For g(x₁^p,…,x_{r + 1}^p) = h(x₁…,x_{r + 1})^p in F^{p – 1}[x₁,…,x_{r – 1}]and if f(x₁…,x_{r – 1}) = g(x₁^p,…,x_{r – 1}^p), then h(a₁…,a_{r – 1}) = 0. Let mi(x₁,…,x_{r – i}), 1 ≤ i ≤ u, be the monomials occurring in h. Then the elements m_i(a₁,…,a_{r – 1}) are linearly dependent over F^{p – 1} so by our hypothesis, these are linearly dependent over F. This gives a non-trivial polynomial relation in a₁… a_{r + 1} with coefficients in F of lower degree than f contrary to the choice of f. We have therefore shown that for some i, 1 ≤ i ≤ r + 1, f(x₁,…,x_{r + 1}) is not a polynomial in x_i^p (and the other x’s). Then a_i is algebraic over F(a₁,…, xâ_i,…,a_{r + 1}) where >_i denotes omission of a_i. It follows that {a₁,…, xâ_i,…,a_{r + 1}} is a transcendency base for F(a₁,…,a_n). Then F[a₁,…, a_{i – 1}, x, a_{i + 1},…, a_{r + 1}] ≅ F[x₁…, x_{r + 1}] in the obvious way and hence f(a₁, …,a_{i – 1},x, a_{i + 1},…, a_{r + 1}) is irreducible in F[a₁ …, a_{i – 1}, x, a_{i + 1},…, a_{r + 1}]. Then this polynomial is irreducible in F(a₁ …,a₁…,â_{r + 1}) [x]. Since a_i is a root of F(a₁,…,a_i-1,x,a_i+1,…,a_r+1.) and this is not a polynomial in x^p, we see that a_i is separable algebraic over F(a₁ …â_i…,a_r+1) and hence over L = F(a₁ …, â_i…,a_n). The induction hypothesis applies to L and gives us a subset {a_i1…, a_i} of {a₁…,â_h… ,a_n] that is a separating transcendency base for L over F. Since a_i is separable algebraic over L, it follows that a_i is separable algebraic over F(a_i1,…,a_ir). Hence {a_i1, …, {a_i1} is a separating transcendency base for F(a₁…,a_n).

We remark that the result is applicable in particular to an algebraic extension E/F. In this case it states that if E and F^p-1 are linearly disjoint over F, then E is separable and if E is separable, then E and F^p-∞ are linearly disjoint over F (which was Lemma 2). This makes it natural to extend the concept of separability for arbitrary extension fields in the following manner.

DEFINITION 8.4.   An extension field E/F is called separable if either the characteristic is 0 or the characteristic is P ≠ 0, and the equivalent conditions of Theorem 8.37 hold.

The implication (3) ⇒ (1) of Theorem 8.37 is due to MacLane. It implies an earlier result due to F. K. Schmidt, which we state as a

COROLLARY.   If F is perfect, then every extension E/F is separable.

Proof.   This is clear since F is perfect if and only if the characteristic is 0 or it is p and F^p-1 = F.

The following grab-bag theorem states some properties and non-properties of separable extensions.

THEOREM 8.40.   Let E be an extension field of F, k an intermediate field. Then (1) If E is separable over F, then k is separable over F. (2) If E is separable over k and k is separable over F, then E is separable over F. (3) If E is separable over F, then E need not be separable over K. (4) If E is separable over F, it need not have a separating transcendency base over F.

Proof. We may assume that the characteristic is p ≠ 0. (1) This is clear since the linear disjointness of E and F^p-1 over F implies that of K and F^{p – 1} over F. (2) The hypothesis is that E and K^{p – 1} are linearly disjoint over K and that K and F^{p – 1} are linearly disjoint over F. Then E and K(F^{p – 1}) are linearly disjoint over K since K(F^{p – 1}) ⊂ K^{p – 1} Hence, by Lemma 1, E and F^p-l are linearly disjoint over F and so E is separable over F. (3) Take E = f(x), x transcendental, and K = F(x^p). (4) Take E = F(x, x^{p – 1}, x^{p – 2},…) where x is transcendental over F. Then E has transcendency degree one over F and E is not separably generated over F.

EXERCISES

        1. Let E₁/F and E₂/F be subfields of E/F such that Ei/F is algebraic and E₂/F is purely transcendental. Show that E₁ and E₂ are linearly disjoint over F.

        2. Let F have characteristic p ≠ 0. Let E = F(a,b,c,d) where a,b,c are algebraically independent over F and d^p = ab^p + c. Show that E is not separably generated over F(a, c).

        3. (MacLane.) Let F be a perfect field of characteristic p, E an imperfect extension field of transcendency degree one over F. Show that E/F is separably generated.

8.16   DERIVATIONS

The concept of a derivation is an important one in the theory of fields and in other parts of algebra. We have already encountered this in several places (first in BAI, p. 434). We consider this notion now first in complete generality and then in the special case of derivations of commutative algebras and fields. In the next section we shall consider some applications of derivations to fields of characteristic p.

DEFINITION 8.5.   Let B be an algebra over a commutative ring K, A a subalgebra. A derivation of A into B is a K-homomorphism of A into B such that

for a, b ∈ A. If A = B, then we speak of a derivation in A (over K).

Let Der_K(A, B) denote the set of derivations of A into B. Then Der_k(A, B) ⊂ hom_K(A, B). If D₁, D₂∈ Der_K(A,B), then the derivation condition (86) for the D_i gives

Hence D₁ + D₂ ∈ Der_K(A, B). Now let k ∈ K, D ∈ Der_K(A, B). Then

Hence kD ∈ Der_K(A, B) and so Der_K(A, B) is a K-submodule of hom_K(A, B).

Now let B = A and write Der_kA for Der_K(A, A). As we shall now show, this has a considerably richer structure than that of a K-module (cf. BAI, pp. 434–435). Let D₁, D₂ ∈ Der_KA, a, b ∈ A. Then

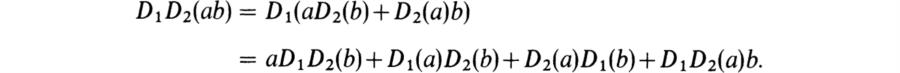
If we interchange D₁ and D₂ in this relation and subtract we obtain

where we have put [D₁D₂] for D₁D₂ – D₂D₁. This result and the fact that Der_kA is a K-module of End_KA amount to the statement that Der_KA is a Lie algebra of K-endomorphisms of A (BAI, p. 434).

There is still more that can be said in the special case in which K is a field of characteristic p ≠ 0. We note first that for any K, if D ∈ Der_KA, we have the Leibniz formula for Dⁿ:

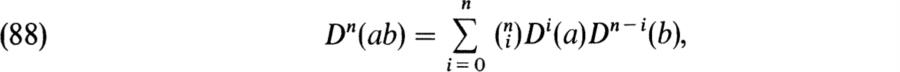
which can be proved by induction on n. If K is a field of characteristic p, then (88) for n = p becomes

This shows that D^p ∈ Der_KA. If V is a vector space over a field K of characteristic p, then a subspace of End_KV that is closed under the bracket composition [D₁D₂] and under pth powers is called a p-Lie algebra (or restricted Lie algebra) of linear transformations in V. Thus we have shown that if A is an algebra over a field of characteristic p, then Der_KA is a p-Lie algebra of linear transformations in A over K.

There is an important connection between derivations and homomorphisms. One obtains this by introducing the algebra of dual numbers over K. This has the base (1,δ) over K with 1 the unit and δ an element such that δ² = 0. If B is any algebra over K, then we can form the algebra B _K and we have the map b → b 1 of B into B _K . Since is K-free, this is an algebra isomorphism and so B can be identified with its image B 1. We can also identify δ ∈ with 1 δ in B _K . When this is done, then B _K appears as the set of elements

This representation of an element is unique and one has the obvious K-module compositions: Moreover, if b_i ∈ B, then

Now let D be a K-homomorphism of A into B. We define a corresponding map α(D) of A into B _K by

which is evidently a K-homomorphism. We claim that α(D) is an algebra homomorphism if and only if D is a derivation. First, we have D(1) = 0 for any derivation since D(l) = D(1²) = 2D(1). Now

and

Thus α(D)(ab)) = (α(D)(a))(α(D)(b)) if and only if D is a derivation and α(D) is an algebra homomorphism if and only if D is a derivation.

The homomorphisms α(D) have a simple characterization in terms of the map

of B _k into B, which is a surjective K-algebra homomorphism of B _K onto B. If a ∈ A, then α(D)a = a + D(a)δ so πα(D)a = a. Hence πα(D) = 1_A. Conversely, let H be a homomorphism of A into B _K. For any a we write H(a) = a₁ + a₂δ. This defines the maps a a₁, a , a₂ of A into B, which are K-homomorphisms. The condition πH = 1_A is equivalent to a₁ = a for all a. Hence if we denote a a₂ by D, then H(a) = a + D(a)δ. The condition H(ab) = H(a)H(b) is equivalent to: D is a derivation.

We summarize our results in

PROPOSITION 8.15.   Let A be a subalgebra of an algebra B and let D be a derivation of A into B. Then α(D): a a + D(a)δ is an algebra homomorphism of A into B _K such that σα(D) = 1_A. Conversely, any homomorphism H of A into B_k such that σH = 1_A has the form a (D), D a derivation of A into B.

The importance of this connection between derivations and homomorphisms is that it enables us to carry over results on algebra homomorphisms to derivations. In this way we can avoid tedious calculations that would be involved in direct proofs of the results for derivations. As an illustration we prove

PROPOSITION 8.16.   Let A be a subalgebra of an algebra B, D, D₁, D₂ derivations of A into B, x a set of generators for A. Call an element a ∈ A a D-constant if D_a = 0. Then

            (1) D₁ = D₂ if |X = D₂|X.

            (2) The set of D-constants is a subalgebra of A. Morever, if A is a division algebra, then it is a division subalgebra.

Proof. (1) The condition D₁|X = D₂|X implies that α(D₁)|X = α(D₂)|X for the algebra homomorphisms of A into B_K. Since X generates A, we have α(D₁) = α(D₂). Hence D₁ = D₂.

(2) The condition that a is a D-constant is equivalent to: a is a fixed element under the homomorphism α(D) of A ⊂ B _K into B_K. Since the set of fixed points of a homomorphism of a subalgebra A of an algebra C is a subalgebra and is a division subalgebra if A is a division algebra, the result on derivations is clear.

We obtain next a formula for D(a^{– 1}) for an invertible element a of A and derivation D of A into B. Since 1 is a D = constant, applying D to aa^{– 1} = 1 gives

Hence we have the formula

which generalizes the well-known formula from calculus.

From now on we consider derivations of commutative algebras into commutative algebras, that is, we assume B commutative. Let D ∈ Der_K(A, B) b ∈ B. If we multiply the relation D(xy) = D(x)y + xD(y), x, y ∈ A, by b we obtain

This shows that bD defined by (bD)(x) = b(D(x)) is again a derivation. It is clear that this action of B on Der_K(A, B) endows Der_K(A, B) with the structure of a B-module.

We now consider the problem of extending a given derivation D of a subalgebra A into B to a derivation of a larger subalgebra A'. Let α(D) be the corresponding homomorphism of A into B_K such that σα(D) = 1_A. The problem of extending D to a derivation of A' amounts to that of extending H = α(D) to a homomorphism H' of A' into B_K such that πH' = 1_A'. Now if H' is a homomorphism of A′ into B_K extending H, then πH' = 1_A. will hold if and only if πH'(x) = x holds for every x in a set of generators for A over A. We shall use these observations in treating the extension problem.

We now suppose that A' = A[u₁…, u_n], the subalgebra generated by A and a finite subset {u₁,…,u_n} of B. Let A[x₁,…,x_n] be the polynomial algebra over A in the indeterminates x_i and let I be the kernel of the homomorphism of A[x₁,…, x_n] onto A', which is the identity on A and sends x_i u_i, 1 ≤ i ≤ n. Suppose that we have a homomorphism s of A into a commutative algebra C and elements v_i 1 ≤ i ≤ n, of C. Then we have the homomorphism

of A[x₁…, x_n] into C (BAI, p. 124). Here sf denotes the polynomial obtained from f by applying s to its coefficients. The homomorphism (95) induces a homomorphism

of A[x₁,…, x_n]/I into C if and only if (sf) (v₁,…, v_n) = 0 for every f ∈ I. Since we have the isomorphism f(x₁,…,x_n) + I f(u₁,…,u_n), we see that we have a homomorphism of A' into C extending s and sending u_i v_i, 1 ≤ i ≤ n, if and only if

for every f ∈ L. Moreover, it is clear that it suffices to have this relation for every F in any set of generators X for the ideal I.

If F(x₁,…, x_n) ∈ A [x₁,…,x_n], we write δf/δx_i for the polynomial obtained from f by formal partial differentiation with respect to x_i. For example

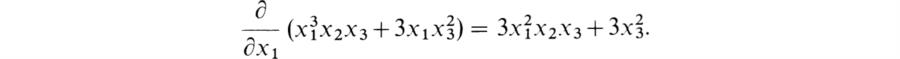
If D is a derivation of A into B, then we shall write (Df)(x₁…,x_n) for the polynomial in B[x₁,…,x_n] obtained by applying the derivation D to the coefficients of f

We can now prove

THEOREM 8.41.   Let B be a commutative algebra, A a subalgebra, A' = A[u₁…, u_n], u_i ∈ B, X a set of generators for the kernel of the homomorphism of A[x₁,… ,x_n] onto A' such that a a for a ∈ A and x_i u_i, 1 ≤ i ≤ n. Let D be a derivation of A into B. Then D can be extended to a derivation of A' into B such that u_i v_i, 1 ≤ i ≤ n, if and only if

for every f ∈ X.

Proof.   The condition that D has an extension of the sort specified is that α(D) is extendable to a homomorphism of A' into B_K sending u_i u_i + v_iδ , 1 ≤ i ≤ n. This will be the case if and only if for every f ∈ X

Now let a ∈ A and consider the monomial . We have

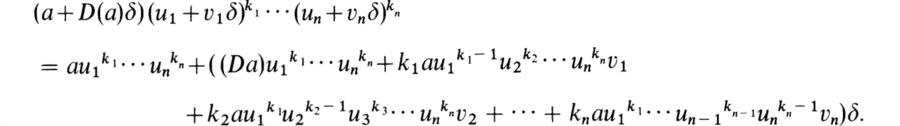
Hence for any f ∈ A[x₁ …, x_n] we have

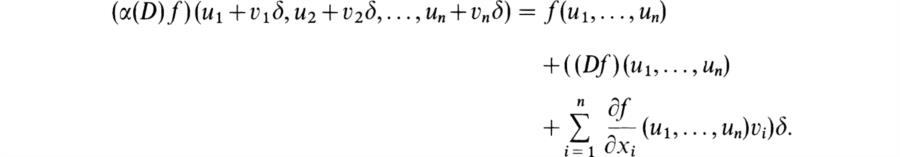
Then the condition that (99) holds for all f ∈ X is equivalent to (98).

We suppose next that S is a submonoid of the multiplicative monoid of A and we consider the localizations A_s and B_s. We can prove

THEOREM 8.42.   Let D be a derivation of A into B (commutative) and let s be a submonoid of the multiplicative monoid of A. Then there exists a unique derivation D_s of a_s into B_s such that

is commutative. Here the horizontal maps are the canonical homomorphisms a a/1 and b b/l respectively.

Proof.   We have the homomorphism α(D) of A into B _K sending a a + D(a)δ and the homomorphism of B_K into B_SK sending b/1u. Hence we have the homomorphism of A into B_SK sending such that a a/1 +(D(a)/l)α. Now if s ∈ S, then s/1 + (D(s)/l)δ is invertible with inverse l/s – (D(s)/s²)δ. Hence by the universal property of A_s we have a unique homomorphism H: A_s B_sK such that

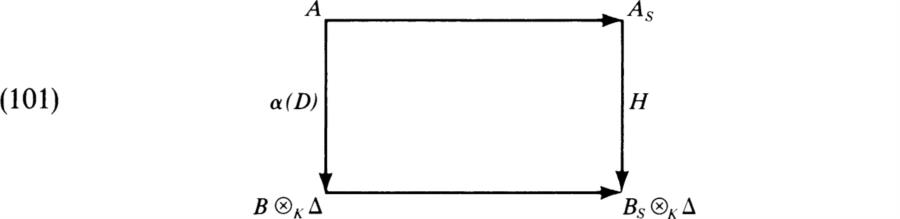
is commutative. If π_s denotes the canonical homomorphism of B_SK onto B_s, then the commutativity of (101) implies that π_sH = 1_As. Hence H has the form α(D_s) where D_s is a derivation of A_s into B_s. Then D_s satisfies the condition of the theorem.

We now specialize to the case of fields. We consider an extension field E/F of a field and regard this as an algebra over F. Suppose K is a subfield of E/F and we have a derivation D of K/F into E/F and a is an element of E. If a is transcendental over K, then Theorem 8.41 shows that for any b∈E there exists a derivation of K[a] into E extending D and mapping a into b. Then Theorem 8.42 shows that this has a unique extension to a derivation of K(a) into E: Hence if a is transcendental over K, then there exists an extension of D to a derivation of K(a) sending a into b. By Proposition 8.16 (and Theorem 8.42) this is unique. Next let a be algebraic over K with minimum polynomial f(x) over K. Then K(a) = K[a] and Theorem 8.41 shows that D can be extended to a derivation of K(a) into E sending a b if and only if

If a is separable, (f(x), f'(x)) = 1 and f′ (a) ≠ 0. Then there is only one choice we can make for fo, namely,

Hence in this case D can be extended in one and only one way to a derivation of K(a) into E. If a is inseparable, then F'(a) = 0. Then (101) shows that D can be extended to a derivation of K(a) if and only if the coefficients of f(x) are D constants and if this is the case, the extension can be made to send a into any b ∈ E. We summarize these results in

PROPOSITION 8.17.   Let E be an extension field of F, k an intermediate field, D a derivation of K/F into E/F, a an element of E. Then

            (1) D can be extended to a derivation of K (a) into E sending a into any b ∈ E if a is transcendental over k.

            (2) D has a unique extension to a derivation of K(a) into E if a is separable algebraic over K.

            (3) D can be extended to a derivation of K(a) into E if a is inseparable algebraic over k if and only if the coefficients of the minimum polynomial of a over k are D-constants. Moreover, if this condition is satisfied, then there exists an extension sending a into any b ∈ E.

We now suppose that E is finitely generated over F: E = F(a₁…,a_n). Let X be a set of generators for the ideal I in F[x₁…, x_n], x_i indeterminates, consisting of the polynomials f such that f(a₁,…,a_n) = 0. Then it follows from Theorems 8.41 and 8.42 that there exists a derivation D of E/F into itself such that Da_i = b_i 1 ≤ i ≤ n, if and only if

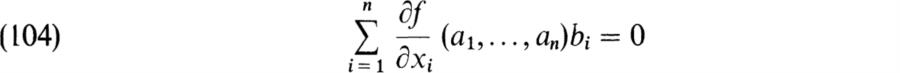
for every f ∈ X. We recall that Der_FE becomes a vector space over E if we define bD for b ∈ E, D ∈ Der_FE by (bD)(x) = b(D(x)) (p. 525). We wish to calculate the dimensionality [Der_FE : E] when E = F(a₁…, a_n). For this purpose we introduce the n-dimensional vector space E⁽ⁿ⁾ of n-tuples of elements of E. If D ∈ Dev_FE, D determines the element (Da₁,…, Da_n) of E⁽ⁿ⁾ and we have the map

of Der_FE into E⁽ⁿ⁾. Evidently this is a linear map of vector spaces over E and since a derivation is determined by its action on a set of generators, λ = λ_a,…,a_n is injective. Hence [Der_FE:E] is the dimensionality of the subspace λ_i(Der_FE) of E⁽ⁿ⁾. Now let g ∈ F[x₁…, x_n]. Then g defines a map dg of E⁽ⁿ⁾ into E by

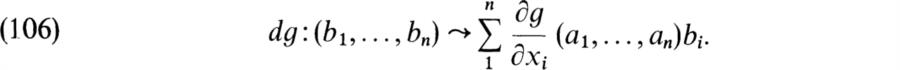
Evidently this is linear. The result we proved before now states that (b₁ …,b_n) ∈ λ (Der_FE) if and only if

for every f ∈ X. This is a system of linear equations that characterizes λ(Der_FE). This leads to a formula for [Der_FE: E], which we give in

THEOREM 8.43.   Let E = F(a₁, … ,a_n) and let x be a set of generators of the ideal of polynomials in F[x₁…x_n] such that f(a₁,…,a_n) = 0. Let dX denote the space of E^(n)* spanned by the linear functions df, f ∈ X. Then

Proof.   We have [Der_FE:E] = [λDer_FE:E], and A Der_FE is the subspace of E⁽ⁿ⁾ of elements such that df(b₁,…, b_n) = 0 for all f ∈ X. Hence (108) follows from linear algebra.

By the Hilbert basis theorem, we can take X = {f₁…, f_m}. Then it follows from linear algebra that [dX: E] is the rank of the Jacobian matrix

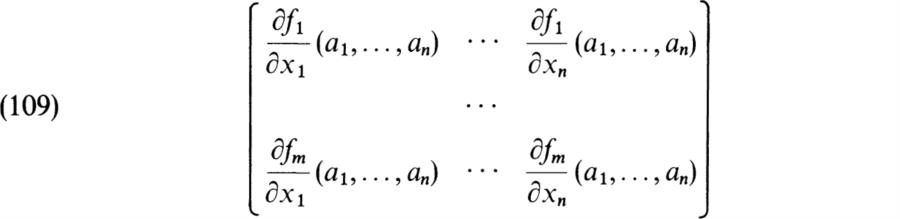
Combining this with Theorem 8.43 we obtain the

COROLLARY.   Let E = F(a₁…, a_n) and let X = {f₁,…, f_m} be a finite set of generators for the ideal of polynomials in F[x₁,…, x_n] such that f(a₁…, a_n) = 0. Then

where J(f₁,…, f_m) is the Jacobian matrix (108).

We obtain next a connection between [Der_FE:E] and the structure of E/F. We prove first

PROPOSITION 8.18.   If E = E(a₁,…,a_n), then Der_FE = 0 if and only if E is separable algebraic over F.

Proof. If a ∈ E is separable algebraic over F, then Proposition 8.17.2 applied to the derivation 0 on F shows that D(a) = 0 for every derivation of E/F. Hence Der_FE = 0 if E is separable algebraic over F. Now suppose that E is not separable algebraic over F. We may assume that {a₁,…,a_r} (r ≥ 0) is a transcendency base for E/F. Let S be the subfield of elements of E that are separable algebraic over F(a₁…,a_r). If S = E, then r > 0 and we have a derivation of F(a₁…,a_r) into E sending a_i 1 ≤ i ≤ r, into any element we please in E. By applying Proposition 8.17.2 successively to a_{r + 1},…,a_n, we obtain extensions of the derivation of F(a₁…, a_r) to E to a derivation of E/F. Hence we can obtain a non-zero derivation of E/F. Now let E S. Then the characteristic is p 0 and E is purely inseparable over S. We have 0 ≠ E [E: S] < ∞ and we can choose a maximal subfield k of E containing S (K ≠ E). If a ∈ E, ∉ EX, then K(a) = E by the maximality of K. Moreover, the minimum polynomial of a over k has the form x^pe – b since E is purely inseparable over S and hence over x. If e > 1, then K(a^{pe – 1}) is a proper subfield of E properly containing x. Hence E = K(a) where x^p– b is the minimum polynomial of a over K. By Proposition 8.17.3 we have a non-zero derivation of E/K. Since this is a derivation of E/F, we have Der_FE≠0 in the case E s also.

We can now prove the following theorem relating [Der_FE:E] and the structure of E/F.

THEOREM 8.44.   Let E = F(a₁,…,a_n). Then [Der_FE: E] is the smallest s such that there exists a subset {a_i1…, a_is} of {a_i1, …,a_n} such that E is separable algebraic over F(a_i1,… ,a_is). Moreover, [Der_FE;E] is the transcendency degree of E over F if and only if E is separable over F.

Proof.   We again consider the map λ = λ_a1,…, a_is of Der_FE into E⁽ⁿ⁾ defined by (105). Let s = [Der_FE: E] = [λ(Der_FE): E] and let D₁, D₂, …, D_s be a base for Der_FE over E. Then s ≤ n and λ(Der_FE) has the base (D₁a₁,…, D₁a_n),…, (D_sa₁,…, D_sa_n) and so the s × n matrix (D_ia_j) has rank s. Hence we may suppose that the a_i are ordered so that

Put k = F(a₁…, a_s) and let D ∈ Der_KE ⊂ Der_FE. Then D = ∑^s₁b_iD_i, b_i ∈ E, and D(a_j) = 0 for 1 ≤ j ≤ s. By (110), this implies that every b_i = 0, so D = 0. Hence Der_KE = 0 and so by Proposition 8.18, E is separable algebraic over x. Conversely, let {ai₁,…, ai_t} be a subset of {a₁,…,a_n} such that E is separable algebraic over F(ai_i… ,a_i). By reordering the a’s we may assume that the subset is {a₁,…,a_t}. We now map Der_FE into E^(t) by D (Dai,„-t ,Da_t). The kernel of this linear map is the set of D such that D(a_k) = 0, 1 ≤ k ≤ t, and hence it is the set of D such that D(K) = 0 for x = F(a_i),…, a_t). Now D(K) = 0 means that D ∈ Der_x(E) and since E is separable algebraic over X, this implies that D = 0. Thus the map D (Da₁,…,Da_t) is injective. Hence t ≥ s = [Der_FE:E]. This completes the proof of the first statement. To prove the second, we note first that if [Der_FE: E] = s, then we may assume that E is separable algebraic over F(a₁,…,a_s). Then {a₁…,a_s} contains a transcendency base for E/F, so s ≤ r = tr deg E/E. Moreover, if r = s, then (a_l,…,s_s} is a transcendency base. Hence this is a separating transcendency base and E is separable over E. Conversely, suppose that E is separable over E. Then the proof of Theorem 8.39 shows that we can choose a separating transcendency base among the a_i so we may assume this is {a_u…,a_r}. Then E is separable algebraic over F(a₁,…,a_r) and hence, as we showed in the first part, r ≥ [Der_FE:E]. Since we had [Der_FE: E] ≥ r, this proves that [Der_FE: E] = r.

EXERCISES

        1. Let E = F(a₁…,a_n). Show that E is separable algebraic over F if and only if there exist n polynomials f₁,…f_n ∈ F[x₁,…,x_n] such that f_i(a₁,…,a_n) = 0 and

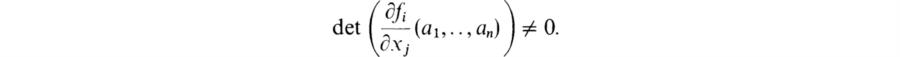
        2. Let D be a derivation in E/F, K the subfield of D-constants. Show that a₁,…, a_m ∈ E are linearly dependent over K if and only if the Wronskian determinant

        3. (C. Faith.) Let E = F(a₁,…,a_n) and let K be a subfield of E/F. Show that [Der_FK: K] ≤ [Der_FE:E].

        4. Let A be a subalgebra of an algebra B over a commutative ring K. Define a higher derivation of rank m of A into B to be a sequence of K-homomorphisms

of A into B such that

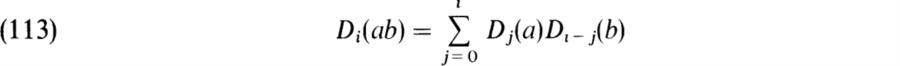
for a, b ∈ A. Let ^(m) be the algebra K[x]/(x^{m + 1}) so ^(m) has a base (1, δ,…, δ^m) where δ = x + (x^{m + 1}) and δ^{m + 1} = 0. Note that B_K^(m) is the set of elements

where b_i = b_i 1, and δ = 1 δ and that an element (113) is 0 if and only if every b_i = 0. Let π denote the homomorphism of B _K ^(m) into B sending b₀ + b₁δ + … + b_mδ^m b₀. Show that a sequence of maps D = (D₀, D₁,…, D_m) of A into B is a higher derivation of rank m of A into B if and only if

is a K-algebra homomorphism of A into B _k ^(m) such that πα(D) = 1_A.

        5. Let A and B be as in exercise 4. Define a higher derivation of infinite rank of A into B to be an infinite sequence of homomorphisms D = (D₀ = l, D₁, D₂,…) of A into B such that (113) holds. Obtain a connection between higher derivations of A into B and homomorphisms of A into B[[x]], the algebra of formal power series in x with coefficients in B.

8.17   GALOIS THEORY FOR PURELY INSEPARABLE EXTENSIONS OF EXPONENT ONE

Let E/F be of characteristic p ≠ 0 and let D be a derivation of E/F. If a ∈ E, then D(a^p) = pa^{p – 1} D(a) = 0. Hence every element of F(E^P) is a constant relative to every derivation of E/F. If c ∈ F(E^p) and a ∈ E, then D(ca) = cD(a) for D ∈ Der_fE. It is natural to replace F by F(E^P) in studying the derivations of E/F. We shall now do this, so with a change of notation, we may assume that E^p ⊂ F, which means that either E = F or E is purely inseparable of exponent one over F (see exercise 8, p. 495). We restrict our attention also to finitely generated extensions E = F(a₁…, a_n).

Let {a₁ …,a_m} be a minimal set of generators for E/F, so m = 0 if and only if E = F. Suppose that m > 0. Then a₁ ∉ F and a_i ∉ F(a_u…,a_{i – 1}) for 1 < i ≤ m. Since a_i^p ∈ F for all i, the minimum polynomial of a_i over F and of a_i over F(a₁…,a_i–1) for i > 1 has the form x^p — b. Hence [F(a₁):F] = p and [F(a₁…, ai): F(a₁…, a_{t – 1}) = p, which implies that [E:E] = p^m. Evidently E = F[a_i,…,a_m] and since a_t^p ∈ F for all i and [E:F]= p^m, the set of monomials

constitutes a base for E/F. It is clear also that E/F is a tensor product of the simple extensions F(a_i)/F.

Put F_i = F(a₁…, â_i,…, a_m). Then E = F_i(a_i) and the minimum polynomial of a_i over F_i has the form x^p – bi, b_i ∈ F. By Proposition 8.17.3 we have a derivation D_i of E/F_t such that D_i(a_i) = 1. Thus we have D_i(a_j) = δ_ij. It follows immediately that the D_i 1 ≤ i ≤ ra, form a base for Der_FE as vector space over E and hence [Der_FE:E] = m. Since [E:F] = p^m, this implies that [Der _FE:F] = mp^m.

We now consider any field E of characteristic p, and derivations of E into itself without reference to a particular subfield of E. These are the endomorphisms D of the group (E, + ,0) that satisfy the condition D(ab) = D(a)b + aD(b). One deduces from this that D(ca) = cD(a) if c is in the prime field P, so D can be regarded as a derivation of E/P. However, we shall simply say that D is a derivation of E into itself. Let Der E denote the set of these maps. Then Der E is a set of endomorphisms of the additive group (E, + ,0) having the following closure properties: (1) Der E is a subspace of End (E, +, 0) regarded as a vector space over E by defining bL for b ∈ E, E ∈ End(E, +, 0) by (bL)(a) = b(L(a)), (2) if D₁, D₂ ∈ Der E, then [D₁, D₂] ∈ Der E, and (3) if D ∈ Der E, then D^pe Der E. We shall now call any subset of End (E, + ,0) having these closure properties a p-E-Lie algebra of endomorphisms of (E, +, 0). We use this terminology for want of anything better, but we should call attention to the fact that a p-F-Lie algebra need not be a Lie algebra over E in the usual sense, since the composition [D₁, D₂] is not F-bilinear.

If F is a subfield of E such that [E: F] < ∞ and E is purely inseparable of exponent ≤ 1 over F, then Der_FE is a p-E-Lie algebra of endomorphisms of (F, + ,0). Moreover, we have seen that [Der_FF:F] < ∞. We shall now show that every p-E-Lie algebra of derivations of E having finite dimensionality over F is obtained in this way. For, we have

THEOREM 8.45 (Jacobson).   Let E be a field of characteristic p ≠ 0, F a subfield such that (1) [F:F] < ∞ and (2) F is purely inseparable of exponent ≤ 1 over E. Then Der_FE is a p-E-Lie algebra of endomorphisms of (F, + ,0) such that p[Der_FE:E] Conversely, let be a p-E-Lie algebra of derivations of E such that [ :E] ∞ and let F be the set of -constants of E, that is, the elements that are D-constants for every D ∈ F. Then [E:F] < ∞ and E is purely inseparable of exponent ≤ 1 over F. Moreover, = Der_FF and if (Di,…, D_m) is a base for over E, then the set of monomials

form a base for End_FE regarded as a vector space over E.

Proof. The first statement has already been proved. To prove the second, we use the same idea we used to establish the results on finite groups of automorphisms in fields: We use the given set of endomorphisms to define a set of endomorphisms L satisfying the conditions in the Jacobson-Bourbaki correspondence. In the present case we take L to be the set of F-linear combinations of the endomorphisms given in (116). Evidently L contains 1 = D₁⁰ … D_m⁰, so L contains E_E = F₁ and [L:F] ≤p^m. It remains to show that L is closed under multiplication by the D_i. We note first that if D is a derivation in F, then the condition D(ab) = D(a)b + aD(b) gives the operator condition

where a_E and D(a)_E denote the multiplications by a and D(a) respectively. Using this relation we see that Di(aD₁^kl … D_m^km) = aD_iD^k₁ … D_m^km + D_i(a)Di^k1 … Dm^m. Hence to prove that D_iL⊂ I, it suffices to show that D_iD₁^k1 ”D_m^m∈L for all i and all k_j such that 0 < kj p. We shall prove this by showing that D_iD^1k₁ 'D_m^km is a linear combination with coefficients in E of the monomials D_i^k” D_m ^m such that 0 ≤ k_j < p and ∑ k_j < k_j+1. The argument for this is very similar to one we used in the study of Clifford algebras (p. 230): We use induction on ∑k_j ∑k_j and for a given k_j induction on i. We have at our disposal the formulas

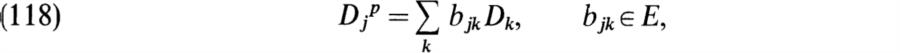
and

that follow from the conditions that is closed under pth powers and under commutators. The result we want to prove is clear if ∑ k_j = 0, so we may suppose that ∑ k_j > 0. Then some k ≠ 0 and we suppose that k_j is the first of the k’s that is > 0. Then D_i^k₁ … D_m^km = D^kj … D_m^km. If i < j, then … D_m^km is one of the monomials (116) for which the sum of the exponents is ∑ _lk_{l + 1}. Hence the result holds in this case. The same thing is true if i = j and k_j < p— 1. Now let i=j, k_j = p– 1. Then D_iD^kj ”D_m^k_m = D_fD_j+^kj^+l ” D_m^k_m and the result follows by induction if we replace D_j^p by ∑ b_jkD_k. Now assume that i > j. Then by (119),

The result follows in this case also by applying both induction hypotheses to the right-hand side. This establishes the key result that L is closed under multiplication. Hence the Jacobson-Bourbaki correspondence is applicable to L, and this shows that if F = {a|a_EB = Ba_E for B ∈ L}, then F is a subfield such that [E:F] = [L:E] and L – End_FE. By definition of L we have [L: E] < p^m and equality holds here if and only if the monomials (116) form a base for L over E. Since ) generates L, the conditions defining F can be replaced by a_ED = Da_E for all D ∈. By (117) this is equivalent to: a is a D-constant for every . Hence F is the set of -constants and ⊂ a Der_FE. Then E is purely inseparable of exponent ≅1 over F. We have [F:F] — [F:F] ≤ p^m, so [E:F] = p^m with m ≤ m. On the other hand, ) contains m linearly independent derivations (over F), so [Der_FE: E] ≥ m and hence [E:F] ≥ p^m. It follows that ) – Der_FF, [Der_FE: F] = m, and [I:F] = [F:F] = p^m. This completes the proof.

EXERCISES

In these exercises we assume that E is purely inseparable of exponent ≤1 over F of characteristic p and that E is finitely generated over F.

        1. (Baer.) Show that there exist a derivation D of E/F such that F is the subfield of E of D-constants.

        2. Let D be a derivation of E/F such that F is the subfield of D-constants. Show that the minimum polynomial of D as a linear transformation in E/F has the form

where p^m = [E: F]. Show that (1, D,…, D^{pm – 1}) is a base for End_FE as vector space over E.

        3. (J. Barsotti, P. Cartier.) Show that if D is a derivation in a field F of characteristic p ≠ 0, then D^{p – 1}(a^{– 1} Da) = a^{– 1} D^pa – (a^{– 1}Da)^p.

        4. (M. Gerstenhaber, m. Ojanguren-M.R. Sridharan.) Let E be a field of characteristic P ≠ 0 and let V be an E subspace of Der E closed under pth powers. Show that V is a Lie subring. Note that this shows that closure under Lie products is superfluous in the statement of Theorem 8.45.

        5. (Gerstenhaber, Ojanguren-Sridharan.) Extend Theorem 8.45 to obtain a 1–1 correspondence between the set of subfields F of E such that E/F is purely inseparable of exponent 1 and the set of p-E-Lie algebras of derivations of E that are closed in the finite topology.

8.18   TENSOR PRODUCTS OF FIELDS

If E/F and K/F are fields over F what can be said about the F-algebra E _FK? In particular, is this a field or a domain? It is easy to give examples where E_FK is not a field. In fact, if E≠F then F _FE is never a field. To see this we observe that by the basic property of tensor products, we have an additive group homomorphism η of E _F E into E such that a b ab, a, b ∈ E. Also it is clear from the definitions that this is an F-algebra homomorphism. Now let a∈E,∈F. Then 1, a are F-independent in E and hence 1 1, 1 a, a 1, and a a are F-independent in F _FE. Hence 1 a – a 1 ≠ 0 but η(l a – a 1) = a – a = 0. Thus ker η is a non-zero ideal in E _FE. The existence of such an ideal implies that F _FE is not a field.

It is readily seen also that if x and y are indeterminates then F(x) _FF(y) is a domain but not a field (see below).

Another fact worth noting is that if F is algebraic over F and F _FK is a domain then this algebra is a field. This is clear if F is finite dimensional over F. For, then E _FK can be regarded as a finite dimensional algebra over K ([F _FK:K] = [F:F]) and a finite dimensional domain is necessarily a field. The general case follows from this since any a∈E _FK is contained in a subalgebra isomorphic to an algebra E_0FK where F₀/F is finitely generated, hence finite dimensional over F. If a ≠ 0 the corresponding element of E_{0 F}K is invertible. Hence a is invertible in E_FK.

We shall now proceed to a systematic study of tensor products of fields. In our discussion separability will mean separability in the general sense of Definition 8.4, pure inseparability of E/F will mean that E is algebraic over F and the subfield of E/F of separable elements over F coincides with F. We shall say that F is algebraically closed (separably algebraically closed) in E if every algebraic (separable algebraic) element of E is contained in F. We prove first

THEOREM 8.46.   Let E/F and K/F be extension fields of F.

            (1) If E/F is separable and K/F is purely inseparable, then E _FK is afield. On the other hand, if E/F ^T’s not separable, then there exists a purely inseparable extension K/F of exponent l such that E _FK contains a non-zero nilpotent element.

            (2) If E/F is separable algebraic, then E _FK has no nilpotent elements for arbitrary K/F, and E _F k is a field if F is separably algebraically closed in K.

            (3) The elements of E _F k are either invertible or nilpotent if either E/F is purely inseparable and K/F is arbitrary, or E/F is algebraic and F is separably algebraically closed in K.

Proof.   In (1) and in the first part of (3) we may assume the characteristic is p ≠ 0.

            (1) Assume E/F is separable and K/F is purely inseparable. The separability implies that if a₁…,a_m are F-independent elements of E then these elements are linearly independent over F^1/pe (contained in the algebraic closure of E) for every e = 0, 1,2,…. This implies that the elements a₁, … a_m^pe are F-independent for every e. Now let K be purely inseparable over F and let z = ∑a_i. c_i ≠ 0 in E_FK where a_t∈E, c_i ∈ K. We may assume that a_i are F-independent and we have an e such that c^pe_i ∈ F, 1 ≤ i ≤ m. Then z^pe = ∑a^pe_i c^pe_i = ∑c^pe_i a^pe_i 1 ≠ 0. Hence ∑c^pe_i a^pe_i ≠ 0 and this element of E is invertible. Thus z^pe is invertible and hence z is invertible in E_FK. Then E _FK is a field.

   Next assume F/F is not separable. Then there are F-independent elements a₁,…,a_m ∈ E that are not F^1/p independent. Hence we have c_i^1/p, c_t ∈ F not all 0 such that ∑^ci^ci ⁼ 0. Then = 0 but ∑c₁a_E ≠ 0 since not every c_t = 0. Consider the field K = F(c^1/p₁a_i = 0,…, c_m^1/p). We have k F since K = F implies the a_i are F-dependent. Now consider the element z = ∑a_i c_i^1/p∈E _FK. This is non-zero since the a_i are F-independent and not every c_j^1/p = 0 in K. On the other hand, z^p = ∑a_i^pc_i = ∑c_ia_i^p 1 = 0. Hence z is a non-zero nilpotent in E _FK.

            (2) Assume E/F is separable algebraic, K/F is arbitrary. We have to show that E _FK has no non-zero nilpotents and that E _FK is a field if F is separably algebraically closed in K. Using the argument at the beginning of this section, we obtain a reduction to the case in which E is finitely generated, hence [E : F] < ∞. In this case since E is separable algebraic, E = F[a] = F(a) where the minimum polynomial M(λ) of a over F is irreducible and separable (meaning, E.g., that (m(λ),m'(λ)) = 1). Then E _FK ≅ K[a] where the minimum polynomial of a over K is m(λ). Hence E _FK ≅ K[λ]/(m(λ)). Since M(λ) is separable, we have the factorization in K[λ] of m(λ) as m(λ) = m₁(λ)…m_r(λ) where the m ≅ λ) are distinct irreducible monic polynomials. Then E _FK ≅ K[λ]/(m(λ)) ≅ ⊕^r₁ K[λ]/(m_i(λ)) (exercise 4, p. 410 of BAI). Since K_i[λ]/(m_i(λ)) is a field we see that E _FK is a direct sum of fields. Clearly an algebra having this structure has no non-zero nilpotent elements. This proves the first assertion of (2).

   The coefficients of the m_i(λ) are separable algebraic over F since they are elementary symmetric polynomials in some of the roots of m(λ) and these are separable algebraic over F. Hence if F is separably algebraically closed in K then m_i(λ) ∈ F[λ]. Then r = 1 and E _FK ≅ K[λ]/(m(λ)) is a field.

            (3) Let E/F be purely inseparable, K/F arbitrary. Let z = ∑₁^ma_i c_i, a_i ∈ C_i ∈ K. We can choose e so that a_i^e ∈ F, 1 ≤ i ≤ m. Then z^pe = ∑a_i^pe c_i^pe = 1 ∑₁^m a_i^pe c_i^pe ∈ 1 K. If z^pe ≅ 0 then z^pe and hence z is invertible. Otherwise, z is nilpotent.

   Next let E/F be algebraic and K/F separably algebraically closed. Let S be the subfield of E/F of separable elements. Then E/S is purely inseparable. Now E _FK ≅ E _s(S _FK) (Exercise 13 (iv), p. 148). Since S/F is separable algebraic and K/F is separable algebraically closed, S _F K is a field by (2). Since E/S is purely inseparable it follows from the first part of this proof that the elements of E _s(S _FK) are either nilpotent or units. Hence this holds for E _FK.

We consider next tensor products of fields in which one of the factors is purely transcendental.

THEOREM 8.47.   Let E/F be purely transcendental, say, E = F(B) where B is a transcendency base and let K/F be arbitrary. Then E _FK is a domain and its field offractions Q is purely transcendental over k = 1 _FK with B = B 1 as transcendency base. Moreover, if F is algebraically closed (separably algebraically closed) in k then E = F(B) is algebraically closed (separably algebraically closed) in Q = K(B).

Proof.   For simplicity of notation we identify E and K with the corresponding subfields E 1 and 1 K of E_FK. These are linearly disjoint over F in A = E _FK. A consequence of this is that if a subset S of E is algebraically independent over F then it is algebraically independent in A over K. It suffices to see this for S = {s₁,…, s_m} In this case algebraic independence over F is equivalent to the condition that the monomials s₁^k1…s^kmm, k_t ≥ 0 are distinct and linearly independent over F. Since this carries over on replacing F by K it follows that S is algebraically independent over K. In particular, this holds for the transcendency base B of E. Consider the subalgebra K[B] If C is a finite subset of B then K[C] is a domain (Theorem 2.13 of BAI, p. 128). It follows thatηK[B] is a domain and this is a subalgebra of A = F(B)_fK. Let z ∈ A. Then z = ∑a_ic_i, a_i ∈ F(B), c_i ∈ K. We can write a_i = p_iq^{– 1} where p_i, q ∈ F[B]. Then z = pq^{– 1} where p = ∑p_ic_i ∈ k[B]. Conversely, if p ∈ K[B] and q ∈ F[B] q ≠ 0, then p and q^{– 1} ∈ A so pq^{– 1} ∈ A. It follows that A is the localization K[B]_F[B]* of K[B] with respect to the multiplicative monoid F[B]* of non-zero elements of F[B]. Since K[B] is a domain, its localization K[B]_F[B]* is a domain. Moreover, this is a subalgebra of the localization K[B]_F[B]* which is the field of fractions Q of K[B] and of A. Evidently Q = K(B) the subfield of Q/K generated by B. Since B is algebraically independent over K we see that Q is purely transcendental over K with transcendency base B. This proves the first assertion of the theorem.

To prove the second assertion we shall show that if K(B) contains an element that is algebraic (separable algebraic) over F(B) not contained in F(B) then K contains an element that is algebraic (separable algebraic) over F not contained in F. Clearly, if such an element exists it exists in K(C) for some finite subset C of B. Hence it suffices to prove the result for finite B and then by induction, it is enough to prove the result for K(x), x an indeterminate. Hence suppose z ∈ K(x) is algebraic over F(x) and z ∉ F(x). Let λⁿ + b₁λ^{n – 1} + & + b_n be the minimum polynomial of z over F(x) so n > 1. Write b_i = p_iq ^{– 1}, p_i q ∈ F[x]. Then w = qz has minimum polynomial λⁿ + P₁λ^{n – 1} + qp₂λ^{n – 2} + … + q^{n – 1}P_n. Replacing z by qz we may assume the Now write z = rs^{– 1} where r, s ∈ k[x] are relatively prime. Then we have

If deg s > 0 then s has a prime factor in K[x]. By (120) this is also a factor of rⁿ, hence of r, contrary to the relative primeness of r and s. Thus s is a unit so we may assume z ∈ K[x] so z = z(x) = c₀ + c₁x+ … + c_mx^m, c_i ∈ K. We claim that the c_i are algebraic over F. We have the relation z(x)ⁿ + b₁z(x)^{n – 1} + … + b_n = 0 where b_i = b_i(x) ∈ F[x]. Hence for every a ∈ F we have

Since b_i(a) ∈ F this shows that the element z(a) of K is algebraic over F. If F is infinite we choose m + 1 distinct elements a₁, a₂,…, a_{m + 1} in F and write

Since the a_j are distinct the Vandermonde determinant det (a^j_k) ≠ 0. Hence we can solve (122) for the c’s by Cramer’s rule to show that every c_k is a rational expression with integer coefficients in the a_i and the z(a_j). Since the a_i and z(a_j) are algebraic over F it follows that every c_k is algebraic over F. If F is finite we replace F by its algebraic closure F which is infinite. Then the argument shows that every c_k is algebraic over F and since is algebraic over F it follows again that the c_k are algebraic over F. Since z ∉ F(x), some c_k∉F and hence we have an element of K that is algebraic over F and is not contained in F.

Finally, we suppose that z is separable algebraic over F. Then F(c₀,…,c_m) contains an element not in F that is separable algebraic over F. Otherwise, this field is purely inseparable over F and hence there exists a p^f, p the characteristic such that c_k^pf ∈ F, 0 ≤ k ≤ m. Then z^pf = c₀^pf + c₁^pf x^pj+ … c_m^pf x^mpf ∈ F(x) contrary to the separability of z over F. Thus if K(x) contains an element that is separable algebraic over F(x) and is not in F(x) then K contains an element separable algebraic over F not in F.

In our next result we weaken the hypothesis that E/F is purely transcendental to separability. Then we have the following

THEOREM 8.48.   Let E/F be separable, K/F arbitrary. Then E _FK has no non-zero nilpotent elements.

Proof.   It is clear that it suffices to prove the theorem in the case in which E/F is finitely generated. In this case E has a transcendency base B over F such that E is separable algebraic over F(B) (Theorem 8.39). Then E _FK ≅ E _F(B)(F(B) _FK). By the last result F(B) _FK is a domain. If Q is its field of fractions then E _F(B)(F(B) _FK) is a subalgebra of E _F(B)Q. Since E is separable algebraic over F(B), E _F(B)Q has no nilpotent elements ≠ 0, by Theorem 8.46 (2). Hence E _F(B)(F(B) _FK) has no non-zero nilpotent elements and this is true also of E _FK.

Next we consider the situation in which F is separably algebraically closed in one of the factors.

THEOREM 8.49.   Let F be separably algebraically closed in E and let K/F be arbitrary. Then every zero divisor of E _FK is nilpotent.

Proof.   Let B be a transcendency base for K/F. Then E _FK≅ (E _FF(B)) _F(B)K. By the last result E _FF(B) is a domain and F(B) is separably algebraically closed in the field of fractions Q of E _F F(B). Since F(B) is separably algebraically closed in Q and K is algebraic over F(B), it follows from Theorem 8.46 (3) that the elements of Q _F(B)K are either invertible or nilpotent. Now let ze(E _FF(B)) _F(B) K be a zero divisor in this algebra. Then z is a zero divisor in the larger algebra Q _F(B) K. Hence z is not invertible in Q _F{B)K SO Z is nilpotent. Since E _FK ≅(E _FF(B)) _F(B)K it follows that every zero divisor of E _FK is nilpotent.

We can now prove our main result on the question as to when the tensor product of two fields is a domain.

THEOREM 8.50.   Let E/F and K/F be extension fields of F. Assume (1) either E/F or K/F is separable and (2) F is separably algebraically closed in either E or K. Then E _F k is a domain.

Proof.   By the last result if one of the factors has the property that F is separably algebraically closed in it then the zero divisors of E _F K are nilpotent. On the other hand, by Theorem 8.48, if one of the factors is separable then E _F K has no non-zero nilpotent elements. Hence E _F K has no zero divisor ≅ 0.

A class of extension fields that is important in algebraic geometry (see Weil’s Foundations of Algebraic Geometry, American Mathematical Society Colloquium Publication v. XXIX, 1946 and 1960) is given in the following

DEFINITION 8.6.   An extension field E/F is called regular if (1) E is separable over F and (2) F is algebraically closed in E.

We remark that a separable extension field E/F contains no purely inseparable subfield. Hence we can replace condition (2) in the definition of regularity by: (2') F is separably algebraically closed in E. The sufficiency part of the following theorem is a special case of Theorem 8.50.

THEOREM 8.51. An extension field E/F is regular if and only if E _F k is a domain for every field K/F.

Proof.   It remains to prove the necessity of the two conditions. The necessity of separability follows from Theorem 8.46 (1). Now suppose F is not algebraically closed in E. Then E contains a finite dimensional subfield K F. Then E _F k contains K _F K that is not a field. Since K K is finite dimensional it is not a domain. Hence we have the necessity of condition (2).

One readily sees that if F is algebraically closed then any extension field E/F is regular. Then E _FK is a domain for any K/F.

In the situation in which E _F K is a domain for the extension fields E/F and K/F we shall denote the field of fractions of E _F K by E · K (or E·_FK).

EXERCISES

        1. Show that if E/F is purely transcendental then E/F is regular.

        2. Show that if E₁/F and E₂/F are regular then E₁ · E₂ is regular.

8.19   FREE COMPOSITES OF FIELDS

Given two extension fields E/F and K/F, a natural question to ask is: What are the possible fields over F that can be generated by subfields isomorphic to E/F and K/F, respectively? To make this precise we define the composite of E/F and K/F as a triple (Γ, s, t) where Γ is a field over F and s and t are monomorphisms of E/F and K/F, respectively, into Γ/F such that Γ/F is generated by the subfields s(E) and t(K), that is, Γ = F(s(E), t(K)). The composites (Γ, s, t) and (Γ', s', t') of E/F and K/F are said to be equivalent if there exists an isomorphism u: Γ → Γ′ such that the following two diagrams are commutative:

Of particular interest for algebraic geometry are the composites that are free in the sense of the following

DEFINITION 8.7.   Afield composite (Γ, s, t) of E/F and K/F is called free if for any algebraically independent subsets C and D of E/F and K/F, respectively, s(C) ∪ t(D) = ∅ and s(C) t(D) is algebraically independent in Γ/F.

Since any algebraically independent subset can be imbedded in a transcendency base, it is clear that the condition that (Γ, s, t) is free is equivalent to the following: for every pair of transcendency bases B and B' of E/F and K/F respectively, s(B) ∩ t(B') = ∅ and s(B) ∪ t(B') is algebraically independent. We now observe that the word “every” can be replaced by “some” in this condition; for, we have

LEMMA 1.   A composite (Γ, s, t) of E/F and K/F is free if and only if there exist transcendency bases B and B' of E/F and K/F respectively such that s(D) ∩ t(D') = ∅ and s(C) ∪ t(D') is algebraically independent in Γ/F.

Proof. The necessity of the condition is clear. To prove sufficiency, suppose we have transcendency bases B and B' for E/F and K/F such that s(B) t(B') = ∅ and s(B) ∪ t(B') is algebraically independent over F. To prove freeness of (Γ, s, t), it obviously suffices to show that if B₁ is another transcendency base for E/F, then s(B₁) ∪ t(B') = ∅ and s(C) ∪ t(C) is algebraically independent over F. Hence it suffices to show that if C is a finite algebraically independent subset of E/F and D is a finite subset of B', then s(C) t(D) = ∅ and s(C) ∪ t(D) is algebraically independent over F. Now there exists a finite subset G of B such that C is algebraically dependent over F on G. Obviously s(G) t(D) = ∅ and s(G) ∪ t(D) is a transcendency base for F(s(G), s(C), t(D))/F, so tr deg F(s(G), s(C), t(D))/F = |G| + |D|. We also have tr deg F(s(G),s(C))/F = tr degF(s(G))/F = |G| and tr deg F(s(C))/F = |C|. It follows that tr deg F(s(G), s(C), t(D))/F(s(C), t(D)) ≤ |G| – |C| (see exercise 1, p. 517). From this and the above formula for tr degF(s(G),s(C),t(D))/F, we know that

Hence s(C) t(D) = ∅ and s(C) ∪ t(D) is algebraically independent over F. Hence (Γ, s, t) is free.

We note also that if B and B' are transcendency bases for E/F and K/F satisfying the conditions of the lemma then s(B) ∪ t(B') is a transcendency base for Γ/F. This is clear since the elements of s(E) and t(K) are algebraic over F(s(B), t(B')) and since Γ is generated by s(E) and t(K), it follows that Γ is algebraic over F(s(B), t(B')). Hence s(B) ∪ t(B') is a transcendency base for Γ/F.

We can use these results to construct a free composite for any two given fields E/F, K/F. Let B and B' be transcendency bases for E/F and K/F. Suppose first that B and B' are finite, say, B = {ξ₁…,ξ_m}, B' = {ξ₁, …, ξ_m}. Let Ω be the algebraic closure of the field F(x₁,…, x_{m + n}) where the x_i are indeterminates. We have monomorphisms s' and t' of F(ξ₁…, ξ_m)/F and F(ξ₁,…, ξ_n/F, respectively, into Ω such that s'ξ_i = x_i 1 ≤ i ≤ m, and t'ξ_j = x_{m + j}, 1 ≤ j ≤ n. Since E is algebraic over F(B) and Ω is algebraically closed, s' can be extended to a monomorphism s of E/F into Ω/F (Exercise 1, p. 475). Similarly, t' can be extended to a monomorphism t of K/F into Ω. Then it is readily seen that if Γ = F(sE, tK) then (Γ, s, t) is a free composite of E and K.

If either B or B' is infinite we modify the procedure used for B and B' finite as follows. We may assume |B'| ≥ |B|. Then let X be a set disjoint from B and B' such that |X| = |B'|. We can decompose X as a disjoint union of two sets Y and Z such that |Y| = |B|, |Z| = |X| = |B'|. Let F(X) be the field of fractions of the polynomial algebra F[x]. Let Ω be the algebraic closure of F(X). Then, as before, we can define a monomorphism s of E/F into Ω/F whose restriction to B is a bijective map of B onto Y and a monomorphism t of K/F into Ω/F whose restriction to B' is a bijective map of B' onto Z. Then (Γ, s, t) for Γ = F(sE, tK) is a free composite of E and K.

We wish to give a survey of the isomorphism classes of the free composites of two given fields E/F and K/F. First, we consider the composites of E and K that need not be free. We form E _F K and let P be a prime ideal in this F-algebra. Then (E _F K)/P is a domain whose field of fractions we denote as Γ_P. We have the homomorphism s_p:a a + P (a = a 1) of E/F into (E _F K)/P and hence into Γ_P/F. Since E is a field this is a monomorphism. Similarly, we have the monomorphism t_P:b b + P of K/F into Γ_P/F. Since E _FK is generated by E and K, (E _F K)/P is generated by its subalgebras s_P(E), t_P(K), and hence Γ_P is generated as a field by S_P(E), t_P(K). Thus (Γ_P, s_P, t_P) is a composite of E/F and K/F.

We note next that distinct prime ideals P and P' of E _F k define inequivalent composites (Γ_P, s_P, t_P) and (Γ_p', s_P', t_P' ). If these are equivalent then we have an isomorphism u of Γ_P onto Γ_p, such that s_p = us_p and t_p. = ut_p. Then u(a + P) = us_pa = S_p'a = a + P' for a ∈ E and u(b + P) = b + P' for b ∈ K. Then u(∑ ^a_ib_i + P) = ∑ ^a_ib_i + P = ^ai^e b_i ∈ K. If ∑ ^a_ib_i + P = 0 so ∑ a_ib_i + p' = 0 and ∑a_ib_i ∈ p'. Thus P ⊂ P' and by symmetry P' a p. Hence P = P' contrary to our hypothesis.

Now let (Γ, s, t) be any composite of E/F and K/F. The homomorphisms s and t give rise to the homomorphism s t of E _F K into Γ which maps ∑a_ib_i a_i ∈ E, b_i ∈ K, into ∑ s(a_i)t(b_i) of Γ. Since the image is a domain the Kernel is a prime ideal P. Hence we have the isomorphism u of (E _FK)/P onto the subalgebra s(E)t(K), which can be extended to an isomorphism u of the field of fractions Γ_P of (E _F K)/P onto Γ = F(s(E),t(E)). It is clear that u is an equivalence of composites. We have therefore established a 1 – 1 correspondence between the set of prime ideals of E _F K and the set of equivalence classes of composites of E/F and K/F.

It remains to sort out the composites (Γ_P, s_P, t_P) that are free. For this we shall prove

THEOREM 8.52.   The composite (T_P, s_P, t_P) is free if and only if every element of P is a zero divisor in E _FK.

We shall identify E and K with their images in E _F K so we regard E and K as subfields of E _F K with the property that if S and S' are linearly independent subsets of E/F and K/F respectively then the map (s,s') ss' is a bijection of S × S' with SS', and SS' is a linearly independent subset of E _F K.

Let B and B' be transcendency bases for E/F and K/F, respectively, and let m and M' be the submonoids of the multiplicative monoids of E and K generated by B and B'. Since B and B' are algebraically independent, M and M' are linearly independent in E/F and K/F and hence MM' is linearly independent in E _F K. Now the subspace FMM' spanned by MM' is the subalgebra F[B ∪ E'] and also the subalgebra F[B]F[B']. Thus MM' is a base for F[B ∪ B'] = F[B]F[B']. Since B ∪ B' is algebraically independent, F[B ∪ B'] is a domain. The field of fractions F(B ∪ B') of this domain contains the subfields F(B) and F(B') and it is readily seen that the subalgebra F(B)F(B') generated by F(B) and F(B') is the set of fractions a(cc') ^{– 1} where a ∈ F[B] F[B'] = F[B]F[B'], c ∈ F[B] and c' ∈ F[B'].

We can now state

LEMMA 2.   The composite (Γ_p, s_p, t_p) is free if and only if F(B)F(B') P = 0.

Proof.   By Lemma 1, (Γ_P, s_P, t_P) is free if and only if s_p(B) ∩ t_p(B') = ∅ and s_P(B) ∪ t_P(B') is algebraically independent over F. Since s_P(B) = {b + P|b ∈ B} and t_P(B') = {b' + P|b' ∈ B'} these conditions hold if and only if the cosets q + P, q ∈ MM', are linearly independent, where m and M' are as above. Hence (Γ_P,s_P, t_P) is free if and only if FMM' ∩ P = 0. Since FMM' = F[B]F[B'] this condition is F[B]F[B'] ∩ P = 0. Since F(B)F(B') = {a(cc') ^{– 1}|a ∈ F[B]F[B'], c ∈ F[B],c' ∈ F[B']}, F[B]F[B'] ∩ P = 0 ⇔ F(B)F(B') ∩ P = 0. Hence {Γ_P, s_P, t_P) is free if and only if F(B)F(B') ∩ P = 0.

We require also

LEMMA 3.   E _F k is integral over F(B)F(B').

Proof.   Since B is a transcendency base for E, E is algebraic, hence, integral over F(B). À fortiori E is integral over F(B)F(B'). Similarly, K is integral over F(B)F(B'). Since the subset of E _F K of elements integral over F(B)F(B') is a subalgebra, it follows that E _F K = EK is integral over F(B)F(B').

We can now give the

Proof of Theorem 8.52. Suppose first that every element of P is a zero divisor in E _FK. Let a ∈ P F(B)F(B'). Then a is a zero divisor in E _FK. We claim that a is a zero divisor in F(B)F(B'). To see this let {c_α} and {dβ} be bases for E/F(B) and K/F(B') respectively, and let {m_γ} and {n_δ} be bases for F(B)/F and F(B')/F respectively. Then {c_αm_γ} is a base for E/F and {d_βn_γ} is a base for K/F. Hence {c_αd_βm_γn_δ} is a base for E _F K over F. Then every element of E _F k can be uniquely written as a finite sum ∑ q_αβC_αdβ where q_αβ ∈ F(B)F(B').

Now we have an element ∑q_αβc_αd_β ≠ 0 such that ∑q_αβc_αd_β = a(∑ q_αβc_αd_β) = 0. Since a ∈ F(B)F(B') this implies that every aq_αβ = 0 and since ∑ q_αβc_αd_β ≠ 0 some q_{αβ ≠ 0} so a is a zero divisor in F(B)F(B'). Since a ∈ F(B)F(B') and F(B)F(B') is a domain this implies that a = 0. Hence we have proved that if every element of P is a zero divisor in E _F K then P ∩ F(B)F(B') = 0 and (Γ_P, s_P, t_P) is free by Lemma 2. Conversely, assume (T_P, s_P, t_P) is free so P ∩ F(B)F(B') = 0. Let b ∈ P. Then b is integral over F(E)JF(E') and hence we have a relation bⁿ + c¹b^{n – 1} + … + E„ = 0 for C_i ∈ F(B)F(B') and we may assume n is minimal. Then we have c_n = – bⁿ – … – bc_{n – 1} ∈ P since b ∈ P. Thus c_n ∈ P ∩ F(B)F(B') and hence c_n = 0. Then b(b^{n – 1} + c_xb^{n – 2} + … + c_{n – x}) = 0 and by the minimality of n, b_{n – 1} + c₁b^{n – 2} + … + c_{n – 2} ≠ 0 so b is a zero divisor. Thus freeness of (Γ p,s_p,tp) implies that every element of P is a zero divisor in E ∩ _F K. This completes the proof.

We now consider an important special case of this theorem, namely, that in which F is separably algebraically closed in E. In this case, by Theorem 8.49, the zero divisors of E _F K are nilpotent. Since the converse holds, nilrad E _F K is the only prime ideal in E _F K that consists of zero divisors. Hence we have

THEOREM 8.53.   If K/F is arbitrary and F is separably algebraically closed in E, then in the sense of equivalence there is only one free composite of E/F and K/F.

This applies in particular if E is a regular extension of F. Then E _FK is a domain for any K so nilrad E _FK = 0. Then the free composite of E/F and K/F is E · K which was defined to be the field of fractions of E (x)_FK.

Finally, we consider a very simple case of composites that will be needed in valuation theory (see section 9.9), that in which one of the fields, say, E/F is finite dimensional. In this case all that we shall require of the foregoing discussion is the 1– 1 correspondence between the set of prime ideals P of E _F K and the equivalence classes of composites (T_P, s_P, t_P). We note also that since E _F K is finite dimensional over K this ring is artinian. Hence the results we derived in section 7.11 are applicable. Using the fact that a domain that is finite dimensional over a field is a field we see that the prime ideals of E (x) _K F are maximal. By Theorem 7.13, there are only a finite number of these. Moreover, the proof of Theorem 7.13 shows how to determine the maximal ideals. We remark also that if E is algebraic over F, E/F has a vacuous transcendency base. It follows from Definition 8.7 that the composites of E/F with any K/F are free.

We now suppose E has a primitive element, say, E = F(θ). This is always true ;if E/F is finite dimensional separable (BAI, p. 291). We have the following

THEOREM 8.54.   Let K/F be arbitrary and let E = F(θ) where θ is algebraic over F with minimum polynomial F(x) of degree n. Let f₁(x),…,f_h(x) be the monic irreducible factors of f(x) in K[x]. Then there are h inequivalent composites (Γ_i, s_i, t_i) of E/F and K/F where Γ_i = K[x]/(f_i(x)), s_i is the monomorphism of E/F into Γ_i/F such that θ x + (f_ix)) and t_i is the monomorphism b b + (f_i(x)) of K/F into Γ_i/F. Any composite of E/F and K/F is equivalent to one of these.

Proof. We have the isomorphism of E = F(θ) over F onto F[x]/(f (x)) such that θ = x + (f(x)). As we have seen before p. 546), E _F K ≅ K[x]/(f(x)). The maximal ideals of K[x]/(f(x)) have the form (f_i(x))/(f(x)) where f_i(x) is a monic irreducible factor of f(x) in K[x]. Then Γ_i = E[x]/(f_i(x)) ≅ (E(x)/(f(x)))/(f_i(x))/f(x))/( f(x)) is a field over F. We have the monomorphism s_i of E/F into Γ_i/F such that θ x + (f_i(x)) and the monomorphism t_i of K/F into Γ_i/F such that b b + (f_i(x)), b ∈ K. Clearly s_i(E) and t_i(K) generate Γ_i. Hence (Γ_i, s_i, t_i) is a composite of E/F and K/F. The rest follows from what we proved before.

EXERCISES

        1. Determine the composites over of with

            (1) (ω), ω a primitive cube root of 1

            (2) ()

        2. Determine the composites over of () and ().

        3. Suppose E/F and K/F are finite dimensional Galois and E _F K is a domain hence a field. Is (E _F K)/F Galois?

REFERENCES

E. Steinitz, Algebraische Theorie den Körpern, Journal fur die reine und angewandete Mathematik, vol. 137 (1909), pp. 167–309.

N. Jacobson, Lectures in Abstract Algebra III. The Theory of Fields and Galois Theory, 1964, New printing, Springer-Verlag, New York.

P. J. McCarthy, Algebraic Extension of Fields, Blaisdell, Waltham, Mass., 1966.

D. J. Winter, The Structure of Fields, Springer-Verlag, New York, 1974.