7
Commutative Ideal Theory:
General Theory and Noetherian Rings
The ideal theory of commutative rings was initiated in Dedekind’s successful “restoration” of unique factorization in the rings of algebraic integers of number fields by the introduction of ideals. Some of these, e.g., ![]() are not factorial, that is, do not have unique factorization of elements into irreducible elements (see BAI, pp. 141 – 142). However, Dedekind showed that in these rings unique factorization does hold for ideals as products of prime ideals (definition on p. 389). A second type of ideal theory, which was introduced at the beginning of this century by E. Lasker and F. S. Macaulay, is concerned with the study of ideals in rings of polynomials in several indeterminates. This has obvious relevance for algebraic geometry. A principal result in the Lasker-Macaulay theory is a decomposition theorem with comparatively weak uniqueness properties of ideals in polynomial rings as intersections of so-called primary ideals (definition on p. 434). In 1921 Emmy Noether gave an extremely simple derivation of these results for arbitrary commutative rings satisfying the ascending chain condition for ideals. This paper, which by its effective use of conceptual methods, gave a new direction to algebra, has been one of the most influential papers on algebra published during this century.
are not factorial, that is, do not have unique factorization of elements into irreducible elements (see BAI, pp. 141 – 142). However, Dedekind showed that in these rings unique factorization does hold for ideals as products of prime ideals (definition on p. 389). A second type of ideal theory, which was introduced at the beginning of this century by E. Lasker and F. S. Macaulay, is concerned with the study of ideals in rings of polynomials in several indeterminates. This has obvious relevance for algebraic geometry. A principal result in the Lasker-Macaulay theory is a decomposition theorem with comparatively weak uniqueness properties of ideals in polynomial rings as intersections of so-called primary ideals (definition on p. 434). In 1921 Emmy Noether gave an extremely simple derivation of these results for arbitrary commutative rings satisfying the ascending chain condition for ideals. This paper, which by its effective use of conceptual methods, gave a new direction to algebra, has been one of the most influential papers on algebra published during this century.
In this chapter we shall consider the ideal theory—once called additive ideal theory—which is an outgrowth of the Lasker-Macaulay-Noether theory. In recent years the emphasis has shifted somewhat away from the use of primary decompositions to other methods, notably, localization, the use of the prime spectrum of a ring, and the study of local rings. The main motivation has continued to come from applications to algebraic geometry. However, other developments, such as the study of algebras over commutative rings, have had their influence, and of course, the subject has moved along under its own power.
We shall consider the Dedekind ideal theory in Chapter 10 after we have developed the structure theory of fields and valuation theory, which properly precede the Dedekind theory.
Throughout this chapter (and the subsequent ones) all rings are commutative unless the contrary is explicitly stated. From time to time, mainly in the exercises, applications and extension to non-commutative rings will be indicated. The first nine sections are concerned with arbitrary commutative rings. The main topics considered here are localization, the method of reducing questions on arbitrary rings to local rings via localization with respect to the complements of prime ideals, the prime spectrum of a ring, rank of projective modules, and the projective class group. The ideal theory of noetherian rings and modules is developed in sections 7.10–7.18. Included here are the important examples of noetherian rings: polynomial rings and power series rings over noetherian rings. We give also an introduction to affine algebraic geometry including the Hilbert Nullstellensatz. Primary decompositions are treated in section 7.13. After these we consider some of the basic properties of noetherian rings, notably the Krull intersection theorem, the Hilbert function of a graded module, dimension theory, and the Krull principal ideal theorem. We conclude the chapter with a section on I-adic topologies and completions.
7.1 PRIME IDEALS. NIL RADICAL
We recall that an element p of a domain D is called a prime if p is not a unit and if p|ab in D implies p|a or p|b in D. This suggests the following
DEFINITION 7.1. An ideal P in a (commutative) ring R is called prime if P ≠ R and if ab ∈ P for a,b ∈ R implies either a ∈ P or b ∈ P.
In other words, an ideal P is prime if and only if the complementary set P′ = R – P is closed under multiplication and contains 1, that is, P′ is a submonoid of the multiplicative monoid of R. In congruence notation the second condition in Definition 7.1 is that if ab ≡ 0(mod P), then a ≡ 0(mod P) or b ≡ 0(mod P). The first condition is that the ring ![]() = R/P ≠ 0. Hence it is clear that an ideal P is prime if and only if R/P is a domain. Since an ideal M in a commutative ring R is maximal if and only if R/M is a field and since any field is a domain, it is clear that any maximal ideal of R is prime. It is clear also that an element p is prime in the usual sense if and only if the principal ideal (p)( = pR) is a prime ideal. Another thing worth noting is that if P is a prime ideal in R and A and B are ideals in R such that AB ⊂ P, then either A ⊂ P B ⊂ P. If not, then we have a ∈ A,
= R/P ≠ 0. Hence it is clear that an ideal P is prime if and only if R/P is a domain. Since an ideal M in a commutative ring R is maximal if and only if R/M is a field and since any field is a domain, it is clear that any maximal ideal of R is prime. It is clear also that an element p is prime in the usual sense if and only if the principal ideal (p)( = pR) is a prime ideal. Another thing worth noting is that if P is a prime ideal in R and A and B are ideals in R such that AB ⊂ P, then either A ⊂ P B ⊂ P. If not, then we have a ∈ A, ![]() P and b ∈ B, ∈
P and b ∈ B, ∈ ![]() P. Then ab ∈ AB ⊂ P, contrary to the primeness of P. It is clear by induction that if P is a prime ideal and a1 a2 … an ∈ P, then some ai ∈ P and if A1 A2…An ⊂ P for ideals Ai, then some Ai ⊂ P.
P. Then ab ∈ AB ⊂ P, contrary to the primeness of P. It is clear by induction that if P is a prime ideal and a1 a2 … an ∈ P, then some ai ∈ P and if A1 A2…An ⊂ P for ideals Ai, then some Ai ⊂ P.
We recall the elementary result in group theory that a group cannot be a union of two proper subgroups (exercise 14, p. 36 of BAI). This can be strengthened to the following statement: If G1, G2, and H are subgroups of a group G and H ⊂ (G1 ∪ G2), then either H ⊂ G1 or H ⊂ G2. The following result is a useful extension of this to prime ideals in a ring.
PROPOSITION 7.1. Let A, I1, …, In be ideals in a ring such that at most two of the Ij are not prime. Suppose A ⊂ ![]() n1 Ij. Then A ⊂ Ij for some j.
n1 Ij. Then A ⊂ Ij for some j.
Proof. We use induction on n. The result is clear if n = 1. Hence we assume n > 1. Then if we have A ⊂ I1 ∪ … ∪ ![]() k ∪ … ∪ In for some k, the result will follow by the induction hypothesis. We therefore assume
k ∪ … ∪ In for some k, the result will follow by the induction hypothesis. We therefore assume ![]() for k = 1, 2,…,n and we shall complete the proof by showing that this leads to a contradiction. Since
for k = 1, 2,…,n and we shall complete the proof by showing that this leads to a contradiction. Since ![]() , there exists an
, there exists an ![]() . Since A ⊂
. Since A ⊂ ![]() Ij, ak ∈ Ik. If n = 2, it is readily seen that (as in the group theory argument) a1 + a2 ∈ A but a1 + a2
Ij, ak ∈ Ik. If n = 2, it is readily seen that (as in the group theory argument) a1 + a2 ∈ A but a1 + a2 ![]() I1 ∪ I2, contrary to hypothesis. If n > 2, then at least one of the Ij is prime. We may assume it is I1. Then it is readily seen that
I1 ∪ I2, contrary to hypothesis. If n > 2, then at least one of the Ij is prime. We may assume it is I1. Then it is readily seen that
![]()
is in A but is not in ![]() Ij. Again we have a contradiction, which proves the result.
Ij. Again we have a contradiction, which proves the result. ![]()
The foregoing result is usually stated with the stronger hypothesis that every Ij is prime. The stronger form that we have proved is due to N. McCoy, who strengthened the result still further by replacing the hypothesis that A is an ideal by the condition that A is a subrng (BAI, p. 155) of the ring R. It is clear that the foregoing proof is valid in this case also. In the sequel we shall refer to Proposition 7.1 as the “prime avoidance lemma.” The terminology is justified since the contrapositive form of the proposition is that if A and I1, …, In are ideals such that A ![]() Ij for any j and at most two of the Ij are not prime, then there exists an a ∈ A such that a
Ij for any j and at most two of the Ij are not prime, then there exists an a ∈ A such that a![]()
![]() I j.
I j.
There is an important way of obtaining prime ideals from submonoids of the multiplicative monoid of R. This is based on
PROPOSITION 7.2. Let S be a submonoid of the multiplicative monoid of R and let P be an ideal in R such that (1) P ∩ S = Ø. (2) P is maximal with respect to property (1) in the sense that if P′ is any ideal such that P′ ![]() P, then P′ ∩ S ≠ Ø. Then P is prime.
P, then P′ ∩ S ≠ Ø. Then P is prime.
Proof. Let a and b be elements of R such that a ![]() P and b
P and b ![]() P. Then the ideals (a) + P and (b) + P properly contain P and so meet S. Hence we have elements p1, p2 ∈ P, x1, x2 ∈ R, s1, s2 ∈ S such that s1 = x1a + p1, s2 = x2b + p2. Then s1 s2 ∈ S and
P. Then the ideals (a) + P and (b) + P properly contain P and so meet S. Hence we have elements p1, p2 ∈ P, x1, x2 ∈ R, s1, s2 ∈ S such that s1 = x1a + p1, s2 = x2b + p2. Then s1 s2 ∈ S and
![]()
Hence if ab ∈ P, then s1s2 ∈ P, contrary to P ∩ S = Ø. Thus ab ![]() P and we have shown that a
P and we have shown that a ![]() P, b
P, b ![]() P implies ab
P implies ab ![]() P, so P is prime.
P, so P is prime. ![]()
If S is a submonoid not containing 0, then the ideal 0 satisfies 0 ∩ S = Ø. Now let A be any ideal such that A ∩ S = Ø and let ![]() be the set of ideals B of R such that B ⊃ A and B ∩ S = Ø. It is an immediate consequence of Zorn’s lemma that
be the set of ideals B of R such that B ⊃ A and B ∩ S = Ø. It is an immediate consequence of Zorn’s lemma that ![]() contains maximal elements. Such an element is an ideal P ⊃ A satisfying the hypotheses of Proposition 7.2. Hence the following result follows from this proposition.
contains maximal elements. Such an element is an ideal P ⊃ A satisfying the hypotheses of Proposition 7.2. Hence the following result follows from this proposition.
PROPOSITION 7.3. Let S be a submonoid of the multiplicative monoid of R and A an ideal in R such that S ∩ A = Ø. Then A can be imbedded in a prime ideal P such that S ∩ P = Ø.
Let N denote the set of nilpotent elements of R. Evidently if z ∈ N so zn = 0 for some n and if a is any element of R, then (az)n = anzn = 0. Hence az ∈ N. If zi ∈ N, i = 1, 2, and ni is an integer such that ![]() = 0, then by the binomial theorem for n = n1 + n2 – 1 we have (z1 + z2)n =
= 0, then by the binomial theorem for n = n1 + n2 – 1 we have (z1 + z2)n = ![]() . This is 0, since if i < n1 then n – i ≥ n2, so
. This is 0, since if i < n1 then n – i ≥ n2, so ![]() and if i ≥ n1, then clearly
and if i ≥ n1, then clearly ![]() . Thus N is an ideal. We call this ideal the nil radical of the ring R and we shall denote it as nilrad R. If
. Thus N is an ideal. We call this ideal the nil radical of the ring R and we shall denote it as nilrad R. If ![]() = z + N is in the nil radical of
= z + N is in the nil radical of ![]() = R/N, N = nilrad R, then zn ∈ N for some n and so zmn = 0 for some integer mn. Then z ∈ N and
= R/N, N = nilrad R, then zn ∈ N for some n and so zmn = 0 for some integer mn. Then z ∈ N and ![]() = 0. Thus nilrad
= 0. Thus nilrad ![]() = 0. We recall that any nil ideal of a ring is contained in the (Jacobson) radical rad R (p. 192). We recall also that rad R is the intersection of the maximal left ideals of R (p. 193), so for a commutative ring rad R is the intersection of the maximal ideals of the ring. The analogous result for the nil radical is the following
= 0. We recall that any nil ideal of a ring is contained in the (Jacobson) radical rad R (p. 192). We recall also that rad R is the intersection of the maximal left ideals of R (p. 193), so for a commutative ring rad R is the intersection of the maximal ideals of the ring. The analogous result for the nil radical is the following
THEOREM 7.1 (Krull). The nil radical of R is the intersection of the prime ideals of R.
Proof. Let N = nilrad R and let N′ = ![]() P where the intersection is taken over all of the prime ideals P of R. If z ∈ N, we have zn = 0 for some integer n. Then zn ∈ P for any prime ideal P and hence z ∈ P. Hence N ⊂ P for every prime ideal P, so N ⊂ N′. Now let s
P where the intersection is taken over all of the prime ideals P of R. If z ∈ N, we have zn = 0 for some integer n. Then zn ∈ P for any prime ideal P and hence z ∈ P. Hence N ⊂ P for every prime ideal P, so N ⊂ N′. Now let s ![]() N, so s is not nilpotent and S = {sn|n = 0, 1, 2, …} is a submonoid of the multiplicative monoid of R satisfying S ∩ {0} = Ø. Then by Proposition 7.3 applied to A = 0 there exists a prime ideal P such that P ∩ S = Ø. Then s
N, so s is not nilpotent and S = {sn|n = 0, 1, 2, …} is a submonoid of the multiplicative monoid of R satisfying S ∩ {0} = Ø. Then by Proposition 7.3 applied to A = 0 there exists a prime ideal P such that P ∩ S = Ø. Then s ![]() P and s
P and s ![]() N′. This implies that N′ ⊂ N and so N = N′ =
N′. This implies that N′ ⊂ N and so N = N′ = ![]() P.
P. ![]()
If A is an ideal in R, we define the nil radical of A, nilrad A (sometimes denoted as ![]() ), to be the set of elements of R that are nilpotent modulo A in the sense that there exists an integer n such that zn ∈ A. This is just the set of elements z such that
), to be the set of elements of R that are nilpotent modulo A in the sense that there exists an integer n such that zn ∈ A. This is just the set of elements z such that ![]() = z + A is in the nil radical of
= z + A is in the nil radical of ![]() = R/A. Thus
= R/A. Thus
![]()
where v is the canonical homomorphism of R onto ![]() . It follows from this (or it can be seen directly) that nilrad A is an ideal of R containing A. It is clear also that iteration of the process of forming the nil radical of an ideal gives nothing new : nilrad (nilrad A) = nilrad A.
. It follows from this (or it can be seen directly) that nilrad A is an ideal of R containing A. It is clear also that iteration of the process of forming the nil radical of an ideal gives nothing new : nilrad (nilrad A) = nilrad A.
We have the bijective map ![]() of the set of ideals of R containing A onto the set of ideals of
of the set of ideals of R containing A onto the set of ideals of ![]() = R/A. Moreover,
= R/A. Moreover, ![]() (BAI, p. 107). Hence B is prime in R if and only if
(BAI, p. 107). Hence B is prime in R if and only if ![]() is prime in
is prime in ![]() . Thus the set of prime ideals of
. Thus the set of prime ideals of ![]() is the set of ideals
is the set of ideals ![]() = P/A where P is a prime ideal of R containing A. Since
= P/A where P is a prime ideal of R containing A. Since ![]() (P/A) = (
(P/A) = (![]() P)/A = (BAI, p. 67, exercise 2), and
P)/A = (BAI, p. 67, exercise 2), and ![]()
![]() taken over the prime ideals of
taken over the prime ideals of ![]() is the nil radical of
is the nil radical of ![]() , we have
, we have
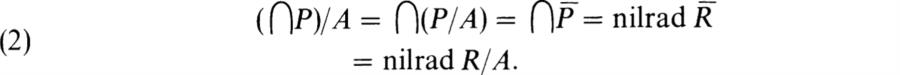
Hence nilrad A = ![]() P taken over the prime ideals P of R containing A. We state this as
P taken over the prime ideals P of R containing A. We state this as
THEOREM 7.2. The nil radical of an ideal A is the intersection of the prime ideals of R containing A.
EXERCISES
1. Let Ai, 1 ≤ i ≤ n, be ideals, P a prime ideal. Show that if P ⊃ ![]() n1 Ai then P ⊃ Ai for some i and if P =
n1 Ai then P ⊃ Ai for some i and if P = ![]() n1 Ai, then P = Ai for some i.
n1 Ai, then P = Ai for some i.
2. Show that if P is a prime ideal, then S = R – P is a submonoid of the multiplicative monoid of R, which is saturated in the sense that it contains the divisors of every s ∈ S. Show more generally that if {Px} is a set of prime ideals, then S = R – ![]() Px is a saturated submonoid of the multiplicative monoid of R. Show that conversely any saturated submonoid of the multiplicative monoid of R has the form R –
Px is a saturated submonoid of the multiplicative monoid of R. Show that conversely any saturated submonoid of the multiplicative monoid of R has the form R – ![]() Px, {Px} a set of prime ideals of R.
Px, {Px} a set of prime ideals of R.
3. Show that the set of zero divisors of R is a union of prime ideals.
4. (McCoy.) Show that the units of the polynomial ring R[x], x an indeterminate, are the polynomials a0 + a1 x + … + anxn where a0 is a unit in R and every ai, i > 0, is nilpotent. (Hint: Consider the case in which R is a domain first. Deduce the general case from this by using Krull’s theorem.)
The next two exercises are designed to prove an important result on the radical of a polynomial ring due to S. Amitsur. In these exercises R need not be commutative.
5. Let f(x) ∈ R[x] have 0 constant term and suppose f(x) is quasi-regular with quasi-inverse g(x) (p. 194). Show that the coefficients of g(x) are contained in the subring generated by the coefficients of f(x).
6. (Amitsur.) Show that R[x] is semi-primitive if R has no nil ideals ≠ 0. (Hint: Assume that rad R[x] ≠ 0 and choose an element ≠ 0 in this ideal with the minimum number of non-zero coefficients. Show that these coefficients are contained in a commutative subring B of R. Apply exercises 4 and 5.)
7.2 LOCALIZATION OF RINGS
The tool of localization that we shall now introduce is one of the most effective ones in commutative algebra. It amounts to a generalization of the familiar construction of the field of fractions of a domain (BAI, pp. 115–119). We can view this generalization from the point of view of a universal construction that is a solution of the following problem:
Given a (commutative) ring R and a subset S of R, to construct a ring Rs and a homomorphism λs of R into Rs such that every λs(s), s ∈ S, is invertible in Rs, and the pair (Rs, λs) is universal for such pairs in the sense that if η is any homomorphism of R into a ring R′ such that every η(s) is invertible, then there exists a unique homomorphism ![]() : Rs → R′ such that the diagram
: Rs → R′ such that the diagram

is commutative.
Before proceeding to the solution of the problem (which is easy), we shall make some remarks about the problem.
1. Since the product of two elements of a ring is invertible if and only if the elements are invertible, there is no loss in generality in assuming that S is a submonoid of the multiplicative monoid of R. The solution of the problem for an arbitrary set S can be reduced to the case in which S is a monoid by replacing the set S by the submonoid ![]() generated by S. For example, if S is a singleton {s}, then we can replace it by
generated by S. For example, if S is a singleton {s}, then we can replace it by ![]() = {sn|n = 0, 1, 2, …}.
= {sn|n = 0, 1, 2, …}.
2. The special case of the field of fractions is that in which R is a domain and S = R*, the submonoid of non-zero elements of R. In this case nothing is changed if we restrict the rings R′ in the statement of the problem to be fields. This is clear since the image under a homomorphism of a field either is the trivial ring consisting of one element or is a field.
3. Since a zero divisor of a ring ( ≠ {0}) is not invertible, we cannot expect λs to be injective if S contains zero divisors.
4. If the elements of S are invertible in R, then there is nothing to do: We can simply take RS = R and λS = 1R, the identity map on R. Then it is clear that ![]() = η satisfies the condition in the problem.
= η satisfies the condition in the problem.
5. If a solution exists, it is unique in the strong sense that if (RS(1), λS(1)) and (RS(2), λS(2)) satisfy the condition for the ring R and subset S, then there exists a unique isomorphism ζ : RS(1) → RS(2) such that

is commutative (see p. 44).
We now proceed to a construction of a pair (Rs, λs) for any ring R and submonoid S of its multiplicative monoid. As in the special case of a domain R and its monoid S = R* of non-zero elements, we commence with the product set R × S of pairs (a, s), a ∈ R, s ∈ S. Since the monoid S may contain zero divisors, it is necessary to modify somewhat the definition of equivalence among the pairs (a, s) that we used in the construction of the field of fractions of a domain. We define a binary relation ~ on R × S by declaring that (a1, s1) ~ (a2, s2) if there exists an s ∈ S such that
![]()
(or ss2a1 = ss1a2). If R is a domain and S does not contain 0, then (4) can be replaced by the simpler condition s2a1 = s1a2. In the general case it is readily verified that ~ is an equivalence relation. We denote the quotient set defined by this equivalence relation as RS and we denote the equivalence class of (a, s) by a/s.
We define addition and multiplication in the set RS by
![]()
and
![]()
It is a bit tedious but straightforward to check that these compositions are well-defined and that if we put 0 = 0/1 ( = 0/s for any s ∈ S) and 1 = 1/1 ( = s/s, s ∈ S), then (RS, + , ·, 0, 1) is a ring. We leave the verifications to the reader.
We now define a map λS (or λSR) of R into RS by
![]()
It is clear from (5) and (6) and the definition of 1 in RS that λS is a homomorphism of R into RS. Moreover, if s ∈ S, then λS(S) = s/1 has the inverse 1/s since (s/1) (1/s) = s/s = 1. Now let η be a homomorphism of R into R′ such that η(s) is invertible for every s ∈ S. It is readily verified that
![]()
is well-defined and this is a homomorphism of RS into R′. Moreover, ![]() λS(a) =
λS(a) = ![]() (a/l = η(a). Thus we have the commutativity of (3). The uniqueness of
(a/l = η(a). Thus we have the commutativity of (3). The uniqueness of ![]() is clear also since a/s = (a/1) (1/s) = (a/1) (s/l)– 1 and hence any
is clear also since a/s = (a/1) (1/s) = (a/1) (s/l)– 1 and hence any ![]() satisfying the commutativity condition satisfies
satisfying the commutativity condition satisfies ![]() (a/s) =
(a/s) = ![]() (λs(a)λs(s)–1) = η(a)η(s) – 1. Thus
(λs(a)λs(s)–1) = η(a)η(s) – 1. Thus ![]() is the map we defined in (8) and (Rs, λs) is a solution of the problem we formulated at the outset. We shall call (Rs, λs) (or simply Rs) the localization of R at S.
is the map we defined in (8) and (Rs, λs) is a solution of the problem we formulated at the outset. We shall call (Rs, λs) (or simply Rs) the localization of R at S.
We shall now study relations between Rs and Rs′ for S′, a submonoid of the monoid S. Note first that λs(s′) is invertible in Rs, s′ ∈ S′. Hence we have a unique homomorphism ζS′, S : Rs′ → Rs such that λs = ζs′, s λs′. Now suppose that λs′(s) is invertible in Rs′ , s ∈ S. Then we also have a unique homomorphism ζs, s′ : Rs → Rs′ such that λs′. = ζs, s′ λs. It follows that ζS, S′ ζS′, S = 1Rs, and ζS′,SζS, S′ = lRs. Hence ζS′, S and ζS, S′ are isomorphisms. We shall now show that in general if S′ ⊂ S, then Rs is, in fact, a localization of Rs′. We state the result in a somewhat imprecise manner as follows.
PROPOSITION 7.4. Let S′ be a submonoid of S and let S/S′ = {s/s′|s ∈ S, s′ ∈ S′}. Then S/S′ is a submonoid of the multiplicative monoid of Rs′ and we have canonical isomorphisms of Rs and (RS′)λS′(S) and of (RS′)λs′(S) and (Rs′)s/s′.
Proof. We shall obtain the first isomorphism by showing that (RS′ )λS′(S) has the universal property of Rs. First, we have the composite homomorphism λλs,(s) λs′ of R into (RS′)λs′(S) obtained from the sequence of homomorphism
![]()
Now let η be a homomorphism of R into R′ such that η(s) is invertible, s ∈ S. Since S′ ⊂ S, we have a unique homomorphism ![]() of Rs′ into R′ such that
of Rs′ into R′ such that ![]() λs′ = η. If s ∈ S, then
λs′ = η. If s ∈ S, then ![]() ′(λS′(s)) = η(s) is invertible in R′. Accordingly, by the universal property of (RS′)λs′(S) we have a unique homomorphism
′(λS′(s)) = η(s) is invertible in R′. Accordingly, by the universal property of (RS′)λs′(S) we have a unique homomorphism ![]() of (Rs′)λs′(s) into R′ such that
of (Rs′)λs′(s) into R′ such that ![]() λλs′(S) =
λλs′(S) = ![]() ′. Then
′. Then ![]() . Moreover,
. Moreover, ![]() is the only homomorphism of (RS′)λs′(s) into R′ satisfying
is the only homomorphism of (RS′)λs′(s) into R′ satisfying ![]() .For, this condition implies that
.For, this condition implies that ![]() , which implies that
, which implies that ![]() by the universality of
by the universality of ![]() . Then we obtain the uniqueness of
. Then we obtain the uniqueness of ![]() by the universality of
by the universality of ![]() . Thus
. Thus ![]() has the universal property of (RS, λS ) and so we have the required isomorphism.
has the universal property of (RS, λS ) and so we have the required isomorphism.
The isomorphism of (RS′)λS′(S) and (Rs′)s/s′ can be seen by observing that λs′(S) is a submonoid of S/S′ . Hence we have the canonical homomorphism of (RS′)λs′(s) into (RS′)S/S′. If s ∈ S, s′ ∈ S′, then s/s′ = (s/1)(s′/l)– 1 in Rs′ and ![]() and
and ![]() are invertible in (RS′)λs′(s). Hence
are invertible in (RS′)λs′(s). Hence ![]() is invertible. It follows from the result we obtained above that the canonical homomorphism of (Rs′)λs′(S) into (Rs′)s/s′ is an isomorphism.
is invertible. It follows from the result we obtained above that the canonical homomorphism of (Rs′)λs′(S) into (Rs′)s/s′ is an isomorphism. ![]()
EXERCISES
1. Let S and T be submonoids of the multiplicative monoid of R. Note that ST = {st|s ∈ S, t ∈ T} is the submonoid generated by S and T. Show that RST ≅ (Rs)λs′(T).
3. Let S be a submonoid of the multiplicative monoid of R. If a, b ∈ S, define ![]() if a|b in S. In this case there is a unique homomorphism
if a|b in S. In this case there is a unique homomorphism ![]() of
of ![]() such that
such that ![]() . Show that
. Show that ![]() (with respect to the ζ ’s).
(with respect to the ζ ’s).
7.3 LOCALIZATION OF MODULES
It is important to extend the concept of localization to R-modules. Let M be a module over R, S a submonoid of the multiplicative monoid of R. We shall construct an Rs-module Ms in a manner similar to the construction of Rs. We consider M × S the product set of pairs (x, s), x∈ M, s ∈ S, and we introduce a relation ~ in this set by (x1, s1) ~ (x2, s2) if there exists an s ∈ S such that
![]()
The same calculations as in the ring case show that ~ is an equivalence. Let Ms denote the quotient set and let x/s be the equivalence class of (x, s). We can make Ms into an Rs-module by defining addition by
![]()
and the action of Rs on Ms by
![]()
We can verify as in the ring case that (10) and (11) are well-defined, that + and 0 = 0/s constitute an abelian group, and that (11) defines a module action of Rs on Ms. We shall call the Rs-module Ms the localization of M at S or the S-localization of M.
Although we are generally interested in Ms as Rs-module, we can also regard Ms as R-module by defining the action of R by a(x/s) = (a/1) (x/s) = ax/s. Since a ![]() a/1 is a ring homomorphism, it is clear that this is a module action. We have a map λs (or λsM if it is necessary to indicate M) of M into Ms defined by x
a/1 is a ring homomorphism, it is clear that this is a module action. We have a map λs (or λsM if it is necessary to indicate M) of M into Ms defined by x ![]() x/1. This is an R-module homomorphism. The kernel of λs is the set of x ∈ M for which there exists an s ∈ S such that sx = 0, that is, if ann x denotes the annihilator ideal in R of x, then ann x ∩ S ≠ Ø. It is clear that λs need not be injective. For example, if Mis a
x/1. This is an R-module homomorphism. The kernel of λs is the set of x ∈ M for which there exists an s ∈ S such that sx = 0, that is, if ann x denotes the annihilator ideal in R of x, then ann x ∩ S ≠ Ø. It is clear that λs need not be injective. For example, if Mis a ![]() -module and S =
-module and S = ![]() – {0}, then the torsion submodule of M is mapped into 0 by λs. It is clear that if S includes 0, then Ms = 0 and ker λs = M. Another useful remark is
– {0}, then the torsion submodule of M is mapped into 0 by λs. It is clear that if S includes 0, then Ms = 0 and ker λs = M. Another useful remark is
PROPOSITION 7.5. If M is a finitely generated module, then Ms = 0 if and only if there exists an s ∈ S such that sM = 0.
Proof. If sM = 0, every x/t = 0 = 0/1 since s(lx) = s(t0) = 0. Conversely, suppose Ms = 0 and let {xl, …, xn} be a set of generators for M. Then xi/1 = 0 implies there exists an si ∈ S such that sixi = 0. Then sxi = 0 for s = ∏n1 si ; hence sx = 0 for any ∑ rixi, ri ∈ R Thus sM = 0. ![]()
Let f : M → N be a homomorphism of .R-modules of M into N. Then we have a corresponding Rs-homomorphism fs of Ms into Ns defined by
![]()
Again we leave the verifications to the reader. The maps M ![]() Ms, f
Ms, f ![]() fs define a functor, the S-localization functor, from the category of R-modules to the category of Rs-modules. We shall now show that this functor is naturally isomorphic to the functor Rs
fs define a functor, the S-localization functor, from the category of R-modules to the category of Rs-modules. We shall now show that this functor is naturally isomorphic to the functor Rs ![]() R from R-mod to Rs-mod. Thus we have
R from R-mod to Rs-mod. Thus we have
PROPOSITION 7.6. For every R-module M we can define an Rs-isomorphism ηM of Ms onto Rs![]() R M that is natural in M.
R M that is natural in M.
Proof. We show first that there is a map ηM of Ms into Rs![]() R M such that
R M such that
![]()
Suppose x1/s1 = x2/s2, which means that we have an s ∈ S such that ss2x1 = ss1x2. Then
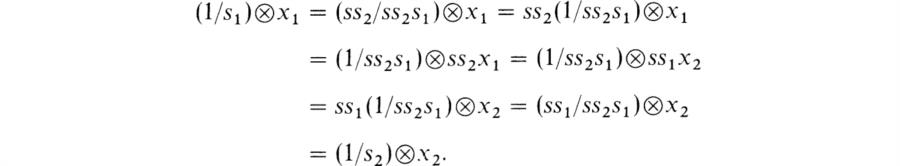
Hence (13) is well-defined. Direct verification shows that ηM is a group homomorphism. We note next that we have a well-defined map of the product set Rs × M into Ms such that
![]()
To check this we have to show that if a1/s1 = a2/s2 in Rs, then a1x/s1 = a2x/s2. Now if a1/s1 = a2/s1, then we have an s ∈ S such that sa1s2 = sa2s1. Then sa1s2x = sa2s1x, which implies the required equality a1x/s1 = a2x/s2. Direct verification shows that (14) satisfies the condition for a balanced product of the .R-modules Rs and M. Hence we have a group homomorphism η′ M of Rs![]() RM into Ms sending (a/s)
RM into Ms sending (a/s)![]() x into ax/s. Following this with ηM we obtain (1/s)
x into ax/s. Following this with ηM we obtain (1/s)![]() ax = (a/s)
ax = (a/s)![]() x. On the other hand, if we apply ηM to x/s, we obtain (l/s)
x. On the other hand, if we apply ηM to x/s, we obtain (l/s)![]() x and the application of η′M to this gives x/s. It follows ηMη′M is the identity map on Rs
x and the application of η′M to this gives x/s. It follows ηMη′M is the identity map on Rs![]() RM and η′MηM is the identity on Ms. Hence ηM is a group isomorphism and so is η′M = η– 1M. Direct verification using the definitions shows that ηM and hence is an Rs-map, hence an Rs-isomorphism. It remains to show the naturality, that is, the commutativity of
RM and η′MηM is the identity on Ms. Hence ηM is a group isomorphism and so is η′M = η– 1M. Direct verification using the definitions shows that ηM and hence is an Rs-map, hence an Rs-isomorphism. It remains to show the naturality, that is, the commutativity of
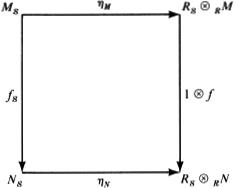
for a given R-homomorphism f : M → N. This follows from the calculation
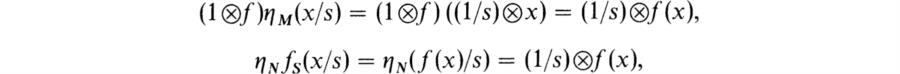
which completes the proof. ![]()
This result gives rise to a useful interplay between tensor products and localization. We recall first that the functor N![]() R is right exact, that is, exactness of
R is right exact, that is, exactness of ![]() implies that of N
implies that of N ![]() . Applying this with N = Rs in conjunction with Proposition 7.6 shows that
. Applying this with N = Rs in conjunction with Proposition 7.6 shows that ![]() is exact. Next we prove directly that if
is exact. Next we prove directly that if ![]() is exact, then
is exact, then ![]() is exact. Suppose fs(x′ /s) = 0, so f(x′)/s = 0. Then we have a t ∈ S such that tf(x′) = 0. Then f(tx′) = 0 and since f is injective, tx′ = 0 and hence x′ /s = 0. Hence ker fs = 0 and so
is exact. Suppose fs(x′ /s) = 0, so f(x′)/s = 0. Then we have a t ∈ S such that tf(x′) = 0. Then f(tx′) = 0 and since f is injective, tx′ = 0 and hence x′ /s = 0. Hence ker fs = 0 and so ![]() is exact. We can now apply Proposition 7.6 to conclude that
is exact. We can now apply Proposition 7.6 to conclude that ![]() is exact. We recall that this is the definition of flatness for Rs as R-module (p. 153). Hence we have the important
is exact. We recall that this is the definition of flatness for Rs as R-module (p. 153). Hence we have the important
PROPOSITION 7.7. Rs is a flat R-module.
We remark also that we have shown that if 0 → M′ → M → M″ → 0 is an exact sequence of R-modules, then 0 → M′s → Ms → M″s → 0 is an exact sequence of Rs-modules. Thus the S-localization functor from R-mod to Rs-mod is exact.
Now let N be a submodule of M. Then the exact sequence ![]() where l is the injection gives the exact sequence
where l is the injection gives the exact sequence ![]() and the definition shows that ls is the injection of Ns. We have the exact sequence
and the definition shows that ls is the injection of Ns. We have the exact sequence ![]() where v is the canonical homomorphism. Hence we have the exact sequence
where v is the canonical homomorphism. Hence we have the exact sequence ![]() , which shows that Ms/Ns ≅ (M/N)s. More precisely, the foregoing exactness shows that the map
, which shows that Ms/Ns ≅ (M/N)s. More precisely, the foregoing exactness shows that the map
![]()
is an isomorphism of Ms/Ns with (M/N)s.
If M and N are R-modules and f is a homomorphism f : M → N, then we have the exact sequence
![]()
where coker f = N/f (M). Hence we have the exact sequence
![]()
This implies that (ker f)S is ker fS. Also (coker f)S = (N/f(M))S ≅ NS/f(M)S = NS/fS(M) = coker fS.
We recall next that we have an RS-isomorphism of ![]() onto
onto ![]() sending
sending ![]() (exercise 13, p. 148). Hence, by Proposition 7.6, we have an Rs-isomorphism of (M
(exercise 13, p. 148). Hence, by Proposition 7.6, we have an Rs-isomorphism of (M![]() RN)s onto Ms
RN)s onto Ms![]() RsNs such that
RsNs such that
![]()
Now let M be an Rs-module. Then M becomes an R-module by defining ax for a ∈ R to be (a/l)x. It is clear that if f is a homomorphism of M as Rs-module, then f is an R-homomorphism. Now consider Ms where M is regarded as an R-module. Since s/1 is invertible in Rs for s ∈ S, sx = (s/l)x = 0 for x ∈ M implies x = 0. Hence the homomorphism λs : x ![]() x/1 of M into Ms is a monomorphism. Since x/s = (l/s)(x/l), λs is surjective. Thus we can identify M as Rs-module with the S-localization Ms of M as R-module.
x/1 of M into Ms is a monomorphism. Since x/s = (l/s)(x/l), λs is surjective. Thus we can identify M as Rs-module with the S-localization Ms of M as R-module.
7.4 LOCALIZATION AT THE COMPLEMENT OF A PRIME IDEAL.
LOCAL-GLOBAL RELATIONS
We recall that an ideal P in R is prime if and only if the complement, R – P of P in R, is a submonoid of the multiplicative monoid of R. Of particular importance are localizations with respect to such monoids. We shall usually write MP for MR–P, fP for fR – P, etc. and call MP the localization of M at the prime ideal P.
We consider first a correspondence between the ideals of R and RP and we shall begin by considering more generally the ideals in R and in Rs for any submonoid S. Let A′ be an ideal in Rs. Then
![]()
is an ideal in R. Clearly (j(A′))s = A′. Again, if we begin with an ideal A in R, then it is easily seen that As = Rs if and only if A contains an element of S. For this reason it is natural to confine our attention to the ideals A of R that do not meet S.
We observe next that if P is a prime ideal of R such that P ∩ S = Ø, then j(PS) = P. For, let a ∈ j(PS). Then we have an element p ∈ P and elements s, t ∈ S such that a/s = p/t. Hence we have a u ∈ S such that uat = ups ∈ P. Since ut∈ S and S ∩ P = Ø, this implies that a ∈ P. Hence j(PS) ⊂ P. Since the reverse inclusion j(As) ⊃ A holds for any ideal A, we have j(PS) = P. It is straightforward to verify two further facts: If P is a prime ideal of R such that P ∩ S = Ø, then Ps is a prime ideal in Rs and if P′ is a prime ideal in Rs, then j(P′) is prime in R that does not meet S. We leave this to the reader. Putting together these results we obtain
PROPOSITION 7.8. The map P ![]() Ps is bijective and order-preserving from the set of prime ideals of R, which do not meet S with the set of prime ideals of Rs. The inverse map is P′
Ps is bijective and order-preserving from the set of prime ideals of R, which do not meet S with the set of prime ideals of Rs. The inverse map is P′ ![]() j(P′) (defined by (18)).
j(P′) (defined by (18)).
We now consider the important case of localization at a prime ideal P. Since Q ∩ (R – P) = Ø means Q ⊂ P, the foregoing result specializes to
PROPOSITION 7.9. The map Q ![]() QP is a bijective order-preserving map of the set of prime ideals Q contained in P with the set of prime ideals of RP. The inverse map is P′
QP is a bijective order-preserving map of the set of prime ideals Q contained in P with the set of prime ideals of RP. The inverse map is P′ ![]() j(P′).
j(P′).
It is clear that Pp contains every prime ideal of RP. It is clear also that the elements not in Pp are units in RP and since RP ≠ Pp, no element of Pp is a unit. Thus Pp is the set of non-units of RP and hence RP is a local ring with rad RP = Pp as its only maximal ideal. We repeat the statement of this result as
PROPOSITION 7.10. RP is a local ring with rad RP = Pp as its only maximal ideal.
This fact accounts for the central importance of localization : It often permits a reduction of questions on commutative rings and modules over such rings to the case of local rings, since in many important instances a result will be valid for R if it holds for every RP, P a prime ideal in R. The following result gives some basic properties of modules that hold if and only if they hold at all the localizations at prime ideals.
PROPOSITION 7.11. (1) Let M be an R-module. If M = 0, then Ms = 0 for every localization and if MP = 0 for every maximal P, then M = 0. (2) If M and N are R-modules and f is a homomorphism of M into N, then f injective (surjective) implies that fs is injective (surjective) for the localizations at every S. On the other hand, if fP is injective (surjective) for every maximal ideal P, then f is injective (surjective). (3) If M is flat, then so is every Ms and if MP is flat for every maximal ideal P, then M is flat.
Proof. (1) Evidently M = 0 implies MS = 0. Now assume M ≠ 0 and let x be a non-zero element of M. Then ann x ≠ R, so this ideal can be imbedded in a maximal ideal P of R. We claim that x/1 ≠ 0 in MP, so MP ≠ 0. This is clear since x/l is the image of x under the canonical homomorphism of M into MP and if x/l = 0, then ann x ∩ (R – P) ≠ Ø. Since ann x ⊂ P, this is ruled out.
(2) Let f : M → N. Then we have seen that ker fs = (ker f)s and coker fs ≅ (coker f)s for any submonoid S of the multiplicative monoid of R. Since a homomorphism is injective (surjective) if and only if its kernel (cokernel) is 0, (2) is an immediate consequence of (1).
(3) Suppose that M is a flat R-module and ![]() is an exact sequence of RS-modules. Regarding N′ and N as R-modules, we see that
is an exact sequence of RS-modules. Regarding N′ and N as R-modules, we see that ![]() is exact, and by (16),
is exact, and by (16), ![]() is exact. We have seen that N′s and Ns can be identified with N′ and N respectively. Hence
is exact. We have seen that N′s and Ns can be identified with N′ and N respectively. Hence ![]() is exact and so MS is RS-flat. Now suppose that M is an R-module such that MP is Rp-flat for every maximal ideal of P of R. Let
is exact and so MS is RS-flat. Now suppose that M is an R-module such that MP is Rp-flat for every maximal ideal of P of R. Let ![]() be an exact sequence of R-modules and consider
be an exact sequence of R-modules and consider ![]() Since MP is flat and
Since MP is flat and ![]() is exact,
is exact, ![]() is exact. Then
is exact. Then ![]() is exact. Since this holds for every maximal
is exact. Since this holds for every maximal ![]() is exact by (2). Hence M is flat.
is exact by (2). Hence M is flat. ![]()
EXERCISES
1. Show that the nil radical of RS is (nilrad R)S.
2. Show that if P is a prime ideal of R, then RP/PP is isomorphic to the field of fractions of the domain R/P.
3. Show that if R is a factorial domain (BAI, p. 141) and S is a submonoid of the multiplicative monoid of R not containing 0, then RS is a factorial domain.
4. Let {Pi| 1 ≤ i ≤ n} be a set of prime ideals in R and let S = ![]() n1(R –Pi). Show that any prime ideal of RS has the form PS where P is a prime ideal contained in one of the Pi.
n1(R –Pi). Show that any prime ideal of RS has the form PS where P is a prime ideal contained in one of the Pi.
7.5 PRIME SPECTRUM OF A COMMUTATIVE RING
Let R be a commutative ring and let X = X(R) denote the set of prime ideals of R. There is a natural way of introducing a topology on the set X that permits the introduction of geometric ideas in the study of the ring R. We proceed to define this topology.
If A is any subset of R, we let V(A) be the subset of X consisting of the prime ideals P containing A. Evidently V(A) = V(I(A)) where I(A) is the ideal generated by A and since the nilradical of an ideal I is the intersection of the prime ideals containing I, it is clear that V(I) = V(nilrad I). Also if P is a prime ideal containing Il I2 for I1, I2 ideals, then either P ⊃ I1 or P ⊃ I2. Hence V(I1 I2) = V(I1) ∪ V(I2). We can now verify that the sets V(A), A a subset of R, satisfy the axioms for closed sets in a topological space:
(1) Ø and X are closed sets, since Ø = V({1}) and X = V({0}).
(2) The intersection of any set of closed sets is closed, since if {Aα} is a set of subsets of R, then
![]()
(3) The union of two closed sets is closed, since we can take these to be V(I1) and V(I2), Ij ideals, and then V(I1) ∪ V(I2) = V(I1 I2).
We shall call X equipped with this topology the prime spectrum of R and denote it as Spec R. The subset Xmax of X consisting of the maximal ideals of R with the induced topology is called the maximum spectrum. This will be denoted as Maxspec R. Such topologies were first introduced by M. H. Stone for Boolean rings and were considered by the present author for the primitive ideals of an arbitrary ring. In the case of commutative rings the topology is called the Zariski topology of X.
The open sets in X = Spec R are the complements X – V(A) = X – ![]() a ∈ A V({a}) =
a ∈ A V({a}) = ![]() a ∈ A(X – V({a})). We denote the set X – V({a}) as Xa for a ∈ R. This is just the set of prime ideals P not containing a, that is, the P such that
a ∈ A(X – V({a})). We denote the set X – V({a}) as Xa for a ∈ R. This is just the set of prime ideals P not containing a, that is, the P such that ![]() = a + P ≠ 0 in R/P. Since any open set is a union of sets Xa, these open subsets of X constitute a base for the open sets in Spec R. It is worthwhile to list the following properties of the map a
= a + P ≠ 0 in R/P. Since any open set is a union of sets Xa, these open subsets of X constitute a base for the open sets in Spec R. It is worthwhile to list the following properties of the map a ![]() Xa of R into the set of open subsets of Spec R:
Xa of R into the set of open subsets of Spec R:
(2) Xa = Ø if and only if a is nilpotent (since nilrad R is the intersection of the prime ideals of R).
(3) Xa = X if and only if a is a unit in R.
If Y is a subset of X, put ΔY = ![]() P ∈ Y P. This is an ideal in R and V(ΔY) is a closed set containing Y. On the other hand, if V(A) ⊃ Y, then P ⊃ A for every P ∈ Y so ΔY ⊃ A and V(A) ⊃ V(Δy). Thus v(ΔY) is the closure of Y, that is, the smallest closed set in X containing Y. In particular, we see that the closure of a point P is the set of prime ideals containing P. If R is a domain, 0 is a prime ideal in R and hence the closure of 0 is the whole space X.
P ∈ Y P. This is an ideal in R and V(ΔY) is a closed set containing Y. On the other hand, if V(A) ⊃ Y, then P ⊃ A for every P ∈ Y so ΔY ⊃ A and V(A) ⊃ V(Δy). Thus v(ΔY) is the closure of Y, that is, the smallest closed set in X containing Y. In particular, we see that the closure of a point P is the set of prime ideals containing P. If R is a domain, 0 is a prime ideal in R and hence the closure of 0 is the whole space X.
EXAMPLES
1. R = ![]() . As we have noted, the closure of the prime ideal 0 is the whole space X(
. As we have noted, the closure of the prime ideal 0 is the whole space X(![]() ). Hence Spec
). Hence Spec ![]() is not a T1-space (a space in which points are closed sets). Now consider Maxspec
is not a T1-space (a space in which points are closed sets). Now consider Maxspec ![]() . The maximal ideals of
. The maximal ideals of ![]() are the prime ideals (p) ≠ 0. Hence the closure of (p) ≠ 0 is (p) and so Maxspec
are the prime ideals (p) ≠ 0. Hence the closure of (p) ≠ 0 is (p) and so Maxspec ![]() is a T1-space. Let Y be an infinite set of primes (p) ≠ 0 in
is a T1-space. Let Y be an infinite set of primes (p) ≠ 0 in ![]() . Evidently
. Evidently ![]() (p)∈y(p) = 0, so V(ΔY) = X. Thus the closure of any infinite subset of Maxspec
(p)∈y(p) = 0, so V(ΔY) = X. Thus the closure of any infinite subset of Maxspec ![]() is the whole space. Hence the closed sets of Maxspace
is the whole space. Hence the closed sets of Maxspace ![]() are the finite subsets (including Ø) and the whole space. Evidently the Hausdorff separation axiom fails in Maxspec
are the finite subsets (including Ø) and the whole space. Evidently the Hausdorff separation axiom fails in Maxspec ![]() .
.
2. R = F[x1, …, xr], F a field, xi indeterminates. For r = 1, the discussion of Spec and Maxspec is similar to that of the ring ![]() . For arbitrary r we remark that F[x1, …, xr]/(x1)
. For arbitrary r we remark that F[x1, …, xr]/(x1) ![]() F[x2, …, xr], so the prime ideals of F[x1, …, xr] containing (x1) are in 1–1 correspondence with the prime ideals of F[x2, …, xr]. Hence the closure of (x1) in Spec F[x1, …, xr] is in 1–1 correspondence with Spec F[x2, …, xr].
F[x2, …, xr], so the prime ideals of F[x1, …, xr] containing (x1) are in 1–1 correspondence with the prime ideals of F[x2, …, xr]. Hence the closure of (x1) in Spec F[x1, …, xr] is in 1–1 correspondence with Spec F[x2, …, xr].
We shall now derive some of the basic properties of the prime spectrum. We prove first
PROPOSITION 7.12. Spec R is quasi-compact.
Proof. This means that if we have a set of open subsets Oα such that ![]() Oα = X, then there exists a finite subset Oα1, …, Oαn of the Oα such that
Oα = X, then there exists a finite subset Oα1, …, Oαn of the Oα such that ![]() Oα1 = X. (We are following current usage that reserves “compact” for “quasi-compact Hausdorff.”) Since the sets Xa form a base, it suffices to show that if
Oα1 = X. (We are following current usage that reserves “compact” for “quasi-compact Hausdorff.”) Since the sets Xa form a base, it suffices to show that if ![]() a∈A Xa = X, then
a∈A Xa = X, then ![]() Xa1 = X for some finite subset {ai} of A. The condition
Xa1 = X for some finite subset {ai} of A. The condition ![]() a∈A Xa = X gives X – V(A) = X and V(A) = Ø. Then V(I(A)) = Ø for the ideal I(A) generated by A and so I(A) = R. Hence there exist ai ∈ A, xi ∈ R such that ∑r1aixi = 1. Retracing the steps, we see that V({ai}) = Ø and
a∈A Xa = X gives X – V(A) = X and V(A) = Ø. Then V(I(A)) = Ø for the ideal I(A) generated by A and so I(A) = R. Hence there exist ai ∈ A, xi ∈ R such that ∑r1aixi = 1. Retracing the steps, we see that V({ai}) = Ø and ![]() Xal = X.
Xal = X. ![]()
Let N = nilrad R, ![]() = R/N, and let v be the canonical homomorphism a → a + N of R onto
= R/N, and let v be the canonical homomorphism a → a + N of R onto ![]() . Any prime ideal P of R contains N and v(P) is a prime ideal of
. Any prime ideal P of R contains N and v(P) is a prime ideal of ![]() . Moreover, every prime ideal of
. Moreover, every prime ideal of ![]() has the form v(P), P a prime ideal of R. We have
has the form v(P), P a prime ideal of R. We have
PROPOSITION 7.13. The map P ![]() v(P) is a homeomorphism of Spec R onto Spec
v(P) is a homeomorphism of Spec R onto Spec ![]() .
.
Proof. The map is injective, since P ⊃ N for every prime ideal P and we have seen that the map is surjective. Now if a ∈ R, v(a) ∈ v(P) if and only if a ∈ P. This implies that if A is a subset of R, then the image of the closed set V(A) in Spec R is V(v(A)) in Spec ![]() and if
and if ![]() is a subset of
is a subset of ![]() , then the inverse image of the closed set V(
, then the inverse image of the closed set V(![]() ) is V(v– 1(
) is V(v– 1(![]() )). Hence P
)). Hence P ![]() v(P) is a homeomorphism.
v(P) is a homeomorphism. ![]()
We recall that a space X is disconnected if it contains an open and closed subset ≠ Ø, ≠ X. We shall show that Spec R is disconnected if and only if R contains an idempotent ≠ 0, 1. This will follow from a considerably stronger result, which gives a bijection of the set of idempotents of R and the set of open and closed subsets of Spec R. To obtain this we shall need the following result on lifting of idempotents, which is of independent interest.
PROPOSITION 7.14. Let R be a ring that is not necessarily commutative, N a nil ideal in R, and ![]() = u + N an idempotent element of
= u + N an idempotent element of ![]() = R/N. Then there exists an idempotent e in R such that
= R/N. Then there exists an idempotent e in R such that ![]() =
= ![]() . Moreover, e is unique if R is commutative.
. Moreover, e is unique if R is commutative.
Proof. We have u2 – u = z where z is nilpotent, say, zn = 0 and z ∈ N. Then (u(l – u))n = unvn = 0 where v = 1 – u. From u + v = 1 we obtain
![]()
where e is the sum of the terms uiv2n – 1 – i in which n ≤ i ≤ 2n– 1 and f is the sum of the terms uiv2n – 1 – i in which 0 ≤ i ≤ n – 1. Since unvn = 0, any term in e annihilates any term in f. Hence ef = 0 = fe. Since e + f = 1, this gives e2 = e, f2 = f. Every term in e except u2n – 1 contains the factor uv = – z. Hence u2n – 1 ≡ e (mod N). Since u ≡ u2 ≡ u3 ≡ … ≡ u2n– 1 (mod N), we have e ≡ u (mod N). This proves the first assertion.
Now assume that R is commutative. The uniqueness of e will follow if we can show that if e is an idempotent, then the only idempotent of the form e + z, z nilpotent, is e. The condition (e + z)2 = e + z gives (1 – 2e)z = z2. Then z3 = (1 – 2e)z2 = (1 — 2e)2z and by induction we have (1 – 2e)nz = zn+1. Since (1 – 2e)2 = 1 – 4e + 4e = 1, this implies that z = 0 and hence e + z = e. ![]()
If e and f are idempotents in R, then so are e′ = 1 – e, ef, and e o f = l – (l – e)(l – f) = e + f – ef. It is readily verified that the set E of idempotents of R is a Boolean algebra with the compositions e ∧ f = ef and e ∨ f = e o f (exercise 1, p. 479 of BAI). We remark next that the open and closed subsets of a topological space X constitute a subalgebra of the Boolean algebra of subsets of X. We can now prove
THEOREM 7.3. If e is an idempotent in R, then Xe is an open and closed subspace of Spec R and the map e ![]() Xe is an isomorphism of the Boolean algebra E onto the Boolean algebra of open and closed subsets of Spec R.
Xe is an isomorphism of the Boolean algebra E onto the Boolean algebra of open and closed subsets of Spec R.
Proof. Let e = e2 ∈ R. Then e(1 – e) = 0 , so any prime ideal P of R contains one of the elements e, 1 – e but not both. Hence Xe ∪ X1 – e = X and Xe ∩ X1 – e = Ø, so Xe is open and closed. Now let Y be an open and closed subset of X, Y′ = X – Y. Let R = R/N, N = nilrad R, v the canonical homomorphism of R onto ![]() . We use the homeomorphism P
. We use the homeomorphism P ![]() v(P) of X = Spec R with
v(P) of X = Spec R with ![]() = Spec
= Spec ![]() to conclude that v(Y) is an open and closed subset of
to conclude that v(Y) is an open and closed subset of ![]() and v(Y′) is its complement. Consider Δv(Y) and Δv(y′) as defined on p. 404. These are ideals in
and v(Y′) is its complement. Consider Δv(Y) and Δv(y′) as defined on p. 404. These are ideals in ![]() and V(Δv(Y)) = v(Y), V(Δv(Y′) = v(Y′) since v(Y) and v(Y′) are open and closed in
and V(Δv(Y)) = v(Y), V(Δv(Y′) = v(Y′) since v(Y) and v(Y′) are open and closed in ![]() . If
. If ![]() is a prime ideal of
is a prime ideal of ![]() containing Δv(y) + Δv(y′), then
containing Δv(y) + Δv(y′), then ![]() ⊃ Δv(y) and
⊃ Δv(y) and ![]() ⊃ Δv(Y′), so
⊃ Δv(Y′), so ![]() ∈ v(Y) ∩ v(Y′). Since v(Y) ∩ v(Y′) = Ø, there are no such
∈ v(Y) ∩ v(Y′). Since v(Y) ∩ v(Y′) = Ø, there are no such ![]() and so Δv(Y) + Δv(Y′) =
and so Δv(Y) + Δv(Y′) = ![]() . If
. If ![]() is any prime in
is any prime in ![]() , either
, either ![]() ⊃ Δv(Y) or
⊃ Δv(Y) or ![]() ⊃ Δv(Y′), so
⊃ Δv(Y′), so ![]() ⊃ Δv(Y) ∩ Δv(Y′). Since this holds for all
⊃ Δv(Y) ∩ Δv(Y′). Since this holds for all ![]() and
and ![]() has no nilpotent elements ≠ 0, Δv(Y) ∩ Δv(y′) = 0. Hence
has no nilpotent elements ≠ 0, Δv(Y) ∩ Δv(y′) = 0. Hence ![]() . Let
. Let ![]() be the unit of Δv(Y′) and let e be the idempotent in R such that v(e) =
be the unit of Δv(Y′) and let e be the idempotent in R such that v(e) = ![]() . Now if P is an ideal in R, the condition P
. Now if P is an ideal in R, the condition P ![]() e is equivalent to v(P)
e is equivalent to v(P) ![]()
![]() , which in turn is equivalent to v(P) ⊃ Δv(Y′) and to v(P) ∈ v(Y′) and P ∈ Y′ . Hence Xe = Y, which shows that the map e
, which in turn is equivalent to v(P) ⊃ Δv(Y′) and to v(P) ∈ v(Y′) and P ∈ Y′ . Hence Xe = Y, which shows that the map e ![]() Xe is surjective. To see that the map is injective, let e be a given idempotent in R,
Xe is surjective. To see that the map is injective, let e be a given idempotent in R, ![]() = v(e). Then we have
= v(e). Then we have ![]() and
and ![]()
![]() and
and ![]() (
(![]() –
– ![]() ) are ideals. Now v(Xe) is the set of prime ideals of
) are ideals. Now v(Xe) is the set of prime ideals of ![]() containing
containing![]() –
– ![]() , hence
, hence ![]() (
(![]() –
– ![]() ), and v(X1 – e) is the set of prime ideals containing
), and v(X1 – e) is the set of prime ideals containing ![]()
![]() . We have shown that
. We have shown that ![]() , we have
, we have ![]() . Since 1 – e is the only idempotent in the coset
. Since 1 – e is the only idempotent in the coset ![]() —
— ![]() , by Proposition 7.14, this implies the injectivity of e
, by Proposition 7.14, this implies the injectivity of e ![]() Xe. If e and f are idempotents, then Xef = Xe ∩ Xf. Also X1 – e = X – Xe, X1 = X, X0 = Ø. These relations imply that e
Xe. If e and f are idempotents, then Xef = Xe ∩ Xf. Also X1 – e = X – Xe, X1 = X, X0 = Ø. These relations imply that e ![]() Xe is an isomorphism of Boolean algebras.
Xe is an isomorphism of Boolean algebras. ![]()
Evidently we have the following consequence of the theorem.
COROLLARY. Spec R is connected if and only if R contains no idempotent ≠ 0, 1.
Because of this result, a commutative ring R is called connected if the only idempotents in R are 0 and 1.
Let f be a homomorphism of R into a second ring R′. If P′ is a prime ideal in R′, then P = f – 1(P′ ) is a prime ideal in R since if ab ∈ P, then f(a)f(b) = f(ab) ∈ P′. Thus either f(a) or f(b) ∈ P′ and hence either a or b ∈ P. This permits us to define a map
![]()
of X′ = Spec R′ into X = Spec R. If a ∈ R, then a prime ideal P′ of R′ does not contain a′ = f (a) if and only if P = f*(P′) does not contain a. Hence
![]()
This implies that the inverse image of any open subset of Spec R under f* is open in Spec R′, so f* is a continuous map of Spec R′ into Spec R. It is clear that if R′ = R and f = 1R, then f* = lspec R and if g is homomorphism of R′ into R″ then (fg)* = g*f*. Thus the pair of maps R ![]() Spec R, f
Spec R, f ![]() f* define a contravariant functor from the category of commutative rings (homomorphisms as morphisms) into the category of topological spaces (continuous maps as morphisms).
f* define a contravariant functor from the category of commutative rings (homomorphisms as morphisms) into the category of topological spaces (continuous maps as morphisms).
EXERCISES
1. Let f be a homomorphism of R into R′, f* the corresponding continuous map of Spec R′ into Spec R. Show that if f is surjective, then f*(Spec R′) is the closed subset V(ker f) of Spec R. Show also that f* is a homeomorphism of Spec R′ with the closed set V(ker f).
2. Same notations as exercise 1. Show that f*(Spec R′) is dense in Spec R if and only if nilrad R ⊃ ker f. Note that this holds if f is injective.
3. Give an example of a homomorrphism f of R into R′ such that for some maximal ideal M′ of R′, f – 1 (M′) is not maximal in R.
4. (D. Lazard.) Show that if P is a prime ideal in R and I is the ideal in R generated by the idempotents of R contained in P, then R/I contains no idempotents ≠ 0, 1. Show that the set of prime ideals P′ ⊃ I is the connected component of Spec R containing P (the largest connected subset containing P). Hint: Let ![]() be an idempotent of
be an idempotent of ![]() = R/I where
= R/I where ![]() = u + I. Then u(l – u) ∈ I ⊂ P and we may assume u ∈ P. Show that there exists an f ∈ I such that f 2 = f and f(u – u2) = u – u2. Then (1 – f)u = g is an idempotent contained in P, so g ∈ I. Then u = g + fu ∈ I and
= u + I. Then u(l – u) ∈ I ⊂ P and we may assume u ∈ P. Show that there exists an f ∈ I such that f 2 = f and f(u – u2) = u – u2. Then (1 – f)u = g is an idempotent contained in P, so g ∈ I. Then u = g + fu ∈ I and ![]() = 0.)
= 0.)
In exercises 5 and 6, R need not be commutative.
5. Let N be a nil ideal in R and let ![]() l, …,
l, …, ![]() n be orthogonal idempotent elements of
n be orthogonal idempotent elements of ![]() . Show that there exist orthogonal idempotents ei in R such that
. Show that there exist orthogonal idempotents ei in R such that ![]() i =
i = ![]() l, 1 ≤ i ≤ n. Show also that if ∑n1
l, 1 ≤ i ≤ n. Show also that if ∑n1![]() i = 1, then necessarily ∑ei = 1
i = 1, then necessarily ∑ei = 1
6. Let R, N, ![]() be as in exercise 5 and let
be as in exercise 5 and let ![]() ij , 1 ≤ i,j ≤ n, be elements of
ij , 1 ≤ i,j ≤ n, be elements of ![]() such that
such that ![]() . Show that there exist eij ∈ R such that
. Show that there exist eij ∈ R such that ![]() .
.
7.6 INTEGRAL DEPENDENCE
In BAI, pp. 278–281, we introduced the concept of R-integrality of an element of a field E for a subring R of E. The concept and elementary results derived in BAI can be extended to the general case in which E is an arbitrary commutative ring. We have the following
DEFINITION 7.2. If E is a commutative ring and R is a subring, then an element u ∈ E is called R-integral if there exists a monic polynomial f (x) ∈ R[x], x an indeterminate, such that f (u) = 0.
If ![]() , then we have the relation un = a0 + a1 u + … + an – 1 un – 1, from which we deduce that if M = R1 + Ru + … + Run – 1, then uM ⊂ M. Evidently M is a finitely generated R-submodule of E containing 1. Since uM ⊂ M, M is an R[u]-submodule of E and since 1 ∈ M, M is faithful as R[u]-module. Hence we have the implication 1
, then we have the relation un = a0 + a1 u + … + an – 1 un – 1, from which we deduce that if M = R1 + Ru + … + Run – 1, then uM ⊂ M. Evidently M is a finitely generated R-submodule of E containing 1. Since uM ⊂ M, M is an R[u]-submodule of E and since 1 ∈ M, M is faithful as R[u]-module. Hence we have the implication 1 ![]() 2 in the following.
2 in the following.
LEMMA. The following conditions on an element u ∈ E are equivalent: 1. u is R-integral. 2. There exists a faithful R[u]-submodule of E that is finitely generated as R-module.
Proof. Now assume 2. Then we have ui ∈ M such that M = Ru1 + Ru2 + … + Run. Then we have the relations uui = ∑nj = 1 aijuj, 1 ≤ i ≤ n, where the aij ∈ R.

If we multiply the ith of these equations by the cofactor of the (i, j)-entry of the matrix u1 – (aij) and add the resulting equations, we obtain the equation f(u)uj = 0, 1 ≤ j ≤ n, where f(x) is the characteristic polynomial of the matrix (aij). Since the uj generate M and M is faithful as R[u]-module, we have f(u) = 0, so u is a root of the monic polynomial f (x). Hence 2 ![]() 1.
1. ![]()
We remark that the argument just used is slightly different from the one given in the field case in BAI, p. 279. If M and N are R-submodules of E that are finitely generated over R then so is MN = {∑mini |mi ∈ M, ni ∈ N}. Moreover, if 1 ∈ M and 1 ∈ N then l ∈ M N and if either uM ⊂ M or uN ⊂ N then uMN ⊂ MN. These observations and the foregoing lemma can be used in exactly the same way as in BAI, pp. 279–280, to prove
THEOREM 7.4. If E is a commutative ring and R is a subring, the subset R′ of elements of E that are R-integral is a subring containing R. Moreover, any element of E that is R′-integral is R-integral and hence is contained in R′.
The subring R′ of E is called the integral closure of R in E. If R′ = E, that is, every element of E is integral over R, then we say that E is integral over R (or E is an integral extension of R).
If A is an ideal of a ring E, then evidently R ∩ A is an ideal in the subring R of E. We call this the contraction of A to R and denote it as Ac. We also have the subring (R + A)/A of E/A and the canonical isomorphism of this ring with the ring R/Ac = R/(R ∩ A). One usually identifies (R + A)/A with R/Ac by means of the canonical isomorphism and so regards E/A as an extension of R/Ac. In this sense we have
PROPOSITION 7.15. If E is integral over R and A is an ideal in E, then ![]() = E/A is integral over
= E/A is integral over ![]() = R/Ac.
= R/Ac.
Proof. Let ![]() = u + A be an element of
= u + A be an element of ![]() . Then we have ai ∈ R, 0 ≤ i ≤ n – 1, such that un = a0 + a1u + … + an–1un – 1. Then
. Then we have ai ∈ R, 0 ≤ i ≤ n – 1, such that un = a0 + a1u + … + an–1un – 1. Then ![]() where
where ![]() i = ai + A. Hence
i = ai + A. Hence ![]() is integral over (R + A)/A, hence over
is integral over (R + A)/A, hence over ![]() = R/Ac.
= R/Ac. ![]()
Next suppose that S is a submonoid of the multiplicative monoid of R. Then the localization Es contains the localization Rs as a subring. Moreover, we have
PROPOSITION 7.16. Let R be a subring of E, R′ the integral closure of R in E, S a submonoid of the multiplicative monoid of R. Then R′S is the integral closure of Rs in Es.
Proof. Any element of R′s has the form u/s, u ∈ R′, s ∈ S. We have a relation un = a0 + a1 u + … + an – 1, un – 1, ai ∈ R. Hence ![]() . Hence u/s is integral over Rs. Conversely, suppose that u/s is integral over Rs where u ∈ E, s ∈ S. To show that u/s = v/t where v ∈ R′, t ∈ S, it suffices to show that there exists an s′ ∈ S such that us′ ∈ R′. For, u/s = us′/ss′ has the required form. Now u/S integral over Rs implies that u/1 is integral over Rs, since s/1 ∈ Rs and u/1 = (u/s)(s/1). Thus we have a relation of the form
. Hence u/s is integral over Rs. Conversely, suppose that u/s is integral over Rs where u ∈ E, s ∈ S. To show that u/s = v/t where v ∈ R′, t ∈ S, it suffices to show that there exists an s′ ∈ S such that us′ ∈ R′. For, u/s = us′/ss′ has the required form. Now u/S integral over Rs implies that u/1 is integral over Rs, since s/1 ∈ Rs and u/1 = (u/s)(s/1). Thus we have a relation of the form ![]() with ai ∈ R, si ∈ S. Multiplication by
with ai ∈ R, si ∈ S. Multiplication by ![]()
![]() where the a′ ∈ R. Hence
where the a′ ∈ R. Hence ![]() . Then there exists a t2 ∈ S such that
. Then there exists a t2 ∈ S such that ![]() . Multiplication of this relation by tn2– 1 shows that s′ u ∈ R′ for s′ = t1 t2.
. Multiplication of this relation by tn2– 1 shows that s′ u ∈ R′ for s′ = t1 t2. ![]()
We prove next
PROPOSITION 7.17. If E is a domain that is integral over the subdomain R, then E is a field if and only if R is afield.
Proof. Assume first that R is a field and let u ≠ 0 be an element of E. We have a relation un + a1un – 1 + … + an = 0 with ai ∈ R and since u is not a zero divisor in E, we may assume an ≠ 0. Then a– 1n exists in R and we have ![]() . Hence u is invertible and E is a field. Conversely, suppose that E is a field and let a ≠ 0 be in R. Then a– 1 exists in E and we have a relation
. Hence u is invertible and E is a field. Conversely, suppose that E is a field and let a ≠ 0 be in R. Then a– 1 exists in E and we have a relation ![]() . Multiplication by an – 1 gives
. Multiplication by an – 1 gives ![]() . Hence a is invertible in R and R is a field.
. Hence a is invertible in R and R is a field. ![]()
An immediate consequence of this result and of Proposition 7.17 is the
COROLLARY 1. Let E be a commutative ring, R a subring such that E is integral over R, and let P be a prime ideal in E. Then Pc = P ∩ R is maximal in R if and only if P is maximal in E.
Proof. ![]() = E/P is a domain and by Proposition 7.15,
= E/P is a domain and by Proposition 7.15, ![]() is integral over
is integral over ![]() = R/Pc. By Proposition 7.17,
= R/Pc. By Proposition 7.17, ![]() is a field if and only if
is a field if and only if ![]() is a field. Hence P is maximal in E if and only if Pc is maximal in R.
is a field. Hence P is maximal in E if and only if Pc is maximal in R. ![]()
We also have the following
COROLLARY 2. Let E and R be as in Corollary 1 and suppose P1 and P2 are ideals in R such that P1 ![]() P2. Then Pc1
P2. Then Pc1 ![]() P2.
P2.
Proof. We have Pc1 ⊃ Pc2. Now suppose p = Pc1 = Pc2. Consider the localization Es for S = R – p. By Proposition 7.16, ES is integral over RS. Since Pi ∩ R = p, Pi ∩ S = Ø. Then, by Proposition 7.8, P1S ![]() P2S. On the other hand PiS ⊃ pS which is the maximal ideal of the local ring RS. Since ES is integral over RS it follows from Corollary 1 that PiS is maximal in ES. This contradicts PlS
P2S. On the other hand PiS ⊃ pS which is the maximal ideal of the local ring RS. Since ES is integral over RS it follows from Corollary 1 that PiS is maximal in ES. This contradicts PlS ![]() P2S. Thus Pc1
P2S. Thus Pc1 ![]() Pc2.
Pc2. ![]()
If P is a prime ideal in E, then it is clear that Pc is a prime ideal in R. Hence we have a map P ![]() Pc of Spec E into Spec R. This is surjective since we have the following
Pc of Spec E into Spec R. This is surjective since we have the following
THEOREM 7.5 (“LYING-OVER” THEOREM). Let E be a commutative ring, R a subring such that E is integral over R. Then any prime ideal p of R is the contraction Pc of a prime ideal P of E.
Proof. We assume first that R is local and p is the maximal ideal of R. Let Pbe a maximal ideal in E. Then Pc is a maximal ideal in R, by the above corollary. Since p is the only maximal ideal in R, we have p = Pc.
Now let R be arbitrary and consider the localizations Rp and Ep. Rp is a local ring and Ep is integral over Rp (Proposition 7.16). Now there exists a prime ideal P′ in Ep whose contraction P′ c = P′ ∩ Rp = pp, the maximal ideal of Rp. By Proposition 7.8 (p. 401), P′ = Pp for a prime ideal P of E such that P ∩ (R – p) = Ø or, equivalently, P ∩ R ⊂ p. Again, by Proposition 7.8, P = j(Pp) = {u ∈ E|u/s ∈ Pp} for some s ∈ R – p. Now p ⊂ j(pp) ⊂ j(Pp) = P. Hence P ∩ R = p. ![]()
EXERCISES
1. Let E be a commutative ring, R a subring such that (1) E is integral over R and (2) E is finitely generated as R-algebra. Show that E is finitely generated as R-module.
2. (“Going-up” theorem). Let E be a commutative ring, R a subring such that E is integral over R. Let p1 and p2 be prime ideals of R such that p1 ⊃ p2 and let P2 be a prime ideal of E such that Pc2 = p2. Show that there exists a prime ideal Pl of E such that P1 ⊃ P2 and Pc1 = p1.
3. Let R be a subring of a commutative ring E, R′ the integral closure of R in E, I an ideal in R, Ie = IR′ its extension to an ideal in R′. An element a ∈ E is integral over I if it satisfies an equation f(a) = 0 where f(λ) = λm + b1λm – l + … + bm, bi ∈ I. The subset I′ of E of elements integral over I is called the integral closure of I in E.
Show that I′ = nilrad Ie in R′. Sketch of proof: If a ∈ E and am + b1 am– 1 + … +bm = 0 with the bi ∈ I then a ∈ R′ and am ∈ Ie. Hence a ∈ nilrad Ie in R′. Conversely, let a∈ nilrad Ie in R′. Then a ∈ R′ and am = ∑niaibi for some m > 0, ai ∈ R′, bi ∈ I. Let A be the R-subalgebra of E generated by the ai. By exercise 1, A has a finite set of generators a1, …, aq, q ≥ n, as R-module. Then ![]() , where the bjk ∈ I. As in the proof of the lemma on p. 408, this implies that am and hence a is integral over I.
, where the bjk ∈ I. As in the proof of the lemma on p. 408, this implies that am and hence a is integral over I.
Remarks, (i) I′ is a subring of E (in the sense of BAI, that is, I′ is a subgroup of the additive group closed under multiplication), (ii) If R is integrally closed in E (R′ = R) then I′ = nilrad I in R.
4. (Basic facts on contractions and extensions of ideals.) Let R be a subring of a commutative ring E. For any ideal I of E, Ic = I ∩ R is an ideal in R and for any ideal i of R, ie = iE is an ideal in E. Note that
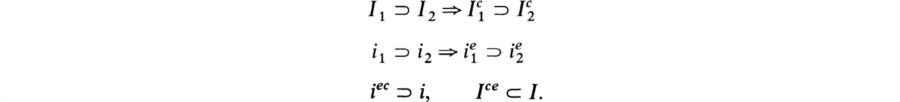
Hence conclude that
![]()
for any ideals i and I. Note that these imply that an ideal i of R is the contraction of an ideal of E ![]() i = iec and an ideal I of E is an extension of an ideal of R
i = iec and an ideal I of E is an extension of an ideal of R ![]() I = Ice
I = Ice
7.7 INTEGRALLY CLOSED DOMAINS
An important property of domains that we shall encounter especially in the study of Dedekind domains (see Chapter 10) is given in the following
DEFINITION 7.3. A domain D is called integrally closed if it is integrally closed in its field of fractions.
It is readily seen that ![]() is integrally closed. More generally any factorial domain is integrally closed (exercise 1, below). Our main objective in this brief section is to prove a “going-down” theorem (Theorem 7.6) for integrally closed domains that will be required later (in the proof of Theorem 8.37). For the proof of this theorem we require
is integrally closed. More generally any factorial domain is integrally closed (exercise 1, below). Our main objective in this brief section is to prove a “going-down” theorem (Theorem 7.6) for integrally closed domains that will be required later (in the proof of Theorem 8.37). For the proof of this theorem we require
PROPOSITION 7.18. Let D be an integrally closed subdomain of a domain E, F the field offractions of D, I an ideal in D. Let a ∈ E be integral over I. Then a is algebraic over F and its minimum polynomial ![]() over F has its coefficients (– 1)jbj ∈ nilrad I, 1 ≤ j ≤ m.
over F has its coefficients (– 1)jbj ∈ nilrad I, 1 ≤ j ≤ m.
Proof. The first statement is clear. For the second let S be a splitting field over F of m(λ) and let m(λ) = (λ – a1)… (λ – am) in S[λ] where a1 = a. For any i we have an automorphism of S/F such that a ![]() ai. Since this stabilizes I it follows that every ai is integral over I. Since bj, 1 ≤ j ≤ m, is an elementary symmetric polynomial in the ai it follows from Remark (i) following exercise 3 of section 7.6 that bj is integral over I. Then, by Remark (ii), bj ∈ nilrad I.
ai. Since this stabilizes I it follows that every ai is integral over I. Since bj, 1 ≤ j ≤ m, is an elementary symmetric polynomial in the ai it follows from Remark (i) following exercise 3 of section 7.6 that bj is integral over I. Then, by Remark (ii), bj ∈ nilrad I. ![]()
We shall need also the following criterion that an ideal be a contraction of a prime ideal.
PROPOSITION 7.19. Let R be a subring of a commutative ring E, p a prime ideal of R. Then p = Pc ≡ P ∩ R for a prime ideal P of E ![]() pec = Ep ∩ R = p.
pec = Ep ∩ R = p.
Proof. If p = Pc then pec = p by exercise 4 of section 7.6. Now assume this holds for a prime ideal p of R. Consider the submonoid S = R – p of the multiplicative monoid of E. Since pec = p, Ep ∩ R = p and hence Ep ∩ S = Ø. Since Ep is an ideal of E and Ep ∩ S = Ø, the extension (Ep)s is a proper ideal of the localization Es of E relative to the monoid S. Then (Ep)s is contained in a maximal ideal Q of Es and P = j(Q) as defined by (18) is a prime ideal of R such that P ∩ (R – p) = P ∩ S = Ø. Then P ∩ R ⊂ p. Since P = j(Q) ⊃ j((Ep)s) ⊃ p we have Pc = P ∩ R = p. ![]()
We can now prove
THEOREM 7.6 (“Going-down” theorem). Let D be an integrally closed subdomain of a domain E that is integral over D. Let p1 and p2 be prime ideals of D such that p1 ⊃ p2 and suppose P1 is a prime ideal of E such that Pc1 = p1. Then there exists a prime ideal P2 of E such that Pc2 = p2 and P2 ⊂ P1.
Proof. Consider the localization Epl ( = EE – P1). It suffices to show that p2EPl ∩ D = p2. For, if this holds, then by Proposition 7.19 there exists a prime ideal Q of EP1 such that D ∩ Q = p2. Then P2 = j(Q) is a prime ideal of E contained in P1 and ![]() .
.
We now proceed to the proof that p2EPl ∩ D = p2. Let a ∈ p2EPl. Then a = b/s where b ∈ Ep2 and s ∈ E – P1 By exercise 3 of section 7.6, b is integral over p2 and hence by Proposition 7.18, the minimum polynomial of b over the field of fractions F of D has the form ![]() , 1 ≤ i ≤ m.
, 1 ≤ i ≤ m.
Suppose a = b/s ∈ p2EPl ∩ D. Then s = b/a and the minimum polynomial of s over F is ![]() . Since s is integral over D, taking I = D in Proposition 7.18, we see that every bi/ai ∈ D. Then (bi/ai)ai ∈ p2 and bi/ai and ai ∈ D. Now suppose a
. Since s is integral over D, taking I = D in Proposition 7.18, we see that every bi/ai ∈ D. Then (bi/ai)ai ∈ p2 and bi/ai and ai ∈ D. Now suppose a ![]() p2. Then, since p2 is prime in D, bi/ai ∈ p2, 1 ≤ i ≤ m. Thus s is integral over p2 and hence over p1. Then again by exercise 3, s ∈ nilrad p1 E ⊂ P1 contrary to s ∈ E – P1 This shows that a ∈ p2 so p2EPl ∩ D ⊂ p2. Since the reverse inequality is clear we have p2EPl ∩ D = p2.
p2. Then, since p2 is prime in D, bi/ai ∈ p2, 1 ≤ i ≤ m. Thus s is integral over p2 and hence over p1. Then again by exercise 3, s ∈ nilrad p1 E ⊂ P1 contrary to s ∈ E – P1 This shows that a ∈ p2 so p2EPl ∩ D ⊂ p2. Since the reverse inequality is clear we have p2EPl ∩ D = p2. ![]()
EXERCISES
1. Show that any factorial domain is integrally closed.
2. Let D be a domain, F its field of fractions. Show that if D is integrally closed then Ds is integrally closed for every submonoid S of the multiplicative monoid of R. On the other hand, show that if DP is integrally closed for every maximal ideal P of D then D is integrally closed. (Hint: Use Proposition 7.11 on p. 402.)
7.8 RANK OF PROJECTIVE MODULES
We have shown in BAI, p. 171, that if R is a commutative ring and M is an R-module with a base of n elements, then any base has cardinality n. Hence the number n, called the rank of M, is an invariant. We repeat the argument in a slightly improved form. Let {ei|l ≤ i ≤ n} be a base for M and let {fj| l ≤ j ≤ m } be a set of generators. Then we have ![]() which gives
which gives ![]() . Assume n ≥ m and consider the n × n matrices
. Assume n ≥ m and consider the n × n matrices

Then we have BA = ln, the n × n unit matrix. Since R is commutative, this implies AB = 1n (BAI, p. 97), which is impossible if n > m. Hence n = m. Thus we see that if M has a base of n elements, then any set of generators contains at least n elements. Hence any two bases have the same cardinality. The argument shows also that any set of n generators fj = ∑aji ei, 1≤ j ≤ n, is a base, since the argument shows that in this case the matrix A = (aij) is invertible in Mn(R), and this implies that the only relation of the form ∑cifi = 0 is the one with every ci = 0. We summarize these results in
PROPOSITION 7.20 Let M be a free module over a commutative ring with base of n elements. Then (1) any base has cardinality n, (2) any set of generators contains at least n elements, and (3) any set of n generators is a base.
We shall now give a method, based on localization, for extending the concept of rank to finitely generated projective modules over commutative rings R. We shall prove first that such modules are free if R is local. For this we require an important lemma for arbitrary rings known as
NAKAYAMA’S LEMMA. Let M be a module over a ring R (not necessarily commutative). Suppose that (1) M is finitely generated and (2) (rad R)M = M. Then M = 0.
Proof. Let m be the smallest integer such that M is generated by m elements xl, x2,…, xm. If M ≠ 0, then m > 0. The condition (rad R)M = M implies that xm = r1x1 + … + rmxm where the ri ∈ rad R. Then we have
![]()
Since rm ∈ rad R, 1 – rm is invertible in R, and acting with (1 – rm)– l on the foregoing relation shows that xm can be expressed in terms of x1,…,xm – 1. Then x1,…, xm –1 generate M, contrary to the choice of m. ![]()
We recall that if B is an ideal in a ring R and M is an R-module, then BM is a submodule and the module M/BM is annihilated by B and so can be regarded in a natural way as R/B-module. In particular this holds for B = rad R. In this case we have the following consequence of Nakayama’s lemma.
COROLLARY. Let M be a finitely generated R-module. Then x1, …, xm ∈ M generate M if and only if the cosets ![]() = x1 + (rad R)M,…,
= x1 + (rad R)M,…, ![]() m = xm + (rad R)M generate M/(rad R)M as R/rad R module.
m = xm + (rad R)M generate M/(rad R)M as R/rad R module.
Proof. If xl, … xm generate M, then evidently ![]() l, …,
l, …, ![]() m generate
m generate ![]() = M/(rad R)M as R-module and, equivalently, as
= M/(rad R)M as R-module and, equivalently, as ![]() = R/rad R-module. Conversely, suppose the
= R/rad R-module. Conversely, suppose the ![]() i generate
i generate ![]() as
as ![]() -module, hence as R-module. Then M = (rad R)M + N where N = ∑Rxi. Then (rad R)(M/N) = M/N and M/N is finitely generated. Hence M/N = 0 by Nakayama’s lemma, so M = N = ∑m1Rxi.
-module, hence as R-module. Then M = (rad R)M + N where N = ∑Rxi. Then (rad R)(M/N) = M/N and M/N is finitely generated. Hence M/N = 0 by Nakayama’s lemma, so M = N = ∑m1Rxi. ![]()
We can now prove
THEOREM 7.7. If R is a (commutative) local ring, then any finitely generated projective module over R is free.
Proof. We may assume that M is a direct summand of a free module F = R(n) : F = M ![]() N where M and N are submodules. Then (rad R)F = (rad R)M + (rad R)N and (rad R)M ⊂ M, (rad R)N ⊂ N. Hence
N where M and N are submodules. Then (rad R)F = (rad R)M + (rad R)N and (rad R)M ⊂ M, (rad R)N ⊂ N. Hence ![]() = F/(rad R)F =
= F/(rad R)F = ![]()
![]()
![]() where
where ![]() = (M + (rad R)F)/(rad R)F,
= (M + (rad R)F)/(rad R)F, ![]() = (N + (rad R)F)/(rad R)F. Now
= (N + (rad R)F)/(rad R)F. Now ![]() = R/rad R is a field and evidently
= R/rad R is a field and evidently ![]() is an n-dimensional vector space over
is an n-dimensional vector space over ![]() , and
, and ![]() and
and ![]() are subspaces. We can choose elements y1, …, yn so that yl … yr ∈ M, yr + 1, …, yn ∈ N and if
are subspaces. We can choose elements y1, …, yn so that yl … yr ∈ M, yr + 1, …, yn ∈ N and if ![]() i = yi + (rad R)F, then {
i = yi + (rad R)F, then {![]() l, …,
l, …, ![]() n} is a base for
n} is a base for ![]() over
over ![]() . Then, by the Corollary to Nakayama’s lemma, yl, …, yn generate F and, by Proposition 7.18, they form a base for F. Then {y1 …, yr} is a base for M so M is free.
. Then, by the Corollary to Nakayama’s lemma, yl, …, yn generate F and, by Proposition 7.18, they form a base for F. Then {y1 …, yr} is a base for M so M is free. ![]()
We now consider finitely generated projective modules over an arbitrary ring K and we prove first
PROPOSITION 7.21. If M is a free R-module of rank n then Ms is a free Rs-module of rank n for any submonoid S of the multiplicative monoid of R. If M is projective with n generators over R, then Ms is projective with n generators over Rs.
Proof. To prove the first statement we recall that S-localization is a functor from R-mod to Rs-mod. Hence a relation M ≅ M1 ![]() …
… ![]() Ms for R-modules implies Ms ≅ M1S
Ms for R-modules implies Ms ≅ M1S![]() …
… ![]() MsS for Rs-modules. Then M ≅ R
MsS for Rs-modules. Then M ≅ R![]() …
… ![]() R (n copies) implies Ms ≅ Rs
R (n copies) implies Ms ≅ Rs![]() …
… ![]() RS (n copies). Next suppose M is projective with n generators. This is equivalent to assuming that M is isomorphic to a direct summand of the free module R(n). Then Ms is Rs-projective with n generators.
RS (n copies). Next suppose M is projective with n generators. This is equivalent to assuming that M is isomorphic to a direct summand of the free module R(n). Then Ms is Rs-projective with n generators. ![]()
In particular, if M is projective with n generators, then for any prime ideal P, MP is projective with n generators over the local ring RP. Hence MP is RP-free of rank nP ≤ n. We call nP the P-rank of M and we shall say that M has a rank if nP = nQ for any two prime ideals P and Q of R. In this case the common value of the local ranks nP is called the rank of the finitely generated projective module M. We shall now show that the map P ![]() nP is a continuous map of Spec R into
nP is a continuous map of Spec R into ![]() endowed with the discrete topology. This will imply that if Spec R is connected or, equivalently, R has no idempotents ≠ 0, 1, then M has a rank.
endowed with the discrete topology. This will imply that if Spec R is connected or, equivalently, R has no idempotents ≠ 0, 1, then M has a rank.
The continuity we wish to establish will be an easy consequence of
PROPOSITION 7.22. Let M be a finitely generated projective R-module, P a prime ideal in R. Then there exists a ![]() P such that M
P such that M![]() is free as R
is free as R![]() -module.
-module.
Proof. MP is a free RP-module of finite rank. If (x1/s1, …, xn/sn), xi ∈ M, si ∈ R – P, is a base for MP, and since the elements si/1 are units in RP, (xl/1, …, xn/l) is also a base. Consider the R-homomorphism f of R(n) into M such that (al, …,an)![]() ∑aixi. We have the exact sequence
∑aixi. We have the exact sequence
![]()
Localizing at P, we obtain the exact sequence
![]()
Since MP is free with base (x1/l, …, xn/l), fP is an isomorphism and hence ker fP = 0, coker fp = 0. Since M is finitely generated, so is its homomorphic image coker f and since coker fp, ≅ (coker f)P, it follows from Proposition 7.5 that we have an element b ![]() P such that b(coker f) = 0. Then (coker f)
P such that b(coker f) = 0. Then (coker f)![]() = 0 and we have the exact sequence
= 0 and we have the exact sequence
![]()
Since M![]() is projective, this splits, so ker f
is projective, this splits, so ker f![]() is isomorphic to a homomorphic image of R(n)
is isomorphic to a homomorphic image of R(n)![]() and hence this is finitely generated. Since
and hence this is finitely generated. Since ![]() is a submonoid of R – P, 0 = (ker f)P ≅ ker fp, is obtained by a localization of (ker f)
is a submonoid of R – P, 0 = (ker f)P ≅ ker fp, is obtained by a localization of (ker f)![]() (Proposition 7.4). Since (ker f)
(Proposition 7.4). Since (ker f)![]() is finitely generated, this implies that there exists an element c/1, c
is finitely generated, this implies that there exists an element c/1, c ![]() P such that (c/1) (ker f)
P such that (c/1) (ker f)![]() = 0. Then ker f
= 0. Then ker f![]() = 0. Hence if we put a = bc, then a
= 0. Hence if we put a = bc, then a ![]() P and we have
P and we have
![]()
so M![]() ≅ R(n)
≅ R(n)![]() is free. This complates the proof.
is free. This complates the proof. ![]()
THEOREM 7.8. The map rM: P ![]() nP(M) of Spec R into
nP(M) of Spec R into ![]() (with discrete topology) is continuous.
(with discrete topology) is continuous.
Proof Let P be any point in Spec R. We have to show that there exists an open set O containing P such that nQ = nP for all Q in O. Take O = Xa where a is as in Proposition 7.20. Then P ∈ Xa and if Q ∈ Xa, then MQ is a localization of M![]() , which is a free R
, which is a free R![]() -module of rank n. Then the rank of MQ is n. Thus nQ = n = nP.
-module of rank n. Then the rank of MQ is n. Thus nQ = n = nP. ![]()
If Spec R is connected, the continuity of the map rM implies that nP = nQ for all P, Q ∈ Spec R. Hence we have the
COROLLARY. If R is connected, that is, R has no idempotents ≠ 0, 1, then the rank is defined for every finitely generated projective R-module.
Again let M be a finitely generated projective module and consider the continuous map rM of Spec R into ![]() . Since
. Since ![]() has the discrete topology, any integer n is an open and closed subset of
has the discrete topology, any integer n is an open and closed subset of ![]() and r–1M(n) is an open and closed subset of Spec R. Moreover, Spec R is a disjoint union of these sets. Since Spec R is quasi-compact, the number of non-vacuous sets r–1M(n) is finite. Thus we have positive integers nl, …, ns such that r–1M(ni) ≠ Ø and X = Spec R =
and r–1M(n) is an open and closed subset of Spec R. Moreover, Spec R is a disjoint union of these sets. Since Spec R is quasi-compact, the number of non-vacuous sets r–1M(n) is finite. Thus we have positive integers nl, …, ns such that r–1M(ni) ≠ Ø and X = Spec R = ![]() r–1M(ni). By Theorem 7.3, the open and closed subset r–1M(ni) has the form Xel for an idempotent ei ∈ R. Since
r–1M(ni). By Theorem 7.3, the open and closed subset r–1M(ni) has the form Xel for an idempotent ei ∈ R. Since ![]() ,
, ![]() . Thus the ei are orthogonal idempotents in R with sum 1 and hence R = R1
. Thus the ei are orthogonal idempotents in R with sum 1 and hence R = R1![]() …
… ![]() RS where Ri = Rei and M = M1
RS where Ri = Rei and M = M1![]() …
… ![]() Ms where Mi = eiM = RiM. It is clear from the dual basis lemma (Proposition 3.11, p. 152) that Mi is a finitely generated projective Ri-module. We claim that Mi has a rank over Ri and this rank is ni. Let Pi be a prime ideal in Ri. Then
Ms where Mi = eiM = RiM. It is clear from the dual basis lemma (Proposition 3.11, p. 152) that Mi is a finitely generated projective Ri-module. We claim that Mi has a rank over Ri and this rank is ni. Let Pi be a prime ideal in Ri. Then ![]() is a prime ideal in R not containing ei, so P ∈ Xel and P contains every ej, j ≠ i. We have
is a prime ideal in R not containing ei, so P ∈ Xel and P contains every ej, j ≠ i. We have ![]() and since ei ∈ P and eiRj = 0 for j ≠ i, RP = RiP. Similarly MP = MiP. Hence the rank of MiP over RiP is ni. We have the homomorphism r
and since ei ∈ P and eiRj = 0 for j ≠ i, RP = RiP. Similarly MP = MiP. Hence the rank of MiP over RiP is ni. We have the homomorphism r ![]() rei of R into Ri in which the elements of R – P are mapped into elements of Ri–Pi. Following this with the canonical homomorphism of Ri into RiPl gives a homomorphism of R into RiPl in which the elements of R–P are mapped into invertible elements. Accordingly, we have a homomorphism of RP into RiPl and we can use this to regard RiPl as RP-module. Then MiPl = RiPl
rei of R into Ri in which the elements of R – P are mapped into elements of Ri–Pi. Following this with the canonical homomorphism of Ri into RiPl gives a homomorphism of R into RiPl in which the elements of R–P are mapped into invertible elements. Accordingly, we have a homomorphism of RP into RiPl and we can use this to regard RiPl as RP-module. Then MiPl = RiPl![]() RpMiPl and since MiP is a free RiP module of rank ni, MiPl is a free RiPl module of rank ni. Since this holds for every prime ideal Pi of Ri, we see that the rank of Mi over Ri is ni. A part of what we have proved can be stated as
RpMiPl and since MiP is a free RiP module of rank ni, MiPl is a free RiPl module of rank ni. Since this holds for every prime ideal Pi of Ri, we see that the rank of Mi over Ri is ni. A part of what we have proved can be stated as
THEOREM 7.9. Let M be a finitely generated projective module over a commutative ring R. Then there are only a finite number of values for the ranks nP(M) for the prime ideal P of R. If these values are n1,…,ns, then R = R![]() …
… ![]() RS where the Ri are ideals such that RiM is finitely generated projective over Ri of rank ni.
RS where the Ri are ideals such that RiM is finitely generated projective over Ri of rank ni.
EXERCISES
1. Let M be a finitely generated projective module over the commutative ring R and let P be a maximal ideal of R. Show that if M has a rank over R, then this is the dimensionality of M/PM regarded as vector space over the field R/P.
2. Let M and R be as in exercise 1 and assume that R is an algebra over R′ such that R is finitely generated projective over R′ . Suppose that M has a rank over R and R has a rank over R′ . Show that M has a rank over R′ and rank M/R′ = (rank M/R) (rank R/R).
3. Show that if D is a domain, then any finitely generated projective module M over D has a rank and this coincides with the dimensionality of F![]() DM over F where F is the field of fractions of D.
DM over F where F is the field of fractions of D.
7.9 PROJECTIVE CLASS GROUP
We now make contact again with the Morita theory. We recall that if R′ and R are rings, an R′ -R-bimodule M is said to be invertible if there exists an R-R′-bimodule M′ such that M′ ![]() R′ M ≅ R as R-R-bimodule and M
R′ M ≅ R as R-R-bimodule and M![]() RM′ ≅ R′ as R′-R′ -bimodule. This is the case if and only if M is a progenerator of mod-R (R′ -mod). Then R′ ≅ End MR as rings and M′ ≅ hom (MR, RR) as R-R′ -bimodule. If R′ = R, the isomorphism classes of invertible bimodules form a group Pic R in which the multiplication is given by tensor products. Now suppose R is commutative. We restrict our attention to the R-R-bimodules in which the left action is the same as the right action. In effect we are dealing with (left) R-modules. The isomorphism classes of invertible modules constitute a subgroup of Pic R that is called the projective class group of the commutative ring R. The following result identifies the modules whose isomorphism classes constitute the projective class group.
RM′ ≅ R′ as R′-R′ -bimodule. This is the case if and only if M is a progenerator of mod-R (R′ -mod). Then R′ ≅ End MR as rings and M′ ≅ hom (MR, RR) as R-R′ -bimodule. If R′ = R, the isomorphism classes of invertible bimodules form a group Pic R in which the multiplication is given by tensor products. Now suppose R is commutative. We restrict our attention to the R-R-bimodules in which the left action is the same as the right action. In effect we are dealing with (left) R-modules. The isomorphism classes of invertible modules constitute a subgroup of Pic R that is called the projective class group of the commutative ring R. The following result identifies the modules whose isomorphism classes constitute the projective class group.
THEOREM 7.10. Let R be a commutative ring, M an R-module. Then M is invertible if and only if it is faithful finitely generated projective and rank M = 1.
Proof. Suppose that M is invertible and M′ is an R-module such that M![]() RM′ ≅ R. Then M and M′ are finitely generated projective. Let P be a prime ideal in R. Then M
RM′ ≅ R. Then M and M′ are finitely generated projective. Let P be a prime ideal in R. Then M![]() RM′ ≅ R implies that MP
RM′ ≅ R implies that MP![]() RpM′ P ≅ RP. Since these modules are free of finite rank over the local ring RP, this relation implies that rank MP/RP = 1. Since this holds for all P, we see that rank M = 1. Conversely, suppose that M satisfies the stated conditions and let M* = homR(M,R). Since M is faithful finitely generated projective, M is a progenerator by Theorem 3.22. Hence, as in the Morita theory, we have the isomorphism μ of M
RpM′ P ≅ RP. Since these modules are free of finite rank over the local ring RP, this relation implies that rank MP/RP = 1. Since this holds for all P, we see that rank M = 1. Conversely, suppose that M satisfies the stated conditions and let M* = homR(M,R). Since M is faithful finitely generated projective, M is a progenerator by Theorem 3.22. Hence, as in the Morita theory, we have the isomorphism μ of M![]() RM* onto EndRM sending x
RM* onto EndRM sending x![]() y*, x ∈ M, y* ∈ M*, into the map y
y*, x ∈ M, y* ∈ M*, into the map y ![]() y*(y)x. Since R is commutative, any r ∈ R determines an R-endomorphism y
y*(y)x. Since R is commutative, any r ∈ R determines an R-endomorphism y ![]() ry. We can identify R with this set of endomorphisms and so EndR M ⊃ R. Hence to show that M
ry. We can identify R with this set of endomorphisms and so EndR M ⊃ R. Hence to show that M ![]() R M* ≅ R, it suffices to prove that EndRM = R. This will follow if we can show that (EndRM)P = RP for every prime ideal P. Now (EndRM)P ≅ RP
R M* ≅ R, it suffices to prove that EndRM = R. This will follow if we can show that (EndRM)P = RP for every prime ideal P. Now (EndRM)P ≅ RP![]() REndRM Since M is finitely generated projective, it is easily seen that RP
REndRM Since M is finitely generated projective, it is easily seen that RP![]() REndRM ≅ EndRpMp (see the proof of Proposition 3.14, p. 154). Now if M is a free module of rank n over a commutative ring R, then EndRM is a free module of rank n2 over R (≅ Mn(R)). By hypothesis, MP has rank 1 over RP. Hence EndRpMP has rank 1 over RP. Thus (EndRM)P has rank 1 over RP and hence (EndRM)P = RP for every P. This completes the proof.
REndRM ≅ EndRpMp (see the proof of Proposition 3.14, p. 154). Now if M is a free module of rank n over a commutative ring R, then EndRM is a free module of rank n2 over R (≅ Mn(R)). By hypothesis, MP has rank 1 over RP. Hence EndRpMP has rank 1 over RP. Thus (EndRM)P has rank 1 over RP and hence (EndRM)P = RP for every P. This completes the proof. ![]()
We shall not give any examples of projective class groups at this point. Later (section 10.6) we shall see that if R is an algebraic number field, then this group can be identified with a classical group of number theory.
7.10 NOETHERIAN RINGS
In the remainder of this chapter we shall be interested primarily in noetherian rings and modules. We recall that the noetherian condition that a module satisfy the ascending chain condition for submodules is equivalent to the maximum condition that every non-vacuous set of submodules contains submodules that are maximal in the set, and equivalent to the “finite basis condition” that every submodule has a finite set of generators (p. 103, exercise 1). We recall also that a (commutative) ring is noetherian if it is noetherian as a module with respect to itself, which means that every properly ascending chain of ideals in the ring terminates, that every non-vacuous set of ideals contains maximal ones, and that every ideal has a finite set of generators. Moreover, any one of these conditions implies the other two. In 1890 Hilbert based a proof of a fundamental theorem in invariant theory on the following theorem :
HILBERT’S BASIS THEOREM. If R is a field or the ring of integers, then any ideal in the polynomial ring R[x1,x2, …, xr], xi indeterminates, has a finite set of generators.
Hilbert’s proof admits an immediate extension of his basis theorem to
HILBERT’S (GENERALIZED) BASIS THEOREM. If R is a ring such that every ideal in R is finitely generated, then every ideal in R[xx,… ,xr] is finitely generated.
Proof. Using induction it evidently suffices to prove the theorem for the case of one indeterminate x. We have to show that any ideal B of R[x] has a finite set of generators. Let j = 0, 1,2,… and let Ij = Ij(B) be the set of elements bj ∈ R such that there exists an element of the form
![]()
It is evident that Ij is an ideal in R, and since fj ∈ B implies that xfj = bjxj+1 + … ∈ B, it is clear that Ij ⊂ Ij+ 1 Hence I = ![]() Ij is an ideal in R. This has a finite set of generators, and we may assume that these are contained in one of the ideals Im. If {bm(1), … ,b{k)m} are these generators, we have polynomials
Ij is an ideal in R. This has a finite set of generators, and we may assume that these are contained in one of the ideals Im. If {bm(1), … ,b{k)m} are these generators, we have polynomials ![]() where deg gm(i) < m. Similarly, since every Ij is finitely generated for j < m, we have polynomials
where deg gm(i) < m. Similarly, since every Ij is finitely generated for j < m, we have polynomials ![]() where deg gj(ij) < j and 1 ≤ ij ≤ kj. We claim that the finite set of polynomials
where deg gj(ij) < j and 1 ≤ ij ≤ kj. We claim that the finite set of polynomials
![]()
generate B. Let f ∈ B. We prove by induction on n = deg f that f = ![]() for suitable hij ∈ R[x]. This is clear if f = 0 or deg f = 0, so we assume that f = bnxn + f1 where bn ≠ 0 and deg f1 < n. Then bn ∈ In ⊂ I. If n ≥ m, then bn =
for suitable hij ∈ R[x]. This is clear if f = 0 or deg f = 0, so we assume that f = bnxn + f1 where bn ≠ 0 and deg f1 < n. Then bn ∈ In ⊂ I. If n ≥ m, then bn = ![]() and has the same leading coefficient as f. Hence deg (f – ∑aixn–mf(i)m) < n. Since this polynomial is in B, the result follows by induction. If n < m, we have bn =
and has the same leading coefficient as f. Hence deg (f – ∑aixn–mf(i)m) < n. Since this polynomial is in B, the result follows by induction. If n < m, we have bn = ![]() . Again the result follows by induction.
. Again the result follows by induction. ![]()
An alternative version of Hilbert’s theorem is that if R is noetherian, then so is the polynomial ring R[x …, xr]. We also have the following stronger result.
COROLLARY. Let R be noetherian and R′ an extension ring of R, which is finitely generated (as algebra) over R. Then R′ is noetherian.
Proof. The hypothesis is that R′ = R[u1, …, ur] for certain u ∈ R′ . Then R′ is a homomorphic image of R[x1, …, xr], xi indeterminates. Since R[x1, …, xr] is noetherian, so is R′ . ![]()
There is another important class of examples of noetherian rings: rings of formal power series over noetherian rings. If R is an arbitrary ring, we can define the ring R[[x]] of formal power series over R as the set of unrestricted sequences
![]()
ai ∈ R with addition defined component-wise, 0 = (0, 0, …), 1 = (1, 0,0, …), and product ab for a as above and b = (b0,b1, …) defined as c = (c0, cl, …) where

It is easily checked that R[[x]] is a ring (exercise 7, p. 127 of BAI). It is clear that R can be identified with the subring of R[[x]] of elements (a0,0, 0, …) and R[x] with the subring of sequences (a0, a1, …, an,0, 0, …), that is, the sequence having only a finite number of non-zero terms (BAI, pp. 116–118).
In dealing with formal power series, the concept of order of a series takes the place of the degree of a polynomial. If a = (a0, al, …), we define the order o(a) by
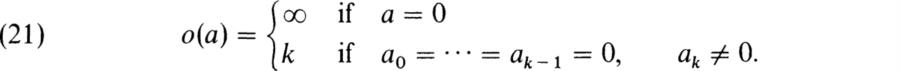
Then we have
![]()
and
![]()
If R is a domain, then (22) can be strengthened to o(ab) = o(a) + o(b). In any case if we define
![]()
(with the convention that 2– ∞ = 0), then we have the following properties of the map a ![]() |a| of R[[x]] into
|a| of R[[x]] into ![]() :
:
(i) |a| ≥ 0 and |a| = 0 if and only if a = 0.
(ii) |a + b| ≤ max (|a|, |b|).
(iii) |ab| ≤ |a| |b|.
The second of these implies that |a + b| ≤ |a| + |b|. Hence (i) and (ii) imply that R[[x]] is a metric space with distance function d(a, b) =|a – b|. We can therefore introduce the standard notions of convergence of sequences and series, Cauchy sequences etc.
We say that the sequence {a{i)}, a(i) ∈ R[[x]], i = 1, 2, 3,…, converges to a ∈ R[[x]] if for any real ε > 0 there exists an integer N = N(ε) such that |a – a(i)| < ε for all i ≥ N. Then we write lim a(i) = a. The sequence {a(i)} is called a Cauchy sequence if given any ε > 0 there exists an integer N such that |a(i) – a(j)| < ε for all i,j ≥ N. R[[x]] is complete relative to its metric in the sense that every Cauchy sequence of elements in R[[x]] converges. For, let {a(i)} be a Cauchy sequence in R[[x]]. Then for any integer n ≥ 0 we have an N such that o(a(i) – a(j)) > n or all i,j ≥ N. Let an be the entry in the (n + l)-st place of a(N). Then every a(i), i ≥ N, has this element as its (n + l)-st entry. It is readily seen that if we take a = (a0,a1,a2, …), then lim a(i) = a.
We can also define convergence of series in the usual way. We say that a(1) + a(2)+ … = a if the sequence of partial sums a(1),a(1) + a(2),… converges to a.
If we put x = (0, 1,0,…), then xi has 1 in the (i + l)th place, 0’s elsewhere. It follows that if a = (a0,al,a2, …) and we identify aj with (aj,0, 0, …), then we can write
![]()
It is clear that if R is a domain, then so is R[[x]]. It is also easy to determine the units of R[[x]], namely, ∑aixi is a unit if and only if a0 is a unit in R. The condition is clearly necessary. To see that it is sufficient, we write ∑∞0 aixi = a0(1 – z) where z = ∑∞1 bjxj and bj = – a0– 1aj. Then o(z) ≥ 1 and o(zk) ≥ k. Hence 1 + z + z2 + … exists. It is readily seen that
![]()
Hence ∑∞0 aixi = a0(l – z) is a unit with inverse a0– 1 ( ∑∞0 zi). It is clear also that the set of power series ∑∞1bixi of order > 0 is an ideal in R[[x]]. An immediate consequence of these remarks is
PROPOSITION 7.23. If F is a field, then F[[x]] is a local ring.
Proof. The set of elements ∑∞0aixi that are not units is the set for which a0 = 0. This is an ideal. Thus the non-units constitute an ideal and hence F[[x]] is local. ![]()
It is easily seen also that if R is local, then so is R[[x]]. We leave the proof to the reader.
We shall prove next the following important
THEOREM 7.11. If R is noetherian, then so is R[[x]].
Proof. The proof is quite similar to the proof of the Hilbert basis theorem. Let B be an ideal. For any j = 0, 1,2,… let Ij be the set of bj ∈ R such that there exists an element fj = bjxj + gj ∈ B where o(gj) > j. Then Ij is an ideal in R and I0 ⊂ I1 ⊂ …, so I = ![]() Ij is an ideal in R. Since R is noetherian, I has a finite set of generators and all of these are contained in Im for some m. Let these generators be bm(1) …, bm(k). It is clear from (22) and (23) that the set of elements of R[[x]] of order ≥ m form an ideal. The intersection of this set with B is an ideal Bm in R[[x]] containing the elements fm(i), 1 ≤ i ≤ k. Now let f ∈ Bm and suppose f = bnxn + g where bn ∈ R, n ≥ m and o(g) > n. Then bn = ∑iaibn(i) for ai ∈ R and
Ij is an ideal in R. Since R is noetherian, I has a finite set of generators and all of these are contained in Im for some m. Let these generators be bm(1) …, bm(k). It is clear from (22) and (23) that the set of elements of R[[x]] of order ≥ m form an ideal. The intersection of this set with B is an ideal Bm in R[[x]] containing the elements fm(i), 1 ≤ i ≤ k. Now let f ∈ Bm and suppose f = bnxn + g where bn ∈ R, n ≥ m and o(g) > n. Then bn = ∑iaibn(i) for ai ∈ R and
Iteration of this process yields a sequence of integers n1 = n – m < n2 < n3… and elements aij ∈ R, 1 ≤ i ≤ k, j = 1, 2,… such that

r = 1, 2,…. Then ai = ∑∞j = 1 aijxnJ is well defined and ![]() . Now consider the ideals Ij, 0 ≤ j < m. Choose a set of generators {b(1)j,…,bj(kJ)} for Ij and
. Now consider the ideals Ij, 0 ≤ j < m. Choose a set of generators {b(1)j,…,bj(kJ)} for Ij and ![]() . Then, as in the polynomial case,
. Then, as in the polynomial case,
![]()
is a set of generators for B. ![]()
We can iterate the process for forming formal power series to construct R[[x, y]]= (R[[x]]) [[y]], etc. We can also mix this construction with that of forming polynomial extensions. If we start with a noetherian R and perform these constructions a finite number of times, we obtain noetherian rings.
Another construction that preserves the noetherian property is described in the following
THEOREM 7.12. Let R be noetherian and let S be a submonoid of the multiplicative monoid ofR. Then the localization Rs is noetherian.
Proof. Let B′ be an ideal in Rs. As on p. 401 let j(B′ ) be the set of elements b ∈ R such that b/s ∈ B′ for some s ∈ S. Then j(B′ ) is an ideal in R and j(B′ )s = B′ . Since R is noetherian, j(B′ ) has a finite set of generators {b1, …, bm}. Then the set {b1/1, …, bm/1} ⊂ = B′ and generates this ideal. ![]()
1. Show that if I is an ideal in a commutative ring R such that I is not finitely generated and every ideal properly containing I is finitely generated, then I is prime. Use this to prove that if every prime ideal in R is finitely generated, then R is noetherian.
2. If R is a ring, we define the ring of formal Laurent series R((x)) over R as the set of sequences (ai), – ∞ < i < ∞, ai ∈ R such that there exists an integer n (depending on the sequence) such that ai = 0 for i < n. Define addition and multiplication as for power series. Show that R((x)) is a localization of R[[x]] and hence that R((x)) is noetherian if R is noetherian. Show that if R is a field, so is R((x)), and R((x)) contains the field R(x) of rational expressions in x.
3. (Emmy Noether’s finiteness theorem on invariants of a finite group.) Let E = F[u1,…,um] be a finitely generated algebra over the field F and let G be a finite group of automorphisms of E/F. Let Inv G = {y ∈ E|sy = y, s ∈ G}. Show that Inv G is a finitely generated algebra over F. (Sketch of proof. Let fi(x) = ∏s∈G(x – sui) = xn – Pi1xn – 1 + Pi2xn – 2 –… , where x is an indeterminate. Then I = F[p11,… ,pmm] ⊂ Inv G and E is integral over I. Hence, by exercise 1, p. 411, E is a finitely generated I-module. Since I is noetherian, Inv G is finitely generated, say by v1, …, vr. Then Inv G = F[p1 1, … pmn,v1, …, vr].)
7.11 COMMUTATIVE ARTINIAN RINGS
The study of artinian rings constitutes a major part of the structure theory of rings as developed in Chapter 4. It is interesting to see how this theory specializes in the case of commutative rings, and to consider relations between the artinian and noetherian conditions. Our first result in this direction is valid for rings that need not be commutative.
THEOREM 7.13. If R is a ring that is left (right) artinian, then R is left (right) noetherian. Moreover, R has only a finite number of maximal ideals.
Proof. Let J = rad R, the Jacobson radical of R. By Theorem 4.3 (p. 202), J is nilpotent, so we have an integer n such that Jn = 0. We have the sequence of ideals R ⊃ J ⊃ J2 ⊃ … ⊃ Jn = 0. We regard R as left R-module. Then we have the sequence of R-modules ![]() i = Ji/Ji + 1 where J0 = R and all of these are annihilated by J, so they may be regarded as modules for the semi-primitive artinian ring
i = Ji/Ji + 1 where J0 = R and all of these are annihilated by J, so they may be regarded as modules for the semi-primitive artinian ring ![]() = R/J. Since all modules of a semi-primitive artinian ring are completely reducible (Theorem 4.4, p. 208), this is the case for the modules
= R/J. Since all modules of a semi-primitive artinian ring are completely reducible (Theorem 4.4, p. 208), this is the case for the modules ![]() i. Moreover, any completely reducible artinian (noetherian) module is noetherian (artinian) and hence has a composition series. Accordingly, for each
i. Moreover, any completely reducible artinian (noetherian) module is noetherian (artinian) and hence has a composition series. Accordingly, for each ![]() i we have a sequence of submodules
i we have a sequence of submodules
![]()
such that every ![]() ij/
ij/![]() i,j + 1 is irreducible, and these can be regarded as R-modules. Corresponding to these we have a sequence of left ideals Mi1 = Ji ⊃ Mi2 ⊃ … ⊃ Mi, n +1 = Ji+1 such that Mij/Mi,j + 1 is an irreducible R-module. Putting together these sequences we obtain a composition series for R as left R-module. The existence of such a series implies that R is left noetherian as well as left artinian. The same argument applies to right artinian rings. This proves the first statement of the theorem.
i,j + 1 is irreducible, and these can be regarded as R-modules. Corresponding to these we have a sequence of left ideals Mi1 = Ji ⊃ Mi2 ⊃ … ⊃ Mi, n +1 = Ji+1 such that Mij/Mi,j + 1 is an irreducible R-module. Putting together these sequences we obtain a composition series for R as left R-module. The existence of such a series implies that R is left noetherian as well as left artinian. The same argument applies to right artinian rings. This proves the first statement of the theorem.
To prove the second, we note that any maximal ideal I of R contains J and ![]() = I/J is a maximal ideal of the semi-primitive artinian ring
= I/J is a maximal ideal of the semi-primitive artinian ring ![]() . We have
. We have ![]() where the
where the ![]() i are minimal ideals. It follows that the only maximal ideals of
i are minimal ideals. It follows that the only maximal ideals of ![]() are the ideals
are the ideals ![]() and that the only maximal ideals of R are the ideals Mj = R1 + … + R j – i + Rj + 1 + … + Rs where Rj is the ideal in R such that
and that the only maximal ideals of R are the ideals Mj = R1 + … + R j – i + Rj + 1 + … + Rs where Rj is the ideal in R such that ![]() j = Rj/J.
j = Rj/J. ![]()
For commutative rings we have the following partial converse to Theorem 7.13.
THEOREM 7.14. If R is a commutative noetherian ring that has only a finite number of prime ideals and all of these are maximal, then R is artinian.
Proof. Since the Jacobson radical J is the intersection of the maximal ideals of R and the nil radical N is the intersection of the prime ideals of R, the hypothesis that the prime ideals are maximal implies that J = N. Hence J is a nil ideal and since R is noetherian, J is finitely generated. As is easily seen, this implies that J is nilpotent. Since R contains only a finite number of maximal ideals, ![]() = R/J is a subdirect product of a finite number of fields. Then
= R/J is a subdirect product of a finite number of fields. Then ![]() is a direct sum of a finite number of fields (Lemma on p. 202) and hence
is a direct sum of a finite number of fields (Lemma on p. 202) and hence ![]() is artinian. As in the proof of Theorem 7.11, we have the chain of ideals R ⊃ J ⊃ … ⊃ Jn – 1 Jn = 0 and every Ji/Ji + 1 is a completely reducible noetherian module for the semi-primitive artinian ring
is artinian. As in the proof of Theorem 7.11, we have the chain of ideals R ⊃ J ⊃ … ⊃ Jn – 1 Jn = 0 and every Ji/Ji + 1 is a completely reducible noetherian module for the semi-primitive artinian ring ![]() . Then Ji/Ji + 1 has a composition series and R has a composition series as R-module. Then R is artinian.
. Then Ji/Ji + 1 has a composition series and R has a composition series as R-module. Then R is artinian. ![]()
It is easy to determine the structure of commutative artinian rings. This is given in the following
THEOREM 7.15. Let R be a commutative artinian ring. Then R can be written in one and only one way as a direct sum R = R1 ![]() R2
R2 ![]() …
… ![]() Rs where the Ri are artinian and noetherian local rings and hence the maximal ideal of Ri is nilpotent. Conversely, if R = R1
Rs where the Ri are artinian and noetherian local rings and hence the maximal ideal of Ri is nilpotent. Conversely, if R = R1 ![]() …
… ![]() Rs where the Ri are noetherian local rings with nilpotent maximal ideals, then R is artinian.
Rs where the Ri are noetherian local rings with nilpotent maximal ideals, then R is artinian.
Proof. We base the proof of the first part on the results on modules that we obtained in connection with the Krull-Schmidt theorem (pp. 110–115) and the fact that for a commutative ring R we have the isomorphism R ![]() EndRR. We have seen that R has a composition series as R-module. Hence R = R1
EndRR. We have seen that R has a composition series as R-module. Hence R = R1 ![]() …
… ![]() Rs where the Ri are indecomposable R-modules with composition series. Hence EndRRi is a local ring. Now Ri
Rs where the Ri are indecomposable R-modules with composition series. Hence EndRRi is a local ring. Now Ri ![]() EndRiRi = EndRRi, so Ri is a local ring. Now there is only one decomposition of a ring into indecomposable ideals (p. 204). Hence the Ri are unique. The artinian property of R carries over to the Ri. Hence, by Theorem 7.13, every Ri is also noetherian. It is clear also that the maximal ideal, rad Ri, of Ri is nilpotent.
EndRiRi = EndRRi, so Ri is a local ring. Now there is only one decomposition of a ring into indecomposable ideals (p. 204). Hence the Ri are unique. The artinian property of R carries over to the Ri. Hence, by Theorem 7.13, every Ri is also noetherian. It is clear also that the maximal ideal, rad Ri, of Ri is nilpotent.
To prove the converse, suppose first that R is a commutative local ring whose maximal ideal J is nilpotent. Let P be a prime ideal in R. Then P ⊂ J and Jn ⊂ P for some n. Since P is prime, this implies that J = P. Hence P is the only prime ideal of R. Since R is noetherian, R is artinian by Theorem 7.14. The general case in which R = R1 ![]() …
… ![]() Rs follows immediately from this special case.
Rs follows immediately from this special case.![]()
If R is an artinian ring and M is a finitely generated R-module, then M has a composition series since R is also noetherian and hence M is artinian and noetherian. We can therefore define the length l(M) of M as the length of any composition series for M. The use of the length provides a tool that is often useful in proving results on modules for artinian rings.
7.12 AFFINE ALGEBRAIC VARIETIES.THE HILBERT NULLSTELLENSATZ
Let F be an algebraically closed field, F(n) the n-dimensional vector space of n-tuples (a1,a2, … ,an), ai ∈ F, and F[x1,x2, … ,xn] the ring of polynomials in n indeterminates xi over F. If S is a subset of F[x1, … ,xn] we let V(S) denote the set of points (a1, … ,an) ∈ F(n) such that f(a1, … , an) = 0 for every f ∈ S and we call V(S) the (affine algebraic) variety defined by S. It is clear that V(S) = V(I) where I = (S), the ideal generated by S, and also V(I) = V(nilrad I). Hence if I1 and I2 are two ideals such that nilrad I1 = nilrad I2, then V(I1) = V(I2). A fundamental result, due to Hilbert, is tha t conversely if V(I1) = V(I2) for two ideals in F[x1, …, xn], F algebraically closed, then nilrad I1 = nilrad I2. There are a number of ways of proving this result. In this section we shall give a very natural proof, due to Seidenberg, which is based on Krull’s theorem that the nil radical of an ideal is the intersection of the prime ideals containing it and on a general theorem of elimination theory that we proved in a completely elementary fashion in BAI, pp. 322–325. For convenience we quote the theorem on elimination of unknowns:
Let K = ![]() or
or ![]() /(p), p a prime, and let A = K[t1, …, tr], B = A[x1, …, xn] where the t’s and x’s are indeterminates. Suppose Fl, …, Fm, G ∈ B. Then we can determine in a finite number of steps a finite collection
/(p), p a prime, and let A = K[t1, …, tr], B = A[x1, …, xn] where the t’s and x’s are indeterminates. Suppose Fl, …, Fm, G ∈ B. Then we can determine in a finite number of steps a finite collection ![]() where
where ![]() such that for any extension field F of K and any (c1, …, cr), ci ∈ F, the system of equations and inequations
such that for any extension field F of K and any (c1, …, cr), ci ∈ F, the system of equations and inequations

is solvable for x’s in some extension field E of F if and only if the ci satisfy one of the systems Γj:
![]()
Moreover, when the conditions are satisfied, then a solution of (27) exists in some algebraic extension field E of F.
For our present purposes the important part of this result is the last statement. This implies the following theorem, which perhaps gives the real meaning of the algebraic closedness property of a field.
THEOREM 7.16. Let F be an algebraically closed field and let f1, …, fm, g ∈ F[x1, …, xn] where the xi are indeterminates. Suppose that the system of equations and inequation
![]()
has a solution in some extension field E of F. Then (29) has a solution in F.
Proof. The field F has one of the rings K = ![]() or
or ![]() /(p) as its prime ring. Now by choosing enough additional indeterminates t1, …, tr we can define polynomials F1, …, Fm, G ∈ B as in the elimination theorem such that Fi(c1, …, cr; x1, …, xn) = fi(x1, …, xn), G(c1, …, cr; x1, …, xn) = g(x1, …, xn). Then it follows from the result quoted that, if (29) has a solution in some extension field E of F, then we have a j for which (28) holds, and this in turn implies that (29) has a solution in an algebraic extension field of F. Since F is algebraically closed, the only algebraic extension field of F is F itself (BAI, p. 216, or p. 460 below). Hence (29) is solvable in F.
/(p) as its prime ring. Now by choosing enough additional indeterminates t1, …, tr we can define polynomials F1, …, Fm, G ∈ B as in the elimination theorem such that Fi(c1, …, cr; x1, …, xn) = fi(x1, …, xn), G(c1, …, cr; x1, …, xn) = g(x1, …, xn). Then it follows from the result quoted that, if (29) has a solution in some extension field E of F, then we have a j for which (28) holds, and this in turn implies that (29) has a solution in an algebraic extension field of F. Since F is algebraically closed, the only algebraic extension field of F is F itself (BAI, p. 216, or p. 460 below). Hence (29) is solvable in F.![]()
Hilbert’s theorem, the so-called Nullstellensatz, is an immediate consequence of this result and the characterization of the nil radical as intersection of prime ideals.
NULLSTELLENSATZ. Let I be an ideal in the polynomial ring F[x1, …, xn] in n indeterminates xi over an algebraically closed field F and let g∈F[x1, …, xn]. Suppose g(al, …, an) = 0 for all (a1, …, an) on the variety V(I) defined by I. Then g ∈ nilrad I.
Proof. Suppose g ![]() nilrad I. Then there exists a prime ideal P ⊃ I such that g
nilrad I. Then there exists a prime ideal P ⊃ I such that g ![]() P. Consider the domain D = F[x1, …, xn]/P = F[
P. Consider the domain D = F[x1, …, xn]/P = F[![]() 1, …,
1, …, ![]() n] where
n] where ![]() i = xi + P. Then for f = f(x1, …, xn) ∈ I, f ∈ P and hence f(
i = xi + P. Then for f = f(x1, …, xn) ∈ I, f ∈ P and hence f(![]() 1, …,
1, …, ![]() n) = 0. On the other hand, g
n) = 0. On the other hand, g ![]() P, so g(
P, so g(![]() 1, …,
1, …, ![]() n) ≠ 0. Now F[x1, …, xn] is noetherian, so I has a finite set of generators f1, …, fm. Let E be the field of fractions of D. Then E is an extension field of F containing the elements
n) ≠ 0. Now F[x1, …, xn] is noetherian, so I has a finite set of generators f1, …, fm. Let E be the field of fractions of D. Then E is an extension field of F containing the elements ![]() 1, …,
1, …, ![]() n such that fi(
n such that fi(![]() 1, …,
1, …, ![]() n) = 0, 1 ≤ i ≤ m, g(
n) = 0, 1 ≤ i ≤ m, g(![]() 1, …,
1, …, ![]() n) ≠ 0. Hence by Theorem 7.14, there exist al, …, an ∈ F such that fi(a1, …, an) = 0, g(a1, … , an) ≠ 0. Since the fi generate I, we have f(a1, …, an) = 0 for all f ∈ I. This contradicts the hypothesis and proves that g ∈ nilrad I.
n) ≠ 0. Hence by Theorem 7.14, there exist al, …, an ∈ F such that fi(a1, …, an) = 0, g(a1, … , an) ≠ 0. Since the fi generate I, we have f(a1, …, an) = 0 for all f ∈ I. This contradicts the hypothesis and proves that g ∈ nilrad I.![]()
Evidently the Nullstellensatz implies that if I1 and I2 are ideals in F[x1, …, xn] such that V(I1) = V(I2), then I1 ⊂ nilrad I2 so nilrad I1⊂ nilrad (nilrad I2) = nilrad I2. By symmetry, nilrad I2 ⊂ nilrad I1 and so nilrad I1 = nilrad I2. An important special case of the Nullstellensatz is
THEOREM 7.17. If I is a proper ideal in F[x1, …, xn], F algebraically closed, then V(I) ≠ Ø.
Proof. If V(I) = Ø, then g = 1 satisfies the condition of the Nullstellensatz so 1 ∈ nilrad I and hence 1 ∈ I, contrary to the hypothesis that I is proper.![]()
The Nullstellensatz permits us also to determine the maximal ideals in F[x1, …, xn]. If (a1, …, an) ∈ F(n), the ideal Ma1, …, an = (x1 – a1, …, xn – an) is maximal in F[x1, …, xn] since F[x1, …, xn]/Ma1, …, an ![]() F. Evidently V(Ma1, …, an) consists of the single point (a1, …, an). If I is any proper ideal, the foregoing result and the Nullstellensatz imply that I ⊂ nilrad Ma1, …, an for some point (a1, …, an). Since Ma1, …, an is maximal, it coincides with its nilradical, so I ⊂ Ma1, …, an. Hence we see that the only maximal ideals of F[x1, …, xn] are those of the form Ma1, …, an. Moreover, since V(Ma1, …, an) = {(a1, …, an)}, we have the following result.
F. Evidently V(Ma1, …, an) consists of the single point (a1, …, an). If I is any proper ideal, the foregoing result and the Nullstellensatz imply that I ⊂ nilrad Ma1, …, an for some point (a1, …, an). Since Ma1, …, an is maximal, it coincides with its nilradical, so I ⊂ Ma1, …, an. Hence we see that the only maximal ideals of F[x1, …, xn] are those of the form Ma1, …, an. Moreover, since V(Ma1, …, an) = {(a1, …, an)}, we have the following result.
COROLLARY. If F is an algebraically closed field, then the map (a1, …, an) ![]() Ma1, …, an = (x1 – a1, …, xn – an) is a bijection of F(n) onto the set of maximal ideals of F[x1, …, xn].
Ma1, …, an = (x1 – a1, …, xn – an) is a bijection of F(n) onto the set of maximal ideals of F[x1, …, xn].
We now suppose that F is any infinite field and we consider again F(n) and F[x1, …, xn], and define the variety V(S) for a subset S of F[x1, …, xn] as in the algebraically closed case. Also if V1 is a variety, we let i(V1) denote the ideal of polynomials f ∈ F[x1, …, xn], which vanish for every (a1, …, an) ∈ V1. The following properties follow directly from the definition:
(1) V(F[x1, …, xn]) = Ø,
(2) V(Ø) = F(n),
(3) V(![]() Sα) =
Sα) = ![]() V(Sα),
V(Sα),
(4) V(S) = V(I) if I = (S), the ideal generated by S,
(5) V(I1I2) = V(I1) ∪ V(I2) for any ideals I1 and I2,
(6) V(S1) ⊃ V(S2) if S1 ⊂ S2,
(7) i(Ø) = F[x1, …, xn]
(8) i(V1) ⊃ i(V2) if V1 ⊂ V2,
(9) i(V(I1)) ⊃ I1 for any ideal I1,
(10) V(i(V1)) ⊃ V1 for any variety V1.
Relations (6), (8), (9), and (10) have the immediate consequences that
(11) V(i(V(I1))) = V(I1),
(12) i(V(i(V1))) = i(V1).
We now recall an important theorem, proved in BAI on p. 136, that if F is an infinite field and f(x1, …, xn) is a non-zero polynomial with coefficients in F, then there exist ai ∈ F such that f(a1, …, an) ≠ 0. Evidently this implies
(13) i(F(n)) = 0.
Relations (1)–(5) show that the set of varieties satisfy the axioms for closed subsets of a topological space. The resulting topology is called the Zariski topology of the space F(n). The open subsets in this topology are the sets F(n) – V, V a variety. If V = V(S), then F(n) – V = ∪f ∈ S (F(n) – V({f})). Thus the open sets 0f = (F(n) – V({f})) form a base for the open subsets of F(n). Evidently 0f is the set of points (a1, …, an) such that f(a1, …, an) ≠ 0.
We now observe that if F is algebraically closed (hence infinite), then F(n) with its Zariski topology is the same thing as the maximum spectrum of the ring F[x1, …, xn]. More precisely, we have a canonical homeomorphism between these two spaces. This is the map (a1, …, an) ![]() Ma1, …, an given in the corollary above. Since the condition that f(a1, …, an) = 0 for a polynomial f(x1, …, xn) is equivalent to f ∈ Ma1, …, an, the map we have defined induces a bijective map of the set of closed sets in F(n) with the set of closed sets in Maxspec (see p. 403). Hence we have a homeomorphism.
Ma1, …, an given in the corollary above. Since the condition that f(a1, …, an) = 0 for a polynomial f(x1, …, xn) is equivalent to f ∈ Ma1, …, an, the map we have defined induces a bijective map of the set of closed sets in F(n) with the set of closed sets in Maxspec (see p. 403). Hence we have a homeomorphism.
When F = ![]() or
or ![]() , the Zariski topology on F(n) has strikingly different properties from the usual Euclidean topology. Let us now consider some of these properties for F(n), F any infinite field. Since any point (a1, …, an) is the variety defined by the ideal Ma1, …, an = (x1 – a1, …, xn – an), it is clear that F(n) is a T1-space. However, it is not a Hausdorff space. On the contrary, F(n) is irreducible in the sense that any two non-vacuous open subsets of F(n) meet. In other words, any non-vacuous open subset is dense in F(n). Since the sets Of constitute a base, it suffices to see that if Of ≠ Ø and Og ≠ Ø, then Of ∩ Og ≠ Ø. The theorem on non-vanishing of polynomials implies that Of ≠ Ø if and only if f ≠ O. It is clear also that Of ∩ Og = Ofg. Since F[x1, …, xn] is a domain, it follows that Of ≠ Ø, Og ≠ Ø imply Of ∩ Og ≠ Ø.
, the Zariski topology on F(n) has strikingly different properties from the usual Euclidean topology. Let us now consider some of these properties for F(n), F any infinite field. Since any point (a1, …, an) is the variety defined by the ideal Ma1, …, an = (x1 – a1, …, xn – an), it is clear that F(n) is a T1-space. However, it is not a Hausdorff space. On the contrary, F(n) is irreducible in the sense that any two non-vacuous open subsets of F(n) meet. In other words, any non-vacuous open subset is dense in F(n). Since the sets Of constitute a base, it suffices to see that if Of ≠ Ø and Og ≠ Ø, then Of ∩ Og ≠ Ø. The theorem on non-vanishing of polynomials implies that Of ≠ Ø if and only if f ≠ O. It is clear also that Of ∩ Og = Ofg. Since F[x1, …, xn] is a domain, it follows that Of ≠ Ø, Og ≠ Ø imply Of ∩ Og ≠ Ø.
We note next that the space F(n) with the Zariski topology is noetherian in the sense that the ascending chain condition holds for open subsets of F(n). Equivalently the descending chain condition holds for varieties. Suppose that V1 ⊃ V2 ⊃ … is a descending chain of varieties. Then we have the ascending chain of ideals i(V1) ⊂ i(V2) ⊂ …, so there exists an m such that i(Vj) = i(Vj + 1) for all j ≥ m. Since Vj = V(i(Vj)), we have Vj = Vj + l for j ≥ m.
Let us now look at the simplest case: n = 1. Here the variety V({f}) defined by a single polynomial f is a finite set f ≠ 0 and is the whole space F if f = 0. Moreover, given any finite set {ai | 1 ≤ i ≤ r} we have V({f}) = {ai} for f = ∏(x – ai). It follows that the closed sets in the Zariski topology are the finite subsets (including the vacuous set) and the whole space. The open subsets of F are the vacuous set and the complements of finite sets. A subbase for the open sets is provided by the complements of single points, since any non-vacuous open set is a finite intersection of these sets.
It should be observed that the Zariski topology provides more open sets than one gets from the product topology obtained by regarding F(n) as product of n copies of F. For example, the open subset of F(n) defined by x1 + … + xn ≠ 0 cannot be obtained as a union of open subsets of the form O1 × 02 × … × On, Oi open in F.
Any polynomial f(x1, …, xn) defines a polynomial function
![]()
of F(n) into F. We have considered such functions in BAI, pp. 134–138. The theorem we quoted on non-vanishing of polynomials shows that the map sending the polynomial f(x1, …, xn) into the function defined by (30) is an isomorphism of F[x1, …, xn] onto the ring of polynomial functions. More generally, consider a second space F(m). Then a sequence (f1, …, fm), fi = fi(x1, …, xn), defines a polynomial map
![]()
of F(n) into F(m) Such maps are continuous of F(n) into F(m), both endowed with the Zariski topology. To see this we take any neighborhood Og of (f1(a1, …, an), …, fm(a1, …, an)). Then we have a polynomial g(x1, …, xm) such that g(f1(a1, …, an), …, fm(a1, …, an)) ≠ 0. Then h(x1, …, xn) = g(f1(x1, …, xn), …, fm(x1, …, xn) ≠ 0 in F[x1, …, xn] and Oh is mapped into Og by (31). Thus (31) is continuous. We remark that since non-vacuous open subsets are dense, to prove that a polynomial map is 0 (that is, sends every element into 0), it suffices to show this for a non-vacuous open subset.
These rudimentary algebraic geometric ideas are often useful in “purely algebraic” situations. Some illustrations of the use of the Zariski topology will be given in the following exercises.
EXERCISES
In all of these we assume F algebraically closed (hence infinite). The topologies are Zariski.
1. Let a ∈ Mn(F) and let fa(λ) = λn – tr(a) λn – 1 + … +(– l)n det a be the characteristic polynomial of a. Show that the maps a ![]() tr a, …, a
tr a, …, a ![]() det a are polynomial functions on the n2-dimensional vector space. Show that the set of invertible matrices is an open subset of Mn(F).
det a are polynomial functions on the n2-dimensional vector space. Show that the set of invertible matrices is an open subset of Mn(F).
2. Let {ρ1, …, ρn } be the characteristic roots of a (in some order) and let g(x1, …, xn) be a symmetric polynomial in the xi with coefficients in F. Show that the map a ![]() g(ρ1, …, ρn) is a polynomial function on Mn(F). Show that the set of matrices, which are similar to diagonal matrices with distinct diagonal entries, is an open subset of Mn(F).
g(ρ1, …, ρn) is a polynomial function on Mn(F). Show that the set of matrices, which are similar to diagonal matrices with distinct diagonal entries, is an open subset of Mn(F).
3. Let f, g ∈ F[x1, …, xn] and suppose that g(a1, …, an) = 0 for every (a1, …, an) such that f(a1, …, an) = 0. Show that every prime factor of f is a factor of g.
4. If a ∈ Mn(F), let Ua denote the linear transformation y ![]() aya of Mn(F) into itself. Let d(a) = det Ua. Use the Hilbert Nullstellensatz and Theorem 7.2 of BAI, p. 418, to prove that d(a) = (det a)2n.
aya of Mn(F) into itself. Let d(a) = det Ua. Use the Hilbert Nullstellensatz and Theorem 7.2 of BAI, p. 418, to prove that d(a) = (det a)2n.
5. Give an alternative proof of the result in exercise 4 by noting that it suffices to prove the relation for a in the open subset of matrices that are similar to diagonal matrices with non-zero diagonal entries. Calculate d(a) and de a for a diagonal matrix.
6. Show that the nil radical of any ideal in F[x1, …, xn] is the intersection of the maximal ideals containing it.
7. Let V be a variety in F(n). A polynomial function on V is defined to be a map p|V where p is a polynomial function on F(n). These form an algebra A(V) over F under the usual compositions of functions. Show that A(V) ![]() F[x1, …, xn]/i(V) = F[
F[x1, …, xn]/i(V) = F[![]() 1, …,
1, …, ![]() n],
n], ![]() i = xi + i(V). The latter algebra over F is called the coordinate algebra of the variety V. V is called irreducible if i(V) is prime. In this case the elements of the field of fractions of the coordinate algebra are called rational functions on V. If V′ is a variety in F(m), a map of V into V′ is called regular if it has the form g|V where g is a polynomial map of F(n) into F(m). Show that if p′ is a polynomial function on V′, then p′g is a polynomial function on V and the map η(g) : p′
i = xi + i(V). The latter algebra over F is called the coordinate algebra of the variety V. V is called irreducible if i(V) is prime. In this case the elements of the field of fractions of the coordinate algebra are called rational functions on V. If V′ is a variety in F(m), a map of V into V′ is called regular if it has the form g|V where g is a polynomial map of F(n) into F(m). Show that if p′ is a polynomial function on V′, then p′g is a polynomial function on V and the map η(g) : p′ ![]() p is an algebra homomorphism of A(V′) into A(V). Show that g
p is an algebra homomorphism of A(V′) into A(V). Show that g ![]() η(g) is a bijection of the set of regular maps of V into V′ and the set of algebra homomorphisms of A(V′) into A(V).
η(g) is a bijection of the set of regular maps of V into V′ and the set of algebra homomorphisms of A(V′) into A(V).
7.13 PRIMARY DECOMPOSITIONS
In this section we consider the classical Lasker-Noether decomposition theorems for ideals in noetherian rings as finite intersections of primary ideals. It is easy to see by using the ascending chain condition that any proper ideal I in a noetherian ring R can be written as an intersection of ideals that are indecomposable in the sense that I ≠ I1 ∩ I2 for any two ideals Ij ≠ I. Moreover, in any noetherian ring, indecomposable ideals are primary in a sense that we shall define in a moment. This type of decomposition is a weak analogue of the decomposition of an element as a product of prime powers. Associated with every primary ideal is a uniquely determined prime ideal. However, primary ideals need not be prime powers and not every prime power is primary. Although the decomposition into primary ideals is not in general unique, it does have some important uniqueness properties. The establishment of these as well as the existence of the primary decomposition are the main results of the Lasker-Noether theory. We shall begin with the uniqueness questions, since these do not involve the noetherian property. The classical results can be generalized to modules and the passage to modules makes the arguments somewhat more transparent. In our discussion we shall consider the general case of modules first and then specialize these to obtain the results on ideals.
If M is a module for R and a ∈ R, then as in section 3.1, we denote the map x ![]() ax, x ∈ M, by aM. Since R is commutative, this is an endomorphism of M as R-module. We have the homomorphism ρM : a
ax, x ∈ M, by aM. Since R is commutative, this is an endomorphism of M as R-module. We have the homomorphism ρM : a ![]() aM of R into the ring of endomorphisms of M and ker ρM is the set of a ∈ R such that ax = 0 for all x. As usual we write annRx for the ideal of elements b ∈ R such that bx = 0. Evidently ker ρM = ∩x ∈ M annRx = annRM. If ax = 0 for some x ≠ 0, then we shall call this element a of the ring R a zero divisor of the module M. The elements a that are not zero divisors are those for which aM is injective. We now look at the nil radical of the ideals ker ρM and annRx for a particular x. By definition, the first of these is the set of elements a ∈ R for which there exists an integer m such that am ∈ ker ρM, that is, amx = 0 for every x or, equivalently, aMm = (am)M = 0. Likewise a ∈ nilrad (annRx) if and only if there exists an m such that amx = 0 or, equivalently, the restriction of aM to the submodule Rx is nilpotent.
aM of R into the ring of endomorphisms of M and ker ρM is the set of a ∈ R such that ax = 0 for all x. As usual we write annRx for the ideal of elements b ∈ R such that bx = 0. Evidently ker ρM = ∩x ∈ M annRx = annRM. If ax = 0 for some x ≠ 0, then we shall call this element a of the ring R a zero divisor of the module M. The elements a that are not zero divisors are those for which aM is injective. We now look at the nil radical of the ideals ker ρM and annRx for a particular x. By definition, the first of these is the set of elements a ∈ R for which there exists an integer m such that am ∈ ker ρM, that is, amx = 0 for every x or, equivalently, aMm = (am)M = 0. Likewise a ∈ nilrad (annRx) if and only if there exists an m such that amx = 0 or, equivalently, the restriction of aM to the submodule Rx is nilpotent.
The case of primary interest is that in which M = R/I where I is an ideal in R. Since we shall need to consider simultaneously such a module and the modules R/I′ for I′ an ideal of R containing I and since ![]() , we need to formulate our definitions and results in terms of a module and a submodule. The style is set in the following
, we need to formulate our definitions and results in terms of a module and a submodule. The style is set in the following
DEFINITION 7.4. A submodule Q of an R-module M is called primary if Q ≠ M and for every a ∈ R either aM/Q is injective or it is nilpotent.
Evidently this means that if a is a zero divisor of M/Q, then there exists an integer m such that amx ∈ Q for every x ∈ M. The set P of elements satisfying this condition is the ideal nilrad (annR M/Q). This ideal is prime since if a ![]() P and b
P and b ![]() P, then aM/Q and bM/Q are injective. Then (ab)M/Q = aM/Q bM/Q is injective and hence ab
P, then aM/Q and bM/Q are injective. Then (ab)M/Q = aM/Q bM/Q is injective and hence ab ![]() P. We shall call P the prime ideal associated with the primary submodule Q. If M = R, the submodules are the ideals. Then the condition amx ∈ Q for every x ∈ R is equivalent to am ∈ Q. Thus in this case an ideal Q is primary if and only if ab ∈ Q, and b
P. We shall call P the prime ideal associated with the primary submodule Q. If M = R, the submodules are the ideals. Then the condition amx ∈ Q for every x ∈ R is equivalent to am ∈ Q. Thus in this case an ideal Q is primary if and only if ab ∈ Q, and b ![]() Q implies that there exists an m such that am ∈ Q. The associated prime of Q is the nilradical of this ideal.
Q implies that there exists an m such that am ∈ Q. The associated prime of Q is the nilradical of this ideal.
EXAMPLES
1. Let R be a p.i.d. and Q = (pe) = (pe), p a prime. It is readily seen that if a ∈ R and a ![]() P = (p), then aR/Q is invertible, hence injective. On the other hand, if a ∈ P, then aeR/Q = 0. Hence Q is primary and P is the associated prime ideal. It is easy to see also that 0 and the ideals (pe) are the only primary ideals in R.
P = (p), then aR/Q is invertible, hence injective. On the other hand, if a ∈ P, then aeR/Q = 0. Hence Q is primary and P is the associated prime ideal. It is easy to see also that 0 and the ideals (pe) are the only primary ideals in R.
2. Let R = ![]() and let M be a finite abelian group written additively and regarded as a
and let M be a finite abelian group written additively and regarded as a ![]() -module in the usual way. Suppose every element of M has order a power of a prime p. Then 0 is a p-primary submodule of M since if a ∈
-module in the usual way. Suppose every element of M has order a power of a prime p. Then 0 is a p-primary submodule of M since if a ∈ ![]() and (a, p) = 1, then aM is injective and if a is divisible by p, then aM is nilpotent. The associated prime ideal of 0 is (P).
and (a, p) = 1, then aM is injective and if a is divisible by p, then aM is nilpotent. The associated prime ideal of 0 is (P).
3. Let R = F[x, y, z]/(xy – z2) where F is a field and x, y , z are indeterminates. If a ∈ F[x, y, z], let ![]() be its image in R under the canonical homomorphism. Let P = (
be its image in R under the canonical homomorphism. Let P = (![]() ,
, ![]() ), the ideal in R generated by
), the ideal in R generated by ![]() ,
, ![]() . Then the corresponding ideal in F[ x, y, z] is (x, z), since this contains xy – z2. Since F[x, v, z]/(x, z)
. Then the corresponding ideal in F[ x, y, z] is (x, z), since this contains xy – z2. Since F[x, v, z]/(x, z) ![]() F [y], it follows that P is prime in R. Since it is clear from Krull’s theorem that the nilradical of any power of a prime ideal is this prime, the ideal P2 of R has P as its nilradical. However, this is not primary since
F [y], it follows that P is prime in R. Since it is clear from Krull’s theorem that the nilradical of any power of a prime ideal is this prime, the ideal P2 of R has P as its nilradical. However, this is not primary since ![]()
![]() P2,
P2, ![]()
![]() P but
P but ![]() .
.
We can obtain many examples of primary ideals by using the following
PROPOSITION 7.24. If P is a maximal ideal in R, any ideal Q between P and Pe, e ≥ 1, is primary with P as associated prime ideal.
Proof. If a ∈ P, then ae ∈ Pe ⊂ Q. If a ![]() P, then we claim that a + Q is a unit in R/Q. For, since P is maximal, R/P is a field. Hence we have an element a′ ∈ R and a z ∈ P such that aa′ = 1 – z. Since z + Q is nilpotent in R /Q, (1 – z) + Q is a unit in R/Q and hence a + Q is a unit in R/Q. It is now clear that if ab ∈ Q, then b ∈ Q. Thus we have shown that if a ∈ P, then aR/Q is nilpotent and if a
P, then we claim that a + Q is a unit in R/Q. For, since P is maximal, R/P is a field. Hence we have an element a′ ∈ R and a z ∈ P such that aa′ = 1 – z. Since z + Q is nilpotent in R /Q, (1 – z) + Q is a unit in R/Q and hence a + Q is a unit in R/Q. It is now clear that if ab ∈ Q, then b ∈ Q. Thus we have shown that if a ∈ P, then aR/Q is nilpotent and if a ![]() P, then aR/Q is injective. Then it is clear that Q is primary and P is the associated prime.
P, then aR/Q is injective. Then it is clear that Q is primary and P is the associated prime.![]()
This result can be used to construct examples of primary ideals that are not prime powers. For instance, let P = (x, y) in F[x, y]. This is maximal, since F[x, y]/P ![]() F. We have
F. We have ![]() . Hence (x2, y) is a primary ideal that is not a prime power.
. Hence (x2, y) is a primary ideal that is not a prime power.
It is clear that if Q is a submodule of M and P is a subset of R such that 1) if a ∈ P, then there exists an integer m such that amx ∈ Q for all x ∈ M and 2) if a ∈ R – P, then aM/Q is injective, then Q is primary with P as associated ideal. We use this to prove
PROPOSITION 7.25. The intersection of a finite number of primary submodules of M having the same associated prime ideal P is primary with P as associated prime ideal.
Proof. It suffices to prove this for two submodules Q1 and Q2. Then Q1 ∩ Q2 is a proper submodule since the Qi are proper. Let a ∈ P. Then we have an integer mi such that ![]() for all x ∈ M. If we take m = max(m1, m2), then amx ∈ Q = Q1 ∩ Q2. Next let a ∈ R – P and let x ∈ M – Q. We may assume that x
for all x ∈ M. If we take m = max(m1, m2), then amx ∈ Q = Q1 ∩ Q2. Next let a ∈ R – P and let x ∈ M – Q. We may assume that x ![]() Q1. Then ax
Q1. Then ax ![]() Q1 so ax
Q1 so ax ![]() Q. Thus aM/Q is injective. Hence Q is primary with P as associated prime ideal.
Q. Thus aM/Q is injective. Hence Q is primary with P as associated prime ideal.![]()
We have noted that for any x the set of a ∈ R such that there exists an integer m such that amx = 0 is the ideal nilrad(ann x). Hence if Q is a submodule and ![]() = x + Q in M/Q, then the set of a for which there exists an m such that amx ∈ Q is the ideal nilrad(annR
= x + Q in M/Q, then the set of a for which there exists an m such that amx ∈ Q is the ideal nilrad(annR![]() ). If Q is primary, we have the following important result.
). If Q is primary, we have the following important result.
PROPOSITION 7.26. Let Q be a primary submodule of M, P the associated prime, and let x ∈ M. Let Ix = {a|amx ∈ Q for some m}. Then Ix = P if x ![]() Q and Ix = R if x ∈ Q.
Q and Ix = R if x ∈ Q.
Proof. Let x ![]() Q. Evidently Ix ⊃ P, since aM/Q is nilpotent for every a ∈ P. On the other hand, if a
Q. Evidently Ix ⊃ P, since aM/Q is nilpotent for every a ∈ P. On the other hand, if a ![]() P, then aM/Q is injective. This precludes amx ∈ Q for any m. Hence Ix = P. The other assertion that if x ∈ Q, then Ix = R is clear.
P, then aM/Q is injective. This precludes amx ∈ Q for any m. Hence Ix = P. The other assertion that if x ∈ Q, then Ix = R is clear.![]()
Now let N be a finite intersection of primary submodules Qi of M: N = ![]() Qi. It may happen that some of these are redundant, that is, that N is an intersection of a proper subset of the Qi. In this case we can drop some of these until we achieve an irredundant decomposition N =
Qi. It may happen that some of these are redundant, that is, that N is an intersection of a proper subset of the Qi. In this case we can drop some of these until we achieve an irredundant decomposition N = ![]() Qi, which means that for every j, N ≠
Qi, which means that for every j, N ≠ ![]() i ≠ j Qi. This is equivalent to assuming that for every j,
i ≠ j Qi. This is equivalent to assuming that for every j, ![]()