10

Dedekind Domains

In this chapter we shall study the domains in which proper non-zero ideals can be factored in one and only one way as products of prime ideals. The most notable examples are the rings of -integral elements of number fields, that is, finite dimensional extension fields of the field (see BAI, pp. 278281), These are the objects of study of algebraic number theory. Another important class of examples are the rings that occur in the study of algebraic curves. Here we begin with a field F(x,y) where F is a base field (usually algebraically closed), x is transcendental over F, and y is algebraic over F(x). Then the subring of elements that are integral over F[x] has the factorization property stated above.

There are many equivalent ways of defining the class of domains, called Dedekind domains, in which the fundamental factorization theorem for ideals into prime ideals holds (see section 10.2). We shall take as our point of departure a definition based on the concepts of fractional ideals and of invertibility. The latter is equivalent to projectivity as a module for the given ring.

The result that the domains mentioned above are Dedekind can be deduced from a general theorem stating that if D is Dedekind with field of fractions F and E is a finite dimensional extension field of F, then the subring D′ of D-integral elements of E is a Dedekind domain. This is proved in section 10.3. In sections 10.4 and 10.5 we consider the central problem of studying the factorization in D′ of extensions of prime ideals of D. This is closely related to the problem of extension of valuations from F to E that was considered in chapter 9.

Besides the study of ideal theory, we consider the structure of finitely generated modules over Dedekind domains. The special case of torsion-free modules is a classical one that was first treated by E. Steinitz (see section 10.6).

Finally, we consider the class group of a Dedekind domain as defined in section 7.9 and we show in section 10.6 that this group has a concrete realization as a classical group defined by the fractional ideals.

10.1   FRACTIONAL IDEALS. DEDEKIND DOMAINS

Let D be a domain, F its field of fractions. It is useful to extend the concept of an ideal in D to certain submodules of F given in the following

DEFINITION 10.1.  If D is a domain and F is its field of fractions, a (D –) fractional ideal I is a non-zero D-submodule of F such that there exists a non-zero a in D such that aI ⊂ D(or, equivalently, aI ⊂ I ∩ D).

The fractional ideals contained in D are the non-zero ideals of D. These are called integral ideals. If I is a fractional ideal and a is a non-zero element of D such that aI ⊂ D, then aI is an integral ideal. If b is any non-zero element of F, then Db = {db\d ∈ D} is a fractional ideal since it is clearly a D-submodule of F and if b = ac^{− 1}, a, c ∈ D, then c(Db) ⊂ D. A fractional ideal of the form Db is called a principal ideal.

If I₁ and I₂ are fractional ideals, then so is the module sum I₁ + I₂ since this is a submodule, and if a_iI_i ⊂ D for a_i ≠ 0 in D, then a₁a₂(I₁ + I₂) ⊂ D. The intersection I₁ ∩ I₂ is a fractional ideal also since this is a D-submodule and I₁ ∩ I₂ ≠ 0 since if b_i ≠ 0 is in I_i we have an a_i ≠ 0 in D such that a_ib_i ∈ D ∩ I_i. Then (a₁ b₁)(a₂ b₂) ≠ 0 is in I₁ ∩ I₂. Moreover, if a ≠ 0 satisfies aI₁ ⊂ D, then a(I₁ ∩ I₂) ⊂ D. We define I₁ I₂ = {∑ b_1i b_2i|b_1i ∈ I₁, b_2i ∈ I₂}. Evidently this is a D-submodule of F and the argument used for I₁ ∩ I₂ shows that I₁ I₂ is a fractional ideal.

We shall need to know what the homomorphisms of a fractional ideal into D look like. This information is given in

PROPOSITION 10.1.  Let f be a D-homomorphism of the fractional ideal I into D and let b be any non-zero element of I. Then f has the form

a ∈ I.

Proof.   Choose a d ≠ 0 in D such that dI ⊂ D. Then db ∈ D and da ∈ D for any a ∈ I. We have

Hence af(b) = bf(a) and so f(a) = b ^{− 1} f(b)a. Thus f has the form given in (1).

If I is a fractional ideal, we define

It is clear that I ^{− l} is a D-submodule of F. Since there exist a ≠ 0 in D such that aI ⊂ D, it is clear that I ^{− 1} ≠ 0. Moreover, if b ≠ 0 is in I ∩ D, then I ^{− l}b ⊂ D. Hence I ^{− 1} is a fractional ideal. If I is the principal ideal Db, b ≠ 0, then it is clear that I⁻¹ = Db⁻¹. It is clear also that I₁ ⊂ I₂ I₁⁻¹ ⊃ I₂⁻¹ .

If I is a fractional ideal, then I^{− 1} I ⊂ D so I^{− 1}I is an integral ideal. We shall now call I invertible if

If I = bD ≠ 0, then I ^{− 1} = b ^{− l}D. Evidently I ^{− l}I = (b ^{− 1}D)(bD) = D. Hence every principal ideal is invertible. The fractional ideals constitute a commutative monoid under multiplication with D as the unit. If I is invertible, then I ^{− 1}I = D so I ^{− 1} is the inverse of I in the monoid of fractional ideals. Conversely, let I have the inverse J in this monoid. Then JI = D implies that J ⊂ I ^{− 1} as defined by (2). Since I ^{− 1} I ⊂ D, we have I ^{− 1}I = D. Since the inverse of an element of a monoid is unique, we have I ^{− 1} = J. Thus the invertible ideals constitute the group of units of the monoid of fractional ideals. We prove next

PROPOSITION 10.2.  Any invertible ideal is finitely generated.

Proof.   Let I be invertible. Then I ^{− 1}I = D implies the existence of elements c_ι ∈ I ^{− 1} , b_i ∈ I such that ∑ ⁿ₁ c_ib_i = 1. Now let b ∈ I. Then b = bl = ∑(bc_i)b_i and a_i = bc_i ∈ D. Thus I = ∑ Db_i and (b_l ,…, b_n) is a set of generators for I.

Next we establish the equivalence of the conditions of invertibility and projectivity for fractional ideals:

PROPOSITION 10.3.  A fractional ideal I is invertible if and only if it is projective.

Proof.  First suppose that I is invertible. Then 1 = ∑ ^m₁ c_ib_i, c_i ∈ I ^{− 1}, b_i ∈ I. The map f_i : a ac_i, a ∈ I, is in hom_D(I,D) and a = ∑(ac_i)b_i = ∑f_i(a)b_i. Hence I is D-projectiveby the “dual basis lemma” (Proposition 3.11, p. 152). Conversely, suppose that I is projective. Then we have a set of generators {b_α} of I and corresponding maps f_α ∈ hom _D(I, D) such that for any a ∈ I, f_α(a) = 0 for all but a finite number of α and a = ∑ f_α(a)b_α. We have shown in Proposition 10.1 that if b is a non-zero element of I, then f_α has the form a b ⁻¹ f_α(b)a. Since f_α(b) = 0 for all α except, say, α = 1, 2, …, m, we have f_α = 0 for α ≠ 1, 2, …, m and a = ∑^m₁ b ⁻¹ f_i(b)ab_i. Then 1 = ∑ b ^{− 1} f_i(b)b_i and since b ⁻¹ f_i(b)a ∈ D for all a ∈ I, c_i = b ⁻¹ f_i(b)∈ I ⁻¹. Thus 1 = ∑ c_ib_i, c_i ∈ I ⁻¹, b_i ∈ I, and hence I ⁻¹I = D. Thus I is invertible.

We say that a fractional ideal I is a divisor of the fractional ideal J if there exists an integral ideal K such that J = IK. Since K ⊂ D and Dl ⊂ I, this implies that J ⊂ I. If I is invertible we have the important fact that the converse holds: If I ⊃ J, then I is a divisor of J. For, D = I ^{− 1}I ⊃ I ^{− 1}J, so k = I ^{− 1}J is integral. Moreover, J = I(I ^{− 1}J) = IK.

We are interested in existence and uniqueness of factorization of ideals into prime ideals. For invertible integral ideals we have the following uniqueness property.

PROPOSITION 10.4.  Let I be integral and invertible and suppose that I = P₁ P₂ … P_m where the P_i are prime ideals of D. Then this is the only factorization of I as a product of prime ideals.

Proof.   We remark first that if M is a commutative monoid and a is a unit in M, then any factor of a is a unit. Applying this remark to the multiplicative monoid of fractional ideals we see that the P _i are invertible. Now let I = Q₁ Q₂ … Q_n where the Q_j are prime ideals. Then P₁ ⊃ Q₁ … Q_n and since P₁ is prime, we may assume that P₁ ⊃ Q₁. Since P₁ is invertible, we have Q₁ = P₁ R₁ where R₁ is integral. Then R₁ ⊃ Q₁. Since Q₁ is prime, either P₁ ⊂ Q₁ or R₁ ⊂ Q₁, so either P₁ = Q₁ or R₁ = Q₁. In the latter case R₁ = P₁ R₁ and since I = Q₁Q₂ … Q_n = P₁ R₁ Q₂ … Q_n, R₁ is invertible. Then D = R₁ ^{− 1} R₁ = R₁ ^{− 1} R₁ P₁ = P₁, contrary to the hypothesis that P₁ is prime (hence proper). Thus Q = P₁, so we have P₁ P₂ … P_m = P₁ Q₂ … Q_n and multiplication by P⁻¹₁ gives D = Q₂ … Q_n if m = 1 and P₂ … P_m = Q₂ … Q_n if m > 1. In the first case we have n = 1 also, and in the second n > 1 and induction on m can be applied since P₂ … P_m is invertible.

We shall now define the class of rings that will concern us in the chapter.

DEFINITION 10.2.  A domain D is called a Dedekind domain if every D-fractional ideal of F (the field of fractions of D) is invertible.

By Proposition 10.3, this is equivalent to assuming that every fractional ideal is projective. It is clear from Proposition 10.2 that any Dedekind domain is noetherian. We have also the following important property:

PROPOSITION 10.5.  Any prime ideal ≠ 0 in a Dedekind domain is maximal.

Proof.     Let I be a non-zero prime ideal ( = integral prime ideal) of the Dedekind domain D. If I is not maximal, we have an ideal J of D such that D J I. Then I = JK where K is integral. Since J ≠ I, we have I J. Also I K since KK ^{− 1} = DK ⊃ JK = I, so I ⊃ K implies I = K and K = JK. Then D = KK^{− l} = JKK ^{− 1} = J, contrary to D ≠ J. Thus we have I = JK with J I and K I. This contradicts the assumption that I is prime.

We have the following fundamental factorization theorem for Dedekind domains:

THEOREM 10.1.  Every proper integral ideal of a Dedekind domain can be written in one and only one way as a product of prime ideals.

Proof.     In view of Proposition 10.4, all we have to do is prove that if I is a proper integral ideal in the Dedekind domain D then I is a product of prime ideals ≠ 0. Suppose that this is not the case, so the set of proper integral ideals that are not products of prime ideals is not vacuous. Then by the noetherian property of D this set contains a maximal element I. Then I is not prime and hence I is not maximal. Then there exists an ideal I₁ in D such that D I₁ I. Then I = I₁ I₂ where I₂ is a proper integral ideal. We have I₂ ⊃ I, and I₂ = I implies that D = II⁻¹ = I₁ I₂ I₂ ^{− 1} = I₁. Thus D I_i I for i = 1, 2. By the maximality of I, I_i is a product of prime ideals. This gives the contradiction that I = I₁ I₂ is a product of prime ideals.

An immediate consequence of this result is

COROLLARY 1.  Suppose that I = P₁ P₂ … P_m where the P_i are primes. Then the integral ideals ≠ D containing I have the form P_i1 P_i2 … P_ir where 1 ≤ i₁ < i₂ < … < i_r ≤ m.

The proof is clear.

It is clear also that we have the following consequence of Corollary 1.

COROLLARY 2.  If I is an integral ideal in a Dedekind domain D, then D/I is artinian.

It is evident that the fractional ideals of a Dedekind domain constitute a group under multiplication with D as the unit and I ^{− 1} as defined by (2) as the inverse of I. The fundamental factorization theorem gives the structure of this group:

THEOREM 10.2.  The group of fractional ideals of a Dedekind domain is a direct product of the cyclic subgroups generated by the prime ideals. These are infinite.

Proof.     Let I be a fractional ideal ≠ D and let a be a non-zero element of D such that aI ⊂ D. Then aI is an integral ideal, so either aI = D or this is a product of prime ideals. Also aD is an integral ideal, so either aD = D or aD is a product of prime ideals. Since I(aD) = aI, I = (aI)(aD)^{− 1}. Then it is clear that we can write I = P₁^k₁ P₂^k₂ … P_r^k_r where the P_i are prime ideals and the k_i are non-zero integers. It follows from Theorem 10.1 that, conversely, if the k_i are non-zero integers and the P_i are prime ideals, then P₁^k₁ P₂^k₂ … P_r^k_r ≠ D. This implies that the representation of a fractional ideal ≠ D as a product P₁^k₁ P₂^k₂ … P_r^k_r is unique. Hence the group of fractional ideals is the direct product of the cyclic subgroups generated by the primes. It is clear also that these are infinite groups.

EXERCISES

        1. Show that any finitely generated D-submodule of F ≠ 0 is a fractional ideal.

        2. Show that if D is Dedekind, then the only fractional ideal I satisfying I ² = I is I = D.

        3. Use Theorem 10.1 to prove that any p.i.d. is factorial.

        4. Give an example of a factorial domain that is not Dedekind.

        5. Let D = [], the subring of F = () of elements a + b , a, b ∈ . Let I be the fractional D-ideal D + Dw where w = − + (a primitive cube root of 1). Compute I ^{− 1} and II ^{− 1}. Is I invertible?

        6. Let D = [] with quotient field F = []. Show that I = D3 + D is a projective D-module that is not free.

        7. Show that any Dedekind domain that is factorial is a p.i.d.

In the remaining exercises, D is a Dedekind domain.

        8. Let I₁ and I₂ be D-integral ideals and write where P_i are distinct prime ideals and the e_jk ≥ 0. Show that I₁ + I₂ = p₁^{min(e_l1, e₂₁)} … P_g^min(e_1g, e_2g) and I₁ ∩ I₂ = P₁^{max(e₁₁, e₂₁})^… P_g^{max(e_1g,e_2g)}.

        9. Show that the lattice of D-integral ideals is distributive (cf. BAI, p. 463).

     10. (Chinese remainder theorem for Dedekind domains.) Let I_l. …, I_n be integral ideals in a Dedekind domain D, a_l, … ,a_n elements of D. Show that the system of congruences x ≡ a_j (mod I_j), 1 ≤ j ≤ n, has a solution x = a in D if and only if for any j, k, 1 ≤ j, k ≤ n, we have a_j ≡ a_k (mod I_j + I_k). (Hint: The necessity of the conditions is clear. The sufficiency is proved by induction on n. For n = 2 we have a₁ − a₂ = b₁ − b₂, b_j ∈ I_j. Then a = a₁ − b₁ = a₂ − b₂ satisfies a ≡ a_j(mod I_j), j = 1, 2. For the inductive step one uses the distributive law ⁿ⁻¹_{j = 1} = ⁿ_{j = 1} I_j + I_n. See exercise 9 and p. 461f of BAI.)

     11. Let I be a fractional ideal, J an integral ideal. Show that there exists an element a ∈ I such that I^{− 1} a + J = D. (Hint: Let P₁, …, P_r be the prime ideals dividing J. For 1 ≤ i ≤ r, choose a_i ∈ IP₁ … P_rP_i ⁻¹, IP₁ … P_r and put a = ∑ ₁^ra_i. Then P_i aI ^{− 1}, 1 ≤ i ≤ r, and aI ^{− 1} + J = D.)

     12. Let I be a fractional ideal and a any non-zero element of I. Show that there exists a b ∈ I such that I = Da + Db. (Hint: Apply exercise 10 to the given I and J = aI^{− 1}.)

     13. Let I be a fractional ideal, J an integral ideal. Show that I/IJ and D/J are isomorphic D-modules.

     14. Let P be a prime ideal ≠ 0 in D. Show that if e ≥ 1 then D/P^e ⊃ P/P^e ⊃ … ⊃ P ^{e − 1}/P^e ⊃ 0 is a composition series for D/P^e as D-module. Show that Pⁱ/P^{i + 1}, i ≥ 0, is a one-dimensional vector space over the field D/P.

     15. Show that if D has only a finite number of ideals P_l, …, P_S, then D is a p.i.d. (Hint: Let I = P₁^e₁ … P_se_s, where the e_i ≥ 0. For each i choose a_i ∈ IP₁ … P_sP_i ^{− 1}, P_i^{e + 1}. Put a = ∑^s_i a_i. Then a ∈ P_i^e,, P_i^{e, + 1} and I = Da.)

10.2   CHARACTERIZATIONS OF DEDEKIND DOMAINS

We shall give a number of characterizations of Dedekind domains. The first one involves the important concept of integral closedness that we introduced in section 7.7.

It is easy to see that any factorial domain D is integrally closed (exercise 1, below). We now prove

PROPOSITION 10.6.  Any Dedekind domain is integrally closed.

Proof. Let D be a Dedekind domain, F its field of fractions, and let u be an element of F that is D-integral. Let f(x) = xⁿ + a₁x^{n − 1} + … + a_n be a monic polynomial with coefficients in D such that f(u) = 0 and put M = D 1 + Du + … + Du^{n − 1}. If u = bc ^{− 1} where b, c ∈ D, then c^{n − 1} M ⊂ D, so M is a fractional ideal. Evidently M² = M, which implies M = D (exercise 2, p. 604). Then u ∈ M = D and hence D is integrally closed.

We have now established the following three properties of Dedekind domains D:

            (1) D is noetherian.

            (2) Every non-zero prime ideal in D is maximal.

            (3) D is integrally closed.

We proceed to show that these properties characterize Dedekind domains. The proof is based on some lemmas that are of independent interest.

LEMMA 1.  Any fractional ideal for a noetherian domain D is finitely generated as D-module.

Proof.     If I is a fractional D-ideal, we have an a ≠ 0 in D such that I ′ = aI ⊂ D. Then I ′ is an ideal in D and since D is noetherian, I ′ is a finitely generated D-module. Then I = a ^{− 1}I ′ is finitely generated.

LEMMA 2.  Any non-zero ideal of a noetherian domain contains a product of non-zero prime ideals.

Proof.     As in the proof of Theorem 10.1, if the result is false we have an ideal I ≠ 0 maximal relative to the property that I does not contain a product of non-zero prime ideals. Then I is not prime and hence there exists ideals I_j, j = 1, 2, such that I_j I and I₁ I₂ ⊂ I. By the maximality of I, I_j contains a product of non-zero prime ideals. Since I ⊃ I₁ I₂, this gives a contradiction.

LEMMA 3.  Let D be an integrally closed noetherian domain, F the field of fractions, I a fractional D-ideal. Then

Proof.     Let s ∈ S. Since I is finitely generated and faithful as D-module and sI ⊂ I, s is D-integral by the lemma on p. 408. Since D is integrally closed, s ∈ D. Then S ⊂ D and since D ⊂ S follows from the definition of a fractional ideal, we have S = D.

LEMMA 4.  Let D be a noetherian domain in which every non-zero prime ideal is maximal and let I be an ideal of D such that I D. Then I ^{− 1} D.

Proof.     Let a ≠ 0 be in I. Then D ⊃ I ⊃ aD, and by Lemma 2, aD ⊃ P₁ P₂ … P_m where the P_i are prime ideals ≠ 0. We assume that m is minimal. By the noetherian condition (or by Zorn’s lemma) there exists a maximal ideal P ⊃ I. Then we have P ⊃ I ⊃ aD ⊃ P₁ … P_m. Since P and the P_i are prime, the hypothesis that non-zero prime ideals are maximal implies that P = P_i for some i, and we may assume that P = P₁. If m = 1 we have aD = I. Then I ^{− 1} = a^{− l}D and since I D, a ^{− 1} D and I^{− 1} = a^{− 1}D D. Next assume that m > 1. Then aD P₂ … P_m by the minimality of m and so we can choose a b ∈ P₂ … P_m, aD. Put c = a^{− l}b. Then c D and cI ⊂ cP = a^{− 1} bP ⊂ a^{− l}bP ⊂ a^{− 1} PP₂ … Pm ⊂ a ^{− 1}(aD) = D. Thus c ∈ I^{− 1} and c D, so again we have I ^{− 1} D.

We can now prove

THEOREM 10.3.  A domain D is Dedekind if and only if (1) D is noetherian. (2)non-zero prime ideal in D is maximal. (Equivalently, D has Krull dimension ≤ 1.)(3)D is integrally closed.

Proof.     We have seen that (1)-(3) hold for any Dedekind domain. Now assume that D is a domain satisfying these conditions and let I be a D-fractional ideal. The fractional ideal I ^{− 1} I is integral and II ^{− 1}(II^{− 1})^{− 1} ⊂ D, so I ^{− 1}(II ^{− 1})^{− 1} ⊂ I^{– 1}. It follows from Lemma 3 that (II ^{− 1})^{− 1} ⊂ D. Since II ^{− 1} ⊂ D, it follows from Lemma 4 that II ^{− 1} = D. Hence every fractional ideal is invertible and D is Dedekind.

Our next characterization of Dedekind domains will be in terms of localizations. Let D be a domain, S a submonoid of the multiplicative monoid of non-zero elements of D. We consider the subring D_s of the field of fractions F of D consisting of the elements as as ^{− 1}, a ∈ D, s ∈ S. It is readily seen that this is isomorphic to the localization of D at S as defined in section 7.2. Hence the results on localization that were developed in sections 7.2 and 7.3 are available for the study of the rings D_s.

Let I be a fractional ideal for D and put I_s = {bs^{− 1}|b ∈ I, s ∈ S}. Then I_sis a D_s-submodule of F, I_s ≠ 0, and if a is a non-zero element of D such that aI ⊂ D, then aI_s ⊂ D_s. Since it is evident that F is the field of fractions for D_s, it follows that I_s is a D_s-fractional ideal. If I₁ and I₂ are D-fractional ideals, then

The first two of these are clear. To verify the third we note that (I₁ ∩ I₂)_S ⊂ I_1S ∩ I_2S is clear. Now let a ∈ I_1S ∩ I_2S, so a = a₁s₁⁻¹ = a₂s₂ ⁻¹ where a_i ∈ I_i, s_i ∈ S. Then b = a₁s₂ = a₂s₁ ∈ I₁ ∩ I₂ and a = b(s₁s₂)⁻¹ ∈ (I₁ ∩ I₂)_s. Hence (6) holds.

We note next that if I is a finitely generated fractional D-ideal, then

For, it follows from the definition of I ^{− 1} that (I₁ + I₂)⁻¹ = I₁⁻¹ ∩ I₂ ⁻¹. It is clear also that if b ≠ 0 in F, then (Db)_s = D_sb. Hence if I = Db₁ + … + Db_m, then I_s = D_sb₁ + … + D_sb_m and I_s ⁻¹ = ^m₁ D_sb_i ⁻¹. On the other hand, I ⁻¹ = ^m₁Db_i ⁻¹, and so by (6), (I ⁻¹)_s = ^m₁D_sb_i ⁻¹ = Is ⁻¹. Hence we have (7).

Now let I′ be a fractional ideal for D_s. Then we have an element as ⁻¹, a ≠ 0 in D, s ∈ S, such that as^{− 1} I′ ⊂ D_s. Then as ^{− 1} I′ is a non-zero ideal contained in the localization D_s. By section 7.2 this has the form I_s for a nonzero ideal I contained in D. Then I ′ = a ⁻¹sI_s = ((a^{− 1}s)I)_s. Thus any fractional D_s-ideal has the form I_s for some fractional D-ideal I.

We can now prove

THEOREM 10.4.  Let D be a domain.

            (1) If D is Dedekind, then D_s is Dedekind for every submonoid of the multiplicative monoid of non-zero elements of D.

            (2) If D is Dedekind and P is a prime ideal ≠ 0 in D, then D_P is a discrete valuation ring.

            (3) If D is noetherian and D_P is a discrete valuation ring for every maximal ideal P in D, then D is Dedekind.

(We recall that if P is prime ideal, D_P ≡ D_s where S is the multiplicative monoid D − P.)

Proof.     (1) Suppose that D is Dedekind and let I′ be a D_s-fractional ideal. Then I′ = I_s for a fractional D-ideal I. Since D is Dedekind, D is noetherian and hence I is finitely generated. Then (I′)⁻¹ = I_s⁻¹ = (I⁻¹)_s by (7) and I′I′⁻¹ = I_s(I⁻¹)_s = (II⁻¹)s (by (5)) = D_s. Hence I′ is invertible and D_s is Dedekind.

(2) The localization D_P at the prime ideal P ≠ 0 is a local ring whose only maximal ideal is P_p. Since D_p is Dedekind, P_p is the only prime ideal ≠ 0 in D_p. Hence D_p is a p.i.d. by exercise 14, p. 605. Then D_p is a discrete valuation ring by Proposition 9.2, p. 570.

(3) Now assume that D is noetherian and that D_p is a discrete valuation ring for every maximal ideal P of D. Then D_p is a p.i.d. and hence D_p is Dedekind. Let I be a fractional D-ideal. Since D is noetherian, I is finitely generated. Hence I_p⁻¹ = (I⁻¹)_p. Then(II ^{− 1})_p = I_p(I⁻¹)_p = I_pI_p⁻¹ = D_P forevery maximal ideal P of D. We can now apply the principal of passage from local to global: We have the injection i: II ^{− 1} D, which localizes to the injection (I I′)_p D_p. Since the latter is surjective for all P, it follows from Proposition 7.11.2 (p. 402) that II ^{− 1} D is surjective. Thus II ^{− 1} = D for every fractional D-ideal I. Hence D is Dedekind.

Dedekind domains can also be characterized by the factorization property given in Theorem 10.1. In fact, we have the following stronger result:

THEOREM 10.5.  Let D be a domain with the property that every proper integral ideal of D is a product of prime ideals. Then D is Dedekind.

Proof(Zariski-Samuel). We show first that any invertible prime ideal P of D is maximal in D. Let a ∈ D, P. Suppose that aD + P ≠ D. Then aD + P = P₁ … P_m, a²D + P = Q₁ … Q_n where the P_i and Q_j are prime ideals. Since aD + P P and a²D + P P (since P is prime), we have P_i P, Q_j P for all i and j. Passing to the domain = D/P we obtain = ₁ … _m and = ₁ … _n where x is the canonical homomorphism of D onto . The principal ideals and are invertible and the _i and _j are prime. Moreover, ₂ = ()², so ₁ … _n = ₁² … _m². By Proposition 10.4, the sequence of prime ideals {₁, …, _n} and {₁, ₁, …, _m, _m} are the same except for order. The corresponding sequences of ideals of D containing P are {Q₁, …, Q_n} and {P₁, P₁, …, P_m P_m}. Hence these coincide except for order. This implies that (aD + P)² = P₁² … P_m² = Q₁ … Q_n = a²D + P. Then P ⊂ (aD + P)² = a²D + aP + P² ⊂ aD + P². Then if p ∈ P, p = ax + y where x ∈ D and y ∈ P². Then ax ∈ P and since a P, x ∈ P. Hence P ⊂ aP + P² ⊂ P, so P = aP + P². Multiplication by P^{− 1} gives D = aD + P, contrary to hypothesis. Thus we have aD + P = D for every a ∈ D, P. This implies that P is a maximal ideal of D.

Now let P be any prime ideal ≠ 0 in D and let b be a non-zero element of P. Then P ⊃ bD and bD = P₁P₂ … P_m where the P_i are prime and are invertible. Hence the P_i are maximal. Since P is prime, we have P ⊃ P_i for some i. Then P = P_i and so P is invertible. Since any proper integral ideal is a product of prime ideals, it follows that every integral ideal is invertible. Since any fractional ideal I ′ = aI for I integral and a ≠ 0, I ′(I ′)^{− 1} = II ^{− 1} = D. Hence every fractional ideal is invertible and D is Dedekind.

The following theorem summarizes the characterizations of Dedekind domains that we have given.

THEOREM 10.6.  The following conditions on a domain are equivalent:

            (i) D is Dedekind.

         (ii) D is integrally closed noetherian and every non-zero prime ideal of D is maximal.

   (iii)   Every proper integral ideal of D can be written in one and only one way as a product of prime ideals.

      (iv) D is noetherian and D_P is a discrete valuation ring for every maximal ideal P in D.

EXERCISES

        1. Prove that any factorial domain is integrally closed.

        2. Prove that the following conditions characterize Dedekind domains: D is integrally closed noetherian and D/I is artinian for every integral ideal I.

        3. (H. Sah.) Show that a domain D is Dedekind if and only if it has the following property:

   If I is any integral ideal of D and a is any non-zero element of I, then there exists a b ∈ I such that I = Da + Db.

   (Sketch of proof: The proof that any Dedekind domain has this property was indicated in exercise 11, p. 605. Now suppose that D has the property. Then D is noetherian. Also it is easily seen that the property is inherited by any localization D_s. Now suppose that D is a local domain having the property and let P ≠ 0 be its maximal ideal. Let I be any ideal ≠ 0 in D. Then I = IP + Db for some b ∈ I. It follows by Nakayama’s lemma that I = Db. Thus D is a p.i.d. and hence a discrete valuation ring (p. 571). Now conclude the proof by using Theorem 10.4.3 (p. 628).

Exercises 4-7 were communicated to me by Tsuneo Tamagawa. The first of these is well known. In all of these exercises, D is Dedekind with F as field of fractions and x is an indeterminate.

        4. If f(x) ∈ D[x], we define the content c(f) to be the ideal in D generated by the coefficients of f(cf. BAI, p. 151). Prove that c(fg) = c(f)c(g) for f, g ∈ D[x].

        5. Let S = {f ∈ D[x]|c(f) = D}. Note that S is a submonoid of the multiplicative monoid. Let D[x]_s denote the subring of F(x) of fractions f(x)/g(x) where f(x) ∈ D[x] and g(x) ∈ S. Show that if f(x), g(x) ∈ D[x], then f(x)/g(x)∈ D[x]_s if and only if c(f) ⊂ c(g).

        6. Show that D[x]_s ∩ F = D. Let I ′ be an ideal in D[x]_s. Show that I = I ′ ∩ D is an ideal in D such that ID[x]_s = I ′. Show that I I ′ = ID[x]_s is a bijective map of the set of ideals of D onto the set of ideals of D[x]_s.

        7. Prove that D[x]_s is a p.i.d.

10.3   INTEGRAL EXTENSIONS OF DEDEKIND DOMAINS

The classical examples of Dedekind domains are the rings of -integers of number fields, that is, of finite dimensional extension fields of and of fields of algebraic functions of one variable. In this section we derive the general result that if D is Dedekind with field of fractions F and E is a finite dimensional extension field of F, then the subring D′ of D-integral elements of E is Dedekind. This implies the Dedekind property of the classical domains and gives the fundamental theorem on the unique factorization of integral ideals as products of prime ideals in these domains.

We prove first

PROPOSITION 10.7.  Let D be a domain, F its field of fractions, E a finite dimensional extension field of F, and D′ the subring of E of D-integral elements. Then any element of E has the form rb^{− 1} where r ∈ D′ and b ∈ D.

Proof.     Let u ∈ E and let g(x) = x^m + a₁x^{m − 1} + … + a_m ∈ F[x] be a polynomial such that g(u) = 0. We can write a_i = c_ib ^{− 1}, c_i, b ∈ D. Then

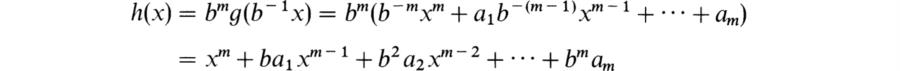
∈ D[x] and h(bu) = 0. Hence r = bu ∈ D′ and u = b ^{− 1}r as required.

Evidently this result implies that E is the field of fractions of D′. Since D′ is the ring of D-integers of E, D′ is integrally closed in E. Hence D′ is an integrally closed domain.

We suppose next that D is integrally closed and we prove

PROPOSITION 10.8.  Let D, E, F, D ′ be as in Proposition 10.7 and assume that D is integrally closed. Let r ∈ E and let m(x),f(x) be the minimum polynomial and characteristic polynomial respectively of r over F. Then the following conditions on r are equivalent:

(1) r is integral.

(2) m(x) ∈ D[x].

(3) f(x) ∈ D[x].

If the conditions hold, then T_E/F(r) and N_E/F(r) ∈ D.

Proof. Since f(x) is a power of m(x), it is clear that (2) (3). Also obviously (3) (1). Now assume (1). Let be an algebraic closure of F containing E. We have m(x) = (x − r_i) in [x] where r₁ = r. For any i we have an automorphism of /F sending r into r_i. Since r is D-integral, there exists a monic polynomial g(x) ∈ D [x] such that g(r) = 0. Applying an automorphism of /F sending r into r_i, we obtain g(r_i) = 0. Hence every root r_i of m(x) is a D-integer. Since the coefficients of m(x) are symmetric polynomials in the r_i, these elements of F are D-integers and since D is integrally closed, they are contained in D. Thus m(x) ∈ D[x] and (1) (2). The last assertion is clear, since f(x) = xⁿ − T_E/F(r)x^{n − 1} + … +(− l)ⁿN_E/F(r).

A key result for the proof of the theorem on integral closures of Dedekind domains is the following

PROPOSITION 10.9.  Let D, E, F, D′ be as in Proposition 10.8 and assume that E/F is separable and D is noetherian. Then D′ is a finitely generated D-module.

Proof.     Since E/F is separable, there exist n = [E:F] distinct monomorphisms σ₁, …, σ_n of E/F into the algebraic closure /F. Moreover, if (u_l, …, u_n) is a base for E/F, then the matrix

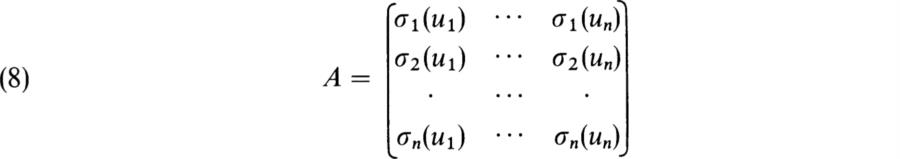
is invertible (BAI, p. 292). We know also that T_E/F(u) = ∑ ⁿ₁ σ_i (u) for u ∈ E (BAI, p. 430). We have (^tA)A = (T_E/F(u_iu_j)). Hence

We have seen in Proposition 10.7 that there exists a b_i ≠ 0 in D such that b_iu_i ∈ D′. Hence we may assume that the u_i ∈ D′. Let r ∈ D′ and write r = ∑ⁿ₁a_iu_i, a_i ∈ F. Then ru_j ∈ D′, 1 ≤ j ≤ n, and ru_j = ∑_ia_iu_iu_j. Hence

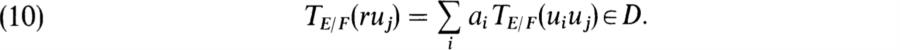
The system of equations (10) for a_i, 1 ≤ i ≤ n, can be solved by Cramer’s rule. This shows that a_i ∈ d⁻¹ D. Since this holds for every r ∈ D ′, we see that D′ is contained in the D-module M = ∑ⁿ₁D(d^{− 1} u_i). Thus D ′ is contained in a finitely generated D-module. Since D is noetherian, M is a noetherian D-module. Hence the submodule D′ is finitely generated.

We can now prove the main result of this section.

THEOREM 10.7.  Let D be a Dedekind domain, F its field of fractions, E a finite dimensional extension field of F, D′ the subring of D-integral elements of E. Then D′ is Dedekind.

Proof.   We assume first that E is separable over F. In this case we shall prove the theorem by showing that D′ has the three properties characterizing Dedekind domains given in Theorem 10.3, namely, (1) D′ is noetherian, (2) every prime ideal ≠ 0 in D′ is maximal, and (3) D′ is integrally closed. The first of these follows from Proposition 10.9, since this proposition implies that D′ is a noetherian D-module. A fortiori D′ is noetherian as D′-module. Now let P′ be a non-zero prime ideal in D′. Let r ≠ 0 be in P′. Then we have f(r) = 0 for the characteristic polynomial f(x) of r. This implies that N_E/F (r) ∈ P ′ and hence, by Proposition 10.8, N_E/F(r) ∈ P = P′ ∩ D. Since N_E/F(r) ≠ 0, we see that P ≠ 0. It is clear also that P is a prime ideal in D. Since D is Dedekind, this implies that P is a maximal ideal in D. By the Corollary to Proposition 7.17, p. 410, we conclude that P′ is maximal in D′. Hence (2) holds. The remark following Proposition 10.7 shows that (3) holds. Hence D′ is Dedekind in the separable case.

We assume next that char F = p and that E is purely inseparable over F. Since [E:F] < ∞, there exists a q = p^e such that u^pe ∈ F for all u ∈ E. Let be an algebraic closure of F containing E and let F^1/q(D^l/q) be the subfield (subring) of of elements v such that v^q ∈ F(D). Then v v^q is an isomorphism of F^1/q onto F mapping D^l/q onto D. Since D is Dedekind, D^1/q is Dedekind. If u ∈ D′, u^q ∈ F and u^q is D-integral. Hence u^q ∈ D and so D′ ⊂ D^1/q. We shall now show that D′ is Dedekind by proving that every D′-fractional ideal I of E is invertible. Let I′ = D^l/qI. Then I′ is a D^1/q-fractional ideal. Hence there exists a D^1/q-fractional ideal J′ such that I′ J′ = D^1/q and since I′ = ID^1/q and D^l/qJ′ = J′, we have elements b_i ∈ I, c′_i ∈ J ′ such that ∑b_ic_i′ = 1. Then ∑b_i^qc^′_i^q = 1 and ∑b_ic_i = 1 where c_i = b_i^q−1 c′_i^q. Now b_i^q−1 c′_i^q ∈ I′ ^q−1J′^q ⊂ J′. Since c′_i^q ∈ F and b_i ∈ E, c_i = b_i ^q−1 c′_i^q ∈ E. Thus c_i ∈ J = J′ ∩ E. Evidently IJ ⊂ D^1/q ∩ E and since the elements of D^1/q are D-integral, D^1/q ∩ E ⊂ D′. Hence IJ ⊂ D′, so J ⊂ I^{− l}. Since the c_i ∈ J and b_i ∈ I and ∑c_ib_i = 1, we have II^{− 1} = D′. Thus I is invertible and D′ is Dedekind.

The general case can be obtained by combining the preceding two cases in the obvious way: If E is arbitrary finite dimensional over F, let K be the maximal separable subfield of E/F. Then E is purely inseparable over K. Now D″ = D′ ∩ K is Dedekind by the first case and since D′ is the set of D″-integral elements of E, D′ is Dedekind by the second case. This completes the proof.

The foregoing result is applicable in particular to F = and D = and to F = K(x) where K is an arbitrary field, x an indeterminate, and D = K[x]. This is clear since these D are p.i.d. and hence are Dedekind. If E is a finite dimensional extension field of F, then the ring D′ of D-integers of E is Dedekind. In the case F = , D = , E is a number field and in the other cases E is an algebraic function field in one variable.

EXERCISES

        1. Let the notations be as in Theorem 10.7. Assume that E/F is separable and that D is a p.i.d. Show that D′ is a free D-module of rank n = [E: F].

Exercises 3, 4, and 5 of BAI, p. 287, are relevant for this section.

        2. (Sah.) Show that if D is a Dedekind domain, then so is the ring D((x)) of Laurent series over D. (Hint: It is easily seen that D((x)) is a domain. If I is an ideal in D((x)), let l(I ) be the set of leading coefficients of the elements of I. Then l(I) is an ideal and if l(I) = Da₁ + … + Da_m where a_i is the leading coefficient of f_i ∈ I, then I = D((x))f₁ + … + D((x))f_m. Use this and exercise 3 on p. 630.

10.4   CONNECTIONS WITH VALUATION THEORY

We give first a valuation theoretic characterization of the integral closure of a subring of a field. This is

THEOREM 10.8 (Krull).  Let D be a subring of a field F and let D′ be the integral closure of D in F (= the subring of D-integral elements of F). Then D′ is the intersection of the valuation rings of F containing D.

Proof.     Let u ∈ D′ and let R be a valuation ring in F containing D, φ a valuation of F having R as valuation ring (e.g., the canonical valuation defined by R). Suppose that u R. Then φ(u^{− 1}) < 1. On the other hand, we have a relation uⁿ + a₁u^{n − 1} + … + a_n = 0, a_i ∈ D, which gives the relation

Since the a_i ∈ D ⊂ R, φ(a_i) ≤ 1. Then φ(a_iu^{− i}) < 1. Since φ(1) = 1, we have the contradiction 1 ≤ max{φ(a_iu ⁻ⁱ)} < 1. Hence u ∈ R and D′ ⊂ R where the intersection is taken over all of the valuation rings R of F containing D. Next, suppose that u D′. Then u⁻¹ is not a unit in the subring D[u⁻¹] of F, since otherwise, its inverse u = a₀ + a_lu⁻¹ + … + a_n−1u⁻⁽ⁿ⁻¹⁾, a_i ∈ D, and hence uⁿ = a₀uⁿ⁻¹ + a₁u^{n − 2} + … + a_{n −1}, contrary to u D ′. Since u⁻¹ is not a unit in D[u⁻¹], u⁻¹ D[u⁻¹] is a proper ideal in D[u^{− 1}] and this can be imbedded in a maximal ideal P₀ of D[u^{− 1}]. Then = D[u^{− 1}]/P₀ is a field and we have the canonical homomorphism of D[u^{− 1}] onto , which can be regarded as a homomorphism ₀ of D[u⁻¹] into an algebraic closure of . By Theorem 9.10 (p. 561), there exists a -valued place extending ₀. If R is the valuation ring on which is defined and P is its maximal ideal, then P is the kernel of . We have R ⊃ D[u^−l] ⊃ D and P ⊃ P₀. Then u^{− 1} D[u^{− 1}]⊂ P₀ ⊂ P;, so (u^{− 1}) = 0 and hence u R. Thus we have shown that if u D′ then u R where R ranges over the valuation rings of Fcontaining D. Hence D′ = R.

Now let D be Dedekind, F its field of fractions. Since D is integrally closed, D is the intersection of the valuation rings of F containing D. We claim that these valuation rings are the localizations D_P, for the prime ideals P of D. We have seen that every D_P is a discrete valuation ring for every prime ideal ≠ 0 in D. This is clear also if P = 0, since D₀ = F. Now let R be a valuation ring in F containing D such that R ≠ F. Let M be the maximal ideal of R and let P = M ∩ D. Then P is a prime ideal in D and if P = 0, every nonzero element of D is invertible in R. Since F is the field of fractions of D, this implies that F = R, contrary to hypothesis. Thus P is an integral prime ideal in D. We have the valuation ring D_P with maximal ideal P_p = PD_p. If a ∈ D − P, then a ∈ R − M and a^{− l} ∈ R. Then R ⊃ D_P. Moreover, since M ⊃ P, M = RM ⊃ D_pP. Now it is easily seen that if R₁ and R₂ are valuation rings with maximal ideals M₁ and M₂ respectively, then R₁ ⊃ R₂ and M₁ ⊃ M₂ imply R₁ = R₂ and M₁ = M₂. Hence R = D_p and M = PD_p. Thus the valuation rings of F containing D (and ≠F) are just the localizations D_p, P a prime ideal ≠ 0 in D. By Theorem 10.8, D = D_p.

A prime ideal P ≠ 0 in a Dedekind domain D determines an exponential valuation v_p for the field of fractions F of D in a manner similar to the definition of the exponential valuation v_p on defined by a prime integer p. If a ≠ 0 in F, we write Da = P^k P₁^k₁ … P_l^k_l where P, P₁, …, P_l are distinct prime ideals and k and the k_i ∈ . Then we put v_p(a) = k. Moreover, we define v_p(0) = ∞. It is readily verified, as in the special case of , that v_p is an exponential valuation of F. Hence if we take a real γ, 0 < γ < 1, then |a|_p = γ ^{v_P (a)} is a non-archimedean absolute value on F. We call this a P-adic absolute value on F. The valuation ring of | |_p evidently contains the localization D_P and the maximal ideal of the valuation ring contains PD_p. Hence the valuation ring of | |_p is D_p and its maximal ideal is PD_p.

Since D_p is Dedekind and PD_p is its only prime ideal ≠ 0, the integral ideals of D_p are the ideals P^kD_p, k ≥0. Evidently, P_k ⊂ P^kD_p ∩ D. On the other hand, if a ∈ P^kD_p ∩ D for k ≥ 1, then a = bc^{− 1} where b ∈ P^k, c ∈ D − P. Then ac ≡ 0 (mod P^k) and c 0 (mod P). The latter condition implies that c + P is a unit in D/P. Then c + P^k is a unit in D/P^k (p. 195). It follows that a ∈ P^k. Hence P^kD_p ∩ D = P^k for k ≥ 0.

Let | | be a non-archimedean absolute value having D_p as valuation ring. We claim that | | = | | _p, a P-adic valuation determined by the prime P. To see this we observe that PD_p = π D_p where π ∈ PD_p, P²D_p. Then P^kD_p = π^kD_p for k ≥ 0 and any element of D_p can be written as uπ^k, u a unit in D_p and k ≥ 0. Then |uπ^k| = γ^k where |π| = γ, 0 < γ < 1. Hence, if a ∈ P^k, P^{k + 1}, then a ∈ P^kD_p, P^{k + 1}D_P, and |a| = γ^k. On the other hand, it is clear that Da = P^k P₁^k₁ … P_l^k_l where P_l, …, P_l are primes distinct from P and hence if | |_P is the P-adic valuation determined by γ, then |a|_p = |a| for a ∈ D. Then | | = | |_p.

We show next that the residue field D_p/P_p of | |_P is canonically isomorphic to D/P. Since P = P_p ∩ D, we have the monomorphism a + P a + P_p of D/P into D_p/P_p. If a, b ∈ D and b P, then since D/P is a field there exists a c ∈ D such that cb ≡ a (mod P). Then ab^{− 1} ≡ c (mod P_p), which implies that a + P a + P_p is surjective on D_p/P_p. Then this map is an isomorphism.

We summarize this collection of results in

PROPOSITION 10.10.  Let D be a Dedekind domain with field of fractions F. Then (1) Any valuation ring in F containing D has the form D_p where P is a prime ideal in D. (2) Any non-archimedean absolute value on F having D_P, P ≠ 0, as valuation ring is a P-adic valuation. (3) The map a + P a + P_p is an isomorphism of D/P onto D_p/P_p.

Now let E be a finite dimensional extension field of F and let D′ be the ring of D-integers of E. Then D′ is Dedekind. If P is an integral ideal of D, then the ideal in D′ generated by P is D′ p. Now D′ P ≠ D′. For, by the “Lying- over” theorem (p. 411), there exists a prime ideal P′ in D′ such that P′ ∩ D = P. Hence P′ ⊃ PD′ and PD′ ≠ D′. It may happen that the extension ideal PD′ of P is not prime. At any rate, we have a factorization

where the P′_i are distinct prime ideals in D′ and the e_i > 0.

We have treated the general problem of extension of an absolute value on a field F to a finite dimensional extension field in Chapter 9 (p. 585). We shall now treat the special case of a P-adic absolute value of the field of fractions F of a Dedekind domain in an alternative manner based on the factorization (12). We prove first

THEOREM 10.9.  Let D be a Dedekind domain, F the field of fractions of D, E a finite dimensional extension field of E, D′ the subring of E of D-integral elements. Let P be an integral prime ideal in D, | |_P a P-adic absolute value on F, (12) the factorization of PD′ into prime ideals in D′. Then for each P′_i there is a unique P′_i-adic absolute value | |_p′i on E extending | |_p. Moreover, | |_p′i and | |_p′j are inequivalent if i ≠ j and the | |_p′i; are the only extensions of | |_P to absolute values on E.

Proof.     Let a ≠ 0 be in F and write Da = Pk Pkl1 … Pkl1 where P and the Pj are distinct prime ideals and k and the kj ∈ . Then vP(d) = k, and by (12),

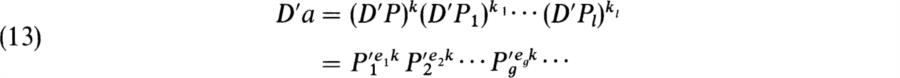
where the terms after P′_ge_gk come from the factorizations of the D′P_j into prime ideals in D′. Now we observe that if P₁ and P₂ are distinct prime ideals in D, then P₁ + P₂ = D and hence D′ P₁ + D′ P₂ = D′. This implies that the prime ideals in D′ dividing D′P₁ are different from those dividing D′P₂. It follows that v_p′j(a) = e_jk. Hence if | |_p = γ ^{v_p( )} for 0 < γ < 1, then we shall have | |_p = | |_p′j on F if and only if ||_p′j = (γ^1/ej)v_p′j^{( )}. This proves the first assertion. We have seen that the valuation ring of | |_p′j (or of v_P′j) is D′_p′j. Since these are distinct for distinct choices of j, it follows that | |_p′i and | |_p′j are inequivalent if i ≠ j. Now let | |′ be any absolute value on E extending | |_P and let R′ denote the valuation ring of | |′. Then R′ ⊃ D_p and since D′ is the integral closure of D in E, R′ ⊃ D′ by Theorem 10.8. By Proposition 10.10.1, R′ = D′_p′ for P′, a prime ideal in D′. Since R′ ⊃ D_p, it follows that P′ ⊃ P. Hence P′ = P′_i for some i. By Proposition 10.10.2, | |′ is a P′_i;-adic valuation.

We recall that the ramification index of | | _p′i relative to | |_p is the index (p. 589). Since | F* | _P is the subgroup of * generated by γ and |E*|_p′i is the subgroup generated by γ^1/e_i, the ramification index is e_i.

We recall also that the residue degree f_i of | |_p′i relative to | | _p is the dimensionality [D′_P′l/P′_ipl : D_p/P_p] where D_P/P_p is imbedded in D′_p/P′_iP by the monomorphism x + P_p x + P′_ipl (p. 589). We also have a monomorphism a + P a + P′_i, a ∈ D, of D/P into D′/P′_i. Hence we can define the dimensionality [D′/P′_i : D/P]. Now we have the isomorphisms σ : a + P a + P_p and s : x + P_i x + P′_ip′l of D/P onto D_p/P_p and of D′_Pl onto D′_p′l /P′_ip^′i respectively. We have s((a + P)(x + P′_i)) = s(ax + P′_i) = ax + P′_ip′l and hence(σ(a + P))(s(x + P′_i)) = (a + P_p)(x + P′_iP′l′ ) = ax + P′_ip′l. Hence s is a semi-linear isomorphism of D′/P′_i over D/P onto D′_p′l/P′_ip′l with associated field isomorphism σ. It follows that the residue degree f_i coincides with the dimensionality [D′/P′_i : D/P].

The results on ramification index and residue degree can be stated as follows:

THEOREM 10.10.  Let the notations be as in Theorem 10.9. Let | |_p be a P-adic absolute value on F, | |_P; a P′_i;-adic absolute value on E extending | |_P. Then e_i is the ramification index and [D′/P′_i : D/P] is the residue degree of | | _p′l relative to | |_p.

An immediate consequence of this result and the main theorem on residue degrees and ramification indices (Theorem 9.15, p. 592) is

THEOREM 10.11.  Let the notations be as in Theorem 10.9. Then Moreover, ∑^g₁e_if_i = n if E/F is separable.

We remark that this result has the consequence that the number g of prime ideals of D′ containing D′P is bounded by n and it gives considerably more information on the factorization (12).

EXERCISES

        1. Let E be the cyclotomic field () when is a primitive lth root of unity, l a prime. Let D = , D′ be the integral closure of in E. Show that lD′ = (( − l)D′)^{p −1} and ( − 1)D′ is a prime ideal in D′. (Hint: [E : Q] = l − 1 and f(x) = x^{l − 1} + x^{l − 2} + … + 1 is the minimum polynomial of . We have f(x) = ₁^{l − 1}(x − ⁱ) in E[x] and every _i, 1 ≤ i ≤ l − 1, is a primitive lth root of 1. (See BAI, p. 154.) Substituting 1 in f(x) gives l = ₁^{l − 1}(1 − ⁱ). Moreover, (1 − ⁱ)/(1 − ) = 1 + + … + ^{i −1} ∈ D′. Show that l + + … + ⁱ⁻¹ is a unit in D′ so lD′ = (( − 1)D′)^{l − 1}. Show that l is not a unit in D′ and use Theorem 10.11 to conclude that ( − 1)D′ is prime.)

The next three exercises are designed to show that in the special case of Theorem 10.11 in which E/F is Galois, the factorization (12) of PD′ = (P′₁ … P′_g)^e and all of the residue degrees are equal. Hence n = [E : F] = efg.

        2. Let E/F be Galois with Gal E/F = G. Show that any σ ∈ G maps D′ into itself. Show that if P′ is a prime ideal in D′ then σP′ is a prime ideal. Show that : a + P′ σ a + σP′ is an isomorphism of D′/P′ onto D′/σP′.

        3. Let P be a non-zero prime ideal of D, PD′ = P′₁^e₁ … P′_g^e_g, the factorization of PD′ into prime ideals in D′ where P′_i ≠ P′_j if i ≠ j. Show that if σ ∈ G, then {σP′₁, …, σP′_g} = {P′, …, P′_g} and that G acts transitively on the set of prime ideals {P′₁, …, P′_g}. (Hint: To prove transitivity of G on {P′₁, …, P′_g} one shows that if P′ is any prime ideal of D′ such that P′ ∩ D = P then any prime ideal Q′ of D′ such that Q′ ∩ D = P is one of the ideals σ P′, σ ∈ G. Otherwise, by Proposition 7.1, p. 390, Q _{σ ∈ G} σ P′. Hence there exists an a ∈ Q′ such that σa P′ for any σ ∈ G. Then N_E/F(a) = _{σ ∈ G} σ a P′ This is a contradiction since N_E/F(a)∈ Q′ ∩ D = P.)

        4. Use the results of exercises 2 and 3 to show that e_i = e_j for every i and j and that the fields D′/P′_i and D′/P′_j are isomorphic over D/P. Hence conclude that [D′/P′_i : D/P] = [D′/P′_j : D/P]. Put e = e_i, f = f_i = [D′P_i : D/P]. Show that n = efg.

10.5   RAMIFIED PRIMES AND THE DISCRIMINANT

As in the previous section, let D be a Dedekind domain, F its field of fractions, E a finite dimensional extension field of F, and D′ the subring of D-integral elements of E. Let P be a non-zero prime ideal in D and let PD′ = P′₁^e₁ … P′_g^e_g where the P′_i are distinct prime ideals in D, as in (12). We consider the ring = D′/PD′, which we can regard also as a module over D′ and by restriction as a module over D. Since P annihilates , can also be regarded as a vector space over = D/P. The action of a + P, a ∈ D, on x + PD′, x ∈ D′, is (a + P)(x + PD′) = ax + PD′. Taking into account the ring structure as well as the -vector space structure, we obtain the algebra over . We shall now consider the structure of this algebra. The main result on this is the following

THEOREM 10.12.  Let D be a Dedekind domain with field of fractions F and let E be a finite dimensional extension field, D′ the subring of E of D-integral elements. Suppose that P is a non-zero prime ideal in D and let PD′ = P′₁^e₁ … P′_g^e_q where the P′_i are distinct prime ideals in D′ and the e_i > 0. Then = D′/PD′ is an algebra over the field = D/P in which (a + P)(x + PD′) = ax + PD′, a ∈ D, x ∈ D′. The dimensionality [ : ] = ∑₁^ge_if_i where f_i is the residue degree [ D′/P′_i : ]. We have [ : ] ≤ n = [E : F] and [ : ] = n if E/F is separable. is a direct sum of g ideals isomorphic to the algebras D′/P′_i^e_i. The radical of is P′₁ … P′_g/PD′ and /rad is a direct sum of g ideals isomorphic to the fields /P′_i.

Proof.     Put . Then

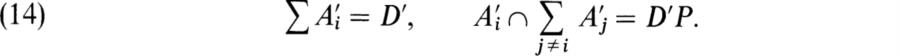
This implies that

and . Hence

We have the chain of ideals

each of which is minimal over the next. Hence

is a composition series for D′/P′_i^e_l as D′-module. The composition factors are isomorphic to D′/P′_i, P′_i/P′²_i, …, P′_i^{e_l− 1}/P′_i^e_l, each of which is annihilated by P′_i and so can be regarded as a vector space over the field D′/P′_i. Since these vector spaces have no non-zero subspaces, they are one-dimensional over D′/P′_i. Hence the composition factors are isomorphic as D′-modules and hence also as D-modules and as vector spaces over . Then [P′_i^{j − 1}/P′_i^j : ] = [D′/P′_i : ] = f_i for j = 1, …, e_i. It follows from (18) that [D′/P′_i^e_l : ] = e_if_i. Since we have [ : ] = Σ₁^ge_if_i. We have shown in Theorem 10.11 that Σ e_if_i ≤ n and Σ e_if_i = n if E/F is separable. Hence [ : ] ≤ n and = n if E/F is separable.

Let e = max{e_i}. Then (P′₁ P′₂ … P′_g)^e ⊂ D′P. Hence P′₁ … P′_g/D′P is a nilpotent ideal in = D′/D′P and . Since every D′/P′_i is a field, it follows that P′₁ … P′_g/D′P = rad and /rad is a direct sum of g ideals isomorphic to the fields D′/P′_i.

We now give the following

DEFINITION 10.4.  A non-zero prime ideal P of D is said to be unramified in D′ if D′P = P′₁ … P′_g where the P′_i are distinct prime ideals in D′ and every D′/P′_i is separable over = D/P. Otherwise, P is ramified in D′.

It is clear from Theorem 10.12 that P is unramified in D′ if and only if = D′/D′P is a direct sum of fields that are separable over = D/P. We shall show that if E/F is separable, then there are only a finite number of prime ideals P of D that are ramified in D′ and in principle we shall determine these prime ideals. For this purpose we give the following

DEFINITION 10.5.  Let D, F, E, D′ be as usual and assume that E/F is separable. Then the discriminant (ideal) d_D′/D of D′ over D is the ideal generated by all of the elements

where (u₁, …, u_n) is a base for E/F consisting of elements u_i ∈ D′.

We have seen in the proof of Proposition 10.9 (p. 612) that det(T_E/F(u_iu_j)) ≠ 0 for every base (u₁, …, u_n) of a separable extension E/F. The main result on ramification is

THEOREM 10.13.  Let D be a Dedekind domain, F its field of fractions, E a finite dimensional separable extension of F, D′ the subring of E of D-integral elements. Then a non-zero prime ideal P of D is ramified in D′ if and only if P is a divisor of the discriminant d_D′/D.

Of course, this implies the finiteness of the set of ramified primes. To achieve the proof of Theorem 10.13 we need to obtain a trace criterion that a finite dimensional commutative algebra A over a field F be a direct sum of ideals that are separable field extensions of F.

If A is a finite dimensional algebra over a field F, we define the trace bilinear form T(a, b) on A/F by

where T_A/F is the trace defined by the regular representation. Since T_A/F is a linear function and T_A/F(ab) = T_A/F(ba), T(a, b) is a symmetric bilinear form (BAI, pp. 424, 426). We recall also that T(a, b) is non-degenerate if and only if det(T(u_i, u_j)) ≠ 0 for any base (u_i, …, u_n) of A/F.

We require the following

LEMMA.  If A is a finite dimensional commutative algebra over a field F, then A/F is a direct sum of ideals that are separable fields over F if and only if the trace bilinear form T(a, b) is non-degenerate on A.

Proof.     Suppose first that where E_i is a separable field extension of F. Let (u_i1, …, u_in1) be a base for E_i. Then (u_ll, …, u_1n1 …, u_g1, …, u_gng) is a base for A/F and

where T_i denotes the trace bilinear form on E_i. Since we have shown (p. 612) that T_i is non-degenerate, the foregoing formula shows that T is non-degenerate on A.

Conversely, suppose that T is non-degenerate on A. We show first that A is semi-primitive. Let z ∈ rad A. Then za = az is nilpotent for every a ∈ A. Since the trace of a linear transformation is the sum of its characteristic roots, the trace of a nilpotent linear transformation is 0. Hence T(a, z) = 0 for all a. Since T is non-degenerate, z = 0. Thus rad A = 0 and A is semiprimitive. Then where E_i is a field extension of F. By (21), the trace bilinear form T_i is non-degenerate on every E_i. On the other hand, if E/F is a/finite dimensional inseparable extension field of F then the trace function is identically 0 on E. For, E S where S is the maximal separable subfield of E. Then E is purely inseparable over S. It follows that there exists a subfield K of E containing S such that [E : K] = p the characteristic. Then the minimum polynomial over K of any a ∈ E is either of the form x^p − α or of the form x − α. In either case the characteristic polynomial is of the form x^p − β (β = α^p in the second case). Then T_E/K(a) = 0 for all a. By the transitivity of the trace (BAI, p. 426) we have T_E/F(a) = T_K/F(T_E/K(a)) = 0. It follows that the trace bilinear form on an inseparable field is identically 0. Hence every E_i is separable.

We can now give the

Proof of Theorem 10.13. We assume first that D is a p.i.d. By Proposition 10.9, D′ is finitely generated as D-module. Since there is no torsion and D is a p.i.d., D′ is a free D-module. Since every element of E has the form r^{− 1}u where r ∈ D and u ∈ D′, the rank of D′ over D = n = [E : F]. Let (v_l, …, v_n) be a D-base for D′. Then det(T(v_i, v_j)) generates d_D′/D, so we have to show that is a direct sum of separable field extensions of if and only if Pdoes not contain the element det(T(v_i, v_j)). Since (v_l, …, v_n) is a D-base for D′, PD′ = Σ Pv_i and if _i = v_i + PD′, then (₁, …, n) is a base for over . It follows that if a ρ(a) is the regular matrix representation of E/F obtained by using the base (v_l, …, v_n), then the regular matrix representation of / using the base (₁, …, n) is ( = a + PD′). This implies that det(T(_i, _j)) = det(T(v_i, v_j)) + P. Hence by the Lemma, is a direct sum of separable fields over if and only if det (T(v_i, V_j)) P. This completes the proof in the case in which D is a p.i.d.

The proof for arbitrary D can be reduced to the p.i.d. case by localizing at the prime P of D. Since we are interested in localizing D′ as well as D and since P is not a prime ideal in D′, we make explicit the localizing monoid as S = D − P. We form D_s and D′_s. By Proposition 7.16, D′_s is the integral closure of D_s in E. Since P′_i ∩ D = P, P′ ∩ S = Ø. Hence P′_is is a prime ideal in D′_s. We have P_s D′_s = P′_1s^e₁ … P′_gs^e_g and the P′_is are distinct. Since P′_is ∩ D′ ⊂ P′_ip′ ∩ D′ = P′_i, we have P′_is ∩ D′ = P′_i. It follows as in the proof of Theorem 10.10 that we have a semi-linear map of D′_s/P′_is over D_s/P_s onto D′/P′_i over D/P, which is a ring isomorphism. Hence D′_s/P′_is is separable over D_s/P_s if and only if D′/P′_i is separable over D/P. Thus P is ramified in D′ if and only if P_s is ramified in D′_s.

We show next that d_D′s/D_s = (d_D′/D)s. Let(u₁, …, u_n) be a base for E/F such that the u_i ∈ D′. Then u_i ∈ D′_s and det(T(u_i, u_j))∈ d_D′s/Ds. Hence d_D′/D ⊂ d_D′s/Ds and (d_D′/D)_s ⊂ d_D′s/Ds. Next let (u′₁, …, u′_n) be a base for E/F such that the u′_i ∈ D′_s. Then the u′_i = u_i s^{− 1}, u_i ∈ D′, s∈ D − P, and det(T(u′_i))= s^{− 2n} det(T(u_i, u_j)) ∈ (d_D′/D)_s. Hence d_D′s/Ds⊂ (d_D′/D)_s so d_D′s/Ds = d_D′s/Ds. It is clear also that P is a divisor of d_D′/D if and only if P_s is a divisor of (d_D′/D)s = d_D′s/Ds. We have therefore achieved a reduction of the theorem to the rings D_s and D′_s. Since D_s is a p.i.d., the result follows from the case we considered first.

EXAMPLE

Let m be a square-free integer, E = (), and let D′ be the integral closure of in E. Then D′ has the base (1, ) over if m ≡ 2 or 3 (mod 4) and D′ has the base (1,(1 + )/2) over if m ≡ 1 (mod 4) (exercises 4 and 5, p. 287 of BAI). Hence in the first case, the discriminant d_D′/ is the principal ideal generated by

Hence the ramified primes (which are the primes p in such that _p is a square of a prime ideal in D′) are 2 and the prime divisors of m.

In the second case (m ≡ 1 (mod 4)), d_D′/ is the principal ideal generated by

Hence the ramified primes are the prime divisors of m.

EXERCISES

        1. Notations as in the example. Show that if p is odd and pD unramified in D′, then pD′ is a prime or a product of two distinct prime ideals in D′ according as the Legendre symbol (m/p) = − 1 or = 1. Show that if m ≡ 1 (mod 4), then 2D′ is prime or a product of two prime ideals in D′ according as m ≡ 5 or m ≡ 1 (mod 8). (Hint: Use Theorems 10.9 and 9.14.)

        2. Let E be the cyclotomic field (), a primitive lth root of unity, l a prime, as in exercise 1, p. 618, which showed that ( − 1)D′ is prime in D′. Show that [D′/( − 1)D′ : /l] = 1 and hence that |D/( − 1)D′| = l Show that D′ = [] + ( − 1)D′ Use exercise 2, p. 276 of BAI, to show that |det T(ⁱ, ^j| = l^{l− 2} if 0 ≤ i, j ≤ l − 2. Hence show that D′ ⊂ l^{−(l + 2)}[] and l^{(l + 2)}D′ ⊂ [] ⊂ D′ Use these results to prove that D′ = [] and that l is the only prime ideal of that is ramified in D′.

        3. Show that a finite dimensional commutative algebra A over a field F is a direct sum of separable fields if and only if A_E is semi-primitive for every field extension E of F. (The latter property was discussed on p. 374 where it was called separability.)

10.6   FINITELY GENERATED MODULES OVER A DEDEKIND DOMAIN

In this section we shall extend the theory of finitely generated modules over a p.i.d. that we treated in BAI (sections 3.6–3.9, pp. 179-194) to finitely generated modules over a Dedekind domain. We recall that if M is a module over a domain D, the subset T of elements x ∈ M for which there exists an a ≠ 0 such that ax = 0 is a submodule called the torsion submodule of M. M is called torsion free if T = 0. Any submodule of a torsion-free module is torsion free. Hence, since any free module is torsion free, any submodule of a free module is torsion free. It is clear also that if T is the torsion submodule of a module M, then M/T is torsion free. We shall derive next a pair of less obvious results on torsion-free modules.

PROPOSITION 10.11.  Any finitely generated torsion-free module M over a domain D is isomorphic to a submodule of a free module of finite rank.

Proof.     Let {u₁, …, u_r} be a set of generators for M. We assume M ≠ 0 and u₁ ≠ 0. We may assume that we have an s, 1 ≤ s, ≤ r such that {u₁, …, u_s} are linearly independent over D in the sense that ∑₁^sd_iu_i = 0 holds only if every d_i = 0, but {u₁, …, u_s, u_{s + j}} are linearly dependent over D for all j, 1 ≤ j ≤ r − s. Then the submodule ∑₁^sDu_i of M is free and hence the result holds if s = r. On the other hand, if s < r, then for each j there exists a nonzero d_j ∈ D such that d_ju_{s + j} ∈ ∑₁^sDu_i. Then du_{s + j} ∈ ∑₁^sDu_i for d = d_j ≠ 0 and so dM ⊂ ∑₁^s Du_i. Hence the D-endomorphism x dx of M maps M into the free submodule ∑₁^s Du_i Since M is torsion free, this map is a monomorphism. Hence M is isomorphic to a submodule of the free module ∑₁^s Du_i.

We shall obtain next a generalization of the theorem that any submodule of a finitely generated free module over a p.i.d. is free (Theorem 3.7 of BAI, p. 179). This is

PROPOSITION 10.12.  Let R be a ring, which is not necessarily commutative, with the property that every left ideal of R is a projective R-module. Then any submodule M of the free module R⁽ⁿ⁾ is a direct sum of m ≤ n submodules isomorphic to left ideals of R. Hence M is projective.

Proof.     The result is clear if n = 1, since the submodules of R = R⁽¹⁾ are left ideals. Hence assume that n > 1. Let S denote the submodule of R⁽ⁿ⁾ of elements of the form (x₁, …, x_{n − 1}, 0). Evidently S ≅ R^{(n − 1]}. Now consider the R-homomorphism p : y = (y_l, …, y_n) y_n of M into R. The image is a left ideal I of R and the kernel is isomorphic to a submodule N of R^{(n − 1)}. We have an exact sequence

Since I is projective, this exact sequence splits (p. 150); hence M ≅ N I. Since N ⊂ R^{(n − 1)}, we may use induction to conclude that N is isomorphic to a direct sum of ≤ n − 1 left ideals. Then M is isomorphic to a direct sum m ≤ n left ideals of R. Since any left ideal is projective, it follows that M is projective.

We now assume that M is a finitely generated module over a Dedekind domain D. The defining property for D that we used is that any fractional ideal of D is invertible and hence is projective (Proposition 10.3). In particular, any integral ideal of D is projective and since 0 is trivially projective, every ideal in D is a projective module. Thus D satisfies the hypothesis of Proposition 10.12. Let T be the torsion submodule of M and put = M/T. Then is finitely generated and torsion free. Hence, by Proposition 10.11, is isomorphic to a submodule of a free module of finite rank. Then, by Proposition 10.12, is projective. Since we have an exact sequence 0 → T → M → → 0 and is projective, M ≅ T. Then T is a homomorphic image of Mand so it, too, is finitely generated. It is clear that we have reduced the problem of classifying finitely generated D-modules into isomorphism classes to the same problem for torsion-free modules and torsion modules.

We consider first the torsion-free modules. We have seen that any such module is projective. On the other hand, if M is projective, M is a direct summand of a free module, and since D is a domain, free modules and hence projective modules over D are torsion-free. Thus M is finitely generated torsion free over D if and only if M is finitely generated projective.

In determining conditions for isomorphism of two such modules, we may assume that the modules have the form M = I₁ … I_n where I_j is an integral ideal. Although there is no gain in generality in doing so, it is somewhat more natural to assume that the I_j are fractional ideals. Consider the localization M_D^* determined by the monoid D^* of non-zero elements of D. We have and since D_D^* is the field F of fractions of D and I_jD^* = F, M_D^* is an n-dimensional vector space over F. Thus M_D^* ≅ F⁽ⁿ⁾. The dimensionality n is the rank of M over D as defined in section 7.7 (Corollary, p. 415). The canonical map x x/1 of M into M_D^* is a monomorphism. It follows that we have an isomorphism of M with the D-submodule of F⁽ⁿ⁾ consisting of the vectors (x₁, …, x_n) where x_j ∈ I_j. Hence we may assume that M consists of this set of vectors.

If η is an isomorphism of M onto a second finitely generated torsion-free module M′, η has a unique extension to a bijective linear transformation of M_D^*/F onto M′_D^*/F. It follows that M and M′ have the same rank n and we may assume also that M′ is the D-submodule of F⁽ⁿ⁾ consisting of the vectors (x′, …, x′_n) where x′_j ∈ I′_j, a fractional ideal in F, 1 ≤ j ≤ n. Taking into account the form of a bijective linear transformation of F⁽ⁿ⁾, we see that η has the form

where A = (a_ij) ∈ GL_n(F), the group of n × n invertible matrices with entries in F. We have x′_k = ∑ x_ja_jk ∈ I′_k and if A^{− 1} = (b_ij), then x_j = ∑ x′_kb_kj ∈ I_j if x′_k ∈ I′_k, 1 ≤ k ≤ n. Conversely, if A ∈ GL_n(F) satisfies these conditions, then (23) is an isomorphism of M onto M′.

If n = 1, the foregoing conditions imply that two fractional ideals I and I′ are isomorphic if and only if there exists an a ≠ 0 in F such that I′ = Ia. We can state this result in terms of the class group of the Dedekind domain D, which we define to be the factor group / where is the multiplicative group of fractional ideals of D and is the subgroup consisting of the principal ideals aD, a ≠ 0 in F. The ideal I and aI = (aD)I are said to be in the same class. Thus we have shown that I and I′ are isomorphic D-modules if and only if I and I′ are in the same class. It is clear that we have a 1-1 correspondence between the isomorphism classes of fractional ideals and hence of torsion-free modules of rank one with the elements of the class group /.

We prove next the

LEMMA.  Let I₁ and I₂ be fractional ideals. Then M = I₁ I₂ ≅ D I₁I₂.

Proof.     We use exercise 10 on p. 605. According to this, if a₁ ≠ 0 in I₁ and J = a₁I₁^{− 1}(⊂ D), then there exists an a₂ ∈ I₂ such that a₁I₁^{− 1} + a₂I₂ ^{− 1} = D. Hence we have b_i ∈ I_i ^{− 1} such that a₁b₁ + a₂b₂ = 1. Then the matrix

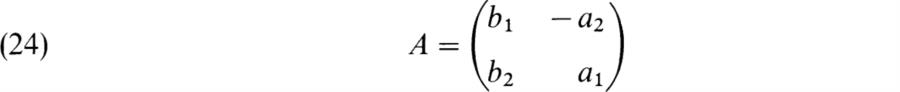
is invertible with A^{− 1} = . If x_j ∈ I_j, then y₁ = x₁b₁ + x₂b₂ ∈ D and y₂ = − x₁a₂ + x₂a₁ ∈ I₁I₂. On the other hand, if y₁ ∈ D and y₂ = c₁c₂, C_j ∈ I_j, then x₁ = a₁y₁ − b₂c₁c₂ ∈ I₁ and x₂ = a₂y₁ + b₁c₁c₂ ∈ I₂. Hence (x₁, x₂) (x₁, x₂)A is an isomorphism of I₁ I₂ onto D I₁ I₂.

We can now prove the main theorem on finitely generated modules without torsion over a Dedekind domain.

THEOREM 10.14.  Any finitely generated torsion-free module M over a Dedekind domain is isomorphic to a direct sum of a finite number of integral ideals. Necessary and sufficient conditions for the isomorphism of M = I₁ … I_n and M′ = I′₁ … I′_m where the I_j and I′_k are fractional ideals are m = n and I₁ … I_n and I′₁ … I′_m are in the same class.

Proof.     The validity of the first statement has been noted before. Now suppose that M ≅ M′ where M and M′ are as in the statement of the theorem. Then m = n and we have a matrix A = (a_ij) ∈ GL_n(F) such that if x_j ∈ I_j, 1 ≤ j ≤ n, then x′_k = ∑_jⁿ = 1 x_ja_jk ∈ I′_k. Moreover, if A^{− 1} = (b_ij) and x′_k ∈ I′_k, 1 ≤ k ≤ n, then x_j = ∑x′_kb_kj ∈ I_j. The first condition implies that x_ja_jk ∈ I′_k for any x_j ∈ I_j. Thus I_ja_jk ⊂ I′_k, so (I′_k)^{− 1}I_ja_jk ⊂ D and a_jk ∈ I_j^{− 1}I′_k. Hence if (k_l, …, k_n) is a permutation of 1, 2, …, n, then a_lk1 … a_nkn, ∈ ( I_j)^{− 1} and (I′_k). This implies that det A ∈ (I_j)^{− 1}(I′_k) and (det A)I_j ⊂ I′_j. Similarly, (det A^{− 1} )I′_j ⊂ I′_j. Hence I′_j = (det A)I_j and so I_j and I′_j are in the same class. Conversely, assume that m = n and that Ij and I′_j are in the same class.By the lemma, M =I₁ I₂ … In ≅ D I₁I₂ I₃ … I_n ≅ D D I₁ I₂ I₃ I₄ … I_n ≅ … ≅ D … D I_j. Similarly, M′ ≅ D … D I′_j. Since I_j and I′_j in the same class, these are isomorphic and hence M ≅ M′.

We consider next the structure of a finitely generated torsion module M over D. Our program for studying M will be to replace it by a closely related module over a p.i.d. Let I = ann_DM. If M = Dx₁ + Dx₂ + … + Dx_n, then

Hence I = ann_DM ≠ 0. Let {P₁, …, P_r} be the prime ideal divisors of I and let

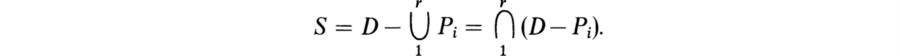
Then S is a submonoid of the multiplicative monoid of D and we can form the ring D_s and the D_s-module M_s = D_{s D}M. Any prime ideal of D_s has the form P_s where P is a prime ideal such that P ∩ S = Ø (p. 401). Then P ⊂ P_i and hence P ⊂ P_i for some i (Proposition 7.1, p. 390), which implies P = P_i. Thus D_s is a Dedekind domain with only a finite number of prime ideals, P′_i = P_is, 1 ≤ i ≤ r. Such a domain is a p.i.d. (exercise 15, p. 625). Moreover, M_s is a torsion D_s-module since I_s ≠ 0 and I_s M_s = 0.

The fundamental theorem on finitely generated modules over a p.i.d. (BAI, p. 187) is applicable to the D_s-module M_s. According to this, M_s = D_sy₁ … Dsy_m where ann_Dsy₁ ⊃ ann_Dsy₂ ⊃ … ⊃ ann_Dsy_m. Moreover, ann_Dsy_i ⊃ I_s ≠ 0 and ann_Dsy_i is a proper ideal in D_s. We shall be able to apply this result to determining the structure of M as D-module, since we can recover M from M_s by using the following

LEMMA.  Let I be a non-zero ideal in D, P₁, …, P_r the prime ideal divisors of I in D, S = (D − P_i). Let N be a D-module such that IN = 0. Then N ≅ (D/I) _DN_s as D-modules.

Proof.     We have (D/I)_DN_s ≅ (D/I)_D(D_{s D}N)≅ ((D/I) _D D_s)_DN ≅ (D/I)_{s D}N. It is readily seen that the elements s + I, s ∈ S, are units in D/I, which implies that (D/I)_s ≅ D/I. Hence (D/I)_{s D}N ≅ N, since IN = 0.

We can now prove the following structure theorem.

THEOREM 10.15.  Let M be a finitely generated torsion module over a Dedekind domain D. Then M is isomorphic to a direct sum of cyclic modules Dz₁ … Dz_m such that ann z₁ ⊃ ann z₂ ⊃ … ⊃ann z_m 0. Moreover, the ideals ann z_i, 1 ≤ i ≤ m, are uniquely determined.

Proof.     Let S be as before. Then M_s = D_sy₁ … D_sy_m where ann_Dsy₁ ⊃ … ⊃ ann_Dsy_m. Then if I′_j = ann_Dsyj, D_sy_j ≅ D_s/I′_j. Let I_j = {a ∈ D|a/s ∈ I′_j for some s ∈ S}. Then I_js = I′_j (p. 401) and D/I_j is a cyclic D-module, Dz_j, such that (D/I_j)_s ≅ D_s/Ij_s = D_s/I′_j. Moreover, ann_Dz_j = I_j and I₁ ⊃ … ⊃ I_m. Now consider the module N = Dz₁ … Dz_m. We have N_s = (Dz₁)_s … (Dz_m)_s ≅ D_sy₁ … D_sy_m ≅ M_s. Hence by the lemma, M ≅ N = Dz₁ … Dz_m. The uniqueness follows also by using S-localization and the corresponding uniqueness result in the p.i.d. case (BAI, p. 192). We leave the details to the reader.

Theorems 10.14 and 10.15 and the fact that any finitely generated module over a Dedekind domain D is a direct sum of its torsion submodule and a torsion-free module constitute a direct generalization of the fundamental theorem on finitely generated modules over a p.i.d. If D is a p.i.d., then the class group / = 1 and the results show that M is a direct sum of copies of D and cyclic modules Dz₁, …, Dz_m with non-zero annihilators I₁, …, I_m such that I₁ ⊃ … ⊃ I_m. This is the fundamental theorem as given in BAI, p. 187. The Dedekind domain is a p.i.d. if and only if / = 1. The group / gives a measure of the departure of D from being a p.i.d. It is a classical group of algebraic number theory. There it is shown by transcendental methods that the class group is finite. On the other hand, it has been shown by L. Claborn (Pacific J. of Math., vol. 18 (1966), 219–222) that any abelian group is the class group of a suitable Dedekind domain.

We shall now show that the class group coincides with the projective class group, which we defined in section 7.4. The latter, denoted as Pic D, is the set of isomorphism classes of faithful finitely generated projective modules of rank one with multiplication defined by the tensor product. Since D is a domain, projective D-modules are automatically faithful. Hence the elements of Pic D can be represented by the fractional ideals, and as we have seen, two such ideals are isomorphic if and only if they are in the same class. Hence we have the bijective map [I] I of Pic D onto / where [I] denotes the isomorphism class of the fractional ideal I. Now we have the canonical module homomorphism of I₁ I₂ into I₁I₂ sending a₁ a₂ into a₁ a₂. Localization at all of the maximal ideals show that this is an isomorphism. Thus I₁ I₂ ≅ I₁I₂ and hence [I] I is a group isomorphism of Pic D with the class group.

REFERENCES

O. Zariski and P. Samuel, Commutative Algebra vol. I, D. van Nostrand, 1958. New printing, Springer-Verlag, New York, 1975.

S. Lang, Algebraic Number Theory, Addison-Wesley, Reading, Mass., 1970.

______,Introduction to Algebraic and Abelian Functions, Addison-Wesley, Reading, Mass., 1972.

G. J. Janusz, Algebraic Number Fields, Academic Press, New York, 1973.