CHAPTER 15

CONFORMAL MAPPING

             71. GENERAL PRINCIPLES OF CONFORMAL MAPPING

It will be recalled that a single-valued function w = f(z) analytic on a domain G is conformal at every point z₀ ∈ G such that f′(z₀) ≠ 0 (see Theorem 3.4). Moreover, according to Theorem 12.9, the image = f(G) of the domain G under the mapping w = f(z) is itself a domain. Thus, given a function f(z) analytic on G, where f′(z) is nonvanishing on G, one might be tempted to describe the mapping of G onto = f(G) as a conformal mapping. However, in any theory involving “mappings,” it seems reasonable to insist that the roles of the domains G and be interchangeable: This leads to the additional requirement that the inverse function z = f^–1(w) be single-valued, or equivalently that the original function w = f(z) be one-to-one:

DEFINITION. Let G and be two domains in the finite plane,¹ and let w = f(z) be a one-to-one analytic function mapping G onto. Then w = f(z) is called a conformal mapping of G onto , and w = f(z) is said to map G conformally onto . Moreover, is called a conformal image of G.

Remark. Note that if f(z) is one-to-one on G, then f′(z) is automatically nonvanishing on G (see Theorem 12.8 and its corollaries). Hence, any conformal mapping of G is conformal at every point of G.

Example 1. Let w = f(z) = e^z, and let G be any domain containing two points z₁, z₂ differing by an integral multiple of 2πi Then f′(z) is non-vanishing on G, and hence f(z) is conformal at every point of G and one-to-one in a sufficiently small neighborhood of every point of G (recall Theorem 12.7). However, f(z) is not one-to-one on G itself, since it takes the same value at the points z₁ and z₂. Therefore w = f(z) is not a conformal mapping of G onto = f(G).

Example 2. Let w = f(z) = e^z as in Example 1, but this time let G be a domain containing no pair of points differing by an integral multiple of 2πi². Then w = f(z) is a conformal mapping of G onto = f(G).

THEOREM 15.1. If is a conformal image of a domain G, then G is a conformal image of .

Proof. Apply Rule 5, p. 48 after noting that the inverse of a one-to-one analytic function is continuous (why?).

THEOREM 15.2. If is a conformal image of a domain G and if * is a conformal image of , then * is a conformal image of G.

Proof. Apply Rule 4, p. 46.

It is now a natural problem to look for classes of domains which are conformal images of each other. For multiply connected domains, this is a complicated matter, but for simply connected domains the problem has a definitive solution given by

THEOREM 15.3 (Riemann’s mapping theorem)³. Any simply connected domain G in the finite plane other than the whole plane is a conformal image of the open unit disk.

COROLLARY. Let G and be any two simply connected domains in the finite plane other than the whole plane. Then G and are conformal images of each other.

Proof. Use Theorems 15.1 and 15.2.

Remark 1. It is clear why the case where G is the whole plane must be excluded in Theorem 15.3. In fact, the existence of a one-to-one analytic function w = f(z) mapping the whole plane onto the unit disk implies |f(z)| < 1 for all z, i.e., f(z) is a bounded entire function. But then by Liouville’s theorem (Theorem 10.7), f(z) ≡ const, which is absurd.

Remark 2. The function w = f(z) mapping G conformally onto = f(G) is not unique. To see this, map G conformally onto the unit disk, then map the unit disk conformally onto itself, and finally map the unit disk conformally onto . The result is a conformal mapping of G onto . However, the unit disk can be mapped conformally onto itself in infinitely many ways (see Example 2, p. 109), and hence G can be mapped conformally onto in infinitely many ways.

The freedom of choice in the conformal mapping of G onto is eliminated in precisely the same way as for the conformal mapping of a disk onto itself (see Sec. 28, Prob. 4):

THEOREM 15.4 (Uniqueness theorem for conformal mappings). Let G be the same as in Theorem 15.3, and let z₀ be an arbitrary point of G. Then there exists a unique function w = f(z) which maps G conformally onto the disk |w| < 1 and satisfies the conditions

Proof. Suppose w = g(z) is another function satisfying the same conditions as w = f(z). Then the function

is analytic on the unit disk, satisfies the conditions

and maps the unit disk conformally onto itself. Therefore, according to Schwarz’s lemma (Theorem 12.12),

i.e.,

for all z ∈ G. But then, interchanging the roles of f(z) and g(z), we obtain

which together with (15.1) implies

or equivalently

Applying Schwarz’s lemma again to (15.2), we conclude that

But φ′(0) > 0 and hence e^iα = 1, i.e.,

It follows that

for all z ∈G, as asserted.

It is often possible to infer that w = f(z) is a conformal mapping of a domain G onto = f(G) from a knowledge of the behavior of f(z) on the boundary of G. The following is a typical result of this kind:

THEOREM 15.5. Given a closed rectifiable Jordan curve γ, suppose f(z) is analytic on and one-to-one on γ. Then f(z) is analytic on I(γ), which it maps conformally onto I(Γ) where Γ = f(γ).

Proof. First we note that Γ is itself a closed rectifiable Jordan curve (see Prob. 7), while f[I(γ)] is a domain (see Theorem 12.9). Let w₁ be an arbitrary point of I(Γ). According to the argument principle (Theorem 12.4), the number of w₁-points of f(z) inside γ minus the number of poles of f(z) inside γ equals v, the number of circuits around the point w₁ made by the point w = f(z) as the point z traverses γ once in the positive direction. A priori, v can only equal –1 or +1, since Γ is a closed Jordan curve.⁴ But f(z) has no poles inside γ, and hence v must equal +1, i.e., f(z) takes every value w₁ ∈ I(Γ) once, and we have incidentally proved that w = f(z) traverses Γ in the same direction as z traverses γ. It follows that

Next let w₂ be an arbitrary point of E(Γ). Then, as z traverses the curve γ, the point w = f(z) traverses the curve Γ and obviously cannot wind around w₂. Again applying the argument principle, and the fact that f(z) has no poles inside γ, we find that f(z) has no w₂-points inside γ, i.e., E(Γ) ∩ f[I(γ)] = 0. We also have Γ ∩ f[I(γ)] = 0, since w ∈ Γ, w ∈ f[I(γ)], implies that some neighborhood (w) is contained in f [I(γ)]. But this contradicts what was just proved, since every neighborhood of a point of Γ must contain points of E(Γ). Therefore

and, together, (15.3) and (15.4) imply the desired result f[I(γ)] = I(Γ). Moreover, as already noted, every point of I(Γ) has precisely one inverse image in I(γ). It follows that f(z) is one-to-one on I(γ), which it maps conformally onto I](γ).

Theorem 15.5 can be generalized in a number of ways. One of these is particularly important in the applications and will be needed in the next two sections:

THEOREM 15.6.⁵ Let γ be the real axis and D the open upper half-plane. Suppose f(z) is continuous on , analytic on except at a finite number of points of γ, and one-to-one on γ which it maps into a closed rectifiable Jordan curveΓ. Then f(z) is one-to -one on D, which it maps conformally onto I(Γ).

Problem 1 (Ml, p. 382). Interpret Schwarz’s lemma geometrically.

Problem 2. Generalize Riemann’s mapping theorem to the case where G is a simply connected domain in the extended plane and simple connectedness has the same meaning as in Sec. 12, Prob. 9.

Hint. Use the preliminary transformation ζ = 1/z to map G conformally onto a domain in the finite plane.

Problem 3. Generalize the corollary to Riemann’s mapping theorem to the case where G and are both simply connected domains in the extended plane.

Hint. The function mapping G onto is now allowed to have one pole.

Problem 4. Can the finite plane with the origin deleted be mapped conformally onto the open unit disk with the origin deleted?

Problem 5 (M2, p. 116). Prove that if f(z) is one-to-one and analytic in the whole plane except for one pole, then f(z) is a Möbius transformation.

Problem 6 (M2, p. 118). Prove that if a sequence {f_n(z)} is uniformly convergent on every compact subset of a domain G and if every term f_n(z) is one-to-one and analytic on G, then the limit function

is also one-to-one and analytic on G, unless f(z) = const.

Hint. Use Hurwitz’s theorem (Theorem 12.6).

Problem 7 (Ml, p. 305). Prove that the analytic image of a rectifiable curve is rectifiable.

Problem 8 (M2, p. 119). Given a closed rectifiable Jordan curve γ, suppose f(z) is analytic on and one-to-one on γ. Prove that f(z) is one-to-one on E(γ), which it maps conformally onto I(Γ) where Γ = f(γ).

72. MAPPING OF THE UPPER HALF-PLANE ONTO A RECTANGLE

To illustrate the application of the results of the preceding section, consider the function

known as the elliptic integral of the first kind (in Legendre’s form), where the path of integration is any rectifiable curve joining the points 0 and z. The function

is double-valued, and has first-order branch points at t = ±1/ and t = ± 1/k (cf. Remark 3, p. 78). Since these points all lie on the real axis, we can define two single-valued analytic branches of (15.6) in the z-plane cut along the segments – 1/k ≤ x ≤ –1 and 1 ≤ x ≤ l/k of the real axis (see Prob. 1), in particular, in the upper half-plane D: Im z > 0. Of these two branches which take values with opposite signs at every point, we choose the one which takes positive values when t belongs to the interval (0, l).⁶ In a neighborhood |z| > l/k of the point at infinity, the integrand in (15.5) has the expansion

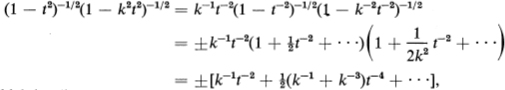
which implies

where C is a constant. Therefore it is clear that both branches of f(z) are analytic at infinity. Moreover, both branches are continuous on .

With a view to eventually applying Theorem 15.6, we now consider the image of γ under the mapping (15.5). In the interval 0 < x < 1, we have

which is positive and increases from 0 to

as x goes from 0 to 1. In the interval 1 < x < 1/k, the integrand in (15.5) becomes

Here the sign cannot be chosen arbitrarily, but must agree with our previous choice of the branch of (15.6), in order to guarantee continuity of this branch on . Writing (1 – t²)(1 – k²t²) in the form

we observe that in going from the interval 0 < x < 1 to the interval 1 < x < 1/k, the change in Arg g(t) equals – π.⁷ In fact, the change in Arg g(t) equals the sum of the changes in arguments of all the separate factors in (15.8), but none of these arguments changes except Arg(t – 1), which changes by – π. Therefore the change in Arg is –π/2, so that Arg becomes

since Arg = 2kπ for 0 < t < 1. Thus we see that of the two values in (15.7), the correct choice is . It follows that

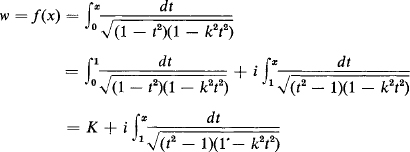
for 1 < x < 1/k. Therefore, as the point z = x traverses the interval 1 < x < 1/k, the image point w = f(x) traverses the line segment parallel to the imaginary axis going from the point K to the point K+ iK′, where

By making the substitution

and then changing τ back to t, we can write the integral for K′ in the same form as the integral for K:

Next we consider the interval l/k < x < + ∞. In this interval, the integrand in (15.5) becomes

where, as before, the sign cannot be chosen arbitrarily. In fact, writing (t² – 1)(1 – k²t²) in the form

we observe that in going from the interval 1 < x < l/k to the interval 1/k < x < + ∞, the change in Arg h(t) equals –π, i.e., the change in Arg [t – (1/k)]. Therefore the change in Arg is –π/2, so that Arg becomes

[cf. (15.9)]. Thus we see that of the two values in (15.10), the correct choice is . It follows that

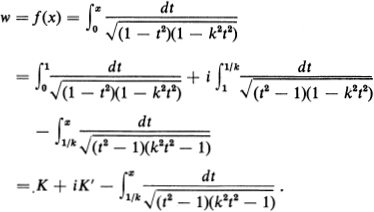
As x increases from 1/k to + ∞, the last integral on the right becomes

where we make the change of variables t = 1/kτ. Correspondingly, the image point w = f(x) describes the line segment parallel to the real axis going from the point K + iK′ to the point iK′

In just the same way, we see that as x moves along the real axis first from 0 to –1, then from –1 to –1/k and finally from – 1/k to – ∞, the point w = f(x) first describes the segment from 0 to – K, then the segment from –K to – K + iK′, and finally the segment from –K + iK′ to iK′. Thus w = f(x) is a one-to-one mapping of the real axis onto the rectangular contour with vertices –K, K, K + iK′ and – K + iK′, where

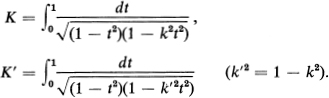
It follows from Theorem 15.6 that w = f(z) is one-to-one in the upper half-plane, which it maps conformally onto the indicated rectangle.

Now consider the expression

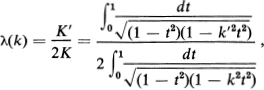
which is the ratio of the altitude of the rectangle to its base. As the parameter k (0 < k < 1) increases from 0 to 1, the denominator increases from

to ∞. At the same time, decreases from 1 to 0, so that the numerator decreases from ∞ to π/2. Therefore, as k increases from 0 to 1, the ratio λ(k) = K′/2K decreases continuously from ∞ to 0. It follows that given any rectangle with base 2a and altitude b, we can find a unique value of k (0 < k <1) such that

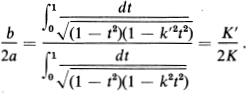
Then the function (15.5) corresponding to this value of k maps the upper half-plane conformally onto a rectangle similar to the given rectangle. To obtain a mapping onto the given rectangle, we need only introduce an extra factor μ = a/K = b/K′, writing

instead of (15.5). Then (15.15) maps the upper half-plane onto the rectangle with vertices

and hence onto any given rectangle, provided the parameters k and π are suitably chosen.

Problem 1 (M1, Sec. 55). Let

where P(z) is an arbitrary polynomial of degree N, with zeros a₁…, a_m of orders α₁…, α_m, respectively, where α₁ +…+ α_m = N. Prove that

a) No point of the finite plane other than a zero of P(z) can be a branch point of f(z);

b) Every zero a_k of P(z) whose order is not a multiple of n is a branch point of f(z) [of what order?];

c) If γ is a closed Jordan curve whose interior contains a set of zeros a_k1,…, a_kq (q ≤ m) of P(z) such that α_k1 +…+ α_kq is a multiple of n and whose exterior contains all the other zeros, then a circuit around γ does not change the value of f(z).

Problem 2. Specialize formula (15.11) to the case of a square.

73. THE SCHWARZ-CHRISTOFFEL TRANSFORMATION

The mapping (15.5) studied in the preceding section is a special case of a more general mapping known as the Schwarz-Christoffel transformation, defined by the integral

Here C is a positive constant, a_l…, a_n are distinct real numbers (assumed to be arranged in increasing order a₁ <…< a_n), and the exponents α₁ – 1,…, α_n – 1 are also real but not necessarily distinct. For example,(15.12) reduces to the elliptic integral (15.5) if we make the following choice of constants

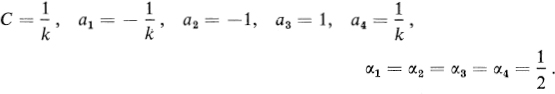
To guarantee convergence of the integral (15.12), we require that

and

where(15.14) stems from the fact that the integrand

behaves like for large t.

Of the various single-valued analytic branches of the function β(t) which can be defined in the upper half-plane, we now choose the branch such that the argument of every factor (t – a₁)^α₁–1,…, (t – a_n)^α_n–1 equals π when all the differences t – a_l,…, t – a_n are negative, i.e., when t belongs to the interval (– ∞, a₁). This corresponds to choosing the value

for the argument of β(t) when t ∈(–∞, a₁).⁸ Then in the other intervals (a_l a₂),…, (a_n–1, a_n), (a_n, + ∞), we assign Arg β(t) values which are consistent with this choice, noting that the only factor in (15.15) whose argument changes when we go from the interval (a_k–1, a_k) to the interval (a_k, a_k+1) is t – a_k, giving rise to a change of – π in Arg (t – a_k) and a change of –(α _k – l)π in Arg β(t) itself (cf. footnote 7, p. 329). Since Arg β(t) has the value (15.16) in the interval (–∞, a₁), it has the value (α₂ – 1)π +…+ (α_n – 1)π in the interval (a_l, a₂), the value (α₃ – 1)π +…+ (α_n– l)π in the interval (a₂, a₃), and so on. In general, we have

where k = 2,…, n. Finally, to the right of all the points a₁,…, a_n, i.e., in the interval (a_n, + ∞), Arg β(t) has the value 0.⁹

Setting

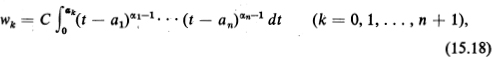
we find that (15.12) can be written in the form

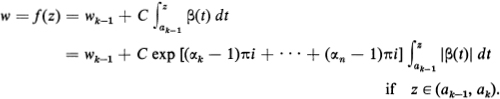
The last term on the right has the same argument for all z ∈ (a_k–1, a_k), but its absolute value increases continuously from 0 to

as z = x increases from a_k–1 to a_k. Therefore, as z traverses the interval (a_k–1, a_k) from left to right, the image point w = f(z) traverses the line segment Δ_k–1 of length l_k, with initial point w_k–1 and final point w_k, making an angle of (α_k – 1)π +…+ (α_n – l)π radians with the positive real axis. This applies equally well to the line segment Δ₀, with initial point

and final point w_l and the line segment Δ_n, with initial point w_n and final point w_n+1 = w₀. It follows that the function (15.12) maps the real axis onto a closed polygonal curve with segments Δ₀, Δ_l…, Δ_n and vertices w₀, w_l,…, w_n, w_n+1 = w₀. It cannot be asserted that this mapping is one-to-one, since the polygonal curve may have self-intersections, i.e., the segments Δ_k may have points in common other than the common end points of consecutive segments. However, if we make the additional assumption that there are no self-intersections [as, for example, in the case of the elliptic integral (15.5)], then A will be a closed rectifiable Jordan curve, bounding a polygon with vertices w₀, w_l,…, w_n. Therefore, in this case, we can apply Theorem 15.6, concluding that the Schwarz-Christoffel transformation (15.12) is one-to-one in the upper half-plane, which it maps conformally onto the indicated polygon.

According to the construction shown in Figure 15.1, the interior angle of the polygon at the vertex w_k(0 < k < n + 1) equals α_kπ. Although all the angles in the figure are only defined to within integral multiples of 2π, it is easy to see that α_kπ gives the interior angle without any correction term, i.e., that the inequality α_k < 2 holds as well as the inequality α_k > 0 assumed in (15.13). In fact, we can write

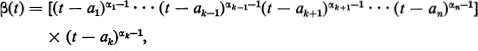
FIGURE15.1

where the expression in brackets is analytic and nonvanishing in a neighborhood of the point a_k, and hence has a power series expansion of the form

which converges uniformly in a neighborhood of a_k. But then

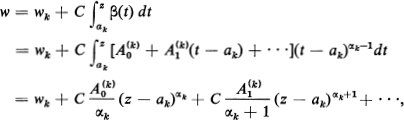
which implies

Therefore

where we use the fact that C > 0, α_k > 0. Thus, as θ varies from 0 to π along an “arbitrarily small” semicircle with center a_k, the image point w = f(z) varies continuously along some Jordan curve joining a point on the segment Δ_k to a point on the segment Δ_k–1, always staying inside the interior angle with vertex at w_k, while Arg w increases from Arg A₀^(k) to Arg A₀^(k) + α_kπ, without winding around the point w = 0 (why?). Therefore α_kπ is just the size of some interior angle of the polygon, and hence must be less than 2π In other words, instead of the condition (5.13), we have the stronger condition

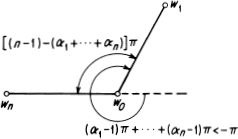
FIGURE 15.2

At the vertex w₀ = w_n+l, the interior angle of the polygon equals

as shown by Figure 15.2. From (15.14) we can only deduce that this quantity is positive. However, our polygon has a total of n + 1 interior angles, whose sum must equal [(n + 1) – 2]π = (n – l)π. Therefore (15.21) is precisely the size of the (n + l)st interior angle, and hence

or

In other words, instead of the condition (15.14), we have the stronger condition

The conditions (15.20) and (15.22) are necessary, but not sufficient, for the Schwarz-Christoffel transformation (15.12) to be a conformal mapping of the upper half-plane onto a bounded polygon, with vertices w₀, w_l,…, w_n, and interior angles

In the special case where

we find that the angle with vertex w₀ equals π Geometrically, this means that w₀ is not really a vertex, but just an interior point of the side with vertices w_n and w₁ (cf. Figure 15.2). Then (15.12) maps the upper half-plane onto an n-gon rather than an (n + l)-gon. This occurs in the case of the elliptic integral (15.5), where

and in the following example:

Example 1. We now use the Schwarz-Christoifel transformation to map the upper half-plane onto a triangle with angles α₁π, α₂π, α₃π (α_k > 0, α₁ + α₂ + α₃ = 1), where the side opposite the angle α₁π has length l. This problem can be solved in two ways. First we use formula (15.12) with n = 3, choosing three arbitrary real points a_l, a₂, a₃, which are mapped into the vertices of the triangle (in this approach, α₁ + α₂ + α₃ = n – 2). Thus, for example, suppose that

Then (15.12) gives

and we need only determine the factor C > 0. But since l must equal

[cf. (15.19)], we have

Therefore (15.23) becomes

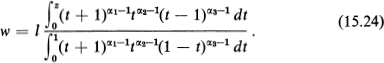
This function actually solves the problem, since it is one-to-one on the real axis, which it maps onto a triangle with the given vertex angles and side length (note that a triangle can have no self-intersections). In particular, (15.24) reduces to

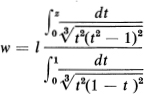
if α₁ = α₂ = α₃ = (corresponding to an equilateral triangle with side length l), and to

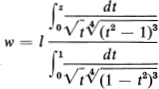
if α₂ = , α₁ = α₃ = (corresponding to an isosceles right triangle with hypotenuse l).

Example 2. Another approach to the problem of mapping the upper half-plane onto a triangle is based on the use of formula (15.12) with n = 2. This time we choose two arbitrary real points a₁ and a₂, which are to be mapped into two vertices of the triangle, with angles α₁π and α₂π. Since α₁ – α₂ cannot equal n – 2 = 0, the point at infinity must go into the third vertex of the triangle, with angle

Thus, for example, suppose that

Then (15.12) gives

and to determine C we have the equation

which implies

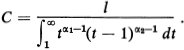
It follows that

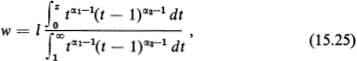
which obviously differs from (15.24). In particular, in the case of an equilateral triangle with side l, (15.25) reduces to

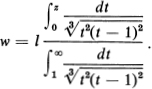
Example 3. In the general case, the upper half-plane is to be mapped onto an n-gon (n ≥ 4) with interior angles α₁π,…, α_nπ and side lengths l₁,…, l_n, where as in Figure 15.3, we associate the angles α_k–1π and α_kπ with the side l_k (k = 2,…, n), and the angles α_nπ and α₁π with the side l₁. Suppose we choose three arbitrary points a_l, a₂ and a₃ of the real axis, which are to go into the vertices w_l w₂ and w₃, with angles α₁π, α₂π and α₃π. Then we must still determine n – 3 points a₄,…, a_n of the real axis, as well as the constant C > 0, which makes n – 2 unknowns n all. At first glance, it appears that there are too many equations available for determining these unknowns, i.e., the n equations expressing the side lengths in terms of appropriate integrals. However, it is immediately apparent from Figure 15.3 that once the angles of n-gon are known, then specifying just n – 2 sides l_l,…, l_n–2 uniquely determines the remaining two sides l_n–1 and l_n¹⁰. In other words, there are actually only n – 2 independent equations of the form

for determining the n – 2 unknowns a₄,…, a_n, C, and these equations can actually be solved. This follows from the fact (not proved here) that apart from a trivial translation and rotation, (15.14) is the most general form of a function mapping the upper half-plane onto an n-gon (see M3, Sec. 47).

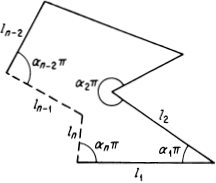
FIGURE 15.3

Problem 1. Justify the arbitrariness in the choice of a_l, a₂, and a₃ in Example 3. Can more points a₄,…, a_n be chosen arbitrarily?

Problem 2. Map the upper half-plane Im z > 0 onto a rhombus with side length l and obtuse angle απ.

Problem 3. Derive the formula for mapping the unit disk |z| < 1 onto the interior of a polygon.

Hint. Make a preliminary Mobius transformation mapping the upper half-plane onto the unit disk.

Problem 4. Show that the function

maps the unit disk onto a square. What is the side length of this square?

Problem 5. Prove that the function

maps the unit disk onto a regular n-gon. What is the side length of this n-gon?

Problem 6. Onto what domain is the unit disk mapped by the function

where

Hint. The domain is starlike (see Sec. 37, Prob. 5).

---

¹ The case of domains in the extended plane (see Sec. 12, Prob. 9) is considered in Probs. 2 and 3.

² Thus G is a domain of univalence for w = e^z as defined on p. 73. (A one-to-one analytic function is often called a univalent function.)

³ The proof of Theorem 15.3 is beyond the scope of this book, but can be found in the more advanced literature on complex analysis (see M3, Sec. 2).

⁴ This fact, which is easily verified in the simplest cases (e.g., where γ is a circle or a polygon), can be proved in complete generality. See e.g., P. S. Aleksandrov, op. cit., Chap. 2.

⁵ We omit the proof of Theorem 15.6 which is a straightforward but rather tedious deduction from the argument principle. The interested reader can prove it by specializing the considerations given in M2, pp. 120–123.

⁶ This is in keeping with what we mean by when a > 0, i.e., the positive square root.

⁷ This is easily seen by drawing a small semicircle in the upper half-plane with center t = 1, and examining the behavior of Arg g(t) as t traverses the semicircle going from left to right.

⁸ In (15.16), (15.17), etc., an extra term + 2kπ (k = 0, ±1, ±2,…) is always understood, since Arg z is only defined to within an integral multiple of 2π.

⁹ Formula (15.17) also holds in the intervals (– ∞, a₁) and (a_n, + ∞), if we introduce extra constants a₀ = – ∞, a_{n + 1} = + ∞ and let k range from 1 to n + 1, regarding the right-hand side as zero if k = n + 1. Similarly, in (15.18), we allow the upper limit of integration to be any of the points –∞ = a₀, a₁,…, a_n, a_n+1 = + ∞. It should be noted that w₀ = w_n+1 (why?).

¹⁰ Obviously, specifying n – 1 angles of an n-gon uniquely determines the remaining angle.