20
BLACK HOLES
J. RICHARD GOTT
This chapter is about the most mysterious objects in the universe, black holes. One of the first exact solutions obtained for Einstein’s equations of general relativity corresponded to a black hole. An exact solution to Einstein’s equations is a spacetime whose geometry has a curvature at each point that solves the equations locally at each point. Of particular interest is the solution for the geometry of the empty space around a point mass. This is called a solution to the vacuum field equations, because they apply in empty space. These were exactly the equations Einstein was trying to solve when he worked out the orbit of Mercury and the light bending around the empty space near the Sun. But this solution was difficult to find, because one had no idea what the geometry of the solution would be like, so Einstein settled for an approximate solution. In his approximate solution, spacetime was approximately flat, just as in special relativity, but with small perturbations (departures from flatness). The equations for the small perturbations were easier to solve, because one knew that one had a flat geometry to start with and with that as a starting point, the equations for the small corrections were easier to solve. Since the velocities of objects orbiting the Sun are small with respect to the speed of light, the geometry around the Sun is only slightly curved. Thus, Einstein’s approximate solution is quite accurate, as are his values for Mercury’s orbit and the bending of light near the Sun. Perhaps Einstein thought that solving the equations exactly would be too difficult. In any case, he contented himself with an approximate solution.
The first person to find an exact solution to Einstein’s field equations for the empty space around a point mass was the German astronomer Karl Schwarzschild. What he found was the solution for a black hole, that is, a point source of mass in otherwise empty space. When Einstein published his work on general relativity, he estimated that there were only 12 people in the world who could understand it. Karl Schwarzschild was one of them. In 1900, Schwarzschild had written a paper about the possible curvature of space. This was even before special relativity. He had reasoned that space might be positively curved, like the surface of a sphere, or even negatively curved, like the surface of a Western saddle. He wanted to know how big that radius of curvature had to be, given the then-current astronomical observations. He was someone who was already willing to think about the curvature of space. When Einstein’s paper came out, Schwarzschild was very receptive: he understood it and, just as important, he was able to deal with the difficult math involving Riemann curvature tensors. He had all the tools he needed to do something new and original with it. Schwarzschild was able to solve the problem, because he came up with a clever coordinate system in which to solve these complex equations, which took advantage of the fact that the problem had spherical symmetry and was unchanging in time. This exact solution to Einstein’s vacuum field equations for the empty space around a point mass turned out to map the exterior of a black hole.
While serving in World War I, Karl Schwarzschild contracted a rare skin disease, which ultimately proved to be fatal; he was sent home sick in 1916 and at that time he learned of Einstein’s paper and found his solution. He sent the solution to Einstein, saying that during the middle of the war he had been pleased to “spend some time in the garden of your ideas.” Schwarzschild died a few months later.
Finding this exact global solution to the vacuum field equations was very much like making a patchwork coat. At each point in spacetime, you are sewing together pieces, where locally there are different curvature terms that sum up to zero. The equations are telling you the rules by which you can stitch the pieces together. You just keep sewing and adding little pieces. But ultimately, you must come up with a global solution—a patchwork coat—that satisfies the rules at every point. This is quite difficult. Karl Schwarzschild was the one who first managed to do this for the curved space around a point mass.
Karl Schwarzschild’s son, Martin Schwarzschild, was our longtime colleague at Princeton (see figure 8.3). He was also an astronomer who made many important contributions. In particular, Martin figured out that a star like the Sun would eventually become a red giant. He definitely followed in his father’s footsteps. Martin never really got to know his father, who died when Martin was only 4 years old. Interestingly, Karl fought in World War I on the German side, whereas his son Martin fled Germany when Hitler came to power, and fought on the American side against Germany in World War II.
To understand black holes, let’s first go back to Newtonian gravity. If I take a ball and throw it up in the air, what will happen? It will go up and then fall back down. There is even a saying about this: “What goes up must come down.” The only trouble with this saying is that it’s wrong. Ignoring air resistance, if you throw a ball up fast enough, at greater than Earth’s escape velocity of 25,000 miles per hour, it will escape the gravitational field of Earth and never come back. Apollo astronauts had to travel at nearly this speed to get out to the Moon. Newtonian theory has a formula for the escape velocity: ves2 = 2GM/r, where G is Newton’s gravitational constant, M is the mass of Earth, and r is the radius of Earth. Now suppose I got an enormous trash compactor and crushed Earth to a smaller size, wadding it up like a ball of paper and crushing it into a smaller radius. What would happen to the escape velocity? Earth’s mass would be the same, but its radius would be smaller, making the escape velocity from its surface rise. Eventually, if I crushed Earth to small enough size, the escape velocity would become equal to the velocity of light c. How small is this? I could just set ves2 = c2 = 2GM/r and solve for r. I would get r = 2GM/c2. We call this radius the Schwarzschild radius, in Karl’s honor. For Earth’s mass, the Schwarzschild radius is 8.88 millimeters. This is about the size of a large marble. If you crush Earth to a size smaller than this radius, the escape velocity would be greater than the speed of light and nothing, not even light, could escape. Einstein showed that nothing can travel faster than the speed of light—if you crush Earth to a radius inside its Schwarzschild radius, it’s never going to re-emerge: it forms a black hole. We call it a “black hole,” because no light from inside it can ever get out. The mass will continue to collapse to still smaller size, where gravity will pull it together even more strongly, increasing the escape velocity even more. Inside the Schwarzschild radius, gravity wins over all other forces, and the mass collapses to a point, a singularity of infinite curvature at the center. General relativity would say that this point is of zero size, but we believe that quantum effects will ultimately smear this out to a size of perhaps 1.6 × 10–33 cm, called the Planck length (we’ll see where this number comes from in chapter 24). This is much smaller than an atomic nucleus. We are left with a point mass at the center, of essentially zero size, surrounded by empty curved spacetime.
If you were to venture inside the Schwarzschild radius, could you ever get back outside? No. You would have to travel faster than light to do so, and Einstein showed that was impossible.
The Schwarzschild radius of a black hole is proportional to its mass. The bigger the mass is, the bigger the Schwarzschild radius will be. The truth is that it would be very hard to crush Earth to be within its Schwarzschild radius. But after they run out of their nuclear fuel, massive stars have dense cores that are in danger of falling inside their Schwarzschild radii. When the Sun dies, it will become a red giant and then shed its envelope, leaving a white dwarf core about the size of Earth. If the core of a dying star is more massive than 1.4 solar masses but less than 2 solar masses, the white dwarf star will collapse to form a neutron star with a radius of about 12 kilometers. A neutron star is only about a factor of 2–3 larger than its Schwarzschild radius, and therefore is close to dangerous ground. If you try to make a neutron star with a mass larger than about 2 solar masses, it is unstable to collapse and collapses inside its Schwarzschild radius, where gravity takes over completely and a black hole is formed. A 10-solar-mass black hole, such as may form when a very massive star collapses at the end of its life, has a Schwarzschild radius of 30 kilometers. A 4-million-solar-mass supermassive black hole, such as we find in the center of our galaxy, has a Schwarzschild radius of 12 million kilometers (a bit less than 1/10 of an AU). One of the largest black holes we have ever found is at the center of the giant elliptical galaxy M87. It has a mass of 3 billion solar masses and thus has a radius of 9 billion kilometers. That’s twice the radius of our entire solar system out to the orbit of Neptune.
Let’s imagine taking a trip inside a Schwarzschild black hole of 3 billion solar masses. Suppose we have a professor and a graduate student; the professor wants to know what happens inside a black hole, so he sends the graduate student to investigate. The professor stays outside the black hole, firing his rocket to stay at a fixed radius of, say, 1.25 Schwarzschild radii. The professor feels an acceleration caused by his rocket to keep at that fixed radius and not fall in. As long as the professor stays outside the black hole, bad things do not happen to him. To investigate the black hole, however, the brave graduate student just free-falls in. AHHHHHH! As the graduate student free-falls in, he sends radio signals outward, back to the professor, to tell the professor how things are going. The first part of his message says, “THINGS.” The radio signal moves outward at the speed of light.
The graduate student falls in farther, and the radio signal reaches the professor. The professor receives the first word of the message: “THINGS.” Meanwhile the graduate student falls in still farther. He sends the second word of his message: “ARE.” This word is sent just outside the Schwarzschild radius. It travels outward at the speed of light, but it is going to take a long time to climb back out and reach the professor. The professor has to fire his rockets just to stand still and avoid falling in, and so he is actually accelerating away from the horizon, so it takes the signal “ARE” a long time to catch up with him.
Meanwhile, the graduate student crosses the Schwarzschild radius. Is this good? No. Will the graduate student ever be getting back out to join the professor? No, unfortunately not. Yet as he crosses this point of no return, there is no special road sign there marking it. Nothing funny happens to the graduate student here. The graduate student doesn’t know that anything bad has happened. Everything looks normal to him. In fact, you might even be crossing inside the Schwarzschild radius of some enormous black hole right now, and from your room where you are reading this, you wouldn’t even know it. Locally a tiny piece of spacetime looks approximately flat, and therefore you have no hint as to what the global solution looks like from local measurements. Just as the graduate student crosses the Schwarzschild radius, he sends the third word of his message: “GOING.” The second word of the message, “ARE,” is still on its way out to the professor. So far, the professor has only received “THINGS.” Now the graduate student falls inside the Schwarzschild radius. The signal saying “GOING” continues outward at the speed of light. But it is like a kid running up on a down escalator and making no progress. At the Schwarzschild radius, the escape velocity is the speed of light; the radio signal traveling outward at the speed of light just stays at the Schwarzschild radius, making no progress. The signal “ARE” continues to make its way outward.
As the graduate student continues to fall farther inside the Schwarzschild radius, something begins to happen. The graduate student is falling in feet first. His feet are closer to the center than his head. Because gravity is a 1/r2 force, the mass at the center is pulling his feet more strongly than his head, with the force on his midsection being intermediate. His head and feet are being pulled apart by this tidal force. It’s like being stretched on a rack. In addition, the graduate student’s left shoulder is being drawn radially inward toward the center, while the right shoulder is also being drawn radially inward toward the center. His shoulders are being wedged together as they are being drawn closer on lines that point toward the center of the black hole. It is like being crushed in an Iron Maiden. So he sends out the last word of his message: “BADLY.” “THINGS ARE GOING BADLY.”
As he gets closer to the center, the forces grow larger and larger. He is being crushed from the sides and stretched head to toe—being turned into a piece of spaghetti. This is called spaghettification. That really is the technical term astronomers use for this process! Eventually the graduate student is ripped apart, crushed, and deposited in the central point. The mass of the central point is now 3 billion solar masses plus a little! The Schwarzschild radius moves just a little bit outward. The signal “ARE” is still working its way out to the professor. The signal “GOING” is still running in place at the Schwarzschild radius. The signal “BADLY” is going outward at the speed of light but is like a kid running up on a down escalator, where the escalator is going faster than the kid can run. Although running up, the kid is being drawn downward. The signal “BADLY,” although running outward, is sucked backward into the center, where it is crushed and deposited on the point singularity as well.
Finally, after a long time, the signal “ARE” is received by the professor. The professor has received the message “THINGS A . . . R . . . E.” He never receives the rest of the message: “GOING BADLY.” “GOING” remains stuck at the Schwarzschild radius, and “BADLY” has been sucked into the pointlike singularity at the center along with the graduate student. “BADLY” is the news of an event occurring inside the Schwarzschild radius. That signal is never going to reach the professor, and he never finds out what happens inside that radius. The professor never sees any events that occur inside the Schwarzschild radius, which is why it is called the event horizon: the boundary of the region containing all the events the professor can see. The professor simply can’t see past the event horizon. In the same way, on Earth you can’t see past the horizon when you look out; it marks the limit of what you can see. Any observer who stays outside the event horizon of the black hole can never see any events that occur inside the event horizon.
If the professor ever wonders what happened to the poor graduate student, he can turn off his rocket motor, which has kept him hovering outside the black hole, and then he will free fall in himself. When he crosses the event horizon, he will see that signal “GOING,” which is still stuck there. As he rides down the “escalator,” he will see the signal “GOING” running past him at the speed of light. Light will always pass him at 300,000 km/sec. But then the professor will fall into the center of the black hole and be killed as well.
For a 3-billion-solar-mass Schwarzschild black hole, the graduate student would have 5.5 hours of free-fall time as measured on his watch before he hit the center and was killed. Luckily for him, the spaghettification process, from the moment the tidal forces begin to hurt him until he is completely ripped apart and killed, only takes up the last 0.09 seconds of his trip. So at least it is a quick end.
We might also like to know what the curved geometry of the exterior of the black hole looks like. I was once asked to appear on the McNeil/Lehrer Newshour, because astronomers using the Hubble Space Telescope had just discovered evidence that the big black hole in M87 existed, and they wanted Kip Thorne and me to explain this to the viewers. I made up a little demonstration. If you cut a plane through the center of the black hole, you might expect that plane to be a flat, two-dimensional surface like a basketball court, with the Schwarzschild radius a circle like the free-throw circle. The singularity would be a point at its center. But that would be wrong. This two-dimensional slice through the black hole is actually curved. It looks like the horn of a trumpet pointing upward (figure 20.1.) The third dimension here is purely to allow us to show you the curvature of two-dimensional funnel surface. The third dimension is not real here. Forget the space above and below the funnel, the only thing that is real is the funnel shape itself. At large distances, the horn of the trumpet flattens out, so that it begins to look flat like a basketball court. Far from the hole the curvature is weak. The extended trumpet horn slopes ever more dramatically downward toward the hole as you approach it. The slope becomes vertical at the Schwarzschild radius. The Schwarzschild radius marks the circumference of the trumpet at its narrowest point. That’s why we call it a black hole—it really is a hole. In fact, in the coordinate system Karl Schwarzschild invented, the coordinate r is called a circumferential radius, because 2πr is the circumference at that point. This circumference lies within the surface of the funnel. You can think of the funnel as a series of smaller and smaller circles reaching a minimum circle at the bottom (where the circumference is equal to 2π times the Schwarzschild radius). The Schwarzschild radius is the radius of the hole at the bottom of the funnel. (Ignore the flange base at the bottom in figure 20.1—it just holds up the model of the funnel.)

FIGURE 20.1. Black hole funnel. The geometry around a black hole is not flat like a basketball court, but curved like a funnel. The funnel becomes vertical at the Schwarzschild radius, indicated by the red band showing the circumference: 2π times the Schwarzschild radius. An astronaut can fall straight in. When he passes the Schwarzschild radius (the red band), that is the point of no return. Ignore the base that holds the funnel up. Also, ignore the inside and outside of the funnel, it is only the funnel shape itself that is real. Photo credit: J. Richard Gott
For my TV demonstration, I used a trumpet-horn-shaped funnel. I set it up with the rim of the bell at the top and the narrowest circumference of the funnel at the bottom (see figure 20.1). Astronomers had detected gas orbiting the black hole in M87 at high velocity. I illustrated this by throwing marbles sideways into the funnel and letting them spin around as they spiraled slowly downward before disappearing through the hole at the bottom. Gas likewise orbits the hole, with the gas farther in orbiting faster such that gas rubs on gas, causing friction. The friction heats the gas, making it glow. We can see this radiation, because it is emitted outside the event horizon. Meanwhile this energy production causes the gas to lose energy and spiral into the hole. This is the power source for quasars: gas spiraling into a supermassive black hole. We see the hot gas while it is spiraling inward toward the event horizon, but we do not see it once it has passed that horizon. My demonstration showed all these things. I thought it was pretty good, and was ready to go for filming the news segment. Then I showed it to my daughter, 7 years old at that time, and she said, why not drop an astronaut in? She went to her room and came back with a cute little one-inch-tall Apollo astronaut wearing his spacesuit and holding a tiny American flag—a toy I didn’t know she had. If you are spiraling around the black hole, like the marbles, you will spiral around as you slowly descend into the black hole, or you can just fall straight in like the graduate student. I put the toy astronaut at the upper edge of the funnel and just let it slide straight in—disappearing into the hole at the bottom. Perfect. A black hole is a hotel where you check in but you don’t check out. The path of the astronaut falling straight in is a curved radial line going straight down into the funnel (it is a geodesic). When I let go of the astronaut, he falls straight down along this line in my model, so it made a good illustration. When a TV crew comes to film you, they usually take hours, filming lots of shots, but for national TV news this usually gets edited down to a short clip. After filming all my elaborate demonstrations with circling marbles spiraling in, what do you think they chose to show in the end? Just the little astronaut falling straight in, of course! Now you know what the geometry of a black hole’s exterior looks like: it looks like a funnel, with a hole at the bottom.
The Schwarzschild solution, found by Karl Schwarzschild in 1916, showed the shape of this funnel. But Schwarzschild’s coordinate system, clever though it was, broke down at the Schwarzschild radius. His solution showed the geometry outside the Schwarzschild radius, but it didn’t show what happens inside. It was like having a map of the world that only showed the Northern Hemisphere—but nothing south of the equator. People thought the exterior solution was all that there was. Finally in the mid-1960s, my colleague Martin Kruskal of the applied math department at Princeton, and George Szekeres of the University of New South Wales, independently found a way to extend the coordinates to cover all the interior of the black hole solution. We can look at a spacetime diagram of the solution, now called a Kruskal diagram (figure 20.2).
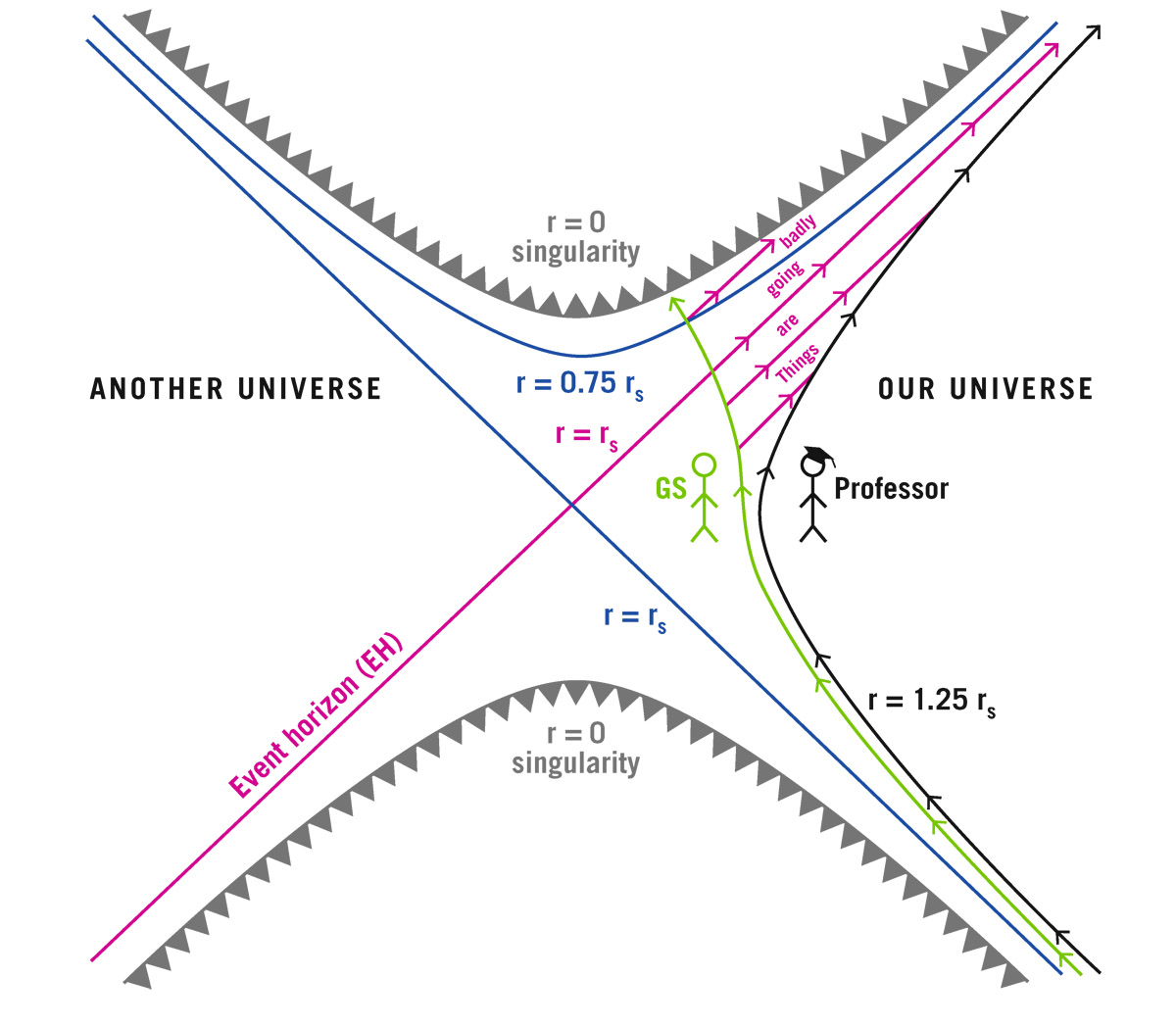
FIGURE 20.2. Kruskal diagram. Spacetime diagram that shows the geometry both outside and inside the Schwarzschild (nonrotating) black hole. The future is toward the top. The diagram represents the curved empty space around a point mass that has lasted forever. Our universe is to the right. The worldlines of a professor and a graduate student (GS) are shown. The professor stays safely outside the black hole at 1.25 Schwarzschild radii (1.25 rS.) The grad student falls into the black hole and hits the singularity at r = 0. The event horizon (EH) runs along a line where the radius is equal to the Schwarzschild radius (r = rS). Credit: J. Richard Gott
This two-dimensional diagram shows one dimension of space horizontally with time shown vertically—the future is toward the top of the diagram. This diagram has the property that light beams travel in straight lines tipped at 45°. The speed of light is constant, and the constant slope of 45° shows that. Let’s illustrate the coordinates by returning to the professor and his ill-fated graduate student. We start by drawing the worldline of the professor in black (see figure). It is not straight, because the professor is accelerating, firing his rocket to stay at 1.25 Schwarzschild radii from the black hole. The professor stays outside the black hole. The worldline is vertical at the point midway up and then bends toward the right. In flat spacetime, this would be a worldline representing a particle that was at rest at the midpoint and accelerated off to the right, picking up velocity. The full worldline of the professor is a hyperbola. It bends over, so that in the far future, it is going upward at about 45° as it approaches the speed of light. Remember the Equivalence Principle, in which an accelerating observer in flat spacetime is like a stationary observer (the professor) in a gravitational field. The professor’s worldline is bent like a hyperbola in the Kruskal diagram.
A horizontal line extending to the right from the point at the center of the X where the two 45° lines cross represents a snapshot of a radial ray extending from the hole at the bottom of the funnel straight out of the funnel, pictured at a single instant of time. (The other dimension of the funnel, the circumferential direction, is left out of the diagram.)
The grad student’s worldline (labeled “GS”) is shown in green. He travels along with the professor at early times, near the bottom of the diagram, where both worldlines track each other side by side until the graduate student leaves the professor at the vertical midpoint of the professor’s worldline. The graduate student is free falling; his worldline falls into the black hole, while the professor accelerates off to the right. The event horizon (labeled “EH,” and r = rs, i.e., a radius equal to the Schwarzschild radius) is a line tipped at 45° that is asymptotic to the professor’s worldline in the far future. It never touches the professor’s worldline. It is tipped at 45°, because the light beam (in this case a radio wave) with the signal “GOING” can travel along it. The grad student’s worldline crosses the diagonal event-horizon line, just as he emits the photon signal “GOING.” The professor will never receive that signal. The professor’s worldline marks the set of points on the diagram where r is equal to 1.25 Schwarzschild radii. The light (radio) signals “THINGS” and “ARE” are two lines tipped at 45° that were emitted before the graduate student crossed the event horizon; those two signals do intersect the worldline of the professor. He receives those signals. You can see now why it takes the signal “ARE” such a long time to reach the professor.
Where are the points lying at 0.75 times the Schwarzschild radius? They are twisted around to form a hyperbola that looks like a smile hovering above the diagonal event-horizon line. At the far right, it approaches the diagonal event-horizon line EH from above but never touches it. The singularity at r = 0 is also a hyperbola-shaped smile lying above the r = 0.75 Schwarzschild radius one. The grad student’s worldline hits this horizontal smile. We put teeth on this grin, for these are jaws that will eat the grad student. The spacetime is so warped that the singularity, which you might expect to be a vertical line over to the far left, has been twisted around until it lies in the future. In fact, once the grad student crosses the event-horizon line, this hyperbola looms in the graduate student’s future. He can’t avoid it any more than you can avoid next Tuesday. No matter how he fires his rocket, he can’t go faster than the speed of light, and he must go upward at more than a 45° angle. Once he has passed that event horizon, the hyperbola representing the singularity looms above him, spanning more than ±45°, and his worldline has to hit it. He is doomed. Likewise, the light signal “BADLY” that he sends out at 45° toward the right after he crosses the event horizon will hit the jaws of the singularity at r = 0 as well.
We can complete the Kruskal diagram to obtain the complete point-mass solution. This represents a point mass that began in the infinite past and lasts into the infinite future, in an otherwise empty universe. The diagonal event-horizon line EH is joined by another diagonal line going in the other direction to form a giant X in the center of the diagram. This X divides the spacetime into four regions. The outside of the black hole, where the professor lives, is to the right of the X. That’s our universe. Above the X is the inside of the black hole, where the singularity looms in the future at the top. Below the X is an initial singularity labeled r = 0, looking like a frown at the bottom in the past. To the left is another universe like ours. It is connected to ours by a wormhole in the middle. If we were to make a horizontal slice through this spacetime in the middle, we would have a slice at a given instant of time. Its geometry is like two funnels joined at their narrowest point. Starting on the far right, the funnel has a large circumference, representing a large radius far from the hole. Going toward the left, the funnel gets narrower and narrower until it has a circumference of 2πrSchwarzschild at the event horizon at the center of the X. It then fans out as again to large radius to make another universe on the left side of the X. The two funnels are joined to form a wormhole. Far away from the hole, the funnels flatten out to look like basketball courts, and they extend to infinity. Imagine a basketball court on the second floor of a building with a curved funnel leading downward into a hole at the center of the court (like the hole on a golf green). This funnel begins to open out again and fans out to make a pretty flat ceiling on the floor below the floor containing the basketball court. The basketball court represents our large universe, and the ceiling of the floor below represents another large universe connected to ours by the small hole smoothly connecting the court surface to the ceiling below it. The two large universes are connected by a wormhole at the instant represented by the horizontal line through the diagram. But you can’t use this wormhole to travel from one universe to the other. That’s because the arms of the X are tipped at exactly 45°. To cross from the region to the right side of the X (our universe) into the region to the left side of the X (another universe), you would have to have a worldline with a slope inclined at more than 45° to the vertical. That would mean you were traveling at greater than the speed of light, and that’s not possible. But you could in principle meet an extraterrestrial from the other universe inside the black hole in the upper (future) quadrant. You could even shake hands. You might say to each other, “Boy, are we in trouble,” before you both died as you hit that smiling singularity in the future. You would hit that singularity in a finite time.
The singularity in the past, at the bottom, is rather like the Big Bang singularity at the beginning of our universe. This part of the solution is called a white hole. It is a time-reversed version of a black hole—like a movie of a black hole run backward. A particle can be created in the white hole singularity at the bottom and have its worldline come out into our universe. If a particle can fall into a black hole, it can come out of a white hole.
The black holes that we might encounter now have not been around forever. In a realistic case, a black hole might be formed from the collapse of a star. In the spacetime Kruskal diagram, imagine that the surface of the collapsing star lies just below the graduate student’s feet: just below the grad student’s feet when he is with the professor and just below the grad student’s feet as he falls in. This represents the situation when the surface of the star maintains a radius of 1.25 Schwarzschild radii for a long time and then free falls inward just below the grad student’s feet as he free falls in. The worldline of the surface of the star is thus parallel to that of the grad student and just to the left of it. Beneath the falling graduate student is the interior of the star, beneath its surface, where the density of matter is greater than zero and the vacuum solution of the Kruskal diagram does not apply. Just ignore that part of the diagram to the left of the graduate student’s worldline—no wormhole, no other universe, no white-hole singularity at the bottom. These are not formed when a star collapses to form a black hole. But the part of the diagram to the right of the graduate student’s worldline is in the vacuum region and it accurately depicts what is happening. The grad student does get crushed as his worldline hits the singularity at r = 0. If you lived inside the star (in an air-conditioned little room), you would find yourself crushed when the volume of the star shrinks to zero and its density blows up to infinity. A curvature singularity awaits your worldline in the future as well: you hit r = 0 when the size of your star collapses to zero.
Here’s some advice: just stay outside the Schwarzschild radius, and you will be okay. You can happily orbit outside the black hole event horizon. If the Sun were to collapse and form a black hole, Earth would stay in its current orbit outside. You could see the black hole, which would appear as a black disk in the sky. It would be surrounded by gravitationally lensed images of stars behind it (figure 20.3).

FIGURE 20.3. Simulated view of a Schwarzschild black hole. It looks like a black disk in the sky, surrounded by gravitationally lensed images of background stars. You can see two images of the galactic plane whose light is bent around opposite sides of the black hole on the way to your eye.
Photo credit: Andrew Hamilton (using Milky Way background image adapted from Axel Mellinger)
In 1963, Roy Kerr discovered an exact solution to Einstein’s field equations for a rotating black hole (one having angular momentum). It has a more complicated geometry inside its event horizon, which we discuss in chapter 21. But its event horizon marks the point of no return, just as in the Schwarzschild black hole. Kerr’s solution was brilliantly vindicated on September 14, 2015, when astronomers from the Laser Interferometer Gravitational-Wave Observatory (LIGO) witnessed the formation of a 62-solar-mass rotating Kerr black hole from the collision of a 29-solar-mass black hole and a 36-solar-mass black hole. The two had formed a tight binary, and spiraled inward, losing energy due to emission of gravitational radiation. By studying these gravitational ripples in the geometry of spacetime, astronomers were able to deduce the masses of the black holes involved. Since the two black holes had orbital angular momentum as they circled each other, it was not surprising that a rotating black hole formed at the center. The ringing oscillations of this final black hole that formed and then settled down matched exactly those expected from the decay of perturbations to a Kerr black hole. Astronomers could even determine that the Kerr black hole had approximately 67% of the maximum angular momentum allowed for a black hole of its mass. The whole collision, including the emission of gravitational waves, could be simulated on a supercomputer that solved Einstein’s equations to calculate the geometry of spacetime. The agreement between the computer simulation and the observed gravitational wave ripples shows that Einstein’s equations work even when spacetime is highly curved—a very important result.
In 1974, Stephen Hawking surprisingly and famously discovered that a black hole actually radiates thermal radiation: energy can, and does, escape from a black hole. How did this discovery come about? Princeton graduate student Jacob Bekenstein was talking with his PhD thesis advisor John Archibald Wheeler. Wheeler was the one who coined the name “black hole.” And it’s a good name! Black holes are holes, and they are black—they emit no light. As Neil has said, astronomers prefer simple names for things—“it’s black and it’s a hole, so why not just call it a ‘black hole’?” Wheeler was the godfather of black hole research and helped revive interest in general relativity in the 1960s. He got people interested in working on the subject and with Charles W. Misner and Kip Thorne wrote an influential textbook on it whose early proofs I studied as a graduate student. When Kruskal discovered his diagram, he sent it to Wheeler to ask his opinion of it and went on vacation. Wheeler read the paper and thought it was so important that he wrote it up himself and sent it immediately to the Physical Review journal with Kruskal’s name alone on it! When Kruskal got back from vacation, he found his paper had already been sent in to the journal.
Wheeler invited his student Bekenstein in for a talk. He brought out a cup of hot tea and mixed some cold water into it. Wheeler said, “I have just committed a crime: I have increased the entropy (disorder) in the universe, and I can’t take it back, because I can’t unmix the tea and water.” Bekenstein knew that the entropy in the universe always increases with time. If you break a vase, the disorder in the universe increases. We don’t often see pieces bounce up and assemble themselves into a vase. In fact, when you see a film showing this by running the film backward, you laugh, because you know that it is unlikely to occur. There is a certain chance that something like that would occur, but it is very small. Statistically, we expect to see the disorder in the universe increasing with time—this principle is called the second law of thermodynamics. People like order; it is a shame to break a beautiful vase into pieces. Following this logic, any increase in entropy, like mixing the tea and water, can be considered a crime. Wheeler went on: “But now I can hide the evidence of my crime by throwing the lukewarm tea and water mixture into a black hole. It will increase the mass of the black hole: it will now have the mass it did before, plus that of the tea and water, but not by any more than if I had thrown the tea and the water separately into the black hole. I have gotten back the result I would have had if I had not mixed the tea and water in the first place, and that seems to violate the second law of thermodynamics. Think about it!”
Bekenstein took Wheeler’s idea seriously and thought about it. The resulting paper struck me as particularly brilliant. Bekenstein noted that Hawking had proved a theorem saying that the total area of all the event horizons in the universe always goes up with time if the mass density everywhere is nonnegative, which seemed reasonable. When mass is added to a black hole, the mass of the black hole increases, and its Schwarzschild radius increases. The surface area of the event horizon, which is 4πrSchwarzschild2, goes up as well. If two black holes collide, as they did in the case discovered by LIGO, they form a black hole that has an event horizon whose total area is larger than the sum of the areas of the event horizons of the two initial black holes. In the LIGO case, for example, calculation shows the area of the event horizon of the final rotating 62-solar-mass Kerr black hole is at least a factor of 1.5 greater than the sum of the areas of the event horizons of the initial 29- and 36-solar-mass black holes. To Bekenstein, this phenomenon of the total area of the event horizons always going up with time sounded to him like entropy, which of course also is always going up with time.
Bekenstein did a thought experiment: he lowered a particle on a string as gently (nearly reversibly) into a Schwarzschild black hole as possible, and calculated how much the area of the black hole went up. He noted that this corresponded to a loss of one bit of information, namely, the information about whether that particle existed or not. Because a loss of information in his thought experiment is equal to a specific increase in entropy, he was able to calculate the relationship between the number of bits of information lost, to the increase in the area of the black hole horizon. He found the loss of one bit of information corresponded to a tiny increase in area—of order (1.6 ×10–33 cm)2 = hG/2πc3 (where these are our old friends, Planck’s constant h, Newton’s gravitational constant G, and the speed of light c). We’ll see this distance of 1.6 ×10–33 cm, called the Planck length, again, in chapter 24. It’s the scale where spacetime geometry becomes uncertain due to Heisenberg’s uncertainty principle in quantum mechanics. When Wheeler dropped his mixed cup of lukewarm tea and water into the black hole, he increased the area of its horizon and its entropy. The entropy in the universe still went up appropriately because the black hole had an entropy that increased as the mixed cup fell in. Black holes had a large but finite entropy, Bekenstein concluded.
Interestingly, Bekenstein’s work puts a limit on the amount of information your 6-inch-diameter hard drive can store—1068 bits = 1.16 × 1058 gigabytes. Try to pack more information than that inside its diameter, and it will become so massive that it collapses and forms a black hole. (To follow the reasoning in detail, see appendix 2.) Bekenstein’s argument also puts limits on the number of bits of information you can cram into the finite radius of the observable universe, and therefore on the number of different visible universes of our size and energy one can have—namely, 10^(10^124), the big number Neil gave you in chapter 1. So, Bekenstein’s paper has a lot of applications.
But Hawking, unlike me, thought Bekenstein’s paper was wrong. If you added a finite amount of energy to a black hole and that increased its entropy by a finite amount, this implied by a simple thermodynamic argument that it had a finite temperature. Hawking thought that must be incorrect. Black holes do not glow like an object of finite temperature would glow. Black holes are black—they have a temperature of zero.
Roger Penrose had shown that in the special case of a rotating black hole, a particle could decay into two particles in a region just outside the black hole event horizon, and one particle could fall inside the event horizon in a counter-rotating way so that it lowered the angular momentum of the black hole, while the second decay particle sailed out with more energy than the total energy the initial particle possessed. In a rotating black hole, some of the hole’s mass is tied up in its rotational energy, and at the end the black hole is rotating more slowly, so its total mass is smaller than it was before. Tapping the rotational energy of the black hole provides the energy to power the high-energy escape of the second decay particle. In this process, the area of the rotating black hole’s event horizon goes up a little. Demetrios Christodoulou, another of Wheeler’s students, investigated these questions, putting limits on how much energy could be extracted from the rotating black hole. In the Soviet Union, Yakov Zeldovich had applied this idea to electromagnetic waves. He presented a heuristic argument that an electromagnetic wave impinging near a rotating black hole could be amplified, gaining more energy, like the Penrose escaping particle. This looked like stimulated emission, the laser effect discovered by Einstein. By that logic, the rotating black hole should have some spontaneous emission as well, slowly losing rotational energy by emitting electromagnetic waves. Alexei Starobinski calculated these effects for waves for a rotating Kerr black hole.
As recounted by his student, Don Page,1 Hawking wanted to put these ideas on a firmer foundation. Hawking set out to apply quantum mechanics in curved spacetime—to calculate the creation and annihilation of particles in the curved Schwarzschild spacetime to discover whether the nonrotating black hole really emitted any radiation. Hawking found, quite to his surprise, that particles were created—the black hole emitted thermal radiation. The black hole had a finite temperature after all! Hawking used the fact that, in the vacuum of empty space, particle pairs are always being created, falling back together, and annihilating again. These are called virtual pairs. They are always popping in and out of existence. Heisenberg’s uncertainty principle of quantum mechanics says that the energy of a system is significantly uncertain over a short enough time period. Thus the energy needed to create an electron and a positron (you need both; the total electric charge still needs to be conserved), can be “borrowed” from the vacuum for a short amount of time. Thus an electron-positron pair can be created near each other out of the vacuum and can fall back together and annihilate again after a short period (of order 3 × 10–22 seconds). But in the black hole case, the electron can be created slightly inside the event horizon and the positron slightly outside the event horizon. The electron created inside the event horizon can’t get back outside to recombine with the positron on the outside. The electron falls into the black hole, and the positron escapes. The electron created inside the event horizon has a gravitational potential energy that is negative and larger in magnitude than its rest mass energy from E = mc2. Thus, its total energy is less than zero and when it falls in, it robs the black hole of some energy and therefore of some of its mass. This makes up for the mass and energy of the emitted positron. There is a quantum vacuum state (now called the Hartle-Hawking vacuum) around the black hole of slightly negative energy density, which violates the positive energy assumption on which the Hawking area-increase theorem was based. In this case, the area of the event horizon goes down slightly as the positron escapes. Alternately, it can be an electron that escapes while a positron falls in. The same effect can produce pairs of photons, where one photon created just inside the horizon falls in and the other created just outside the horizon escapes. Hawking found that black holes give off thermal radiation (now called Hawking radiation). This causes black holes to shrink, and eventually evaporate. This thermal radiation has a characteristic wavelength (λmax) about 2.5 times the size of the Schwarzschild radius of the black hole. For a 10-solar-mass black hole, this means it is giving off 75-kilometer-long radio waves—far too feeble to be detected; this thermal radiation is very low temperature, 6 × 10–9 K (with very few positrons and electrons in the mix). This is why Stephen Hawking has not garnered a Nobel Prize yet. If the radiation were strong enough to have been detected by now, he would surely have gone to Stockholm by now. No one, I think, doubts that the radiation exists; but the radiation is predicted to be extremely weak. Black holes of stellar mass or larger are actually absorbing more radiation from the cosmic microwave background (CMB) than they are emitting. Only in the far future will the microwave background redshift and cool enough to allow the evaporation process to proceed.
It takes black holes a long time to evaporate. A 3 × 109-solar-mass black hole like the one in M87 currently should be emitting thermal radiation with a temperature of about 2 × 10–17 K—mostly in the form of photons and gravitons. According to calculations by Don Page, a 3 × 109-solar-mass black hole will take 3 × 1095 years to evaporate. Today it is accreting more radiation from the CMB than it is emitting in thermal radiation. Its loss of mass will not really start until the CMB temperature has dropped below 2 × 10–17 K. That should occur about 700 billion years from now. Ultimately, due to evaporation, it will finally shrink to a size of about 10–33 cm and then go out of existence in a blaze of ultra-high-energy gamma rays. It is thought that the information lost when the black hole formed eventually leaks back out in the Hawking radiation that is emitted as it evaporates, but in a scrambled (disordered) form.
The details of how this evaporation affects the interior of the black hole are still being hotly debated. Some physicists believe that the antiparticles (or particles) just inside the event horizon paired with the Hawking particles (or antiparticles) being emitted outside the horizon can form a firewall, a wall of hot photons, just inside the event horizon that will kill any astronaut falling in. This effect might become important only after the black hole has evaporated more than half its mass, something that would only occur in the far future. The details depend on the quantum vacuum state that forms around the black hole.
James Hartle and Hawking found a quantum vacuum state that did not blow up on the event horizon and in which an infalling astronaut would not get burned up as he passed through to the inside. When a particle and an antiparticle (such as a positron and an electron) are created out of the vacuum, their quantum states are entangled. The two particles have angular momentum and spins that are opposite. If you measure the spin of one relative to a particular direction, you instantly know that the spin of the other relative to that same direction is the opposite. This remains true even as the particles separate to large distances. This effect puzzled Einstein, who called it “spooky action at a distance.” It was one of the things that troubled him about quantum mechanics. In a recent paper, Juan Maldacena and Leonard Susskind, two of the leading experts in the field, have argued that quantum entanglement between the particles being emitted and their partners on the inside of the horizon can keep the astronaut cool as he falls through, just as Hartle and Hawking intended. They argue that the particle and its antiparticle are connected by a tiny microscopic wormhole. They are essentially touching each other through the wormhole while being separated by a large distance in regular space. The wormhole is like a hole in a dining room tabletop that allows an ant to get from the top surface of the tabletop to its underside. Yet the two wormhole openings, or mouths, are separated by a large distance if one must follow a path along the table’s big surfaces. An ant would have to crawl a long way to get from the upper wormhole mouth to the lower wormhole mouth this way. She would first need to crawl along the top of the table to reach its side edge; then she would have to crawl around the side, underneath the tabletop, and then along the bottom surface of the tabletop until she reached the lower wormhole mouth. That traveling ant would say the upper and lower mouths of the wormhole were widely separated, whereas an ant zipping through the wormhole would realize that they were actually quite close to each other. This could solve Einstein’s “spooky action at a distance” problem. The particle and antiparticle are always close to each other through the wormhole. Interestingly, Wheeler had already commented that electric field lines converging on a wormhole mouth could look like an electron (on the underside of the tabletop), but when they emerged and fanned out on the top of the table, they would look like a positron. Thus, he argued that particles and antiparticles could be linked by a wormhole like that occurring in a black hole, such as we encountered in the Kruskal diagram connecting two universes (in that case called an Einstein–Rosen bridge). Einstein’s paper on spooky action at a distance was co-authored with Nathan Rosen and Boris Poldowski. Thus, Maldacena and Susskind argued, the Einstein, Rosen, Poldowski paradox of spooky action at a distance can be resolved using a microscopic Einstein–Rosen bridge! Surprisingly, Einstein and Rosen (and everyone else) missed the connection! If this picture is correct, it looks safe for the graduate student to pass inside the event horizon, as Hawking had originally supposed. This example points out some of the deep connections that Hawking’s work has illuminated.
I remember well the excitement when Hawking came to Caltech to tell us of his discovery that black holes would evaporate. Kip Thorne, one of the world’s experts on black holes, introduced him. Nobel laureate Murray Gell-Mann was in the audience. Thorne assured us all of the revolutionary importance of this research. I agree—it is the most important result in the theory of general relativity since Einstein’s day. You’ve heard of Stephen Hawking—this is how he became world famous. Some of these exciting events have been recounted in the 2014 movie The Theory of Everything, which earned Eddie Redmayne an Oscar for his compelling and accurate portrayal of Hawking.