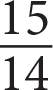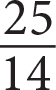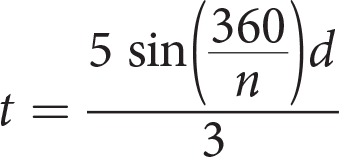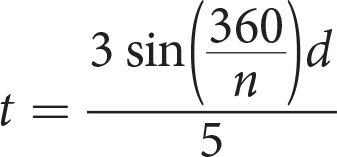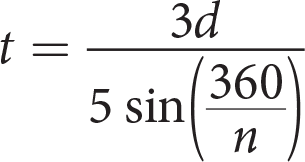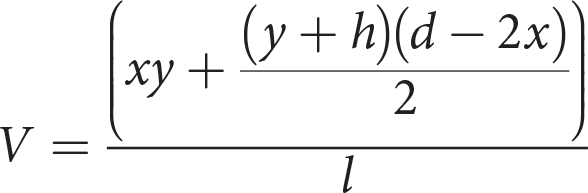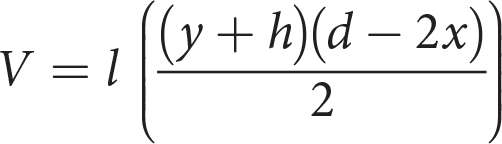Chapter 16
SAT Math: Timing and Section Management Strategies
SAT Math Timing and Triage
The non-calculator section has 20 questions to be completed in 25 minutes, which means you’ll have 1 minute and 15 seconds per question; the calculator section has 38 questions to be completed in 55 minutes, which means you’ll have a little less than a minute and a half per question. This is an average, though. Some questions will be straightforward, meaning that you can get the correct answer in 30 seconds or less. Others will be more difficult and time consuming. Test takers who start at the beginning of the section, attempt the questions in order, and only move on to the next question when the previous one is complete often find that they get bogged down and don’t make it to the end of the section, potentially missing questions that they could have answered correctly. Flexibility can earn you more points.
A better approach would be to make your way through the section with a plan to deal with each question. Each time you read a new question, take a moment to gauge your gut reaction:
- Does this question seem quick and easy? Do it immediately.
- Does this question seem time consuming but manageable? Skip it for now. Put a circle around it and try it on a second pass through the section.
- Does this question look confusing or difficult? Skip it. Don’t worry about circling or marking questions like this. You’ll approach them only after you have worked on the other questions in the section, and only if you have time.
Try to make this decision quickly. The more you practice, the easier it will be to recognize which questions are easier and which are more challenging for you.
Page 474When you approach a section this way, you’ll end up taking two or three passes through it. This technique ensures that you’ll get all of the easy points first, and that if you run out of time, you’ll know that the questions you didn’t attempt were the hardest in the section and that it would have been tougher to get those questions right anyway.
Before the end of the section, make sure you have something bubbled in for every question since there is no penalty for guessing. Also, be very careful when bubbling your answers. It’s easy to skip a question but forget to skip a line on the grid and bubble your answer to the next question in the wrong place.
The questions in each Math section will be in approximate order of difficulty, with the easiest questions at the beginning of the section and the most difficult questions at the end of the section. There are two exceptions:
- The difficulty resets with the Grid-in questions. That is, the first Grid-in question is much easier than the last multiple-choice question. If the multiple-choice questions start getting too tough, skip to the Grid-ins.
- The individual questions in a two- or three-part question set might be easier or harder than the questions around them. It’s a good idea to attempt them in order, since sometimes the work you did for an earlier question will help you with a later question, but you should still be ready to skip questions within one of these sets if they get too tough.
If you tend to finish the Math sections early but find that you are making speed mistakes, you may consider pausing at the confirmation step to check your logic and calculations before bubbling your response to each question.Page 475
Try on Your Own
Directions: Use this question set to practice effective question triage. Skip those questions that you feel will take too long; come back to them if you have time. Try to get as many questions correct as you can in 15 minutes. As always, be sure to study the explanations, even for questions you got correct. They can be found at the end of this chapter.

-
Quadrilateral ABEF is a rectangle and the length of side FE is 9. If quadrilateral BCDE is a square, what is its area?
- 27
- 36

- 81
-
If
 , what is the value of x ?
, what is the value of x ? -
If f(x) = 2x2 − 5x + 7, what is the value of f(8) − f(3) ?
-
Anthony recently completed a trip in 3 hours. If his average speed had been 20 percent faster, how long would the same trip have taken?
- 2.2 hours
- 2.4 hours
- 2.5 hours
- 2.8 hours

-
If tan ∠B = 1, and the length of side BC is
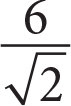 , what is the length of side AC ?
, what is the length of side AC ?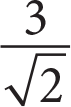
- 3

- 6
Page 476
x2 + 12x = −30
What is the absolute value of the difference between the two solutions for x in the equation above?

- 4

- 12

-
Given the equations above, what is the value of x + y ?

-
-
Questions 8–10 refer to the following information.
-

A diagram of a gambrel roof attic is shown above. Gambrel roofs are common on barns because they allow the maximum space for storage while still having a sloped roof. The steepness of the slope of a roof is called its pitch. Gambrel roofs are unique because they have a pitch break where the pitch changes. In a standard plan, the pitch break is calculated so that the four roof trusses all have the same truss length, t. The formula for the length of the base where t is the truss length and n is the number of trusses is as follows:
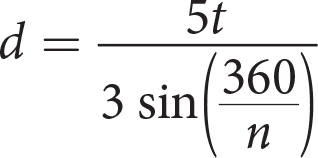
A cross-section of a typical gambrel roof, which is symmetrical about the vertical axis, is shown in the diagram above.
-
Which of the following expresses truss length in terms of the length of the base and the number of trusses?
Page 477
-
The Greer family is building a new barn and calculating the dimensions based on how much winter hay storage space they need in the gambrel roof attic. If l is the length of the barn from front to back, which one of the following equations can be used to calculate the volume, V, of the attic roof space?
-
After completing the volume calculations, the family decides to use a standard plan for the gambrel roof where the base, d, is 30 feet and the length of the barn from front to back, l, is 40 feet. All four surfaces of the barn roof will need to be shingled at a rate of $3.17 per square foot. Approximately how much will the Greer family spend to have the gambrel roof shingled?
- $2,300
- $3,800
- $9,100
- $15,200
-
Page 478
Answers and Explanations
SAT Math Timing and Triage
-
A
Difficulty: Easy
Category: Geometry (Chapter 13)—Special Right Triangles
Getting to the Answer: The fact that the figures are a rectangle and a square means that all the angles other than those formed by the diagonal are 90°, which means that △BEF is a 30-60-90 triangle. If you don’t recall the side ratios of such a triangle, you might consider skipping this question even though you can look up the side ratios on the formula sheet. (It’s best to memorize the higher-yield information on the formula sheet so you won’t have to spend time looking it up on test day.)
The side ratios of the triangle are
 . Since the length of the longer leg, FE, is 9,
. Since the length of the longer leg, FE, is 9,  and the lengths are
and the lengths are  . Thus, the side length of the square, BE, is
. Thus, the side length of the square, BE, is 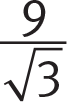 , and the area of square BCDE is
, and the area of square BCDE is  . (A) is correct.
. (A) is correct. -
B
Difficulty: Easy
Category: Linear Equations and Graphs (Chapter 4)—Solving Equations
Getting to the Answer: If you recall that the way to simplify multiple fractions is to clear the denominators by multiplying all terms by a common denominator, then proceed with this question. The numbers appear manageable, so you probably won’t even need to use the calculator.
The lowest common denominator (LCD) of the fractions is 18, so multiply all terms by 18. (If you didn’t notice that LCD, you could have multiplied by 9 × 6 = 54.)
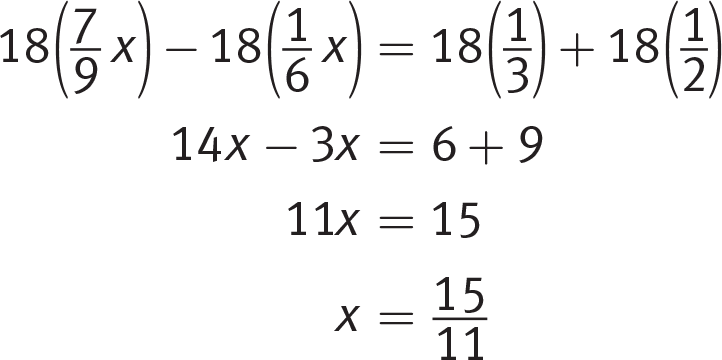
(B) is correct.
-
85
Difficulty: Easy
Category: Functions (Chapter 10)—Function Notation
Getting to the Answer: Although this is a Grid-in question, the amount of calculations needed to get the answer are minimal since all that is required is to evaluate a single-variable function twice and make one subtraction. Therefore, you would probably choose to answer this question on a first pass. Even though the question permits the use of the calculator, you are certainly not required to use it. Usually, if you are comfortable making the calculations without the calculator, you will save time and avoid keying errors.
Substitute the two values given into the function. Notice that since you will be subtracting f(3) from f(8), the constant term, 7, will cancel out. Therefore, the calculation is 2(8)2 − 5(8) − [2(3)2 − 5(3)], which is 2(64) − 5(8) − 2(9) + 5(3). This simplifies to 128 − 40 − 18 + 15, which is 85. Grid in 85 and move on.
-
C
Difficulty: Medium
Category: Linear Equations and Graphs (Chapter 4)—Word Problems
Getting to the Answer: Your time management decisions often depend on whether you are able to quickly identify the strategy you can use to answer a question. For this question, you will use the formula Distance = rate × time to determine the answer. Since distance is the constant factor and rate and time vary, you’ll set rate × time for both scenarios equal to each other. If you don’t see this approach fairly quickly, you should move on and mark this question to come back to later.
Set the initial rate to r and the time to make the trip at the new rate to t. The distance for the actual trip is 3r and the distance if Anthony increases his average speed is t(1.2r). Set these two equal to each other, 3r = t(1.2r). The r’s cancel out, so you can write that
Page 479 . (C) is correct.
. (C) is correct. -
B
Difficulty: Medium
Category: Trigonometry (Chapter 14)—Sine, Cosine, and Tangent
Getting to the Answer: The key to unraveling this question is recognizing that ∠B = ∠C = 45°. That fact enables you to set up a side ratio and solve for the length of side AC. If you are unable to make this determination, pass on this question for now and move on.
Given that
 , tan ∠B = 1 means that the sides opposite and adjacent to vertex B are equal. Triangle ABC is an isosceles right triangle. The side ratio for a 45-45-90 triangle is
, tan ∠B = 1 means that the sides opposite and adjacent to vertex B are equal. Triangle ABC is an isosceles right triangle. The side ratio for a 45-45-90 triangle is  , so
, so 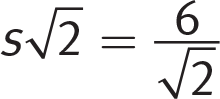 , and
, and  . (B) is correct.
. (B) is correct. -
A
Difficulty: Medium
Category: Quadratics (Chapter 12) – The Quadratic Formula
Getting to the Answer: Add 30 to each side to get x2 + 12x + 30 = 0. Since there are not any integer factors of 30 that add to 12, you’ll have to use either completing the square or the quadratic formula to solve for the possible values of x. If you see a question like this on test day and are not comfortable with those techniques or feel that this question could take too much time to answer, come back to it on a second pass.
If you choose to solve via the quadratic equation,
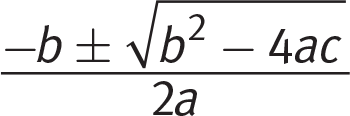 , substitute 1 for a, 12 for b, and 30 for c, to get
, substitute 1 for a, 12 for b, and 30 for c, to get  . This simplifies to
. This simplifies to 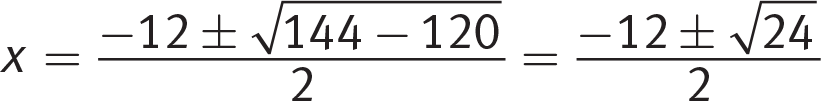 . Since
. Since  , this further simplifies to
, this further simplifies to  . The question asks for the difference between the two solutions which is
. The question asks for the difference between the two solutions which is 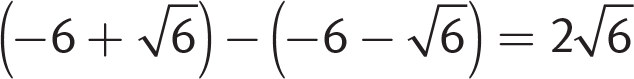 . (A) is correct.
. (A) is correct.To complete the square, add the square of half of 12, or 36, to both sides to get x2 + 12x + 36 = (x + 6)2 = 6. Take the square root of both sides to get
 , so
, so  . The absolute difference is twice
. The absolute difference is twice  , or
, or  , which confirms that (A) is correct. Note that the technique of completing the square takes less calculation than using the quadratic formula.
, which confirms that (A) is correct. Note that the technique of completing the square takes less calculation than using the quadratic formula. -
12
Difficulty: Hard
Category: Systems of Equations (Chapter 5)—Combination
Getting to the Answer: Even though you are solving for x + y and you are given equations in terms of 3x and 3y, merely adding the two equations to get 3x + 3y = 4y − 13 + 31 − 2x and dividing both sides by 3 does not work. You’ll need to solve the system of equations by substitution or combination (elimination) for the values of both variables and add them.
First, put the equations in the same format such as 3x − 4y = −13 and 2x + 3y = 31. Using substitution would likely result in working with fractions, so use combination. The x-coefficients are smaller values than the y-coefficients, so the calculations might be a little easier. Create a common x-coefficient of 6 by multiplying the first equation by 2 and the second by 3, then subtracting the second equation from the first:

So y = 7. You can plug y = 7 into either of the original equations to find x, but because x is already isolated on one side in the first equation, use it: 3x = 4(7) − 13 = 15, so x = 5. The sum of x and y is thus 7 + 5 = 12. Grid in 12.
Page 480 -
B
Difficulty: Medium
Category: Linear Equations and Graphs (Chapter 4) – Solving Equations
Getting to the Answer: Even when an equation looks complicated, to solve for a specific variable, you only need to move everything else in the equation to the other side of the equal sign. The original equation gives the length of the base, d, in terms of the truss length, t, and the number of trusses, n. To solve for t, multiply both sides of the expression by the
 term and divide by 5:
term and divide by 5: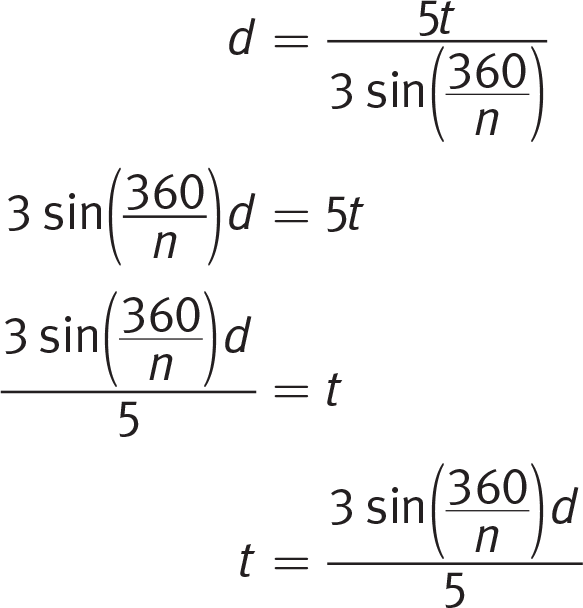
(B) is correct. (A), (C), and (D) all contain the incorrect expression in the denominator.
-
C
Difficulty: Hard
Category: Geometry (Chapter 13)—Three-Dimensional Figures
Getting to the Answer: The volume for any 3-D prism can be found by taking the area of the base and multiplying it by the height (or in this case, the length of the barn). You can eliminate (B) immediately because it divides by the length instead of multiplying by it. The cross-section of the barn is not a standard shape, but, since it is symmetrical about the vertical axis, it can be broken up into simpler shapes: two equal right triangles and two equal trapezoids.
Start with the area that is easier to calculate: the area of the two right triangles. The base and height of the two triangles are x and y, and plugging those values into the triangle area formula results in
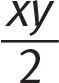 . There are two equal triangles, so multiply by 2 to get xy as the area of the two triangles. At this point on test day, you could make the strategic leap to eliminate (D) because it does not include the xy term and (A) because it divides the xy term by 2. (C) is correct.
. There are two equal triangles, so multiply by 2 to get xy as the area of the two triangles. At this point on test day, you could make the strategic leap to eliminate (D) because it does not include the xy term and (A) because it divides the xy term by 2. (C) is correct.If you continue with the calculations, the area formula for a trapezoid is (average of parallel bases) × (height of the trapezoid). Based on the cross-section diagram those values will be:
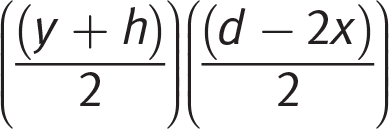
Again, there are two trapezoids, so multiply the expression by 2:

Next, add the area of both triangles and both trapezoids:
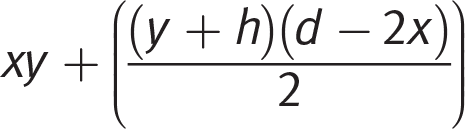
(C) is the only choice that multiplies this value by l, which confirms that it is the correct choice. Recognizing that you are building the volume formula from the area of simple shapes allows for powerful strategic elimination (and fewer calculations!).Page 481
-
C
Difficulty: Medium
Category: Linear Equations and Graphs (Chapter 4) – Solving Equations
Getting to the Answer: If the cross-section of the roof shown in the diagram is stretched over the 40-foot length of the barn, then the four sections of the roof are four equal rectangles where one dimension is the length and the other dimension is the truss length. Find the truss length by plugging the number of trusses, 4, and the base length, 30 feet, into the truss length formula that you solved for in question 8:

Now that you have the dimension for one section of the roof, 18 feet by 40 feet, find the area of all four sections:

Finally, the price per square foot needs to be multiplied by the total area of the roof:
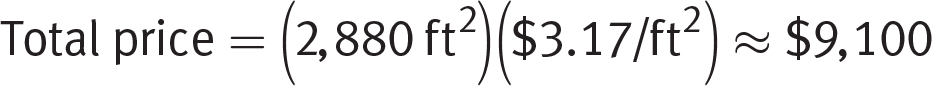
(C) is correct.