CHAPTER 26
Cryptographic Concepts
In this chapter, you will
• Identify the different types of cryptography
• Learn about current cryptographic methods
• Understand how cryptography is applied for security
• Given a scenario, utilize general cryptography concepts
• Compare and contrast basic concepts of cryptography
Cryptography is the science of encrypting, or hiding, information—something people have sought to do since they began using language. Although language allowed them to communicate with one another, people in power attempted to hide information by controlling who was taught to read and write. Eventually, more complicated methods of concealing information by shifting letters around to make the text unreadable were developed. These complicated methods are cryptographic algorithms, also known as ciphers. The word “cipher” comes from the Arabic word sifr, meaning empty or zero.
Certification Objective This chapter covers CompTIA Security+ exam objective 6.1, Compare and contrast basic concepts of cryptography.
General Cryptographic Concepts
Historical ciphers were simple to use and also simple to break. Because hiding information was still important, more advanced transposition and substitution ciphers were required. As systems and technology became more complex, ciphers were frequently automated by some mechanical or electromechanical device. A famous example of a modern encryption machine is the German Enigma machine from World War II. This machine used a complex series of substitutions to perform encryption, and interestingly enough, it gave rise to extensive research in computers.
When setting up a cryptographic scheme, it is important to use proven technologies. Proven cryptographic libraries and proven cryptographically correct random number generators are the foundational elements associated with a solid program. Homegrown or custom elements in these areas can greatly increase risk associated with a broken system. Most groups don’t possess the abilities to develop their own cryptographic algorithms. Algorithms are complex and difficult to create. Any algorithm that has not had public review can have weaknesses. Most good algorithms are approved for use only after a lengthy test and public review phase.
When material, called plaintext, needs to be protected from unauthorized interception or alteration, it is encrypted into ciphertext. This is done using an algorithm and a key, and the rise of digital computers has provided a wide array of algorithms and increasingly complex keys. The choice of specific algorithm depends on several factors, and they will be examined in this chapter.
Cryptanalysis, the process of analyzing available information in an attempt to return the encrypted message to its original form, required advances in computer technology for complex encryption methods. The birth of the computer made it possible to easily execute the calculations required by more complex encryption algorithms. Today, the computer almost exclusively powers how encryption is performed. Computer technology has also aided cryptanalysis, allowing new methods to be developed, such as linear and differential cryptanalysis. Differential cryptanalysis is done by comparing the input plaintext to the output ciphertext to try to determine the key used to encrypt the information. Linear cryptanalysis is similar in that it uses both plaintext and ciphertext, but it puts the plaintext through a simplified cipher to try to deduce what the key is likely to be in the full version of the cipher.
Fundamental Methods
Modern cryptographic operations are performed using both an algorithm and a key. The choice of algorithm depends on the type of cryptographic operation that is desired. The subsequent choice of key is then tied to the specific algorithm. Cryptographic operations include encryption for the protection of confidentiality, hashing for the protection of integrity, digital signatures to manage non-repudiation, and a bevy of specialty operations such as key exchanges.
While the mathematical specifics of these operations can be very complex and are beyond the scope of this level of material, the knowledge to properly employ them is not complex and is subject to being tested on the CompTIA Security+ exam. Encryption operations are characterized by the quantity and type of data, as well as the level and type of protection sought. Integrity protection operations are characterized by the level of assurance desired. Data is characterized by its usage: data-in-transit, data-at-rest, or data-in-use. It is also characterized in how it can be used, either in block form or stream form, as described next.
Symmetric Algorithms
Symmetric algorithms are a form of encryption that is older and a simpler method of encrypting information. The basis of symmetric encryption is that both the sender and the receiver of the message have previously obtained the same key. This is, in fact, the basis for even the oldest ciphers—the Spartans needed the exact same size cylinder, making the cylinder the “key” to the message, and in shift ciphers, both parties need to know the direction and amount of shift being performed. All symmetric algorithms are based upon this shared secret principle, including the unbreakable one-time pad method.
Figure 26-1 is a simple diagram showing the process that a symmetric algorithm goes through to provide encryption from plaintext to ciphertext. This ciphertext message is, presumably, transmitted to the message recipient, who goes through the process to decrypt the message using the same key that was used to encrypt the message. Figure 26-1 shows the keys to the algorithm, which are the same value in the case of symmetric encryption.
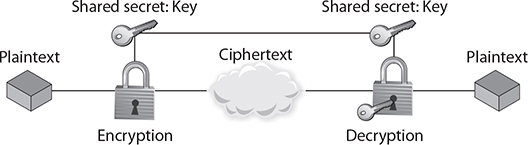
Figure 26-1 Layout of a symmetric algorithm
Unlike with hash functions, a cryptographic key is involved in symmetric encryption, so there must be a mechanism for key management. Managing the cryptographic keys is critically important in symmetric algorithms because the key unlocks the data that is being protected. However, the key also needs to be known or transmitted in a secret way to the party with whom you wish to communicate. This key management applies to all things that could happen to a key: securing it on the local computer, securing it on the remote one, protecting it from data corruption, protecting it from loss, and, probably the most important step, protecting it while it is transmitted between the two parties. Later in the chapter we will look at public key cryptography, which greatly eases the key management issue, but for symmetric algorithms, the most important lesson is to store and send the key only by known secure means.

EXAM TIP Common symmetric algorithms are 3DES, AES, Blowfish, Twofish, and RC4.
Symmetric algorithms are important because they are comparatively fast and have few computational requirements. Their main weakness is that two geographically distant parties both need to have a key that matches exactly. In the past, keys could be much simpler and still be secure, but with today’s computational power, simple keys can be brute forced very quickly. This means that larger and more complex keys must be used and exchanged. This key exchange is difficult because the key cannot be simple, such as a word, but must be shared in a secure manner. It might be easy to exchange a 4-bit key such as b in hex, but exchanging the 128-bit key 4b36402c5727472d5571373d22675b4b is far more difficult to do securely. This exchange of keys is greatly facilitated by asymmetric, or public key, cryptography, discussed after modes of operation.
Modes of Operation
In symmetric or block algorithms, there is a need to deal with multiple blocks of identical data to prevent multiple blocks of ciphertext that would identify the blocks of identical input data. There are multiple methods of dealing with this, called modes of operation. There are five common algorithmic modes that are detailed in NIST SP 800-38A, Recommendation for Block Cipher Modes of Operation: Methods and Techniques. These algorithms are covered in detail in Chapter 27, and are, Electronic Code Book (ECB), Cipher Block Chaining (CBC), Cipher Feedback Mode (CFB), Output Feedback Mode (OFB), and Counter Mode (CTR).
Asymmetric Algorithms
Asymmetric algorithms comprise a type of cryptography more commonly known as public key cryptography. Asymmetric cryptography is in many ways completely different from symmetric cryptography. While both are used to keep data from being seen by unauthorized users, asymmetric cryptography uses two keys instead of one. It was invented by Whitfield Diffie and Martin Hellman in 1975. The system uses a pair of keys: a private key that is kept secret and a public key that can be sent to anyone. The system’s security relies upon resistance to deducing one key, given the other, and thus retrieving the plaintext from the ciphertext.
Public key systems typically work by using complex math problems. One of the more common methods is through the difficulty of factoring large numbers. These functions are often called trapdoor functions, as they are difficult to process without the key, but easy to process when you have the key—the trapdoor through the function. For example, given a prime number, say 293, and another prime, such as 307, it is an easy function to multiply them together to get 89,951. Given 89,951, it is not simple to find the factors 293 and 307 unless you know one of them already. Computers can easily multiply very large primes with hundreds or thousands of digits, but cannot easily factor the product.
The strength of these functions is very important: because an attacker is likely to have access to the public key, he can run tests of known plaintext and produce ciphertext. This allows instant checking of guesses that are made about the keys of the algorithm. RSA, Diffie-Hellman, elliptic curve cryptography (ECC), and ElGamal are all popular asymmetric protocols.
Asymmetric encryption enables digital signatures and also corrects the main weakness of symmetric cryptography. The ability to send messages securely without senders and receivers having had prior contact has become one of the basic concerns with secure communication. Digital signatures enable faster and more efficient exchange of all kinds of documents, including legal documents. With strong algorithms and good key lengths, security can be assured.
Asymmetric cryptography involves two separate but mathematically related keys. The keys are used in an opposing fashion. One key undoes the actions of the other and vice versa. So, as shown in Figure 26-2, if you encrypt a message with one key, the other key is used to decrypt the message. In the top example, Alice wishes to send a private message to Bob. So, she uses Bob’s public key to encrypt the message. Then, since only Bob’s private key can decrypt the message, only Bob can read it. In the lower example, Bob wishes to send a message, with proof that it is from him. By encrypting it with his private key, anyone who decrypts it with his public key knows the message came from Bob.
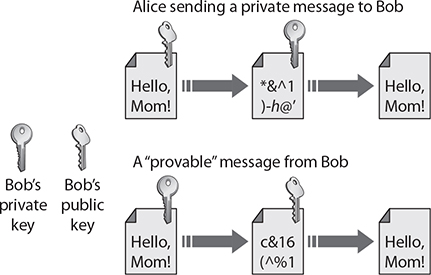
Figure 26-2 Using an asymmetric algorithm
Asymmetric keys are distributed using certificates. A digital certificate contains information about the association of the public key to an entity, and additional information that can be used to verify the current validity of the certificate and the key. When keys are exchanged between machines, such as during an SSL/TLS handshake, the exchange is done by passing certificates.

EXAM TIP Public key cryptography always involves two keys, a public key and a private key, which together are known as a key pair. The public key is made widely available to anyone who may need it, while the private key is closely safeguarded and shared with no one.
Symmetric vs. Asymmetric
Both symmetric and asymmetric encryption methods have advantages and disadvantages. Symmetric encryption tends to be faster, is less computationally involved, and is better for bulk transfers. But it suffers from a key management problem in that keys must be protected from unauthorized parties. Asymmetric methods resolve the key secrecy issue with public keys, but add significant computational complexity that makes them less suited for bulk encryption.
Bulk encryption can be done using the best of both systems by using asymmetric encryption to pass a symmetric key. By adding in ephemeral key exchange, you can achieve perfect forward secrecy, discussed later in the chapter. Digital signatures, a highly useful tool, are not practical without asymmetric methods.
Hashing
Hashing functions are commonly used encryption methods. A hashing algorithm is a special mathematical function that performs one-way encryption, which means that once the algorithm is processed, there is no feasible way to use the ciphertext to retrieve the plaintext that was used to generate it. Also, ideally, there is no feasible way to generate two different plaintexts that compute to the same hash value. Figure 26-3 shows a generic hashing process.
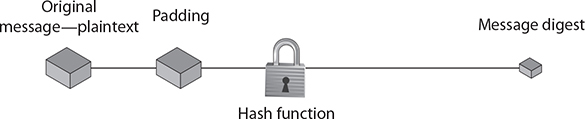
Figure 26-3 How hashes work
Common uses of hashing algorithms are to store computer passwords and to ensure message integrity. The idea is that hashing can produce a unique value that corresponds to the data entered, but the hash value is also reproducible by anyone else running the same algorithm against the data. So you could hash a message to get a message authentication code (MAC), and the computational number of the message would show that no intermediary has modified the message. This process works because hashing methods are typically public, and anyone can hash data using the specified method. It is computationally simple to generate the hash, so it is simple to check the validity or integrity of something by matching the given hash to one that is locally generated. HMAC, or Hashed Message Authentication Code, is a special subset of hashing technology. It is a hash algorithm applied to a message to make a MAC, but it is done with a previously shared secret. So, the HMAC can provide integrity simultaneously with authentication.
A hash algorithm can be compromised with what is called a collision attack, in which an attacker finds two different messages that hash to the same value. This type of attack is very difficult and requires generating a separate algorithm that will attempt to find a text that will hash to the same value of a known hash. This must occur faster than simply editing characters until you hash to the same value, which is a brute-force type attack. The consequence of a hash function that suffers from collisions is that integrity is lost. If an attacker can make two different inputs purposefully hash to the same value, she might trick people into running malicious code and cause other problems. Popular hash algorithms are the Secure Hash Algorithm (SHA) series, the RIPEMD algorithms, and the Message Digest (MD) hash of varying versions (MD2, MD4, MD5).

EXAM TIP The hashing algorithms in common use are MD2, MD4, MD5, SHA-1, SHA-256, SHA-384, and SHA-512.
Hashing functions are very common, and they play an important role in the way information, such as passwords, is stored securely and the way in which messages can be signed. By computing a digest of the message, less data needs to be signed by the more complex asymmetric encryption, and this still maintains assurances about message integrity. This is the primary purpose for which the protocols were designed, and their success will allow greater trust in electronic protocols and digital signatures.
Salt, IV, Nonce
To provide sufficient entropy for low-entropy inputs to hash functions, the addition of a high-entropy piece of data concatenated with the material being hashed can be used. The term salt refers to this initial data piece. Salts are particularly useful when the material being hashed is short and low in entropy. For example, the addition of a high-entropy, 30-character salt to a 3-character password greatly increases the entropy of the stored hash.
As introduced in Chapter 2, an initialization vector, or IV, is used in several ciphers, particularly in the wireless space, to achieve randomness even with normally deterministic inputs. IVs can add randomness and are used in block ciphers to initiate modes of operation.
A nonce is similar to a salt or an IV, but it is only used once, and if needed again, a different value is used. Nonces provide random, nondeterministic entropy in cryptographic functions and are commonly used in stream ciphers to break stateful properties when the key is reused.
Elliptic Curve
Elliptic curve cryptography (ECC) works on the basis of elliptic curves. An elliptic curve is a simple function that is drawn as a gently looping curve on the X,Y plane. Elliptic curves are defined by this equation:
y2 = x3 + ax2 + b
Elliptic curves work because they have a special property—you can add two points on the curve together and get a third point on the curve.
For cryptography, the elliptic curve works as a public key algorithm. Users agree on an elliptic curve and a fixed curve point. This information is not a shared secret, and these points can be made public without compromising the security of the system. User 1 then chooses a secret random number, K1, and computes a public key based upon a point on the curve:
P1 = K1×F
User 2 performs the same function and generates P2. Now user 1 can send user 2 a message by generating a shared secret:
S = K1×P2
User 2 can generate the same shared secret independently:
S = K2×P1
This is true because
K1×P2 = K1× (K2×F ) = (K1×K2) ×F = K2× (K1×F ) = K2×P1
The security of elliptic curve systems has been questioned, mostly because of lack of analysis. However, all public key systems rely on the difficulty of certain math problems. It would take a breakthrough in math for any of the mentioned systems to be weakened dramatically, but research has been done about the problems and has shown that the elliptic curve problem has been more resistant to incremental advances. Again, as with all cryptography algorithms, only time will tell how secure they really are. The big benefit of ECC systems is that they require less computing power for a given bit strength. This makes ECC ideal for use in low-power mobile devices. The surge in mobile connectivity has brought secure voice, e-mail, and text applications that use ECC and AES algorithms to protect a user’s data.
Weak/Deprecated Algorithms
Over time, cryptographic algorithms fall to different attacks or just the raw power of computation. The challenge is understanding which algorithms have fallen to attacks and avoiding their use, even if they are still available for use in software libraries. Although this list will continue to grow, it is important to consider this topic, for old habits die hard. Hash algorithms, such as MD5, should be considered inappropriate, as manufactured collisions have been achieved. Even newer hash functions have issues, such as SHA-1 (and soon SHA-256). The Data Encryption Standard, DES, and its commonly used stronger form 3DES, have fallen from favor. The good news is that new forms of these functions are widely available, and in many cases, such as AES, are computationally efficient, providing better performance.
Key Exchange
Cryptographic mechanisms use both an algorithm and a key, with the key requiring communication between parties. In symmetric encryption, the secrecy depends upon the secrecy of the key, so insecure transport of the key can lead to failure to protect the information encrypted using the key. Key exchange is the central foundational element of a secure symmetric encryption system. Maintaining the secrecy of the symmetric key is the basis of secret communications. In asymmetric systems, the key exchange problem is one of key publication. Because public keys are designed to be shared, the problem is reversed from one of secrecy to one of publicity.
Early key exchanges were performed by trusted couriers. People carried the keys from senders to receivers. One could consider this form of key exchange to be the ultimate in out-of-band communication. With the advent of digital methods and some mathematical algorithms, it is possible to pass keys in a secure fashion. This can occur even when all packets are subject to interception. The Diffie-Hellman key exchange is one example of this type of secure key exchange. The Diffie-Hellman key exchange depends upon two random numbers, each chosen by one of the parties and kept secret. Diffie-Hellman key exchanges can be performed in-band, and even under external observation, as the secret random numbers are never exposed to outside parties.

EXAM TIP Security+ exam objective 6.1 is to compare and contrast basic concepts of cryptography. Understanding the differences between symmetric, asymmetric, and other concepts from a description of events is important to master.
Cryptographic Objectives
Cryptographic methods exist for a purpose: to protect the integrity and confidentiality of data. There are many associated elements with this protection to enable a system-wide solution. Elements such as perfect forward secrecy, non-repudiation, key escrow, and others enable successful cryptographic implementations.
Digital Signatures
A digital signature is a cryptographic implementation designed to demonstrate authenticity and identity associated with a message. Using public key cryptography, a digital signature allows traceability to the person signing the message through the use of their private key. The addition of hash codes allows for the assurance of integrity of the message as well. The operation of a digital signature is a combination of cryptographic elements to achieve a desired outcome. The steps involved in digital signature generation and use are illustrated in Figure 26-4. The message to be signed is hashed, and the hash is encrypted using the sender’s private key. Upon receipt, the recipient can decrypt the hash using the sender’s public key. If a subsequent hashing of the message reveals an identical value, two things are known: First, the message has not been altered. Second, the sender possessed the private key of the named sender, so is presumably the sender him- or herself.
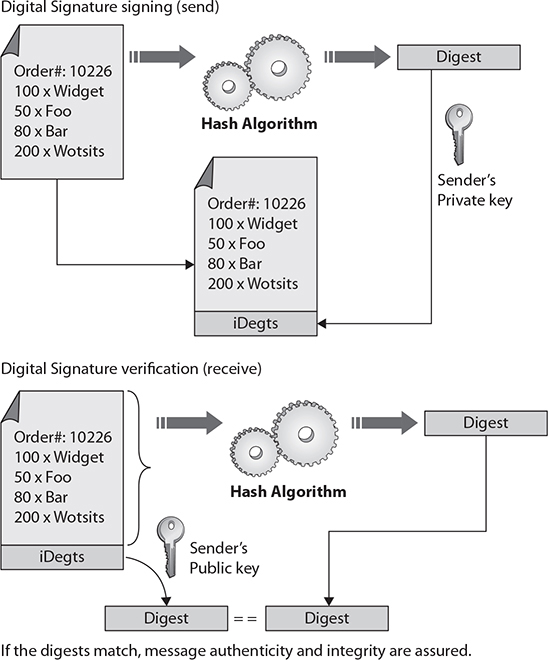
Figure 26-4 Digital signature operation
A digital signature does not by itself protect the contents of the message from interception. The message is still sent in the clear, so if confidentiality of the message is a requirement, additional steps must be taken to secure the message from eavesdropping. This can be done by encrypting the message itself, or by encrypting the channel over which it is transmitted.
Diffusion
Diffusion is a principle that the statistical analysis of plaintext and ciphertext results in a form of dispersion rendering one structurally independent of the other. In plain terms, a change in one character of plaintext should result in multiple changes in the ciphertext in a manner that changes in ciphertext do not reveal information as to the structure of the plaintext.
Confusion
Confusion is a principle to affect the randomness of an output. The concept is operationalized by ensuring that each character of ciphertext depends on several parts of the key. Confusion places a constraint on the relationship between the ciphertext and the key employed, forcing an effect that increases entropy.
Collision
A collision is when two different inputs have the same output on a cryptographic function such as a hash. Since inputs to a hash function are technically infinite (unlimited in length) and the number of unique outputs is limited by hash size, collisions have to occur. The issue is whether one can manufacture a collision using cryptanalysis methods. As mentioned earlier in the chapter, this form of attack is known as a collision attack, and practical forms of this attack are possible with the computer power available on a desktop. If two inputs can be generated that produce the same hash value, this enables the movement of a digital signature from an original to a near duplicate, resulting in the failure of the digital signature to protect an original.

EXAM TIP Understanding the difference between diffusion and confusion is important. Collision seems like it fits with these terms, but it is about something totally different. Do not allow some common words to confuse you in the heat of the exam. Learn the definitions of the vocabulary terms.
Steganography
Steganography, an offshoot of cryptography technology, gets its meaning from the Greek word “steganos,” meaning covered. Invisible ink placed on a document and hidden by innocuous text is an example of a steganographic message. Another example is a tattoo placed on the top of a person’s head, visible only when the person’s hair is shaved off.
Hidden writing in the computer age relies on a program to hide data inside other data. The most common application is the concealing of a text message in a picture file. The Internet contains multiple billions of image files, allowing a hidden message to be located almost anywhere without being discovered. The nature of the image files also makes a hidden message difficult to detect. While it is most common to hide messages inside images, they can also be hidden in video and audio files.
The advantage to steganography over cryptography is that the messages do not attract attention, and this difficulty in detecting the hidden message provides an additional barrier to analysis. The data that is hidden in a steganographic message is frequently also encrypted, so should it be discovered, the message will remain secure. Steganography has many uses, but the most publicized uses are to hide illegal material, often pornography, and allegedly for covert communication by terrorist networks. Terrorists have used steganography to distribute materials via the web, and the techniques have been documented in some of their training materials.
Steganographic encoding can be used in many ways and through many different media. Covering them all is beyond the scope of this book, but we will discuss one of the most common ways to encode into an image file, LSB encoding. LSB, Least Significant Bit, is a method of encoding information into an image while altering the actual visual image as little as possible. A computer image is made up of thousands or millions of pixels, all defined by 1s and 0s. If an image is composed of Red Green Blue (RGB) values, each pixel has an RGB value represented numerically from 0 to 255. For example, 0,0,0 is black, and 255,255,255 is white, which can also be represented as 00000000, 00000000, 00000000 for black and 11111111, 11111111, 11111111 for white. Given a white pixel, editing the least significant bit of the pixel to 11111110, 11111110, 11111110 changes the color. The change in color is undetectable to the human eye, but in an image with a million pixels, this creates a 125KB area in which to store a message.
Obfuscation
Obfuscation is the masking of an item to render it unreadable yet still usable. Consider source code as an example. If the source code is written in a manner that it is easily understood, then its functions can be easily recognized and copied. Code obfuscation is the process of making the code unreadable by adding complexity at the time of creation. This “mangling” of code makes it impossible to easily understand, copy, fix, or maintain. Using cryptographic functions to obfuscate materials is more secure in that it is not reversible without the secret element, but this also renders the code unusable until it is decoded.
Program obfuscation can be achieved in many forms, from tangled C functions with recursion and other indirect references that make reverse engineering difficult, to proper encryption of secret elements. Storing secret elements directly in source code does not really obfuscate them, because numerous methods can be used to find hard-coded secrets in code. Proper obfuscation requires the use of cryptographic functions against a non-reversible element. An example is the storing of password hashes. If the original password is hashed with the addition of a salt, reversing the stored hash is practically not feasible, making the key information, the password, obfuscated.
Stream vs. Block
When encryption operations are performed on data, there are two primary modes of operation, block and stream. Block operations are performed on blocks of data, enabling both transposition and substitution operations. This is possible when large pieces of data are present for the operations. Stream data has become more common with audio and video across the Web. The primary characteristic of stream data is that it is not available in large chunks, but either bit by bit or byte by byte, pieces too small for block operations. Stream ciphers operate using substitution only and therefore offer less robust protection than block ciphers. A table comparing and contrasting block and stream ciphers is presented in Table 26-1.

Table 26-1 Comparison of Block and Stream Ciphers

EXAM TIP Compare and contrast are common objectives in the Security+ exam—comparing and contrasting block and stream ciphers is a prime exam target.
Key Strength
The strength of a cryptographic function typically depends upon the strength of a key: a larger key has more entropy and adds more strength to an encryption. Because different algorithms use different methods with a key, direct comparison of key strength between different algorithms is not easily done. Some cryptographic systems have fixed key lengths, such as 3DES, while others, such as AES have multiple lengths, AES-128, AES-192, and AES-256.
Session Keys
A session key is a symmetric key used for encrypting messages during a communication session. It is generated from random seeds and is used for the duration of a communication session. When correctly generated and propagated during session setup, a session key provides significant levels of protection during the communication session and also can afford perfect forward secrecy (described later in the chapter). Session keys offer the advantages of symmetric encryption, speed, strength and simplicity, and, with key exchanges possible via digital methods, significant levels of automated security.
Ephemeral Key
Ephemeral keys are cryptographic keys that are used only once after generation. When an ephemeral key is used as part of the Diffie-Hellman scheme, it forms an Ephemeral Diffie-Hellman (EDH) key exchange. An EDH key exchange generates a temporary key for each connection, never using the same key twice. This provides for perfect forward secrecy.
Secret Algorithm
Algorithms can be broken into two types: those with published details and those whose steps are kept secret. Secrecy has its uses in security. Keeping your password secret, for instance, is an essential element in its proper functionality. Secrecy in how to apply security elements can assist in thwarting reverse engineering. An example of this is the use of multiple rounds of multiple hash functions to provide password security. Although the developers of a secret algorithm must understand how many rounds to use and the proper order of algorithmic application, users don’t need to know those details because they are encoded into the application itself. Keeping this secret can enhance security because it makes reverse engineering difficult, if not impossible.
The drawback of keeping a cryptographic algorithm secret is that it reduces the testing of the algorithm by cryptographers. The most secure algorithms are those that have survived over time the onslaught of cryptographic researchers attacking them.
Data-in-Transit
Transport encryption is used to protect data-in-transit, or data that is in motion. When data is being transported across a network, it is at risk of interception. An examination of the OSI networking model shows a layer dedicated to transport, and this abstraction can be used to manage end-to-end cryptographic functions for a communication channel. When utilizing the TCP/IP protocol, Transport Layer Security (TLS) is one specific method of managing security at the transport level. Secure Sockets Layer (SSL) is another example. Managing a secure layer of communications is an essential element in many forms of computer operations.
Data-at-Rest
Protecting data-at-rest is the most prominent use of encryption, and is typically referred to as data encryption. Whole disk encryption of laptop data to provide security in the event of device loss is an example of data-at-rest protection. The same concept applies to data being stored in the cloud, where encryption can protect against unauthorized reading.
Data-in-Use
Data-in-use is the term used to describe data that is stored in a non-persistent state of either RAM, CPU caches, or CPU registers. Data-in-use is of increasing concern to security professionals as attacks such as RAM scraping malware are occurring. Data-in-use is still data that requires protection, and in modern secure systems, this data can be encrypted. New techniques, such as Intel’s Software Guard Extensions (SGX), promise a future where sensitive data can be protected from all other processes on a system, even those with higher levels of authority, such as root.

EXAM TIP Data-in-transit, data-at-rest, and data-in-use are terms commonly used to describe states of data in a computing system. Understanding how to differentiate these terms based on their similarities and differences when it comes to cryptography is a very testable item.
Random/Pseudo-Random Number Generation
Many cryptographic functions require a random number. A true random number has no correlation to previous random numbers, nor future random numbers, and has a uniform frequency distribution over the range of interest. This means that even given all previous numbers, the next number cannot be predicted with any greater probability than by chance. True random numbers are virtually impossible to generate from physical or algorithmic processes because of the influences associated with the underlying process. This leads to the field of pseudo-random numbers, a set of numbers that while statistically appearing to be random with respect to frequency distribution, because they are algorithmically generated, if one knows the algorithm and the seeds, one can predict future values.
For cryptographic purposes, the importance of the unpredictability cannot be overstated. This has led to a series of specialized random/pseudo-random number generation algorithms that minimize the predictability element, making them nearly perfect from a true randomness point of view. When selecting random number generators to be used in cryptographic algorithms, it is very important to use cryptographically secure random number generation methods to prevent introducing flaws into the encryption protections.
Key Stretching
Key stretching is a mechanism that takes what would otherwise be weak keys and “stretches” them to make the system more secure against brute force attacks. Computers have gained so much computational power that hash functions can be computed very quickly, leading to a need for a manner of increasing the workload when computing hashes so that an attacker can’t merely compute them all. In the case of a short key, the chance of randomly matching the hash function by use of computational guessing attacks has increased. To make the problem more difficult, either the keyspace must be increased or the computation must be slowed down. Key stretching involves increasing the computational complexity by adding iterative rounds of computations, rounds that cannot be done in parallel. The increase in computational workload becomes significant when done billions of times, making attempts to use a brute force attack much more expensive.
Implementation vs. Algorithm Selection
When using cryptography for protection of data, several factors need to be included in the implementation plan. One of the first decisions is which algorithm to select. The algorithm must be matched to the intended use, and deprecated algorithms must be avoided.
Crypto Service Provider
A cryptographic service provider (CSP) is a software library that implements cryptographic functions. CSPs implement encoding and decoding functions, which computer application programs may use, for example, to implement strong user authentication or for secure e-mail. In Microsoft Windows, the Microsoft CryptoAPI (CAPI) is a CSP for all processes that need specific cryptographic functions. This provides a standard implementation of a complex set of processes.
Crypto Modules
A cryptographic module is a hardware or software device or component that performs cryptographic operations securely within a physical or logical boundary. Crypto modules use a hardware, software, or hybrid cryptographic engine contained within the boundary, and cryptographic keys that do not leave the boundary, maintaining a level of security. Maintaining all secrets within a specified protected boundary is a foundational element of a secure cryptographic solution.
Perfect Forward Secrecy
Perfect forward secrecy is a property of a public key system in which a key derived from another key is not compromised even if the originating key is compromised in the future. This is especially important in session key generation, where the security of all communication sessions using the key may become compromised; if perfect forward secrecy were not in place, then past messages that had been recorded could be decrypted.
Security Through Obscurity
Security through obscurity is the concept that security can be achieved by hiding what is being secured. This method alone has never been a valid method of protecting secrets. This has been known for centuries. But this does not mean obscurity has no role in security. For example, naming servers after a progressive set of objects, like Greek gods, planet names, or rainbow colors, provides an attacker an easier path once they start obtaining names. Obscurity has a role, making it hard for an attacker to easily guess critical pieces of information, but should not be relied upon as a singular method of protection.
Common Use Cases
Cryptographic services are being employed in more and more systems, and there are many common use cases associated with them. Examples include implementations to support situations such as low power, low latency, and high resiliency, as well as supporting functions such as confidentiality, integrity, and non-repudiation.
Low Power Devices
Low power devices, such as mobile phones and portable electronics, are ubiquitous and require cryptographic functions. Because cryptographic functions tend to take significant computational power, special cryptographic functions, such as elliptic curve cryptography, are well suited for low-power applications.
Low Latency
Some use cases involve low latency operations, requiring specialized cryptographic functions to support operations that have extreme time constraints. Stream ciphers are examples of low latency operations.
High Resiliency
High resiliency systems are characterized by functions that are capable of resuming normal operational conditions after an external disruption. The use of cryptographic modules can support resiliency through a standardized implementation of cryptographic flexibility.
Supporting Confidentiality
Protecting data from unauthorized reading is the definition of confidentiality. Cryptography is the primary means of protecting data confidentiality—at rest, in transit, and in use.
Supporting Integrity
Integrity of data is needed in scenarios such as during transfers. Integrity can demonstrate that data has not been altered. The use of message authentication codes (MACs) supported by hash functions is an example of cryptographic services supporting integrity.
Supporting Obfuscation
There are times where information needs to be obfuscated, protected from causal observation. In the case of a program, obfuscation can protect the code from observation by unauthorized parties. It is common for computer programs to have variable and function names changed to random names masking their use. Some people will write down things like PIN codes, but change the order of the digits so it is not immediately obvious.
Supporting Authentication
Authentication is a property that deals with the identity of a party, be it a user, a program, or piece of hardware. Cryptographic functions can be employed to demonstrate authentication, such as the validation that an entity has a specific private key, associated with a presented public key, proving identity.
Supporting Non-repudiation
Non-repudiation is a property that deals with the ability to verify that a message has been sent and received so that the sender (or receiver) cannot refute sending (or receiving) the information. An example of this in action is seen with the private key holder relationship. It is assumed that the private key never leaves the possession of the private key holder. Should this occur, it is the responsibility of the holder to revoke the key. Thus, if the private key is used, as evidenced by the success of the public key, then it is assumed that the message was sent by the private key holder. Thus, actions that are signed cannot be repudiated by the holder.
Resource vs. Security Constraints
Cryptographic functions require system resources. Using the proper cryptographic functions for a particular functionality is important for both performance and resource reasons. Determining the correct set of security and resource constraints is an essential beginning step when planning a cryptographic implementation.

EXAM TIP Understanding the different common use cases for cryptography and being able to identify the applicable use case given a scenario is a testable element associated with this section’s objective.
Chapter Review
In this chapter, you became acquainted with the principles of cryptography. The chapter opened with the concepts of cryptography, including the description of vocabulary elements associated with general cryptography. It then examined the fundamental concepts of cryptography, encryption, and hashing in terms of the types of algorithms and the types of data. Next, cryptographic objectives, including digital signatures, steganography, diffusion and confusion, as well as others, were presented, followed by an examination of issues such as session keys, key strength, ephemeral keys, and key stretching. The chapter concluded with topics associated with use cases and implementation details, including an introduction to cryptographic service providers and modules; use of cryptology for confidentiality, integrity, and non-repudiation; and adoptions of cryptology in low-power, high-resiliency, and low-latency situations.
Questions
To help you prepare further for the CompTIA Security+ exam, and to test your level of preparedness, answer the following questions and then check your answers against the correct answers at the end of the chapter.
1. What is the difference between linear and differential cryptanalysis?
A. Differential cryptanalysis can examine symmetric and asymmetric ciphers, whereas linear cryptanalysis only works on symmetric ciphers.
B. Linear cryptanalysis puts the input text through a simplified cipher, whereas differential cryptanalysis does not.
C. Unlike differential cryptanalysis, linear cryptanalysis is deprecated because it does not work on newer ciphers.
D. Differential cryptanalysis cannot take advantage of computational improvements, whereas linear cryptanalysis makes full use of newer computations.
2. What is the oldest form of cryptography?
A. Asymmetric
B. Hashing
C. Digital signatures
D. Symmetric
3. What kind of cryptography makes key management less of a concern?
A. Asymmetric
B. Hashing
C. Digital signatures
D. Symmetric
4. Why are computers helpful in the function of public key systems?
A. They can store keys that are very large in memory.
B. They provide more efficient SSL key exchange for servers.
C. They can easily multiply very large prime numbers.
D. They can encrypt large amounts of data.
5. What is the best way, if any, to get the plaintext from a hash value?
A. Use linear cryptanalysis.
B. Factor prime numbers.
C. You cannot get the plaintext out of a hash value.
D. Use an ephemeral key.
6. What does a salt do?
A. It tells the algorithm how many digits of primes to use.
B. It primes the algorithm by giving it initial noncritical data.
C. It adds additional rounds to the cipher.
D. It provides additional entropy.
7. What makes a digitally signed message different from an encrypted message?
A. A digitally signed message has encryption protections for integrity and non-repudiation, which an encrypted message lacks.
B. A digitally signed message uses much stronger encryption and is harder to break.
C. An encrypted message only uses symmetric encryption, whereas a digitally signed message use both asymmetric and symmetric encryption.
D. There is no difference.
8. Why is LSB encoding the preferred method for steganography?
A. It uses much stronger encryption.
B. It applies a digital signature to the message.
C. It alters the picture the least amount possible.
D. It provides additional entropy.
9. Why is the random number used in computing called a pseudo-random number?
A. They could have an unknown number.
B. Algorithms cannot create truly random numbers.
C. The numbers have deliberate weaknesses placed in them by the government.
D. They follow a defined pattern that can be detected.
10. What is the advantage of a crypto module?
A. Custom hardware adds key entropy.
B. It performs operations and maintains the key material in a physical or logical boundary.
C. It performs encryption much faster than general-purpose computing devices.
D. None of the above.
11. If you need to ensure authentication, confidentiality, and non-repudiation when sending sales quotes, which method best achieves the objective?
A. Key stretching
B. Asymmetric encryption
C. Digital signature
D. Ephemeral keys
12. Given a large quantity of data in the form of a streaming video file, what is the best type of encryption method to protect the content from unauthorized live viewing?
A. Symmetric block
B. Hashing algorithm
C. Stream cipher
D. Asymmetric block
13. Why does ECC work well on low-power devices?
A. Less entropy is needed for a given key strength.
B. Less computational power is needed for a given key strength.
C. Less memory is needed for a given key strength.
D. None of the above.
14. What does Diffie-Hellman allow you to do?
A. Exchange keys in-band
B. Exchange keys out-of-band
C. Both A and B
D. Neither A nor B
15. In developing a system with a logon requirement, you need to design the system to store passwords. To ensure that the passwords being stored do not divulge secrets, which of the following is the best solution?
A. Key stretching
B. Salt
C. Obfuscation
D. Secret algorithms
Answers
1. B. Differential cryptanalysis works by comparing the input plaintext to the output ciphertext, while linear cryptanalysis runs plaintext through a simplified version of the cipher to attempt to deduce the key.
2. D. Symmetric is the oldest form of cryptography.
3. A. Asymmetric cryptography makes key management less of a concern because the private key material is never shared.
4. C. Computers can easily multiply prime numbers that are many digits in length, improving the security of the cipher.
5. C. Hash ciphers are designed to reduce the plaintext to a small value and are built to not allow extraction of the plaintext. This is why they are commonly called “one-way” functions.
6. D. The salt adds additional entropy, or randomness, to the encryption key.
7. A. The digital signature includes a hash of the message to supply message integrity and uses asymmetric encryption to demonstrate non-repudiation, the fact that the sender’s private key was used to sign the message.
8. C. LSB, or Least Significant Bit, is designed to place the encoding into the image in the least significant way to avoid altering the image.
9. B. Random numbers in a computer are generated by an algorithm, and it is not possible to create truly random numbers, so only numbers that are very close to being random, called pseudo-random numbers, are possible.
10. B. Crypto modules, such as smartcards, maintain the key material inside a physical or logical boundary and perform cryptographic operations inside the boundary. This ensures that private key material is kept secure.
11. C. Digital signatures can support confidentiality, integrity, and authentication of “signed” materials.
12. C. Stream ciphers work best when the data is in very small chunks to be processed rapidly, such as live streaming video. Block ciphers are better for large chunks of data.
13. B. ECC uses less computational power for a given key strength than traditional asymmetric algorithms.
14. A. Diffie-Hellman allows an in-band key exchange even if the entire data stream is being monitored, because the shared secret is never exposed.
15. B. Salts are used to provide increased entropy and eliminate the problem of identical passwords between accounts.