The four cardinal points of the compass were extremely important to the Egyptians. The human world ran north-south along the Nile. Trade, raw materials, and people continuously moved up and down the river. The life-bringing flood came from the south and worked its way to the north. Throughout their entire lives most Egyptians rarely moved significantly in any other direction.
Death was another matter entirely. At this time, Egyptians hoped to join their gods, who moved east to west when embodied as the sun, moon, and stars. The entrance into the netherworld was in the land of the setting sun, and hence all tombs were built on the western side of the Nile. Many had a false door painted on or carved into the western inner wall of the tomb. Appearing as mere decoration to the living, this door was accessible only by the spirits of the deceased. Shortly after death, an Egyptian’s soul would begin the journey to the Hall of Osiris.
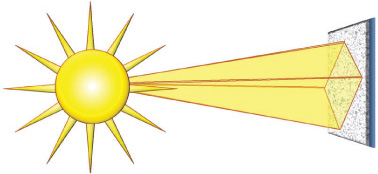
The pharaohs made a much grander entrance into the afterlife, and the pyramid was instrumental to this end. The shape of the pyramid is usually thought of as mimicking the primordial mound from which the Egyptian universe was formed. It is probably more accurate to think of it as symbolic of a ray of light. The benbenet was the sacred icon of Heliopolis, the Egyptian city of the sun. It was shaped exactly like a pyramid but smaller. Benbenet were often placed on top of obelisks, forming the pointy tips, such as the one on the top of the Washington Monument. The cult of the sun chose the benbenet as the shape of their icon presumably because it looked like a ray of sunshine. This shape was selected for the tomb of a pharaoh because the dead king walked up to the stars on a ray of sunlight; hence, the pyramid can literally be thought of as a representation of a ramp to heaven.

A ray of sunshine is similar to a pyramid.
For the ramp to work, it needs to be pointed to the west; as a result, pyramids were aligned with their sides running east-west and north-south. The precision of the alignment is remarkably accurate. The angular alignment of the Great Pyramid of Khufu is off by only 3 minutes and 26 seconds of arc, which is about a seventeenth of 1 degree.
In order to get a rough estimate of the magnitude of the error, we need to remember that objects look bigger when they make a bigger angle with your eye. The farther away something is, the smaller it looks because it forms a smaller angle.
If you hold out your thumb at arm’s length, it has an angular width of about 2 degrees. This means that the error of the Egyptians’ north-south line is about a thirty-fourth of this. This is equivalent to an error of roughly 1 inch every 100 feet.
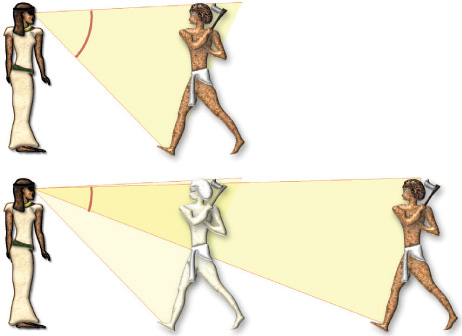
They probably found the north-south orientation using the stars, which move in a complete circle about once every day. The center of these circles falls on the earth’s polar axis, which by definition points north-south. One way the ancient Egyptians could have found true north is by seeing where a star in the northern hemisphere rises and sets. Halfway between these two points is true north.
Farther objects make smaller angles with the eye.

The thick blue line represents a thirty-fourth of a thumb width at arm’s length.
It’s easier to measure objects on the ground than in the sky, and in measuring the former, the Egyptians were even more accurate. The seked of the Great Pyramid of Kufu was 5 s, which is 51 degrees, 50 minutes, and 34 seconds of arc. The actual angular slopes of the above two pyramids are both 51 degrees and 50 minutes. Including possible rounding errors, this means that the slope is off from 5 s seked by at most 1 minute of arc. This extraordinarily accurate slope is off by less than one-hundredth of a thumb width.
True north is halfway between where a star rises and sets.
Such accurate measurements were presumably accompanied by similarly accurate computations. To attain this kind of precision, the numbers used would have many fractional components. As we’ve seen, in Egyptian mathematics fractions beget fractions. For example, doubling an odd fraction usually increases the number of fractions in an expression by one or two. The scribes would have had to reduce these numbers quickly and efficiently. To do so, they would have applied the identities we’ve mastered to transform the resulting clutter of fractions into simple, useable numbers.
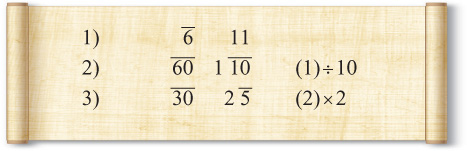
In the last chapter we learned of many different types of identities. Our goal in this section is to learn how to put them all together. In Ahmose’s papyrus there’s a problem of calculating the pesu of 80 loaves made of 3 s hekat of grain. Since the pesu is the number of loaves per hekat, the former is calculated by dividing 80 by 3 s. The division is done as follows. I’ve added line 7 to include a step I assume the scribe did in his head.

The multiplication itself is interesting and far from obvious. I’d love to talk about it, but we need to focus first on simplification. It’s not immediately clear that the right column adds to 80. When confronted with the sum of 70, 7, 2 d, s, and h, we first add the integer parts, getting 79 s d h. When trying to simplify the fractional part, we first add equal fractions, of which there are none. Then we look for applications of the G rule. Start with 2 and see if it goes into 3 or 6 evenly. Clearly, it doesn’t go into 3, but it does go into 6 three times, although 6 divided by 1 more than 3, which is 4, is not a whole number. We then go on to 3 and notice that if it is doubled, we get 6, and when we divide by 3, we get 2. This means that d h is just s.
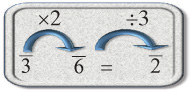
This means that we have 79 s s. Of course s s is just 1, bringing the total to 80. The Egyptians always did such simplifications without writing anything down; however, if they were to write out these computations, it might appear as follows:
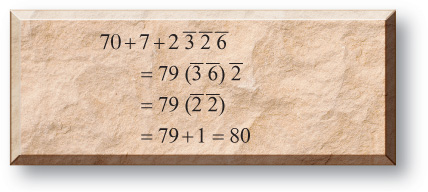
After Ahmose performed this division, he did a check. If his solution of 80 ÷ 3 s is 22 ' j sa was correct, then 22 ' j sa × 3 s should be 80. Ahmose performed the following straightforward multiplication.
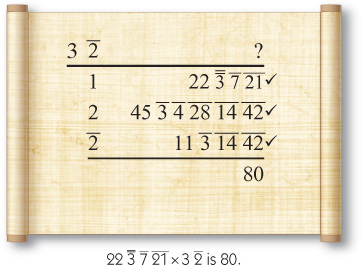
Once again it’s not clear that the sum of the fractions is 80. The mass of fractions seems overwhelming to a beginner. As you gain experience it does get easier. The strategy I use is broken down into the following steps:
• Add integers.
• Add ' to ' or d.
• Add equal fractions, such as f f or j j, using doubling.
• Apply the G rule, for example, g s; = f.
• Look for special relations found on the Egyptian Mathematical Leather Roll.
• Use parts if necessary.
Our job is to add the ugly collection of numbers found in the above multiplication that supposedly add up to 80:
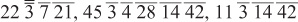
Start by applying the first three steps at once, grouping whole numbers, d and ', and equal fractions. Doing this we get
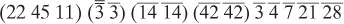
The integers add up to 78. The ' and d sum to 1, a fact that every Egyptian mathematician had to have known. The two afs and fss are easy to add because they are even, giving j and sa, respectively. This process results in
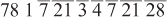
Notice that once again we have multiple whole numbers and repeated fractions, so we repeat some of the steps we just took. First we group them:
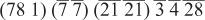
Then we add. Note: to add the js and the sas we need to consult Ahmose’s doubling table. Doing so we get
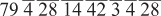
Once again we group and add.
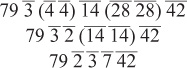
At this point, the first three rules are played out. We now consider the fourth rule. In order to apply the G rule, we check for which numbers go into which evenly and then see if when we divide by 1 more than the result, we get a whole number. For the s, we see that 2 goes into 42 twenty-one times, but 42 ÷ 22 is not whole. However, 7 goes into 42 six times, and 42 ÷ (6 + 1) is 6, so j fs is just h. We now get

Once again the G rule applies since 3 goes into 6 two times, and the result of 6 ÷ (2 + 1) is a whole number; hence, d h is just s. Finally we are left with two ss, which add up to a, which is just 1. We get 80, just as we knew we should.
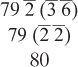
It seems like a coincidence that the fractions simplified so well, but as I’ve often said, “coincidences” are common in Egyptian mathematics. Here’s another example:
EXAMPLE: Add 4 ' fh + 5 fh h; + 3 ' sd.

Now try this one:
PRACTICE: Add 8 ' ag as; + 2 a; as; + 9 d ag.
ANSWER: 20 f.
Accurate measurements beget fractions. Operating on these numbers magnifies the problem, but as we see, the proper application of identities can help contain the resulting mess. You may have noticed that I didn’t use the last one of the six steps to simplify fractions. The step “use parts if necessary” requires a bit more sophistication and will be discussed in the next section.
Thoth, the god of wisdom and scribes, had two tasks to perform. He had no choice because it was a direct command from Ra. The first task was completed when he found Ra’s eye, the Solar Eye, in the land of Nubia. Thoth knew that the second task, bringing the eye home, would be both difficult and dangerous.
According to ancient Egyptian myths, the eyes of the gods were beings in their own right, having their own personalities and some degree of free will. They embodied the very power of the god and could be sent out independently of the rest of the divine body to accomplish difficult tasks. Ra’s eye had refused to come home because she was angry. Even worse, she had transformed herself into a lioness, the form female goddesses take when they want to commit acts of violence. Hence Thoth found himself face to face with the full power of Ra at a time when she was uncontrolled, angry, and looking for a fight.
The eye had already killed everyone in human form who had approached her. Thoth only avoided destruction by transforming himself into a baboon. Now that Thoth had found the eye of Ra, he needed to convince her that she belonged with Ra. Thoth tried pleas and taunts, but none of these tactics seemed to work. Eventually he won her over with amusing but pointed tales. One of the stories, about a lion and a mouse, goes like this. Once upon a time, a powerful lion of the mountains noticed that the other animals were in great distress. They were each wounded, chained, or tortured. When the lion asked who had done this, each animal had the same reply: man. The lion had never seen a man but vowed that he would avenge the animals of his land.

The Solar Eye in lioness form.
As the lion searched for man, he accidentally stepped on a mouse. The mouse begged mercy and promised that if the lion spared his life, he would save the lion one day. The thought of a tiny mouse saving the great lion amused him so much that he let the mouse go. Although the lion never found man, he did find one of his traps. The lion fell in to a covered pit and became ensnared in the net below. For hours the lion tried to break free, but to no avail. Finally the mouse came and freed the lion by chewing through his bonds, repaying his debt.
The point of the story, of course, is that even the mighty, like the Solar Eye, need the aid of the meek and that acts of goodness are repaid by the universe. So the eye returned to Ra, where she was met with music and dancing. These helped pacify Ra’s eye, transforming her from her deadly lioness form.
My point in telling this story is to emphasize that there is a big difference between finding something and justifying that what you’ve found is what you want. Thoth found Ra’s eye, but his task was not finished until he could convince her that she belonged to Ra. Thoth essentially had to prove what he found was the Solar Eye. Consider the following mathematical equation:
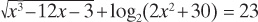
One solution is x = 7. Any math student familiar with the above functions and the use of a calculator can replace the x’s above with 7’s on the left side and get 23, verifying the solution. Once presented with the solution, it’s easy to check. However, I dare anyone to try to solve this equation and arrive at x = 7 as a solution. Finding and proving are very different operations.
As we’ve seen, the ancient Egyptians frequently checked their answers, at least in their texts, if not in practice. We’ve also seen that they were unable to prove many of their statements, at least in the modern sense, because they were unable to abstract, as we do through algebra. This does not mean they ignored proof. The Egyptians proved much of what they did, but they reserved proof for specific as opposed to general statements. One place we see this is in Ahmose’s justification of the table of doubling odd fractions.
I’ve portrayed Ahmose’s table in a modern way: as two columns, the first as the fraction to be doubled and the second as its value when doubled. But this is not how it appears in Ahmose’s papyrus. For example, I’ve given the entry j, f sk to mean that 2 × j = f sk. But in fact, the beginning of the entry appears as f 1 s f, sk f. The f and the sk are in red in the scroll, and oddly enough, the 7 doesn’t even appear except as part of a multiplication next to the entry, which looks roughly as follows:

The key to understanding what’s happening here is to realize that the calculation is determining the value of 2 ÷ 7, which is in fact equivalent to 2 × j. Notice that the checked rows have 1 s f and f, which are precisely the black numbers that appear in the table entry, f 1 s f, sk f. It’s possible that the line of numbers should be read as “a fourth of 7 is 1 s f and a twenty-eighth of 7 is f.” The important mathematical property of the 1 s f and the f is that they add up to 2, and hence the checked entries of the right column of the division will add up to 2.
There’s a lot going on here and it’s mildly confusing, especially because there are at least two valid interpretations. One is that they are deriving the value for the table, and the other is that they are proving it. Mathematicians often use the two terms interchangeably, but they really are different. A derivation is how you find something, and a proof is how you verify that what you found is what you claim it to be. Most modern texts greatly favor the latter, so students see mathematical ideas being verified, but they are woefully ignorant of the process of mathematical discovery and creation.
If we view the above calculation as a derivation, then we are dividing 2 by 7 and get the lines f, 1 s f, and sk, f. Note that 1 s f and f add up to 2, as is demonstrated by the following:
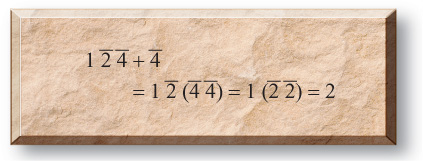
We now know that 2 ÷ 7 is f sk. I personally disagree with this interpretation because the divisions for the other elements of the table make no sense. Consider the division in the calculation of 2 ÷ 65.

Interpreting the above calculation as a division makes no sense. The first line follows from the second by a “division” of 39. Never have we encountered a one-step division by 39 in any Egyptian problem, and I have no idea how it could be done. Even if steps were skipped, it’s impossible to see how or why the problem was done this way.
Let’s instead view these calculations as proofs. In other words, the scribe knows the answer before he starts. Now when we consider the first calculation of 2 ÷ 7 = f sk, we assume the scribe is already aware of this and instead wants to verify it.
Division is the opposite of multiplication. If I divide 15 by 3 to get 5, I can verify this solution by multiplying 3 by 5 to get 15. Similarly if a scribe wants to verify 2 ÷ 7 = f sk, he can perform the multiplication of 7 × f sk in order to get 2. Note the following multiplication of 7 by f sk. Except for the column headings and sums, it looks precisely like the division of 2 by 7.

You should also realize that these column headings and sums don’t actually appear in the Egyptian papyrus; rather, I put them in for clarity. So it’s unclear if this is 7 × f sk or 2 ÷ 7; hence the two interpretations. I’m not even sure whether an Egyptian would greatly distinguish between the two. In fact, they often would phrase something like 2 ÷ 7 as something that loosely translates to “multiply by 7 to get 2.” Now the f and sk are not byproducts of the calculation but rather numbers that are consciously constructed by the scribe. When the second column adds to 2, the proof that 2 ÷ 7 is f sk is provided by the fact that 7 × f sk is 2.
Let’s accept this interpretation and try to provide our own proofs. Consider the following identity from Ahmose’s table: 2 × ag = a; d;. We need to realize that this means that 2 ÷ 15 is a; d;, and to prove that this identity is true, we will show that 15 × a; d; is 2. Starting with 1 and 15 in the first row, we will need to create a a; and a d; in the first column. When we check off the corresponding rows, we should get a total of 2.
We have four basic tools at our disposal. They are doubling, taking ', dividing by 10, and switching. Creating the a; is trivial. We have 1 initially in the first column, and dividing by 10 will immediately give us a;. The d; has an additional factor of 3 in it. Taking ' of the a; puts the 3 in, and dividing by 2 finishes the job. Here’s the calculation.

As you can see, the 1 s and the s add up to 2, proving that 2 ÷ 15 is a; d;.
Now let’s look at the table entry for 2 ÷ 11 is h hh. We’ll need to show that 11 × h hh is 2. Constructing the h is easy. We start with 1, divide it by 2 and then by 3. The division by 3 is performed by multiplying by and then dividing by 2. So the proof starts as follows:
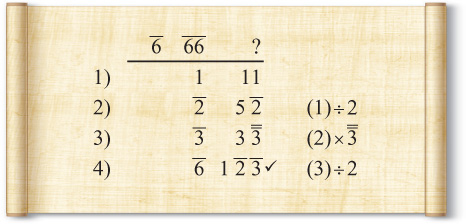
Now that we’ve got the h, we need to construct the hh. This number can be more difficult to construct because it has an 11 as a factor. There is no natural way I know to construct an 11, but we always need to remember that Egyptian numbers are not random. The hh is there precisely because we are dividing by 11. If we switch the first row, we get aa in the first column. In order to get hh, we need to divide by 2 and then by 3, giving

We can verify that the sum is 2 with the following calculation:

A sharp reader will notice that we could have built the 66 on the right and then switched, but I wanted to provide more practice in constructing fractions.
In general we give our fractions the factors of 2, 3, and 5 by using division by 2, multiplication by ', and division by 10, respectively. The first is the most obvious. If I have a j and I want a af, I simply divide the j by 2.
EXAMPLE: Build a s; in the first column when the first row is g, 9.
Note that since we start with a g and need a s;, we’re off by a factor of 4, which is two 2s. Hence we divide by 2 twice.
SOLUTION:

PRACTICE: Build a gh in the first column when the first row is j, 12 g.
ANSWER: The fourth row should be gh, 1 s f;.
Sometimes we need a factor of 3 in our fraction, such as if we had a j and wanted a sa. This can be accomplished by a division by 3, which is the combination of dividing by 2 and multiplying by '.
EXAMPLE: Build a sa in the first column when the first row is j, 8.
SOLUTION:

PRACTICE: Build a ag in the first column when the first row is g, 11 s.
ANSWER: The third row should be ag, 3 ' h.
Now when we need a factor of 5 in a fraction, we divide by 10. This also adds a factor of 2 that often needs to be eliminated by doubling.
EXAMPLE: Build a d; in the first column when the first row is h, 11.
Note that since we start with a h and need a d;, we’re off by a factor of 5.
SOLUTION:
PRACTICE: Build a sg in the first column when the first row is g, 7 f.
ANSWER: The third row should be sg, 1 d ag s;.
We simply combine the methods to obtain factors of 2, 3, and/or 5.
EXAMPLE: Build a h; in the first column when the first row is s, 10 g.
Note that since 60 has a 5 and a 3 in it that is not found in the 2, we start by inserting them.
SOLUTION:

PRACTICE: Build a d;; in the first column when the first row is s;, 15 d.
ANSWER: The third row should be d;;, 1 fg.
The last skill we need to master is switching. This moves missing factors from the right column to the left column.
EXAMPLE: Build a dg in the first column when the first row is f, 14.
Note that we need a 7 in the 35, but we know how to build only 2, 3, and 5. However, there is a 7 in the 14 that can be moved to the left by switching. Once there, we will need to get the 5 by dividing by 10 and then getting rid of extraneous 2s.

PRACTICE: Build a dd in the first column when the first row is k, 11.
ANSWER: The fourth row should be dd, 2 '.
Now we’re ready to do some proofs. Below I’ll show that 2 ÷ 79 is h; sdj dah jl;. Although this looks difficult, it’s important to note that 237, 316, and 790 are all multiples of 79. While this is not obvious in the proof, perhaps it was clear in the derivation. In other words, perhaps the scribe found this identity in a way in which 237, 316, and 790 were found by taking multiples of 79. I’m going to construct these in the Egyptian manner of creating them fully formed in the right column before switching.
EXAMPLE: Prove that 2 ÷ 79 is h; sdj dah jl;.
SOLUTION: We will do this by showing that 79 × h; sdj dah jl; is 2, as shown at the top of the next column on this page.
The right column sums to 2, as can be seen in the following computation:
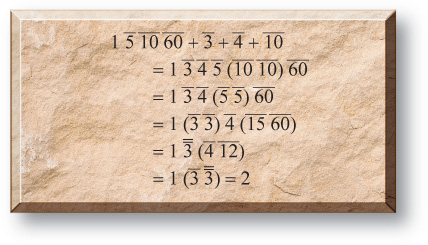

PRACTICE: Prove that 2 ÷ 27 is ak gf.
PRACTICE: Prove that 2 ÷ 17 is as ga hk.
Ancient Egypt existed more or less intact for almost three thousand years, but in this book I’ve misleadingly presented a unified view of the Egyptian mythos. In the first chapter I told you that Ptah, the craftsman god, created the world. If you were to ask this question of someone from Memphis, the capital of Egypt during the Old Kingdom, they’d probably agree with me. However, if you asked another Egyptian from another place or time, they could easily disagree; for example, if you asked someone from Hermopolis or Heliopolis, they might answer Thoth or Ra, respectively.
As time progressed, the cities of Egypt waxed and waned. As a city grew in importance, so did their gods. At the end of the Old Kingdom, about 2700–2200 BCE, the city of Memphis lost its primacy. After a period of disorder, Thebes, in southern Egypt, took over. Their chief god, Amun, the hidden one, became the king of the gods. They smoothed the transition by merging their gods with one of the old gods, Ra, creating Amun-Ra, the new creator of the universe. Some priests tried to work the old mythology into the new. The merging of gods and the reworking of divine family trees led to a twisted sense of history. Kings claimed to be both the son of Ra and the protector of their father Osiris and did not see any contradiction in having two dads. Perhaps they didn’t think it was their place to question the gods or perhaps they didn’t take such familial associations as literally as they might be interpreted today.
Views of the importance and roles of the gods varied not only by time and place, but also by profession and social class. Kings seemed to favor Ra, the god of the all-powerful sun, and Horus, the embodiment of the living god king. High priests leaned toward gods of knowledge, such as Ptah, the craftsman god; Thoth, the god of wisdom and learning; and Ma’at, the goddess of order. Scribes worshipped Imhotep, the deified architect of the first stone pyramid, god of scribes, dreams, and healing.
Competing theologies led to competing views of the afterlife. Those persons who favored Ra believed that the blessed spent eternity on the Boat of Millions. This giant ship carried Ra in the form of the sun around the earth each day. In Abydos, they worshiped Osiris, the benevolent god of the dead. Osiris ruled the underworld from the Field of Reeds, where he was joined by the souls of the dead who achieved salvation.
Although Abydos was never as politically powerful as cities like Memphis or Thebes, the cult of Osiris grew in importance among the people. While circling the universe daily in the Boat of Millions might be exciting, most Egyptians preferred the idyllic, peaceful existence in the Field of Reeds. Osiris’s realm was very much like a perfect version of Egypt itself. Despite the insistence by the theocracy that the Boat of Millions would be one’s final resting place, belief in the Field of Reeds persisted. It was so pervasive that it lasted until Christianity dominated Egypt, and even then it merged with that religion, forming the conceptual basis of the Christian heaven. The people chose the afterlife that most suited them.

Osiris, god of the underworld.
There’s an unusual parallel in Egyptian mathematics. The Egyptians had a fair amount of choice in the fractions they used. They could decide if the answers to a calculation were to their liking. If not, they would change them. As we will see, they could even choose the first terms in their identities, carefully picking the numbers they liked.
Just as every entry in Ahmose’s times-2 table was checked, the same is true for most entries of the division-by-10 table. The check was done in an unusual way. After the 9-entry table, there are six word problems, each of which serves as proof that one of the table entries is correct. For example, the table tells us that 2 ÷ 10 is g. The second problem after the table states that two loaves of bread divided between 10 men is g of a loaf for each. The answer is clearly pulled off the table. However, it then proceeds to check the solution by multiplying 10 by g, showing that the result is 2. The check appears as follows:
The sum of the entries in the right column can be initially calculated as follows:

Now we know the answer should be 2, but instead we got the long sequence 1 ' g a; d;. As we’ve seen, this can be simplified using parts. Each of the fractions is easily measured as parts of 30. We know that ' of 30 is 20, g of 30 is 6, a; of 30 is 3, and d; of 30 is 1. So when calculating parts we get the following:
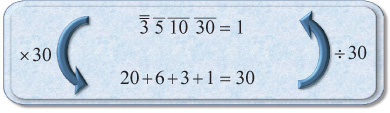
Since the fractions add up to 1, the answer 1 ' g a; d; becomes 2, exactly the answer we expected.
In this case, we knew ahead of time that the answer was 2, so clearly the four fractions had to simplify. But what if we don’t know the answer? Some answers the ancient Egyptians left as is and others they simplified. For example, in the eyes of an Egyptian, 8 h s; would probably be deemed acceptable, whereas 8 h a; might require simplification.
The answer is not black and white. It has its roots in the ideas we discussed in the section “What Makes a Good Identity,” in chapter 4. Recall that a number expressed as the sum of fractions can be evaluated on a number of criteria. Perhaps the most important one is whether or not the fraction forms a good approximation.
Imagine we solved a problem and obtained a solution of h a;. The pair of fractions h a; is not a good approximation. The error is more than 50% since 10 is less than 6 × 2. A tenth is just too large when compared with a sixth. I might then be tempted to simplify the fractions using parts of 30 as follows:

The answer of g ag is a better approximation since a fifth is three times larger than a fifteenth. Thus the error is about 33%. However, you might remember that the Egyptians favored even fractions over odd ones, so in some ways, the original solution of h a; is better than g ag. Even fractions are better because you don’t need to consult Ahmose’s table to double them. However, if this is a final answer to a problem, we’re not going to double it again. Hence g ag is better unless we planned on using it in another computation. There’s no hard-and-fast rule, but the Egyptians seemed content with a difference of around three times as large. So, for example, a; ds would probably be acceptable because 32 is more than 3 × 10, but k s; might not be because 20 is less than 3 × 8.
This rule of thumb seems to get weaker the farther down the line of fractions you get. For example, Ahmose’s table tells us that 2 × al is as jh aaf. The fraction jh is less than a sixth of as, since 6 × 12 < 76 and hence is a good separation of fractions. However the jh and the aaf are very close. Somehow this was not a deal breaker to the ancient scribes. I’m not sure if this was because aaf is so small that they felt it didn’t matter or just because finding a better set of fractions led to other mathematical difficulties. For the following problems, aim to have the third fraction at least twice as large as the previous one.
EXAMPLE: Simplify s j ag or explain why there is no need.
SOLUTION: 7 is more than 3 × 2, so the first pair are fine. While 15 is roughly twice 7, it’s the second pair in the sequence, so it is fine.
EXAMPLE: Simplify f h ak or explain why there is no need.
SOLUTION: 6 is much less than 3 × 4 so we will use parts of 36, the least common multiple.

The terms f, h, and ak turn into 9 + 6 + 2 = 17. We now need to break 17 into whole parts of 36. The larger the initial part, the better the approximation will be. The largest part no more than 17 is 12, a third of 36. This leaves five parts, which can be broken into 4 + 1, which represent a ninth and a thirty-sixth of 36.

So f h ak simplifies to d l dh.
EXAMPLE: Simplify h ak sf or explain why there is no need.
SOLUTION: While 18 is 3 × 6, the 18 and 24 are too close. Simplify with parts of 72.

So h ak sf simplifies to f js.
PRACTICE: Simplify the following or explain why there is no need.
• g sa f;
• d f dh
• h s; sf
ANSWERS:
• It is simplified.
• s l
• f as;
You should not think of the difference between fractions as isolated conditions. Each one adds or subtracts from the total suitability of a fractional expression. So we may tolerate f ah k; and s ah sf, but we would not tolerate f ah sf. Neither pair is bad enough to be a deal breaker but together they are unacceptable. There’s a good reason for this. If we just had f ah, the error in approximating this as f is ah; however, if we approximate f ah sf as f, then the error is ah sf. This is a significantly large number relative to f, so we might simplify it as follows:

There are other considerations for when to simplify, like the simplicity of computation. For example, we would probably try to reduce a; s; g; but not aa sa ga. The common factor of 10 would make the number of parts smaller in the first expression. The factors of 2 and 5 within the 10 would provide us with more options when breaking the total into parts. The 11, 21, and 51 of the other fractions would lead to difficult computations and extended answers if we tried to reduce it.
Occasionally using parts doesn’t seem to simplify an answer. Consider f g. It’s an obvious candidate for simplification because the two fractions are so close together. However, when we choose the obvious number of parts, 20, we get the following:

We can’t break up the total of 9 into a better sum. That’s because there is no factor of 20 greater than 5 but less than 9. There’s a trick to dealing with this problem. It more or less requires us to estimate the answer before we start. Obviously f g is a little less than f f, which is s. Since s is already bigger than f g, our answer can’t start with s because all we can do is add other fractions that simply make it larger. So what could our answer start with? We can’t start with a s, since it’s too big, but if we start with f, it’s too small, because the error, g, is too large. Hopefully a little common sense should tell us if s is too big and f is too small, then perhaps d is what we need.
So now we’re confronted with the question, why didn’t we get d as the start of our solution when we simplified f g with parts of 20? The problem is, there just isn’t any nice number of parts that is a third of 20. In order to get a d, we need the number of parts to be a multiple of 3. Hence we should have used 60 parts. Let’s try it and see what happens.
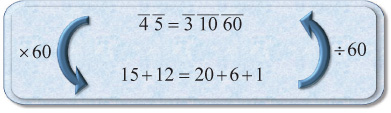
What we just did was essentially pick the first term in our simplification. We could have written the d down before multiplying by 60, getting 15 + 12 = 20 + ?? on the bottom row. At this point we need to realize that we need 7 more, which must then be broken into nice parts of 60.
EXAMPLE: Simplify a; aa so that the solution starts with h.
For this problem, the obvious number of parts is 110. However, this is not easily split into six parts. We’re missing a factor of 3, so we’ll use 330 instead. Note that a sixth of 330 will be 55.
SOLUTION:

PRACTICE: Simplify d g so the solution starts with s.
ANSWER: s d;
It’s possible to mess up when choosing the first term. Let’s try to simplify a; s; so that it starts with h and see what happens.
EXAMPLE: Try to simplify a; s; starting with h. What goes wrong and why?
SOLUTION:
There’s nothing (positive) we can add to 10 to get 9. Hence h is more than a; s; and we can’t add other fractions to h to make them equal.
PRACTICE: Try to simplify k ds starting with g. What goes wrong and why?
Now that we know how to start a simplification with any fraction, we need to know how to choose this value. There seem to be three primary considerations: it should be a good approximation, share common factors, and be easy to break into parts.
Consider ad ag. It’s obviously bad. It turns out that j is the best approximation for this sum. So we could try to start our simplification with j. This will lead to unruly fractions.

There are problems with using the best approximations. It’s unlikely that an Egyptian scribe would even be sure of what the best approximation was. If I were to describe to modern mathematicians how to find the best approximation for ad ag, I would tell them to take the harmonic mean of 13 and 15, divide by 2, and round up, giving the number to put under the fraction bar. If you don’t understand what I just said, don’t worry, an Egyptian scribe probably wouldn’t understand it either. Even if you find the best approximation, it often leads to ugly answers because they tend to involve odd fractions and huge parts that make for tedious hand calculations.
An easy way to get a good estimate of the best approximation is to pick an even number somewhere from 13 to 15, making sure it’s at least as close to the larger number as to the smaller. The closer it is to the middle, the better the approximation. Take half of this number and write it as a fraction. In our example the only even number in this range is 14, and half of it is 7, so j is our good approximation. In this case, it found the best.
EXAMPLE: Find a good approximation for sa sh.
SOLUTION: The even numbers between the two are 22 and 24. 24 is at least as close to 26 as 21, so half of 24 as a fraction, as, is a decent approximation.
As you try the following practice problem, remember it’s better to pick a number closer to the top than to the bottom.
PRACTICE: Find a good approximation for dd dj.
ANSWER: ak.
Once we find a good approximation, we need to find one that works well. Let’s go back to ad ag. The fraction j makes a good approximation. If we make the number under the bar larger, the fraction gets smaller, which is fine, but the approximation gets worse and worse. We can’t make the number smaller because it might get larger than the sum itself. As long as we stay above but close to the good approximation, we should be fine. So we need to consider fractions like k, l, and a; instead of j. As we will see, all of these are reasonable choices.
The choice of k is a good one because it’s filled with factors that are easy to break into parts. The more 2s and 3s a number is composed of, the better, and 8 is composed of all 2s. So when we use k as our first fraction, the following fractions will be relatively easy to find as parts.

It turns out that k is probably not the best choice. It does have some advantages: the 2s in the 8 make all the fractions in the identity even and hence easier to work with. But its main flaw is that the number of parts, 1560, is enormous. What if we used a; instead? The reason it’s a good choice is that there is already a 5 in the ag, so all we need is a 2 to complete the a;. This greatly reduces the number of parts and we still get a 2 in them.

EXAMPLE: Consider the simplification of s; sd. Which is the best fraction to start with: aa, as, ad, or af? Explain and simplify with this fraction.
SOLUTION: as is the best since it has many small factors and shares a 4 with s;.

PRACTICE: Consider the simplification of ak sa. Which is the best fraction to start with: aa, as, or ad? Explain and simplify with this fraction.
ANSWER: as gf jgh, as hd sgs, or as kf ash
While I have to admit that simplifying fractions is perhaps the most tedious part of Egyptian mathematics, it generally needs to be done only at the end of a problem and only when the answer doesn’t “feel” right. You could get by without reducing at all. Your answers would still be technically correct; however, there would be differences between your solutions and those of the ancient scribes.
The units people work in tend to be fixed by practice and not by mathematicians. I’m sure at one time a foot was literally the length of a foot. Similarly a yard is the distance from your nose to the tip of your outstretched hand. The problem is that feet and arms vary in size, so sooner or later a civilization needs to standardize its units.
This is where the insight of the mathematician comes in. While it’s possible to make a foot just the average foot length, it is foolish to do so because different units need to work together. My foot is about 10 inches long and my “yard” is about 36 inches. This means that I would need to multiply by 3.6 to convert from feet to yards. A good mathematician would realize that this is an overly difficult number to work with, so she would fudge the units, altering the lengths to make exactly 3 feet in a yard. Hence our foot of 12 inches is much larger than a typical human foot. Math needs to be easy to be practical, and easy numbers make for easy computations.
The Egyptians were clearly aware of this because all of their units were relatively easy to convert. We already know a palm is 4 fingers. To go from one to the other, all we need to do is double twice, or conversely, take half, and half again. A standard cubit is 6 palms. To convert palms into the standard cubit, we simply need to divide by 2 and then divide by 3. A khet is 100 cubits. As we’ve seen, multiplying and dividing by 10 usually requires only a change in symbol. For example, HH cubits is FF khet.
The same ease of conversions also holds for volumes. A hekat is roughly equal to the modern gallon. The volume of a box a cubit on each side is equal to 30 hekat. Larger volumes were measured in double or quadruple hekat, which simply required doubling to convert. A khar is 20 hekat, just a doubling followed by a multiplication by 10. Converting from cubic cubits, for example, 30 hekat, into khar required multiplying by '.
Everything was easy until some pharaoh demanded that his royal cubit have one more palm than everyone else’s. I imagine that he made this proclamation to two scribes, the first of whom declared that 7 palms in a royal cubit was no good since division by 7 was awkward. After the first scribe was decapitated, the second agreed that the royal cubit was a wonderful idea. I wonder how many scribes lost their heads before they agreed that there should be 5280 feet in a mile?
Remember that when performing conversions, the operations work “backward” from the table. For example, since 1 palm = 4 fingers, then 4 times the number of palms is the number of fingers.
The moral is that math needs to be easy to be useful. Any and all methods suggested by historians of mathematics should be relatively easy to perform given the knowledge and techniques of the ancients. There’s a serious problem with the interpretation of Egyptian mathematics that I’ve put forward. In order to work with the fractions, we’ve needed to work in parts. This requires multiplications and divisions to convert back and forth between the original fractions and the parts. So doing a multiplication requires us to do more multiplications, and this process violates the principle that math needs to be easy to be practical. My goal in this section is to convince you that working in parts doesn’t require nearly as much multiplication and division as you might think.

Unit conversions.
Let’s consider the problem of adding g and h. The obvious number of parts is 30, and the computation might look like this.

Notice that the first two terms of the top row, g and h, and the first two of the bottom row, 6 and 5, seem interchanged. This is not a coincidence. In order to understand this, we need to realize that the 30 parts we picked is just 5 × 6.
When we multiplied g by the 30 parts to get 6, we really just multiplied g by 5 × 6. Algebraically we can think of the g and the 5 as cancelling each other. An Egyptian might think of it in the following way. When we multiply 5 × 6 by g, we’re really asking, what is a fifth of five groups of six? The answer is of course, one group of six. Similarly, when we multiply h by 5 × 6 to get 5, we are acknowledging that a sixth of six groups of five is one group of five.
Now consider adding aj and sd. I don’t know the value of 17 × 23, but it really doesn’t matter. I know that aj as parts of 17 × 23 is 23 and that sd as parts of 17 × 23 is 17.

If we think in these terms, certain problems become simple. If I needed to know what j is as parts of 7 × 11, I’d answer 11, because the j and 7 cancel each other.
EXAMPLE: Fill in the bottom left of the following parts table.
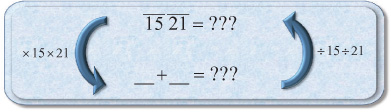
SOLUTION: ag as parts of 15 × 21 is 21, and sa as parts of 15 × 21 is 15, so we get
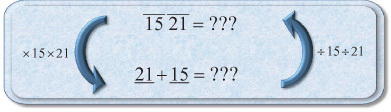
PRACTICE: Fill in the bottom left of the following parts table.

ANSWER: The bottom row is 31 + 27.
Sometimes we add extra parts. When we simplify aj sd, one strategy is to select the first fraction. A good number to select is a;, and this adds an extra factor of 10 into the mix. All we need to do is to multiply our parts by 10. So if aj of 17 × 23 parts is 23, then aj of 17 × 23 × 10 is 23 × 10, or 230. While we still have to perform a multiplication, we need to remember that we selected the first fraction in part because it was an easy number to work with.
EXAMPLE: What is j in parts of 5 × 7 × 2?
SOLUTION: 5 × 2 = 10.
PRACTICE: What is g as parts of 3 × 5 × 11?
ANSWER: 33
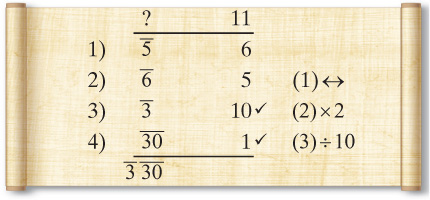
Let’s go back to our original example of adding g and h. We turned them into parts of 6 and 5, respectively. The next step is to add these to get 11 and then break the 11 into parts. Here’s the standard solution. The key for us to solve this problem is to break 11 into factors of 30. We know that both 10 and 1 are factors of 30 and that 11 = 10 + 1, so we get the following solution:

The problem is that we know factors of many numbers because we’ve memorized multiplication tables. For example, since we know 4 × 7 is 28, we also know 4 and 7 are factors of 28. Egyptians would not realize this as readily as we do. However, I believe that the ancient scribes could easily have performed the above calculations in their head. I will now try to convince you that the above calculations are almost exactly like the Egyptians’ standard multiplication method.
The trick is to “tip” the above table 90 degrees. In essence, the rows above become the columns of an Egyptian operation. Let’s start with just the 6 and 5, which are trivially derived from the g and h.
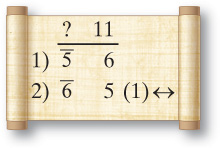
Notice that the first column is just the original g and h from the problem. These numbers are found in the first row of our above parts calculation. The second column contains 5 and 6. These are just the parts from the second row above. So the first column represents the original numbers, while the second represents the corresponding parts. Note that we can think of the second row as a standard row switch. The g and 6 change places becoming h and 5.
We put 11 over the second column because it’s the number of parts we need. While 5 and 6 work, it produces the bad approximation h g. We need to start with a number closer to 11 than 6 to get a better answer. A sharp scribe would realize that if he doubled the 5, he got 10, a number very close to 11.

Since we now have 10 of 11 parts, there’s only one more part to go. We can easily get 1 by dividing the 10 by 10. This gives us the solution of d d;.
The significance of the above operation is clear only when you compare it to the following parts calculation. The first column above is g h d d; while the first row below is g h = d d;, exactly the same numbers. Now compare the second column above with the second row below. Once again, they are the same.
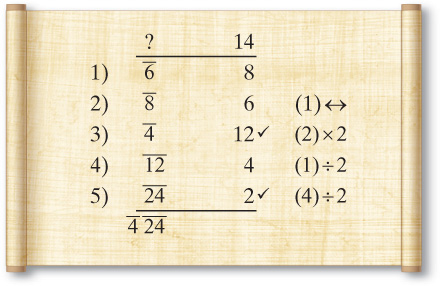
Let’s look at another example. Consider adding h and k. Let’s use parts of 6 × 8. We could use the LCM, but there’s really no need because the parts will be easy to compute. We know that the corresponding parts will be the terms reversed, 8 and 6, whose total is 14.

At this point, let’s switch to an Egyptian-style computation. Note that the total number of parts we need is 14. We need a “nice” number of them close to but under 14. If we double 6 we get 12, which will do nicely. This leaves 2 parts. There are a number of ways to obtain 2. I’ll do it by halving 8 twice.
Now let’s put this into a parts-styled computation. Remember the columns above become the rows below. We leave some terms, like row 4 above, because they are not used in the identity.

The truth is we don’t know how Egyptians did part calculations. Clearly when we use our knowledge of factors, we’re taking liberties applying our modern methods. Yet it is encouraging that similar operations resemble Egyptian-styled computations. Here’s one more example without all the explanation.
EXAMPLE: Add h a; as parts of 6 × 10. Use Egyptian multiplication tricks to figure out their parts and the parts of the final solution. Include a multiplication-like document to show their derivation.

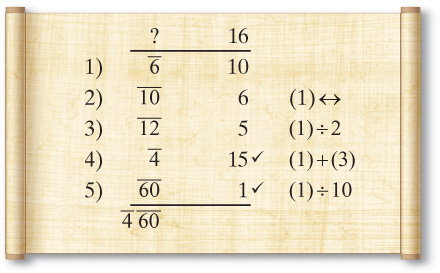
Most of the operations are so simple that I doubt the Egyptians would have had the need to write such a document to compute their parts. Try this one on your own. Realize that to go from 20 parts to 4 parts you can divide by 10 to get 2 parts then double.
PRACTICE: Add a; af as parts of 10 × 14. Use Egyptian multiplication tricks to figure out their parts and the parts of the final solution. Include a multiplication-like document to show their derivation.
ANSWER: j dg
Let’s use these skills to find another way to construct Ahmose’s doubling table. I’m going to focus on the doubling of odd primes because the factor method I introduced earlier in the book doesn’t produce nice answers. Let’s start with 2 × j. We can think of this as a simplification problem by rewriting it as j j. There are no evens between 7 and 7, but remember that larger numbers also work, so let’s choose 8. Half of 8 is 4, which is a nice number as well as a good approximation. So let’s write j j as f and something else.
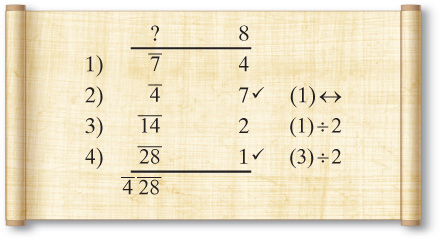
To do this let’s work in parts of 7 × 4. We immediately know that the corresponding parts of j and f are 4 and 7, respectively. This gives us the following partial solution.

Clearly we need one more part on the right, and we can calculate it by dividing the 4 parts by 2 twice. The calculations and final answer appear as follows:

Let’s try doubling dj. Half of 38 is 19, a lousy number because it’s odd and has no whole parts except for 1 and itself. The number 20 isn’t a bad choice since it is a good approximation and has parts comprising 2s and a 5. However, the author of the scroll used 24. It’s a better number because it is all 2s and 3s, although it’s a slightly worse approximation. Here’s the problem as an example.
EXAMPLE: Construct Ahmose’s doubling of dj starting with the fraction sf. Do all parts as a table.
SOLUTION:

Both of the preceding answers are exactly the same as the entries in Ahmose’s table. Try these two practice problems.
PRACTICE: Construct Ahmose’s doubling of aa starting with the fraction h. Do all parts as a table.
ANSWER: h hh
PRACTICE: Repeat for ad starting with an k.
ANSWER: k gs a;f
In the above “doubling” problems we selected f, sf, h, and k as the starting fractions of our solution. These are all extremely easy numbers to work with in Egyptian math since they all contain 2s and 3s. These choices made the breakup of the remainder into parts much easier. While it’s impossible to know the exact method used to create the Ahmose’s table, he seems to have followed exactly the same strategy. Let’s look at the entries on the doubling table and focus on the prime fractions. Let’s ignore d, since doubling it is just '. The next 22 prime fractions when doubled start with the fractions d, f, h, k, as, s;, sf, d;, dh, f;, fs, and h;. Many occur a number of times, of course. With the exception of 42, which appears only once, all of the other numbers are composed of only 2s, 3s, and 5s. Even the 5s occur only if there are at least two 2s or 3s. This is probably not pure chance. It appears as if the creators of the table were intentionally selecting numbers that were easy to work with, and that should hardly come as a surprise.
You can see most of the stars visible at your latitude at some time in the night. While at any given moment, only half the sky is visible, the celestial sphere rotates, continually “lifting” new stars into the heavens. At a given time of year, some stars are simply too close to the sun and are hidden by the glare. However, the sun moves around the sphere of stars once a year and will, in a couple of months, move away, allowing the star to reappear in the eastern sky minutes before the dawn. The first such appearance of a star is called its helical rising.
Sopdet, now called Sirius, is by far, the brightest star in the sky. The Egyptian name translates into something like “she who is sharp,” and her helical rising marked the beginning of the Egyptian year. It was a particularly important time for the residents of the Nile valley since by this day all the canals had to be dredged and the dikes repaired in preparation for the coming flood.
Nilometers, the device Egyptians use to measure the depth of the Nile, were continually checked. At the appropriate time, canal gates were opened and anything valuable had to be moved to higher ground. The rising waters were directed by canals into every region of the valley. When the canals were full, the gates were closed and the water was held captive by dikes that partitioned the arable land of Egypt. The fertile silt would settle to the bottom of the standing water, reinvigorating the soil. The water would slowly be absorbed into the ground, waiting to be taken up by the crops. Finally the canal gates would be reopened, draining any excess water back into the receding Nile. At this point the soil was ready for the wheat, barley, and flax that the Egyptians needed for their sustenance and clothing, but there was one problem.
The force of the water and the new layer of silt could push away or cover the markers or landmarks that distinguished one Egyptian’s property from another’s. Even worse, the very course of the Nile could easily change, making old boundaries obsolete. Every year the educated, math-literate class of Egyptians had to engage in a massive land survey, redrawing the property lines of an entire nation.
A farmer would want a plot equal to the one he had in previous years. It was often difficult to guarantee exactly the same stretch of land. However, if the farmer was given the same amount of land of the same quality as his old plot, it’s unlikely that there would be an objection. Hence the area of a plot was its vital feature. As a result, many of the area problems that come down to us from ancient Egypt are phrased as determining the size of fields. A common unit of area used in ancient times was a cubit strip, which was equal to 100 square cubits. While this is equal to the area of a square 10 cubits on a side, it is more properly thought of as an area of a 1-cubit-by-100-cubit rectangle. If a row of fields were 100 cubits long, you could then find the area in cubit strips simply by measuring the width in cubits.

The area in cubit strips of a field 100 cubits deep is the width.
When we calculate areas today using familiar equations, such as “one-half base times height” for triangles, our answers come in simple units. If our lengths are measured in inches, the formulas give us areas in square inches. Similarly using measurements in feet produces solutions in square feet, and so on. A cubit strip is not such a unit. Egyptians typically measured such lengths in cubits, so standard modern equations will produce areas in square cubits not cubit strips. Hence, we need a way to convert square cubits into cubit strips, just as a modern surveyor might need a way to convert square feet into acres.
Using base times height, we can calculate the area of the above 23-cubit-strip strip field to be 100 × 23, or 2300 square cubits. So 23 cubit strips is equal to 2300 square cubits. Hopefully you realize that we can convert from cubit strips into square cubits by multiplying by 100, a very easy operation. Similarly square cubits can be converted into cubit strips by dividing by 100.
We’ve already seen how to calculate the area of a rectangle and a triangle. However, one of the field shapes discussed in Egyptian mathematics is a truncated triangle, known to mathematicians as a trapezoid. Humans like order. They want their fields to be nice rectangles all in a row. However nature doesn’t always comply. The walls of the Nile valley are not straight, and the river meanders in a seemingly random path within the confines of the canyon walls. A field cut on one side by such a barrier closely resembles a trapezoid.
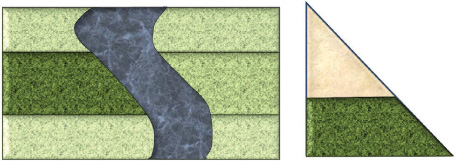
A rectangular field cut by a river forms a truncated triangle.
Fortunately, as the Egyptians knew, these areas are easy to compute. Instead of multiplying the height by the base, you simply multiply the height by the average base. Consider the following trapezoid with a height of 20 and bases of 4 and 6. The average base is just the sum of the two bases divided by 2.

A trapezoid with a height 20 and bases of 6 and 4.
EXAMPLE: Find the area of a trapezoid with a height of 20 and bases of 6 and 4. Give the answer in square cubits and cubit strips.
SOLUTION: Add the bases to get 10. Take half to get 5, the average base. The area is average base times the height, so multiply 5 by the height of 20, to get 100:
The above answer, 100, is in square cubits. Since the Egyptians measured fields in cubit strips, we need to convert. Multiply by a;;, the number of cubit strips in a square cubit, to get the answer, 1, in cubit strips.
PRACTICE: Find the area of a trapezoid with a height of 9 and bases of 10 and 13. Give the answer in cubits and cubit strips.
ANSWERS: 103 s cubits and 1 f; a;; cubit strips
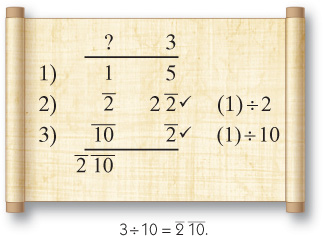
The area problem I want to consider is actually much simpler than finding the area of a trapezoid. The problem simply states that ten fields have an area of seven setat, a unit of 10,000 square cubits. What’s the area of each? The problem is solved by simply calculating 7 ÷ 10. The division is performed as follows:
Although it’s not a complicated solution, it’s short and sweet and doesn’t follow the usual pattern. Immediately after this problem is the same type of problem with different numbers.
EXAMPLE: Five fields have an area of 3. What’s the area of each?
Both solutions get their answers in just a few lines and the computations seem unsystematic. It is the nature of Egyptian mathematics to offer surprising solutions, giving the mathematician freedom to compute as she pleases. In the hands of a skilled practitioner, this can result in unexpectedly short computations.
While it’s important to know what the Egyptians knew, it’s as important to think like they did. Their system of computation gave them great flexibility, and knowing how to exploit this is what gives their mathematics such power. Consider the options you have when going from one line in a multiplication to another. You can double, halve, take the ', divide by 10, sometimes multiply by 10, and switch the terms. You don’t even have to do this with the previous line, but rather, you can use any line above it. When you include the option of adding any pair of lines together, the number of choices you’re confronted with is enormous.
Egyptian math presents us with a series of choices, and to make choices you have to think. Modern math gives us rules and steps. Performing its operations requires rote memorization, repetition, and perseverance. It may be tedious and boring, but if you follow the instructions to the letter, eventually you will be rewarded with the correct answer. This is the exact opposite of Egyptian math. To the uninitiated it often seems impossible, but that’s because they don’t know which choices to make and continually make the wrong ones. An Egyptian computation can take untold pages or a handful of lines depending upon the skill of a mathematician.
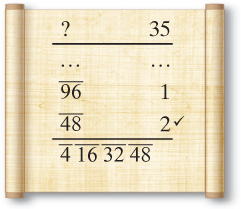
Let’s consider the example of 35 ÷ 96. Someone only mildly familiar with the Egyptian method would set up the table and begin mindlessly taking half until they’re about to hit a fraction. Here’s how it might look.
After the amateur mathematician checks off the appropriate numbers, he realizes he still needs 2 to get to 35. Mindlessly he switches the top row and then doubles it. The continuation might look like this.
After he gets the answer of f ah ds fk, his teacher glares at him, and he begins to simplify, repeatedly applying the G rule.
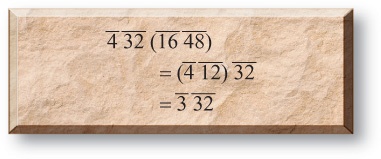
Now that he’s done, he declares Egyptian mathematics to be awkward and pointlessly tedious. But then, to his horror he glances at the work of the student sitting next to him and he sees this.
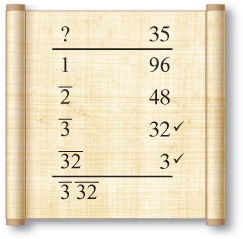
In a mere four lines with no simplification, she got the same answer as he did. How did she know to take the ' of the second line and then to switch the third line? She must have got lucky, he thinks, but he doesn’t realize that she has the insight. Someone with insight sees the number 15 and immediately then gets the numbers 30, 7 s, 10, 150, ag, and 1 s in her head, which are the double, half, ', times 10, switch, and tenth of 15. Not only that, but she will instinctively know how these numbers relate to other numbers in the problem. She saw 48 and immediately thought of its ', 32, and knew it was close to 35. In fact, it was the switch of d away.
Thinking this way is at first difficult, but the brain adapts. Just as riding a bicycle seems to go from impossible to easy overnight, so does Egyptian math. It just takes practice, and that’s exactly what this section is for. In the following problems I will give you a starting line and a goal. The goal number has to appear in the right column in four lines or less. Let’s look at an example.
EXAMPLE: Starting with ad, 20, create the number 150 on the right in four lines or less.
SOLUTION:

I like the four-lines-or-less exercise. The numbers you need to create are just far enough away that the solutions are not obvious, but they are close enough that a little trial and error will usually find them. The exercises I’m providing here are the same questions I give my students in an hour-long math lab. Working in groups, they can usually find all the solutions in the time allotted. I can do it in a few minutes. I’m not trying to brag but rather convince you that anyone with practice will be able to do this easily.
Each of the problems can be solved with three applications of the following operations:
• Double
• Halve
• Multiply by '
• Divide by 10
• Switch a line
• Add any number of lines
In special circumstances, Egyptians multiplied by 10. I’m going to disallow this because it doesn’t always work. Also remember that you can’t switch lines that contain fractions consisting of more than one term, such as d a; or 2 j. Good luck.
PRACTICE: Starting with the given rows, create the last number on the right in four lines or less.
• 11, 90 to 3
• 1, 45 to 31
• 11, 18 to 45
• 12, 9 to dh
• f, 50 to 58
• 4, 150 to 5
• h, 80 to 89
• 10, 36 to 48
• h, 40 to 100
• 20, 12 to fg
By now you should realize that solving these problems is like solving puzzles. It requires more wit than repetition and patience. You’re now beginning to understand the true nature of Egyptian computation.
The tenth problem of the Moscow Mathematical Papyrus asks the reader to determine the area of an nb.t. Unfortunately this word never appears anywhere else, and hence it’s untranslatable. It’s similar to the word for “hill,” which gives us some clue. The problem also states that the nb.t has a diameter of 4 s, which suggests that some part of it is circular. Further confusing matters, it also has a “[?]” followed by the Egyptian equivalent of d. The “[?]” means that the word is unreadable, possibly damaged. The d is untranslatable without some context. There are many possible shapes that loosely resemble a hill and have a radius. The math doesn’t help much. Any area involving circles can only be approximated, so any shape with roughly the area calculated in the exercise is a candidate.
Possible shapes of an nb.t.
We may never know what an nb.t is, but we can examine the mathematical calculations. Part of the procedure of finding this unknown figure’s area has the student remove a ninth from 8. Taking l of a number is relatively straightforward.

We now need to remove this ninth from 8. The answer given is a simple 7 l, but how did they get it? We’ve never subtracted fractions. Adding is easy. You put the two answers side by side and simplify if it suits you, but pulling ' h ak out of a whole number seems difficult at first. But just as division is like multiplication, Egyptian subtraction is much like addition.
Ancient civilizations thought in positive terms, not negative, and hence avoided inverse operations. When they phrased inverse operations, they usually stated them in terms of the standard operations. So you usually don’t ask, “What is 8 divided by 2?” but rather, “What do I multiply 2 by to get 8?” You don’t take the square root of 25, but rather ask, “What do I multiply by itself to get 25?” The ancient Egyptians would not have removed 4 from 7 in a subtraction but rather completed 4 to 7.
Completions on whole numbers were considered trivial in Ahmose’s text on fractions, but the papyrus does give examples of the subtraction of fractions. True to the ways of thinking in the ancient world, it’s treated as an addition problem with an unknown. Fortunately it’s done with a method very similar to our computation of parts. It’s simple enough that it’s best to learn it by examining an example or two.
EXAMPLE: Complete f s; to s.
To solve this we are going to literally express this as f s; plus what, is s. I’m going to express this in the parts diagram that we’re all familiar with.

We now pick a good number of parts for these fractions. An obvious choice here is 20.
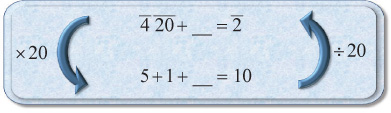
Looking at the problem on the bottom, you should realize that we’re essentially asking what we should add to 6 to get 10. The answer is 4, and we fill it in.
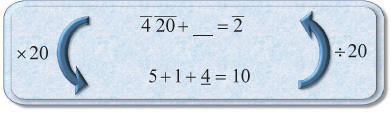
The only thing left to do is take 4 back to the top line by dividing it by 20, giving g. The final solution appears as follows:
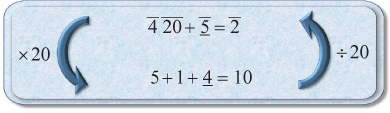
SOLUTION:
Note that we’ve essentially shown that s minus f s; is g.
EXAMPLE: Complete d h to ' ag.
Once again we try to find an easy number of parts to work with. In this problem, a good number of parts is 30. Multiplying by 30 we get the following:
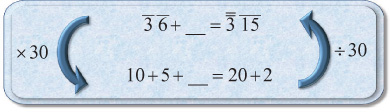
We have 15 on the left and 22 on the right, so the left needs 7 more. Unfortunately 7 is not a nice part of 30. Hence we need to break it into pieces. The obvious choice is 6 + 1. When we divide these by 30 to get the fractions, the solution looks like this.
SOLUTION:
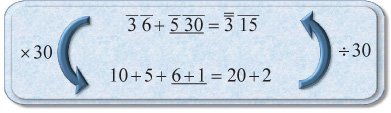
Hence (' ag) - (d h) is g d;. Try these.
PRACTICE: Complete f g to s.
ANSWER: s;
PRACTICE: Complete aa hh to h.
ANSWER: ss hh
Sometimes we don’t have enough parts. For example, if we were to try to complete j to 1, an obvious but wrong choice for parts is 7. We would be confronted with 1 + ___ = 7. Of course a 6 could fill in the blank, but the problem is that 7 has only 1 and 7 as parts, and there’s no good way to make 6. A good choice for parts is 28, a number the Egyptians used frequently when dealing with sevenths. A better choice of parts is 42. In order to understand why, we need to remember that Egyptians often estimated answers before calculating them. The fraction j is near 0, and we’re completing it to 1. This fraction is huge, and an Egyptian would have realized that it’s going to be at least '. So we need a 3 in the number of parts. If we throw in a 2 for good measure, the number of parts is 7 × 3 × 2, or 42. We can put the ' in the answer ahead of time, giving the following:
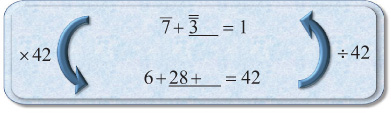
At this point we see that we’re 8 shy of 42. Since 8 is easily broken into 7 and 1 we get this solution.
EXAMPLE: Complete j to 1.
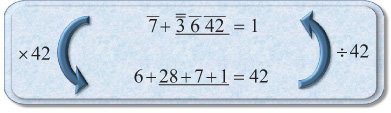
When computing parts, it never hurts to throw in a 2 or two, especially when the “obvious” number of parts is odd. In the following practice problem, the obvious number of parts is 3 × 5 = 15. Notice that it’s odd. If we put a 2 in it, this will give us more flexibility in selecting parts. So, instead of 15, use 3 × 5 × 2 = 30 parts.
PRACTICE: Complete d g to 1.
ANSWER: d a; d;
Sometimes you will know that the answer will be a large fraction very close to 1. The only single fraction near 1 is '. In these cases it helps to throw a 3 into the parts if it is not already there. Otherwise you will never get thirds.
EXAMPLE: Complete af to 1.
Here the obvious choice for parts is 14. However af is tiny, and hence the distance to 1 is large. Therefore we should use 3 × 14 = 42 for the parts. Normally we think of the “nice” parts of 42 as its factors. But remember that 28 is ' × 42, so 28 also is a part of 42. The solution is unpleasantly long, but this often happens to fractions near 1.
SOLUTION:

The following problem uses the same trick. You need to add a 3 to get ' into your answer. Since 3 × 11 is odd, adding a 2 for good measure gives 3 × 11 × 2 = 66 parts. Remember that 44 is ' of 66 and hence is a valid part.
PRACTICE: Complete aa to 1.
ANSWER: ' h ss dd
Here are a few final tricks. If we want to complete 4 d k to 5 k s;, we can cancel from both sides. Hence we could remove 4 from both sides and completely eliminate the k. Hence the solution would be equivalent to the answer to “complete d to 1 s;. Finally, there’s no need to use this method to complete whole numbers. So if we were asked to complete d a; to 8, we should complete it to 1. Then we add 7 to our fractional answer to go from 1 to 8.
PRACTICE: Complete 8 s a; to 12 s g.
More than two thousand years ago the mathematician and engineer Archimedes was contemplating a diagram of circles he had drawn on the floor. The aging Sicilian was apparently unaware of the commotion outside. Archimedes’ king had made the mistake of talking with the Carthaginians, the mortal enemies of the Romans. For this offense, the vengeful and violent leaders of Rome decided that the inhabitants of Syracuse must die. For three years the war machines invented by Archimedes held off the Roman legions, who simply camped outside the city walls waiting. Finally, after a festival filled with drunken revelry, Roman spies opened the city gates and the slaughter began. When a Roman soldier entered Archimedes’ room, the mathematician told the warrior to not disturb his diagrams. For this, Archimedes received a spear plunged through his chest. Thus died a great, perhaps the greatest, mathematician.
Archimedes was a favored son of Syracuse. As the father of mechanics, the numerization of the physical laws of the universe, he created machines of unprecedented power. Those for war had kept the most powerful army in the world at bay for years. At the same time, he paralleled his mechanical creations with pure mathematics. He used math to justify his new laws, and hypothetical machines as examples to discover new laws in math. He was a mathematician literally thousands of years ahead of his time.
Archimedes is credited for finding, with proof, the area and volumes of many shapes. In particular, he found the area of a circle and the volume and surface area of a sphere, all of the equations involving the elusive constant π. The proofs he provided were done with a method that the Greeks called exhaustion. It is a complicated but rote method of proving the measure of a figure. The main problem with the method of exhaustion is that it’s preferable to know the answer before you start. In other words, it’s better at verifying a guess rather than finding a solution.
In the ancient world, mathematicians didn’t know that the π involved in the circumference of a circle was related to the constant involved in other aspects of circles and spheres. Archimedes had to know the relation between the two constants before he applied exhaustion, and he explained how he knew the answer in his masterful book, The Method. This book had been long forgotten but was rediscovered at the dawn of the twentieth century. A copy of the text had survived to the modern day. Unfortunately, it had been erased and overwritten with a medieval religious text. For a long time no one knew of the treasure hidden under the ink of the holy tome. Upon its discovery, scholars were able to read the remnants of most of the barely visible, original text.
The argument Archimedes gives for the area of a circle is both imaginative and beautiful in its simplicity. Imagine a circular rug made of concentric strands in loops. Cut the rug in a straight line from somewhere on the outside to the center.

The circular rug cut to the middle.
Each circular loop is now a length of rope that can be straightened out. The resulting figure is basically a triangle. This is a result of the linear relation of curves, something Archimedes would have known well. In simple terms, if you go twice as far from the center of the circle, the loop gets twice as long. Similarly, if you go twice as far down from the peak of a triangle, the corresponding line gets twice as long.

When straightened out, the loops form a triangle.
The height of the triangle is just the radius of the old circle. If you don’t see this, just count the bands in both diagrams. Both the height of the triangle and the radius of the circle in the above diagrams consist of six bands of equal width. The base of the triangle is just the outside loop, whose length is the circumference of the circle. The area of a triangle is just ½ base × height. If we replace “base” with the modern equation for the circumference, 2πr, and r for the height, where r is just a name for the radius, then the area of the triangle becomes ½ 2πr × r. This simplifies to the equation that is familiar to many math students, πr2.
This abstract cutting of a figure into thin pieces is often called slicing. Archimedes used slicing arguments to find many things, like the volume and surface area of a sphere and the volume of a paraboloid. He used such arguments to find centers of mass. His understanding of center of mass led him to the law of the lever and pulley, which in turn aided his construction of the war machines that defended Syracuse from the Romans. He also used the notion of the center of mass to develop his theory of hydrostatics, with which he determined whether an object would float, how far it would sink in the water, and whether it would be stable or tip over. Perhaps his understanding of the center of mass led him to conclude, almost two thousand years before Copernicus, that the sun, not the earth, was the center of the solar system.
Just like Leibniz, Newton, and others from the Age of Reason would do, Archimedes thought of shapes as consisting of the sum of infinitely thin slices. Just like they would, he applied these ideas to find areas, volumes, slopes, and centers of mass. Just like they would, he applied his methods and conclusions to the physical world. Archimedes died a few steps away from the invention of calculus The only real difference is that he determined his numerical solutions by comparative arguments rather than by algebraic rules such as Leibnitz’s dx2 = 2xdx. In my opinion, at the time of his death, Archimedes had brought mathematics within a generation of the invention of calculus.
So why did it take almost two thousand years for these ideas to reappear? Some blame the Romans, who had no time for the intellectual musings of those of Greek descent. While partly true, the great intellectual center of Alexandria in Egypt would remain free of Roman control for another two hundred years, which was plenty of time to develop calculus. Some blame the Greek preference for the theoretical over the practical. This explanation again is partly true, but there are many exceptions, such as their laws of reflection and refraction. It also assumes there is no theoretical appeal to the notions of calculus.
I, being completely biased and never missing a good opportunity for self-righteous moralizing, have my own opinion: Archimedes didn’t follow the rules. The method of exhaustion had clearly defined steps, each of which had clearly defined justifications. Greek mathematicians probably balked at the notion of adding infinitely thin items, a method that at the time had no precise theoretical justification. By supplying exhaustion proofs as well as slicing proofs, Archimedes allowed the intellectually fettered to stay within their comfort zone.
The newborn calculus was presented to the mathematical establishment to receive its judgment. They looked it over and applied the standards for what used to be mathematics, thereby hindering the growth of the new mathematics. They examined the baby calculus and in essence declared, “It can’t hold a job, drive a car, or even use a toilet!” But people like Archimedes, Newton, and Leibniz would look at the child and could see it for what it could become. They had the imagination to see its potential worth and not be chained by the existing standards and procedures of the so-called intellectual world. The old rules simply didn’t apply, and those predisposed to following rules just couldn’t understand. Even in the Age of Reason, two thousand years later, the ideas of calculus had many detractors. Fortunately Newton and Leibnitz were able to win the debate that Archimedes had lost.
Because Archimedes was able to relate the area of a circle to the area of a triangle whose base was the circumference of the circle, he was able to connect the constant of π used in the circumference equation with constants used to compute area. Unfortunately for the author of Ahmose’s papyrus, this understanding was well over one thousand years into his future.
As we’ve seen, some in the ancient world knew that if they multiplied the diameter of a circle by 3 k, they would obtain a number close in length to the circumference of a circle. Moderns would interpret this as the equation Circ. = π × Diam. We would also obtain the area of a circle by computing π × Radius2. Note the Radius2 in the equation. It has been long known that areas are related to the squares of numbers. For the actual shape of a square, a simple square is taken. For other shapes, the square needs to be multiplied by some constant, like ½ in the formula for the area of a triangle or π in the formula for the area of a circle. In theory, it doesn’t matter if you multiply before or after you square the number; however, which you choose will change the value of the constant.
Consider the following example. Imagine the zigzag shape pictured below where the two long sides are twice as long as the short sides. You could find the area of this figure by multiplying the short side by 2 and then squaring it. So if the short edges were 5 inches long, we can find the area by doubling it to get 10 and then squaring it to get 100.

The zigzag with the top and bottom lengths exactly twice as long as the other six.
However, we could just as easily have squared 5 first to get 25 and then multiplied this result by the new constant, 4, to get 100. Notice when we multiplied before squaring the constant was 2 and when we multiplied after, it was 4. Both methods will always give the same answer. When computing the area of a circle, we’re confronted with the same choice.
We moderns use the equation πr2. In other words, we square the r first and then multiply by the constant π. The Egyptians chose the other route, multiplying first and then squaring. As a result, their constant is not as recognizably similar to our π as is their 3 k. They choose the constant 8/9, used this to multiply the diameter, and then squared the result. You can obtain an approximation for our π by taking 8/9, doubling it, and then squaring it to get 3 l sj ka. It’s easy to see how anyone without Archimedes’ insight would miss the relation between the approximations 8/9 and 3 k. Would anyone even realize that 8/9 is actually an approximation for half of the square root of π? Archimedes’ discovery that these numbers are in fact related is far from obvious.
There have been many attempts to determine where the approximation of 8/9 came from. I suspect it came from empirical measurements. In other words, they got the value from practical experience. For example, some scribe may have kept a record of how many tiles it took to cover some circular floor. After a minute or two of computation, it would become apparent that it was about the same number of tiles required to cover a square floor of with a side of eight-ninths of the diameter. It turns out that other fractions close to the actual value have denominators that are difficult to work with in Egyptian math or are excessively large. So even though this is just an estimate, it’s not surprising that they settled on this value.
The Egyptians inadvertently made a huge mistake by choosing to multiply before squaring. The computations are just extremely complex and lengthy. The reason for this lies in the fraction 8/9 itself. Recall that in chapter 2 we added to the standard list of fractions because we needed reasonable approximations to numbers between s and 1. So we added one tick mark to our ruler in this region. For small fractions, the ruler is dense with tick marks. It’s easy to approximate fractions in this range. However, near 1 the gaps are relatively huge, even with the addition of '. The closer you are to 1, the worse the problem is. Unfortunately 8/9 is very close to 1. From personal experience, I can tell you that Egyptian math just becomes more difficult in this region.
This section, “Finding the Area of a Circle,” is somehow out of place. I’m not going to teach you a new technique, but rather give you problems to solve that incorporate many of the ideas from this chapter in a few good problems. (By the way, you should always run in fear when a mathematician refers to an exercise as “a good one.”) These problems will give you practice and in the name of fairness to modern math show you that Egyptian math doesn’t always work out easily.
On its surface, the Egyptian method for finding the area of a circle is trivial. You first remove a ninth of the diameter using completion and then square the result. Let’s start with a problem that won’t give us any trouble. There are trickier, faster ways to solve it, but I want to do it in a way that won’t change significantly when we pick harder numbers. Just so the method is clear, here are the steps the Egyptians used to estimate the area of a circle:
• Multiply l by the diameter.
• Subtract the answer from the diameter.
• Square the new answer.
EXAMPLE: Use the steps above to estimate the area of a circle with a diameter of 18.
SOLUTION: First calculate l of 18 to remove l from the diameter.

Now remove the ninth; in other words, subtract 2 from 18. The Egyptians would do this by completing 2 to 18.
The answer is 16.
All that’s left to do is to square this value, basically turning it into an area. So we need to square 16.
256 is the area of the circle.
That wasn’t so bad, but that’s just because we started with a number whose l was trivial. It should come as no surprise that this is the very example in Ahmose’s papyrus that first shows how to find the area of a circle. He used simple numbers to keep the focus on the method and not on the computation. We can test this approximation by using the modern equation πr2. Since the diameter is 18, the radius is 9 and π × 92 is roughly 254.47, which is a little over a half of 1 percent away from the Egyptian’s value of 256.

PRACTICE: Use the steps above to estimate the area of a circle of diameter 27.
ANSWER: 576
Now let’s try one whose solution is far from trivial.
EXAMPLE: Use the steps above to estimate the area of a circle of diameter 10.
SOLUTION: First calculate l of 10.

Complete 1 l to get 10.
When we complete l to get 1 we get
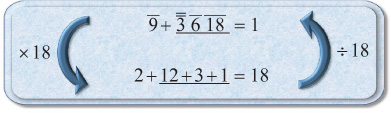
Square 8 ' h ak.

We now have the unenviable job of adding 71 l, 5 ' h ak sj, 1 d as ak a;k, and d l dh gf dsf. The whole numbers add to 77. The fractional parts can be added as follows:

So the total is 77 and 2 ka, or 79 ka. I have to admit that the above computation was painful, but it still amazes me how much it simplifies. Nothing we did above was difficult; the number of fractions involved just made the computation particularly tedious.
If the Egyptians had squared and then multiplied by the constant, things would have been much easier. They could have used s f ds as their multiplier, which is essentially equivalent to using the Babylonian value of π, 3 k. Now the problem would have gone like this.
EXAMPLE: Find the area of a circle of diameter 10 squaring first.
SOLUTION: Square the 10.
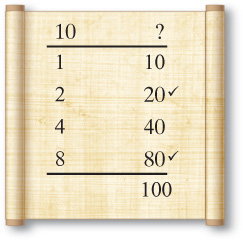
Now multiply by the constant s f ds.
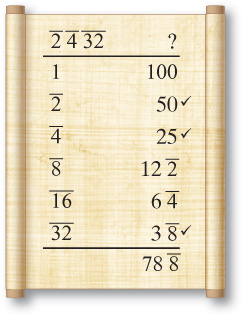
We obtained almost the same answer in a tiny fraction of the time. We could get a closer answer by tweaking our constant a little higher. Say, perhaps s f d;, which would actually take fewer steps to calculate.
PRACTICE: Find the area of a circle of radius 12. Then redo using the square-first method.
ANSWERS: 113 ' l and 112 s
PRACTICE: Find the area of a circle of radius 7. Then redo using the square-first method.
ANSWERS: 38 ' sj ka and 38 f ds
In some chapters, the historical context of this book writes itself. However, in this chapter I’ve been frequently confronted with the difficulty of finding some historical connection with a subtle math technique. In this section, please forgive me because I’ve decided to tell you about something that I personally find amusing but that has no link to the mathematics that follows.
In popular culture, the portrayal of college life rarely centers on the classroom. Comedic movies and television shows focus on parties, drug use, and sex. How exaggerated these depictions are probably varies from school to school and student to student; however, the stereotype dominates our imagination. You might be surprised to find out that this outlook is thousands of years old.
Young Egyptian scribes learned by copying texts. In some sense it doesn’t matter what they wrote as long as they learned the many symbols of hieroglyphs and hieratic. The teachers in the House of Wisdom often used these copying exercises to teach other things in the content of the texts. Sometimes the content was the format of a document like an official letter. Other times the content was a moralizing speech. Here’s an example of a faux letter from a teacher to a less-than-serious student.
I hear … that you are neglecting your writing and spending all your time dancing, going from tavern to tavern, always reeking of beer. […] If only you realized that wine is a thing of the devil. … You sit in the house with girls around you. […] You sit in front of the wench, sprinkled with perfume. … You reel and fall on your belly and are filthied with dirt.
As we’ve seen, multiplications and divisions can often be performed in multiple ways. Sometimes one way is far more efficient than the other. Consider the following two calculations for the division of 12 by 36. The first scribe mindlessly took half repeatedly and switched when he had gone too far. The second scribe noticed the 12 and realized she could get this using the division-by-3 trick of taking half and then taking '. By noticing a relationship between 12 and 36, she was able to shorten the computation. In some sense she was lucky that 12 was exactly one of the numbers easily reached from 36.
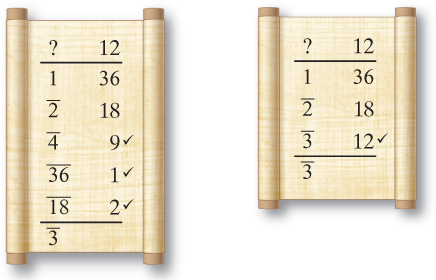
36 ÷ 12 done by a careless (left) and a careful (right) scribe.
Now consider the following two divisions of 13 by 36. The two numbers in the quotient are no longer precisely related. While we can’t easily get 13 from 36, it often helps just to get close, and 12 is close to 13. The first division is mindless and long. The second proceeds as above, getting 12. We’re now 1 away from 13, which can easily be obtained with a switch. While we didn’t get 13 immediately, the smaller gap is relatively easy to make up. Also notice that the approximation d dh is better than f l. This is because “getting close” really means being more accurate.
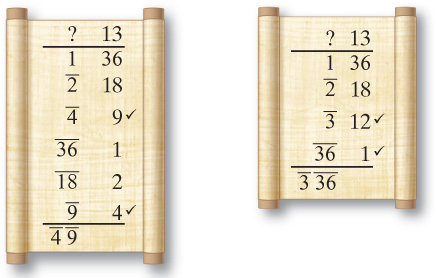
Since 12 is closer to 13 than 9, the second method is more efficient and gets a better answer.
PRACTICE: Divide 15 by 42 in four lines.
ANSWER: ' fs
In general, if you are close enough to the target value that taking ' will put you below it, use ' instead of s. You don’t always have to obey this rule, particularly when your number is not a multiple of 3 because taking the ' introduces fractions into the problem. Egyptians were not that worried about such fractions, but it can add a level of difficulty. It’s your choice.
If you do decide to perform this operation on a whole number, the only fractions you’ll get are d and '. Here are two divisions of 7 by 10, one avoiding and one using the trick. Below, we will get 6 ' when we’re trying to get 7. Realize that we need d more and hence we must construct this answer.

The trick on a non-multiple of 3.
Notice that the time it takes to get the d we need to reach 7 takes more steps than if we didn’t, particularly since we were able to construct the 2 on the left using a switch. However, the answer on the right is better than the one on the left because it is a better approximation. We probably would be expected to simplify the solution on the left using parts, eliminating any time saved.
Try this one. Note that you will need the right column to add to 16, but you will get 14 '. This means you will need 1 and d more, which can be constructed separately. Do this problem both ways. After simplifying you should get the same answer.
PRACTICE: Divide 16 by 22.
ANSWER: ' ss hh
If you end up with a d in your answer, you will need to construct a ' in order to obtain the answer.
EXAMPLE: Divide 18 by 52.

The trick on a non-multiple of 3.
As we can see again, the trick may not save time, but it generally gives better answers. Now that we’re no longer terrified by fractions, we can take ' instead of half if it gets us closer to the desired value. Compare these two divisions. The first is the standard procedure, and the second takes advantage of the fact that 5 s is close to 6. Of course we need s more to make 6.
EXAMPLE: Divide 6 by 22.
SOLUTIONS:
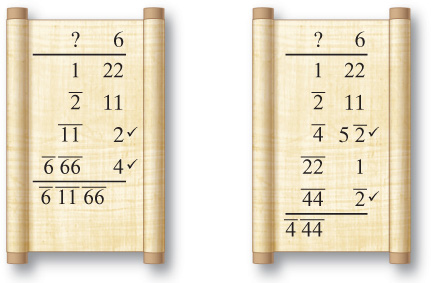
Getting closer with an extra division by 2.
ANSWER: s fs
The last trick of this section is, in a sense, almost the exact opposite of the ' trick. Above we multiplied by ' instead of s because we didn’t want the number to shrink that much. That’s because we were close to the target number. However, if you’re far from the target, you want to shrink quickly. In order to do this, division by 10 helps. For now we’ll apply this only on multiples of 10, although we do have the division-by-10 table in Ahmose’s papyrus. Try to do the following problem using only doubling and halving and see how difficult it becomes.
EXAMPLE: Divide 86 by 7400.

PRACTICE: Divide 31 by 2000.
ANSWER: a;; s;; s;;;
All that’s left to do is mix and match. In the next example we first divide by 10 because we want to get small quickly, and then we take the ' because it gets us closer.
EXAMPLE: Divide 660 by 45.
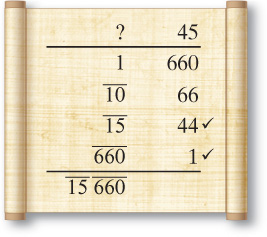
See if you can do this next problem in four lines using both the ' and the 10 tricks.
PRACTICE: Divide 66 by 840.
ANSWER: ag kf
Time was of the essence for Alexander the Great. He had defeated the army of the great Persian Empire well over a year prior and the Persians were beginning to rebuild. The sieges of Tyre and Gaza had taken longer than expected. Fortunately, on his arrival in Egypt, he was welcomed as a liberator. Despite the need to return to Mesopotamia in order to meet the Persian forces once again, he ordered his armies to wait while he took a pilgrimage to the Temple of Amun in the oasis of Siwa. He told his men that there was something he needed to know about himself.
Perhaps he felt motivated by destiny. His mother’s and father’s sides claimed to be descended from Perseus and Hercules, respectively. Both of these fabled Greek heroes had sought divine guidance from the priests of Amun during their quests. Alexander’s mother had instilled in him the notion that his true father was in fact Zeus, whom the Greeks identified with Amun. So it’s no surprise that Alexander imitated the actions of his mythological ancestors.
As Alexander arrived at the temple, a priest greeted him as the son of Amun and took him into the holiest sanctum of the temple. In order for the priest to consult the god, a number of Egyptian men came in carrying a boat that was suspended on poles and within which was the god symbol of Amon. The men moved about, supposedly being directed by the god as the seer watched. He then interpreted their motions as omens, forming an oracle given only to Alexander. After leaving, Alexander simply declared that he had received the answer his soul desired.
In Egypt, divination doesn’t seem to have had as strong an influence as it had in Mesopotamia or Greece. However, there were notable exceptions, such as the seers in the above story. For example, the priests of Imhotep were skilled in the interpretation of dreams. If Egyptians could truly foretell the future, I’m not sure they would have liked what they would have seen. They would be dominated by Greek rulers for about three hundred years. After that, less tolerant Roman leaders would hold the reins of power for over four hundred more. The Roman period would end shortly after the rise of Christianity, which finished the distinct Egyptian culture for good.
Yet I’m not sure they would have been surprised. The Egyptian culture had been in a state of decline since the rule of Ramses. They had suffered two periods of Persian domination, ended only by the arrival of Alexander. The Egyptians had grown so weak that their army consisted of Greek mercenaries whose pay drained the country’s resources. The seat of power in Egypt continually moved south in an effort to stay a safe distance from the aggressive Mediterranean cultures. Eventually the pharaohs were Nubian kings who ruled lands that were originally south of Egypt’s borders.
The lack of foresight in political matters stands in direct contrast to the foresight required in mathematical computation. As we’ve seen, Egyptian mathematics was not algorithmic. The practitioners had to use finesse rather than rote computation. Here I will show you that to perform Egyptian math effectively, you not only need to know where you are, but also where you are going. Being aware of what lies ahead is as important as any step in the calculation.
When Ahmose checked his value for 2 × aj, he paused in the middle and gave a “remainder.” Here’s how the division started.

In order to understand what’s being done, we need to notice what’s missing. Ahmose wanted the right column to add to 2. He got as far as 1 f h and needed to know how much further he had to go. So he performed a completion to see what was left. Of course, completing 1 f h to 2 is the same as completing f h to 1.

The remainder d f is the amount needed to get to two. Ahmose quickly constructed 3 and 4 on the left-hand side of the tablet in steps 7 and 9. He then switched them in steps 8 and 10 to get the required d f on the right. The full division looks something like this.

You can tell by looking at Egyptian multiplication that they always had a sense of what they needed to finish the problem. Their goal was to get one of the columns to add up to a given value. The numbers they created in that column varied depending upon what they required. They seemed to know how much more they needed in that column and then figured out how to generate that amount. Sometimes it’s easy. If, for example, you need 10 and have 8, you want 2 more. But when fractions are involved, especially Egyptian fractions, it’s not always clear what’s needed. So if you need 10 s l and have 8 d aa, you’re more or less forced to do a completion.
Let’s say we are dividing 8 ' by 34. We’d probably start as follows:
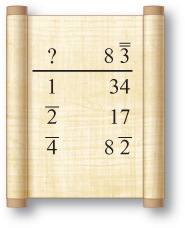
At this point we should realize that we’re close. We need 8 ' and we’ve got 8 s. So to finish the division, we need to determine how much more we require; therefore, we complete s to '.

We now know that we need h in the right column, so we finish the division by switching the first row and forming a h from the 1. Remember that the Egyptians didn’t know how to divide by 6, so they would divide by 2 and then by 3. The division by 3 consists of first taking half and then taking '.

EXAMPLE: Divide 10 by 13 using completions.
We start off the same way as before.

Now we’re at 9 s f, which is very close to 10. So we need to complete 9 s f to 10, which is the same as s f to 1.

This means we need f more, which is very easy to construct.
SOLUTION:

In the following practice problem, repeatedly divide by 2 until you get the line f, 2 s f, then perform a completion.
PRACTICE: Divide 14 by 11 using completions.
ANSWER: 1 f ff
I was sloppy in the last example when I divided 10 by 13. I took half of 13 to get 6 s, which is well under 10. I could have taken ' of the value to get 8 ', which is still under 10. We would now need 1 d to finish this division, both values are easy to make. Let’s try another problem being more careful.
EXAMPLE: Divide 7 s a; by 11 using completions.
The number 7 s a; is close to 11, so taking half is probably too much. So we’ll start off by taking ' of 11.

We can tell we’re close, so we need to perform a completion.
I’ll now create the missing g and ag by switching the 11, dividing it by 10, then both doubling and taking ' of this value.
SOLUTION:

In the next practice problem, perform the completion after you obtain the line d, 7 '.
PRACTICE: Divide 8 h by 23 using completions.
ANSWER: d fh
Let’s do a less trivial example.
EXAMPLE: Divide 35 g a; by 80 using completions.
In this problem we start off by taking half of 80 to get 40.
Our answer 40 is close to 35, our target. If we take half of 40 to get 20, we way undershoot 35. So it seems to be a good idea to take ' instead of half. This gives us 26 '.

Now 26 ' is a little more than 8 away from 35 g a;. This is fortunate since 8 is very easy to get from 80.

The two checked values total 34 '. At this point we should realize that we are very close to the answer. However, it is very difficult to know exactly how far 34 ' is from 35 g a;. Hence it’s time for a completion.
So, all we’re missing is s a; d;. Luckily these are all easy numbers to obtain from 1 since the only factors in them are 2, 3, and 5. So we finish by creating the missing fractions.
SOLUTION:

The scribe Amennakhte didn’t do his job; he couldn’t. The tomb workers of the Valley of the Kings had waited eighteen days after payday for their monthly wages, but Amennakhte had nothing to give them. The workers, hungry and disgusted, went to the back rooms of Thutmose III’s temple and just sat down, beginning the first strike known in recorded history. The shouts and threats of Amennakhte had no effect—the workers just stayed where they were. The next day the scribe Pentaweret brought fifty-five loaves of bread, but apparently it was too little, too late. The workers complained of hunger and thirst. They had run out of fish and vegetables and needed new clothes.
In response, they were paid some but not all of their back wages. The chief of police sided with the workers and had promised to talk with the mayor of Thebes. Five days into the strike, the workers were each given half a sack of barley, used to brew beer, and the police managed to scrounge up a few rations, but the partial pay was not enough to sway the strikers. On the seventh day of the strike, they were finally paid that month’s wages.
The next month came with no pay, and the strike started once again. One worker declared that if he were taken away, he’d begin to make plans to rob the tombs they had built. A letter arrived from the vizier himself. He explained that he had recently been appointed and that his predecessor was supposed to have paid them. When the new vizier went to the granaries supposedly containing the grain owed the workers, he had found them empty. It seems his corrupt predecessor had taken the grain on his way out. The best the new vizier could do was give the workers half of their due.
On the advice of the foreman, the crew took the half rations and immediately left work anyway. The scribe Amennakhte apparently had had enough. He stopped the crew at a guard post and began to threaten them. Now that they had been paid, he declared that there wasn’t a court in the land that would not convict them. The workers changed their minds and went back to work. They were later paid directly by the mayor of Thebes. The ancient account of this story ends with the workers muttering in anger, claiming that they will exact revenge on those who have wronged them. Apparently they had some knowledge of the wrongdoings of their superiors and would soon make them public, including charges of tomb robbing, cattle theft, and adultery.
All of these events took place two years before the end of the reign of Ramses III, the last great pharaoh of Egypt. Earlier in his reign he had fought off the Peoples of the Sea, seafaring warrior nomads who had brought great disruption to the entire Mediterranean. He also had fended off a Libyan invasion. But Egyptian control outside its borders was gone. Seafaring technology had rendered their isolation moot. Gradually the great Egyptians would become subordinate to their more powerful neighbors. If this story is any indication, the corruption and disorder that weakened a once-mighty empire was already ongoing.
Let’s examine through a simple example how wages were computed in ancient Egypt. Imagine two friends and I start a business and make 16 f bags of gold. Since I’m the only one in the group who knows math, I’m put in charge of dividing it up. Not trusting me, they demand a full share. When I agree, they smile approvingly. I then inform them that due to my accounting duties, I deserve a full 1 f share. In order to divide up the money, I first have to calculate the total number of shares. This is easy since the sum of 1, 1, and 1 f is clearly 3 f. Now I need to find the value of a 1 share. This is done by dividing up the 16 f bags of gold between the 3 f shares.
This means a 1 share, my friends’ “fair” portion, is worth 5 bags of gold. My 1 f share can be computed by multiplying 1 f by the value of a 1 share.
So my friends each get 5 bags and I get 6 f bags. The next time, we get 5 s as bags of gold to split up. I begin my calculations just as before. There are still 3 f shares, so we divide 5 s as by this to find the number of bags per share.
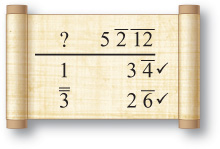
At this point in the computation I know I’m close. I’ve got 5 f h and need 5 s as. So I do a completion, but I don’t finish it because I know a trick.
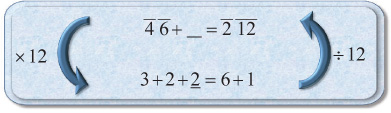
In the above completion I never return the 2 parts of 12 back into a h. For one thing it wouldn’t help me much. How could I make a h out of a 3 f? By the operations known to Egyptians, there is no easy way. There are nice numbers in the first column, but I can’t switch sums because of the entries in the right column. There is no nice way to switch 3 f to the other side. You can switch only single whole numbers or fractions, not mixed numbers. There are tricks that could make a whole number out of 3 f, like multiplying by 4 first and then switching, but this doesn’t work well in all such problems.
What you need to realize is that I already have all I need to know. I need 2 parts of 12. As long as I work in parts of 12, this is easy. The first line has a 3 f in the second column. In parts of 12, the 3 becomes 3 × 12, or 36, and the f becomes 3, for a total of 39. What’s important about the 39 is that it is a whole number that can be switched. So we rewrite the first line expressing the second column in parts of 12 and resume the computation knowing we need 2 more.
If you still don’t see why this works, think in terms of feet and inches. Let’s reinterpret the previous problem as fence building. I want to build 5 s as feet of fence. I know that 3 f feet costs a piece of gold. I use this to determine that 2 h feet costs ' a piece of gold. So by spending 1 ', I can build 5 f h feet of fence. What I’ve just described is essentially the first two lines of the above division.
Now I have 5 f h feet of fence and need 5 s as feet. The obvious question is, how much more do I need? Specifically, I need to know how much larger s as feet is than f h feet. To simplify the problem by eliminating fractions, I decide to convert into inches. I know s as feet is 6 and 1 inches and f h feet is 3 and 2 inches. So I have 5 inches and need 7. Therefore I need 2 inches more. In the above math, I’ve intuitively done the completion. In the original problem I determined I needed 2 more parts of 12. In this problem I need 2 more inches out of the 12 in a foot. Notice that the numbers are identical.
The remaining question is how much will those 2 inches cost? I know that 1 bag of gold buys 3 f feet, but this is just 36 and 3 inches, for a total of 39 inches. So if 1 bag buys 39 inches, then dl of a bag buys 1 inch. I double this to get sh jk to get the cost of the remaining 2 inches. Finally I add this to the cost of the fence I’ve already bought for a total of 1 ' sh jk bags of gold. This finishes the problem.
Below is the multiplication. Note that we determined after the first two lines that we were short 2 parts of 12. The line that follows simply converts the 3 f into parts of 12, which is 39. The computation continues until the 2 parts are calculated.

As we’ve seen, computations by parts can be thought of as unit conversions. The first part of the division is done in feet, and the completion tells us how much more we need in inches. So we finish the computation in inches. While we can’t add some of the numbers in the second column because some are in feet and some in inches, the first column always remains in “bags of gold,” and hence all the entries are summable. The best part of this method is that completions, like any parts calculation, eliminate fractions and make the problems easier. It also uses the same completion that is needed to finish the problem anyway, so it requires almost no extra work. Here’s one more example and a practice problem.
EXAMPLE: Divide 10 d by 1 k.
SOLUTION: First we divide as usual until we get close to 10 d.

The total is 10 k, which is close to 10 d, so we calculate how many parts we’re short.

From the above computation we can see that we’re short 5 parts of 24. We can now continue our above computation. We start from the first line, 1, 1 k, but convert the right-hand side into parts of 24, giving 1, 27 since 1 k × 24 is 27. We now need to make the 5 missing parts in the right column.
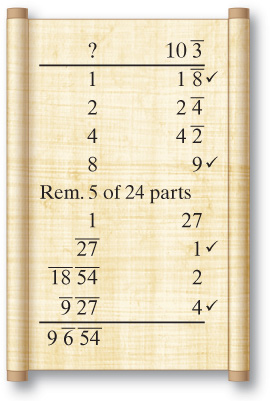
PRACTICE: Finish the following multiplication by forming a completion and finishing in parts. Divide 8 g by 2 d.
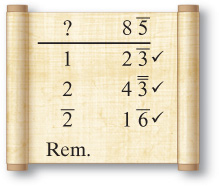
ANSWER: 3 s j;
In theory, this method can be used to make short work of any division. For those of you who know algebra, this is essentially equivalent to multiplying through by the denominator of an equation to eliminate the fractions. In practice, this is not the case.
Consider the division of 6 j by 6 sa. In the very first line of the division we get close to the answer.

So far everything seems fine. All we need to do is complete j to sa.

So we need 2 parts of 21. When we convert 6 sa into parts of 21 we get 127. It looks easy until we try to double asj.

The problem is we can’t double asj because it’s not on our table. This method often produces huge numbers, creating fractions that are too big. How did the Egyptians deal with this problem? I have no idea. If we simply doubled ask instead, we’d be off by less than one part in eight thousand. While this is not a big error, one of the attractions of the Egyptian method is that it provides exact answers. Using the sliced bread method, it’s easy to see that 2 × asj is hf kask. The difficulty with this is that the fraction size is so large, it exacerbates the problem.
Unfortunately, just as we were examining the last method of Egyptian mathematics, we see a nearly fatal flaw. To be fair, a mixed number divided by a mixed number is problematic in any system. Even so, it’s still sad that we seem to have reached the limits of Egyptian computation.