10 LOOKING UNDER THE HOOD OF DEEP NEURAL NETWORKS
COMPUTER-GENERATED IMAGES
On June 10, 2015, a strange and mysterious image showed up on the internet, posted anonymously on the website Imgur.com. At first glance, the picture looked like one or two squirrels relaxing on a ledge. But the resemblance ended there: as you looked more closely, you could make out bizarre detail—and objects—at every scale. The image on the internet was psychedelic, like a fractal, with a dog’s snout on the squirrel’s face, a mystical pagoda here, a human torso there, and a bird-giraffe creature over there, seamlessly embedded into the fine detail of the image. Uncanny eyes peered out from every nook and cranny. Looking at this image felt like looking for objects in clouds, except that it wasn’t your imagination. Or was it? You had to look again to see.
It was clear that the image hadn’t been created by a human. It was too bizarre to be a photograph, and its detail was too fine to be an illustration. The anonymous user who had posted the picture on Imgur.com described it only with this note:
This image was generated by a computer on its own (from a friend working on AI).1
As the image began to spread and the denizens of the internet tried to make sense of it, engineers over at Google were generating more images just like this and sharing them with one another. A week later, they published a blog post explaining the phenomenon. The image had indeed been generated by AI—specifically an artificial neural network. The phenomenon became known as Deep Dream. With the arrival of these images, people began asking some uncomfortable questions that had been lurking beneath the surface. Are these really android dreams? Do we even understand what’s going on in these networks? Have researchers gone too far in their efforts to recreate human thinking?
These concerns about intelligent machines had been further stirred up because the likes of modern industrialist Elon Musk were voicing their own worries. Musk, who had reportedly invested in DeepMind to keep an eye on the progress of AI, worried that his good friend Larry Page—one of Google’s founders—might “produce something evil by accident,” including, rather specifically, “a fleet of artificial intelligence–enhanced robots capable of destroying mankind.”2
When these images came out, we already knew that neural networks could be useful in playing Atari games and in understanding the content of images. The images did stir up some uncomfortable questions, but as we’ll see, the reasons neural networks can be good at playing Atari games and the reasons they’re able to produce psychedelic dreamscapes are actually closely related. And even though these dreamscapes seemed at first to make deep neural networks more mysterious, it turns out that they can also make them less mysterious.
SQUASHING FUNCTIONS
In the history of neural networks, there was a period during which researchers eschewed deep architectures. They had the universal approximation theorem, which suggested that maybe they didn’t need to go so deep, and they also knew in practice that deep networks were difficult to train. But these networks were difficult to train because researchers hadn’t yet discovered the best way for neurons in their networks to light up.
Remember that in a neural network, each neuron is a simple classifier. The neuron takes a weighted sum of its inputs and squashes this weighted-sum in some way to produce an output, as we saw in figure 8.2. This squashing function might seem like a footnote, but it turns out to be extremely important in enabling us to train deep networks. For a long time, researchers’ favorite squashing function in neural networks followed the S-shaped curve I show in figure 10.1a.3 This S-shaped curve takes the weighted sum of the neurons’ brightness in the previous layer and squashes it into the range 0 to 1. If the weighted sum of the neuron’s inputs is very small, the output of the neuron will be close to 0. If it is very large, the output of the neuron will be very close to 1.
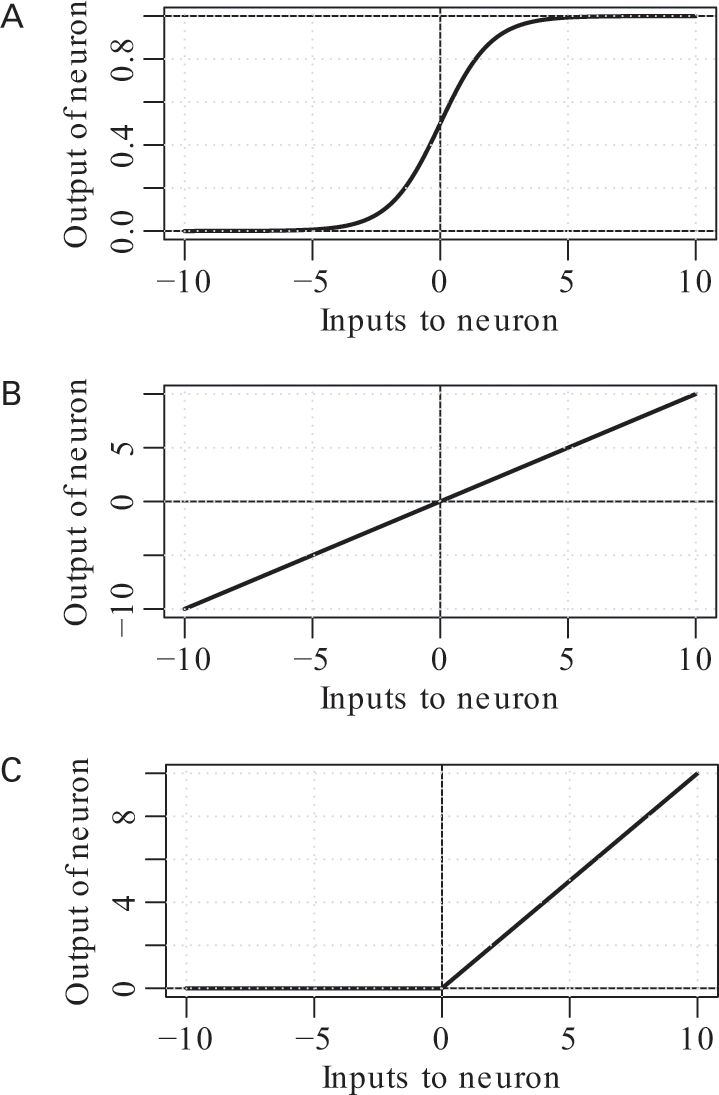
Activation functions for neural networks. The S-curve (a) (formally known as a sigmoid) was used for a long time, but ReLU activation functions (c) have become popular because they make training deep neural networks easier.
The benefit of using this S-curve is that neurons’ output values are all “well-behaved”: no neuron will output a ridiculously high or low value, and there is a smooth relationship between the inputs and the outputs. These are good properties to have when you’re training or using the network, because otherwise the edge weights could blow up to infinity when you’re using the network. Having a smooth function means that you always know how much you should adjust the network weights if you adjust the network’s input or output just a little bit. Researchers also liked to point out that this function was biologically inspired—but remember, using something because it’s biologically inspired can sometimes be “fraught with danger.”
The problem with using the S-shaped curve is that it tends to “dilute” messages passed through the network. If the weighted-sum input to the neuron is high, the neuron doesn’t care whether the input is large or really large: it outputs the number 1 either way. It’s the same at the other extreme: whether the input to the neuron is somewhat negative or really negative, the neuron outputs 0 regardless. This may not be a problem when we “run” the network, but it can become a problem when we’re trying to train it. The message we send backward through the network to adjust the weights will become diluted as it passes through the network. One of the benefits we originally thought we had—that we know how much to adjust the weights when we’re training the network—isn’t much of a benefit, because the training algorithm may think it doesn’t need to adjust the weights at all, when they should in fact be changed a lot. This problem is sometimes known as a “vanishing gradient.” The gradient is the direction that weights in a neural network must move for it to learn from a sample of training data. If the gradient vanishes—that is, if it appears to be zero when the network training is not complete—then this means the network can’t learn from its training examples: it will ignore the training example, even if the example is useful. Because of this problem, researchers continued to poke around at other activation functions.4
At the opposite extreme, what if we don’t squash the output of the neurons at all, and instead pass the weighted sum computed by each neuron directly through as the output of that neuron, using the activation function in figure 10.1b? This doesn’t have the problem we had with the vanishing gradient, and in fact it will be really easy to update the network weights if we use this squashing function. But this poses a different problem: if we use this squashing function for all of the neurons in our network, then the entire network will collapse mathematically into the equivalent of a single-layer network. Any benefits we thought we’d gained from having a deep network simply vanish. Assuming that we want the benefits of a multilayer network—and we do—this won’t work either.
RELU ACTIVATION FUNCTIONS
Since about 2010, we’ve been seeing much better results with an activation function that’s somewhere in-between these two extremes: the one shown in figure 10.1c. This activation function—used by AlexNet in 2012 and a variety of other networks since then—is called the rectified linear unit, or “ReLU” for short.5 The ReLU is zero if the sum of the neuron’s inputs is less than zero, and it’s equal to the sum of the inputs if that sum is greater than zero. For a while researchers were worried that this would have the same problem as the S-shaped curve—namely, that the network would dilute a message passed through many layers. But this doesn’t seem to happen in practice.6
Instead, the ReLU activation function appears to have some rather nice properties. For any fixed input, some subset of the network’s neurons will be dark, while others will be lit up. If you vary the input a little bit in any direction, the set of neurons set to on or off typically won’t change. The brightness of the on neurons will change as you vary the input a small amount, but the on ones will stay on, and the off ones will stay off. But more importantly, the network will behave in the small vicinity of this input exactly like a single-layer network—that is, like a bunch of weighted-average classifiers.
As you continue to vary the input to the network, moving it further from the initial input, the set of on neurons will begin to change. The output will still vary smoothly as you change the input smoothly—that is, it will never make a sudden jump in value as long as you don’t make a sudden change in the input.7 The relationship between the inputs and outputs, however, will change. You can think of the overall network as a patchwork of single-layer networks, stitched together to agree with the training data. Which single-layer network handles the input depends on which neurons are turned on or off by the input. In fact, it’s possible for there to be an exponentially large number of single-layer networks encoded within the overall network.8
When I say there are an “exponentially large” number of networks, I don’t mean this casually or carelessly. I mean “exponential” in the mathematical sense. The number of possible single-layer networks hidden within the overall network is described by all of the possible ways the neurons in the network can be switched on or off. For a ReLU network with just 60 neurons, the number of ways to assign its neurons to on/off—and, hence, the number of single-layer networks we could hide within it—is about the number of grains of sand on all the beaches and in all the deserts of the world.9 A network with 270 neurons has the potential to represent as many combinations as there are atoms in the known universe.10 And remember: modern neural networks can easily have millions of neurons. If the network only needs to use a simple function to represent its input, it can do so; and if it needs to use a more complicated function—as with a patchwork of single-layer networks—it can do that instead.11
Why doesn’t the ReLU have the same problem the S-curve had, given that large parts of the ReLU are also flat? Let’s say you have a training example you want the network to learn. Although many of the neurons will be turned off for a typical input, as long as there is at least some path of lit-up neurons from the input of the network to its output, then the network can adjust the weights along that path to learn the training example. The weights along that path will take the credit or the blame for the training example, as information from the example propagates through those lit-up neurons.12 Later, when the network sees an input that’s similar to examples it saw during training, it will “remember” those training examples by lighting up some or all of the same neurons that were lit up when it saw a similar example during training.
This benefit of ReLUs is similar to another popular trick for training deep neural networks in which neurons are temporarily “suppressed” during training. Any time a training example is used to train the network, a random subset—say, 50 percent—of the neurons are temporarily suppressed, by setting their outputs temporarily to zero.13 The remaining neurons’ weights are then updated using the training example, as if the suppressed neurons never existed. As with the ReLUs, there are an exponentially large number of ways these neurons might be suppressed—and, hence, a virtually infinite number of networks to train.
When the resulting network is used for prediction, the output of each neuron is scaled down, so that the input to each neuron becomes the average of many independently trained models. The overall network effectively becomes a giant blend of a huge number of networks that were trained, reminiscent of the model-averaging techniques that were successful in the Netflix Prize.14
This combination of tricks for training deep neural networks—that is, ReLU activation functions and the random suppression of neurons during training, along with having lots of data, using depth instead of width, and using convolutional layers—were some of the main factors in creating networks that could classify images as well as, or better than, humans.
Although it was technically true that neural networks have done better than humans at identifying objects in images, this fact requires a large asterisk. At least one network did indeed exceed humans’ ability to recognize very fine-grained categories, but the network had an advantage in that it was trained on narrow, specific categories of objects, such as the 120 dog breeds from the training data. In many cases, the network could correctly identify narrow types of objects, such as “coucal,” “Komondor,” and “yellow lady’s slipper,” when a typical human would have only recognized these items based on their broad categories: “cuckoo,” “sheepdog,” and “orchid,” or possibly just “bird,” “dog,” and “flower.” The humans compared with the computer had the chance to study these categories, and the researchers behind the ImageNet Challenge found that humans did better the more they studied, but the fact remains: humans are imperfect.15
And neural networks have their own weaknesses. The same algorithms that beat humans can still make mistakes identifying objects in images that humans would have had no trouble recognizing.16 It’s even possible to create optical illusions for neural networks that can “trick” them into being extremely confident that they are seeing objects that aren’t really there, when to a human the illusion looks like abstract art. In one case, a white background with five columns of red stitch-marks could trick a neural network into thinking it was looking at a baseball; in another, a rippling pattern of black, gray, and orange convinced a neural network that it was looking at a king penguin; and in yet another, a grid of carefully positioned rectangles convinced a neural network that it was looking at a remote control. It’s also possible to construct illusions that look to humans like one object, while they look to neural networks like entirely different objects.17 This happens because of the unique way a neural network interprets the picture.
ANDROID DREAMS
Suppose that we take a photo of your pet dog and pass that photo through a convolutional neural network like the ones we trained in the last chapter. As long as you know the network weights, the layers of the network will activate predictably, layer by layer. In each layer, some neurons will remain dark while others will light up as they respond to different patterns in the image. Since we passed a photo of your pet dog into the network, then when we look deep enough in the network—say, at the fourth or fifth level—the neurons will represent object parts that we’ll likely recognize. Those neurons that respond to things like fur and parts of a dog’s face will be glowing brightly. If we look at the final layer, the dog neuron(s) will be lit up, while most of the remaining neurons will be dark.
Now here’s where it gets interesting. When we first trained the network in the last chapter, I glossed over some details about how we adjusted the weights of the network for each training example. Remember that the algorithm to train the network adjusted its weights based on how “incorrect” the dog neuron at the end of the network was. It used a mathematical function that measured how close the output of the network was to the training example’s label. That label was just a 1 or a 0 describing whether the image did or didn’t have a dog. The algorithm to train the network then calculated, using high school calculus, in which direction it should adjust the network’s weights so the network could predict the output values just a bit more accurately the next time around.
What if, instead of adjusting the network’s weights to agree more with the image, we instead adjusted the image to agree more with the network? In other words, once we’ve already trained the network, what would happen if we keep the network’s weights fixed to what they are, and adjust the input image—say, a photograph of a cloud—so that the dog neuron is more bright while the other neurons remain dark?
If we adjust the image like this, adjusting the pixels a bit at a time and then repeating, then we would actually start to see dogs in the photo, even if there weren’t dogs there to begin with!18 In fact, this is how some of the images in the last chapter were generated: a group of deep learning researchers took a network just like AlexNet and adjusted input images so that certain neurons—representing a great white shark or an hourglass, for example—became bright, while other neurons remained dark.19 Google’s researchers used a similar method to analyze their own neural networks. When they wrote about how they did this, they gave several examples. In one of these examples, they looked at images generated from a neuron that recognized dumbbells, the equipment that you would find in a gym. They found that the images indeed showed dumbbells; but they also showed muscular arms attached to these dumbbells. Apparently, they observed, the network learned that an important distinguishing characteristic of dumbbells isn’t just the hardware itself; but also the context in which it they’re used.20
Google created its Deep Dream images in a similar way, except that instead of forcing the network to generate pictures of dogs or other specific objects, they let the network create more of whatever it saw in the image. As the Deep Dream engineers wrote on Google’s research blog:
Instead of exactly prescribing which feature we want the network to amplify, we can also let the network make that decision. In this case we simply feed the network an arbitrary image or photo and let the network analyze the picture. We then pick a layer and ask the network to enhance whatever it detected. Each layer of the network deals with features at a different level of abstraction, so the complexity of features we generate depends on which layer we choose to enhance. For example, lower layers tend to produce strokes or simple ornament-like patterns, because those layers are sensitive to basic features such as edges and their orientations.
If we choose higher-level layers, which identify more sophisticated features in images, complex features or even whole objects tend to emerge. Again, we just start with an existing image and give it to our neural net. We ask the network: “Whatever you see there, I want more of it!” This creates a feedback loop: if a cloud looks a little bit like a bird, the network will make it look more like a bird. This in turn will make the network recognize the bird even more strongly on the next pass and so forth, until a highly detailed bird appears, seemingly out of nowhere.21
And that’s how the mysterious image from Imgur.com was created. You can see the results of a Deep Dream created by feeding a photograph of kittens into a similar algorithm in figure 10.2b.

A photo of foster kittens, (a), along with a reinterpretation of the photo based on what the network sees after many iterations of the Deep Dream algorithm, (b), and style transfer algorithms, (c) and (d). Image (c) uses style from a Vincent van Gogh painting, while image (d) uses a style created from The Simpsons. All images except (a) were generated via https://
Soon after Google’s blog post, other researchers began using a similar idea to reimagine artistic style. They created tools that would enable anyone to transfer the style from an artist’s painting to an entirely different image. If you wanted to make a photo of your family look like Vincent van Gogh painted it, you simply needed to run your photo through one of these programs.
In these programs, a style image—the Van Gogh painting—is passed through the network so that the neurons light up as usual. The neurons that light up would include some low-level edge detectors in the first few layers as well as high-level object detectors in the higher layers. Then, the style-transfer algorithm measures how the filters in each layer correlate with one another across the entire image. This correlation is exactly how these algorithms define the style of an artist. If certain filters tend to consistently light up with each other across different parts of the image, the reasoning goes, then this indicates something important about the style of the artist. If the artist tends to use only a few, simple colors with many small dots, then the neurons that explain these small dots tend to co-occur with each other. If the artist tends to use sharp brush strokes, then any neuron that captures these sharp brush strokes will tend to occur next to itself wherever it occurs.
After this, a “content” image—your family photo—is passed through another copy of the same network, and we select a specific layer of the network to capture the essence of what’s in the image. Once we’ve selected this layer, the algorithm adjusts the family photo so that the neurons in each layer correlate with one another in the same way they did with the style image, without allowing the neurons in the layer we’ve selected deviate too far from their original values. As long as we were correct in assuming that the correlation in filters expressed at each layer can capture the style of an artist, then this will cause the new image to take on the style of the first photo. This appears to be a reasonable assumption in practice, as the results of the algorithm match our intuition: when the algorithm finishes running, your family photo will have been reimagined as a Van Gogh painting—or as just about any other painting style that you used for the style image!22 I’ve applied this same method to some photos of the three kittens in figure 10.2c and 10.2d. As you can see, the resulting images capture the intuition we expect in different artistic styles: one of them has the intense brush strokes we associate with some of Van Gogh’s most famous work, such as his self-portrait; while the other image has a style reminiscent of a cartoon image; this style was called a “Simpsons” style.
When this algorithm “reimagines” your family photo, remember that no actual “imagining” happens. The network simply processes the style image and the content image, its neurons lighting up in predictable ways for each, and then the algorithm adjusts the content image to optimize a well-defined mathematical function so that the network’s activated neurons correlate in a way that agrees with the style image. The end result may seem spectacular for a computer program, but that’s mostly because these networks perform their operations with higher-level abstractions than what we usually expect from computer programs. Until recently, we’ve come to expect computers to operate on images at a very primitive level, because that’s all they’ve been able to do. Your home photo-editing software has tools that let you adjust the color balance of a photograph or apply softening to it. Up until recently, these operations could have been implemented with the lowest level of a convolutional neural network. But the algorithms I’ve described in this chapter operate on images at a much more abstract level, interpreting and adjusting images by using neurons several layers deep in the network. This is the primary strength of these networks, and it’s one of the reasons they can be applied in many unique and non-intuitive applications.
In the past few chapters, we’ve gained some intuition for how deep neural networks can enable computers both to interpret and manipulate images in remarkably “human” ways. But up until now, our focus has been exclusively on using deep neural networks to interpret visual information. Is it possible to use deep neural networks to better interpret and manipulate other types of media, like audio recordings or written text? As we’ll see in the next chapter, the answer is a clear yes. Deep neural networks can work well in these domains, in part because we have large amounts of data in these other domains as well. But as we’ll soon see, we’ll need to develop some new neural network tools—akin to convolutional filters, but for time-series data—to work with these different types of data.