The reader will no doubt have gathered by this time that the chess pieces, being possessed of intrinsic qualities of movement and capture, may also be compared, one with the other, on the yardstick of relative values.
The correlation of the powers of the pieces is deceptive, however, as in any position each piece will be possessed of a power peculiar to that position. In diagram 9, page 29, for example, both black rooks are out of play, whereas the humble pawn on d2, threatening, if unwatched, to become a queen, is an apparent force. However, the pawn may soon fall, and the black rooks may bring their long-range guns to bear down the vital files. A game is therefore in a permanent state of flux, and the values of the pieces change from move to move. The scale of relative values can only remain a guide for the exchange of pieces (an exchange is when one side captures an opposing piece, giving up one of its own pieces in the process) when other considerations are approximately equal. The ability to assess the true value of a position and, in consequence, the temporary values of the pieces composing the position, is a gift with which only really strong chess players are endowed.
The king, since he cannot be captured, and is only used as an attacking piece towards the end of the game when his powers are approximately equal to those of a bishop, is excluded from the assessment.
Queen = 9 points
Bishop or knight = 3 points or 3 pawns
Rook = 5 points (or a bishop/knight and 2 pawns)
These are approximations. The bishop is normally worth a fraction more than the knight (although there are many positions where knights are stronger than bishops). The queen is perhaps slightly undervalued in this table, but two rooks working together are usually slightly stronger than the queen.
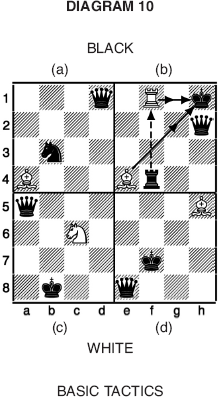
As we have seen in position (c), diagram 8, page 25, a piece is pinned if, in moving, it would expose the king to a hostile check. In diagram 10(a), the knight is also said to be pinned, for although it may be legally moved, the white bishop would then capture the black queen which would be a poor bargain for Black even should the bishop be captured.
The term “pin” is thus extended to signify any position in which the movement of a piece would expose an undefended piece to attack, or a stronger piece to attack from a weaker piece. If there was another black knight at c7 (that is, on the diagonal between the queen and the other knight), the setup would be known as a half-pin as the movement of either knight would automatically result in the pinning of the other.
In the second example (diagram 10(b)), we see a double check, when a king is exposed to attack from two hostile pieces simultaneously. White has just moved the rook, as indicated. In a double check the king must move, since he cannot capture both attacking pieces or interpose two of his own pieces in one move.
If he cannot move, as in diagram 10(b), he is checkmated. Note that Black can apparently capture either piece with the rook, or interpose a piece between either the king and rook or the king and bishop, but none of these resources is open to him because, whichever he adopts, the king will still be in check from the remaining white piece.
The extraordinary power of the double check is apparent, and it is something a player should endeavour to avoid unless he is certain that such check would be innocuous – which is very rarely the case.
This is similar to the double check, but not as dangerous, as the piece moved does not itself give check. If in diagram 10(b), the white rook had moved to f7 instead of f8 it would then have been a “discovered” and not a “double” check. Black could thus have avoided mate, but would have lost the queen.
The knight, by virtue of its irregular move, can create an embarrassing attack known as a “fork”. In the position 10(c), the knight is attacking both king and queen, and as the king must move out of check, the queen is doomed. The most common fork of the knight is of king and rook, when the rook, which, as we have seen, is the stronger piece, is lost. Forks by other pieces are possible. In diagram 4(b), on page 19, for example, the white pawn has forked the black rook and bishop. The term is self-explanatory.
The position in 10(d) is something to guard against. Here the black king, in check, is compelled to move, when the bishop will capture the black queen.
In order to acquaint the reader with the practical power of the pieces, we will examine one or two game endings.
Assuming that Black has only a king left, White will be able to force mate with a minimum force of:
1. King and queen. The white king will, of course, be on the board. If White has a pawn which he can safely promote, then it can be reckoned as a queen.
2. King and rook.
3. King and two bishops.
4. King, bishop and knight.
Mate cannot be forced against a lone king with:
1. King alone – this is obvious.
2. King and bishop.
3. King and knight or king and two knights.
It is interesting to observe that two knights (the joy of the novice!) are unable to force mate, whereas a mere pawn which can be promoted is sufficient for the purpose.
Let us examine the system of forcing mate by king and queen against a bare king.
This performance should not demand more than ten moves, in most positions considerably fewer (when we talk about moves in chess we mean moves of both sides).
Place the white king on e1, the white queen on e8, and the black king on g5. White can mate in a number of ways, but the principle remains the same in every case – the lone king must be driven to the edge of the board where the queen will deliver the mate, the white king assisting.
A series of checks with the queen will achieve nothing. (All beginners assume that checks are stronger than quiet moves (i.e. moves that are not checks), in the hope, presumably, that “it might be mate”.) White, therefore, moves Qe8–f7!, restricting the movements of the doomed monarch.
Notice that in chess, moves are numbered in pairs.
|
White |
Black |
1. |
Qe8–f7 |
Kg5–g4 |
Not Kg5–h4, when Qf7–g6 further restricts the king.
2. |
Ke1–f2 |
Kg4–g5 |
3. |
Kf2–g3 |
Kg5–hg |
The only square.
4. |
Qf7–g8 |
|
4. Kg3–f4? would be a grave error since the black king would then be without a move – stalemated, in other words – and the game would be drawn.
4. |
. . . |
Kh6–h5 |
Again the only move.
5. |
Kg3–f4 |
Kh5–h6 |
Not Kh5–h4 allowing White to mate immediately.
6. |
Kf4–f5 |
|
And now mate next move is unavoidable.
6. |
. . . |
Kh6–h5 |
7. |
Qg8–g5# |
|
The black king has been forced to the edge of the board and is there checkmated. King and queen cannot mate a bare king anywhere except at the side: the same applies to king and rook against bare king, as the following example shows.
Set up the kings as before, and substitute a white rook for the queen. Since this mate is more difficult, as might be expected, and as it is one which you are likely to encounter (if your opponent obstinately refuses to resign), it is essential to be familiar with the correct procedure.
|
White |
Black |
1. |
Re8–f8 |
|
1. |
. . . |
Kg5–g4 |
2. |
Ke1–e2 |
Kg4–g3 |
3. |
Ke2–e3 |
Kg3–g4 |
4. |
Rf8–f1 |
Kg4–g5 |
Black is playing the best defence.
5. |
Ke3–e4 |
Kg5–g6 |
6. |
Ke4–e5 |
Kg6–g7 |
7. |
Ke5–e6 |
Kg7–g6 |
8. |
Rf1–g1+ |
|
The king is now forced to the edge of the board. Note the position of the white king at the precise moment of the check: it is directly opposite the black king, thereby controlling the three squares between them that would otherwise have been open to the fugitive. The black king is now confined to the h file. White aims to set up the same position to deliver checkmate.
8. |
. . . |
Kg6–h5 |
9. |
Ke6–f5 |
Kh5–h4 |
10. |
Rg1–g8 |
Kh4–h3 |
11. |
Kf5–f4 |
Kh3–h2 |
12. |
Kf4–f3 |
Kh2–h1 |
13. |
Kf3–f2 |
Kh1–h2 |
The black king is forced to face the white king: the curtain falls.
14. |
Rg8–h8# |
The maximum number of moves required for this type of ending is seventeen – and this only in extreme cases.
This is a very easy ending, the two rooks being moved rank by rank or file by file, to the edge of the board where the lone king is checkmated.
Place the white king on e1, the two white rooks on a1 and h1, and the black king on e4. White mates in eight moves by:
1. Ra1–a3 Ke4–f4 2. Rh1–h4+ Kf4–g5 3. Rh4–b4 Kg5–f5 4. Ra3–a5+ Kf5–e6 5. Rb4–b6+ Ke6–d7 6. Ra5–a7+ Kd7–c8 7. Ra7–h7 Kc8–d8 8. Rb6–b8#.
This is not the quickest way to force mate but it is the easiest to understand.
The ending with king and two bishops embraces the same idea of driving the lone king to the edge of the board, the pieces working in conjunction to cut off the escape squares (or flight squares, as they are more commonly called). The king must be mated on a corner square, and in this respect the mate differs from the endings with queen and rook given above.
The ending with king, bishop and knight against bare king is conducted in the same manner as the ending with the two bishops, except that the victim must be mated on a corner square of the same colour as that on which the bishop stands.
Most elementary textbooks on chess give pages of analysis on these two endings which serve only to bewilder the student. Many experienced players are unable to force the mate with bishop and knight. And, indeed, why worry? This ending is very rare in actual play and the procedure is beyond the scope of this book.
When the tumult of the middle game has subsided into the comparative quiet of the end game, it is usual for each side to be left with three or four pieces. With only a few pieces remaining it is easier to calculate with precision the best line of play – indeed, the end game of chess is a fine art, and there are many books devoted to this subject alone.
With only a limited force available, it is unlikely that either king is in danger of being mated. The play is therefore concentrated on the task of queening (promoting) pawns – which does not mean to say that either player should lose sight of mating possibilities.
As soon as one side succeeds in promoting a pawn, he will obviously have a decided, if not decisive, advantage, and can then turn his attention to destroying the enemy force preparatory to the final checkmate.
On a crowded board the likelihood of a pawn surviving the hazardous march from the second to the eighth rank is remote; but, as the forces decrease, its power augments. It will be seen, therefore, that in the end game the pawn takes on a new importance, since the longer it survives, the greater are its chances of eventual promotion.
To understand even the simplest end games, it is necessary to study the movements of the pawn in conjunction with the movements of the two kings.
Look at diagram 11. Here are four simple examples of king and pawn endings.
In (a) Black to move is a draw, since the king is stalemated. White, to move, wins, however. 1. Kb6–c6 Kb8–a7 (the only move) 2. Kc6–c7 (still guarding the pawn and preventing Black returning to the promotion square) Ka7–a6 3. b7–b8Q and White mates in two more moves.
In (b) Black to move is a draw (stalemate). If White to move, he is in a quandary. The only square to which he can play the king and still guard the pawn (g6) leaves the black king in stalemate, whilst any other king move permits Black to capture the pawn. From which we derive the important precept that if, in a king and rook’s pawn v king ending, the solitary king can reach the queening square before the pawn, the game is drawn.
The difference between 11(a) and 11(b) will now be apparent. In (a) the white king penetrates by forcing the black king out on the opposite file; whereas in (b) he is not able to do this.
In (c) the king is unable to capture either pawn without permitting the other to queen. For example, 1. Kb2–c3 a4–a3 2. Kc3xc4 a3–a2 and queens (promotes to queen) next move. The white king can only shuffle impotently between b2 and b1 until the black king arrives on the scene to force the issue. Black loses both pawns in an attempt to promote one without assistance:
1. Kb2–b1 c4–c3 2. Kb1–c2 a4–a3 3. Kc2xc3 a3–a2 4. Kc3–b2.
In (d) White can again do nothing but move his king around until the black king arrives. If he captures the unprotected pawn, he cannot stop the other one queening.
A simple rule for determining whether a pawn, advancing alone to promotion, can be captured by the king before it reaches the queening square, is illustrated in diagram 12.
Imagine a square with one side marking out the path from pawn to queening square. If the black king can move inside this square, he can capture the pawn. In the diagram, Black, with the move, draws by playing Kb3–c3 or c4. White, with the move, wins by h3–h4, and the pawn cannot be stopped. If the pawn were at h2, White would still win by virtue of the initial double pawn move 1. h2–h4. This rule only applies to a pawn advancing alone: if the White king or other piece can in any way influence the play, the formula does not apply.
You should now have a reasonable grasp of the elementary principles of the game. In order that you may not become over-wearied with theory, we shall proceed to play over a short game or two, assessing the value of each move as we go.
Before passing on, however, try the following brief test based on the points we have examined (answers on page 46):
1. Place WK on a8, WN on e3; BK on h6, BQ on h2, BB on b8. Black plays Bb8–a7 attacking the knight and threatening Qh2–b8#. What result?
2. In the king and queen ending given in this chapter, after Black played 6. . . . Kh6–h5, White mated by 7. Qg8–g5. Can you see any alternative mates for White in this position (one move)?
3. Place WK on a1, WP on a4; BK on f5. Can Black, to move, prevent the WP queening?
4. Place WK on d6, WR on d1; BK on e8. White to play. Mate in how many moves?
5. Place WK on h5, WP on f7; BK on h7. White to play. What result?
6. Place WK on b5, WP on b6; BK on b8. (i) White to move – what result? (ii) Black to move – what result?
1. Draw. White can play Ne3–g4+! forking king and queen, thus leaving both sides with insufficient mating force. If White plays Ka8xa7?, Black plays simply Qh2–f2 pinning the knight, capturing it next move and winning easily with king and queen against king.
2. Qg8–h8 or h7 – here the queen, notice, is only exercising her powers as a rook.
3. Yes, by Kf5–e6, e5 or e4.
4. Two: 1. Rd1–f1! Ke8–d8 2. Rf1–f8#.
5. White wins: 1. f7–f8R etc. Not 1. f7–f8Q stalemate, or 1. f7–f8B or N with insufficient mating force. Black to play draws by Kh7–g7 winning the pawn.
6. Draw in each case. (i) 1. Kb5–a6 Kb8–a8 (not 1. . . . Kb8–c8? 2. Ka6–a7); 2. b6–b7+ Ka8–b8 and White must now give up the pawn or stalemate the black king. (ii) 1 . . . Kb8–b7! and White can do nothing except move about on the fifth rank as Black alternates between b8 and b7. If the white king tries to penetrate, the sequel is as in (i). Note that 1. . . . Kb8–a8 (or c8) would be fatal: 2. Kb5–a6 (or c6) Ka8–b8 3. b6–b7 wins (see diagram 11(a)). On examination it will be seen that if one side can play a pawn to the seventh rank in this type of ending without giving check, and provided that the pawn is not a rook’s pawn, he will win.