Perceiving Loudness, Pitch, and Location
Responding to Loud and Soft Sounds
How do we detect loudness? If you guessed that it’s related to the intensity of a hair cell’s response, you’d be wrong. Rather, a soft, pure tone activates only the few hair cells attuned to its frequency. Given louder sounds, neighboring hair cells also respond. Thus, your brain interprets loudness from the number of activated hair cells.
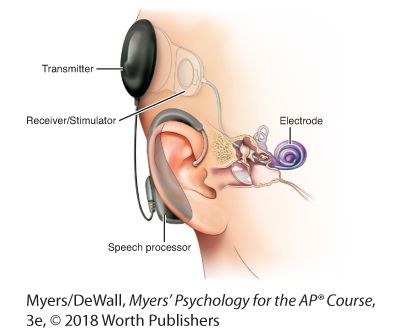
Hardware for hearing Cochlear implants work by translating sounds into electrical signals that are transmitted to the cochlea and, via the auditory nerve, relayed to the brain.
If a hair cell loses sensitivity to soft sounds, it may still respond to loud sounds. This helps explain another surprise: Really loud sounds may seem loud to people with or without normal hearing. As a person with hearing loss, I [DM] used to wonder what really loud music must sound like to people with normal hearing. Now I realize it sounds much the same; where we differ is in our perception of soft sounds. This is why we hard-of-hearing people do not want all sounds (loud and soft) amplified. We like sound compressed, which means harder-to-hear sounds are amplified more than loud sounds (a feature of today’s digital hearing aids).
Hearing Different Pitches
 Flip It Video: Theories of Hearing
Flip It Video: Theories of Hearing
How do we know whether a sound is the high-frequency, high-pitched chirp of a bird or the low-frequency, low-pitched roar of a truck? Current thinking on how we discriminate pitch combines two theories.
- PLACE THEORY presumes that we hear different pitches because different sound waves trigger activity at different places along the cochlea’s basilar membrane. Thus, the brain determines a sound’s pitch by recognizing the specific place (on the membrane) that is generating the neural signal. When Nobel laureate-to-be Georg von Békésy (1957) cut holes in the cochleas of guinea pigs and human cadavers and looked inside with a microscope, he discovered that the cochlea vibrated, rather like a shaken bedsheet, in response to sound. High frequencies produced large vibrations near the beginning of the cochlea’s membrane. Low frequencies vibrated more of the membrane and were not so easily localized. So there is a problem: Place theory can explain how we hear high-pitched sounds but not low-pitched sounds.
- FREQUENCY THEORY (also called temporal theory) suggests an alternative: The brain reads pitch by monitoring the frequency of neural impulses traveling up the auditory nerve. The whole basilar membrane vibrates with the incoming sound wave, triggering neural impulses to the brain at the same rate as the sound wave. If the sound wave has a frequency of 100 waves per second, then 100 pulses per second travel up the auditory nerve. But frequency theory also has a problem: An individual neuron cannot fire faster than 1000 times per second. How, then, can we sense sounds with frequencies above 1000 waves per second (roughly the upper third of a piano keyboard)? Enter the volley principle: Like soldiers who alternate firing so that some can shoot while others reload, neural cells can alternate firing. By firing in rapid succession, they can achieve a combined frequency above 1000 waves per second.
So, place theory and frequency theory work together to enable our perception of pitch. Place theory best explains how we sense high pitches. Frequency theory, extended by the volley principle, also explains how we sense low pitches. Finally, some combination of place and frequency theories likely explains how we sense pitches in the intermediate range.
Locating Sounds
Why don’t we have one big ear—perhaps above our one nose? “All the better to hear you with,” as the wolf said to Little Red Riding Hood. Thanks to the placement of our two ears, we enjoy stereophonic (“three-dimensional”) hearing. Two ears are better than one for at least two reasons (Figure 20.4). If a car to your right honks, your right ear will receive a more intense sound, and it will receive the sound slightly sooner than your left ear.
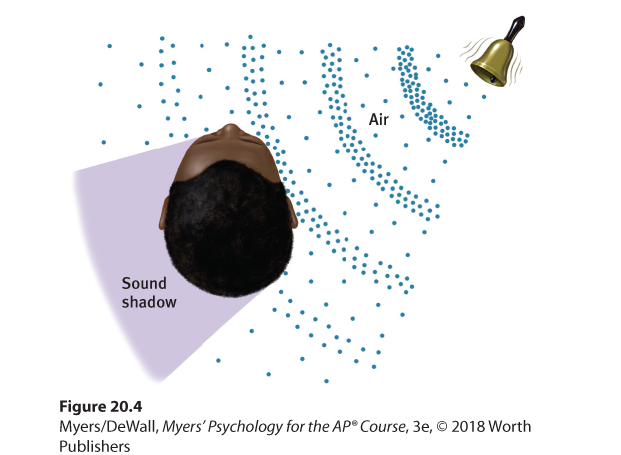
Figure 20.4 How we locate sounds
Sound waves strike one ear sooner and more intensely than the other. From this information, our nimble brain can compute the sound’s location. As you might therefore expect, people who lose all hearing in one ear often have difficulty locating sounds.
Because sound travels 761 miles per hour and human ears are but 6 inches apart, the intensity difference and the time lag are extremely small. A just noticeable difference in the direction of two sound sources corresponds to a time difference of just 0.000027 second! Lucky for us, our supersensitive auditory system can detect such minute differences—and locate the sound (Brown & Deffenbacher, 1979; Middlebrooks & Green, 1991).