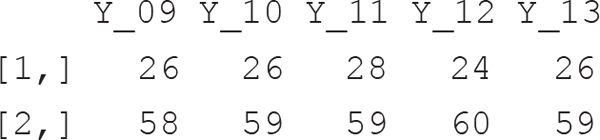Camera Trapping for Wildlife Research

Static and dynamic occupancy models were orginally intended to investigate occurrence and occupancy dynamics of single species (see Chapter 6). Among the wide variety of extensions proposed for this class of models, those allowing the investigation of community-level metrics and dynamics are certainly relevant for readers who want to extend inference to a higher hierarchical level of ecological organisation, from populations of individuals to populations of species (i.e. community) or populations of spatially organised communities (metacommunities) (Royle and Dorazio 2008). In fact, as ecological systems are fundamentally hierarchical, the correspondence between ecological levels of organisation (population, metapopulation, community and metacommunity) and the levels of a hierarchical model can be very important in the modelling process. Population size, i.e. the number of individuals comprising a population, can be viewed as conceptually equivalent to species richness, which defines the number of species in a community. When our system state is allowed to vary temporally, the classic population dynamic parameters, survival and recruitment of individuals, have their analogues in local extinction and local colonisation of species, respectively, and can provide a description of changes in the pool of species over time. In addition, sampling a population or a community results in binary data (i.e. mutually exclusive outcomes, such as ‘observed’ and ‘not observed’) on individuals or species and we can thus use similar model formulations to describe the observation process relating to ecological systems at different scales. This conceptual equivalence, i.e. the fact that the observation and the state models often translate across systems (from populations to metacommunities), facilitated the extension of single-species occupancy models to a multi-species framework. The latter is flexible enough to be relevant for abundance, occurrence and species richness, the three main state variables in ecology (Royle and Dorazio 2008). It is also important to recall, as additional background information, that occupancy models are hierarchical models, expressed using the so-called ‘state-space’ formulation (e.g. De Valpine and Hastings 2002) whereby two models are in fact specified, one for the latent ecological or state process (the primary object of inference) and, conditional on that, a model for the observation process.

In this chapter, we extend the single-species occupancy models described in Chapter 6 to a hierarchical, multi-species framework that allows modelling of species occurrence separately from detectability and, at the same time, can be used to estimate community-level parameters and derive measures of community size and structure. The approach can thus be useful to study spatial and temporal changes in biodiversity. We illustrate static (single-season) and dynamic (multi-season) models using the same camera trapping data for a community of medium-to-large mammals collected in the Udzungwa Mountains of Tanzania in the framework of the TEAM Network, and already showcased in Chapters 5 and 6.

Measuring and assessing biological diversity and understanding the relationship between living organisms and their environment are major goals in ecology. Biodiversity is commonly measured by species richness, Shannon entropy (also called Shannon’s diversity index or Shannon–Wiener index) and the Gini–Simpson index (e.g. Jost 2006; Chao et al. 2014). Species richness, i.e. the number of species in a community, is the simplest and most common measure of biodiversity. However, species richness alone does not distinguish between species with different abundances. Two communities may contain the same number of species, but their composition in terms of the number of individuals belonging to each species can differ, making one community more diverse than the other (Gotelli et al. 2013). In other words, species richness counts all species equally, weighting rare species the same as common ones. However, the Shannon entropy and the Gini–Simpson index incorporate information about the relative abundance of species. The Shannon entropy ‘quantifies the uncertainty in the species identity of a randomly chosen individual in the assemblage’, whereas the Gini–Simpson index ‘measures the probability that two randomly chosen individuals (selected with replacement) belong to two different species’ (Gotelli et al. 2013). Variations to the latter index include the Simpson concentration, the inverse Simpson concentration, the second-order Renyi entropy or the Hurlebert–Smith–Grassle index (Jost 2006).

A common attribute of these estimators is that they do not take imperfect detection into account (see Chapter 6 for details on imperfect detection) and they are sensitive to sample size. Concepts such as rarefaction and extrapolation have been proposed to deal with unequal sample sizes (Chao and Jost 2012) but the issue of imperfect detection has been solved only with the advent of the multi-species occupancy framework (Dorazio and Royle 2005). In general, multi-species occupancy models provide more precise and less biased estimates of species richness than single-visit approaches, such as the jackknife and the Chao estimators (Kéry and Royle 2008; McNew and Handel 2015). Since detectability will not be equal across sites, species and sampling occasions, diversity measures should account for the mismatch between the proportion in which individuals are detected vs. their actual proportion in the community. In fact, information on communities is often available as apparent presence or absence of each species. However, a proportion of zeros in these data will likely stem from an imperfect detection process, and these false zeros have to be separated from true zeros, which are associated with the absence of a species. Bias in biodiversity estimators can be higher in communities that contain a large proportion of rare or difficult-to-detect species. In occupancy models we can account for this source of bias since species occurrence and detection can be estimated separately within the same framework using presence–absence data or, more precisely, detection/non-detection data.

In addition to the above-mentioned measures of biodiversity, many others can be derived from a multi-species occupancy model, such as alpha, beta and gamma diversities, and the Sorensen and Jacard coefficients (Magurran and McGill 2011). For an example of beta diversity derivation, see Dorazio et al. (2011). Furthermore, Broms et al. (2014) showed that Hill numbers can also be easily derived through a multi-species occupancy model. Hill numbers provide a unifying framework to summarise all three measures of biodiversity (alpha, beta and gamma diversity) into a single expression (Hill 1973; Chao et al. 2014).

In an occupancy-based approach to modelling communities, both community- and species-level attributes can be estimated, as these are combined in the same framework. We need replicated detection/non-detection data to estimate species occurrence separately from detectability and to resolve the ambiguity of an observed zero, which can indicate either that the species is absent, or present but not detected. All models developed for the analysis of replicated detection–non-detection data include parameters for an incidence matrix (e.g. Gotelli 2000) which contains the binary occupancy state (presence or absence) for each species at each sample location. As a consequence of imperfect detection the incidence matrix is only partly observed, but can be estimated along with any quantity derived from the matrix itself, such as species richness and other diversity measures. Multi-species occupancy models were first developed by Dorazio and Royle (2005) and Dorazio et al. (2006). Further extensions included spatial covariates of occupancy and detectability (Royle and Dorazio 2008; Kéry and Royle 2009) and quantification of anthropogenic and natural factors affecting community size and other community-level attributes (Burton et al. 2012; Zipkin et al. 2009; 2010; Carrillo-Rubio et al. 2014).

We start from data collected at multiple sample locations, or sites, which can correspond to an array of J cameras. The latter remain active for a certain number of days K, and thus each site is sampled on K > 1 occasions. The data we collect (y_ij) are encounter frequencies of species i = 1, …, n at each of j = 1, …, J sites, sampled k = 1, …, K times, and can be summarised in a n × J matrix (Y) so that rows are associated with distinct species and columns with distinct sites. Note that the number of visits, K, need not to be identical for all sites, but here we assume K is fixed for the sake of clarity. We assume that the occupancy state of each species, and thus the number of species, at each sample site remains constant during the time required to perform the K replicate observations.

The detection frequency matrix Y is a subset of the (imperfectly observable) N × J matrix Z of latent occupancy states of each species in each site (z_ij). N is the actual number of species in the community, and the number of undetected species (with all-zero encounter histories) is N – n. To estimate the ‘true’ occupancy states in Z we use the repeated detection/non-detection information contained in Y. Note that in estimating species richness N, the number of observed species n represents a lower bound for the estimate of N.

Multi-species occupancy models cannot be fitted in a classical (or frequentist) framework since the evaluation of the marginal likelihood function involves analytically intractable, high-dimensional integrations. We can, however, adopt a Bayesian mode of inference with Markov chain Monte Carlo (MCMC) methods (Robert and Casella 2004) (Box 6.1). However, one main challenge in this framework is that the dimension of the parameter vector for community size N can change at every iteration of the MCMC algorithm. The solution adopted to overcome this difficulty is called parameter-expanded data augmentation (Tanner and Wong 1987; Dorazio and Royle 2005; Dorazio et al. 2006; Royle et al. 2007; Royle and Young 2008; Royle and Dorazio 2011). In practice, this technique implies the addition of an arbitrary number of all-zero trap frequencies, which can be seen as potentially unobserved species, to the detection matrix Y, and thus the analysis of the augmented matrix. The latter has dimension M × J, where M >> N,¹ and we can estimate which of the M – n species (rows of the augmented data set) are members of the community (sampling zeros) or not (structural zeros). We do this by adding an indicator ω_i for whether a row of the augmented data matrix represents a ‘real’ species (ω_i = 1) or not (ω_i = 0), for i = 1, …, M. By assuming ω_i ~ Bern(Ω) we can estimate the probability Ω that the species is a member of the community of size N.

Note that data augmentation converts the problem of estimating N into the equivalent problem of estimating Ω, and species richness N is computed as a derived parameter by summing up the latent indicators ω_i, since the expectation of N is equal to MΩ (Kéry and Schaub 2012). Elements of the augmented matrix Z, of dimension M × J, indicate whether species i is present at sample site j (z_ij = 1) or not (z_ij = 0). Since z_i is defined conditional on the value of ω_i, each element of z_i is equal to zero if species i is not a member of the community (i.e. ω_i = 0), with Z treated as a random variable: z_ij ~ Bern(ψ_ij ω_i). Matrix Z can be used as the already-mentioned incidence matrix to derive community-level attributes. For instance, the number of species present at each sample site (alpha diversity) is obtained by summing the columns of Z. We can also express differences in species composition among sites (beta diversity) by comparing columns of Z. For an example of derivation of alpha, gamma and beta diversity (Jaccard index), see Dorazio et al. (2011). Dorazio and Royle (2005) and Royle and Dorazio (2008) report the estimation of the similarity of species present at two different sampling locations, the Dice (1945) index of similarity, also known as the coefficient of community (Pielou 1977). In addition, Dorazio et al. (2006) derive species-accumulation curves (Gotelli and Colwell 2001) from estimates of species richness and species occurrence. Species-accumulation curves can be used to compare the size of different communities at similar levels of sampling effort, to improve the efficiency of future surveys, and to select priority areas for conservation (Dorazio et al. 2006).

Conditional on the state model for z_ij, the simplest assumption we can make about the observation process is that if species i is present at site j (i.e. z_ij = 1) its probability of capture p_ij is the same at each sampling site and occasion: y_ij ~ Bin(K; p_ij z_ij). Note that if a species is absent at site j, i.e. z_ij = 0, then the camera trap in that site will not record contacts for that species and the probability that y_ij = 0 is 1.

In many cases covariates are thought to affect species occurrence and detection. We can easily incorporate site- and/or replicate-level covariates, such as measures of environmental features or sampling effort. For instance, we can assume that detectability is affected by seasonality, in relation to species phenology, and occurrence differs with elevation. We might also expect a peak in both detection and occurrence for certain values of the related covariate, and thus include a quadratic effect. We can write the relationships in two linear predictors for the observation and the state process, on the logit-scale, as follows:

Note that detection can vary among species (i), sites (j) and sampling occasions (k), whereas occurrence has to be fixed for all replicates. In this case intercepts a_i0 and b_i0 denote, respectively, the probability (on the logit-scale) of occurrence and detection of species i at the average value of the covariates. It is advisable to standardise covariates to have zero mean and unit variance, in order to avoid numerical issues during the calculations.

At this point, further model assumptions are needed (i) to characterise the heterogeneity in occurrence and detectability among species, and (ii) to estimate the occurrence of species members of the community that are not observed at any sampling site. A common approach is to assume ecological similarity among species, that is to say that species are likely to have a similar, but not identical, response to environmental changes (Dorazio et al. 2006, 2011; Kéry and Royle 2009). We must note that in the case of interspecific interactions where occurrence of a species is affected by the presence or absence of another species, as expected between competing species or between predator and prey, the ecological similarity assumption does not hold and patterns of co-occurrence should instead be considered (MacKenzie et al. 2004; Waddle et al. 2010). When the assumption of ecological similarity is reasonable, we can model unobserved sources of heterogeneity in occurrence and detection among species by adding one hierarchical level and assuming that the species-specific parameters in the related linear predictors (such as a_i and b_i in eqs (1) and (2)) are independent random effects. That can be written as a_il ~ Normal(α_l, σ_al²) with l = 1, …, P (where P is the number of parameters in the linear predictor), and b_il ~ Normal(β_l, σ_bl²), for detectability and occurrence parameters, respectively. We can thus estimate the community-level hyperparameters, the means (α_l, β_l) and variances (σ_al², σ_bl²) of the distributions. In this way we can estimate parameters for species observed a small number of times (often the rarest ones) or never observed, in a framework that borrows information from any individual species in the sample. In this way, occurrence and detectability estimates of individual species depend not only on the data of that species but also on the information available for every other species. In practice, species-specific estimates are ‘shrunk’ toward the mean parameter value of the community.

In addition, we might expect that occupancy and detection probability increase as the abundance of species increase, and the model can thus be extended to define a correlation structure between the two probabilities. For further details about the model component for heterogeneity among species and related distributional assumptions, see e.g. Dorazio (2007) and Royle and Dorazio (2008).

Different approaches exist to assess the effect of covariates on the occurrence and detectability of each species, in a Bayesian framework. Unfortunately, these approaches can be difficult to implement and there is no ‘canned’ method for model selection like the AIC in a classical analysis based on maximum likelihood. Readers who want to deepen their understanding of Bayesian model selection and averaging can refer to Link and Barker (2006), Link and Barker (2009), O’Hara and Sillanpää (2009), Hooten and Hobbs (2014) and Tenan et al. (2014). For a direct application of a Bayesian variable selection approach to multi-species occupancy models, see Dorazio et al. (2011) and Burton et al. (2012). In conclusion, we want to emphasise the usefulness of multi-species occupancy models in estimating the community’s incidence matrix while accounting for imperfect detection. The estimated incidence matrix is key, since all measures of biodiversity are directly derived from it. Note that, under the multi-species occupancy framework, biodiversity measures are derived for a single spatial unit or ‘region’ sampled at different sites. Single-region models have been recently extended to simultaneously estimating species richness across communities from multiple regions. This new, multi-region framework allows direct modelling of spatial variation in species richness using region-specific covariates, representing a formal mechanism to test hypotheses on the drivers of geographic variation of community size and structure (Sutherland et al. 2016; Tenan et al. 2016).

The case study is based on the same dataset from the TEAM Network project in the Udzungwa Mountains of Tanzania as used for Chapters 5 and 6 (file ‘team.yr2009_2013.csv’), and contains five years of repeated camera trapping at 60 locations within the target forest. The ensuing analysis requires the extraction from the database of yearly matrices of species (arranged in rows) by sampling locations (columns) and populated by the number of ‘independent’ events, i.e. separated by 1 day (see Chapter 5 for details of this raw metric). The analysis also requires the sampling effort (camera days) by sampling unit.

We first load the TEAM libraries, the data and the packages for data checking and inclusion of taxonomic attributes as done in Chapters 5 and 6:

source("TEAM library 1.7.R")

library(chron)

library(reshape)

team_data <-read.csv(file="teamexample.csv", sep=",",h=T,stringsAsFactors=F)

iucn.full<-read.csv("IUCN.csv", sep=",",h=T)

iucn<-iucn.full[,c("Class","Order","Family","Genus","Species")]

team<-merge(iucn, team_data, all.y=T)

data<-fix.dta(team)

data<- droplevels(data[data$bin!="Homo sapiens", ])

mam<-data[data$Class=="MAMMALIA",]

We can now extract the events year by year (the code below refers to the baseline year, 2009), using the same function event.sp as in Chapter 5. Note that the thresh value set at 1440 min is indeed equivalent to 1 day:

ev2009<-event.sp(dtaframe=mam, year=2009.01, thresh=1440)

rownames(ev2009)<-ev2009[["Sampling.Unit.Name"]]

The resultant matrix needs to be transposed for the subsequent analysis, before being saved as a .TXT file:

sp<-t(ev2009)

write.table(sp,"spudz_2009.txt")

The sampling effort is also extracted and saved in .TXT, using the function cam. days:

camera_days<-cam.days(data,2009.01)

write.table(camera_days, file="camera_days_2009.txt",quote=F, sep="\t",row.names = F)

Detection frequencies collected in 2009 are related to 58 camera trap points, whereby each camera trap was active from a minimum of 7 to a maximum of 37 days (median 31). In total, 26 species of mammals were detected.

As a simple case study, we assume constant occurrence and detection probabilities across sites, i.e. logit(ψ_ij) = b_i0 and logit(p_ij) = a_i0, with b_i0 ~ Normal(β₀, σ_b0²) and a_i0 ~ Normal(α₀, σ_a0²).

The model is implemented in the program JAGS (Plummer 2003; see also Chapter 6 and Box 6.1), which we execute from R (R Core Team 2012; see also the case study in Chapter 6, section 6.6.2) with the R packages rjags (Plummer 2013) and dclone (Sólymos 2010). We can reduce computational time by parallelising the process with the jags.parfit() function of the dclone package. This allows us to use one CPU per chain. Summaries of the parameter posterior distribution are calculated from three Markov chains initialised with random starting values, run 30,000 times after a 10,000 burn-in and thinned every 10 draws. The script is shown below, with lines beginning with ‘#’ being descriptive notes for the ensuing code (see the file in Appendix 9.1 for a downloadable version of the R script).

# load detection data

Y <- as.matrix(read.table(file="spudz_2009.txt",header=T,sep=" "))

# load effort

effort <- read.table(file="camera_days_2009.txt",header=T, sep="\t")

# load libraries

library(rjags)

library(dclone)

# set seed

set.seed(1980)

# BUGS model

modelFilename = "smsom.txt"

cat("

model {

# Priors for community-level parameters

omega ~ dunif(0,1)

psi.mean ~ dunif(0,1)

beta <- log(psi.mean) - log(1-psi.mean) # logit(psi.mean)

p.mean ~ dunif(0,1)

alpha <- log(p.mean) - log(1-p.mean) # logit(p.mean)

sigma.psi ~ dunif(0,10)

sigma.p ~ dunif(0,10)

tau.psi <- pow(sigma.psi,-2)

tau.p <- pow(sigma.p,-2)

# Likelihood

for (i in 1:M) {

w[i] ~ dbern(omega)

# occupancy

phi[i] ~ dnorm(beta, tau.psi)

# detectability

eta[i] ~ dnorm(alpha, tau.p)

logit(psi[i]) <- phi[i]

mu.psi[i] <- psi[i]*w[i]

logit(p[i]) <- eta[i]

for (j in 1:n.site) {

Z[i,j] ~ dbern(mu.psi[i])

mu.p[i,j] <- p[i]*Z[i,j]

Y[i,j] ~ dbin(mu.p[i,j], K[j])

}

# compute species richness

N <- sum(w[])

}

", fill=TRUE, file=modelFilename)

# number of sampling occasions for each trap

K <- effort$ndays

# number of traps

nsites <- dim(Y)[2]

# number of observed species

nspecies <- dim(Y)[1]

# Augment data set

nzeros <- 100

Y_aug <- rbind(Y,matrix(0,nrow=nzeros,ncol=nsites))

# Latent states

w <- c(rep(1, nspecies), rep(NA, nzeros))

# parameters monitored

parameters <- c("omega","psi.mean","sigma.psi","p.

mean","sigma.p","N")

# data

bugs.data <- list(M=(nspecies+nzeros),n.site=nsites,K=K,Y=Y_aug,

Z=(Y_aug>0)*1,w=w)

# initial values

inits <- function() { list(omega=runif(1),

psi.mean=runif(1), p.mean=runif(1),

sigma.psi=runif(1,0,4), sigma.p=runif(1,0,4))}

#mcmc settings

n.adapt <- 5000	# adaptation
n.update <- 10000	#burnin
n.iter <- 30000	#iterations post-burnin

thin <- 10

chains<-3

# run the model and record the run time

cl <- makeCluster(chains, type = "SOCK")

start.time = Sys.time()

out <- jags.parfit(cl, data = bugs.data,

params = parameters,

model = "smsom.txt",

inits = inits,

n.adapt = n.adapt,

n.update = n.update,

n.iter = n.iter,

thin = thin, n.chains = chains)

end.time = Sys.time()

elapsed.time = difftime(end.time, start.time, units='mins')

cat(paste(paste('Posterior computed in ', elapsed.time, sep=''), ' minutes\n', sep=''))

stopCluster(cl)

#Posterior computed in 3.37720005909602 minutes

# Summarize posteriors

summary(out)

Iterations = 15010:45000

Thinning interval = 10

Number of chains = 3

Sample size per chain = 3000

1. Empirical mean and standard deviation for each variable, plus standard error of the mean:

2. Quantiles for each variable:

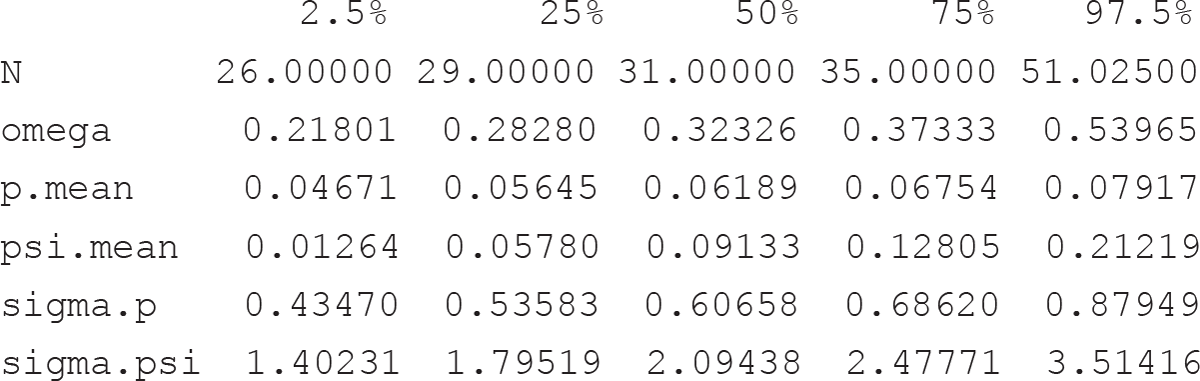
Thus, while in this case study the observed species richness was 26, our model estimates a community size of 31 species (median; 26–51 95% credible interval). The inclusion probability Ω, i.e. the probability with which a species member of the augmented data set (with dimension M) is included in the community of size N, is estimated at 0.34 (0.22–0.54). The average (among species) probabilities of detection and occurrence are indicated by p.mean and psi.mean, respectively, and are reported on the probability scale. Heterogeneity in detection and occurrence probability among species are indicated by sigma.p and sigma.psi, which are on the logit scale.

Convergence is achieved quickly. We can use the diagnostics in the coda package in R to check for convergence by inspecting plots of the chains visually using the xyplot() function (originally implemented in the lattice package). We can also display the posterior density distributions of the parameters with the densityplot() function. Autocorrelation in the MCMC series can be explored with the acfplot() function. A more formal convergence check is based on the Gelman–Rubin statistics (Brooks and Gelman 1998; gelman.plot() function), which needs more than one chain started at randomly selected values. When this statistic is close to 1 it indicates likely convergence; as a rule of thumb, it can be safe to assume convergence of an MCMC algorithm for values <1.1 (Gelman et al. 2004).

# check model output

xyplot(out[,c("omega","psi.mean","sigma.psi","p.mean","sigma.p"), drop=F])

densityplot(out[,c("omega","psi.mean","sigma.psi", "p.mean","sigma.p"), drop=F])

acfplot(out[,c("omega","psi.mean","sigma.psi", "p.mean","sigma.p"), drop=F])

gelman.plot(out[,c("omega","psi.mean","sigma.psi", "p.mean","sigma.p"), drop=F])

We can now plot (see Figure 9.1) the posterior distribution of the estimated richness for the local community using the following code:

# bind chains for the plot

out2 <- mcmc(do.call(rbind, out))

# plot

par(mar = c(5,4.5,4,1.5)+.1, cex.axis=1.5, cex.lab=2, tcl = 0.25)

hist(out2[,"N"],breaks=seq(20,100,by=1),main="", xlab="Species richness",ylab="Posterior probability",freq=F)

abline(v=nspecies,col="red",lwd=3)

The bar chart shows very clearly how the estimated richness is greater than the observed one. For more details on the ecological interpretation of this result, see Rovero et al. (2014), which uses the same data set as in this example.

Finally we remember that, in a Bayesian analysis, we need to assess the sensitivity of the posterior distributions to alternative priors. For further details on prior sensitivity analysis, see e.g. King (2009).

Detection/non-detection data gathered during multiple, instead of single, sampling periods can be used to assess changes in communities over time, similarly to what has been described for species-level occupancy models (Chapter 6). Hence, we need a ‘robust design’ (Pollock 1982), whereby K replicate visits to sampling sites correspond to secondary periods nested within T primary periods (e.g. seasons or years), during which we repeated our sampling protocol. In this case, we need to account for the fact that during the time between primary sampling periods, which is assumed to be long relative to secondary periods, community composition and size can change.

Dynamics in species composition and occurrence can be analysed by means of an extension of the multi-species occupancy modelling framework (section 9.3) to multiple time periods. Once again, the previously mentioned incidence matrix represents the core of this statistical modelling framework, where community and metacommunity dynamics are specified at the species level by modelling changes in the incidence matrix (Dorazio et al. 2010). For each primary period t = 1, …, T we define an incidence matrix Z_t of dimension N × J, where N denotes the number of species in the (meta)community and J the number of sampling sites. The sequence of incidence matrices Z₁, Z₂, …, Z_T is partially observed, due to imperfect detectability. By estimating that sequence we can infer the spatial and temporal dynamics of (meta)community composition. At least three different formulations are available to describe the state process of the dynamic model, and an overall comparison is provided by Royle and Dorazio (2008). In the first formulation, temporal changes in species occurrence are modelled conditional on changes in covariate values between primary periods (Kéry et al. 2009). A second kind of model includes a form of conditional dependence in the occurrence of a species over time at a specific site, and a third formulation represents a hybrid between the first two (autologistic parameterization; Royle and Dorazio 2008).

We describe here the second model type, where changes in species occurrence depend on a set of species- and site-specific extinction and colonisation probabilities, and are modelled using a first-order Markov process (MacKenzie et al. 2003). The approach is similar to the single-species dynamic occupancy model described in Chapter 6. The initial occupancy state at t = 1 of species i at site j is modelled as z_ij1 ~ Bern(ψ_ij1 ω_i), where ψ_ij1 denotes the occurrence probability and ω_i indicates whether species i is a member of the community of size N exposed to sampling during any of the T primary periods. The Markov process is specified by assuming that states in primary periods t = 2, …, T depend on the states at t – 1: z_ij,t+₁ ~ Bern(π_ijt ω_i), for t = 1, …, T – 1, where π_ijt = φ_ijt z_ijt + γ_ijt(1 – z_ijt). φ_ijt denotes the probability that a site occupied at time t remains occupied at t + 1 by species i (i.e. species i ‘survives’ or persists at site j). The complement of φ_ijt is the local extinction probability, ε_ijt = 1 – φ_ijt. Local colonisation is denoted by γ_ijt ,the probability that a site not occupied at time t becomes occupied at t + 1 by species i. With this formulation, occurrence probability for primary sampling periods from 2 to T is expressed as a function of local persistence and colonisation ψ_ij,t+₁ = φ_ijt ψ_ijt + γ_ijt(1 – ψ_ijt).

The observation process can be specified in the same way we did with the static multi-species occupancy model, for the observed number of detections y_ijt of species i at site j and primary period t: y_ijt ~ Bin(K_jt ; p_ijt z_ijt). Here p_ijt indicates detection probability, and K_jt the number of sampling occasions for each trap in each primary period. We can extend this general model by including covariates thought to be informative of species occurrence (only occurrence at t = 1 with this formulation), detection, colonisation and persistence, in the same way we did in section 9.3. An advantage of the autologistic parameterisation is that it can be extended to include spatial or temporal covariates of occurrence probability (Royle and Dorazio 2008). For details about modelling heterogeneity among species, see Dorazio et al. (2010).

We can use this framework to derive quantities of ecological interest for individual species, local communities or an entire metacommunity. From the estimated incidence matrices Z₁, Z₂, …, Z_T, and thus for every primary period, we can compute the number of species present at different subsamples of sites, which can represent biogeographic regions as in Dorazio et al. (2010) or treatment plots as in Russell et al. (2009). Among the quantities of scientific interest we can also derive turnover rates, defined as the probability that a site occupied at time t was not occupied at t – 1 by a randomly selected species (Nichols et al. 1998; Royle and Dorazio 2008; Russell et al. 2009; Ruiz-Gutiérrez and Zipkin 2011; Walls et al. 2011), as well as growth rate which is the ratio of species occurrence probability at time t + 1 and t (MacKenzie et al. 2003). An important biodiversity index derived from camera trapping data is the Wildlife Picture Index (WPI, O’Brien et al. 2010; see Chapter 10 for details on this index which is an official indicator of the Convention on Biological Diversity). The WPI can be estimated within the dynamic multi-species model fitted in a Bayesian framework, to fully account for the uncertainty in the estimated occurrence probabilities (Nichols 2010; see case study below, section 9.4.1). The index can be computed for an entire group of target species or for different subgroups of species, in relation to their conservation status or functional group (Ahumada et al. 2013).

Finally, we note that multi-species occupancy models assume a constant camera trap layout (i.e. data must be collected at the same sites during all primary periods) and they are thus not suited to model species occurrence across multiple sites or time periods if the camera trap layout changes. To this end, Tobler et al. (2015) provided a multi-session multi-species occupancy model that can combine data from multiple camera trap surveys.

We again use the data collected by the TEAM Network in the Udzungwa Mountains of Tanzania during the period 2009–2013 (as in the example above and in Chapters 5 and 6), whereby of the 60 camera trap sites originally set, 56 operated for more than 1 day during each of the 5 years of repeated sampling. Note that each camera operated a different number of days among the years, with the default sampling effort being set at 30 days per camera trap. From 24 to 28 species were detected during the 5 year period.

The reader should first extract the data needed in the following analysis by using the same code reported in section 9.3.1 to obtain the 2009 matrix of detection events for species by sampling sites events, and repeating the six lines beginning with the following one, for the remaining 4 years. Thus, for year 2010 the matrix extraction starts with this line of code:

ev2010<-event.sp(dtaframe=mam, year=2010.01, thresh=1440)

The five detection matrices, as they were extracted, contain sites (i.e. camera traps) that for the last 2 days of sampling did not operate every year. In addition, detection matrices have different number of rows in relation to the number of species detected every year, and the order of the species in the rows can vary among years. We thus first need to manipulate the data in order to remove camera trap sites that were not active all years and keep the same species order along the rows of every detection matrix. The following code performs this task. Readers will need to customise some parts of the following code to manipulate their data.

# load detection data and effort for the period 2009-2013

# get files' names

filesY <- list.files(pattern="spudz_")

names_objY <- paste("Y_",substring(filesY, first=9, last=10),sep="")

fileseff <- list.files(pattern="camera_days_")

names_objeff <- paste("effort_",substring(fileseff, first=15, last=16),sep="")

# open files and assign them names

for(i in seq(along=filesY)) {

assign(names_objY[i],

as.matrix(read.table(filesY[i],header=T,sep=" ")))

assign(names_objeff[i], read.table(fileseff[i],

header=T,sep="\t"))

}

# check dimensions of each data set

dimcheck <- sapply(mget(names_objY),FUN=dim)

dimcheck

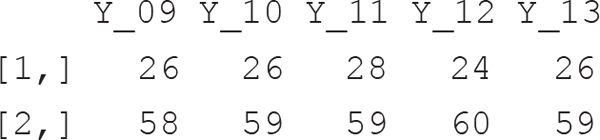
We can see from the table above that the number of detected species ranged from 24 to 28, whereas the number of active cameras ranged from 58 to 60.

### keep only sites active every year for at

# least two sampling occasions

# get trap names for each year

Yl <- list()

for (i in 1:length(names_objeff)){

Yl[[i]] <- get(names_objeff[i])[,1]

}

# homogenize trap names between detection matrices

# and effort data sets

Yl2 <- lapply(Yl,function(x) gsub("-",".",x))

for (i in 1:length(names_objeff)){

tmp <- get(names_objeff[i])

tmp[,1] <- Yl2[[i]]

assign(paste(names_objeff[i],"b",sep=""),tmp)

}

# check which traps in a specific year (Yl2[[n]])

# were not active in other years (unlist(Yl2[-n]))

traptodel <- lapply(1:length(Yl2), function(n) setdiff(unlist(Yl2[-n]),Yl2[[n]]))

traptodel2 <- unlist(traptodel)

traptodel3 <- traptodel2[-duplicated(unlist(traptodel2))]

traptodel3

[1] "CT.UDZ.3.13" "CT.UDZ.1.08" "CT.UDZ.1.12" "CT.UDZ.2.16"

# delete traps not active every year

names_objeff_b <- objects(pattern="b$")

for(i in 1:length(names_objeff_b)){

col_todel_Y <- which(colnames(get(names_objY[i]))

%in% traptodel3)

row_todel_eff <- which(Yl2[[i]] %in% traptodel3)

assign(paste("Y",i,sep=""),get(names_objY[i])[,-col_todel_Y])

assign(paste("effort",i,sep=""),get(names_objeff_b[i])

[-row_todel_eff,])

}

### insert all-zero rows for species not detected

# in a certain year

names_objY_b <- objects(pattern="^Y[1-5]")

# get species names for each year-specific dataset and

# a list of species names detected at least once

colnamesYs <- data.frame(matrix(nrow=28, ncol=5))

allnames <- NULL

for(i in 1:(length(names_objY_b))){

tmp <- rownames(get(names_objY_b[i]))

colnamesYs[(1:length(rownames(get(names_objY_b[i])))),i]

<- tmp

allnames <- c(allnames,tmp)

}

allnames2 <- allnames[-(which(duplicated(allnames)==T))]

allnames3 <- allnames2[order(allnames2)]

# total number of observed species during the period 2009-2013

allnames3

[1]	"Atilax paludinosus"	"Bdeogale crassicauda"
[3]	"Cephalophus harveyi"	"Cephalophus spadix"
[5]	"Cercocebus sanjei"	"Cercopithecus mitis"
[7]	"Civettictis civetta"	"Colobus angolensis"
[9]	"Cricetomys gambianus"	"Crocuta crocuta"
[11]	"Dendrohyrax arboreus"	"Genetta servalina"
[13]	"Hystrix africaeaustralis"	"Leptailurus serval"
[15]	"Loxodonta africana"	"Mellivora capensis"
[17]	"Mungos mungo"	"Nandinia binotata"
[19]	"Nesotragus moschatus"	"Panthera pardus"
[21]	"Papio cynocephalus"	"Paraxerus vexillarius"
[23]	"Petrodromus tetradactylus"	"Potamochoerus larvatus"
[25]	"Procolobus gordonorum"	"Rhynchocyon cirnei"
[27]	"Rhynchocyon udzungwensis"	"Syncerus caffer"
[29]	"Thryonomys swinderianus"	"Tragelaphus scriptus"

# see which species are not present in the different years

for(i in 1:(length(names_objY_b))){

print(which(sapply(allnames3,"%in%",colnamesYs[,i])==FALSE))

print("---------------------------")

}

1] "---------------------------"

[1] "---------------------------"

# edit the detection matrices in order to incorporate

# undetected species

not_detected <- rep(0,dim(Y1)[2])

Y1b <- rbind(Y1[1:9,],not_detected,Y1[10:12,], not_detected,Y1[13:26,],not_detected,not_detected)

Y2b <- rbind(Y2[1:6,],not_detected,Y2[7:12,],not_ detected,Y2[13:18,],not_detected,Y2[19:25,],not_ detected,Y2[26,])

Y3b <- rbind(Y3[1:6,],not_detected,Y3[7:11,], not_detected,Y3[12:28,])

Y4b <- rbind(Y4[1:6,],not_detected,Y4[7:8,], not_detected,Y4[9:11,],not_detected,Y4[12:13,], not_detected,Y4[14:16,],not_detected,Y4[17:20,], not_detected,Y4[21:24,])

Y5b <- rbind(Y5[1:6,],not_detected,Y5[7:8,], not_detected,Y5[9:10,],not_detected,not_detected,Y5[11:26,])

Following this rather long data handling, we can begin analysis by first augmenting the five year-specific detection matrices and bundle all the data into a three-dimensional matrix (Yaug_tot).

# augment detection data

names_objY_c <- objects(pattern="^Y[1-5]b")

nzeros <- 100

for(i in 1:(length(names_objY_c))){

nc <- dim(get(names_objY_c[i]))[2]

assign(paste(names_objY_c[i],"_aug",sep=""),

rbind(get(names_objY_c[i]), matrix(0, nrow=nzeros, ncol=nc))

)

}

# bind augmeted matricies

library(abind)

Yaug_tot <- abind(Y1b_aug,Y2b_aug,Y3b_aug,Y4b_aug,Y5b_aug, along=3)

attr(Yaug_tot, "dimnames") <- NULL

# number of sampling occasions for each camera in each year

names_objeff_c <- objects(pattern="^effort[1-5]")

K_tot <- matrix(NA, nrow=dim(Yaug_tot)[2],

ncol=length(names_objeff_c))

for(i in 1:length(names_objeff_c)){

K_tot[,i] <- get(names_objeff_c[i])[,"ndays"]

}

Finally, to derive subsequently the WPI within the model we need to define the target species for which the WPI is computed. For simplicity we choose a pool of only 10 species which includes carnivores, forest ungulates and the elephant.

# Target species for the WPI

speciesWPI <- c("Atilax paludinosus",

"Bdeogale crassicauda",

"Cephalophus harveyi",

"Cephalophus spadix",

"Genetta servalina",

"Loxodonta africana",

"Mellivora capensis",

"Nandinia binotata",

"Nesotragus moschatus",

"Panthera pardus")

nspeciesWPI <- length(speciesWPI)

# find out to which rows of the detection matrix

# these target species correspond

id_speciesWPI <- which(allnames3 %in% speciesWPI)

Now we are ready to write the model in BUGS language and run it. We define occurrence, detection, colonisation and persistence rates constant across sites, as follows:

logit(ψ_ij1) = b_i0, with b_i0 ~ Normal(μ_ψ1, σ_ψ1²)

logit(p_ijt) = a_it0, with a_it0 ~ Normal(μ_p, σ_p²)

logit(γ_ijt) = c_it0, with c_it0 ~ Normal (μ_γ, σ_γ²)

logit(φ_ijt) = d_it0, with d_it0 ~ Normal (μ_φ, σ_φ²).

# load libraries

library(rjags)

library(dclone)

# set seed

set.seed(1980)

# BUGS model

modelFilename = "dmsom.txt"

cat("

model {

# priors

omega ~ dunif(0,1)

psiMean ~ dunif(0,1)

for (t in 1:T) {

pMean[t] ~ dunif(0,1)

}

for (t in 1:(T-1)) {

phiMean[t] ~ dunif(0,1)

gamMean[ t] ~ dunif(0,1)

}

lpsiMean <- log(psiMean) - log(1-psiMean)

for (t in 1:T) {

lpMean[t] <- log(pMean[t]) - log(1-pMean[t])

}

for (t in 1:(T-1)) {

lphiMean[t] <- log(phiMean[t]) - log(1-phiMean[t])

lgamMean[t] <- log(gamMean[t]) - log(1-gamMean[t])

}

lpsiSD ~ dunif(0,10)

lpsiPrec <- pow(lpsiSD,-2)

lpSD ~ dunif(0,10)

lphiSD ~ dunif(0,10)

lgamSD ~ dunif(0,10)

for (t in 1:T) {

lpPrec[t] <- pow(lpSD,-2)

}

for (t in 1:(T-1)) {

lphiPrec[t] <- pow(lphiSD,-2)

lgamPrec[t] <- pow(lgamSD,-2)

}

# likelihood

for (i in 1:M) {

# initial occupancy state at t=1

w[i] ~ dbern(omega)

b0[i] ~ dnorm(lpsiMean, lpsiPrec)T(-12,12)

lp[i,1] ~ dnorm(lpMean[1], lpPrec[1])T(-12,12)

p[i,1] <- 1/(1+exp(-lp[i,1]))

for (j in 1:n.site) {

lpsi[i,j,1] <- b0[i]

psi[i,j,1] <- 1/(1 + exp(-lpsi[i,j,1]))

mu.z[i,j,1] <- w[i] * psi[i,j,1]

Z[i,j,1] ~ dbern(mu.z[i,j,1])

mu.y[i,j,1] <- p[i,1]*Z[i,j,1]

Y[i,j,1] ~ dbin(mu.y[i,j,1], K_tot[j,1])

}

# model of changes in occupancy state for t=2, ...,

# T for (t in 1:(T-1)) {

lp[i,t+1] ~ dnorm(lpMean[t+1], lpPrec[t+1])T(-12,12)

p[i,t+1] <- 1/(1+exp(-lp[i,t+1]))

c 0[i,t] ~ dnorm(lgamMean[t], lgamPrec[t])T(-12,12)

d0[i,t] ~ dnorm(lphiMean[t], lphiPrec[t])T(-12,12)

for (j in 1:n.site) {

lgam[i,j,t] <- c0[i,t]

gam[i,j,t] <- 1/(1+exp(-lgam[i,j,t]))

lphi[i,j,t] <- d0[i,t]

phi[i,j,t] <- 1/(1+exp(-lphi[i,j,t]))

psi[i,j,t+1] <- phi[i,j,t]*psi[i,j,t] +

gam[i,j,t]*(1-psi[i,j,t])

mu.z[i,j,t+1] <- w[i] * (phi[i,j,t]*Z[i,j,t] +

gam[i,j,t]*(1-Z[i,j,t]))

Z[i,j,t+1] ~ dbern(mu.z[i,j,t+1])

mu.y[i,j,t+1] <- p[i,t+1]*Z[i,j,t+1]

Y[i,j,t+1] ~ dbin(mu.y[i,j,t+1], K_tot[j,t+1])

}

# Derive total species richness for the metacommunity

N_tot <- sum(w[])

# Derive yearly species richness

for (i in 1:M) {

for (t in 1:T) {

tmp[i,t] <- sum(Z[i,,t])

tmp2[i,t] <- ifelse(tmp[i,t]==0,0,1)

}

for (t in 1:T) {

N[t] <- sum(tmp2[,t])

}

# Derive WPI

for (i in 1:nspeciesWPI) {

for (t in 1:T) {

psi_ratio[i,t] <- psi[id_speciesWPI[i],1,t]/psi[id_

speciesWPI[i],1,1]

log_psi_ratio[i,t] <- log(psi_ratio[i,t])

}

for (t in 1:T) {

WPI[t] <- exp((1/(nspeciesWPI))*sum(log_psi_

ratio[1:nspeciesWPI,t]))

}

# rate of change in WPI

for (t in 1:(T-1)) {

lambda_WPI[t] <- WPI[t+1]/WPI[t]

}

", fill=TRUE, file=modelFilename)

# number of traps

nsites <- dim(Yaug_tot)[2]

# number of primary periods (years)

T <- dim(Yaug_tot)[3]

# latent states

w <- c(rep(1,length(allnames3)),rep(NA,nzeros))

# Parameters monitored

parameters <- c("omega","psiMean","pMean","phiMean","gamMean", "lpsiSD","lpSD","lphiSD","lgamSD","N" ,"N_tot","WPI","lambda_WPI")

# data

bugs.data <- list(M=dim(Yaug_tot)[1],n.site=nsites, K_tot=K_tot,Y=Yaug_tot,T=T,nspeciesWPI=nspeciesWPI, id_speciesWPI=id_speciesWPI)

# Initial values

inits <- function() { list(omega=runif(1),Z=(Yaug_tot>0)*1,w=w, psiMean=runif(1),pMean=runif(T),phiMean=runif(T-1), gamMean=runif(T-1),lpsiSD=runif(1,0,4),lpSD=runif(1,0,4), lphiSD=runif(1,0,4),lgamSD=runif(1,0,4))}

#mcmc settings

n.adapt <- 5000	#pre-burnin
n.update <- 10000	#burnin
n.iter <- 50000	#iterations post-burnin

thin <- 10

chains<-3

# run the model and record the run time

cl <- makeCluster(chains, type = "SOCK")

start.time = Sys.time()

out <- jags.parfit(cl, data = bugs.data,

params = parameters,

model = "dmsom.txt",

inits = inits,

n.adapt = n.adapt,

n.update = n.update,

n.iter = n.iter,

thin = thin, n.chains = chains)

end.time = Sys.time()

elapsed.time = difftime(end.time, start.time, units='mins')

cat(paste(paste('Posterior computed in ', elapsed.time, sep=''), ' minutes\n', sep=''))

stopCluster(cl)

#Posterior computed in 137.004419155916 minutes

# Summarize posteriors

summary(out)

Iterations = 15010:65000

Thinning interval = 10

Number of chains = 3

Sample size per chain = 5000

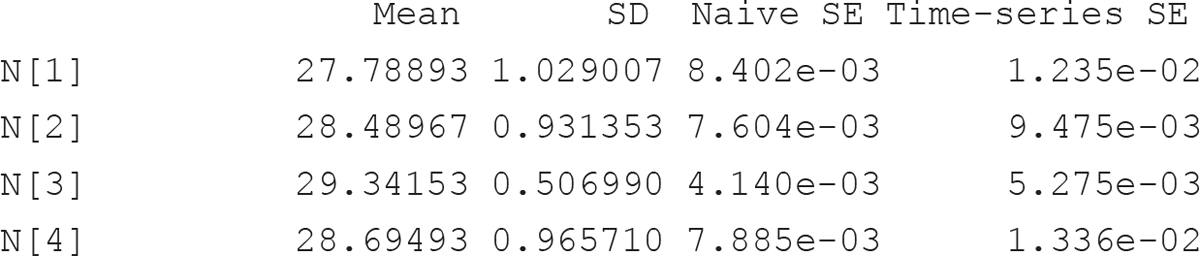
1. Empirical mean and standard deviation for each variable, plus standard error of the mean:

2. Quantiles for each variable:

# check output (there are many parameters monitored,

# therefore it is advisable to plot them in separate bunches)

xyplot(out[,c("omega","psiMean","lpsiSD","lpSD","lphiSD", "lgamSD"), drop=F])

xyplot(out[,c("pMean[1]","pMean[2]","pMean[3]","pMean[4]", "pMean[5]"), drop=F])

xyplot(out[,c("gamMean[1]","gamMean[2]","gamMean[3]", "gamMean[4]"), drop= F])

xyplot(out[,c("phiMean[1]","phiMean[2]","phiMean[3]", "phiMean[4]"), drop= F])

We have derived both species richness for each year (N; Figure 9.2) and total species richness for the 5 year period (N_tot; Fig. 9.3). Note that the median value for the latter corresponds to the total number of observed species, but the 99% credible interval for the estimate is 30–31, indicating that almost all species (exposed to sampling) of the (meta) community were overall observed during the 5 years of study. The average (among species) probabilities of detection, persistence and colonisation are indicated in the model output, for each year, by pMean (which corresponds to expit(μ_p), where expit is the inverse-logit function), phiMean (expit(μ_φ)) and gamMean (expit(μ_γ)), respectively, and are all reported on the probability scale. The average occurrence probability for the first year is denoted by psiMean (expit(μ_ψ1)). Heterogeneity among species of these probabilities are indicated by lpSD (σ_p), lphiSD (σ_φ), lgamSD (σ_γ) and lpsiSD (σ_ψ1), respectively. Parameter omega (ω) denotes the probability that a species is a member of the community of size N exposed to sampling during the 5 years. Persistence and colonisation probabilities are nearly constant among years and their 95% credible intervals largely overlap.

We derived the WPI (Figure 9.3) directly within the dynamic multi-species occupancy model, an advantage only provided by the latter framework. As an alternative, we may choose to monitor the matrix of year-specific occurrence probabilities of target species in JAGS, and then export it to R where the WPI can be derived. An example of this approach can be found in Ahumada et al. (2013), where WPI was not derived directly in JAGS since the authors used single-species dynamic occupancy models.

Note that we also derived the rate of change in WPI from year t to t + 1 (lambda_WPI) calculated as WPI_t _{+ 1}/WPI_t.

We have described multi-species occupancy models, a versatile framework that can be used to estimate quantities of ecological interest at different levels of ecological organisation, from single species, to local communities of species, and even to metacommunities. In this framework, estimates for species richness and other biodiversity measures that account for imperfect detection can be derived within the model. This statistical approach is flexible, allowing for modelling covariates on species occurrence and detection probabilities and, in a dynamic, multi-season version, on persistence and colonisation probabilities. In the latter case, the spatiotemporal dynamics of biodiversity estimators can be also analysed.

We have to be aware of the fact that estimates of community-level parameters can be sensitive to the underlying assumptions of the model, such as the type of the distribution chosen to model heterogeneity among species and sites. Standard goodness-of-fit approaches might not be adequate to test these assumptions. The models presented here also rely on a closure assumption (replicated observations of species are made over a short time interval during which occurrence states of species are assumed constant). Currently the closure assumption has been relaxed only for single-species dynamic occupancy models (Chambert et al. 2015). Another assumption of these models is the absence of false-positives, i.e. all species are assumed to be correctly identified (an assumption which is usually easily met by camera trapping data). False-positive errors in detection tend to positively bias estimates of occurrence probability because species detections are erroneously assigned to sites where the species is not present (Royle and Link 2006). Finally, Yamaura et al. (2011) developed a multi-species abundance model for presence–absence data that can estimate species abundance in space and time by using the Royle–Nichols formulation (Royle and Nichols 2003) of detection heterogeneity.

The author is grateful to Jorge Ahumada and Fridolin Zimmermann for valuable comments on a previous version of this chapter.

For dataset and extraction of detection matrices, see the following appendices to Chapter 5:

Ahumada, J.A., Hurtado, J. and Lizcano, D. (2013) Monitoring the status and trends of tropical forest terrestrial vertebrate communities from camera trap data: a tool for conservation. PLoS ONE 8: e73707.

Broms, K.M., Hooten, M.B. and Fitzpatrick, R.M. (2014) Accounting for imperfect detection in Hill numbers for biodiversity studies. Methods in Ecology and Evolution 6: 99–108.

Brooks, S.P. and Gelman, A. (1998) Alternative methods for monitoring convergence of interative simulations. Journal of Computational and Graphical Statistics: 434–455.

Burton, A.C., Sam, M.K., Balangtaa, C. and Brashares, J.S. (2012) Hierarchical multi-species modeling of carnivore responses to hunting, habitat and prey in a West African protected area. PLoS ONE 7: e38007.

Carrillo-Rubio, E., Kéry, M., Morreale, S.J., Sullivan, P.J., Gardner, B., Cooch, E.G. and Lassoie, J.P. (2014) Use of multispecies occupancy models to evaluate the response of bird communities to forest degradation associated with logging. Conservation Biology 28: 1034–1044.

Chambert, T., Kendall, W.L., Hines, J.E., Nichols, J.D., Pedrini, P., Waddle, J.H., Tavecchia, G., Walls, S.C. and Tenan, S. (2015) Testing hypotheses on distribution shifts and changes in phenology of imperfectly detectable species. Methods in Ecology and Evolution 6: 638–647.

Chao, A. and Jost, L. (2012) Coverage-based rarefaction and extrapolation: standardizing samples by completeness rather than size. Ecology 93: 2533–2547.

Chao, A., Gotelli, N.J., Hsieh, T., Sander, E.L., Ma, K., Colwell, R.K. and Ellison, A.M. (2014) Rarefaction and extrapolation with Hill numbers: a framework for sampling and estimation in species diversity studies. Ecological Monographs 84: 45–67.

De Valpine, P. and Hastings, A. (2002) Fitting population models incorporating process noise and observation error. Ecological Monograph 72: 57–76.

Dice, L.R. (1945) Measures of the amount of ecologic association between species. Ecology 26: 297–302.

Dorazio, R.M. (2007) On the choice of statistical models for estimating occurrence and extinction from animal surveys. Ecology 88: 2773–2782.

Dorazio, R.M. and Royle, J.A. (2005) Estimating size and composition of biological communities by modeling the occurrence of species. Journal of the American Statistical Association 100: 389–398.

Dorazio, R.M., Royle, J.A., Söderström, B. and Glimskär, A. (2006) Estimating species richness and accumulation by modeling species occurrence and detectability. Ecology 87: 842–854.

Dorazio, R.M., Kéry, M., Royle, J.A. and Plattner, M. (2010) Models for inference in dynamic metacommunity systems. Ecology 91: 2466–2475.

Dorazio, R.M., Gotelli, N.J. and Ellison, A.M. (2011) Biodiversity loss in a changing planet. In: Grillo, O. and Venora, G. (eds), Modern Methods of Estimating Biodiversity from Presence– Absence Surveys. Rijeka, Croatia: InTech. pp. 277–302.

Gelman, A., Carlin, J.B., Stern, H.S., Rubin, D.B. (2004) Bayesian Data Analysis, 2nd edn. Boca Raton, FL: CRC/Chapman & Hall.

Gotelli, N.J. (2000) Null model analysis of species co-occurrence patterns. Ecology 81: 2606–2621.

Gotelli, N. and Colwell, R. (2001) Quantifying biodiversity: procedures and pitfalls in the measurement and comparison of species richness. Ecology Letters 4: 379–391.

Gotelli, N., Chao, A. and Levin, S. (2013) Measuring and estimating species richness, species diversity, and biotic similarity from sampling data. Encyclopedia of Biodiversity 5: 195–211.

Hill, M.O. (1973) Diversity and evenness: a unifying notation and its consequences. Ecology 54: 427–432.

Hooten, M.B. and Hobbs, N.T. (2014) A guide to Bayesian model selection for ecologists. Ecological Monographs 85: 3–28.

Kéry, M. and Royle, J. (2008) Hierarchical Bayes estimation of species richness and occupancy in spatially replicated surveys. Journal of Applied Ecology 45: 589–598.

Kéry, M. and Royle, J.A. (2009) Inference about species richness and community structure using species-specific occupancy models in the national Swiss breeding bird survey. In: Thomson, D.L., Cooch, E.G. and Conroy, M.J. (eds), Modeling Demographic Processes in Marked Populations. Berling: Springer. pp. 639–656.

Kéry, M. and Schaub, M. (2012) Bayesian Population Analysis Using WinBUGS: A Hierarchical Perspective. New York: Academic Press.

Kéry, M., Royle, J.A., Plattner, M. and Dorazio, R.M. (2009) Species richness and occupancy estimation in communities subject to temporary emigration. Ecology 90: 1279–1290.

King, R. (2009) Bayesian Analysis for Population Ecology. Boca Raton, FL: CRC Press.

Link, W.A. and Barker, R.J. (2006) Model weights and the fundations of multimoldel inference. Ecology 87: 2626–2635.

Link, W.A. and Barker, R.J. (2009) Bayesian Inference: With Ecological Applications. New York: Academic Press.

MacKenzie, D.I., Nichols, J.D., Hines, J.E., Knutson, M.G. and Franklin, A.B. (2003) Estimating site occupancy, colonization, and local extinction when a species is detected imperfectly. Ecology 84: 2200–2207.

MacKenzie, D.I., Bailey, L.L. and Nichols, J.D. (2004) Investigating species co-occurrence patterns when species are detected imperfectly. Journal of Animal Ecology 73: 546–555.

Magurran, A.E. and McGill, B.J. (2011) Biological Diversity: Frontiers in Measurement and Assessment, Vol. 12. Oxford: Oxford University Press.

McNew, L.B. and Handel, C.M. (2015) Evaluating species richness: biased ecological inference results from spatial heterogeneity in detection probabilities. Ecological Applications, in press.

Nichols, J. (2010) The wildlife picture index, monitoring and conservation. Animal Conservation 13: 344–346.

Nichols, J.D., Boulinier, T., Hines, J.E., Pollock, K.H. and Sauer, J.R. (1998) Estimating rates of local species extinction, colonization, and turnover in animal communities. Ecological Applications 8: 1213–1225.

O’Brien, T., Baillie, J., Krueger, L. and Cuke, M. (2010) The wildlife picture index: monitoring top trophic levels. Animal Conservation 13: 335–343.

O’Hara, R.B. and Sillanpää, M.J. (2009) A review of Bayesian variable selection methods: what, how and which. Bayesian Analysis 4: 85–118.

Plummer, M. (2003) JAGS: a program for analysis of Bayesian graphical models using Gibbs sampling. Proceedings of the 3rd International Workshop on Distributed Statistical Computing ( DSC 2003), Technische Universität Wien, Vienna, Austria. https://www.r-project.org/conferences/DSC-2003/Proceedings/Plummer.pdf

Plummer, M. (2013) rjags: Bayesian graphical models using MCMC. R package v. 3-10.

Pollock, K.H. (1982) A capture–recapture design robust to unequal probability of capture. Journal of Wildlife Management 46: 757–760.

R Core Team (2012) R: A Language and Environment for Statistical Computing. Vienna: R Foundation for Statistical Computing. ISBN 3-900051-07-0.

Robert, C. and Casella, G. (2004) Monte Carlo Statistical Methods. New York: Springer.

Rovero, F., Martin, E., Rosa, M., Ahumada, J.A. and Spitale, D (2014) Estimating species richness and modelling habitat preferences of tropical forest mammals from camera trap data. PLoS ONE 9(7): e103300.

Royle, J.A. and Nichols, J.D. (2003) Estimating abundance from repeated presence–absence data or point counts. Ecology 84: 777–790.

Royle, J.A. and Link, W.A. (2006) Generalized site occupancy models allowing for false positive and false negative errors. Ecology 87: 835–841.

Royle, J.A. and Dorazio, R. (2008) Hierarchical Modeling and Inference in Ecology: The Analysis of Data from Populations, Metapopulations and Communities. San Diego: Academic Press.

Royle, J.A. and Young, K.V. (2008) A hierarchical model for spatial capture–recapture data. Ecology 89: 2281–2289.

Royle, J.A. and Dorazio, R. (2011) Parameter-expanded data augmentation for Bayesian analysis of capture–recapture models. Journal of Ornithology 152 (Suppl. 2): S521–S537.

Royle, J.A., Dorazio, R.M. and Link, W.A. (2007) Analysis of multinomial models with unknown index using data augmentation. Journal of Computational and Graphical Statistics 16: 67–85.

Ruiz-Gutiérrez, V. and Zipkin, E.F. (2011) Detection biases yield misleading patterns of species persistence and colonization in fragmented landscapes. Ecosphere 2: art61.

Russell, R.E., Royle, J.A., Saab, V.A., Lehmkuhl, J.F., Block, W.M. and Sauer, J.R. (2009) Modeling the effects of environmental disturbance on wildlife communities: avian responses to prescribed fire. Ecological Applications 19: 1253–1263.

Sutherland, C., Brambilla, M., Pedrini, P. and Tenan, S. (2016) A multi-region community model for inference about geographic variation in species richness. Methods in Ecology and Evolution doi: 10.1111/2041-210X.12536.

Tanner, M.A. and Wong, W.H. (1987) The calculation of posterior distributions by data augmentation. Journal of the American Statistical Association 82: 528–540.

Tenan, S., O’Hara, R.B., Hendriks, I. and Tavecchia, G. (2014) Bayesian model selection: the steepest mountain to climb. Ecological Modelling 283: 62–69.

Tenan, S., Brambilla, M., Pedrini, P. and Sutherland, C. (2016) Evaluating biodiversity gradients while accounting for ecological stratification of communities (in review).

Tobler, M.W., Zúñiga Hartley, A., Carrillo-Percastegui, S.E. and Powell, G.V. (2015) Spatiotemporal hierarchical modelling of species richness and occupancy using camera trap data. Journal of Applied Ecology 52: 413–421.

Waddle, J.H., Dorazio, R.M., Walls, S.C., Rice, K.G., Beauchamp, J., Schuman, M.J. and Mazzotti, F.J. (2010) A new parameterization for estimating co-occurrence of interacting species. Ecological Applications 20: 1467–1475.

Walls, S.C., Waddle, J.H. and Dorazio, R.M. (2011) Estimating occupancy dynamics in an anuran assemblage from Louisiana, USA. Journal of Wildlife Management 75: 751–761.

Yamaura, Y., Andrew Royle, J., Kuboi, K., Tada, T., Ikeno, S. and Makino, S. (2011) Modelling community dynamics based on species-level abundance models from detection/nondetection data. Journal of Applied Ecology 48: 67–75.

Zipkin, E.F., DeWan, A. and Andrew Royle, J. (2009) Impacts of forest fragmentation on species richness: a hierarchical approach to community modelling. Journal of Applied Ecology 46: 815–822.

Zipkin, E.F., Andrew Royle, J., Dawson, D.K. and Bates, S. (2010) Multi-species occurrence models to evaluate the effects of conservation and management actions. Biological Conservation 143: 479–484.

1 M can be either arbitrary large, or can be set on the basis of prior information about the total diversity of species known for the region (Dorazio et al. 2011).

logit(p_ijk) = a_i0 + a_i1 date_jk + a_i2 date_jk²	(9.1)
logit(ψ_ij) = b_i0 + b_i1 elevation_j + b_i2 elevation²_j.	(9.2)