So far, you’ve done everything right. You dug deep to define the right problem. You balanced the true requirements with a careful selection of algorithms and data structures. You used the techniques of program verification to write elegant pseudocode that you’re pretty sure is correct. How do you incorporate the resulting gem into your big system? All that’s left is, well, a small matter of programming.
Programmers are optimists, and they are tempted to take the easy path: code up the function, slip it into the system, and fervently hope that it runs. Sometimes that works. But the other 999 times out of 1000, it leads to disaster: one has to grope around in the huge system to manipulate the little function.
Wise programmers instead build scaffolding to give them easy access to the function. This column is devoted to implementing the binary search described in pseudocode in the last column as a trustworthy C function. (The code would be very similar in C++ or Java, and the approach works for most other languages.) Once we have the code, we’ll probe it with scaffolding, then move on to test it more thoroughly and conduct experiments on its running time. For a tiny function, our path is long. The result, though, is a program we can trust.
We’ll assume that the array x and the target item t are both of type DataType, which is defined by a C typedef statement like
typedef int DataType;
The defined type might be long integer, floating point, or whatever. The array is implemented by two global variables:
int n;
DataType x[MAXN];
(Although this is poor style for most C programs, it reflects the way that we access data within a C++ class; global variables can also result in smaller scaffolding.) Our goal is this C function:
int binarysearch(DataType t)
/* precondition: x[0] <= x[1] <= ... <= x[n-1]
postcondition:
result == -1 => t not present in x
0 <= result < n => x[result] == t
*/
Most of the pseudocode statements in Section 4.2 translate line-by-line into C (and most other languages, for that matter). Where the pseudocode stores a value in the answer variable p, the C program will return the value. Replacing the pseudocode loop with the C infinite loop for (;;) yields this code:
for (;;) {
if (1 > u)
return -1;
... rest of loop ...
}
We can transform that to a while loop by reversing the test:
while (1 <= u) {
... rest of loop ...
}
return -1;
The final program is then:
int binarysearch(DataType t)
/* return (any) position if t in sorted x[0..n-1] or
-1 if t is not present */
{ int l, u, m;
l = 0;
u = n-1;
while (l <= u) {
m = (l + u) / 2;
if (x[m] < t)
l = m+1;
else if (x[m] == t)
return m;
else /* x[m] > t */
u = m-1;
}
return -1;
}
The first step in exercising the function is, of course, to walk through a few test cases by hand. Tiny cases (zero-, one- and two-element arrays) often suffice to smoke out bugs. On larger arrays such tests become tedious, so the next step is to build a driver to call the function. Five lines of C scaffolding can do the job:
while (scanf("%d %d", &n, &t) != EOF) {
for (i = 0; i < n; i++)
x[i] = 10*i;
printf(" %d\n", binarysearch(t));
}
We can start with a C program of about two dozen lines: the binarysearch function and the above code in the main function. We should expect to grow the program as we add additional scaffolding.
When I type the input line “2 0”, the program generates the two-element array with x[0] = 0 and x[1] = 10, then reports (on the next, indented, line) that the result of searching for 0 was that it was in location 0:
2 0
0
2 10
1
2 -5
-1
2 5
-1
2 15
-1
The typed input is always in italics. The next pair of lines shows that 10 is correctly found in location 1. The final six lines describe three correct unsuccessful searches. The program thus correctly handles all possible searches in an array of two distinct elements. As the program passed similar tests on inputs of other sizes, I grew more and more confident of its correctness and more and more bored with this laborious hand testing. The next section describes scaffolding to automate this job.
Not all testing proceeds this smoothly. Here is a binary search proposed by several professional programmers:
int badsearch(DataType t)
{ int l, u, m;
l = 0;
u = n-1;
while (l <= u) {
m = (l + u) / 2;
/* printf(" %d %d %d\n", l, m, u); */
if (x[m] < t)
l = m;
else if (x[m] > t)
u = m;
else
return m;
}
return -1;
}
(We’ll return shortly to the commented-out printf statement.) Can you spot any problems in the code?
The program passed the first two little tests. It found 20 in position 2 of a 5-element array, and found 30 in position 3:
5 20
2
5 30
3
5 40
...
When I searched for 40, though, the program went into an infinite loop. Why?
To solve the puzzle, I inserted the printf statement that appears as a comment above. (It is outdented to the left margin to show that it is scaffolding.) It displays the sequence of values of l, m and u for each search:
5 20
0 2 4
2
5 30
0 2 4
2 3 4
3
5 40
0 2 4
2 3 4
3 3 4
3 3 4
3 3 4
...
The first search finds 20 on the first probe, and the second search finds 30 on the second probe. The third search is fine for the first two probes, but on the third probe goes into an infinite loop. We could have discovered that bug as we tried (in vain) to prove the termination of the loop.
When I have to debug a little algorithm deep inside a big program, I sometimes use debugging tools like single-stepping through the huge program. When I work on an algorithm using scaffolding like this, though, print statements are usually faster to implement and more effective than sophisticated debuggers.
Assertions played several key roles as we developed the binary search in Column 4: they guided the development of the code, and they allowed us to reason about its correctness. We’ll now insert them into the code to ensure that the run-time behavior matches our understanding.
We’ll use an assert to state that we believe a logical expression to be true. The statement assert(n > 0) will do nothing if n is zero or greater, but will raise an error of some sort if n is negative (perhaps invoking a debugger). Before reporting that binary search has found its target, we might make this assertion:
...
else if (x[m] == t) {
assert(x[m] == t);
return m;
} else
...
This weak assertion merely repeats the condition in the if statement. We might want to strengthen it to assert that the return value is in the input range:
assert(0 <= m && m < n && x[m] == t);
When the loop terminates without finding the target value, we know that l and u have crossed, and we therefore know that the element is not in the array. We might be tempted to assert that we have found a pair of adjacent elements that bracket it:
assert(x[u] < t && x[u+1] > t);
return -1;
The logic is that if we see 1 and 3 adjacent in the sorted table, then we know with certainty that 2 is not present. This assertion will sometimes fail, though, even for a correct program; why?
When n is zero, the variable u is initialized to -1, so the indexing will access an element outside the array. To make the assertion useful, we must therefore weaken it by testing for the edges:
assert((u < 0 || x[u] < t) && (u+1 >= n || x[u+1] > t));
This statement will indeed find some bugs in faulty searches.
We proved that the search always halts by showing that the range decreases in each iteration. We can check that property during execution with a little extra computation and an assertion. We initialize size to n + 1, then insert the following code after the for statement:
oldsize = size;
size = u – l + 1;
assert(size < oldsize);
I would be embarrassed to admit in public how many times I’ve tried in vain to debug a “broken” binary search, only to find that the array to be searched was not sorted. Once we define this function
int sorted()
{ int i;
for (i = 0; i < n-1; i++)
if (x[i] > x[i+1])
return 0;
return 1;
}
we can assert(sorted()). We should be careful, though, to make this pricey test only once before all searches. Including the test in the main loop could result in a binary search that runs in time proportional to n log n.
Assertions are helpful as we test the function in its scaffolding, and as we move from component test through system test. Some projects define assert with a preprocessor so the assertions can be compiled away and thereby incur no run-time overhead. On the other hand, Tony Hoare once observed that a programmer who uses assertions while testing and turns them off during production is like a sailor who wears a life vest while drilling on shore and takes it off at sea.
Chapter 2 of Steve Maguire’s Writing Solid Code (Microsoft Press, 1993) is devoted to the use of assertions in industrial-strength software. He describes in detail several war stories of the use of assertions in Microsoft’s products and libraries.
You’ve played with the program enough to be pretty sure it is correct, and you’re bored feeding it cases by hand. The next step is to build scaffolding to attack it by machine. The main loop of the test function runs n from the smallest possible value (zero) to the largest reasonable value:
for n = [0, maxn]
print "n=", n
/* test value n */
The print statement reports the progress of the test. Some programmers hate it: it produces clutter but no substantial information. Others find solace in watching the progress of the test, and it can be useful to know what tests were passed when you see the first bug.
The first part of the testing loop examines the case in which all elements are distinct (it also puts a spare at the top of the array to ensure that the search does not locate it).
/* test distinct elements (plus one at the end) */
for i = [0, n]
x[i] = 10*i
for i = [0, n)
assert(s(10*i) == i)
assert(s(10*i - 5) == -1)
assert(s(10*n – 5) == -1)
assert(s(10*n) == -1)
To make it easy to test various functions, we define the function to be tested:
#define s binarysearch
The assertions test every possible position for successful and unsuccessful searches, and the case that an element is in the array but outside the search bounds.
The next part of the testing loop probes an array of equal elements:
/* test equal elements */
for i = [0, n)
x[i] = 10
if n == 0
assert(s(10) == -1)
else
assert(0 <= s(10) && s(10) < n)
assert(s(5) == -1)
assert(s(15) == -1)
This searches for the element that is there, and for a lesser and greater element.
These tests poke around most of the program. Testing n from zero to 100 covers the empty array, common sizes for bugs (zero, one and two), several powers of two, and many numbers one away from a power of two. The tests would have been dreadfully boring (and therefore error prone) by hand, but they used an insignificant amount of computer time. With maxn set to 1000, the tests require only a few seconds of run time on my computer.
The extensive testing supports our belief that the search is correct. How can we similarly bolster our belief that it does the job using about log2 n comparisons? Here is the main loop of the timing scaffolding:
while read(algnum, n, numtests)
for i = [0, n)
x[i] = i
starttime = clock()
for testnum = [0, numtests)
for i = [0, n)
switch (algnum)
case 1: assert(binarysearchl(i) == i)
case 2: assert(binarysearch2(i) == i)
clicks = clock() - starttime
print algnum, n, numtests, clicks,
clicks/(1e9 * CLOCKS_PER_SEC * n * numtests)
This code computes the average run time of a successful binary search in an array of n distinct elements. It first initializes the array, then performs a search for each element of the array a total of numtests times. The switch statement selects the algorithm to be tested (scaffolding should always be prepared to test several variants). The print statement reports the three input values and two output values: the raw number of clicks (it is always crucial to inspect those numbers), and a value easier to interpret (in this case, the average cost of a search in nanoseconds, given by the conversion factor 1e9 in the print statement).
Here is an interactive session with the program on a 400MHz Pentium II, with typed input, as usual, in italics:
1 1000 10000
1 1000 10000 3445 344.5
1 10000 1000
1 10000 1000 4436 443.6
1 100000 100
1 100000 100 5658 565.8
1 1000000 10
1 1000000 10 6619 661.9
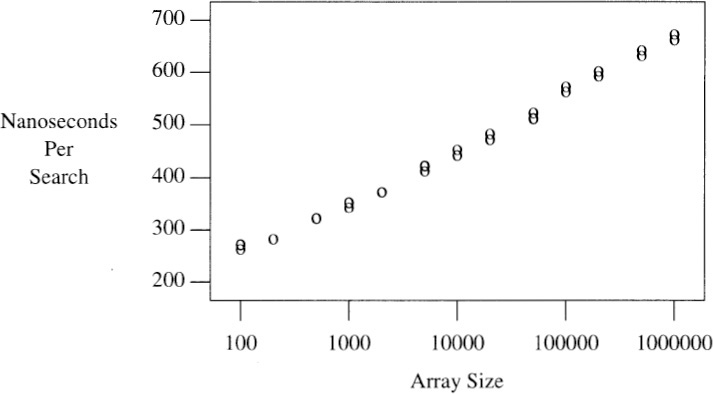
The first line tests algorithm 1 (the binary search we’ve studied so far) on an array of size 1000, and performs the tests 10000 times. It takes 3445 clock ticks (reported on this system in milliseconds), which translates to an average cost of 344.5 nanoseconds per search. Each of the three subsequent trials increases n by a factor of 10, and decreases the number of tests by the same factor. The run time for a search seems to be roughly 50 + 30log2 n nanoseconds.
I next wrote a three-line program to generate input for the timing scaffolding. The output is plotted in the graph, which shows that the average search cost indeed grows as log n. Problem 7 observes a potential timing bug in this scaffolding; be sure to study that before you put too much faith in such numbers.
I believe that the C implementation of binary search is correct. Why? I carefully derived the pseudocode in a convenient language, then used analytic techniques to verify its correctness. I translated it into C line-by-line, and fed the program inputs and watched the output. I sprinkled assertions through the code to ensure that my theoretical analysis matched the behavior in practice. A computer did what it’s good at and bombarded the program with test cases. Finally, simple experiments showed that its run time was as low as theory predicted.
With this background, I’d feel comfortable using the code to search a sorted array in a big program. I’d be pretty surprised if a logic bug showed up in this C code. I wouldn’t be shocked to find many other kinds of bugs, though. Did the caller remember to sort the table? Is –1 the desired return value when the search item isn’t in the table? If the target item occurs many times in the table, this code returns an arbitrary index; did the user really want the first or the last? And so on and so on.
Can you trust this code? You could take my word for it. (If you are inclined in this direction, I currently own a very nice bridge that you might be interested in purchasing.) Alternatively, you can get a copy of the program from this book’s web site. It includes all of the functions we’ve seen so far, and several variants of binary search that we’ll study in Column 9. Its main function looks like:
int main(void)
{ /* probe1(); */
/* test(25); */
timedriver();
return 0;
}
By commenting out all but one call, you can play with particular inputs, deluge it with test cases, or run timing experiments.
This column has thrown a lot of effort at a little problem. The problem may be small, but it’s not easy. Recall from Section 4.1 that while the first binary search was published in 1946, the first binary search that works correctly for all values of n did not appear until 1962. If early programmers had taken the approach in this column, it might not have taken them 16 years to derive a correct binary search.
Scaffolding. The best kind of scaffolding is usually that which is easiest to build. For some tasks, the easiest scaffolding consists of a graphical user interface implemented in a language like Visual Basic or Java or Tcl. In each of those languages, I’ve whipped up little programs in half an hour with point-and-click control and fancy visual output. For many algorithmic tasks, though, I find it easier to ignore those powerful tools in favor of the simpler (and more portable) command-line techniques that we’ve seen in this column.
Coding. I find it easiest to sketch a hard function in a convenient high-level pseudocode, then translate it into the implementation language.
Testing. One can test a component much more easily and thoroughly in scaffolding than in a large system.
Debugging. Debugging is hard when a program is isolated in its scaffolding, and much harder yet when it is embedded in its real environment. Section 5.10 tells tales of debugging large systems.
Timing. If run time doesn’t matter, linear search is much simpler than binary search; many programmers can get it right on the first try. Because run time is important enough for us to introduce the additional complexity of binary search, we should conduct experiments to ensure that its performance is what we expect.
1. Comment on the programming style used in this column, and in this book, in general. Address issues such as the variable names, the form and specification of the binary search function, the code layout and so forth.
2. Translate the pseudocode description of binary search into languages other than C, and build scaffolding to test and debug your implementation. How do the language and system help and hinder?
3. Introduce errors into the binary search function. How are your errors caught by the tests? How does the scaffolding help you chase down the bugs? (This exercise is best carried out as a two-player game, in which the attacker introduces bugs that the defender must then track.)
4. Repeat Problem 3, but this time, leave the binary search code correct and introduce errors into the functions that call it (such as forgetting to sort the array).
5. [R. S. Cox] A common bug applies binary search to an unsorted array. Completely checking whether the array is sorted before each search has the exorbitant cost of n – 1 extra comparisons. How can you add partial checking to the function at significantly less cost?
6. Implement a graphical user interface for studying binary search. Is the bang (in increased debugging effectiveness) worth the buck (in development time)?
7. The timing scaffolding in Section 5.5 has a potential timing bug: by searching for each element in order, we get particularly beneficial caching behavior. If we know that the searches in the potential application will exhibit similar locality, this is an accurate framework (but binary search is probably not the right tool for that job). If we expect the searches to probe the array randomly, though, then we should probably initialize and shuffle a permutation vector
for i = [0, n)
p[i] = i
scramble(p, n)
and then perform the searches in a random order
assert(binarysearchl(p[i]) == p[i])
Measure the two versions to see if there is any difference in observed run times.
8. Scaffolding is underused and rarely described in public. Inspect any scaffolding you can find; desperation may drive you to this book’s web site. Build scaffolding to test a complex function that you have written.
9. Download the search.c scaffolding program from this book’s web site, and experiment to find the run time of binary search on your machine. What tools will you use to generate the input and to store and to analyze the output?
Kernighan and Pike’s Practice of Programming was published by Addison-Wesley in 1999. They devote fifty pages to debugging (Chapter 5) and testing (Chapter 6). They cover important topics such as non-reproducible bugs and regression testing that are beyond the scope of this little column.
The nine chapters of their book will be interesting and fun for every practicing programmer. In addition to the two chapters mentioned above, other chapter titles include programming style, algorithms and data structures, design and implementation, interfaces, performance, portability and notation. Their book gives valuable insight into the craft and style of two journeymen programmers.
Section 3.8 of this book describes Steve McConnell’s Code Complete. Chapter 25 of that book describes “Unit Testing” and Chapter 26 describes “Debugging”.
Every programmer knows that debugging is hard. Great debuggers, though, can make the job look simple. Distraught programmers describe a bug that they’ve been chasing for hours, the master asks a few questions, and minutes later the programmers are staring at the faulty code. The expert debugger never forgets that there has to be a logical explanation, no matter how mysterious the system’s behavior may seem when first observed.
That attitude is illustrated in an anecdote from IBM’s Yorktown Heights Research Center. A programmer had recently installed a new workstation. All was fine when he was sitting down, but he couldn’t log in to the system when he was standing up. That behavior was one hundred percent repeatable: he could always log in when sitting and never when standing.
Most of us just sit back and marvel at such a story. How could that workstation know whether the poor guy was sitting or standing? Good debuggers, though, know that there has to be a reason. Electrical theories are the easiest to hypothesize. Was there a loose wire under the carpet, or problems with static electricity? But electrical problems are rarely one-hundred-percent consistent. An alert colleague finally asked the right question: how did the programmer log in when he was sitting and when he was standing? Hold your hands out and try it yourself.
The problem was in the keyboard: the tops of two keys were switched. When the programmer was seated he was a touch typist and the problem went unnoticed, but when he stood he was led astray by hunting and pecking. With this hint and a convenient screwdriver, the expert debugger swapped the two wandering keytops and all was well.
A banking system built in Chicago had worked correctly for many months, but unexpectedly quit the first time it was used on international data. Programmers spent days scouring the code, but they couldn’t find any stray command that would quit the program. When they observed the behavior more closely, they found that the program quit as they entered data for the country of Ecuador. Closer inspection showed that when the user typed the name of the capital city (Quito), the program interpreted that as a request to quit the run!
Bob Martin once watched a system “work once twice”. It handled the first transaction correctly, then exhibited a minor flaw in all later transactions. When the system was rebooted, it once again correctly processed the first transaction, and failed on all subsequent transactions. When Martin characterized the behavior as having “worked once twice”, the developers immediately knew to look for a variable that was initialized correctly when the program was loaded, but was not reset properly after the first transaction.
In all cases the right questions guided wise programmers to nasty bugs in short order: “What do you do differently sitting and standing? May I watch you logging in each way?” “Precisely what did you type before the program quit?” “Did the program ever work correctly before it started failing? How many times?”
Rick Lemons said that the best lesson he ever had in debugging was watching a magic show. The magician did a half-dozen impossible tricks, and Lemons found himself tempted to believe them. He then reminded himself that the impossible isn’t possible, and probed each stunt to resolve its apparent inconsistency. He started with what he knew to be bedrock truth — the laws of physics — and worked from there to find a simple explanation for each trick. This attitude makes Lemons one of the best debuggers I’ve ever seen.
The best book I’ve seen on debugging is The Medical Detectives by Berton Roueché, published by Penguin in 1991. The heroes in the book debug complex systems, ranging from mildly sick people to very sick towns. The problem-solving methods they use are directly applicable to debugging computer systems. These true stories are as spellbinding as any fiction.