
The next three columns describe three different approaches to run-time efficiency. In this column we’ll see how those parts fit together into a whole: each technique is applied at one of several design levels at which computer systems are built. We’ll first study one particular program, and then turn to a more systematic view of the levels at which systems are designed.
Andrew Appel describes “An efficient program for many-body simulations” in the January 1985 SIAM Journal on Scientific and Statistical Computing 6, 1, pp. 85-103. By working on the program at several levels, he reduced its run time from a year to a day.
The program solved the classical “n-body problem” of computing interactions in a gravitational field. It simulated the motions of n objects in three-dimensional space, given their masses, initial positions and velocities; think of the objects as planets, stars or galaxies. In two dimensions, the input might look like

Appel’s paper describes two astrophysical problems in which n = 10,000; by studying simulation runs, physicists could test how well a theory matches astronomical observations. (For more details on the problem and later solutions based on Appel’s approach, see Pfalzner and Gibbon’s Many-Body Tree Methods in Physics, published by Cambridge University Press in 1996.)
The obvious simulation program divides time into small “steps” and computes the progress of each object at each step. Because it computes the attraction of each object to every other, the cost per time step is proportional to n2. Appel estimated that 1,000 time steps of such an algorithm with n = 10,000 would require roughly one year on his computer.
Appel’s final program solved the problem in less than a day (for a speedup factor of 400). Many physicists have since used his techniques. The following brief survey of his program will ignore many important details that can be found in his paper; the important message is that a huge speedup was achieved by working at several different levels.
Algorithms and Data Structures. Appel’s first priority was to find an efficient algorithm. He was able to reduce the O(n2) cost per time step to O(n log n)† by representing the physical objects as leaves in a binary tree; higher nodes represent clusters of objects. The force operating on a particular object can be approximated by the force exerted by the large clusters; Appel showed that this approximation does not bias the simulation. The tree has roughly log n levels, and the resulting O(n log n) algorithm is similar in spirit to the divide-and-conquer algorithm in Section 8.3. This change reduced the run time of the program by a factor of 12.
† The “big-oh” notation O(n2) can be thought of as “proportional to n2”; both 15n2 + 100n and n2/2–10 are O(n2). More formally, f(n) = O(g(n)) means that f(n)<cg(n) for some constant c and sufficiently large values of n. A formal definition of the notation can be found in textbooks on algorithm design or discrete mathematics, and Section 8.5 illustrates the relevance of the notation to program design.
Algorithm Tuning. The simple algorithm always uses small time steps to handle the rare case that two particles come close to one another. The tree data structure allows such pairs to be recognized and handled by a special function. That doubles the time step size and thereby halves the run time of the program.
Data Structure Reorganization. The tree that represents the initial set of objects is quite poor at representing later sets. Reconfiguring the data structure at each time step costs a little time, but reduces the number of local calculations and thereby halves the total run time.
Code Tuning. Due to additional numerical accuracy provided by the tree, 64-bit double-precision floating point numbers could be replaced by 32-bit single-precision numbers; that change halved the run time. Profiling the program showed that 98 percent of the run time was spent in one function; rewriting that code in assembly language increased its speed by a factor of 2.5.
Hardware. After all the above changes, the program still required two days of time on a departmental machine that cost a quarter of a million dollars, and several runs of the program were desired. Appel therefore moved the program to a slightly more expensive machine equipped with a floating point accelerator, which halved its run time again.
The changes described above multiply together for a total speedup factor of 400; Appel’s final program ran a 10,000-body simulation in about one day. The speedups were not free, though. The simple algorithm may be expressed in a few dozen lines of code, while the fast program required 1200 lines. The design and implementation of the fast program required several months of Appel’s time. The speedups are summarized in the following table.
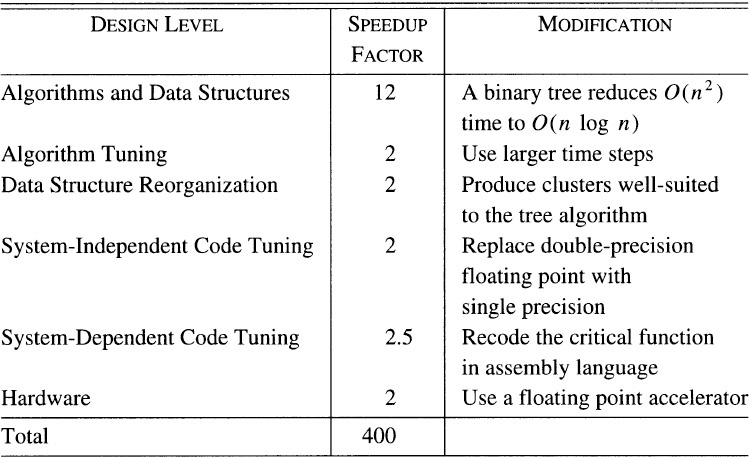
This table illustrates several kinds of dependence among speedups. The primary speedup is the tree data structure, which opened the door for the next three changes. The last two speedups, changing to assembly code and using the floating point accelerator, were in this case independent of the tree. The tree structure would have had less of an impact on the supercomputers of the time (with pipelined architectures well suited to the simple algorithm); algorithmic speedups are not necessarily independent of hardware.
A computer system is designed at many levels, ranging from its high-level software structure down to the transistors in its hardware. The following survey is an intuitive guide to design levels; please don’t expect a formal taxonomy.†
† I learned the theme of this column from Raj Reddy and Allen Newell’s paper “Multiplicative speedup of systems” (in Perspectives on Computer Science, edited by A. K. Jones and published in 1977 by Academic Press). Their paper describes speedups at various design levels, and is especially rich in speedups due to hardware and system software.
Problem Definition. The battle for a fast system can be won or lost in specifying the problem it is to solve. On the day I wrote this paragraph, a vendor told me that he couldn’t deliver supplies because a purchase order had been lost somewhere between my organization and my company’s purchasing department. Purchasing was swamped with similar orders; fifty people in my organization alone had placed individual orders. A friendly chat between my management and purchasing resulted in consolidating those fifty orders into one large order. In addition to easing administrative work for both organizations, this change also sped up one small piece of a computer system by a factor of fifty. A good systems analyst keeps an eye out for such savings, both before and after systems are deployed.
Sometimes good specifications give users a little less than what they thought was needed. In Column 1 we saw how incorporating a few important facts about the input to a sorting program decreased both its run time and its code length by an order of magnitude. Problem specification can have a subtle interaction with efficiency; for example, good error recovery may make a compiler slightly slower, but it usually decreases its overall time by reducing the number of compilations.
System Structure. The decomposition of a large system into modules is probably the single most important factor in determining its performance. After sketching the overall system, the designer should do a simple “back-of-the-envelope” estimate to make sure that its performance is in the right ballpark; such calculations are the subject of Column 7. Because efficiency is much easier to build into a new system than to retrofit into an existing system, performance analysis is crucial during system design.
Algorithms and Data Structures. The keys to a fast module are usually the structures that represent its data and the algorithms that operate on the data. The largest single improvement in Appel’s program came from replacing an O(n2) algorithm with an O(n log n) algorithm; Columns 2 and 8 describe similar speedups.
Code Tuning. Appel achieved a speedup factor of five by making small changes to code; Column 9 is devoted to that topic.
System Software. Sometimes it is easier to change the software on which a system is built than the system itself. Is a new database system faster for the queries that arise in this system? Would a different operating system be better suited to the realtime constraints of this task? Are all possible compiler optimizations enabled?
Hardware. Faster hardware can increase performance. General-purpose computers are usually fast enough; speedups are available through faster clock speeds on the same processor or multiprocessors. Sound cards, video accelerators and other cards offload work from the central processor onto small, fast, special-purpose processors; game designers are notorious for using those devices for clever speedups. Special-purpose digital signal processors (DSPs), for example, enable inexpensive toys and household appliances to talk. Appel’s solution of adding a floating point accelerator to the existing machine was somewhere between the two extremes.
Because an ounce of prevention is worth a pound of cure, we should keep in mind an observation Gordon Bell made when he was designing computers for the Digital Equipment Corporation.
The cheapest, fastest and most reliable components of a computer system are those that aren’t there.
Those missing components are also the most accurate (they never make mistakes), the most secure (they can’t be broken into), and the easiest to design, document, test and maintain. The importance of a simple design can’t be overemphasized.
But when performance problems can’t be sidestepped, thinking about design levels can help focus a programmer’s effort.
If you need a little speedup, work at the best level. Most programmers have their own knee-jerk response to efficiency: “change algorithms” or “tune the queueing discipline” spring quickly to some lips. Before you decide to work at any given level, consider all possible levels and choose the one that delivers the most speedup for the least effort.
If you need a big speedup, work at many levels. Enormous speedups like Appel’s are achieved only by attacking a problem on several different fronts, and they usually take a great deal of effort. When changes on one level are independent of changes on other levels (as they often, but not always, are), the various speedups multiply.
Columns 7, 8 and 9 discuss speedups at three different design levels; keep perspective as you consider the individual speedups.
1. Assume that computers are now 1000 times faster than when Appel did his experiments. Using the same total computing time (about a day), how will the problem size n increase for the O(n2) and O(n log n) algorithms?
2. Discuss speedups at various design levels for some of the following problems: factoring 500-digit integers, Fourier analysis, simulating VLSI circuits, and searching a large text file for a given string. Discuss the dependencies of the proposed speedups.
3. Appel found that changing from double-precision arithmetic to single-precision arithmetic doubled the speed of his program. Choose an appropriate test and measure that speedup on your system.
4. This column concentrates on run-time efficiency. Other common measures of performance include fault-tolerance, reliability, security, cost, cost/performance ratio, accuracy, and robustness to user error. Discuss how each of these problems can be attacked at several design levels.
5. Discuss the costs of employing state-of-the-art technologies at the various design levels. Include all relevant measures of cost, including development time (calendar and personnel), maintainability and dollar cost.
6. An old and popular saying claims that “efficiency is secondary to correctness — a program’s speed is immaterial if its answers are wrong”. True or false?
7. Discuss how problems in everyday life, such as injuries suffered in automobile accidents, can be addressed at different levels.
Butler Lampson’s “Hints for Computer System Design” appeared in IEEE Software 1, 1, January 1984. Many of the hints deal with performance; his paper is particularly strong at integrated hardware-software system design. As this book goes to press, a copy of the paper is available at www.research.microsoft.com/~lampson/.