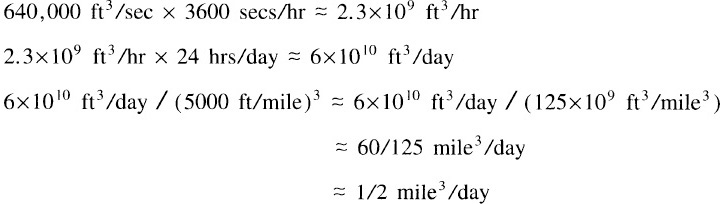
It was in the middle of a fascinating conversation on software engineering that Bob Martin asked me, “How much water flows out of the Mississippi River in a day?” Because I had found his comments up to that point deeply insightful, I politely stifled my true response and said, “Pardon me?” When he asked again I realized that I had no choice but to humor the poor fellow, who had obviously cracked under the pressures of running a large software shop.
My response went something like this. I figured that near its mouth the river was about a mile wide and maybe twenty feet deep (or about one two-hundred-and-fiftieth of a mile). I guessed that the rate of flow was five miles an hour, or a hundred and twenty miles per day. Multiplying
1 mile × 1/250 mile × 120 miles/day ≈ 1/2 mile3/day
showed that the river discharged about half a cubic mile of water per day, to within an order of magnitude. But so what?
At that point Martin picked up from his desk a proposal for the communication system that his organization was building for the Summer Olympic games, and went through a similar sequence of calculations. He estimated one key parameter as we spoke by measuring the time required to send himself a one-character piece of mail. The rest of his numbers were straight from the proposal and therefore quite precise. His calculations were just as simple as those about the Mississippi River and much more revealing. They showed that, under generous assumptions, the proposed system could work only if there were at least a hundred and twenty seconds in each minute. He had sent the design back to the drawing board the previous day. (The conversation took place about a year before the event, and the final system was used during the Olympics without a hitch.)
That was Bob Martin’s wonderful (if eccentric) way of introducing the engineering technique of “back-of-the-envelope” calculations. The idea is standard fare in engineering schools and is bread and butter for most practicing engineers. Unfortunately, it is too often neglected in computing.
Two Answers Are Better Than One. When I asked Peter Weinberger how much water flows out of the Mississippi per day, he responded, “As much as flows in.” He then estimated that the Mississippi basin was about 1000 by 1000 miles, and that the annual runoff from rainfall there was about one foot (or one five-thousandth of a mile). That gives
1000 miles × 1000 miles × 1/5000 mile/year ≈ 200 miles3/year
200 miles3/year / 400 days/year ≈ 1/2 mile3/day
or a little more than half a cubic mile per day. It’s important to double check all calculations, and especially so for quick ones.
As a cheating triple check, an almanac reported that the river’s discharge is 640,000 cubic feet per second. Working from that gives
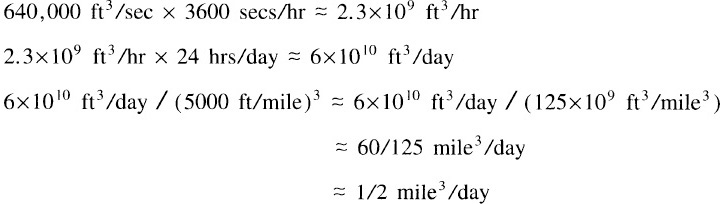
The proximity of the two estimates to one another, and especially to the almanac’s answer, is a fine example of sheer dumb luck.
Quick Checks. Polya devotes three pages of his How to Solve It to “Test by Dimension”, which he describes as a “well-known, quick and efficient means to check geometrical or physical formulas”. The first rule is that the dimensions in a sum must be the same, which is in turn the dimension of the sum — you can add feet together to get feet, but you can’t add seconds to pounds. The second rule is that the dimension of a product is the product of the dimensions. The examples above obey both rules; multiplying
(miles + miles) × miles × miles/day = miles3/day
has the right form, apart from any constants.
A simple table can help you keep track of dimensions in complicated expressions like those above. To perform Weinberger’s calculation, we first write down the three original factors.
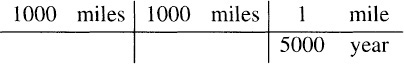
Next we simplify the expression by cancelling terms, which shows that the output is 200 miles3/year.

Now we multiply by the identity (well, almost) that there are 400 days per year.
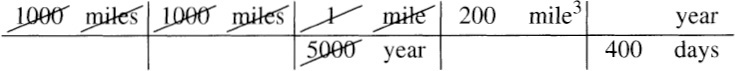
Cancellation yields the (by now familiar) answer of half a cubic mile per day.
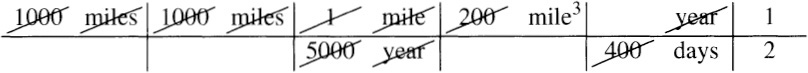
These tabular calculations help you keep track of dimensions.
Dimension tests check the form of equations. Check your multiplications and divisions with an old trick from slide rule days: independently compute the leading digit and the exponent. One can make several quick checks for addition.
3142 3142 3142
2718 2718 2718
+1123 +1123 +1123
----- ----- -----
983 6982 6973
The first sum has too few digits and the second sum errs in the least significant digit. The technique of “casting out nines” reveals the error in the third example: the digits in the summands sum to 8 modulo 9, while those in the answer sum to 7 modulo 9. In a correct addition, the sums of the digits are equal after “casting out” groups of digits that sum to nine.
Above all, don’t forget common sense: be suspicious of any calculations that show that the Mississippi River discharges 100 gallons of water per day.
Rules of Thumb. I first learned the “Rule of 72” in a course on accounting. Assume that you invest a sum of money for y years at an interest rate of r percent per year. The financial version of the rule says that if r×y = 72, then your money will roughly double. The approximation is quite accurate: investing $1000 at 6 percent interest for 12 years gives $2012, and $1000 at 8 percent for 9 years gives $1999.
The Rule of 72 is handy for estimating the growth of any exponential process. If a bacterial colony in a dish grows at the rate of three percent per hour, then it doubles in size every day. And doubling brings programmers back to familiar rules of thumb: because 210 = 1024, ten doublings is about a thousand, twenty doublings is about a million, and thirty doublings is about a billion.
Suppose that an exponential program takes ten seconds to solve a problem of size n = 40, and that increasing n by one increases the run time by 12 percent (we probably learned this by plotting its growth on a logarithmic scale). The Rule of 72 tells us that the run time doubles when n increases by 6, or goes up by a factor of about 1000 when n increases by 60. When n = 100, the program should therefore take about 10,000 seconds, or a few hours. But what happens when n increases to 160, and the time rises to 107 seconds? How much time is that?
You might find it hard to memorize that there are 3.155×107 seconds in a year. On the other hand, it is hard to forget Tom Duffs handy rule of thumb that, to within half a percent,
π seconds is a nanocentury.
Because the exponential program takes 107 seconds, we should be prepared to wait about four months.
Practice. As with many activities, your estimation skills can only be improved with practice. Try the problems at the end of this column, and the estimation quiz in Appendix 2 (a similar quiz once gave me a much-needed dose of humility about my estimation prowess). Section 7.8 describes quick calculations in everyday life. Most workplaces provide ample opportunities for back-of-the-envelope estimates. How many foam “packing peanuts” came in that box? How much time do people at your facility spend waiting in line every day, for morning coffee, lunch, photocopiers and the like? How much does that cost the company in (loaded) salary? And the next time you’re really bored at the lunch table, ask your colleagues how much water flows out of the Mississippi River each day.
Let’s turn now to a quick calculation in computing. Nodes in your data structure (it might be a linked list or a hash table) hold an integer and a pointer to a node:
struct node { int i; struct node *p; };
Back-of-the-envelope quiz: will two million such nodes fit in the main memory of your 128-megabyte computer?
Looking at my system performance monitor shows that my 128-megabyte machine typically has about 85 megabytes free. (I’ve verified that by running the vector rotation code from Column 2 to see when the disk starts thrashing.) But how much memory will a node take? In the old days of 16-bit machines, a pointer and an integer would take four bytes. As I write this edition of the book, 32-bit integers and pointers are most common, so I would expect the answer to be eight bytes. Every now and then I compile in 64-bit mode, so it might take sixteen bytes. We can find out the answer for any particular system with a single line of C:
printf("sizeof(struct node)=%d\n", sizeof(struct node));
My system represented each record in eight bytes, as I expected. The 16 megabytes should fit comfortably into the 85 megabytes of free memory.
So when I used two million of those eight-byte records, why did my 128-megabyte machine start thrashing like crazy? The key is that I allocated them dynamically, using the C malloc function (similar to the C++ new operator). I had assumed that the eight-byte records might have another 8 bytes of overhead; I expected the nodes to take a total of about 32 megabytes. In fact, each node had 40 bytes of overhead to consume a total of 48 bytes per record. The two million records therefore used a total of 96 megabytes. (On other systems and compilers, though, the records had just 8 bytes of overhead each.)
Appendix 3 describes a program that explores the memory cost of several common structures. The first lines it produces are made with the sizeof operator:
sizeof(char)=1 sizeof(short)=2 sizeof(int)=4
sizeof(float)=4 sizeof(struct *)=4 sizeof(long)=4
sizeof(double)=8
I expected precisely those values from my 32-bit compiler. Further experiments measured the differences between successive pointers returned by the storage allocator; this is a plausible guess at record size. (One should always verify such rough guesses with other tools.) I now understand that, with this space-hogging allocator, records between 1 and 12 bytes will consume 48 bytes of memory, records between 13 and 28 bytes will consume 64 bytes, and so forth. We will return to this space model in Columns 10 and 13.
Let’s try one more quick computing quiz. You know that the run time of your numerical algorithm is dominated by its n3 square root operations, and n = 1000 in this application. About how long will your program take to compute the one billion square roots?
To find the answer on my system, I started with this little C program:
#include <math.h>
int main(void)
{ int i, n = 1000000;
float fa;
for (i = 0; i < n; i++)
fa = sqrt(10.0);
return 0;
}
I ran the program with a command to report how much time it takes. (I check such times with an old digital watch that I keep next to my computer; it has a broken band but a working stopwatch.) I found that the program took about 0.2 seconds to compute one million square roots, 2 seconds to compute ten million, and 20 seconds to compute 100 million. I would guess that it will take about 200 seconds to compute a billion square roots.
But will a square root in a real program take 200 nanoseconds? It might be much slower: perhaps the square root function cached the most recent argument as a starting value. Calling such a function repeatedly with the same argument might give it an unrealistic advantage. Then again, in practice the function might be much faster: I compiled the program with optimization disabled (optimization removed the main loop, so it always ran in zero time). Appendix 3 describes how to expand this tiny program to produce a one-page description of the time costs of primitive C operations for a given system.
How fast is networking? To find out, I type ping machine-name. It takes a few milliseconds to ping a machine in the same building, so that represents the startup time. On a good day, I can ping a machine on the other coast of the United States in about 70 milliseconds (traversing the 5000 miles of the round-trip voyage at the speed of light accounts for about 27 of those milliseconds); on a bad day, I get timed out after waiting 1000 milliseconds. Measuring the time to copy a large file shows that a ten-megabit Ethernet moves about a megabyte a second (that is, it achieves about 80 percent of its potential bandwidth). Similarly, a hundred-megabit Ethernet with the wind at its back moves ten megabytes a second.
Little experiments can put key parameters at your fingertips. Database designers should know the times for reading and writing records, and for joins of various forms. Graphics programmers should know the cost of key screen operations. The short time required to do such little experiments today will be more than paid in the time you save by making wise decisions tomorrow.
The output of any calculation is only as good as its input. With good data, simple calculations can yield accurate answers that are sometimes quite useful. Don Knuth once wrote a disk sorting package, only to find that it took twice the time predicted by his calculations. Diligent checking uncovered the flaw: due to a software bug, the system’s one-year-old disks had run at only half their advertised speed for their entire lives. When the bug was fixed, Knuth’s sorting package behaved as predicted and every other disk-bound program also ran faster.
Often, though, sloppy input is enough to get into the right ballpark. (The estimation quiz in Appendix 2 may help you to judge the quality of your guesses.) If you guess about twenty percent here and fifty percent there and still find that a design is a hundred times above or below specification, additional accuracy isn’t needed. But before placing too much confidence in a twenty percent margin of error, consider Vic Vyssotsky’s advice from a talk he has given on several occasions.
“Most of you”, says Vyssotsky, “probably recall pictures of ‘Galloping Gertie’, the Tacoma Narrows Bridge which tore itself apart in a windstorm in 1940. Well, suspension bridges had been ripping themselves apart that way for eighty years or so before Galloping Gertie. It’s an aerodynamic lift phenomenon, and to do a proper engineering calculation of the forces, which involve drastic nonlinearities, you have to use the mathematics and concepts of Kolmogorov to model the eddy spectrum. Nobody really knew how to do this correctly in detail until the 1950’s or thereabouts. So, why hasn’t the Brooklyn Bridge torn itself apart, like Galloping Gertie?
“It’s because John Roebling had sense enough to know what he didn’t know. His notes and letters on the design of the Brooklyn Bridge still exist, and they are a fascinating example of a good engineer recognizing the limits of his knowledge. He knew about aerodynamic lift on suspension bridges; he had watched it. And he knew he didn’t know enough to model it. So he designed the stiffness of the truss on the Brooklyn Bridge roadway to be six times what a normal calculation based on known static and dynamic loads would have called for. And, he specified a network of diagonal stays running down to the roadway, to stiffen the entire bridge structure. Go look at those sometime; they’re almost unique.
“When Roebling was asked whether his proposed bridge wouldn’t collapse like so many others, he said, ‘No, because I designed it six times as strong as it needs to be, to prevent that from happening.’
“Roebling was a good engineer, and he built a good bridge, by employing a huge safety factor to compensate for his ignorance. Do we do that? I submit to you that in calculating performance of our real-time software systems we ought to derate them by a factor of two, or four, or six, to compensate for our ignorance. In making reliability/availability commitments, we ought to stay back from the objectives we think we can meet by a factor of ten, to compensate for our ignorance. In estimating size and cost and schedule, we should be conservative by a factor of two or four to compensate for our ignorance. We should design the way John Roebling did, and not the way his contemporaries did — so far as I know, none of the suspension bridges built by Roebling’s contemporaries in the United States still stands, and a quarter of all the bridges of any type built in the U.S. in the 1870’s collapsed within ten years of their construction.
“Are we engineers, like John Roebling? I wonder.”
Most back-of-the-envelope calculations use obvious rules: total cost is unit cost times number of units. Sometimes, though, one needs a more subtle insight. Bruce Weide wrote the following note about a surprisingly versatile rule.
“The ‘operational analysis’ introduced by Denning and Buzen (see Computing Surveys 10, 3, November 1978, 225-261) is much more general than queueing network models of computer systems. Their exposition is excellent, but because of the article’s limited focus, they didn’t explore the generality of Little’s Law. The proof methods have nothing to do with queues or with computer systems. Imagine any system in which things enter and leave. Little’s Law states that ‘The average number of things in the system is the product of the average rate at which things leave the system and the average time each one spends in the system.’ (And if there is a gross ‘flow balance’ of things entering and leaving, the exit rate is also the entry rate.)
“I teach this technique of performance analysis in my computer architecture classes at Ohio State University. But I try to emphasize that the result is a general law of systems theory, and can be applied to many other kinds of systems. For instance, if you’re in line waiting to get into a popular nightspot, you might figure out how long you’ll have to wait by standing there for a while and trying to estimate the rate at which people are entering. With Little’s Law, though, you could reason, ‘This place holds about 60 people, and the average Joe will be in there about 3 hours, so we’re entering at the rate of about 20 people an hour. The line has 20 people in it, so that means we’ll wait about an hour. Let’s go home and read Programming Pearls instead.’ You get the picture.”
Peter Denning succinctly phrases this rule as “The average number of objects in a queue is the product of the entry rate and the average holding time.” He applies it to his wine cellar: “I have 150 cases of wine in my basement and I consume (and purchase) 25 cases per year. How long do I hold each case? Little’s Law tells me to divide 150 cases by 25 cases/year, which gives 6 years.”
He then turns to more serious applications. “The response-time formula for a multi-user system can be proved using Little’s Law and flow balance. Assume n users of average think time z are connected to an arbitrary system with response time r. Each user cycles between thinking and waiting-for-response, so the total number of jobs in the meta-system (consisting of users and the computer system) is fixed at n. If you cut the path from the system’s output to the users, you see a meta-system with average load n, average response time z + r, and throughput x (measured in jobs per time unit). Little’s Law says n = x×(z + r), and solving for r gives r = n/x – z.”
When you use back-of-the-envelope calculations, be sure to recall Einstein’s famous advice.
Everything should be made as simple as possible, but no simpler.
We know that simple calculations aren’t too simple by including safety factors to compensate for our mistakes in estimating parameters and our ignorance of the problem at hand.
The quiz in Appendix 2 contains additional problems.
1. While Bell Labs is about a thousand miles from the mighty Mississippi, we are only a couple of miles from the usually peaceful Passaic River. After a particularly heavy week of rains, the June 10, 1992, edition of the Star-Ledger quoted an engineer as saying that “the river was traveling about 200 miles per hour, about five times faster than average”. Any comments?
2. At what distances can a courier on a bicycle with removable media be a more rapid carrier of information than a high-speed data line?
3. How long would it take you to fill a floppy disk by typing?
4. Suppose the world is slowed down by a factor of a million. How long does it take for your computer to execute an instruction? Your disk to rotate once? Your disk arm to seek across the disk? You to type your name?
5. Prove why “casting out nines” correctly tests addition. How can you further test the Rule of 72? What can you prove about it?
6. A United Nations estimate put the 1998 world population at 5.9 billion and the annual growth rate at 1.33 percent. Were this rate to continue, what would the population be in 2050?
7. Appendix 3 describes programs to produce models of the time and space costs of your system. After reading about the models, write down your guesses for the costs on your system. Retrieve the programs from the book’s web site, run them on your system, and compare those estimates to your guesses.
8. Use quick calculations to estimate the run time of designs sketched in this book.
a. Evaluate programs and designs for their time and space requirements.
b. Big-oh arithmetic can be viewed as a formalization of quick calculations — it captures the growth rate but ignores constant factors. Use the big-oh run times of the algorithms in Columns 6, 8, 11, 12, 13, 14 and 15 to estimate the run time of their implementation as programs. Compare your estimates to the experiments reported in the columns.
9. Suppose that a system makes 100 disk accesses to process a transaction (although some systems need fewer, some systems require several hundred disk accesses per transaction). How many transactions per hour per disk can the system handle?
10. Estimate your city’s death rate, measured in percent of population per year.
11. [P. J. Denning] Sketch a proof of Little’s Law.
12. You read in a newspaper article that a United States quarter-dollar coin has “an average life of 30 years”. How can you check that claim?
My all-time favorite book on common sense in mathematics is Darrell Huff’s 1954 classic How To Lie With Statistics; it was reissued by Norton in 1993. The examples are now quaint (some of those rich folks make a whopping twenty-five thousand dollars per year!), but the principles are timeless. John Allen Paulos’s Innumeracy: Mathematical Illiteracy and Its Consequences is a 1990 approach to similar problems (published by Farrar, Straus and Giroux).
Physicists are well aware of this topic. After this column appeared in Communications of the ACM, Jan Wolitzky wrote
I’ve often heard “back-of-the-envelope” calculations referred to as “Fermi approximations”, after the physicist. The story is that Enrico Fermi, Robert Oppenheimer, and the other Manhattan Project brass were behind a low blast wall awaiting the detonation of the first nuclear device from a few thousand yards away. Fermi was tearing up sheets of paper into little pieces, which he tossed into the air when he saw the flash. After the shock wave passed, he paced off the distance travelled by the paper shreds, performed a quick “back-of-the-envelope” calculation, and arrived at a figure for the explosive yield of the bomb, which was confirmed much later by expensive monitoring equipment.
A number of relevant web pages can be found by searching for strings like “back of the envelope” and “Fermi problems”.
The publication of this column in Communications of the ACM provoked many interesting letters. One reader told of hearing an advertisement state that a salesperson had driven a new car 100,000 miles in one year, and then asking his son to examine the validity of the claim. Here’s one quick answer: there are 2000 working hours per year (50 weeks times 40 hours per week), and a salesperson might average 50 miles per hour; that ignores time spent actually selling, but it does multiply to the claim. The statement is therefore at the outer limits of believability.
Everyday life presents us with many opportunities to hone our skills at quick calculations. For instance, how much money have you spent in the past year eating in restaurants? I was once horrified to hear a New Yorker quickly compute that he and his wife spend more money each month on taxicabs than they spend on rent. And for California readers (who may not know what a taxicab is), how long does it take to fill a swimming pool with a garden hose?
Several readers commented that quick calculations are appropriately taught at an early age. Roger Pinkham wrote
I am a teacher and have tried for years to teach “back-of-the-envelope” calculations to anyone who would listen. I have been marvelously unsuccessful. It seems to require a doubting-Thomas turn of mind.
My father beat it into me. I come from the coast of Maine, and as a small child I was privy to a conversation between my father and his friend Homer Potter. Homer maintained that two ladies from Connecticut were pulling 200 pounds of lobsters a day. My father said, “Let’s see. If you pull a pot every fifteen minutes, and say you get three legal per pot, that’s 12 an hour or about 100 per day. I don’t believe it!”
“Well it is true!” swore Homer. “You never believe anything!”
Father wouldn’t believe it, and that was that. Two weeks later Homer said, “You know those two ladies, Fred? They were only pulling 20 pounds a day.”
Gracious to a fault, father grunted, “Now that I believe.”
Several other readers discussed teaching this attitude to children, from the viewpoints of both parent and child. Popular questions for children were of the form “How long would it take you to walk to Washington, D.C.?” and “How many leaves did we rake this year?” Administered properly, such questions seem to encourage a life-long inquisitiveness in children, at the cost of bugging the heck out of the poor kids at the time.